Тест по математике «Неравенства» (2 класс)
Неравенства 2 класс
МатематикаКласс
2
Учебник
Математика. 2 класс. В 2 ч. Моро М.И. и др. 6-е изд. — М.: 2015. —
Ч.1 — 96с., Ч.2 — 112с.
Вопрос №1
Поставь знак вместо звёздочки
12+5 * 12+3

<
>
Вопрос №2
Какое неравенство верно?
20 + 10 > 10 + 10
30 — 20 > 10 + 30

1
2
Вопрос №3
Какое число нужно поставить вместо *, чтобы неравенство было верным?
15 + 10 > 30 — *

5
Вопрос №4
Поставь знак вместо *
35 — 5 * 25 — 5

<
>
Вопрос №5
Поставь число вместо * так, чтобы получилось верное неравенство
25 < *5

1
3
Вопрос №6
Поставь число вместо * так, чтобы неравенство было верным
* — 40 > 30

60
80
Вопрос №7
Какое неравенство верно?
60 – 30 > 100 – 50
70 – 40 < 80 – 20

1
2
Вопрос №8
Поставь знак вместо *
85 — 40 * 55

<
>
Вопрос №9
Поставь число вместо * так, чтобы получилось верное неравенство
48 > 4*

7
9
Вопрос №10
Выбери верное равенство
99 – 9 > 80
78 + 2 < 70

1
2
Вопрос №11
Поставь знак вместо *
37 – 30 * 47 – 7

<
>
- Главная
- Справочник по математике для начальной школы
- Сравнение чисел
- Равенства и неравенства
Сначала повтори тему «Больше. Меньше» и вспомни, что такое больше, меньше, поровну, столько же.
Рассмотри рисунок.
Сколько синих кругов? 5.
Сколько красных кругов? 5.
Каких кругов больше? Каких меньше?
Синих кругов столько же, сколько красных. Их поровну.
Красных кругов столько же, сколько синих. Их поровну.
Составим запись к рисунку:
5 = 5.
Прочитаем запись: пять равно пяти.
Это равенство.
Запись, в которой есть знак РАВНО, называется РАВЕНСТВОМ.
Рассмотри рисунок.
Сколько синих кругов? 5.
Сколько красных кругов? 6.
Каких кругов больше? Красных.
Каких кругов меньше? Синих.
Синих кругов меньше, чем красных.
Красных кругов больше, чем синих.
Составим запись к рисунку:
6 > 5
Прочитаем запись: шесть больше пяти.
Это неравенство.
5 < 6
Прочитаем запись: пять меньше шести.
Это неравенство.
Запись, в которой есть знак БОЛЬШЕ или МЕНЬШЕ, называется НЕРАВЕНСТВОМ.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Уменьшить на… Увеличить на…
Сравнение чисел
Правило встречается в следующих упражнениях:
1 класс
Страница 48, Моро, Волкова, Степанова, Учебник, 1 часть
Страница 115, Моро, Волкова, Степанова, Учебник, 1 часть
Страница 121, Моро, Волкова, Степанова, Учебник, 1 часть
Страница 39, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 40, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 12. Вариант 1. № 3, Волкова, Проверочные работы
Страница 52. Вариант 1. Тест, Волкова, Проверочные работы
Страница 55, Моро, Волкова, Степанова, Учебник, 2 часть
Страница 57, Моро, Волкова, Степанова, Учебник, 2 часть
2 класс
Страница 57, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Задание 126, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 12. Вариант 1. Тест 1, Моро, Волкова, Проверочные работы
Страница 60. Вариант 1. № 2, Моро, Волкова, Проверочные работы
Страница 61. Вариант 2. № 2, Моро, Волкова, Проверочные работы
Страница 63. Вариант 2. № 3, Моро, Волкова, Проверочные работы
Страница 58, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 21, Моро, Волкова, Рабочая тетрадь, 2 часть
Страница 64, Моро, Волкова, Рабочая тетрадь, 2 часть
3 класс
Страница 52, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 85, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 29, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 28. Вариант 1. Тест 2, Моро, Волкова, Проверочные работы
Страница 47. Вариант 2. Проверочная работа 1, Моро, Волкова, Проверочные работы
Страница 68. Вариант 1. Тест 1, Моро, Волкова, Проверочные работы
Страница 21, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 73, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 11, Моро, Волкова, Рабочая тетрадь, 2 часть
Страница 12, Моро, Волкова, Рабочая тетрадь, 2 часть
4 класс
Страница 28, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 75, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 70, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 77. Тест. Вариант 2, Моро, Волкова, Проверочные работы
Страница 14, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 32, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 64, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 69, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 74, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 92, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
5 класс
Задание 626, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Упражнение 120, Мерзляк, Полонский, Якир, Учебник
Упражнение 121, Мерзляк, Полонский, Якир, Учебник
Упражнение 122, Мерзляк, Полонский, Якир, Учебник
© budu5.com, 2020
Пользовательское соглашение
Copyright
По теме: методические разработки, презентации и конспекты
 Сценарий урока математики по теме «Понятие о равенствах и неравенствах», 3 класс
Сценарий урока математики по теме «Понятие о равенствах и неравенствах», 3 классУрок-сказака с применением на уроке игры…
Урок математики в 1 классе по системе Л. В. Занкова «Верные и неверные равенства и неравенства»Тема урока: «Верные и неверные равенства и неравенства». К уроку прилагается презентация….
Презентация по теме «Решение неравенства» 4 класс по программе Л. Г. ПетерсонПрезентация используется на уроках математики по программе Л. Г. Петерсон 4 класс. Тема «Решение неравенства» с использованием проектора и интерактивной доски…..
Урок математики в первом классе(учебник А. А. Аргинской) по теме: «Преобразование равенств в неравенства и неравенств в равенства».Представлен урок математики»Преобразование равенств в неравенства и неравенств в равенства», проведенный в первом классе, в рамках программы развивающего обучения Л. В. Занкова. Обучающиеся расш…
Математика. 1 класс » Школа России». Тема : » Равенство. Неравенство».Материал содержит конспект , в котором отражены цели и задачи изучения данной темы. Урок носит ознакомительный характер. Содержит большое количество материала на повторение пройденного. Так как …
 Урок математики в1 классе по теме: «Понятие о неравенстве. Знаки >,
Урок математики в1 классе по теме: «Понятие о неравенстве. Знаки >, Урок математики в1 классе по теме: «Понятие о неравенстве. Знаки >, <. Запись и чтение числовых равенств и неравенств» адресован учителям начальных классов, работающих по УМК «Система Л.В….
 конспект урока по математике в 1 классе «Неравенства»
конспект урока по математике в 1 классе «Неравенства»урок математики в 1 классе по программе «Начальная школа 21 века»…
Урок 61
Тема: ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО: РАВЕНСТВА
И НЕРАВЕНСТВА
Педагогические задачи: повторить понятия «равенство», «неравенство»; развивать вычислительные навыки, мышление.
Планируемые образовательные результаты:
Личностные: овладевают начальными навыками адаптации в обществе; принимают и осваивают социальную роль обучающегося; стремятся развивать внимание, память, логическое мышление, навыки сотрудничества со сверстниками и со взрослыми; проявляют самостоятельность, личную ответственность.
Предметные: знают: различные приемы сложения и вычитания двузначного числа с однозначным и двузначного числа с двузначным; что такое равенство и неравенство; что значит «сравнить числа или числовые выражения»; устную и письменную нумерацию чисел в пределах 100; как проверить результат действия сложения, разные способы проверки результата действия вычитания; умеют: проверять результат действия сложения вычитанием, результат действия вычитания сложением и вычитанием, выражения изученных видов; сравнивать числовые выражения.
Метапредметные (критерии сформированности/оценки компонентов УУД): регулятивные: формулируют учебную задачу урока; составляют план и последовательность действий, прогнозируют результат собственной деятельности, контролируют и оценивают свою деятельность и деятельность партнеров по образовательному процессу, при необходимости вносят корректировки; способны к саморегуляции; познавательные: формулируют познавательную цель; осознанно и произвольно строят речевое высказывание в устной форме; создают алгоритм деятельности; строят логическую цепочку рассуждений, анализируют, сравнивают, устанавливают причинно-следственные связи; контролируют и оценивают процесс и результаты деятельности; коммуникативные: знают правила ведения диалога и применяют их на практике; достаточно полно и точно выражают свои мысли, аргументируют свою точку зрения, при этом уважают всех участников образовательного процесса; эффективно сотрудничают как со сверстниками, так и со взрослыми.
методы и формы обучения: частично-поисковый; индивидуальная, фронтальная, групповая.
Образовательные ресурсы: http://www.liveinternet.ru/users/byxtelka/post104646979 – Цитатник
Основные понятия и термины: сравнить, сложить, вычесть, слагаемое, сумма, значение суммы, уменьшаемое, вычитаемое, разность, значение разности, проверка, геометрические фигуры, треугольник, квадрат, круг, прямоугольник.
организационная структура (сценарий) урока
I. Каллиграфическая минутка.
2 12 20 2 12 20… 3 13 30 3 13 30…
II. Устный счет.
1. «Цепочка».
2. Какое число пропущено?
62 + = 70 – 6 = 9
+ 8 = 30 33 – =28
3. Вставьте знаки арифметических действий (+ или –) так, чтобы равенства были верными.
72 * 8 * 35 = 45 62 * 20 * 7 = 49
54 * 9 * 20 = 25 36 * 30 * 8 = 58
III. Подготовка к восприятию учебного материала. Сообщение темы и целей. Повторение понятий «равенство», «неравенство».
На доске запись:
15 + 5 = 28 – 8 9 + 4 > 14 – 6
39 + 30 + 9 40 < 40 + 8
1 м = 10 дм 2 м > 20 см
– Рассмотрите внимательно запись на доске. Что вы заметили?
– Чем похожи записи каждого столбика?
– Как называется запись, в которой есть знак «равно» (=)? (Равенство.)
– Как называется запись, в которой есть знаки: «больше» (>), «меньше» (<)? (Неравенство.)
– Вы догадались, чему будет посвящен урок? (Мы будем составлять равенства и неравенства, сравнивать и решать выражения.) Верно. Тема нашего урока: «Равенства и неравенства».
– Составьте верные равенства и неравенства, используя выражения:
6 + 8, 17 – 10, 24 – 10, 37 – 30.
IV. Сравнение выражений.
На данном этапе урока ученикам может быть предложено задание 6 (с. 90), которое они выполняют с устным объяснением, а затем в качестве самостоятельной работы – задание по карточкам:
К-1. 63 + 17 * 17 + 63 25 + 20 * 25 + 2
59 – 34 * 59 – 36 45 – 17 * 55 – 17
К-2. 80 – 31 * 80 – 21 18 + 4 * 18 + 40
72 + 8 * 8 + 72 67 – 24 * 47 – 24
К-3. 82 + 8 * 8 + 82 15 + 7 * 7 + 15
91 – 40 * 91 – 42 74 – 38 * 84 – 38
Дети утром рано встали, За грибами в лес пошли. Приседали, приседали, Белый гриб в траве нашли. | (Ходьба на месте.) (Приседания.) |
На пеньке растут опята, Наклонитесь к ним, ребята, Наклоняйся, раз-два-три, И в лукошко набери! Вон на дереве орех. Кто подпрыгнет выше всех? Если хочешь дотянуться, Надо сильно потянуться. Три часа в лесу бродили, Все тропинки исходили. Утомил всех долгий путь – Дети сели отдохнуть. | (Наклоны.) (Прыжки.) (Потягивания – руки вверх.) (Ходьба на месте.) (Дети садятся за парты.) |
V. Решение выражений.
– Выполните с подробным устным объяснением задание 2 (с. 90). Найдите значения данных выражений, а затем проверьте их.
После этого выполняется задание 8 (с. 90) следующим образом: учащиеся рассматривают выражения 1-го столбика и приходят к выводу: для решения выражений необходимо воспользоваться приемом группировки слагаемых; данный столбик выполняется с комментированием.
Запись в тетради:
40 + 7 + 3 + 18 = 40 + (7 + 3) + 18 = 40 + 10 + 18 = 50 + 18 = 68
50 + 26 + 8 + 2 = 50 + 26 + (8 + 2) = 50 + 10 + 26 = 60 + 26 = 86
30 + 9 + 6 + 1= 30 + (9 + 1) + 6 = 30 + 10 + 6 = 40 + 6 = 46
Далее учитель предлагает ученикам рассмотреть выражения 2-го столбика.
– Чем интересны выражения этого столбика?
– Как, по вашему мнению, будут изменяться значения данных выражений? Решите выражения.
Групповая работа.
Учащимся могут быть предложены задания 1, 3 (с. 90). Выполняя задание 1, ученики находят ошибки и исправляют их. В задании 3 ставят скобки таким образом, чтобы записи были верными.
VI. Задание на смекалку.
Учащиеся выполняют задание 9 (с. 90), в котором заполняют таблицу с геометрическими фигурами. (Вторая строка – в зеленом квадрате красный круг, в синем треугольнике красный круг, в желтом прямоугольнике красный круг, в белом круге красный круг; третья строка – в зеленом квадрате черный треугольник, в синем треугольнике черный треугольник, в желтом прямоугольнике черный треугольник, в белом круге черный треугольник.)
VII. Самостоятельная работа обучающихся.
В заключение урока ученикам может быть предложена самостоятельная работа: проверочные задания (с. 38, 39 тетради для проверочных работ).
VIII. Рефлексия учебной деятельности.
– Какие понятия, правила повторяли сегодня на уроке?
– Как вы сегодня работали? Что бы хотели выполнить еще?
Урок математики по теме «Неравенства» 2 класс
Тема: НЕРАВЕНСТВА. Цель: к концу урока учащиеся научатся сравнивать любые числа, выражения, величины , выражения с величинами; записывать результат сравнения, используя знаки <, >, =: различать равенства и неравенства: читать равенства и неравенства Задачи создать условия для развития вычислительных навыков как устных, так и письменных (в столбик) совершенствования умений сравнивать числа, числовые выражения, величины контроля и самооценки своих действий учащимися создания алгоритма деятельности по сравнению выражений и выражений с величинами анализа, сравнения развития умения высказывать свои мысли, аргументируя свою точку зрения содействовать воспитанию дисциплинированности и культуры поведения при работе в группе и паре Ход урока. 1. Организационный этап. Эмоциональный настрой на работу. Аутотренинг.(сидя) 2. Этап проверки домашнего задания. Взаимопроверкаобмен тетрадями, ответы по д/з на доске (взаимооценка на полях тетради) 3. Этап актуализации субъектного опыта учащихся. 1) Каллиграфическая минутка. Сколько раз ваше число повторяется в ряде чисел от 0 до 100? ( учащиеся пишут в тетради и считают, 2 ученика у доски. Взаимопроверка в тетрадях по результату на доске) Девочки – 2, 12, 20, 21,22,….… мальчики 3, 13, 23, 30, 31, ……..… 2) Устный счет. ( карточказадание ряду; чей ряд быстрее и правильнее) 1) «Цепочка». +30 7 40 +25 +12 30 +90 20 …..……..……..…….…… ……. …… задание ряду. Чей ряд быстрее пройдёт ряд заданий. Последний говорит число, которое получилось последним ( Ответ 100) Ряд получает балл. 2) Игра «Данетка»( с сигнальными карточками – «ручками» ) – молча. предлагаю учащимся примеры с ответами на карточках. если пример решён правильноподнимают зелёную»ручку», если неправильнокрасную «ручку». Чей ряд без ошибок – зарабатывает балл. 22 + 13 = 35 80 + 12 = 91 82 – 20 = 52 94 – 14 = 80 35 + 20 = 55 100 – 41 = 22 64 – 60 = 4 57 + 3 = 60 100 – 11 = 89 31 + 31 = 64 3) Математический диктант. ( 3 учащийся у доски каждый за свой ряд) А) запиши наибольшее число четвёртого десятка Б) запиши число большее 28 на 2 В) запиши число меньшее 30 на 1 Г) первое слагаемое 8, второе на 5 больше. Найди сумму Д) уменьшаемое 38, вычитаемое 13. Найди разность. Е) на сколько 87 больше числа 7 Ж) увеличь 9 на 6 З) сторона квадрата 6 см. Найди периметр И) запиши число, в котором десятков на 3 больше, чем единиц. Взаимопроверка по ключу( на доске). Оценка в тетради на полях. По результату выполнения ряд получает балл. 4) Задачи на смекалку. ( 2 задачи ряду 1 балл ряду за правильный ответ) 1.Заяц вытащил 25 морковок и съел все, кроме 3. Сколько морковок осталось? Устно. 2. У животного 2 левые ноги, 2 правые, 2 спереди и 2 сзади. Сколько ног у животного? 3. Когда гусь стоит на одной ноге , то весит 3 кг. Сколько будет весить гусь, если встанет на две ноги? 4. У бабушки Даши был внучок Паша, котик Пушок, собака Дружок. Сколько внучат у бабушки Даши? 5. Сколько орехов в пустом стакане? 6. Сколько ложек соли нужно положить в стакан с чаем, чтобы чай был сладким? Физкультминутка для глаз. 4. Подготовка к восприятию учебного материала. Сообщение темы и целей. Повторение понятий «равенство», «неравенство». 5) На карточках (в парах) запись: 10 + 70 = 80 80 – 20 = 60 9 + 4 > 14 – 6 Х + 14 = 100 40 < 40 + 8 39 + 30 + 9 2 м > 20 см 15 + 5 = 28 – 8 1 м = 10 дм – Рассмотрите внимательно записи. – Чем похожи записи каждого столбика? – Как называется запись, в которой есть знак «равно» (=)? (Равенство.) – Как называется запись, в которой есть знаки: «больше» (>), «меньше» (<)? (Неравенство.) Как называется выделенное равенство? ( равенство с неизвестной – уравнение) Найдите лишнюю запись…( это 39 + 30 + 9 ). Измените эту запись так, чтобы она стала НЕРАВЕНСТВОМ. ( 30 + 30> 9) – Вы догадались, чему будет посвящен урок? (Мы будем составлять неравенства, сравнивать числа и величины; различать равенства и неравенства) Тема нашего урока: «Неравенства». Какую цель мы перед собой поставим? (научиться сравнивать выражения и величины) 6) – Составьте верные неравенства, используя выражения и величины ( на карточке в паре) 6 + 8 17 – 10 24 – 10 37 – 30 11 см 1 дм 8 см 2 дм – 5 см ……………………. ……………………. ……………………. ……………………… …………………….. ……………………… ……………………… ……………………… ……………………… ………………………. ( устная фронтальная проверка) Вывод: Чему научились, выполнив это задание? различать равенства и неравенства: читать равенства и неравенства составлять неравенства и читать их. 5. Этап первичного закрепления. 7) Работа по учебнику. Стр.82 № 1 . Кто из вас может выполнить с объяснением это задание на доске? ( выполняет ученик у доски с комментированием) 8) Дифференцированное задание ( на доске) Сравните, поставив знаки > < = 6 дм * 1 м – 5 дм 98 см 8 см * 10 дм 2 ч * 20 мин 8 дм – 70 см * 1 дм * Сравните, поставив знаки > < = 3 дм * 3 см 5 дм – 2 дм * 4 дм 80 мин * 1 ч 2 дм 3 см * 22 см ( Учащиеся поднимаются с мест, когда выполнят задание. Проверка по рядам. Балл ряду, если учащийся правильно сделал задание. Самооценка на полях тетради) Вывод : Что позволило нам усвоить выполнение данного задания? ( выполнять действия с величинами и сравнивать их) Физкультминутка двигательная. ( Прыгаем –если я показала пример на сравнение правильный; топаем на месте – если знак сравнения неправильный) 9) работа по учебнику № анализ и решение задачи. + высокомотивированным учащимся другое задание на карточке. Проверьте, являются ли квадраты магическими. 9 14 7 40 15 20 8 10 12 5 25 45 13 6 11 30 35 10 10) работа в группах. Найдите ошибки в сравнениях. ( чья группа быстрее и правильнее тому ряду балл) 6 дм 5 см + 5 см > 70 см 34 см + 2 дм = 52 см 8 дм < 7 дм + 11 см 110 мин > 2 ч – 60 мин Ребята, наш урок подходит к концу. Скажите, вы достигли на уроке поставленных перед собою целей составлять неравенства, сравнивать числа и величины; различать равенства и неравенства? ( ответы детей) 6. Этап закрепления и проверки знаний. А это мы сейчас проверим, выполнив минитест по данной теме. Выполнив его вы сможете оценить себя по ключу. Мини тест. 1. Отметь неравенства а) 56 = 50 + 6 К) 37 – 31 >100 – 98 О) 1 дм 3 см < 1 дм 4 см г) 1 ч 15 мин = 75 мин 2. Отметь правильные сравнения 1 ) 6 дм > 54 см в) 92 – 80 < 40 36 О) 25 мин > 70 мин – 1 ч г) 2 дм – 2 см > 20 см Ключ: ОК 10 ( учащиеся по ключу определяют свои знания по теме урока) Итог – те , кто получили по минитесту ОК 10 ( встают) достигли поставленных целей на урок, а те, у кого возникли затруднения мы продолжим работу на поддерживающих занятиях). 7. Этап подведения итогов. Рефлексия. Итог по соревнованию между рядами подводится. Победивший ряд имеет право первым свои стикеры с именем разместить на « Горе успеха» на вершине если вы всё поняли и можете объяснить другому; на склоне горы по середине если поняли. Но объяснить не сможете; внизу горы если вы не поняли и вам нужно ещё объяснение данной темы. ( учащиеся рядами подходят к доске и размещают стикер). – Какие понятия, правила повторяли сегодня на уроке? – Как вы сегодня работали? Что бы хотели выполнить еще? Кому хотели бы сказать спасибо за урок или похвалить? 8. Этап сообщения о домашнем задании. Д.з.Стр.83 № 1.( комментарии учителя) Р.S. – если хватит времени Задачи о животных.( учащимся предлагается не только назвать ответ задачи, но и записать сравнение животных) 1. Лягушкарогатка, имея длину тела 19 см, может в несколько приёмов проглотить змею длиной 1 м. На сколько см длина змеи превышает длину тела лягушки? 2. Лев живёт 25 лет, а слон на 75 лет дольше. Сколько лет живёт слон? 3. Туловище японского гигантского краба достигает 60 см, а крабагорошинки – 2 см. На сколько туловище краба – гиганта больше туловища краба горошинки?
Конспект урока «Числовые неравенства»
Тип урока: урок объяснения нового материала (урок формирования первоначальных предметных навыков и УУД, овладения новыми предметными умениями) – «Введение понятия числовые неравенства»
Цель урока: Сформировать у школьников умения читать и записывать числовые неравенства; преобразовывать графическую и текстовую информацию в знаково-символическую.
Формируемые УУД:
- Образовательные (предметные):
Сформировать умение моделировать сравнение чисел на числовом луче; сравнивать количество предметов в двух совокупностях и
записывать результат, используя знаки «>» и «
Развить умение распознавания изученных геометрических фигур
Развивать умение применения счета на пальцах, отыскивая правильный ответ.
Совершенствовать навыки счета с помощью числового луча.
- Развивающие (метапредметные):
- Регулятивные:
Фиксировать индивидуальное затруднение в пробном действии.
Способствовать выполнению пробного учебного действия – построению числового луча.
Создать возможность планирования совместно с учителем своих действий в соответствии с поставленной задачей и условиями ее реализации.
Развивать умение младшего школьника контролировать свою деятельность по ходу выполнения задания.
- Познавательные:
Развивать умение анализировать, сравнивать, сопоставлять и обобщать.
Подвести под понятие числовое неравенство.
Помочь выделить и сформулировать познавательную цель.
Развивать умение работать с разными видами информации.
Продолжать работать над формированием умений ориентироваться в учебнике и тетради для самостоятельных работ.
Работать над формированием умений выполнения действий по образцу.
Работать над использованием знаково-символичных средств.
Способствовать высказыванию детьми своего мнения, оцениванию своей деятельности на уроке.
- Коммуникативные:
Создать условия для учебного сотрудничества с учителем и сверстниками.
Способствовать осуществлению взаимодействия ребенка с соседом по парте.
Помочь ребенку в аргументации своего мнения.
- Воспитательные (личностные):
Сформировать мотивационную основу учебной деятельности, положительное отношение к уроку, понимание необходимости учения.
Понимать и следовать в деятельности нормам эстетики.
Работать над самооценкой и адекватным пониманием причин успеха/неуспеха в учебной деятельности.
Развивать умение адаптироваться к сложным ситуациям.
Следовать установке на здоровый образ жизни и ее реализации в реальном поведении.
Способствовать проявлению познавательной инициативы в оказании помощи соученикам (посредством системы заданий, ориентирующей младшего школьника на оказание помощи героям учебника).
Следовать в поведении моральным и этическим требованиям.
Способствовать проявлению самостоятельности в разных видах детской деятельности.
Работать над осознанием ответственности за общее дело.
Этап урока | Цели этапа | Деятельность учителя | Деятельность учащихся | Планируемые результаты | ||
Личностные | Метапредметные | Предметные | ||||
1. Организацион-ный момент | Организовать направленное внимание на начало урока. | Проверка готовности рабочих мест. Создание положительного настроя учащихся на урок. Ребята, сегодня у нас необычный урок. У нас на уроке гости. Посмотрите на них, чтобы потом не отвлекаться. Поздоровайтесь. Теперь глазки все на меня. Всем, всем добрый день! Прочь с дороги наша лень! Не мешай трудиться, Не мешай учиться! | Приготовление к уроку. Приветствие учителя. | Положительное отношение к уроку, понимание необходимости учения. Следование в поведении моральным и этическим требованиям. | Учебное сотрудничество с учителем и сверстниками. | — |
2. Актуализация знаний | Дальнейшее успешное усвоение новых знаний или учебных действий. | Учитель создает ситуацию, при которой возникает необходимость получения новых знаний: — А для чего надо учиться математике? (ответы детей) — Ну что, будем учиться? Мудрая Сова просит вас, ребята, посчитать. | Повторение системы ранее усвоенных учебных действий, необходимых и достаточных для восприятия нового материала, осознание необходимости получения новых знаний: | Проявление познавательной инициативы в оказании помощи соученикам (посредством системы заданий, ориентирующей младшего школьника на оказание помощи героям учебника). Умение адаптироваться к сложным ситуациям. | Аргументация своего мнения и позиции в коммуникации. Развитие умения анализировать, сравнивать и сопоставлять. | Ведение счета как в прямом, так и в обратном порядке (от 0 до 20) Запись цифр от 1 до 9 |
3. Постановка цели урока | Сформировать представления детей о том, что нового они узнают на уроке, чему научатся. | Ребята, давайте вспомним,какие математические знаки мы уже знаем? 1. Сравни числа ( > ,) 1…1 1…2 2…2 2…1 На какие группы можно разбить эти записи? Какие названия к ним можно придумать? | Ученики самостоятельно пытаются сформулировать тему и цель урока: на уроке будем работать с числовыми равенствами и неравенствами. | Формирование мотивационной основы учебной деятельности. | Выделение и формулирование познавательной цели с помощью учителя. Планирование совместно с учителем своих действий в соответствии с поставленной задачей и условиями ее реализации. | — |
4. Первичное восприятие и усвоение нового теоретического учебного материала | Привлечение внимания детей к принципиально новым сведениям, развитие умения сравнивать числа на числовом луче. | Учебник с. 76 № 169, 170. | Отвечают на поставленный вопрос, выполняют построение | Проявление самостоятельности в разных видах детской деятельности | Работа с разными видами информации. Использование знаково-символичных средств. Выполнение пробного учебного действия –изображение числового луча. Выполнение действий по образцу. | Совершен-ствование навыков сравнения чисел по числовому лучу. |
5. Применение теоретических положений в условиях выполнения упражнений и решения задач | Сформировать навыки записи | Тетрадь с.43 | Объясняют как сравнивают числа. | Осознание ответственности за общее дело. Понимание и следование в деятельности нормам эстетики. | Высказывание своего мнения. Аргументация своего мнения. Выполнение действий по заданному алгоритму. Контроль деятельности по ходу выполнения задания. | Работа с числовым лучом. Запись чисел на числовом луче, постановка знаков в неравенствах. |
6. Динамическая пауза (этап физической разрядки) | Смена вида деятельности | Любопытная Варвара Смотрит влево, смотрит вправо. Смотрит вверх, смотрит вниз. Чуть присела на карниз И с него свалилась вниз. | Повторение движений учителя | Установка на здоровый образ жизни и ее реализация в реальном поведении | Выполнение действий по образцу. | — |
7. Обобщение усвоенного и включение его в систему ранее усвоенных ЗУНов и УУД | Закрепить, повторить, продолжить формирование УУД. | Работа с компьютером. | Индивидуальная работа. | Нравственно-этическое оценивание усваиваемого содержания. | Ориентация в учебнике и тетради для самостоятельных работ. Взаимодействие с соседом по парте. Анализ, синтез, сравнение и обобщение. | Составление неравенств |
8. Рефлексия деятельности | Сформировать личную ответственность за результаты деятельности | Подводит итоги совместной и индивидуальной деятельности учеников | Фиксируют материал, изученный на уроке, выявляют недостаток тех знаний и умений, которых им не хватает для решения новых проблем, оценивают личный вклад в результаты коллективной деятельности | Адекватное понимание причин успеха/неуспеха в учебной деятельности Самооценка на основе критерия успешности | Рефлексия способов и условий действия. Оценка своей деятельности на уроке. Выражение своих мыслей с достаточной полнотой и точностью. Формулирование и аргументация своего мнения, учет разных мнений. | — |
Конспект урока по математике во 2 классе по программе «Перспективная начальная школа»
Тема: «ЧИСЛОВЫЕ РАВЕНСТВА И ЧИСЛОВЫЕ НЕРАВЕНСТВА»
Цели: — познакомить с понятием «круглые» двузначные числа;
— учить читать и записывать «круглые» двузначные числа, считать десятками;
— развивать умение анализировать и сравнивать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Расставьте числа в пустые клетки квадрата так, чтобы по всем направлениям сумма чисел была равна 15.
2. Разгадайте, как связаны числа и рисунки, и запишите верные равенства: 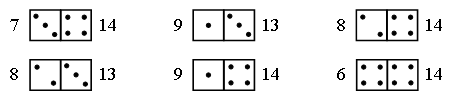
3. Назовите признаки, по которым изменяются фигуры в каждом ряду.
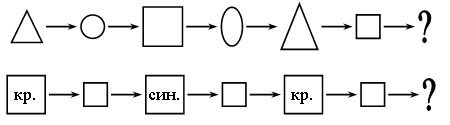
4. Решите задачу.
Мальвина загадывала Буратино и Пьеро загадки.
Буратино отгадал 5 загадок, а Пьеро – 12. Кто отгадал загадок больше и на сколько?
– Сколько всего загадок отгадали Буратино и Пьеро?
III. Сообщение темы урока.
– Рассмотрите записи на доске:
– Сравните записи в каждом столбике. Чем они похожи? Чем отличаются?
– Сегодня на уроке мы узнаем, как называются данные математические записи, если в «окошко» вставить числа.
IV. Работа по теме урока.
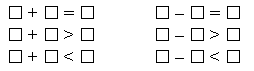
1. Задание 1.
– Дополните записи так, чтобы они получились верными.
Запись:
2. Задание 2.– Прочитайте математические записи слева и справа. Чем они похожи? Чем отличаются?
– Все ли записи являются верными?
– В столбике слева написаны числовые равенства. А в столбике справа написаны числовые неравенства. Почему эти записи так называются?
3. Задание 3.
– Прочитайте данные математические записи.
– Как они называются? (Это числовые равенства.)
– Выберите верные числовые равенства и запишите их.
Запись:
Какие знания помогли вам выполнить это задание?4. Задание 4.
– Прочитайте данные математические записи.
– Как они называются? (Это числовые неравенства.)
– Выберите верные числовые неравенства и запишите их.
Запись:
Физкультминутка5. Работа в парах.
– Составьте и запишите 5 верных числовых равенств и 5 верных числовых неравенств.
Взаимопроверка в парах.
6. Задание 6.
– Запишите все числа, при подстановке которых запись становится верным неравенством.
 < 10 4 < 10
< 10 4 < 10
9 < 10 3 < 10
8 < 10 2 < 10
7 < 10 1 < 10
6 < 10 0 < 10
5 < 10
7. Задание 7.
– Запишите десять чисел, при подстановке которых данная запись становится верным неравенством.
10 <  10 < 16
10 < 16
10 < 11 10 < 17
10 < 12 10 < 18
10 < 13 10 < 19
10 < 14 10 < 20
10 < 15
V. Итог урока.
– Что нового узнали на уроке?
– Какие записи называют «числовыми равенствами»?
– Какие записи называют «числовыми неравенствами»?
Домашнее задание: учебник, с. 14, № 5.
Введение в неравенства
Неравенство говорит нам о относительном размере двух значений.
Математика не всегда о «равных», иногда мы только знаем, что что-то больше или меньше.
Пример: Алекс и Билли участвуют в гонке, и Билли побеждает!
Что мы знаем?
Мы не знаем , как быстро они бежали , но мы знаем, что Билли был быстрее, чем Алекс:
Билли был быстрее, чем Алекс
Мы можем записать это так:
б> а
(где «b» означает, насколько быстрым был Билли, «>» означает «больше чем», а «a» означает, насколько быстрым был Алекс)
Мы называем такие вещи неравенства (потому что они не «равны»)
больше или меньше
Два наиболее распространенных неравенства:
Символ | слов | Пример использования |
|---|---|---|
| > | больше | 5> 2 |
| < | менее | 7 <9 |
Их легко запомнить: «маленький» конец всегда указывает на меньшее число, например:
Символ больше БОЛЬШОЙ> маленький
Пример: Алекс играет в футбол до 15 лет.Сколько лет Алексу?
Мы не знаем точно , сколько лет Алексу, потому что он не говорит «равно»
Но мы знаем «меньше 15», поэтому мы можем написать:
Возраст <15
Маленький конец указывает на «Возраст», потому что возраст меньше 15 лет.
… или равно!
Мы также можем иметь неравенства, которые включают в себя «равно», как:
Символ | слов | Пример использования |
|---|---|---|
| ≥ | больше или равно | x ≥ 1 |
| ≤ | меньше или равно | лет ≤ 3 |
Пример: вам должно быть 13 лет или больше, чтобы посмотреть фильм.
«Неравенство» находится между вашего возраста и возраста 13 .
Ваш возраст должен быть «больше, чем или , равный 13», что написано:
Возраст ≥ 13
Сравнение значений
Практика>, <и = с номерами для сравнения с 10
Узнайте больше о неравенствах меньше или больше, чем
,Сложное неравенство
Сложное неравенство — это утверждение, в котором два неравенства связаны словом «и» или словом «или».
Например, x> 5 и x ≤ 7 и x ≤ -1 или x> 7 являются примерами сложных неравенств.
Когда слово, связывающее оба неравенства, равно «и», решением является любое число, которое делает оба неравенства истинными
Когда слово который соединяет оба неравенства, это «или», решение — любое число, которое делает либо неравенства истинными.
Например, нарисуйте следующее сложное неравенство: x ≥ 2 и x <4
. выглядеть так:
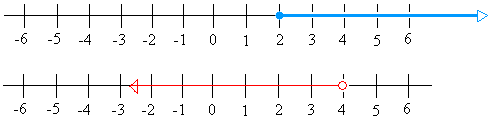 |
Соединение двух графиков дает следующее:
 |
Решением является та часть графика, где вы видите красный и синий цвета одновременно (или часть, заштрихованная дважды)
Если вы вытащите это из графика выше, мы получим:
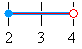 |
Это означает, что решением может быть любое число от 2 до 4, включая 2, но не 4.
Обратите внимание, что открытый кружок (красным) означает, что число 4 не включено
График x ≥ — 2 и x> 1
Графики для x ≥ — 2 и x> 1 должны выглядеть следующим образом:
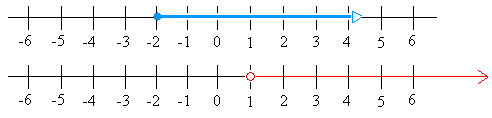 |
Соединение двух графиков дает следующее:
 |
Решением является та часть графика, где вы видите красный и синий цвета одновременно (или часть, заштрихованная дважды)
Если вы вытащите это из графика выше, мы получим:
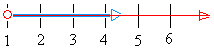 |
Решение — любое число после 1
Однако, если мы закрутим ту же проблему выше и на графике x ≥ — 2 или x>, это будет другая история
Так как «или» означает либо, решение будет затенено область, которая включает в себя оба неравенства.
Решение, таким образом, любое число после -2
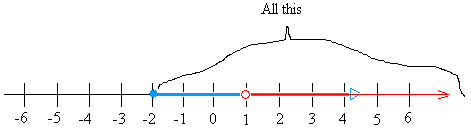 |
График х> 2 или х <-3
Вот оно!
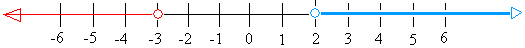 |
Однако, если для той же самой проблемы, указанной выше, я заменю «или» на «и», для этого соединения не будет решений.
Еще раз внимательно посмотрите на график справа, и вы увидите, что синий и красный не встреча.Вот почему у них нет ничего общего и, следовательно, нет решений
Новые уроки математики
Ваша электронная почта в безопасности с нами. Мы будем использовать его только для информирования вас о новых уроках математики.
,Свойства неравенства
Покажем 6 свойств неравенства. При необходимости мы проиллюстрируем на практике примеры свойств неравенства. Пусть x, y и z представляют действительные числаСвойство сложения:
Если x Пример: предположим, что вес Сильвии <вес Дженнифер, затем вес Сильвии + 4 <вес Дженнифер + 4 Или предположим, что 1 <4, то 1 + 6 <4 + 6 Если x> y, то x + z> y + z Пример: допустим, что вес Сильвии> вес Дженнифер, затем вес Сильвии + 9> Вес Дженнифер + 9 Или предположим, что 4> 2, то 4 + 5> 2 + 5 Свойство вычитания: Если x Пример: Предположим, вес Сильвии < Вес Дженнифер, затем вес Сильвии - 4 <вес Дженнифер - 4 Или предположим, что 4 <8, тогда 4 - 3 <8 - 3 Если x> y, то x — z> y — z Пример: Предположим, Сильвия вес> вес Дженнифер, затем вес Сильвии — 9> вес Дженнифер — 9 Или предположим, 8> 3, затем 8 — 2> 3 — 2 Multiplicatio n свойство: z> 0 Если x Пример: предположим, что 2 <5, затем 2 × 10 <5 × 10 (обратите внимание, что z = 10 и 10> 0) Если x> y и z> 0, то x × z> y × z Пример: предположим, что 20> 10, тогда 20 × 2> 10 × 2 z Если x Пример: предположим, что 2 <5, тогда 2 × -4> 5 × -4 (-8> -20.z = -4 и -4 <0) Если x> y и z <0, то x × z Пример: предположим, что 5> 1, тогда 5 × -2 <1 × -2 (- 10 <-2) Работает точно так же, как умножение z> 0 Если x Пример: Предположим, что 2 <4 , тогда 2 ÷ 2 <4 ÷ 2 Если x> y и z> 0, то x ÷ z> y ÷ z Пример: предположим, что 20> 10, затем 20 ÷ 5> 10 ÷ 5 z Если x Пример: Предположим, 4 <8, тогда 4 ÷ -2> 8 ÷ -2 (-2> -4) Если x> y, и z <0, затем x ÷ z Пример: Предположим, 5> 1, затем 5 ÷ -1 <1 ÷ -1 (-5 <-1) Переходное свойство: Если x> y и y> z, затем x> z Пример: предположим, что 10> 5 и 5> 2, затем 10> 2 x 5 <10 и 10 <20, затем 5 <20 Свойство сравнения: Если x = y + z и z> 0, то x> y Пример: 6 = 4 + 2, тогда 6> 4 Свойства неравенства сложнее понять, чем свойство равенства. Позвольте себе побольше времени проходить этот урок. Есть вопросы о свойствах неравенства, дайте мне знать. Новые уроки математики Ваша электронная почта в безопасности с нами. Мы будем использовать его только для информирования вас о новых уроках математики. Это график линейного неравенства: Вы можете видеть линию y = x + 2, а заштрихованная область — это где y меньше или равно x + 2 Линейное неравенство похоже на линейное уравнение (например, y = 2x + 1 ) … … но оно будет иметь неравенство вроде <,>, ≤ или ≥ вместо = . Сначала нарисуйте линию «равно», затем заштрихуйте правильную область. Есть три шага: Давайте попробуем несколько примеров: 1. Неравенство уже имеет «y» слева и все остальное справа, поэтому нет необходимости переставлять 2. График y = 2x-1 (как сплошная линия, потому что y≤ включает , равный ) 3. Заштрихуйте область ниже (потому что у меньше, чем или равно) 1.Нам нужно изменить это так, чтобы «у» было слева: Начните с: 2y — x ≤ 6 Добавьте x в обе стороны: 2y ≤ x + 6 Разделите все на 2: y ≤ x / 2 + 3 2. Теперь построите график y = x / 2 + 3 (как сплошная линия, потому что y≤ включает , равный ) 3. Заштрихуйте область ниже (потому что у меньше, чем или равно) 1.Нам нужно изменить это так, чтобы «у» было слева: Начните с: y / 2 + 2> x Отнимите 2 с обеих сторон: y / 2> x — 2 Умножить все на 2: y> 2x — 4 2. Теперь построите график y = 2x — 4 (как пунктирная линия, потому что y> не включает в себя равно) 3. Заштрихуйте область выше (потому что у на больше, чем на ) Пунктирная линия показывает, что неравенство , а не включает в себя линию y = 2x-4 . Вы также можете иметь горизонтальную или вертикальную линию: Вот таблица, суммирующая свойства неравенства.
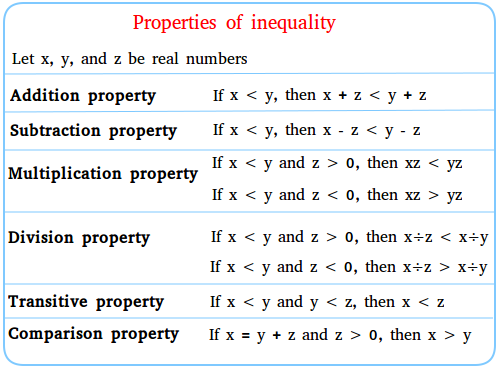
График линейных неравенств
Неравенство y ≤ x + 2 линейное неравенство
Как построить график линейного неравенства
или ниже линии для «меньше чем» ( y < или y≤ ). Пример: y≤2x-1
Пример: 2y — x ≤ 6
Пример: г / 2 + 2> х
Два особых случая
, Это показывает, где у меньше 4
(от, но не включая линию у = 4 вниз)
Обратите внимание, что у нас есть пунктирная линия, чтобы показать, что она не включает где у = 4 У этого даже нет y!
Имеет линию x = 1 и закрашивается для всех значений x больше (или равно) 1