Урок 11. равенство. неравенство. знаки «>», «
Математика, 1 класс
Урок 11. Равенство. Неравенство. Знаки «>», «<», «=»
Перечень вопросов, рассматриваемых на уроке:
1. Определять место знаков больше, меньше, равно
2. Писать знаки >,<,=
3. Называть равенство, неравенство.
Глоссарий
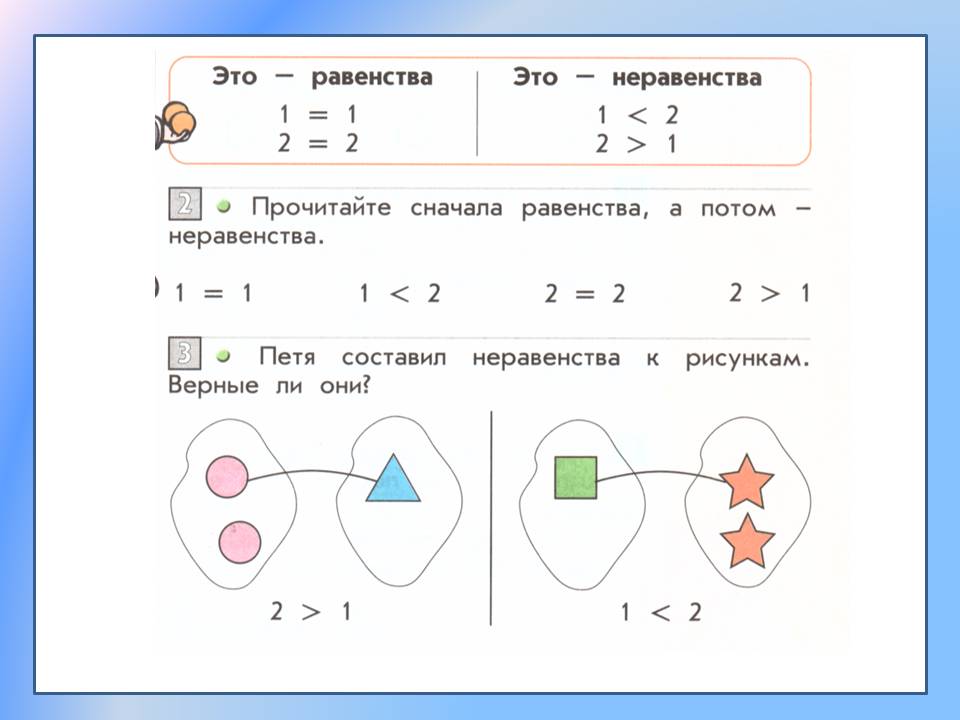
Равенство – это когда одно количество равно другому.
Неравенство – это когда одна сторона выражения не равна второй.
Если носик галочки смотрит направо — это знак больше (>).
Если носик галочки смотри налево – это знак меньше (<).
Знак равенства (=) в математике, в логике и других точных науках — символ, который пишется между двумя одинаковыми по своему значению выражениями.
Ключевые слова
Знак >; знак <; знак =
Основная литература:
1.Моро М. И., Волкова С. И., Степанова С.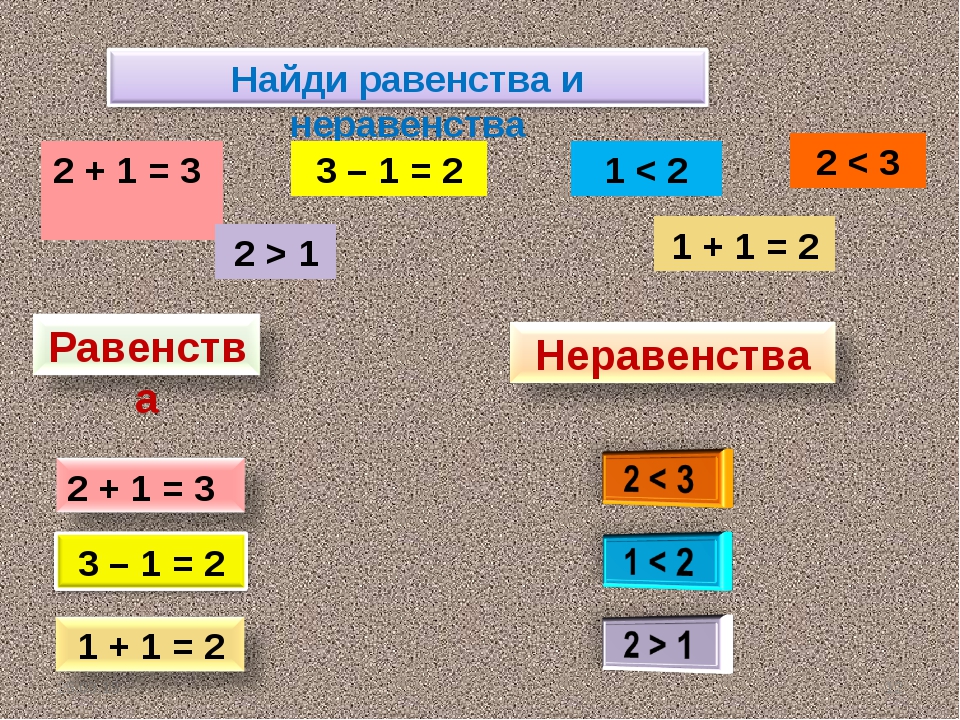
Дополнительная литература:
1. Моро М. И., Волкова С. И. Математика. Рабочая тетрадь. 1 кл. В 2 ч. пособие для общеобразовательных организаций. — М.: Просвещение, 201 с.
Основное содержание урока
1. Сегодня мы отправляемся в магазин, чтобы купить Оле и Ане к уроку технологии все учебные принадлежности.
Для урока понадобится 1 пачка пластилина и две пачки картона.
По сколько пачек пластилина получили девочки? ( по одной пачке)
Можно сказать, что девочки получили одинаковое количество пластилина.
2. Для технологии необходимо две пачки картона.
По сколько пачек картона получили девочки? (по две пачки)
Можно сказать, что девочки получили одинаковое количество картона.
3. В математике используется специальный значок, чтобы записать, что число предметов одинаковое.
Можно записать цифрами и использовать для слов «одинаково», «равно» специальный значок «=»,1 = 1
=
2 = 2 (аналогично)
Две палочки напишут дети,
И что получится в ответе,
Ведь каждый выучил давно,
Как пишется тот знак: РАВНО!
Такие записи называются равенствами.
Это равенства. Записать равенства можно с помощью знака «=».
Докажем, что одинаковое количество предметов с помощью стрелочек образует пары.
На схеме каждый предмет обозначим кружочком и образуем пары. Покажем стрелочкой.
Оля Аня
Лишних фигур не осталось. Значит, поровну, одинаково.
Можно записать 1 = 1
6. 2 + 1 = 3
Как можно прочитать эту запись?
(Числовое равенство)
Под этим высказыванием понимают два числовых выражения, которые стоят по обе стороны от знака « =».
Обе части записи равны между собой.
- В каком количестве нужно было для урока картона? А пластилина?
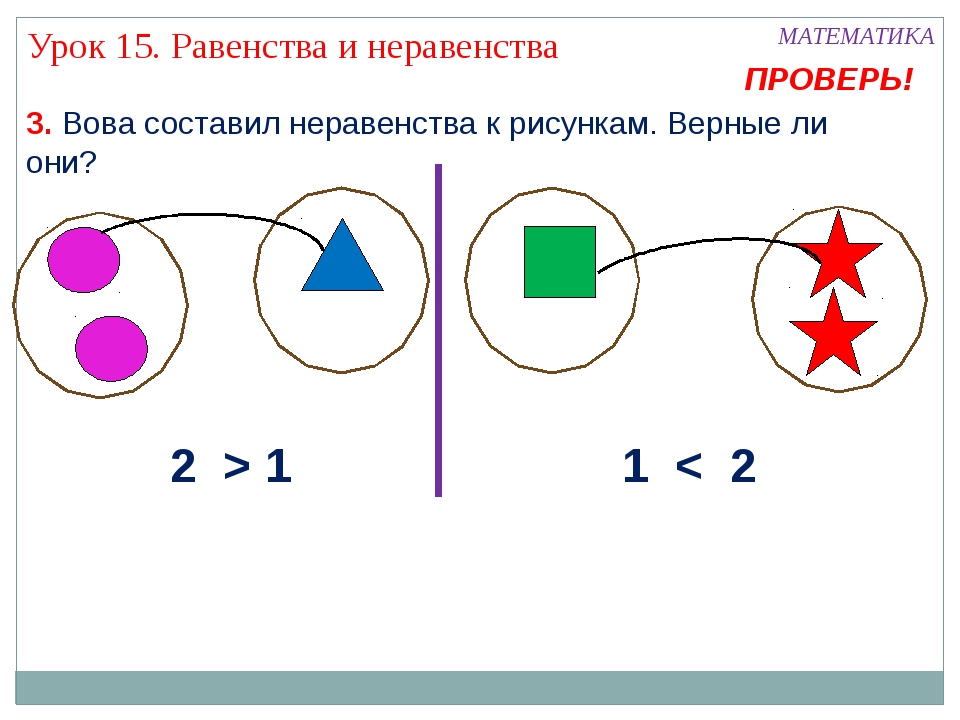
Чтобы узнать, каких предметов потребовалось больше или меньше, используют специальные значки «>», « <».
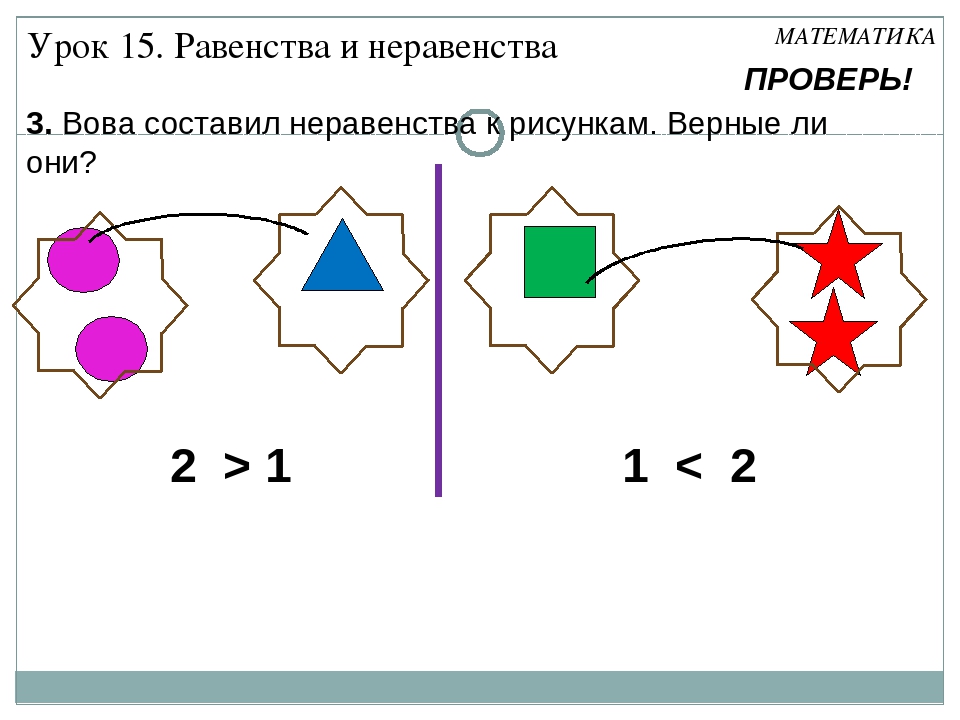
Если с какой- то стороны больше или меньше, то запись будет называться «неравенство».
Два больше одного.
Картон Пластилин
Если слева больше число, чем справа, то используют знак «>».
2 > 1
- А если число слева меньше, чем справа, то ставим знак меньше «<».
1 < 2
- Такие записи называются неравенства:
4 > 3, 4 < 5
Разбор типового тренировочного задания
Выберите нужный знак и распределите на две группы.
Дополните каждую группу своими записями.
6 (=, >, <) 9
1 (=, >, <) 3
2 (=, >, <) 2
3 (=, >, <) 3
Правильный ответ:
Равенства: 2 = 2, 3 = 3
Неравенства: 6 < 9, 1 < 3
Открытый урок «Равенства и неравенства»
I.Организационный момент.
Громко прозвенел звонок –
Начинается урок.
Слушаем , запоминаем
Ни минутки не теряем.
— Ребята , сегодня к нам на урок пришли гости. Давайте повернемся и поприветствуем гостей.
— Посмотрите друг на друга , улыбнитесь , пожелайте себе и другим успешной работы.
— Вспомним наш девиз « Повторять да учить – ум точить»
— Тихо садимся . Вспоминаем правила посадки. Спинки прямые , ножки ровненько поставили. Приготовились трудиться.
II. Подготовительный этап.
Сейчас я загадаю вам загадку.
Кто, угадай-ка?
Сегодня хозяйка!
Тряхнет перинки-
Над миром пушинки? (зима)
-Кто любит это время года? А за что? Очень весело детворе зимой, появляется много игр, забав.
3.Постановка цели урока.
-Сегодня на уроке математики мы будем лепить снеговика, играть в снежки, ловить причудливые красивые снежинки, разгребать сугробы. Но мы будем не просто играть, а математические понятия закреплять, складывать и вычитать числа, решать «зимние» задачи.
Деление класса на 3 группы.
— И я предлагаю Вам поиграть в снежки. У каждого учащегося на парте лист со словами «больше», «less», «тең». Скомкайте лист бумаги и давайте поиграем в снежки. Дети кидают друг другу снежки, затем раскрывают снежок и рассаживаются по группам: «больше», «less», «тең».
— Объяснение слов:
— Как вы думаете, о чем мы будем говорить на уроке? Чем мы будем заниматься?
Вы –команда!
Будьте активны!
Слушайте друг друга!
Спорьте честно, искренне!
Сделайте работу интересной!
II
 Устный счет. Урок проходит с сопровождением раздачи жетонов за каждый правильный ответ, дети составляют композицию.
Устный счет. Урок проходит с сопровождением раздачи жетонов за каждый правильный ответ, дети составляют композицию.
1 группа:
Учитель просит учащихся хором посчитать от 1 до 20.
2 группа:
Затем учитель на числовой прямой изображает числа от 0 до 20.
– Из расположенных на числовой прямой чисел назовите все чётные.
3 группа:
– Назовите все нечётные числа.
1 группа:
– Назовите число, которое следует за числом 12.
2 группа:
– Число, которое предшествует числу 15.
3 группа:
– Число, которое на числовой прямой находится между числами 17 и 19.
1 группа:
– Назовите «соседей» числа 19.
2 группа:
– Назовите число, в котором: 1 десяток 5 единиц; 1 десяток 2 единицы; 1 десяток 9 единиц; 2 десятка.
3 группа:
– Посчитайте в обратном порядке числа от 20 до 10.
Вопросы по группам:
1 группа:
2. Какой день недели идёт после среды? Перед средой?
3. Назовите летние месяцы.
Назовите летние месяцы.
2 группа:
4. Сколько месяцев в году?
5. Каким месяцем заканчивается год? А начинается?
6. Сколько времён года вы знаете? Перечислите.
3 группа:
7. Назовите осенние месяцы.
8. Назовите зимние месяцы.
9. Назовите весенние месяцы.
«Зимние задачки»:
1.На берёзе 3 синички
Продавали рукавички.
Прилетело ещё 5,
Сколько будут продавать? 3+5=8
2. Как-то четверо ребят
Как-то четверо ребят
С горки покатились.
Двое в саночках сидят,
А сколько в снег свалились? 4-2=2
3. Семь ребят каталось с горки.
Убежал домой Егорка,
А потом ушел Вадим
И Сережа вслед за ним.
Сколько на горке осталось детей?
Кто посчитал, отвечайте скорей! 7-1-1-1=4
4. В снег упал Сережа
А за ним Алеша
А за ним Ирина
А за ней Марина
А потом упал Игнат
Сколько на снегу ребят? (пять)
5. Ежик по лесу шел,
На обед грибы нашел:
Два — под березой,
Один — у осины,
Сколько их будет
В плетеной корзине? (3)
6. В класс вошла Маринка,
В класс вошла Маринка,
А за ней — Аринка,
А потом пришел Игнат.
Сколько стало всех ребят? (3)
Найдите лишнее:
1 группа: 10 20 30 40 55 60
2 группа: 1 2 31 4 5 6 7 8
3 группа: 10 11 15 17 9 18
Прикрепляем на бумагу 1 круг. Жетоны собирают в коробочку.
Физкультминутка для глаз «Снеговик»
Игровое упражнение «Помогите снеговикам» 9 10 8
5+5 7+3 1+8 5+4 8+2 9+1 6+4 7+2 6+3 9+0 4+4 5+3 1+7 2+6 8+0
Ответы.
 Учебник. Часть 2 (с. 103)
Учебник. Часть 2 (с. 103)Числа от 1 до 100
Что узнали, чему научились во 2 классе?
Числовые и буквенные выражения
1. Запиши сумму и разность, произведение и частное чисел 18 и 2.
18 + 2, 18 – 2, 18 • 2, 18 : 2 – числовые выражения.
Что значит найти значение выражения?
Выполни вычисления.
Найти значение выражения значит произвести вычисления в этом выражении.
18 + 2 = 20
18 – 2 = 16
18 • 2 = 36
18 : 2 = 9
2. Запиши выражения и вычисли их значения.
1) Из числа 80 вычесть сумму чисел 20 и 7.
2) К числу 12 прибавить разность чисел 11 и 3.
1) 80 – (20 + 7) = 80 – 27 = 53
2) 12 + (11 – 3) = 12 + 8 = 20
3. 1) Что нужно знать, чтобы можно было найти значения буквенных выражений: α + 5, d – 8, k + 14, c • 3, b : 2?
2) Найди значения выражений при α = 8, d = 28, k = 30, k = 10, k = 6, c = 4, b = 10.
1) Чтобы найти значения буквенных выражений нужно значть числовое значение букв в этих выражениях
2) α = 8, 8 + 5 = 13
d = 28, 28 – 8 = 20
k = 30, 30 + 14 = 44
k = 10, 10 + 14 = 24
k = 6, 6 + 14 = 20
c = 4, 4 • 3 = 12
b = 10, 10 : 2 = 5
Равенство. Неравенство. Уравнение
1. Объясни, почему верно неравенство
3 + 4 > 10 – 5. Как это можно доказать?
Надо вычислить выражения справа и слева от знака неравенства: 3 + 4 = 7, 10 – 5 = 5. При счёте 7 следует после 5, поэтому 7 больше 5. Соответственно, 3 + 4 будет больше 10 – 5.
2. Рассмотри рисунки и составь по ним верные неравенства или равенства.
3 + 4 > 8 – 2
5 – 2 = 8 – 5
5 – 1 < 6 + 1
3.
25 + 8 < 25 + 9
43 – 9 < 43 – 6
27 + 2 > 27 – 2
64 + 3 = 3 + 64
18 < 81
21 > 19
4. Что обозначает буква в записи уравнения? Что значит решить уравнение?
Что обозначает буква в записи уравнения? Что значит решить уравнение?
Реши уравнения: х – 8 = 2, 16 – х = 6, 5 + х = 5.
Неизвестное число, которое надо найти. Найти такое число, при подстановке которого в уравнение оно превратится в равенство.
х – 8 = 2
х = 2 + 8
х = 10
16 – х = 6
х = 16 – 6
х= 10
5 + х = 5
х = 5 – 5
х = 0
ЗАДАНИЕ НА ПОЛЯХ
НАБЕРИ 16
16 = 7 + 4 + 5 = 6 + 9 + 1 = 2 + 4 + 8 + 2 = 3 + 4 + 9
Математика. 2 класс. Ответы к заданиям
1 / 5 ( 5 голосов )
Конспект урока математики по теме Равенства-неравенства
Урок математики в 1 классе. Программа «Школа России»
Тема: Равенства и неравенства.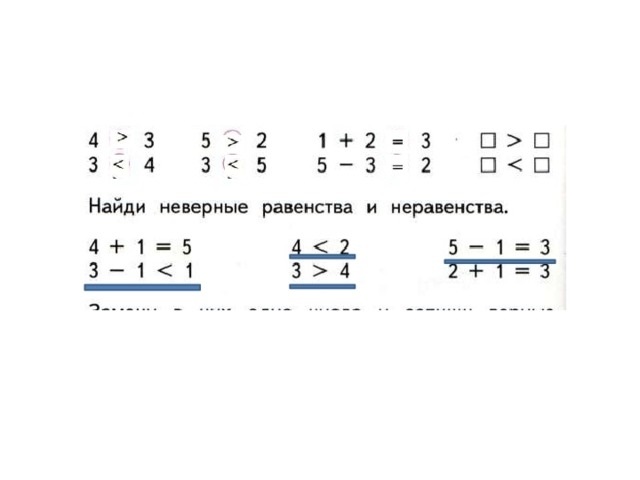
Лялина Ирина Анатольевна
ГКОУ «Бежецкая школа-интернат»
учитель начальных классов
Тема предыдущего урока: «Знаки «>», «<», «=».
13 урок в разделе «Числа от 1 до 10 и число 0. Нумерация.»
Цели урока:
1.Обучающие:
Познакомить учащихся с терминами «равенство», «неравенство».
Формировать умение детей сравнивать числа и правильно использовать знаки сравнения «больше», «меньше», «равно».
2. Развивающие:
Способствовать развитию мыслительных операций: анализа, синтеза, обобщения, сравнения.
Развивать логическое мышление, речь, внимание.
Развивать умение грамотно, логично полно давать ответы на вопросы, уметь доказывать, аргументировать своё мнение.
3. Воспитательные:
Воспитывать интерес к математике, создавать мотивацию к дальнейшему изучению предмету.
Воспитывать стремление использовать математические знания в повседневной жизни.
Содействовать развитию у детей умения общаться, радоваться успехам товарищей.
Планируемые образовательные результаты
Предметные УУД.
Знают термины «равенство», «неравенство».
Умеют сравнивать числа и правильно использовать знаки сравнения «больше», «меньше», «равно».
Метапредметные УУД.
Познавательные:
умеют анализировать, сравнивать и обобщать полученную информацию на уроке.
Регулятивные:
умеют ставить учебные задачи и самостоятельно формулировать выводы;
умеют слушать собеседника, излагать своё мнение и аргументировать свою точку зрения.
Личностные:
осуществлять сотрудничество в парах, группах при выполнении учебных задач.
Коммуникативные:
вступать в учебное сотрудничество с одноклассниками; участвовать в совместной деятельности;
участвовать в диалоге, в общей беседе, взаимопомощь; осуществлять взаимоконтроль;
проявлять доброжелательное отношение к партнёрам.
Место занятия – учебный кабинет.
Тип урока: урок — «открытие» новых знаний.
Форма урока: урок-исследование.
Межпредметные связи: русский язык, физкультура.
Формы организации работы учащихся: фронтальная, индивидуальная, парная, дифференцированная.
Методы и приёмы: словесный, наглядный, объяснительно-иллюстративный, опора, частично-поисковый, доказательство, рассуждение, инструктаж, наблюдение, конкретизация, целеполагание, сравнение.
Методы и формы контроля: наблюдение, самооценка, самоконтроль, рефлексия.
Конспект урока по математике.
1 класс.
Тема: Равенства. Неравенства. Знаки «<», «>» «=».
Ι. Орг. момент
Психологический настрой
Улыбнитесь друг другу, подарите улыбки, и мне тоже. Ведь улыбки располагают к приятному общению, а теперь настроимся на работу – откроем ладошки новым знаниям.
Ведь вокруг нас так много интересного, стоит только оглянуться по сторонам. Но в любом деле необходимо соблюдать определенные правила. Давайте вспомним наши правила.
Но в любом деле необходимо соблюдать определенные правила. Давайте вспомним наши правила.
Не выкрикивай, не перебиваем друг друга
Мы слышим друг друга, учимся работать сообща.
ΙΙ. Устный счёт.
1)- Назвать предыдущее число: 3, 5, 2, 4
— Что значит, предыдущее?
— Назвать последующее число: 4, 5, 3, 2
— Что значит, следующее?
2) — Листья желтеют и опадают – это приметы чего? (осени )
— Ветер осенью летал, ветер листики считал:
Красный лист, зеленый лист.
Липы лист, клена лист.
Хорошо ли ты считал? Сколько листьев насчитал? 4
— Назовите соседей числа 4
— Как получить число 4? (состав числа 4)
— Какой сегодня день недели? (пятница)
— А по счёту какой? ( Повторение состава «5»)
ΙΙΙ. Работа по теме.
Объяснение нового материала поисковым методом.
— Кого больше белочек или утят?
— Кого меньше мышат или зайчат?
— Что мы делали? (сравнивали)
— Тогда скажите, что мы будем делать на уроке?
— Сегодня на уроке мы будем сравнивать числа и выражения, узнаем, что такое равенство и неравенство.
— Сколько синих квадратов? (3)
— Сколько красных квадратов? (3)
– то можно сказать о количестве синих и красных? (Их поровну. Столько же.)
–Какой знак поставим между цифрами? (Равно.)
Учитель записывает на доске 3=3.
— Прочти выражение.
— Это равенство.
— Как думаете, почему мы называем это выражение равенство? ( Если количество равное, то такое математическое выражение называется равенством)
— Сколько синих треугольников? (3)
— Сколько зеленых треугольников? (2)
– Что можно сказать о количестве синих и зеленых треугольников? (Синих треугольников больше.)
– Какой знак поставим между цифрами? (Больше.)
Учитель записывает на доске 3>2.
— Прочти выражение.
— Это неравенство.
— Как думаете, почему мы называем это выражение неравенство? (Если количество неравное, то математическое выражение называется неравенством.)
– Какой вывод можно сделать? (Если между числами или числовыми выражениями стоит знак «равно», то это равенство, если между числами или числовыми выражениями стоит знак « > » или « < », то это – неравенство. )
)
Первичное закрепление. Игра.Показываю карточки (2=2, 4>2, 4=4,1<3,1=1,4>3). Если показываю равенство, вы стоите ровно, если неравенство, делаете наклон.
Работа по учебнику с.48
Прочитай равенства, затем неравенства
Сравни( устно)
4. Работа в тетради на печатной основе с.19
IV.Итог урока.
Я научился….
Сегодня мне удалось….
Теперь я умею…
Я буду стараться, чтобы….
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/374808-konspekt-uroka-matematiki-po-teme-ravenstva-n
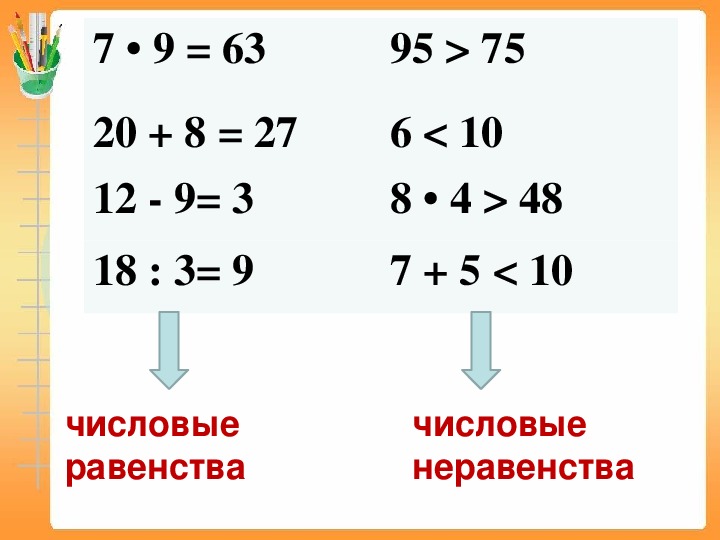
Урок математики в 3 классе по теме: «Числовые равенства и неравенства»
Муниципальное бюджетное общеобразовательное учреждение Зимовниковская средняя общеобразовательная школа №1
Зимовниковский район, Ростовская область
Урок математики
в 3 классе
по теме: «Числовые равенства и неравенства»
разработала: учитель начальных классов
Московченко Галина Васильевна
класс: 3, 9 лет
п. Зимовники
Зимовники
2014 г.
ТЕМА: «Числовые равенства и неравенства»
Цели: создать условия для знакомства с терминами «равенство» и «неравенство», формирования навыков употребления в своей речи слов: «верное» и «неверное» равенство и неравенство; развития навыков математического счета, смекалки, мышления; воспитания положительных нравственных качеств.
Ход урока
1.Организационный момент.
Каждый день всегда, везде
На занятиях, в игре
Смело, четко говорим
И тихохонько сидим.
Ну-ка, проверь дружок,
Ты готов начать урок?
Всё ль на месте? Все в порядке
Книжка, ручка и тетрадка?
Все ли правильно сидят?
Все ль внимательно глядят?
Каждый хочет получать только лишь оценку пять.
2.Устный счёт
А сейчас посчитаем устно.
-Назовите числа в порядке возрастания:
61, 70, 68 , 62, 65, 63.
_ Посчитаем:
300 + 400 520 +4
254 – 54 738 -30
— Ребята « Книга – источник знаний»
-Что я произнесла? (пословицу, предложение)
-А как в математике мы называем такие предложения? (высказывания)
-Верно ли оно? Докажите. (книги учат жизни. много полезной информации)
— В выражении 24: 8 *9 нужно выполнить действия по порядку слева направо.
-Верно ли это высказывание? Найдите значение этого выражения.(27)
— В следующем выражении 64- 5*7 +5 сначала надо выполнить вычитание. Верно ли это высказывание. Почему? (надо выполнить сильное действие – умножение, а затем по порядку).
-Найдите значение этого выражения. (34)
3.Работа по теме урока.
А)Это дети, равенства, потому что стоит знак =.
Прочитайте тему нашего урока.
— Можете ли вы сказать, что такое числовое равенство и неравенство? (равенство ,когда стоит знак =: неравенство—знаки Б,М)
— Посмотрите на рисунок, скажите, в каком столбике записаны равенства, в каком неравенство? Почему?
— проверим (решаем по картинке)
Б) Совершенствование знаний.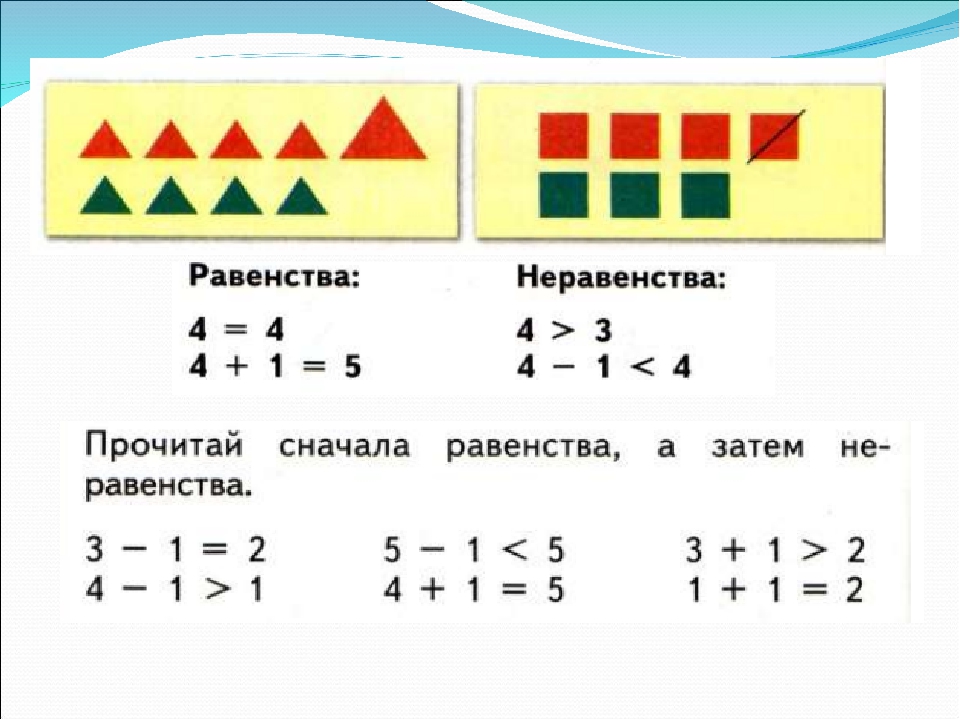
№2,стр.4
— Что мы выписали? (мы выписали верные равенства)
№3.Читаем задание.
А почему неравенства? (потому что стоят знаки сравнения)
— Что мы выписывали? (мы выписывали верные неравенства)
4.Работа в парах.
А сейчас поиграете вдвоём, со своим соседом (соседкой): вы придумайте и запишите —1 ряд (верное равенство), 2 ряд (неверное равенство).
1 ряд (неверное неравенство), 2 ряд (верное неравенство).
Молодцы
5.Физминутка
Чья пара лучше справилась с заданием? Давайте поаплодируем.
6.Самостоятельная работа
— Сейчас выполните самостоятельно №4.
-Ваша задача проверить, верна ли каждая запись?
1вариант—1столбик
2 вариант —2столбик ПРОВЕРКА.
7.Повторение пройденного материала.
— Откройте рабочие тетради на стр.4,№9 (и выполним 3-4столбик)
8.Итог урока.
Подведем итог урока
—Я познакомилась с новыми терминами: числовые равенства и неравенства.
Я понял, что равенством называют тогда, когда стоит знак =,
А неравенством- когда стоят знаки больше и меньше.
Я научилась определять, когда равенство верно, а когда неверно.
А мне понравилось, когда помогает соседка.
Ребята спасибо вам за работу на уроке, вы были моими самыми лучшими друзьями и помощниками.
9.Домашнее задание.
Стр.4(р.т.) №9(1,2 столбик)
Список литературы
Истомина Н.Б. Учимся решать комбинаторные задачи/ Н.Б. Истомина, Е.П. Виноградова. – Смоленск: Ассоциация XXI век, 2004.
Кравченко В.С. Устные упражнения по математике в 1-3 классах/ В.С. Кравченко. – М. Просвещение, 1979.
Рудницкая В.М. Математика 3 кл.: учебник для учащихся общеобразовательных учреждений: в 2 ч./В.М. Рудницкая, Т.В. Юдачева. – М.: Вентана-Граф, 2008.
Рудницкая В.М. Математика: рабочая тетрадь для 3 класса: № 2/ В.М. Рудницкая, Т.В. Юдачева. – М.: Вентана-Граф, 2008.

Энциклопедический словарь юного математика/ сост. Н.П. Ернылев. – М.: Педагогика, 1980.
Интернет-ресурсы
http://migranov.ru/photoalbum/fall/12.php
http://images.yandex.ru/yandsearch?text=смайлики веселые и грустные
*В контексте тем: | «Путешествие», «Традиции и фольклор» | ||||||
Школа: | |||||||
Дата: «____»____________20___г. | ФИО учителя: | ||||||
Класс: 1 «____» класс. | Количество присутствующих: отсутствующих: | ||||||
Тема урока: | Равенства и неравенства. | ||||||
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу): | |||||||
1.5.2.2 использовать знаки «+», «-», «≠», «=», «», « 1.2.2.1 распознавать равенство, неравенство, уравнение; различать верные и неверные равенства | |||||||
Цели урока: | Раскрыть понятия «равенство» и «неравенство»; сформировать навык различения равенства и неравенства; развивать умение записывать равенства, используя знак «=», записывать неравенства, используя знак ≠. | ||||||
Критерии успеха | К концу урока учащиеся научатся различать равенства и неравенства. | ||||||
Привитие ценностей | Ценности, основанные на национальной идее «Мәңгілік ел»: казахстанский патриотизм и гражданская ответственность; уважение; сотрудничество; труд и творчество; открытость; образование в течение всей жизни. | ||||||
Межпредметные связи | Межпредметные связи содержат перечень ссылок на другие предметы, которые имеют отношение к уроку. Разнообразные виды заданий выполняются на уроке с целью осуществления интеграции с другими предметами. Например, задачи обучения в рамках конкретного урока по предмету «Математика» можно рассмотреть через такие предметы, как «Естествознание» и «Художественный труд». | ||||||
Навыки использования ИКТ | На данном уроке учащиеся не используют ИКТ. Возможный уровень:
| ||||||
Предварительные знания | Имеющиеся представления о длине, массе, вместимости | ||||||
Ход урока | |||||||
Этапы урока | Запланированная деятельность на уроке | Ресурсы | |||||
Начало урока | Вводное задание. Если нет возможности предоставить весы каждой группе детей, ограничьтесь демонстрацией. Положите на каждую чашу весов по 3 монеты. Спросите у учащихся: Сообщите, что равновесие в математике называется равенством. Для обозначения равенства используется специальный математический знак «=» (равно). Результат записывают так: 3=3. Продолжите демонстрацию: снова положите на одну чашу весов 3 монеты. Предложите одному ученику взять из мешочка несколько монет и положить их на другую чашу весов. Спросите у учащихся:
| ||||||
Критерии успеха | Выслушайте предложения детей и сообщите, что отсутствие равновесия в математике называется неравенством. | ||||||
Середина урока | Сравни количество конфет в коробках. Обсудите с первоклассниками способ соотношения «один к одному», когда одному объекту из первого набора соответствует единственный объект из второго набора. Спросите, в каком соотношении находятся конфеты в данных наборах: равенства или неравенства. Уточните, почему они сделали такой вывод. Предложите составить и записать неравенство на листах ламинированной бумаги и продемонстрировать результат работы классу. Равенство или неравенство. Парная работа. Устные ответы следует сопроводить записью на листах ламинированной бумаги. В ходе проверки работы в парах учащиеся могут поднять свои листы как сигнал для учителя при затруднении в различении равенств и неравенств. А) 5=5 Б) 6≠9 Реши. парах и обсудить, какими способами можно разложить 12 игрушек в 2 коробки так, чтобы при первом раскладывании образовывались равенства, а при втором — неравенства. Варианты ответов дети могут записать в 2 столбика. Первый столбик — «равенства», второй столбик — «неравенства». В ходе обсуждения школьники могут обменяться результатами и выяснить, у кого получилось составить большее количество равенств и неравенств. Попробуй. Предложите учащимся оценить ситуацию с чашечными весами, которые не уравновешены. В группах они обсуждают, как привести весы в равновесие, т. е, превратить неравенство в равенство, и выступают перед классом со своими гипотезами. После обсуждения всех путей решения данной ситуации предоставьте ребятам возможность проверить теоретические предположения на практике, используя чашечные весы и муляжи фруктов или кубики при условии, что данные предметы будут одинаковыми. | Учебник: Равенства и неравенства, с. 28—29. Рабочая тетрадь: Рабочий лист 23 «Равенства и неравенства», с. 25, Рабочий лист 24 «Знаки «=» и ≠, с. 26. Ресурсы:
| |||||
Критерии успеха | Ответы а) убрать 1 яблоко слева или доложить 1 яблоко на правую сторону весов; б) переложить 1 яблоко с левой чаши весов на правую или добавить на правую сторону 2 яблока (или убрать слева 2 яблока). | ||||||
Конец урока | Для закрепления ключевых слов проведите игру. Разделите класс на группы по 4 или 6 человек. По команде ведущего «Равенство!» участники игры внутри групп должны разделиться на равные подгруппы. Например, по 2 или по 3 человека. По команде ведущего «Неравенство!» дети в группах делятся на неравные подгруппы. | ||||||
Критерии успеха | Например, если в группе 4 человека, они делятся на 1 и 3. Если в группе 6 человек, то возможны варианты: 2 и 4, 1 и 5. | ||||||
Дифференциация Каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися? | Оценивание Как Вы планируете проверить уровень усвоения материала учащимися? Используйте данный раздел для записи методов, которые Вы будете использовать для оценивания того, чему учащиеся научились во время урока. | Здоровье и соблюдение техники безопасности Здоровьесберегающие технологии. Используемые физминутки и активные виды деятельности. | |||||
Дополнительные задания Найди на рисунках равенства. Учащиеся должны выбрать картинки с равенствами и раскрасить цветным карандашом любого цвета кружок рядом с изображением. Справа от изображения с равенством нужно записать его числовой эквивалент. Ответы а) равенство 2 = 2; б) неравенство 3≠4; в) равенство 4 = 4. Расставь знаки. Цель задания — сравнить пары групп объемных фигур под буквами а) и б) и поставить между ними знак равенства или неравенства. Под картинкой нужно записать соответствующее ей числовое выражение. Для дифференциации предназначена вторая часть задания, под буквами в) и г). Ответы а) 8 = 8; б) 5 ≠ 6. | Чтобы выявить уровень овладения знаниями по данной теме, предложите им следующие вопросы и задания:
У Гульмиры 5 книг о животных, а у Светы 5 книг о приключениях. У кого больше? Составьте и назовите выражение. (Равенство: 5 = 5.) | Физкультминутка. Чтоб все выполнить заданья, | |||||
Конспект урока математики на тему: «Равенство. Неравенство» в 1 классе (УМК «Школа России»)
Технологическая карта урока математики
Технологическая карта урока математики Тема урока: Задачи с величинами цена, количество, стоимость.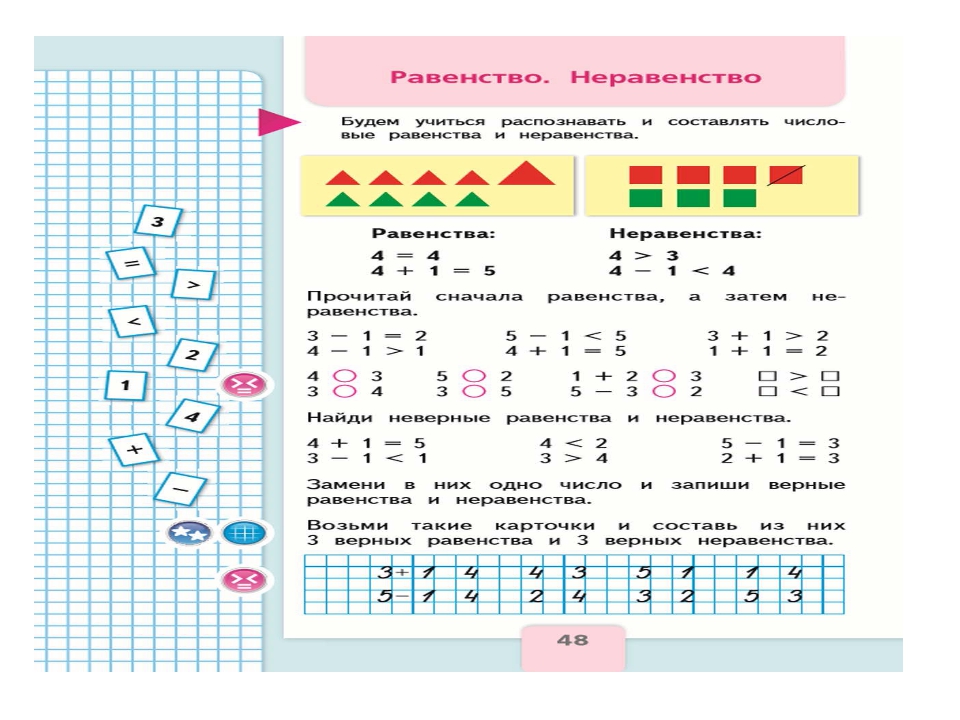 Тип урока: открытие нового знания (в технологии деятельностного метода) Класс: 2 класс Учитель: Волошина
Тип урока: открытие нового знания (в технологии деятельностного метода) Класс: 2 класс Учитель: Волошина
Цели. Планируемый результат
Тема Цели Предмет: математика Класс: 2-а класс Тип урока: Изучение нового материала. Учитель: Турайханова Г.Ф. Технологическая карта изучения темы Прямой угол. Острые и тупые углы. Угольник. Образовательные:
ПодробнееПредмет математика класс 2 г
Предмет математика класс 2 г Тема урока Место урока по теме (в разделе/главе) Закрепление изученного по теме «Умножение и деление» «Умножение и деление» 18 из 20 Тип урока Форма урока, форма учебной деятельности,
ПодробнееТехнологическая карта урока математики
Технологическая карта урока математики Изучаемая тема: Устные и письменные приемы вычисления вида 32-5, 51-27 Место урока в изучаемой теме: 5 Дата проведения: 14. 04.2017 г. Класс: 2 Программа: УМК «Перспектива»
04.2017 г. Класс: 2 Программа: УМК «Перспектива»
Технологическая карта урока математики
АДМИНИСТРАЦИЯ ГОРОДСКОГО ОКРУГА ПОДОЛЬСК КОМИТЕТ ПО ОБРАЗОВАНИЮ Муниципальное общеобразовательное учреждение «Лицей 1» (МОУ «Лицей 1») Технологическая карта урока математики Урок математики в 6 классе
ПодробнееТехнологическая карта урока
Технологическая карта урока Предмет: математика УМК «Гармония» Класс 1а Тема урока: Состав числа 8 Цель урока: рассмотреть состав числа 8 Планируемые результаты: Предметные: развить умение распознавание
ПодробнееТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА Предмет: русский язык Класс: 4 Учитель: Недодева Ольга Николаевна УМК: Перспективная начальная школа Тема урока: «Орфограммы в окончаниях глаголов: безударные личные окончания»
ПодробнееТехнологическая карта урока
Технологическая карта урока ФИО Попенкова Татьяна Сергеевна КЛАСС 3 УМК «Начальная школа XXI век» ПРЕДМЕТ Математика ТЕМА Умножение многозначного числа на двузначное.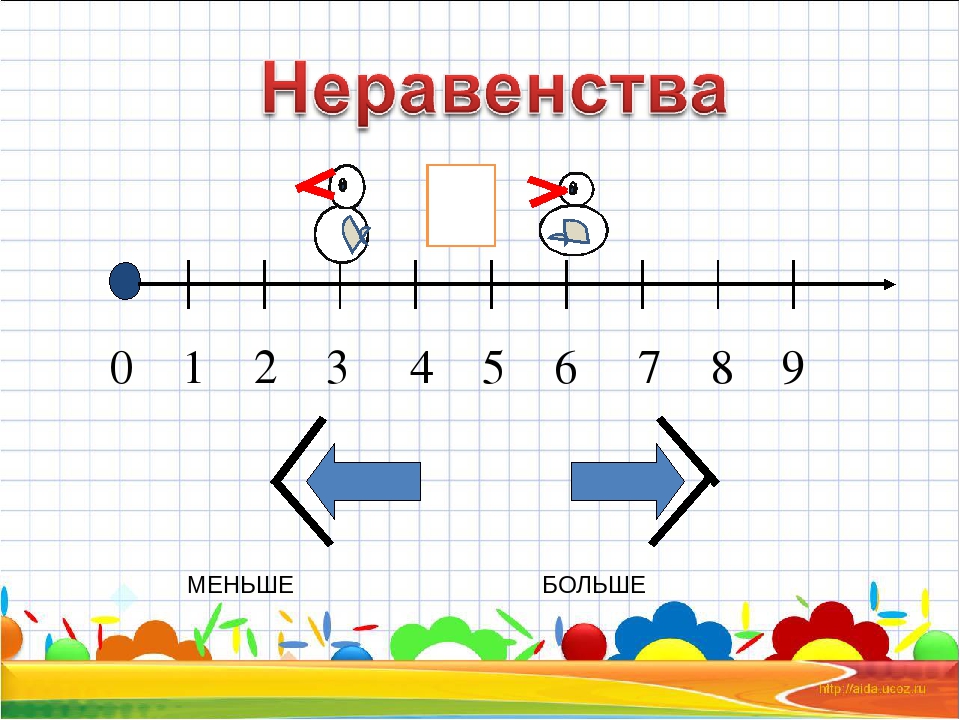 ТИП Урок открытия нового знания. ЦЕЛЬ
ТИП Урок открытия нового знания. ЦЕЛЬ
Технологическая карта урока математики.
Технологическая карта урока математики. Андреева Надежда Николаевна Тема урока «Умножение десятичных дробей на натуральное число» (5 класс) Цели (задачи) урока образовательные: Формировать умения выполнять
ПодробнееВершинина Анна Владимировна
МБОУ «СОШ 76» Урок математики ( 27) Сложение и вычитание в пределах 100. Образовательная программа: Материально-техническое обеспечение: Тип урока: Цель: Задачи: Формируемые УУД: Вершинина Анна Владимировна
ПодробнееТехнологическая карта урока
Технологическая карта урока Ф.И.О. Ковалева Юлия Сергеевна Предмет: Математика Класс: 5 класс Автор УМК: Математика 5 класс: учебник для общеобразовательных учреждений А. Г. Мерзляк и др. Тема урока: Сложение
Г. Мерзляк и др. Тема урока: Сложение
Открытый урок по математике в 1 классе.
Автор: Матющенко М.А., учитель начальных классов Предмет: Математика Класс: 1 класс Тип урока: урок изучения новой темы Открытый урок по математике в 1 классе. Оборудование: учебник «Математика» (Дорофеев
ПодробнееКонспект урока математики
Конспект урока математики Класс: 1а ГБОУ СОШ 185 с углублённым изучением английского языка Учитель: Федотова Н. Н. Тема урока: «Задачи в два действия» Цель урока: познакомить с составными задачами, состоящими
ПодробнееТехнологическая карта урока по геометрии
Технологическая карта урока по геометрии Автор: Турукина Светлана Ивановна, учитель математики, МБОУ «СОШ 6» города Обнинска Предмет: Геометрия Класс: 9 класс Тип урока: урок «открытия нового знания» Тема:
Подробнеедействия деятельности
Технологическая карта урока Предмет алгебра Класс 9 Автор УМК Алгебра 9 класс. Учебник для учащихся общеобразовательных учреждений / С.М.Никольский, М.Н. Потапов, Н.Н.Решетников, А.В. Шевкин Москва «Просвещение»
Учебник для учащихся общеобразовательных учреждений / С.М.Никольский, М.Н. Потапов, Н.Н.Решетников, А.В. Шевкин Москва «Просвещение»
Технологическая карта урока
Технологическая карта урока Учитель: Кривцовой О. И. Класс: 2 «Б» УМК: «Школа России» Предмет: математика. Тема урока: Периметр прямоугольника. Вычисление периметра. урока: урок открытия новых знаний Место
ПодробнееТехнологическая карта урока
Технологическая карта урока Учитель: Марахина Ольга Анатольевна Предмет: алгебра 7 класс УМК: А.Г. Мордкович, Алгебра 7 класс Тема урока: Взаимное расположение графиков линейных функций Тип урока: изучение
ПодробнееТехнологическая карта урока
Технологическая карта урока Учитель: Можаева Т.П., учитель нач. классов 1 квалификационной категории Предмет: русский язык Класс: 4 Тип урока: обобщение и закрепление знаний Тема: «Падежные окончания имён
ПодробнееПояснительная записка
Пояснительная записка Данный урок является уроком открытия нового знания по теме «Свойства степени с натуральным показателем», расширяющий кругозор учащихся. Урок может быть проведён учителем, работающим
Урок может быть проведён учителем, работающим
Конспект урока во 2 классе
Конспект урока во 2 классе Тема: Вычитание двузначных чисел с переходом через разряд Цель: Знакомство с приемами вычитания двузначного числа из двузначного с переходом через разряд Задачи: — познакомить
ПодробнееРешайте неравенства — 2-й класс по математике
Научитесь решать неравенства
Вы помните, что означает знак равно ?
=
👉 Он говорит нам, что обе части уравнения имеют одинаковое значение.
Что делать, если две стороны уравнения не имеют одинакового значения?
Мы можем использовать специальный символ, чтобы показать это!
Жадный аллигатор
Это жадный аллигатор. Он настолько жаден, что всегда выбирает большее число .
Он настолько жаден, что всегда выбирает большее число .
Мы знаем, что 5 больше 3.
Мы используем символ больше чем:
Вот еще несколько примеров, когда больше :
6> 2
6 больше 2
4> 1
4 больше 1
7> 3
7 больше 3
Есть еще один символ, когда левое число на меньше справа.
Только подумайте о Жадном Аллигаторе! Он всегда откроет рот большему числу!
Это означает, что 2 меньше 7.
Это символ меньше чем.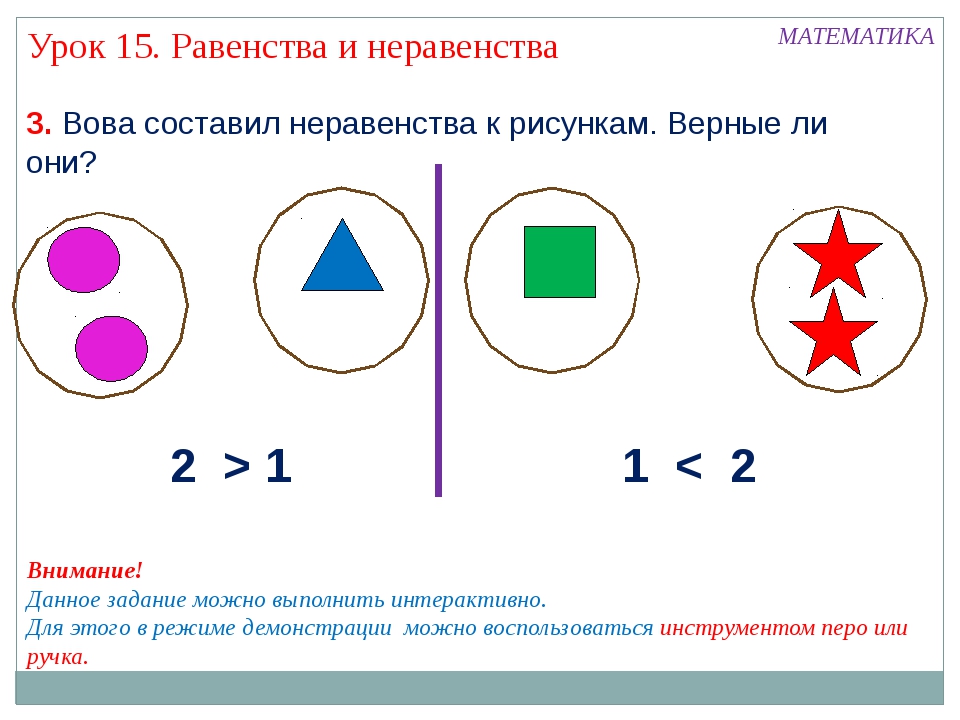
Вот еще несколько примеров, где на меньше:
2 <6
2 менее 6
1 <4
1 меньше 4
3 <7
3 меньше 7
Устранение неравенств
Еще вас попросят заполнить отсутствующий знак!
Какой знак завершает это неравенство?
Поскольку 5 на больше 1, мы используем знак больше .
Теперь попробуйте неравенство с задачей сложения:
🌟 Сначала складываем, чтобы вычислить, что 5 + 1 = 6.
5 — меньше 6
Мы используем знак меньше , чтобы завершить это неравенство.
Вы поняли!
Смотри и учись
Поздравляем, вы научились решать неравенств! 🤗 Теперь попробуйте практиковаться.
Устранение неравенств — объяснения и примеры
Что такое неравенство в математике?
Слово неравенство означает просто математическое выражение, в котором стороны не равны друг другу.По сути, неравенство сравнивает любые два значения и показывает, что одно значение меньше, больше или равно значению на другой стороне уравнения.
Как правило, для представления уравнений неравенства используются пять символов неравенства.
Символы неравенства
Эти символы неравенства: меньше ( <), больше (> ), меньше или равно ( ≤ ), больше или равно ( ≥ ) и символ неравенства ( ≠ ) .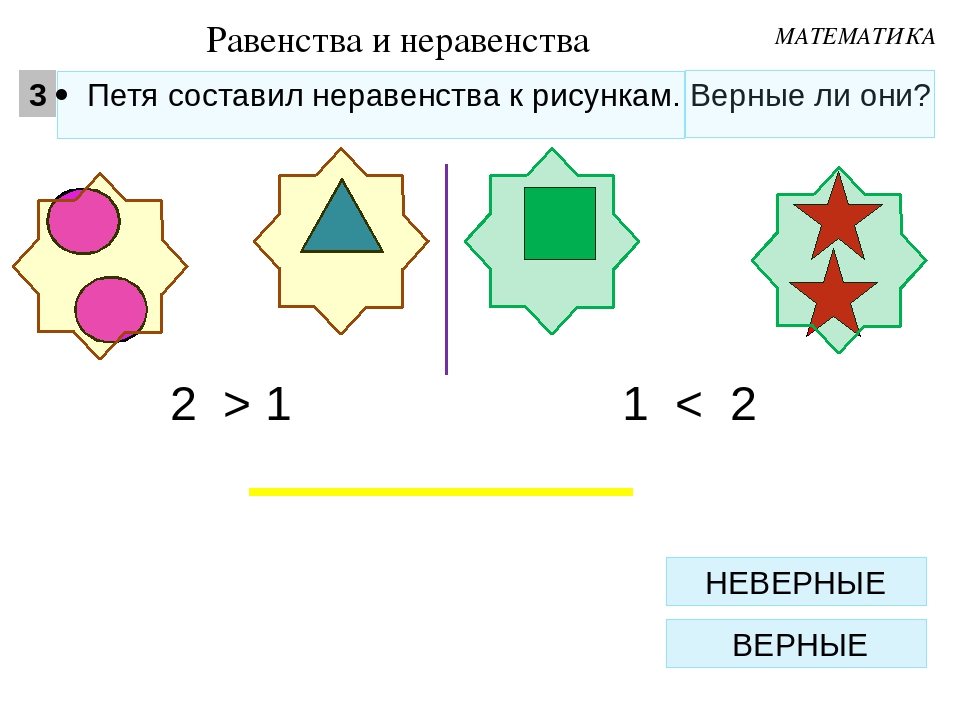
Неравенства используются для сравнения чисел и определения диапазона или диапазонов значений, которые удовлетворяют условиям данной переменной.
Операции с неравенствами
Операции с линейными неравенствами включают сложение, вычитание, умножение и деление. Общие правила этих операций показаны ниже.
Хотя мы использовали символ <для иллюстрации, следует отметить, что те же правила применяются к>, ≤ и ≥.
- Символ неравенства не меняется, когда одно и то же число добавляется к обеим сторонам неравенства.Например, если a
- Вычитание обеих частей неравенства на одно и то же число не меняет знака неравенства. Например, если a
- Умножение обеих частей неравенства на положительное число не меняет знака неравенства. Например, если a
- Разделение обеих сторон неравенства на положительное число не меняет знака неравенства. Если a
- Умножение обеих сторон уравнения неравенства на отрицательное число изменяет направление символа неравенства.
 Например, если a b *
Например, если a b *- Аналогичным образом, разделение обеих сторон уравнения неравенства на отрицательное число изменяет символ неравенства. Если a b / c
- Вычитание обеих частей неравенства на одно и то же число не меняет знака неравенства. Например, если a
Как устранить неравенства?
Неравенства, как и линейные уравнения, можно решить, применяя аналогичные правила и шаги, за некоторыми исключениями. Единственная разница при решении линейных уравнений — это операция умножения или деления на отрицательное число.Умножение или деление неравенства на отрицательное число изменяет символ неравенства.
Линейные неравенства могут быть решены с помощью следующих операций:
- Сложение
- Вычитание
- Умножение
- Деление
- Распределение собственности
Решение линейных неравенств с помощью сложения
, чтобы увидеть ниже несколько примеров это понятие.
Пример 1
Решите 3x — 5 ≤ 3 — x.
Решение
Начнем с добавления обеих сторон неравенства на 5
3x — 5 + 5 ≤ 3 + 5 — x
3x ≤ 8 — x
Затем сложим обе стороны на x.
3x + x ≤ 8 — x + x
4x ≤ 8
Наконец, разделите обе части неравенства на 4, чтобы получить;
x ≤ 2
Пример 2
Вычислите диапазон значений y, который удовлетворяет неравенству: y — 4 <2y + 5.
Решение
Сложите обе части неравенства на 4.
y — 4 + 4 <2y + 5 + 4
y <2y + 9
Вычтем обе части на 2y.
y — 2y <2y - 2y + 9
−y <9 Умножьте обе части неравенства на −1 и измените направление символа неравенства. y> — 9
Решение линейных неравенств с вычитанием
Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию.
Пример 3
Решите x + 8> 5.
Решение
Изолируйте переменную x, вычтя 8 из обеих сторон неравенства.
x + 8-8> 5-8 => x> −3
Следовательно, x> −3.
Пример 4
Решите 5x + 10> 3x + 24.
Решение
Вычтите 10 из обеих сторон неравенства.
5x + 10-10> 3x + 24-10
5x> 3x + 14.
Теперь вычтем обе части неравенства на 3x.
5x — 3x> 3x — 3x + 14
2x> 14
x> 7
Решение линейных неравенств с умножением
Давайте посмотрим на несколько примеров ниже, чтобы понять эту концепцию.
Пример 5
Решить x / 4> 5
Решение:
Умножить обе части неравенства на знаменатель дроби
4 (x / 4)> 5 x 4
x > 20
Пример 6
Решите -x / 4 ≥ 10
Решение:
Умножьте обе стороны неравенства на 4.
4 (-x / 4) ≥ 10 x 4
-x ≥ 40
Умножьте обе стороны неравенства на -1 и измените направление символа неравенства на противоположное.
x ≤ — 40
Решение линейных неравенств с делением
Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию.
Пример 7
Решите неравенство: 8x — 2> 0.
Решение
Прежде всего, сложите обе стороны неравенства на 2 9000 — 2
+ 2> 0 + 2
8x> 2
Теперь решите, разделив обе части неравенства на 8, чтобы получить;
x> 2/8
x> 1/4
Пример 8
Решите следующее неравенство:
−5x> 100
Divide both Решение сторон неравенства на -5 и измените направление символа неравенства
= −5x / -5 <100 / -5
= x <- 20
Решение линейных неравенств с использованием распределительного свойства
Давайте см. несколько примеров ниже, чтобы понять эту концепцию.
несколько примеров ниже, чтобы понять эту концепцию.
Пример 9
Решить: 2 (x — 4) ≥ 3x — 5
Решение
2 (x — 4) ≥ 3x — 5
Примените свойство распределения для удаления скобок.
⟹ 2x — 8 ≥ 3x — 5
Сложить обе стороны на 8.
⟹ 2x — 8 + 8 ≥ 3x — 5 + 8
⟹ 2x ≥ 3x + 3
Вычесть обе части на 3.
⟹ 2x — 3x ≥ 3x + 3 — 3x
⟹ -x ≥ 3
⟹ x ≤ — 3
Пример 10
Студент набрал 60 баллов за первый тест и 45 баллов во втором тесте заключительного экзамена.Сколько минимальных баллов должен набрать ученик в третьем тесте, чтобы получить в среднем 62 балла.
Решение
Пусть в третьем тесте будет получено х баллов.
(60 + 45 + x) / 3 ≥ 62
105 + x ≥ 196
x ≥ 93
Следовательно, учащийся должен набрать 93 балла, чтобы поддерживать среднее значение не менее 62 баллов.
Пример 11
Джастину требуется не менее 500 долларов на празднование дня рождения.Если он уже накопил 150 долларов, до этой даты осталось 7 месяцев. Какую минимальную сумму он должен откладывать ежемесячно?
Решение
Пусть минимальная ежемесячная экономия = x
150 + 7x ≥ 500
Решите для x
150-150 + 7x ≥ 500-150
x ≥ 50
Следовательно, Джастин должен экономить 50 долларов и более
Пример 12
Найдите два последовательных нечетных числа, которые больше 10 и имеют сумму меньше 40.
Решение
Пусть меньшее нечетное число = x
Следовательно, следующее число будет x + 2
x> 10 ………. больше 10
x + (x + 2) <40 …… сумма меньше 40
Решите уравнения.
2x + 2 <40
x + 1 <20
x <19
Объедините два выражения.
10 Следовательно, последовательные нечетные числа следующие: 11 и 13, 13 и 15, 15 и 17, 17 и 19. Лучшим инструментом для представления и визуализации чисел является числовая линия. Числовая линия определяется как прямая горизонтальная линия с числами, расположенными на равных отрезках или интервалах. У числовой прямой есть нейтральная точка в середине, известная как начало координат. Справа от начала координат на числовой прямой находятся положительные числа, а слева от начала координат — отрицательные числа. Линейные уравнения также могут быть решены графическим методом с использованием числовой прямой.Например, чтобы построить x> 1 на числовой прямой, вы просто обведите цифру 1 на числовой прямой и проведете линию, идущую от круга в направлении чисел, которые удовлетворяют утверждению о неравенстве. Пример 13 Если символ неравенства больше или равен или меньше или равен знаку (≥ или ≤), нарисуйте круг над числовым числом и заполните или заштрихуйте круг. Пример 14 x ≥ 1 Та же процедура используется для решения уравнений, включающих интервалы. Пример 15 –2 < x <2 Пример 16 –1 ≤ –1 Неравенства и числовая линия
 Наконец, проведите линию, идущую от заштрихованного круга в направлении чисел, которые удовлетворяют уравнению неравенства.
Наконец, проведите линию, идущую от заштрихованного круга в направлении чисел, которые удовлетворяют уравнению неравенства.
Пример 17
–1 < x ≤ 2
Практические вопросыРешите следующие неравенства и представьте свой ответ на числовой прямой.
- 2x> 9
- x + 5> 13
- −3x <4
- 7x + 11> 2x + 5
- 2 (x + 3)
- — 5 ≤ 2x — 7 ≤ 1
- 4x — 8 ≤ 12
Ответы
- x> 9/2
- x> 8
- x> −4/3
- x> −6/5
- x <−5.

- 1 ≤ x ≤ 4.
- x ≤ 5
Математика для 6-го класса — Блок 6: Уравнения и неравенства
Сводка по установке
В Блоке 6 шестиклассники переходят от выражений к уравнениям и неравенствам.Они пересматривают знакомые диаграммы, такие как ленточные диаграммы, для моделирования уравнений, и они открывают новые модели, такие как весы и подвесные мобильные. Учащиеся изучают, что значит быть решением уравнения или неравенства и как использовать уравнения и неравенства для моделирования взаимосвязей между величинами. При использовании уравнения или неравенства для представления ситуаций реального мира учащиеся должны деконтекстуализировать ситуацию, чтобы представить ее с помощью переменных и символов, а затем реконструировать текст, чтобы интерпретировать то, что их ответ означает в отношении данной ситуации (MP.2). В этом модуле учащиеся объединяют концепции из трех областей: соотношения и пропорции, чувство числа и выражения и уравнения. Они повторно посещают проценты из Блока 2 и решают процентные задачи с помощью уравнений. Они изучают взаимосвязи между различными количествами и, при необходимости, используют свои соображения относительно соотношения. Замечание о беглости речи: решение уравнений дает учащимся хорошую возможность продолжить развитие и продемонстрировать свободное владение десятичными операциями и дробным делением.Некоторые проблемы связаны с вычислениями с десятичными знаками и делением на дроби; по мере необходимости включать дополнительные задачи в практику для студентов.
Они повторно посещают проценты из Блока 2 и решают процентные задачи с помощью уравнений. Они изучают взаимосвязи между различными количествами и, при необходимости, используют свои соображения относительно соотношения. Замечание о беглости речи: решение уравнений дает учащимся хорошую возможность продолжить развитие и продемонстрировать свободное владение десятичными операциями и дробным делением.Некоторые проблемы связаны с вычислениями с десятичными знаками и делением на дроби; по мере необходимости включать дополнительные задачи в практику для студентов.
В этом модуле учащимся поддерживаются некоторые предыдущие навыки. В пятом классе ученики анализировали закономерности и отношения, когда изучали стандарт 5.OA.3. Они также наблюдали, что произошло, когда эти отношения были нанесены на координатную плоскость. В предыдущих разделах шестого класса ученики изучали алгебраические и числовые выражения и наборы эквивалентных соотношений.В этом модуле учащиеся используют все эти концепции и навыки.
В этом устройстве есть много будущих соединений со стандартами. В седьмом классе ученики будут глубоко исследовать пропорциональные отношения в форме $$ y = rx $$, понимая значение $$ r $$ как константу пропорциональности. Они дополнительно исследуют графики этих уравнений, и в восьмом классе ученики сравнят различные представления пропорциональных отношений. Студенты также будут сталкиваться со все более сложными уравнениями и неравенствами, которые предстоит решить.
Темп: 17 учебных дней (14 уроков, 2 гибких дня, 1 контрольный день)
Инструкции по корректировке темпа обучения на 2020-2021 учебный год из-за закрытия школ см. В нашем разделе «Рекомендуемые корректировки объема и последовательности занятий для 6-го класса».
Преподавание одно- и двухступенчатого неравенства
Когда я впервые увидел преподавание одно- и двухступенчатого неравенства в стандартах Common Core 6 и 7 классов, я чуть не умер. Это кажется таким абстрактным — попросить студентов решить неравенство и построить график на числовой прямой. Но затем я подумал об основах математики и о том, как неравенство действительно укоренилось в базовом числовом смысле. В начальной школе ученики сравнивают числа и часто используют утверждения о неравенстве. Это звучит примерно так:
Но затем я подумал об основах математики и о том, как неравенство действительно укоренилось в базовом числовом смысле. В начальной школе ученики сравнивают числа и часто используют утверждения о неравенстве. Это звучит примерно так:
- Какое число меньше?
- Какое число больше?
- Сколько еще нужно, чтобы числа сравнялись?
6.EE.B8 Запишите неравенство в форме x > c или x < c , чтобы представить ограничение или условие в реальной или математической задаче.Признайте, что неравенства вида x > c или x
7.EE.4 Используйте переменные для представления величин в реальной или математической задаче и создавайте простые уравнения и неравенства для решения проблем, рассуждая о величинах.
7.EE.4A Решите задачи со словами, приводящие к уравнениям вида пикселей + q = r и p ( x + q ) = r , где p , q и r — конкретные рациональные числа.
Бегло решать уравнения этих форм. Сравните алгебраическое решение с арифметическим, определяя последовательность операций, используемых в каждом подходе. Например, периметр прямоугольника равен 54 см. Его длина 6 см. Какая у него ширина?
7.EE.4B Решите проблемы со словами, приводящие к неравенствам в виде пикселей + q > r или пикселей + q < r , где p , q и r — конкретные рациональные числа.Изобразите набор решений неравенства и интерпретируйте его в контексте проблемы. Например: вам, как продавцу, платят 50 долларов в неделю плюс 3 доллара за продажу. На этой неделе вы хотите, чтобы ваша зарплата составляла не менее 100 долларов. Напишите неравенство для количества продаж, которые вам необходимо совершить, и опишите решения .
Ниже я изложил несколько идей и вещей, которые следует учитывать при планировании обучения одно- и двухступенчатому неравенству.
Фирменный фундамент выражений и их свойства
Чтобы решать неравенства, учащиеся должны иметь прочный фундамент выражений и различных математических свойств. Я знаю, что это огромная борьба! Фактически, даже будучи учителем, мне действительно приходилось думать о различных свойствах и сохранять их все в порядке.
Я знаю, что это огромная борьба! Фактически, даже будучи учителем, мне действительно приходилось думать о различных свойствах и сохранять их все в порядке.
Я не думаю, что этот урок должен быть чрезвычайно формальным, и я бы не стал предлагать модели Фрейера с разными свойствами. Тем не менее, я бы предложил практическое применение, чтобы убедиться, что студенты действительно понимают, почему 3x и 4x можно комбинировать, а 3x и 3 — нет. В моем классе это включало использование плиток алгебры для представления различных терминов и много работы с выражениями, прежде чем переходить к уравнениям и неравенствам.
Может читать заявление о неравенстве
Еще одно большое заблуждение, которое я обнаружил, — это «аллигатор». Конечно, «аллигатор ест большее число» работает, когда вы сравниваете 3 и 7, но что насчет того, когда это -3 и -7 или 4x и 6? Учащиеся должны уметь прочитать заявление о неравенстве и объяснить его значение с помощью цифр вокруг него. Им нужно чувствовать себя уверенно, выбирая число для x, чтобы проверить неравенство.
Им нужно чувствовать себя уверенно, выбирая число для x, чтобы проверить неравенство.
Использование числовых строк
Я знаю, что виновен в том, что учу студентов решать проблемы неравенства, а затем, в конце концов, просто говорю студентам строить его график.Может показаться, что график — это еще одна вещь, которую нужно сделать, но на самом деле решение и размышления лежат внутри графика. Числовая линия — это идеальный наглядный материал, чтобы на самом деле побудить учащихся рассказать о решении и его значении. Некоторые вопросы для размышления учащихся:
- Какое значение x содержится в наборе решений? Есть другой?
- Почему _____ не является решением проблемы неравенства? Какие еще цифры не были бы решением?
- Опишите процесс построения графика решения.
- Какое утверждение о неравенстве лучше всего описывает этот график?
Распространенные заблуждения
- Забыв поменять знак неравенства при делении на отрицательное число
- Общая путаница, когда ответ «4> x» или написано с константой слева
- Непонятно, какое число считается решением проблемы
- Невозможно установить связь между неравенством и фактическим решением в числовой строке
- Написание утверждений о неравенстве в ситуациях, когда термины «меньше чем» или «больше чем» не включены
Якорные диаграммы Идеи
Якорные диаграммы — отличный способ визуально продемонстрировать содержание, чтобы студенты могли сослаться на него. Их можно легко создать перед уроком или во время преподавания, в зависимости от содержания. Этот пример включает упор на словарный запас, поскольку ученики, как правило, борются с неравенством в написании.
Их можно легко создать перед уроком или во время преподавания, в зависимости от содержания. Этот пример включает упор на словарный запас, поскольку ученики, как правило, борются с неравенством в написании.
ИДЕЙ ДЛЯ БОРЬБЫ УЧАЩИХСЯ
- Вынесите манипуляторы — плитки алгебры, блоки шаблонов и т. Д. — попросите учащихся сгруппировать предметы
- Разбейте шаги в простой контрольный список
- Вернитесь к положительным целым числам, чтобы увидеть, испытывают ли учащиеся трудности с концепцией или математическими навыками
- Предложите учащимся возможное решение и попросите их работать в обратном направлении
Надеюсь, это даст вам некоторые идеи для обучения одно- и двухступенчатому неравенству или даже понимание того, с какими знаниями приходят ваши ученики.Я хотел бы услышать другие замечательные занятия или идеи, которые вы использовали! Не стесняйтесь делиться в комментариях.
Обязательно ознакомьтесь с этими различными концепциями и упражнениями, которые включены в мои Блоки по уравнениям и неравенствам для 6-х классов и Пакет действий, Блок по неравенствам в 7-м классе и Пакет действий.
Решение линейных неравенств | Уравнения и неравенства
4.7 Решение линейных неравенств (EMA3H)
Линейное неравенство похоже на линейное уравнение в том, что наибольший показатель степени переменной равен \ (\ text {1} \).Ниже приведены примеры линейных неравенств.
\ begin {align *} 2x + 2 & \ le 1 \\ \ frac {2 — x} {3x + 1} & \ ge 2 \\ \ frac {4} {3} x — 6 & <7x + 2 \ end {выровнять *} Методы, используемые для решения линейных неравенств, аналогичны тем, которые используются для решения линейных уравнений. Единственная разница возникает при умножении или делении со знаком минус.Например, мы знаем, что \ (8> 6 \). Если обе части неравенства разделить на \ (- \ text {2} \), то мы получим \ (- 4> -3 \), что неверно. Следовательно, знак неравенства нужно поменять местами, чтобы получить \ (- 4 <-3 \).
Чтобы сравнить неравенство с нормальным уравнением, мы сначала решим уравнение.
Решить \ (2x + 2 = 1 \):
\ begin {align *} 2х + 2 & = 1 \\ 2x & = 1-2 \\ 2x & = -1 \\ х & = — \ frac {1} {2} \ end {выровнять *}Если представить этот ответ в числовой строке, получим:
Теперь решим относительно \ (x \) в неравенстве \ (2x + 2 \ le 1 \):
\ begin {align *} 2x + 2 & \ le 1 \\ 2x & \ le 1-2 \\ 2x & \ le -1 \\ х & \ le — \ frac {1} {2} \ end {выровнять *}Если представить этот ответ в числовой строке, получим:
Мы видим, что для уравнения существует только одно значение \ (x \), для которого уравнение верно. Однако для неравенства существует диапазон значений, для которых неравенство верно. В этом главное отличие уравнения от неравенства.
Однако для неравенства существует диапазон значений, для которых неравенство верно. В этом главное отличие уравнения от неравенства.
Помните: , когда мы делим или умножаем обе стороны неравенства на отрицательное число, направление неравенства меняется. Например, если \ (x <1 \), то \ (- x> -1 \). Также обратите внимание, что мы не можем делить или умножать на переменную.
Следующее видео знакомит с линейными неравенствами.
Видео: 2FGH
Обозначение интервалов (EMA3J)
Примеры:
\ (\ left (4; 12 \ right) \) | Круглые скобки указывают на то, что номер не включен. Этот интервал включает в себя все действительные числа, большие, но не равные \ (\ text {4} \) и меньшие, но не равные \ (\ text {12} \). |
\ (\ left (- \ infty; -1 \ right) \) | Круглые скобки всегда используются для положительной и отрицательной бесконечности.Этот интервал включает все действительные числа, меньшие, но не равные \ (- \ text {1} \). |
\ (\ left [1; 13 \ right) \) | Квадратная скобка означает, что номер включен. Этот интервал включает все действительные числа, большие или равные \ (\ text {1} \) и меньшие, но не равные \ (\ text {13} \). |
Важно отметить, что это обозначение может использоваться только для представления интервала действительных чисел.
Представим приведенный выше ответ в обозначении интервалов как \ (\ left (- \ infty; — \ frac {1} {2} \ right] \)
Рабочий пример 17: Решение линейных неравенств
Решить относительно \ (r \):
\ [6 — r> 2 \]Представьте ответ в числовой строке и в виде интервалов.
Переставьте и решите для \ (r \)
\ begin {align *} -r &> 2-6 \\ -r &> -4 \ end {align *}Умножить на \ (- \ text {1} \) и отменить знак неравенства
\ [г <4 \]Изобразите ответ в числовой строке
Представьте ответ в виде интервалов
\ [\ влево (- \ infty; 4 \ вправо) \]Рабочий пример 18: Решение линейных неравенств
Решить относительно \ (q \):
\ [4q + 3 Представьте ответ в числовой строке и в виде интервалов.
Раскладной кронштейн
\ begin {align *} 4q + 3 & <2 (q + 3) \\ 4q + 3 & <2q + 6 \ end {align *}Переставьте и решите для \ (q \)
\ begin {align *} 4q + 3 & <2q + 6 \\ 4q - 2q & <6 - 3 \\ 2q & <3 \ end {align *}Разделите обе стороны на \ (\ text {2} \)
\ begin {align *} 2q & <3 \\ д & <\ frac {3} {2} \ end {align *}Представьте ответ в числовой строке
Представьте ответ в виде интервалов
\ (\ left (- \ infty; \ frac {3} {2} \ right) \)Рабочий пример 19: Решение сложных линейных неравенств
Решите относительно \ (x \):
\ [5 \ le x + 3 Представьте ответ в числовой строке и в интервальной записи.
Вычтем \ (\ text {3} \) из всех частей неравенства
\ [\ begin {array} {ccccc} 5 — 3 & \ le & x + 3 — 3 & <& 8 - 3 \\ 2 & \ le & x & <& 5 \ конец {массив} \]Изобразите ответ в числовой строке
Представьте ответ в виде интервалов
\ (\ left [2; 5 \ right) \)Вы можете это сделать! Позвольте нам помочь вам учиться с умом для достижения ваших целей.Siyavula Practice направит вас в удобном для вас темпе, когда вы задаете вопросы в Интернете.
Зарегистрируйтесь, чтобы улучшить свои оценки Упражнение 4.6\ (x <-1 \ text {и} x \ ge 6; x \ in \ mathbb {R} \)
\ (3 <х <6; х \ в \ mathbb {R} \)
\ (x \ neq 3; x \ neq 6; x \ in \ mathbb {R} \)
\ (х> -10; х \ в \ mathbb {R} \)
\ begin {align *} 3х + 4 &> 5х + 8 \\ 3х — 5х &> 8 — 4 \\ -2x> 4 \\ 2xОбозначается в числовой строке:
В интервальном обозначении: \ ((- \ infty; -2) \)
\ (3 (x — 1) — 2 \ le 6x + 4 \)
\ begin {align *} 3 (x — 1) — 2 & \ le 6x + 4 \\ 3x — 5 & \ le 6x + 4 \\ 3х — 6х & \ ле 4 + 5 \\ -3x \ le 9 \\ х \ ge — \ frac {9} {3} \\ х \ ge -3 \ end {выровнять *}Обозначается в числовой строке:
В интервальном обозначении: \ ([- 3; \ infty) \)
\ (\ dfrac {x — 7} {3}> \ dfrac {2x — 3} {2} \)
\ begin {align *} \ frac {x — 7} {3} &> \ frac {2x — 3} {2} \\ 2 (х — 7) &> 3 (2x — 3) \\ 2х — 14> 6х — 9 \\ -4x> 5 \\ xОбозначается в числовой строке:
В интервальном обозначении: \ ((- \ infty; — \ frac {5} {4}) \)
\ begin {align *} -4 (x — 1) & \ frac {2} {5} \ end {выровнять *}Обозначается в числовой строке:
В интервальном обозначении: \ ((\ frac {2} {5}; \ infty) \)
\ (\ dfrac {1} {2} x + \ dfrac {1} {3} (x — 1) \ ge \ dfrac {5} {6} x — \ dfrac {1} {3} \)
\ begin {align *} \ frac {1} {2} x + \ frac {1} {3} (x — 1) & \ ge \ frac {5} {6} x — \ frac {1} {3} \\ \ frac {1} {2} x + \ frac {1} {3} x — \ frac {1} {3} & \ ge \ frac {5} {6} x — \ frac {1} {3} \ \ \ frac {1} {2} x + \ frac {1} {3} x — \ frac {5} {6} x & \ ge \ frac {1} {3} — \ frac {1} {3} \ \ \ frac {3} {6} x + \ frac {2} {6} x — \ frac {5} {6} x & \ ge 0 \\ 0x \ ge 0 \ end {выровнять *} Неравенство верно для всех действительных значений \ (x \).
Обозначается числовой строкой:
В интервальном обозначении: \ ([- 1; 4) \)
\ [\ begin {array} {ccccc} -5 &Обозначается в числовой строке:
В интервальном обозначении: \ ((- 1; 5] \)
\ (7 (3x + 2) — 5 (2x — 3)> 7 \)
\ begin {align *} 7 (3x + 2) — 5 (2x — 3) &> 7 \\ 21х + 14 — 10х + 15 &> 7 \\ 11x &> -22 \\ х &> -2 \ end {выровнять *}Обозначается в числовой строке:
В интервальном обозначении: \ ((- 2; \ infty) \)
\ (\ dfrac {5x — 1} {- 6} \ ge \ dfrac {1 — 2x} {3} \)
\ begin {align *} \ frac {5x — 1} {- 6} & \ ge \ frac {1 — 2x} {3} \\ 5x — 1 & \ ge -2 (1 — 2x) \\ 5x — 1 & \ ge -2 + 4x \\ 5x — 4x & \ ge -1 \\ х & \ ge -1 \ end {выровнять *}Обозначается в числовой строке:
В интервальном обозначении: \ ([- 1; \ infty) \)
\ [\ begin {array} {ccccc} 3 & \ le & 4 — х & \ le & 16 \\ -1 & \ le & -x & \ le & 12 \\ 1 & \ ge & x & \ ge & -12 \ конец {массив} \]Обозначается в числовой строке:
В интервальном обозначении: \ ([1; 12] \)
\ (\ dfrac {-7y} {3} — 5> -7 \)
\ begin {align *} \ frac {-7y} {3} — 5 &> -7 \\ -7л — 15 &> -21 \\ -7лет &> -6 \\ y &Обозначается в числовой строке:
В интервальном обозначении: \ ((- \ infty; \ frac {6} {7}) \)
\ [\ begin {array} {ccccc} 1 & \ le & 1-2y & & -4 \\ -4 &Обозначается в числовой строке:
В интервальном обозначении: \ ((- 4; 0] \)
\ (- 2 <\ dfrac {x - 1} {- 3} <7 \)
\ [\ begin {array} {ccccc} -2 & & x — 1 &> & -21 \\ 7 &> & x &> & -20 \\ -20 иОбозначается в числовой строке:
В интервальном обозначении: \ ((- 20; 7) \)
\ begin {align *} 2 х -1 & <3 (х +11) \\ 2 х -1 & <3 х +33 \\ 2 х -3 х & <33 +1 \\ -1 х & <34 \\ \ поэтому x &> -34 \ end {align *}
\ [\ влево (-34; \ infty \ вправо) \]
\ begin {align *} х -1 & <-4 (х -6) \\ х -1 & <-4 х +24 \\ х +4 х & <24 +1 \\ 5 х & <25 \\ \ поэтому x & <5 \ end {align *}
\ [\ влево (- \ infty; 5 \ вправо) \]
\ (\ dfrac {x-1} {8} \ leq \ dfrac {2 (x-2)} {3} \)
\ begin {align *} \ frac {x-1} {8} & \ leq \ frac {2 (x-2)} {3} \\ 3 (х-1) & \ leq 16 (х-2) \\ 3х-3 & \ leq 16х-32 \\ 3х -16х & \ leq -32 +3 \\ -13x & \ leq -29 \\ \ поэтому x & \ geq \ frac {29} {13} \ end {выровнять *} \ (\; x \ in \ left [\ frac {29} {13}; \ infty \ right) \).
\ (\ dfrac {x + 2} {4} \ leq \ dfrac {-2 (x-4)} {7} \)
\ begin {align *} \ frac {x + 2} {4} & \ leq \ frac {-2 (x-4)} {7} \\ 7 (х + 2) & \ leq -8 (х-4) \\ 7x + 14 & \ leq -8x + 32 \\ 7x + 8x & \ leq 32-14 \\ 15x & \ leq 18 \\ \ поэтому x & \ leq \ frac {6} {5} \ end {выровнять *}\ (\; x \ in \ left (- \ infty; \ frac {6} {5} \ right] \).
\ (\ dfrac {1} {5} x — \ dfrac {5} {4} (x + 2)> \ dfrac {1} {4} x + 3 \)
\ begin {align *} \ frac {1} {5} x — \ frac {5} {4} (x + 2) &> \ frac {1} {4} x +3 \\ 4х — 25 (х + 2) &> 5х +60 \\ 4х — 25х-50 &> 5х +60 \\ 4х — 25 х -5х &> 60 + 50 \\ -26x &> 110 \\ \ поэтому x & <- \ frac {55} {13} \ end {align *}
Интервал: \ [\ left (- \ infty; — \ frac {55} {13} \ right) \]
\ (\ dfrac {1} {5} x — \ dfrac {2} {5} (x + 3) \ geq \ dfrac {4} {2} x +3 \)
\ begin {align *} \ frac {1} {5} x — \ frac {2} {5} (x + 3) & \ geq \ frac {4} {2} x +3 \\ 2x — 4 (x + 3) & \ geq 20x +30 \\ 2х — 4 х-12 & \ geq 20x +30 \\ 2х — 4 х -20х & \ geq 30 + 12 \\ -22x & \ geq 42 \\ \ поэтому x & \ leq — \ frac {21} {11} \ end {align *}
Интервал: \ [\ left (- \ infty; — \ frac {21} {11} \ right] \]
\ (4x +3 <-3 \ quad \ text {или} \ quad 4x +3> 5 \)
Решите неравенство: \ [\ begin {array} {rclcrcl} 4x +3 & <& -3 & \ text {или} & 4x +3 &> & 5 \\ 4x & <& -3-3 & \ text {or} & 4x &> & 5-3 \\ x & <& \ frac {-3-3} {4} & \ text {или} & x &> & \ frac {5-3} {4} \\ x & <& - \ frac {3} {2} & \ text {или} & x &> & \ frac {1} {2} \\ \ end {array} \]
\ [\ left (- \ infty; — \ frac {3} {2} \ right) \ cup \ left (\ frac {1} {2}; \ infty \ right) \]
Решите неравенство: \ [\ begin {array} {rcccl} 4 & \ ge & -6x -6 & \ ge & -3 \\ 4 + 6 & \ ge & -6x & \ ge & -3 + 6 \\ \ frac {4 + 6} {- 6} & \ le & x & \ le & \ frac {-3 + 6} {- 6} \\ — \ frac {5} {3} & \ le & x & \ le & — \ frac {1} {2} \\ \ end {array} \]
\ [\ left [- \ frac {5} {3}; — \ frac {1} {2} \ right] \]
\ (6b — 3> b + 2, ~ b \ in \ mathbb {Z} \)
\ begin {align *} 6b — 3> b + 2, ~ b \ in \ mathbb {Z} \\ 5b> 5 \\ b> 1 \ end {выровнять *}\ (3a — 1 <4a + 6, ~ a \ in \ mathbb {N} \)
\ begin {align *} 3а — 1-7 \ end {выровнять *} Однако нам говорят, что \ (a \ in \ mathbb {N} \) и поэтому \ (a> 0 \).
\ (\ dfrac {b-3} {2} + 1 <\ dfrac {b} {4} - 4, ~ b \ in \ mathbb {R} \)
\ begin {align *} \ frac {b-3} {2} + 1\ (\ dfrac {4a +7} {3} — 5> a — \ dfrac {2} {3}, ~ a \ in \ mathbb {N} \)
\ begin {align *} \ frac {4a +7} {3} — 5> a — \ frac {2} {3} \\ 4а + 7-15> 3а — 2 \\ а> 6 \ end {выровнять *}Рабочих листов по неравенству
Советы по написанию неравенств для моделирования математических ситуаций
Существует множество различных ситуаций, в которых вы можете использовать свои математические навыки, чтобы лучше понять свое окружение или событие во времени.Самая важная концепция, с которой вам нужно начать, — это понимание контекста неравенства. Они помогут нам моделировать события, в которых мы не пытаемся быть точными, а пытаемся понять тенденцию данных, которую они представляют. Есть много финансовых транзакций, которые мы используем эту форму моделирования, чтобы понять, есть ли у нас достаточный или дополнительный капитал, который мы можем применить к вторичным транзакциям. Если мы посмотрим на типичную транзакцию, в которой оказывается большинство подростков, мы сможем увидеть, как это применимо.Что, если бы Джим хотел узнать, сколько часов ему нужно поработать, чтобы купить пару накладных наушников для учебы. Нам нужно знать финансовое положение Джима и сколько он зарабатывает на своей работе. Если Джим зарабатывает девять долларов в час на своей работе и накопил тридцать пять долларов, это дает нам хорошую отправную точку. Затем мы должны понять, сколько стоят эти наушники. Если включить налог, наушники будут стоить сто пятьдесят три доллара. Имея всю эту информацию, мы можем быстро создать неравенство.Сначала мы представим количество часов, которые Джиму нужно для работы, с термином 9h. 9, указывающая сумму, которую ему платят за час, и переменная h, указывающая, сколько часов ему нужно будет работать. Затем мы представляем константу, которая является суммой денег, которую он уже имеет, равной 35. Если сложить эти термины, мы получим начало нашего неравенства как: 9h + 35.
Если мы посмотрим на типичную транзакцию, в которой оказывается большинство подростков, мы сможем увидеть, как это применимо.Что, если бы Джим хотел узнать, сколько часов ему нужно поработать, чтобы купить пару накладных наушников для учебы. Нам нужно знать финансовое положение Джима и сколько он зарабатывает на своей работе. Если Джим зарабатывает девять долларов в час на своей работе и накопил тридцать пять долларов, это дает нам хорошую отправную точку. Затем мы должны понять, сколько стоят эти наушники. Если включить налог, наушники будут стоить сто пятьдесят три доллара. Имея всю эту информацию, мы можем быстро создать неравенство.Сначала мы представим количество часов, которые Джиму нужно для работы, с термином 9h. 9, указывающая сумму, которую ему платят за час, и переменная h, указывающая, сколько часов ему нужно будет работать. Затем мы представляем константу, которая является суммой денег, которую он уже имеет, равной 35. Если сложить эти термины, мы получим начало нашего неравенства как: 9h + 35. Затем мы должны представить сумму, которую он должен накопить: 153. Он необходимо иметь эту сумму денег или больше, чтобы купить наушники. Мы бы изобразили это символом, который означает, что у него есть такое же или большее количество с символом (≥).Собрав все это вместе, мы бы смоделировали транзакцию как: 9h + 35 ≥ 153. Чтобы найти количество часов, которое ему нужно для работы, нам нужно переставить его, чтобы выделить количество часов. Мы можем сделать это, убедившись, что выполняем операции с обеих сторон символа ≥. Сначала мы избавимся от константы, вычтя обе части на 35. В результате получим: 9h ≥ 118. Затем мы разделим обе части на 9. В результате получим: h ≥ 13,11. Это означает, что Джиму нужно будет работать не менее 13 лет.11 часов на покупку наушников.
Затем мы должны представить сумму, которую он должен накопить: 153. Он необходимо иметь эту сумму денег или больше, чтобы купить наушники. Мы бы изобразили это символом, который означает, что у него есть такое же или большее количество с символом (≥).Собрав все это вместе, мы бы смоделировали транзакцию как: 9h + 35 ≥ 153. Чтобы найти количество часов, которое ему нужно для работы, нам нужно переставить его, чтобы выделить количество часов. Мы можем сделать это, убедившись, что выполняем операции с обеих сторон символа ≥. Сначала мы избавимся от константы, вычтя обе части на 35. В результате получим: 9h ≥ 118. Затем мы разделим обе части на 9. В результате получим: h ≥ 13,11. Это означает, что Джиму нужно будет работать не менее 13 лет.11 часов на покупку наушников.
Факты о неравенстве для детей
Неравенство — это когда один объект равен:
- Меньше другого (означает, что a меньше b )
- Больше, чем другой (означает, что a больше, чем b )
- Не меньше другого (означает, что a не меньше b , то есть либо больше, либо равно b )
- Не больше другого (означает, что a не больше b или меньше или равно b )
Неравенство иногда используется для обозначения утверждения, что одно выражение меньше, больше, не меньше или не больше другого.
Работа с неравенствами
Неравенство 1 Это решение уравнения x + 4> 12Неравенство в математике — это когда два решения или ответа сравниваются на большее или меньшее чем. Это когда сравниваются два или еще много решений, не равных по количеству. Решить неравенство — значит найти его решения. Когда вы подставляете число в переменную и утверждение истинно, тогда это решение. Когда вы подставляете число в переменную, а утверждение неверно, число не является решением этого утверждения.
Решение неравенства — это поиск решения заданной переменной. Это нахождение относительного порядка набора. Неравенство может иметь множество решений, но обычно мы ищем только решения, так как действительные числа. Правильный способ чтения неравенства — слева направо, как и другие уравнения, но с той лишь разницей, что они имеют разные правила для каждого уравнения.
Например, рассмотрим неравенство x + 4> 12, где x — действительное число. Во-первых, нужно найти x и убедиться, что это действительно решение. Ответ будет x> 8, и это верное утверждение. Это выражение касается положения x в наборе действительных чисел. Числовая линия — это один из способов показать местоположение относительно всех других действительных чисел (см. Рисунок Неравенство 1)
Ответ будет x> 8, и это верное утверждение. Это выражение касается положения x в наборе действительных чисел. Числовая линия — это один из способов показать местоположение относительно всех других действительных чисел (см. Рисунок Неравенство 1)
Различные виды неравенства
Линейное неравенство Пример линейного неравенстваСуществует пять различных видов неравенства:
- Первый вид — это линейные неравенства, которые представляют собой неравенства, различающие выражения на меньшее или равное, меньшее или большее или равное, большее чем.Если мы заменим неравенство отношением равенства, результатом будет линейное уравнение.
- Второй вид — это комбинации неравенств, которые должны удовлетворять неравенствам. Здесь нужно сначала иметь число в наборах решений, так что числа, удовлетворяющие неравенствам, будут значениями в пересечении двух наборов решений.
- Третий вид — это неравенства, включающие абсолютные значения, что означает, что значения можно перефразировать как комбинации неравенств, включающих абсолютные значения.

- Четвертый тип неравенств называется полиномиальными неравенствами, что означает, что они непрерывны и их графики не имеют скачков или разрывов.
- И последнее, но не менее важное, это рациональные неравенства, что означает, что это форма одного полинома, деленного на другой многочлен. Другими словами, графики рациональных функций не имеют разрывов и не представлены в нулях знаменателя.
Четыре способа решения неравенств
Пример добавления неравенств.Есть четыре способа решить квадратные уравнения:
- Сложите или вычтите одинаковые числа с обеих сторон.
- Сдвиньте стороны и измените расположение знака неравенства.
- Умножьте одинаковое число с обеих сторон.
- Разделите одинаковое положительное или отрицательное число на обе стороны. пример умножения неравенства
Кроме того, для устранения неравенства потребуется два шага. Первый — это упростить, используя обратное сложение или вычитание.Второй — еще больше упростить, используя обратную величину умножения или деления. Обратите внимание, что при умножении или делении неравенства на отрицательное число символ неравенства необходимо перевернуть.
Первый — это упростить, используя обратное сложение или вычитание.Второй — еще больше упростить, используя обратную величину умножения или деления. Обратите внимание, что при умножении или делении неравенства на отрицательное число символ неравенства необходимо перевернуть.
Примеры решения неравенств
Неравенство 2 Решение уравнения -6yНеравенство — это математическое утверждение, объясняющее, что эти два значения не равны и различны. Уравнение a ≠ b означает, что a не равно b .Неравенство одинаково с любым уравнением, с той (единственной) разницей, что неравенство не использует знак равенства, а символы неравенства. Неравенство b> a означает, что b больше a. Ограничения скорости, знаки и другие используют неравенство, чтобы выразить их.
При решении неравенства человеку необходимо иметь верное утверждение. Когда вы делите или умножаете неравенство с отрицательным числом с обеих сторон, утверждение неверно. Чтобы утверждение было правильным с отрицательным числом, нужно изменить направление символа неравенства.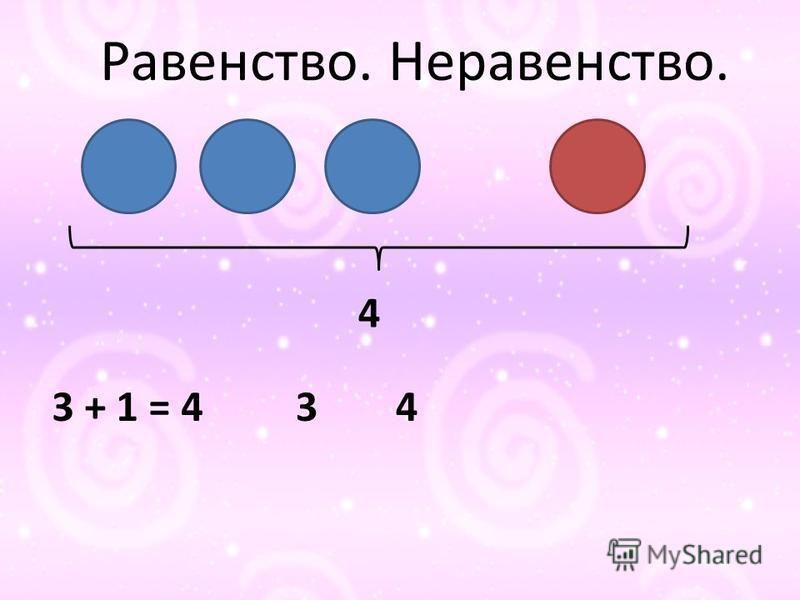 Когда число является положительным числом, переворачивать символ не нужно. Неравенство — это правдивое заявление.
Когда число является положительным числом, переворачивать символ не нужно. Неравенство — это правдивое заявление.
Например, начните с истинного утверждения -6 y <-12. Когда обе стороны разделены на -6, результат станет y <2. В этом утверждении символ необходимо перевернуть, чтобы получить истинное утверждение, которое дает y> 2 как правильный ответ. В числовой строке (см. Рисунок Неравенство 2) замкнутый заштрихованный кружок указывает на то, что он включен в набор решений.Открытый кружок указывает на то, что он не входит в набор решений.
Связанные страницы
.



 Исследовательская работа в группах. У каждой группы должны быть чашечные весы и монеты одинаковой номинальной стоимости (одинаковой массы).
Исследовательская работа в группах. У каждой группы должны быть чашечные весы и монеты одинаковой номинальной стоимости (одинаковой массы). Неравенство обозначается знаком ≠ (не равно). Результат записывается так: 3≠5.
Неравенство обозначается знаком ≠ (не равно). Результат записывается так: 3≠5. Предложите школьникам выполнить задание в
Предложите школьникам выполнить задание в

 Первоклассники продвинутого уровня могут самостоятельно составить равенство или неравенство из объемных фигур, поставить знаки равенства или неравенства между группами фигур и записать соответствующее выражение.
Первоклассники продвинутого уровня могут самостоятельно составить равенство или неравенство из объемных фигур, поставить знаки равенства или неравенства между группами фигур и записать соответствующее выражение.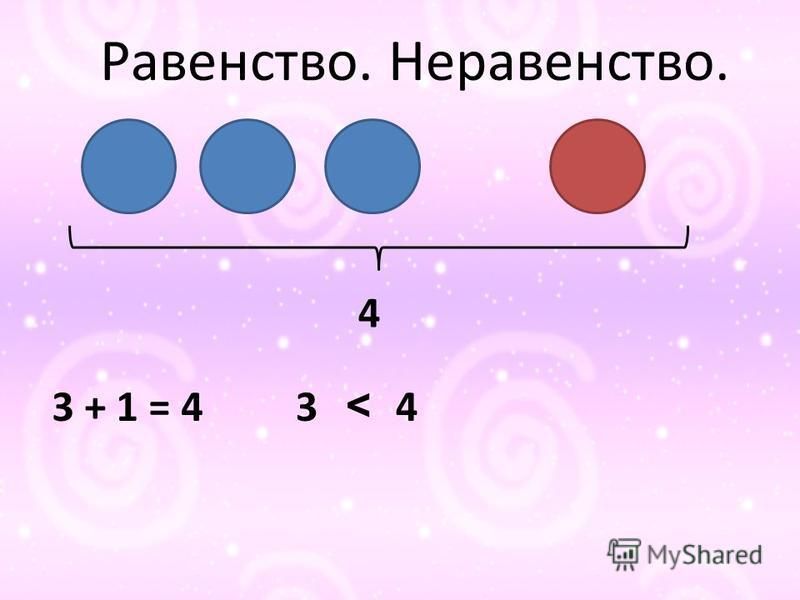
 Например, если a b *
Например, если a b *
 Бегло решать уравнения этих форм. Сравните алгебраическое решение с арифметическим, определяя последовательность операций, используемых в каждом подходе. Например, периметр прямоугольника равен 54 см. Его длина 6 см. Какая у него ширина?
Бегло решать уравнения этих форм. Сравните алгебраическое решение с арифметическим, определяя последовательность операций, используемых в каждом подходе. Например, периметр прямоугольника равен 54 см. Его длина 6 см. Какая у него ширина? 
