Центральная симметрия ℹ️ определение, свойства, построение и доказательство, пример фигур, обладающих центральной симметрией, интересные факты
Центральная симметрия – самая интересная и познавательная тема в геометрии, которую изучают в начальных классах школы и более тщательно — в 8 — 11 классах. Знания по этой теме обязательно пригодятся ученику в жизни.
Что такое центральная симметрия
Начнём с определения: центральная симметрия — одно из свойств определённой геометрической фигуры, при котором точке В соответствует некая точка В1, находящая в таком же пространственном положении относительно точки С. Точка С лежит на середине отрезка ВВ1. Точка С называется центром симметрии. Это определение соответствует курсу планиметрии.
Центральную симметрию можно построить и в пространстве. В пространстве центральной симметрией называется словно зеркальное отображение какой-либо геометрической фигуры. Она представляет собой две одинаковые фигуры, соответственные точки которых попарно симметричны относительно точки пространства О.
Свойства центральной симметрии
Основные свойства следующие:
1. Центральную симметрию называют движением, при котором соответствующие точки также остаются симметричными, то есть расстояние между ними остаётся прежним.
Посмотрим на рисунок. Треугольники АВС и А1В1С1
симметричны в пространстве относительно точки О. При каком либо преобразовании пространства сохраняются условия: АО=А
Однако если представить геометрическую фигуру в виде векторов, то при преобразовании пространства эти векторы поменяют свои направления;
2. Центральная симметрия имеет только одну центральную точку, которая является неподвижной при преобразовании пространства;
3. Если прямая проходит через центр симметрии, то она соответствует самой себе, то есть симметрична;
4. Центральная симметрия переводит прямую, не проходящую через центр симметрии, в параллельную ей прямую.
Доказывается это свойство достаточно просто. Для этого нужно построить две параллельные прямые АВ и А1В1 относительно точки О.
Далее соединяем симметричные точки и получаем отрезки АА1 и ВВ1. Далее легко заметить, что отрезки АО и А1О будут равны. Соответственно равны и отрезки ВО и В1О. Углы, которые образуются при пересечении двумя прямыми точки О также равны.
Значит, треугольники равны по двум сторонам и углу между ними. Следовательно, равны углы А,А1 и В,В1. Значит они являются накрест лежащими при секущих АА
5. При центральной симметрии отрезки симметричны отрезкам, лучи симметричны лучам, прямые симметричны прямым.
Примеры фигур, обладающих центральной симметрией
Фигур, как имеющих углы, так и без углов, но при этом обладающих центральной симметрией не так уж мало:
-
параллелограмм;
-
окружность;
-
ромб и квадрат;
-
Интересные факты о центральной симметрии
Вся окружающая нас природа – сплошная центральная симметрия. Многие растения и насекомые обладают центральной симметрией.
Практически у каждого фрукта есть своя симметрия. Например, кокос в разрезе представляет собой окружность с центром в некоторой точке.
Ещё один очевидный пример – бабочка.
Великолепные узоры на её крылышках – четкая и яркая симметрия.
Каждый знает, что видовое разнообразие морских ракушек бесконечно. Наверняка, вы сможете найти несколько как с осевой, так и центральной симметрией.
Великолепные примеры с элементами центральной симметрии можно наблюдать и в архитектуре. Потолки различных храмов и церквей украшаются орнаментами, основой которых является центральная симметрия.
Собор Парижской Богоматери имеет прекрасный, утончённый узор, основанный на центральной симметрии.
Рукодельницы в своих произведениях искусства применяют симметрию, которая заметна в удивительных и затейливых узорах.
Таким образом, центральная симметрия – основа, которая составляет природу, архитектуру и даже иногда музыку. Именно это проявление так радует человеческий глаз при появлении первых снежинок или при знакомстве с сооружениями архитектуры.
Осевая и центральная симметрия — урок. Математика, 6 класс.
Симметрия — слово греческого происхождения, как и многие другие слова, которые связаны с математикой. Оно означает соразмерность, наличие определённого порядка, закономерности в расположении частей. Смотря на объекты вокруг, мы не раз восклицаем: «Какая симметрия!»

Люди с давних времён использовали симметрию в рисунках, орнаментах, предметах быта, в архитектуре, художестве, строительстве.
Но симметрия широко распространена и в природе, где не было вмешательства человеческой руки. Её можно наблюдать в форме листьев и цветов растений, в расположении различных органов животных, в форме кристаллических тел, в порхающей бабочке, загадочной снежинке, морской звезде.

Пока рассмотрим две симметрии на плоскости: относительно точки и прямой.
Центральная симметрия
Симметрию относительно точки называют центральной симметрией.
Точки M и M1 симметричны относительно некоторой точки \(O\), если точка \(O\) является серединой отрезка MM1.

Точка \(O\) называется центром симметрии.
Алгоритм построения центрально-симметричных фигур.

Построим треугольник A1B1C1, симметричный треугольнику \(ABC\) относительно центра (точки) \(O\):
1. для этого соединим точки \(A\), \(B\), \(C\) с центром \(O\) и продолжим эти отрезки;
2. измерим отрезки \(AO\), \(BO\), \(CO\) и отложим с другой стороны от точки \(O\) равные им отрезки AO=OA1;BO=OB1;CO=OC1;
3. соединим получившиеся точки отрезками и получим треугольник A1B1C1, симметричный данному треугольнику \(ABC\).
Фигуры, симметричные относительно некоторой точки, равны.
Фигура симметрична относительно центра симметрии, если для каждой точки этой фигуры симметричная ей точка также лежит на этой фигуре. Такая фигура имеет центр симметрии (фигура с центральной симметрией).
Есть фигуры с центральной симметрией, это, например, окружность и параллелограмм. У окружности центр симметрии — это её центр, у параллелограмма центр симметрии — это точка, в которой пересекаются его диагонали. Есть очень много фигур, у которых нет центра симметрии.Осевая симметрия — это симметрия относительно проведённой прямой (оси).
Точки M и M1 симметричны относительно некоторой прямой (оси симметрии), если эти точки лежат на прямой, перпендикулярной данной, и на одинаковом расстоянии от оси симметрии.

Алгоритм построения фигуры, симметричной относительно некоторой прямой.

Построим треугольник A1B1C1, симметричный треугольнику \(ABC\) относительно красной прямой:
1. для этого проведём из вершин треугольника \(ABC\) прямые, перпендикулярные оси симметрии, и продолжим их дальше на другой стороне оси.
2. Измерим расстояния от вершин треугольника до получившихся точек на прямой и отложим с другой стороны прямой такие же расстояния.
3. Соединим получившиеся точки отрезками и получим треугольник A1B1C1, симметричный данному треугольнику \(ABC\).
Фигуры, симметричные относительно прямой, равны.
Фигура считается симметричной относительно прямой, если для каждой точки рассматриваемой фигуры симметричная для неё точка относительно данной прямой также находится на этой фигуре. Прямая является в этом случае осью симметрии фигуры.
Иногда у фигур несколько осей симметрии:
- для неразвёрнутого угла существует единственная ось симметрии — это биссектриса данного угла.
- Для равнобедренного треугольника есть единственная ось симметрии.
- Для равностороннего треугольника — три оси.
- Для прямоугольника и ромба существуют две оси симметрии.
- Для квадрата — целых четыре.
- Для окружности осей симметрии бесчисленное множество — это каждая прямая, которая проходит через центр этой фигуры.
- Есть фигуры без осей симметрии — это параллелограмм и треугольник, все стороны которого различны.
Центральная и осевая симметрии [wiki.eduVdom.com]
Центральная симметрия
Две точки А и А1 называются симметричными относительно точки О, если О — середина отрезка АА1 (рис.1). Точка О считается симметричной самой себе.
Пример центральной симметрии
Точки А и А1 – симметричные относительно точки О
Рис.1
Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией.
Примерами фигур, обладающих центральной симметрией, являются окружность и параллелограмм (рис.2).
Центральная симметрия
Фигуры, обладающие центральной симметрией
Рис.2
Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма — точка пересечения его диагоналей. Прямая также обладает центральной симметрией, однако в отличие от окружности и параллелограмма, которые имеют только один центр симметрии (точка О на рис.2), у прямой их бесконечно много — любая точка прямой является ее центром симметрии.
Осевая симметрия
Две точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему (рис.3). Каждая точка прямой а считается симметричной самой себе.
Осевая симметрия
Точки А и А1 — симметричные относительно прямой а
Рис.3
Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая а называется осью симметрии фигуры.
Примеры таких фигур и их оси симметрии изображены на рисунке 4.
Осевая симметрия
Рис.4
Заметим, что у окружности любая прямая, проходящая через ее центр, является осью симметрии.
Сравнение симметрий
Центральная и осевая симметрии
Построение треугольника (а) симметрично относительно оси (б) и точки (в)
Рис.5
Пример
Сколько всего осей симметрии имеет фигура, изображённая на рисунке?
Дополнительно
subjects/geometry/центральная_и_осевая_симметрии.txt · Последние изменения: 2013/10/12 02:02 — ¶
Центральная симметрия — это… Что такое Центральная симметрия?
Центра́льной симме́три́ей относительно точки A называют преобразование пространства, переводящее точку X в такую точку X′, что A — середина отрезка XX′. Центральная симметрия с центром в точке A обычно обозначается через , в то время как обозначение можно перепутать с осевой симметрией. Фигура называется симметричной относительно точки A, если для каждой точки фигуры симметричная ей точка относительно точки A также принадлежит этой фигуре. Точка A называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией.
Другие названия этого преобразования — симметрия с центром A. Центральная симметрия в планиметрии является частным случаем поворота, точнее, является поворотом на 180 градусов.
Формальная запись
- Пусть G — оператор центральной симметрии, точка A задана радиус-вектором , а преобразовываемая точка задается радиус-вектором . Тогда имеет место следующая формула:
Связанные определения
Если фигура переходит в себя при симметрии относительно точки A, то A называют центром симметрии этой фигуры.
Общие свойства
- В n-мерном пространстве для преобразования R, заданного последовательным отражением относительно n взаимно перпендикулярных гиперплоскостей всегда такая точка A, что R — центральная симметрия относительно A. В частности — если все n плоскостей имеют общую точку, то R — центральная симметрия относительно этой точки. Кроме того:
- В чётномерных пространствах центральная симметрия сохраняет ориентацию, а в нечётномерных — не сохраняет.
- Центральную симметрию можно представить также как гомотетию с центром A и коэффициентом −1 ().
Симметрия на прямой
В одномерном пространстве (на прямой) центральная симметрия является зеркальной симметрией.
На плоскости
На плоскости (в 2-мерном пространстве) симметрия с центром A представляет собой поворот на 180° с центром A (). Центральная симметрия на плоскости, как и поворот, сохраняет ориентацию.
В трёхмерном пространстве
Центральную симметрию в трёхмерном пространстве называют также сферической симметрией.
Её можно представить как композицию отражения относительно плоскости, проходящей через центр симметрии, с поворотом на 180° относительно прямой, проходящей через центр симметрии и перпендикулярной вышеупомянутой плоскости отражения.
В четырёхмерном пространстве
В 4-мерном пространстве центральную симметрию можно представить как композицию двух поворотов на 180° вокруг двух взаимно перпендикулярных плоскостей (перпендикулярных в 4-мерном смысле, см. Перпендикулярность плоскостей в 4-мерном пространстве), проходящих через центр симметрии.
См. также
Центральная симметрия — Википедия
Материал из Википедии — свободной энциклопедии
Не следует путать с инве́рсией — преобразованием пространства с выколотой точкой.Центра́льной симметри́ей относительно точки A называют преобразование пространства, переводящее точку X в такую точку X′, что A — середина отрезка XX′. Центральная симметрия с центром в точке A обычно обозначается через Z A {\displaystyle Z_{A}} , в то время как обозначение S A {\displaystyle S_{A}} можно перепутать с осевой симметрией. Фигура называется симметричной относительно точки A, если для каждой точки фигуры симметричная ей точка относительно точки A также принадлежит этой фигуре. Точка A называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией.
Другие названия этого преобразования — симметрия с центром A. Центральная симметрия в планиметрии является частным случаем поворота, точнее, является поворотом на 180 градусов.
Векторная запись
- Пусть G — оператор центральной симметрии, точка A задана радиус-вектором
r
A
→
{\displaystyle {\vec {r_{A}}}}
, а преобразовываемая точка задается радиус-вектором
x
→
{\displaystyle {\vec {x}}}
. Тогда имеет место следующая формула:
- G ( x → ) = 2 r A → − x → {\displaystyle G({\vec {x}})=2{\vec {r_{A}}}-{\vec {x}}}
Связанные определения
- Если фигура переходит в себя при симметрии относительно точки A, то A называют центром симметрии этой фигуры.
- При этом сама фигура называется центрально-симметричной.
Свойства
 Композиция двух центральных симметрий.
Композиция двух центральных симметрий.- В n-мерном пространстве если преобразование R является последовательным отражением относительно n взаимно перпендикулярных гиперплоскостей, то R — центральная симметрия относительно общей точки этих гиперплоскостей. Как следствие:
- В чётномерных пространствах центральная симметрия сохраняет ориентацию, а в нечётномерных — не сохраняет.
- Центральную симметрию можно представить также как гомотетию с центром A и коэффициентом −1 ( H A − 1 {\displaystyle H_{A}^{-1}} ).
- На плоскости (в 2-мерном пространстве) симметрия с центром A представляет собой поворот на 180° с центром A ( R A 180 {\displaystyle R_{A}^{180}} ). Центральная симметрия на плоскости, как и поворот, сохраняет ориентацию.
- Центральную симметрию в трёхмерном пространстве можно представить как композицию отражения относительно плоскости, проходящей через центр симметрии, с поворотом на 180° относительно прямой, проходящей через центр симметрии и перпендикулярной вышеупомянутой плоскости отражения.
- В 4-мерном пространстве центральную симметрию можно представить как композицию двух поворотов на 180° вокруг двух взаимно перпендикулярных плоскостей (перпендикулярных в 4-мерном смысле, см. Перпендикулярность плоскостей в 4-мерном пространстве), проходящих через центр симметрии.
См. также
Литература
Осевая и центральная симметрии. — Студопедия
Осевая и центральная симметрии
Симметрия (означает «соразмерность» ) — свойство геометрических объектов совмещаться с собой при определенных преобразованиях. Под «симметрией» понимают всякую правильность во внутреннем строении тела или фигуры.
Центральная симметрия — симметрия относительно точки.
Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры.
В одномерном пространстве (на прямой) центральная симметрия является зеркальной симметрией.
На плоскости ( в 2-мерном пространстве) симметрия с центром А представляет собой поворот на 180 градусов с центром А. Центральная симметрия на плоскости, как и поворот, сохраняет ориентацию.
Центральную симметрию в трёхмерном пространстве называют также сферической симметрией. Её можно представить как композицию отражения относительно плоскости, проходящей через центр симметрии, с поворотом на 180° относительно прямой, проходящей через центр симметрии и перпендикулярной вышеупомянутой плоскости отражения.
В 4-мерном пространстве центральную симметрию можно представить как композицию двух поворотов на 180° вокруг двух взаимно перпендикулярных плоскостей, проходящих через центр симметрии.
Осевая симметрия — симметрия относительно прямой.
Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая а называется осью симметрии фигуры.
Осевая симметрия имеет два определения:
— Отражательная симметрия.
В математике осевая симметрия — вид движения (зеркального отражения), при котором множеством неподвижных точек является прямая, называемая осью симметрии. Например, плоская фигура прямоугольник в пространстве осимметрична и имеет 3 оси симметрии, если это не квадрат.
— Вращательная симметрия.
В естественных науках под осевой симметрией понимают вращательную симметриею, относительно поворотов вокруг прямой. При этом тела называют осесимметричными, если они переходят в себя при любом повороте вокруг этой прямой. В этом случае, прямоугольник не будет осесимметричным телом, но конус будет.
Изображения на плоскости многих предметов окружающего нас мира имеют ось симметрии или центр симметрии. Многие листья деревьев и лепестки цветов симметричны относительно среднего стебля.
С симметрией мы часто встречаемся в искусстве, архитектуре, технике, быту. Фасады многих зданий обладают осевой симметрией. В большинстве случаев симметричны относительно оси или центра узоры на коврах, тканях, комнатных обоях. Симметричны многие детали механизмов, например зубчатые колеса.



Симметрия в архитектуре.
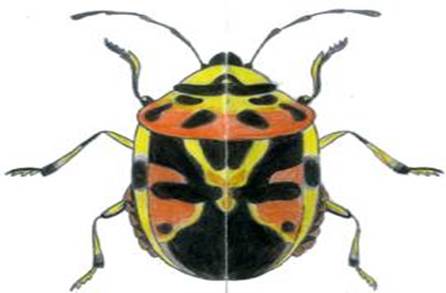

Симметрия в природе.
Симметрия в искусстве.


Осевая и центральная симметрии. Проводим урок с ЭФУ
Статьи
Линия УМК А. Г. Мерзляка. Математика (5-6)
Математика
Разберемся, как провести урок в 6 классе по теме «Осевая и центральная симметрии» с использованием ЭФУ.05 февраля 2020
- Зайдите на бесплатный сервис «Классная работа» от LECTA. В помощь учителю на сервисе «Классная работа» представлены поурочные планы по математике — календарно-тематическое планирование и методические рекомендации к каждому этапу урока. Поурочные разработки по математике содержат интерактивные материалы для изучения каждой темы и интерактивные задания для каждого урока, математические диктанты и проверочные работы для организации проверки знаний.
- Откройте ЭФУ «Математика. 6 класс» (УМК А.Г. Мерзляка). Нужная нам тема рассматривается в параграфе 44.
- Откройте в сервисе «Классная работа» поурочные разработки к этому учебнику. Тема «Осевая и центральная симметрии» рассматривается на трех занятиях — 127-129. Планы данных уроков вы можете скачать в этой статье, ко всем остальным занятием — по ссылке выше.
Повторение материала
Из курса математики 5 класса учащиеся уже узнали, как выглядят и строятся фигуры, имеющие ось симметрии. Перед изучением темы «Осевая и центральная симметрии» будет целесообразно повторить материал 5 класса. Следует разъяснить учащимся, что построение фигуры во многих случаях возможно по положению ключевых точек.
Учитель: Отрезок можно определить положением концов, треугольник — расположением вершин. Какие еще примеры вы можете назвать?
Ученики: Квадрат по 4 точкам, например… И ромб!
Учитель: Верно. Чтобы построить фигуру, которая будет симметрична нашему треугольнику или ромбу, нам необходимо отразить ее ключевые точки.
Для закрепления этого интуитивно-наглядного понимания, учитель может предложить детям перегнуть лист бумаги, на котором изображены симметричные фигуры.
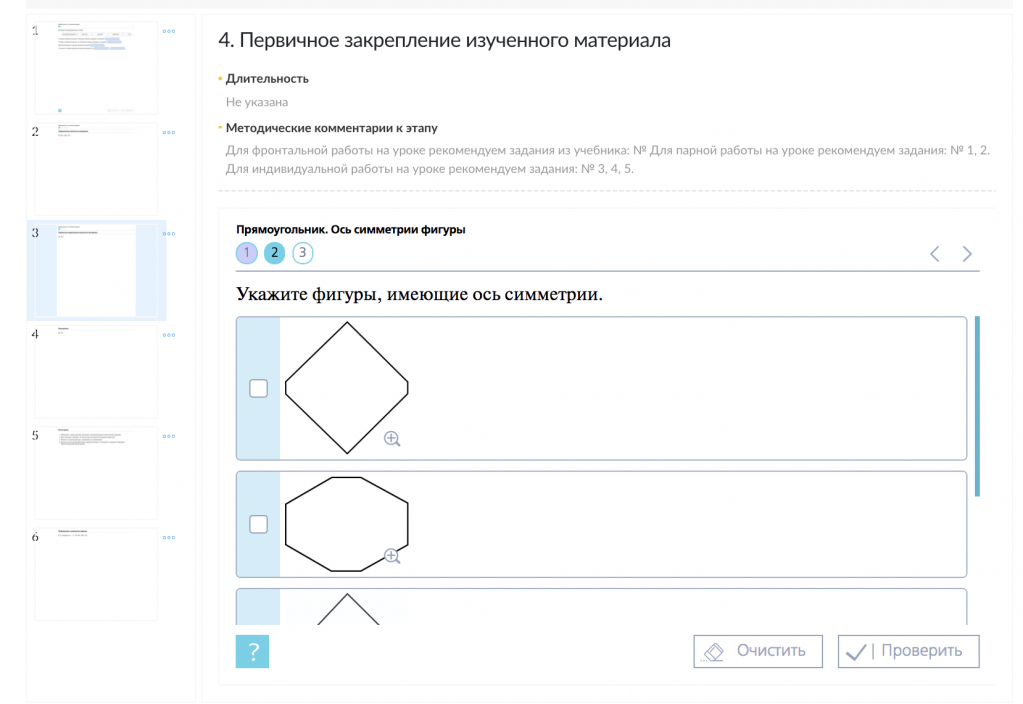 .
.
Понятие симметрии
Слово «симметрия» происходит от греческого symmetria, что означает соразмерность. В нашем случае, симметрия — это свойство геометрических фигур к отображению.Учитель: Симметрия используется в рисунках, орнаментах, архитектуре с давних времен. Где еще симметрию могут использовать люди?
Ученики: при строительстве домов; в изготовлении предметов быта.
Учитель: верно, но ведь симметрия распространена не только там, где творил человек! Мы видим симметричные объекты природы каждый день. Назовите мне три таких объекта!
Ученики: Бабочка, цветы, форма листа! Морская звезда, снежинка, яблоко в разрезе.
Симметрий, как это не покажется вам странным и любопытным, много, но мы будем рассматривать две симметрии на плоскости: относительно точки и прямой.
Осевая симметрия
Осевая симметрия — это симметрия относительно проведённой прямой (оси).
Заметим, что любые две фигуры, симметричные относительно некоторой прямой, равны (Рис.131). Все точки фигуры, имеющей ось симметрии, не принадлежащие этой оси, можно разделить на пары симметричных точек (Рис. 132).

Центральная симметрия
Фигуры, имеющие центр симметрии — понятие, воспринимающееся учащимися сложнее, чем фигуры, имеющие ось симметрии. Для удобства восприятия и понимания, рекомендуется привести как можно больше примеров из окружающей природы.Симметрию относительно точки называют центральной симметрией.
В зависимости от уровня математической подготовки учащихся класса, можно обратить их внимание на то, что прямая — это фигура, имеющая бесконечно много осей и центров симметрии.
С помощью заданий из «Классной работы» материал можно закрепить в различных графических форматах.

Актуализация знаний
Для каждого параграфа в учебнике подобраны задачи для самостоятельного решения. Задания распределены по трем уровням сложности — от простых к трудным. Для дополнительной мотивации учащихся и практического применения полученных знаний предлагается решить специальную задачу «От мудрой совы» — здесь школьникам понадобится проявить смекалку и изобретательность. Еще одна рубрика, которая неизменно заинтересует как юных первооткрывателей, так и учителей, — рубрика «Когда сделаны уроки», в которой можно узнать о важных математических объектах и истории их появления.Предложите ребятам решить задание № 1260. Какие печатные буквы русского алфавита имеют 1) вертикальную ось симметрии; 2) горизонтальную ось симметрии; 3) горизонтальную и вертикальную оси?
Готовый яркий раздаточный материал «Алфавит» вы можете скачать в конце этой статьи.

Также рекомендуем вам применять на уроке различные методы преподнесения информации: как визуальный, так и аудио. Попробуйте аудиодиктант.
Осевая и центральная симметрия

Осевая симметрия — это преобразование, поэтому каждая точка $$ P $$ на плоскости отображает другую точку $$ P ‘$$ также плоскости, так что ось $$ e $$ будет серединным перпендикуляром сегмента. $$ PP ‘$$. Осевые симметрии являются обратными изометриями, потому что они сохраняют расстояния между его точками и его гомологом, но его ориентация является обратной. Осевая симметрия возникает не только между объектом и его отражением, поскольку многие фигуры, которые могут разделиться на две части с помощью линии, симметричны относительно линии.Эти объекты имеют одну (или несколько) осей симметрии.
Осевая симметрия возникает, когда точки одной фигуры совпадают с точками другой фигуры, при этом за точку отсчета берется линия, известная под названием оси симметрии. В осевой симметрии мы находим то же явление, что и в отраженном в зеркале изображении.
Мы называем точки, принадлежащие симметричной фигуре, гомологичными точками, т. Е. $$ A ‘$$ гомологичен $$ A $$, $$ B’ $$ гомологичен $$ B $$ и $$ C ‘$$ является гомологом $$ C $$.Кроме того, существующие расстояния между точками исходной фигуры равны расстояниям между точками симметричной фигуры. В этом случае: Осевая симметрия также может иметь место в объекте относительно одной или нескольких осей симметрии.
Если мы согнем фигуру на начерченной оси симметрии, мы сможем ясно увидеть, что точки противоположных частей совпадают, то есть обе части соответствуют.
Далее мы изучим выражение в координатах осевой симметрии.
Пусть $$ P = (x, y) $$ и $$ P ‘= (x’, y ‘) $$ — две точки плоскости, дадим ее выражение в координатах в соответствии с положением ее оси:
Ось симметрии — это ось координат y:

В этом случае алгебраическое представление преобразования может быть выполнено с помощью следующей системы:
$$$ \ begin {pmatrix} x ‘\\ y’ \ end {pmatrix} = \ begin {pmatrix} -1 & 0 \\ 0 & 1 \ end {pmatrix} \ cdot \ begin {pmatrix} x \\ y \ end {pmatrix} $$$
Далее мы собираемся вычислить симметрию точки $$ P $$ с помощью симметрии, ось которой является осью их координат.Пусть $$ P = (2,2) $$ — точка на плоскости, тогда ее симметричность вычисляется с помощью следующей системы уравнений:
$$$ \ begin {pmatrix} x ‘\\ y’ \ end {pmatrix} = \ begin {pmatrix} -1 & 0 \\ 0 & 1 \ end {pmatrix} \ cdot \ begin {pmatrix} 2 \\ 2 \ end {pmatrix} \ Rightarrow \ left \ {\ begin {array} {l} x ‘= — 2 \\ y’ = 2 \ end {array} \право. $$$
Следовательно, симметричной точкой относительно оси y является точка $$ P ‘= (- 2,2) $$.
Ось симметрии — это ось координат x:

В этом случае алгебраическое представление преобразования может быть выполнено с помощью следующей системы: $$$ \ begin {pmatrix} x ‘\\ y’ \ end {pmatrix} = \ begin {pmatrix} 1 & 0 \\ 0 & -1 \ end {pmatrix} \ cdot \ begin {pmatrix} x \\ y \ end {pmatrix} $$$
Продолжаем предыдущий пример, давайте вспомним, что у нас была точка P с координатами $$ (2,2) $$ и в предыдущем примере мы вычислили ее симметричность относительно оси координат $$ y $$.Теперь мы собираемся вычислить ее симметричную относительно координатной оси $$ x $$ — и назовем эту новую точку $$ P «$$. Мы вычисляем ее координаты с помощью следующей системы уравнений:
$$$ \ begin {pmatrix} x ‘\\ y’ \ end {pmatrix} = \ begin {pmatrix} 1 & 0 \\ 0 & -1 \ end {pmatrix} \ cdot \ begin {pmatrix} 2 \\ 2 \ end {pmatrix} \ Rightarrow \ left \ {\ begin {array} {l} x ‘= 2 \\ y’ = — 2 \ end {array} \право. $$$
Следовательно, точка симметрии относительно оси координат x — это $$ P » = (2, -2) $$.
В заключение, об осевой симметрии, мы собираемся изучить, что происходит с композицией осевых симметрий:
Композиция двух симметрий с параллельными осями $$ e $$ и $$ e ‘$$ является трансляцией, вектор которой имеет длину, вдвое превышающую расстояние между осями, направление перпендикулярно осям и его смысл равен одному. который меняется от $$ e $$ до $$ e ‘$$.

- Композиция двух симметрий с перпендикулярными осями $$ e $$ и $$ e ‘$$ является центральной симметрией относительно точки, где встречаются две оси симметрии.

Снова возьмем точку $$ P = (2,2) $$ и применим к ней симметрию относительно оси координат y, а затем симметрию относительно оси координат $$ x $$. В последнем примере симметричной точкой для оси координат $$ y $$ — была точка $$ P ‘= (-2,2) $$. Затем для вычисления симметричной относительно оси координат $$ x $$ — решаем следующую систему уравнений:
$$$ \ begin {pmatrix} x ‘\\ y’ \ end {pmatrix} = \ begin {pmatrix} 1 & 0 \\ 0 & -1 \ end {pmatrix} \ cdot \ begin {pmatrix} -2 \\ 2 \ end {pmatrix} \ Rightarrow \ left \ {\ begin {array} {l} x ‘= — 2 \\ y’ = — 2 \ end {array} \право.$$$
Если сначала мы выполним симметрию относительно оси координат x, а затем симметрию относительно оси координат y, мы получим ту же точку $$ Q = (- 2, -2) $$. Как мы скоро увидим, это преобразование называется осевой симметрией.
Центральная симметрия с центром в точке $$ O $$ — это движение плоскости, при котором каждая точка $$ P $$ плоскости должна отображаться в другую точку $$ P ‘$$, являющуюся $$ O $$ средняя точка сегмента конечных точек $$ P $$ и $$ P ‘$$. Обратите внимание, что центральная симметрия эквивалентна повороту на $$ 180 ^ \ circ $$.
Точка — это центр симметрии фигуры, если она определяет центральную симметрию.

Далее мы увидим выражение в координатах центральной симметрии, изменяющей центр симметрии.
Координаты с помощью симметрии центра $$ O = (0,0) $$:
На следующем изображении мы видим, как ведет себя центральная симметрия, когда центр является началом координат точки:

Далее треугольник и его гомолог видны посредством симметрии:

В обоих случаях преобразование имеет следующего системного партнера: $$$ \ begin {pmatrix} x ‘\\ y’ \ end {pmatrix} = \ begin {pmatrix} -1 & 0 \\ 0 & -1 \ end {pmatrix} \ cdot \ begin {pmatrix} x \\ y \ end {pmatrix} $$$
Для отрезка $$ AB $$, образованного точками $$ A = (1,0) $$ и $$ B = (2,3) $$, мы собираемся вычислить его симметрию относительно центра координат.Для этого вычислим симметрию точек $$ A $$ и $$ B $$. Точнее, симметрично $$ A $$ — это $$ A ‘$$:
.$$$ \ begin {pmatrix} x ‘\\ y’ \ end {pmatrix} = \ begin {pmatrix} -1 & 0 \\ 0 & -1 \ end {pmatrix} \ cdot \ begin {pmatrix} 1 \\ 0 \ end {pmatrix} \ Rightarrow \ left \ {\ begin {array} {l} x ‘= — 1 \\ y’ = 0 \ end {array} \право. $$$
Следовательно, $$ A ‘= (-1,0) $$. Симметричная точка $$ B $$ равна $$ B ‘$$:
$$$ \ begin {pmatrix} x ‘\\ y’ \ end {pmatrix} = \ begin {pmatrix} -1 & 0 \\ 0 & -1 \ end {pmatrix} \ cdot \ begin {pmatrix} 2 \\ 3 \ end {pmatrix} \ Rightarrow \ left \ {\ begin {array} {l} x ‘= — 2 \\ y’ = — 3 \ end {array} \право.$$$
Следовательно, симметрией отрезка $$ AB $$ является отрезок $$ A’B ‘$$, который проходит через точки $$ A’ = (-1,0) $$ и $$ B ‘= (- 2, -3) $$.
Координаты с помощью центральной симметрии $$ O = (a, b) $$:
Точка $$ P ‘$$, гомологичная точке $$ P = (x, y) $$ посредством центральной симметрии центра $$ O = (a, b) $$:

А фигура, гомологичная треугольнику, имеет такую форму:

Следовательно, связанная с ним система: $$$ \ begin {pmatrix} x ‘\\ y’ \ end {pmatrix} = \ begin {pmatrix} -1 & 0 \\ 0 & -1 \ end {pmatrix} \ cdot \ begin {pmatrix} x \\ y \ end {pmatrix} + \ begin {pmatrix} 2a \\ 2b \ end {pmatrix} $$$
, где мы помним, что значения $$ (a, b) $$ — это co
Симметрия отражения
Симметрия отражения
Симметрия отражения (иногда называемая Line Symmetry или Mirror Symmetry ) легко увидеть, потому что одна половина является отражением другой половины.
Здесь у моей собаки «Flame» мордочка была сделана идеально симметричной Белая линия по центру — это линия симметрии |
Отражение в этом озере также имеет симметрию, но в данном случае:
- Линия симметрии проходит слева направо
- это не идеальная симметрия, потому что изображение немного меняется из-за поверхности озера.
Линия симметрии
Линия симметрии (также называемая Зеркальной линией ) может быть в любом направлении .
Но есть четыре общих направления, и они названы в честь линии, которую они образуют на стандартном графике XY.
См. Эти примеры (изображение было создано с помощью Symmetry Artist):
Плоскости
Не все фигуры имеют линии симметрии или могут иметь несколько линий симметрии.Например, треугольник может иметь 3 , 1 или без линий симметрии:
| Равносторонний треугольник (все стороны равны, все углы равны) | Равнобедренный треугольник (две стороны равны, два угла равны) | Чешуйчатый треугольник (без равных сторон, без равных углов) | ||
| 3 Линии симметрии | 1 Линия симметрии | Нет Линии симметрии |
Я собрал еще несколько примеров в Линии симметрии плоских форм.
.Симметрия | Размышляя о геометрии
Глядя на изображения ниже, вы сразу поймете, какое из них симметрично, а какое нет. Симметрия — это то, что мы все понимаем инстинктивно; кажется, это встроено в наш мозг. Что касается математических понятий, то, возможно, людям проще всего понять симметрию.
 Симметрии
СимметрииНо что такое симметрия? Если вы раньше не задумывались об этом, ответ может быть не таким очевидным: симметрия — это невосприимчивость к изменениям.Изображение бабочки, показанное ниже, является симметричным, потому что мы можем отразить его в вертикальной линии, идущей вниз по центру, и полученное изображение будет таким же, как то, с которого мы начали.
 Бабочка
БабочкаИзображение снежинки также имеет зеркальную симметрию (есть много осей, в которых мы можем ее отразить), но, кроме того, она симметрична относительно вращения: поверните ее вокруг центральной точки на шестую часть полного оборота (это 60 градусов) и то, что мы видим, совпадает с исходным изображением.
 Снежинка
СнежинкаКартина облицовки ванной комнаты симметрична, потому что если мы возьмем ее, сдвинем на один квадрат по горизонтали, вертикали или диагонали, а затем снова положим, мы получим тот же узор, с которого начали — по крайней мере, если мы представьте, что мозаика бесконечно простирается в обоих направлениях.
 Сетка плитки
Сетка плиткиИтак, фигура является симметричной, если она остается неизменной, когда мы применяем к ней определенную операцию. В случае фигур, нарисованных на двумерной плоскости, нас интересуют операции, которые перемещают фигуру без изменения расстояния между точками.Мы уже встречали три типа таких жестких движений: отражения, вращения и перемещения (перемещение объекта в определенном направлении и на определенное расстояние). И это почти все. В двух измерениях единственное оставшееся изображение описывает симметрию линии следов на песке. В этом случае картина остается прежней, когда мы переводим ее на определенную величину, а затем отражаем ее в горизонтальной линии между отпечатками ваших ног. Этот тип жесткого движения называется скользящим отражением.2-1 \). Это сложно, но поскольку все задействованные степени четны, его значение одинаково для \ (x \) и \ (- x \). Выражение симметрично относительно преобразования \ (x \ rightarrow -x \). Уметь замечать это чрезвычайно полезно. Например, мы часто хотим найти значения \ (x \), для которых выражение равно нулю. Симметрия означает, что как только мы нашли такое значение, его отрицательный результат также дает нам ответ на вашу проблему. Симметрия также означает, что при рисовании графика функции \ (f (x) = 7x ^ 6-10x ^ 4 + 4x ^ 2-1 \) нам нужно только определить его форму для неотрицательных значений \ ( х \), а остальное следует.Граф, который снова является визуальным объектом, симметричен относительно отражения по оси \ (y \) -.
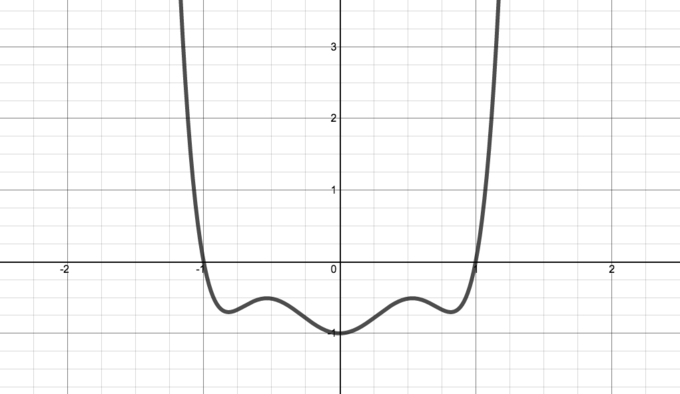 График
ГрафикПроблемы тоже могут содержать симметрии. Например, предположим, что нам дана сетка \ (3 \ times 3 \), и нас просят поместить числа \ (0 \) и \ (1 \) в ячейки так, чтобы не было двух одинаковых строк и не было двух столбцы такие же. Здесь есть внутренняя симметрия: как только мы нашли решение, замена \ (0 \) s и \ (1 \) s также является решением.
| \ (1 \) | \ (0 \) | \ (0 \) |
| \ (1 \) | \ (1 \) | \ (0 \) |
| \ (0 \) | \ (1 \) | \ (1 \) |
| \ (0 \) | \ (1 \) | \ (1 \) |
| \ (0 \) | \ (0 \) | \ (1 \) |
| \ (1 \) | \ (0 \) | \ (0 \) |
Эта симметрия упрощает задачу поиска решений.Как только мы его нашли, мы сразу же получаем второй, меняя местами \ (0 \) s и \ (1 \) s. И если частично заполненная сетка оставляет нас в тупике, потому что ее невозможно завершить без нарушения правил, тогда мы сразу понимаем, что симметричная частичная сетка тоже не стоит рассматривать:
| \ (0 \) | \ (0 \) | \ (0 \) |
| \ (1 \) | \ (1 \) | \ (1 \) |
| \ (0 \) | \(ИКС\) | \(ИКС\) |
| \ (1 \) | \ (1 \) | \ (1 \) |
| \ (0 \) | \ (0 \) | \ (0 \) |
| \ (1 \) | \(ИКС\) | \(ИКС\) |
Многие проблемы, которые возникают в реальной жизни, связаны с заполнением сеток с определенными ограничениями, например, с созданием расписания для школ или планированием приспособлений для футбольной лиги.Эти проблемы могут быть чрезвычайно сложными и обычно решаются с помощью компьютерных программ, которые по сути пробуют все возможные способы заполнения сетки. Программы, использующие присущую им симметрию, могут работать значительно быстрее, чем те, которые этого не делают.
В физике симметрия стала играть еще более фундаментальную роль. Законы природы, например, те, которые описывают, как работает гравитация, симметричны относительно перемещений в пространстве. Роняем ли мы яблоко здесь, на Гавайях или в 2000 световых годах от нас, одни и те же законы могут быть использованы для описания того, что с ним произойдет.Точно так же законы природы симметричны относительно вращений. Мы вправе изменить определение Севера, чтобы он был направлен к Эйфелевой башне, а не к Северному полюсу — любые эксперименты, которые мы проводим, все равно будут иметь тот же результат. Эти симметрии чрезвычайно полезны: если законы природы меняются в зависимости от того, где вы находитесь или куда вы смотрите, тогда не было бы никакой надежды когда-либо их понять.
В начале двадцатого века Альберт Эйнштейн решил, что симметрия является настолько важной особенностью природы, что ее следует поставить на первое место.Его теория относительности возникла из идеи, что законы природы должны выглядеть абсолютно одинаково для всех наблюдателей , независимо от того, едут ли они на слоне или ускоряются от Земли на космическом корабле. С тех пор соображения симметрии играли важную роль в физике. Например, они позволили физикам предсказывать частицы, которые никогда не наблюдались, но позже были обнаружены в экспериментах. В физике симметрия стала руководящим принципом. Как сказал лауреат Нобелевской премии П. В. Андерсон, «сказать, что физика — это исследование симметрии, будет лишь немного преувеличением».
Изучение симметрии — важная часть математики не только потому, что она полезна, но и потому, что это прекрасный предмет сам по себе. Одна вещь, которую вы заметите, когда играете, скажем, с симметрией прямоугольника, — это то, что когда вы следуете одной симметрии за другой, результатом также является симметрия: прямоугольник будет выглядеть так же, как и в начале. Например, сначала отражение по горизонтальной оси, а затем по вертикальной оси имеет тот же конечный результат, что и поворот на \ (180 \) градусов.
 Преобразования прямоугольника
Преобразования прямоугольникаМы можем представить все различные симметрии в прямоугольнике в таблице, которая показывает нам, как они сочетаются. Написав \ (a \) для отражения по горизонтальной оси, \ (b \) для отражения по вертикальной оси, \ (c \) для поворота на \ (180 \) градусов и \ (e \) для ничего не делая, получаем
| \ (е \) | \ (а \) | \ (Ь \) | \ (с \) | |
|---|---|---|---|---|
| \ (е \) | \ (е \) | \ (а \) | \ (Ь \) | \ (с \) |
| \ (а \) | \ (а \) | \ (е \) | \ (с \) | \ (Ь \) |
| \ (Ь \) | \ (Ь \) | \ (с \) | \ (е \) | \ (а \) |
| \ (с \) | \ (с \) | \ (Ь \) | \ (а \) | \ (е \) |
Здесь запись в данной строке и столбце сообщает нам, что мы получаем, когда выполняем симметрию, соответствующую строке, за которой следует симметрия, соответствующая столбцу.Удивительно то, что совершенно другая ситуация может дать нам такую же таблицу. Возьмем, например, линию из четырех одинаковых точек. Предположим, мы поменяем местами точки 1 и 2 и точки 3 и 4.
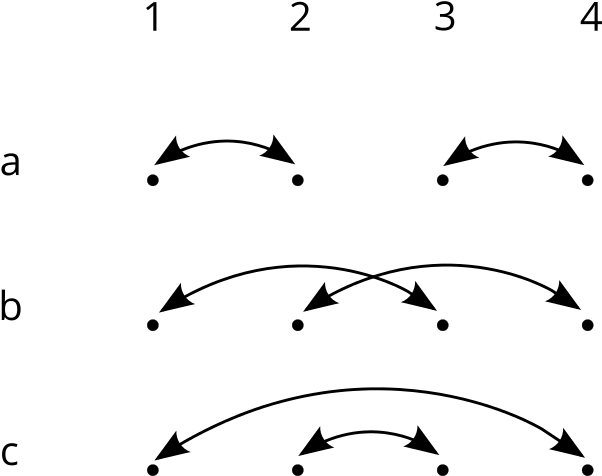 Точечные транспозиции
Точечные транспозицииКартинка будет выглядеть так же, это симметрия, для которой мы будем писать \ (a \). Перестановка точек 1 и 3 и точек 2 и 4 также является симметрией, для которой мы будем писать \ (b \). Оставшаяся возможность состоит в том, чтобы поменять местами 1 и 4 и 2 и 3, которые мы обозначим через \ (c \).Записывая таблицу, снова используя букву \ (e \), чтобы ничего не делать, мы видим, что эти симметрии сочетаются точно так же, как симметрии прямоугольника!
| \ (е \) | \ (а \) | \ (Ь \) | \ (с \) | |
|---|---|---|---|---|
| \ (е \) | \ (е \) | \ (а \) | \ (Ь \) | \ (с \) |
| \ (а \) | \ (а \) | \ (е \) | \ (с \) | \ (Ь \) |
| \ (Ь \) | \ (Ь \) | \ (с \) | \ (е \) | \ (а \) |
| \ (с \) | \ (с \) | \ (Ь \) | \ (а \) | \ (е \) |
Этот пример показывает, что симметрии можно рассматривать абстрактно: вместо изучения реальных объектов, паттернов или проблем, которые демонстрируют симметрии, математики изучают таблицы, подобные приведенной выше, состоящие из набора из элементов , которые объединяются разными способами которые следуют определенным правилам.Такие коллекции называются группами . Теория групп — это основная часть математики, которая, что неудивительно, находит приложения во всех областях, от фундаментальной физики до решения сложных задач реальной жизни.
.линий симметрии плоских форм
Линия симметрии
Здесь моя собака «Пламя» имеет лицо Белая линия по центру — это линия симметрии |
Тест складывания
Чтобы узнать, есть ли у формы Линию симметрии, сложите ее .
Когда сложенная деталь идеально сидит сверху (все края совпадают), тогда линия сгиба является линией симметрии.
Вот я сложил прямоугольник в одну сторону, а не получилось .
Итак, это , а не Линия симметрии
Но когда я пробую таким образом, действительно работает (сложенная часть идеально сидит сверху, все края совпадают):
Итак, это — это линия симметрии
Треугольники
Треугольник может иметь 3 или 1 или без линий симметрии:
| Равносторонний треугольник (все стороны равны, все углы равны) | Равнобедренный треугольник (две стороны равны, два угла равны) | Масштабный треугольник (без равных сторон, без равных углов) | ||
| 3 линий симметрии | 1 Линия симметрии | Нет Линии симметрии |
Четырехугольники
Различные типы четырехугольников (четырехсторонняя плоскость):
| Квадрат (все стороны равны, все углы 90 °) | Прямоугольник (противоположные стороны равны, все углы 90 °) | Неровное Четырехугольник | ||
| 4 линий симметрии | 2 Линий симметрии | Нет Линии симметрии |
| Воздушный змей | Ромб (все стороны одинаковой длины) | |
| 1 Линия симметрии | 2 Линий симметрии |
Правильные многоугольники
У правильного многоугольника все стороны равны и все углы равны:
И образец продолжается:
- Правильный многоугольник с 9 сторонами имеет 9 линий симметрии
- Правильный многоугольник с 10 сторонами имеет 10 линий симметрии
- …
- Правильный многоугольник с «n» со сторонами имеет «n» линий симметрии
КругЛиния (проведенная под любым углом), проходящая через его центр, является линией симметрии. Итак, круг имеет бесконечных линий симметрии. |







