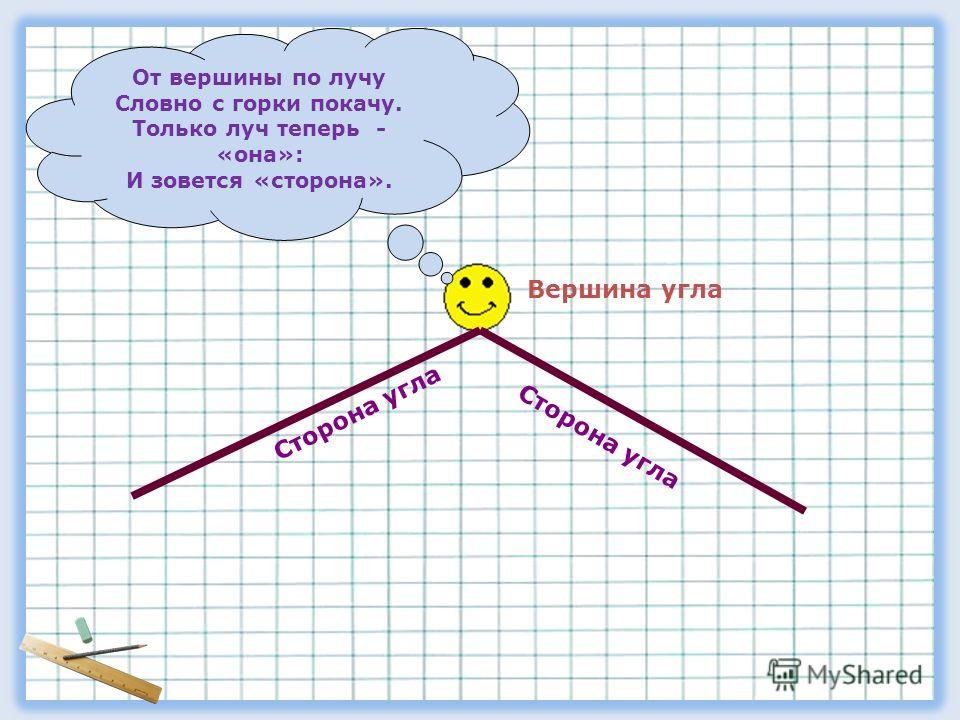
Что такое луч кратко. Что такое луч в математике и геометрии
Наряду с такими понятиями как точка, отрезок, прямая, в геометрии существует и еще одно понятие. Оно имеет название луч. Луч — это часть прямой, ограниченная с одной стороны точкой, а с другой стороны — бесконечная, т.е. ни чем не ограниченная.
Можно провести аналогию с природой. Например, луч света, который мы можем направить с земли в космос. С одной стороны он ограничен, а с другой стороны — нет. Каждый луч имеет одну крайнюю точку, в которой он начинается. Она называется началом луча .
Если взять произвольную прямую a , и отметим на ней некоторую точку О , то эта точка разобьет нашу прямую на две части. Каждая из которых будем лучом. Точка О будет принадлежать каждому из этих лучей. Точка О будет в данном случае началом этих двух лучей.
Луч обычно обозначают одной латинской буквой. На рисунке ниже представлен луч k .
Также можно обозначать луч двумя большими латинским буквами.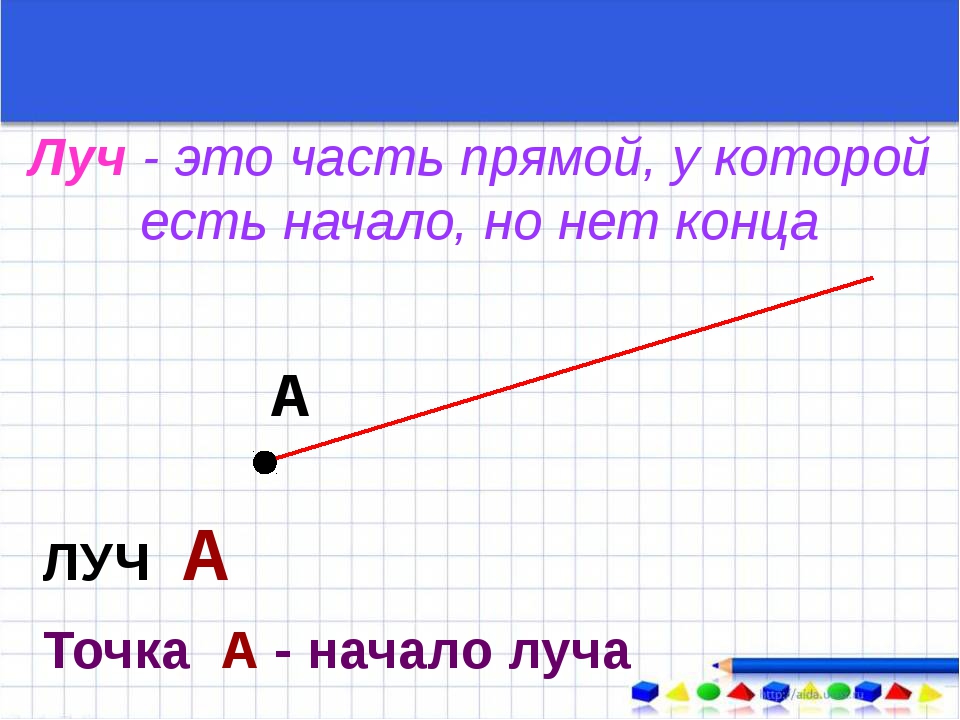
На рисунке представлен луч ОС.
Еще одним способом обозначения луча, является указание начальной точки луча и прямой, которой этот луч принадлежит. Например, на рисунке ниже представлен луч Оk.
Иногда говорят, что луч исходит из точки О. Это значит, что точка О является началом луча. Лучи еще иногда называют полупрямыми .
Задача:
Проведите прямую, и отметьте на ней точки A B и на отрезке AB отметьте точку C. Среди лучей АB, BC, CA, AC и BA найдите пары совпадающих лучей.
Лучи совпадают, если они лежат на одной прямой и имеют общее начало и ни один из них не является продолжением другого луча.
По рисунку видно, что этим условиям удовлетворяют лучи AB и AC, а также лучи BC и BA. Следовательно, они являются совпадающими.
Из курса школьной геометрии мало у кого остались точные сведения о том, что представляет собой отрезок, как он обозначается, что такое ломаная линия, прямая, точка и как обозначаются лучи.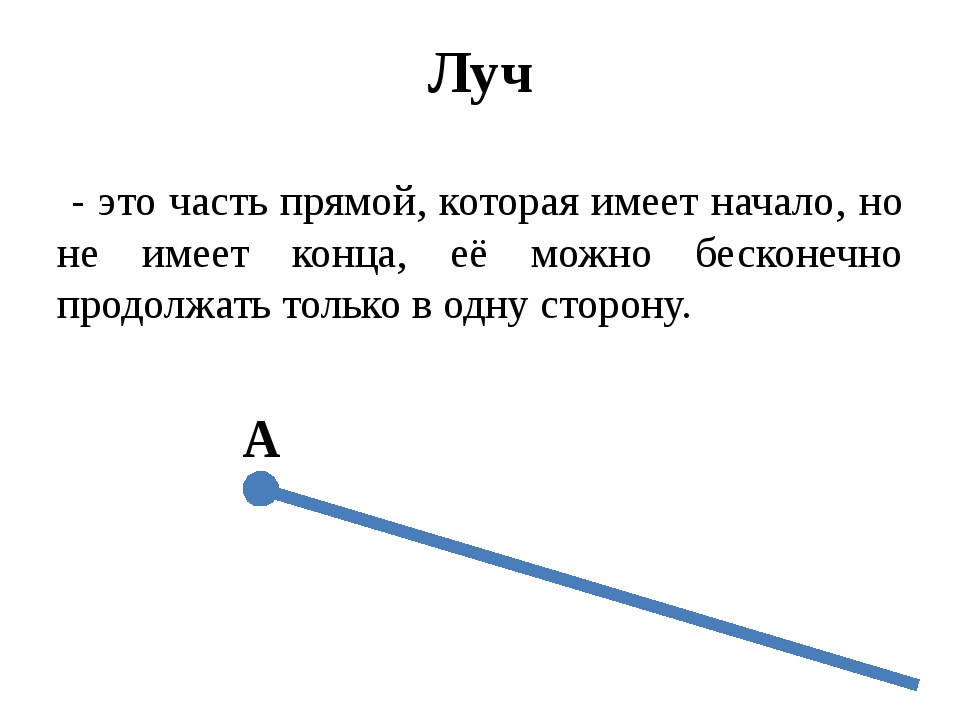 Если вы не можете вспомнить начальный курс геометрии, достаточно ознакомиться с этой статьей.
Если вы не можете вспомнить начальный курс геометрии, достаточно ознакомиться с этой статьей.
Что такое геометрия? Это математический раздел, в котором школьник знакомится с геометрическими фигурами и их свойствами. Информации много, иногда недостаточно времени для того, чтобы все охватить и запомнить. Некоторые знания необходимо освежить спустя несколько месяцев и даже лет. Например, вспомнить, что такое лучи и как они обозначаются.
Что такое луч в геометрии
Луч – это прямая, с одной стороны ограниченная точкой, а с другой стороны – свободная, то есть не имеющая ограничений. Чтобы быстрее запомнить, как обозначаются лучи и как они выглядят, можно привести простой пример: мы ведь можем направить лучик света из фонарика в небо? С одной стороны луч ограничен – с того места, откуда он выходит, то есть – из фонарика. С другой стороны – он не имеет ограничений. Получается, что крайняя точка начала луча только одна, она и называется «начало». Второй точки не существует, потому что луч уходит в бесконечность.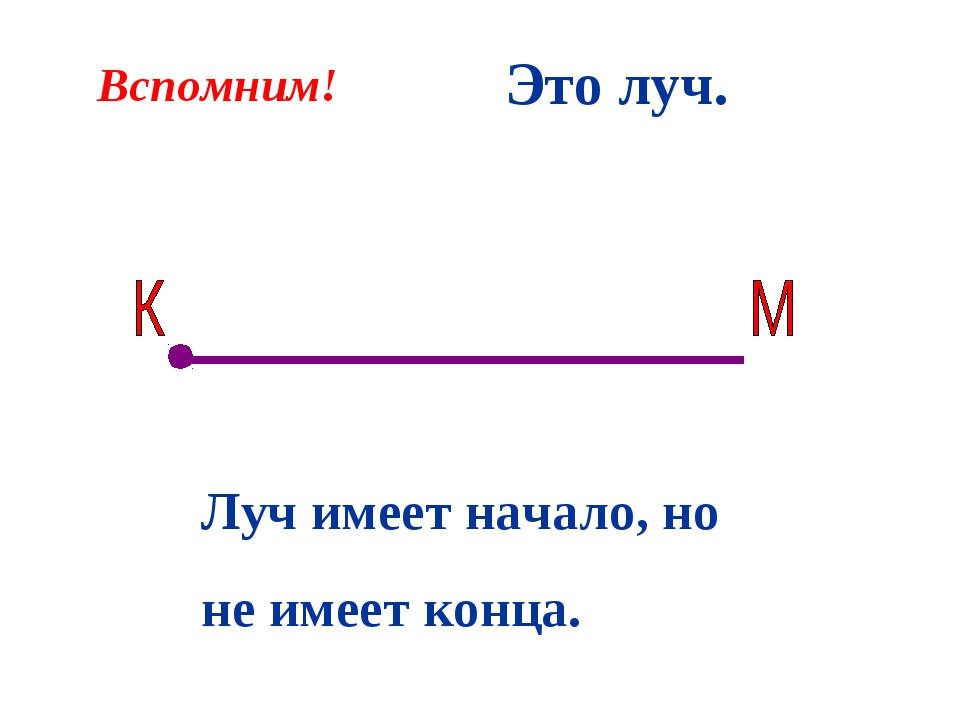
Чтобы понимать, как обозначить луч на листке бумаги, нужно начертить прямую линию. Например, пусть это будет отрезок, равный 10 см. С правой стороны поставим ограничение – точку, это начало луча. Второй точки на конце отрезка не будет.
Как обозначаются лучи
Продолжим вспоминать, что представляет собой луч и как его обозначить.
Вариантов обозначения несколько:
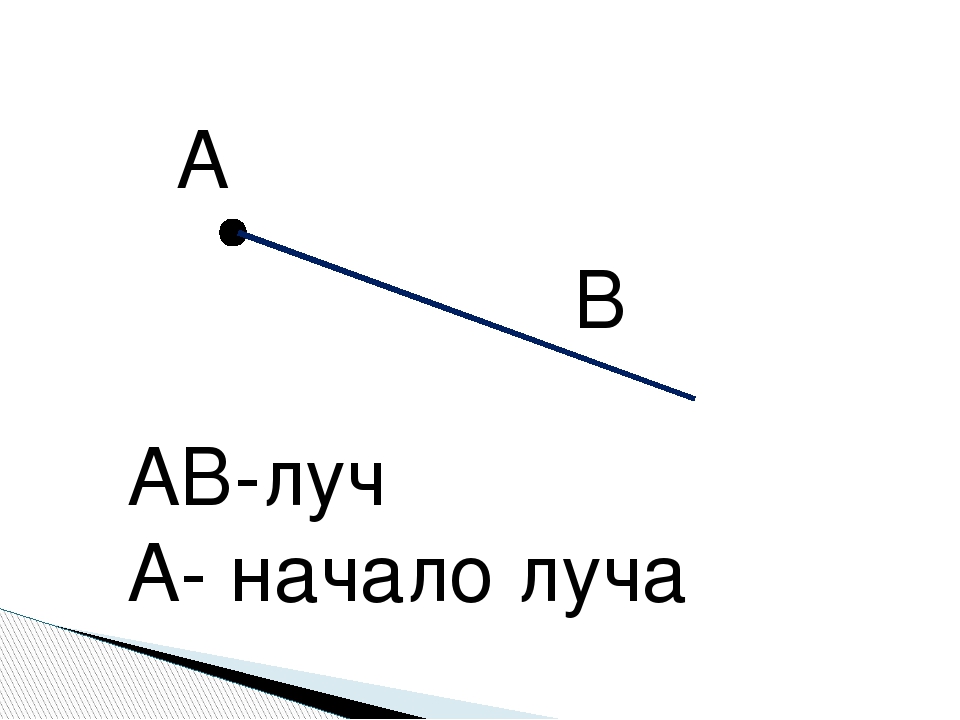
- Второй вариант поинтереснее: луч можно обозначить несколькими буквами. Например, на одном луче может быть 2 буквы. Первая – это начало луча, пусть это будет буква А, а вторая может располагаться с определенным шагом. Допустим, на отрезке длиной 10 см начало луча обозначено буквой А, а на расстоянии 4 см от начала луча имеется вторая точка, точка В.
 Тогда луч нужно обозначить, как луч «АВ». Чтобы было понятнее, читать можно так: вторая точка В – это точка, через которую проходит луч.
Тогда луч нужно обозначить, как луч «АВ». Чтобы было понятнее, читать можно так: вторая точка В – это точка, через которую проходит луч. - Лучи еще можно обозначить и третьим способом, когда начальная точка будет находиться не в начале луча, а с небольшим отступлением. Например, чертим прямую длиной 10 см, отступаем от левого края 1 см, ставим точку – это будет начало луча. Обозначаем, например, буквой О. Посередине луча точку не ставим, но обозначаем эту часть луча буквой К. В данном случае буква О, будет началом этого луча, он исходит из этой точки. Читается луч так: «ОК», он является полупрямым.
Как обозначается луч в тетрадке
Обозначение на письме луча нужно один раз запомнить: записываются лучи латинскими заглавными буквами. Если это прямая, то записать луч нужно АВ в круглых скобочках: (АВ). Если перед вами отрезок, то он записывается только в квадратных скобках.
Наряду с такими понятиями как точка, отрезок, прямая, в геометрии существует и еще одно понятие.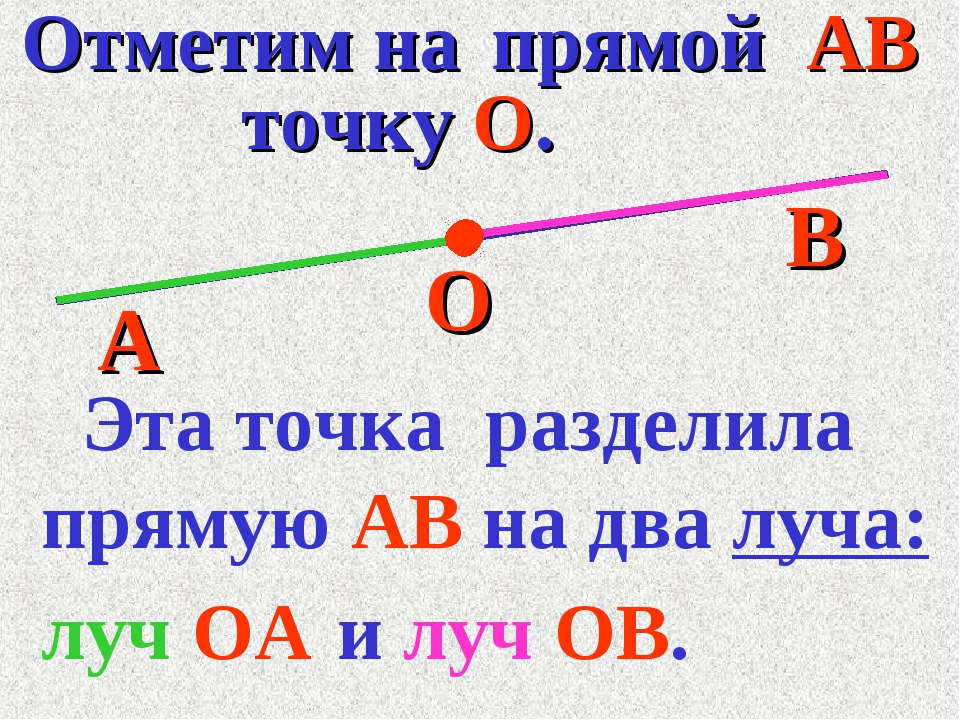 Оно имеет название луч. Луч — это часть прямой, ограниченная с одной стороны точкой, а с другой стороны — бесконечная, т.е. ни чем не ограниченная.
Оно имеет название луч. Луч — это часть прямой, ограниченная с одной стороны точкой, а с другой стороны — бесконечная, т.е. ни чем не ограниченная.
Можно провести аналогию с природой. Например, луч света, который мы можем направить с земли в космос. С одной стороны он ограничен, а с другой стороны — нет. Каждый луч имеет одну крайнюю точку, в которой он начинается. Она называется
Если взять произвольную прямую a , и отметим на ней некоторую точку О , то эта точка разобьет нашу прямую на две части. Каждая из которых будем лучом. Точка О будет принадлежать каждому из этих лучей. Точка О будет в данном случае началом этих двух лучей.
Луч обычно обозначают одной латинской буквой. На рисунке ниже представлен луч k .
Также можно обозначать луч двумя большими латинским буквами. При этом первая из них — это точка, в которой лежит начало луча. Вторая — это точка которая принадлежит лучу или другими словами — через которую луч проходит.
На рисунке представлен луч ОС.
Еще одним способом обозначения луча, является указание начальной точки луча и прямой, которой этот луч принадлежит. Например, на рисунке ниже представлен луч Оk.
Иногда говорят, что луч исходит из точки О. Это значит, что точка О является началом луча. Лучи еще иногда называютполупрямыми .
Задача:
Проведите прямую, и отметьте на ней точки A B и на отрезке AB отметьте точку C. Среди лучей АB, BC, CA, AC и BA найдите пары совпадающих лучей.
Решение:
Лучи совпадают, если они лежат на одной прямой и имеют общее начало и ни один из них не является продолжением другого луча.
Ответ: AB и AC, BC и BA.
Чаще всего этот вопрос задают в школах, на уроках геометрии, а также понятие достаточно популярно в оптике. Однако, как это часто бывает, слово имеет довольно много значений. Стоит подробнее остановиться на самых ключевых.
Стоит подробнее остановиться на самых ключевых.
Геометрия
Для того, чтобы понять, что такое луч с точки зрения геометрии, нужно рассмотреть одно из фундаментальных понятий этой науки, а именно – прямую.
Дать определение этому термину достаточно трудно, так как оно является одним из исходных, и именно с помощью прямой объясняются другие различные слова. Существует довольно мало аксиом в этом вопросе. Тем не менее, прямую можно трактовать как линию, находящуюся между двумя точками.
Прямая имеет свои свойства, согласно евклидовой геометрии.
- Через любую точку можно провести сколько угодно прямых, а вот через две несовпадающие точки – лишь одну.
- Прямые могут находиться лишь в трех состояниях – они могут пересекаться, быть параллельными друг другу, а также могут скрещиваться.
- Существует линейное уравнение, задающее прямую на плоскости.
Итак, стоит вернуться к понятию луча. Он является частью прямой. Если на такой линии поставить точку, то автоматически получится два луча, при этом они не будут иметь второй ограничивающей их точки.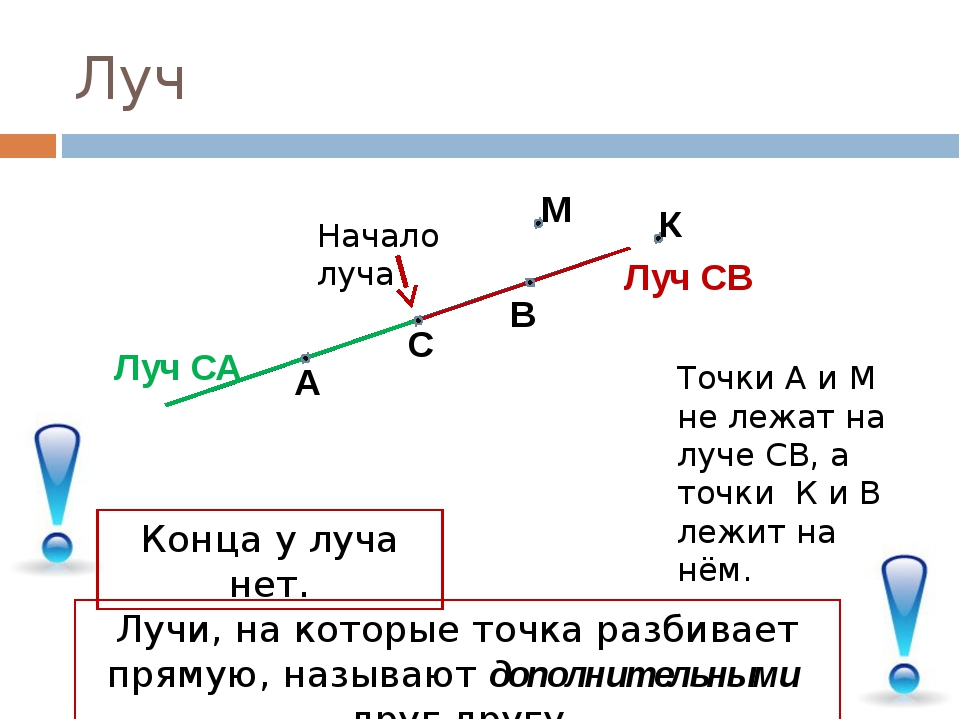
Таким образом, луч – это часть прямой , имеющая начало, но не имеющая конца.
Световой луч
Геометрическая оптика рассматривает понятие светового луча довольно схожим образом. Здесь он тоже будет являться линией, однако она будет использоваться световой энергией. Иначе говоря, световой луч – это небольшой пучок света .
Как и понятие прямой в геометрии, так и понятие луча в оптике является довольно базовым явлением. Однако, в отличие от геометрического луча, световой не имеет какого-то четкого направления, так как происходит дифракция. Однако, если свет очень большой, то расходимостью принято пренебрегать. В этом случае можно выделить четкое направление.
Помимо базовых терминов в точных науках, этим словом обозначают самые разнообразные объекты. Например, около семи спортивных клубов носили такое название, а некоторые из них существуют до сих пор. Множество деревень, поселков и хуторов на территории России, Украины и Белоруссии тоже называются Лучами.
От них не отстают и суда – причем в этом случае Луч является маркой пассажирских судов, а также целым классом яхт.
Эти яхты являются одноместными и используются для гонок. Часто их применяют в качестве обучающего снаряда для детей, однако на нем проводятся и соревнования.
Существуют и другие значения:
- Этим словом называются три российских спутника-ретранслятора.
- В Удмуртии и Предуралье выходит журнал с таким названием.
- Лучом назвали и объединение атомной промышленности.
- С таким названием есть часовой завод и обувная фабрика в Минске.
- Луч – это псевдоним чувашского писателя, официальное имя которого Григорий Васильевич Васильев.
Возможно, будет полезно почитать:
Прямая. Луч. Отрезок. Задачи по математике 2 класс
Математика 2 класс
Задачи для 2 класса
Контрольные работы
Задача 1
Точка О разбивает прямую AB на две части.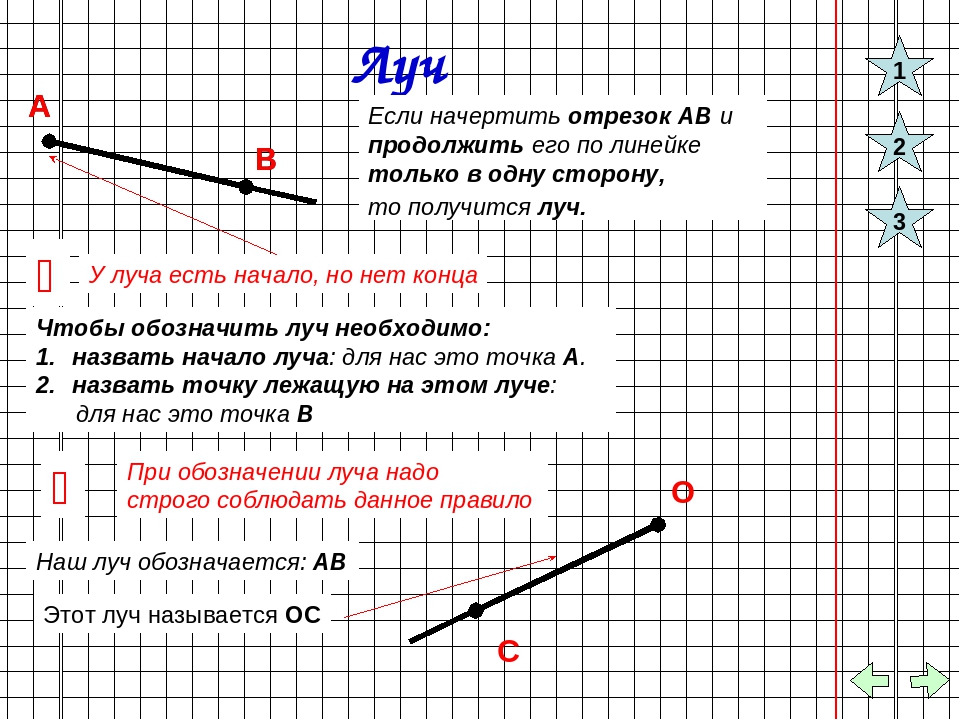 Что напоминает каждая из частей? Чем каждая часть отличается от прямой и отрезка?
Что напоминает каждая из частей? Чем каждая часть отличается от прямой и отрезка?
Решение
- 1) Каждая из частей напоминает луч.
- 2) Луч имеет начальную точку, но не имеет конечной точки. Отрезок имеет начальную и конечную точки. Прямая не имеет ни начальной ни конечной точек.
Задача 2
Отметь цветным карандашом начало каждого луча. Как обозначен первый луч? Можно ли поменять местами буквы? Почему? Обозначь остальные лучи.
Решение
- Луч обозначен: первая буква — начальная точка луча, вторая конец.
- Буквы нельзя менять мстами, потому что первая буква обозначает начало луча.
Задача 3
- а) Подбери правильные названия для чертежей и проведи линии:
- б) Начерти в тетради прямую, луч и отрезок и обозначь их.

Решение
- а)
Задача 4
Обведи с помощью линейки на чертеже прямые линии красным карандашом, лучи — синим, а отрезки — зелёным:
Решение
Задача 5
«Машенька испекла вчера 32 пирожка, а сегодня — на 4 пирожка больше».
Какие вопросы можно поставить к этому условию, чтобы получилась задача:
- 1) Сколько пирожков испекла Машенька вчера?
- 2) Сколько пирожков испекла она сегодня?
- 3) С какой начинкой были пирожки?
- 4) Сколько пирожков испекла Машенька за 2 дня?
- Подбери к полученным задачам подходящие схемы и реши их:
Решение
- 2) Сколько пирожков испекла она сегодня?
- 4) Сколько пирожков испекла Машенька за 2 дня?
Задача 6
В одном вагоне поезда едут 46 человек, а в другом — на 18 человек меньше.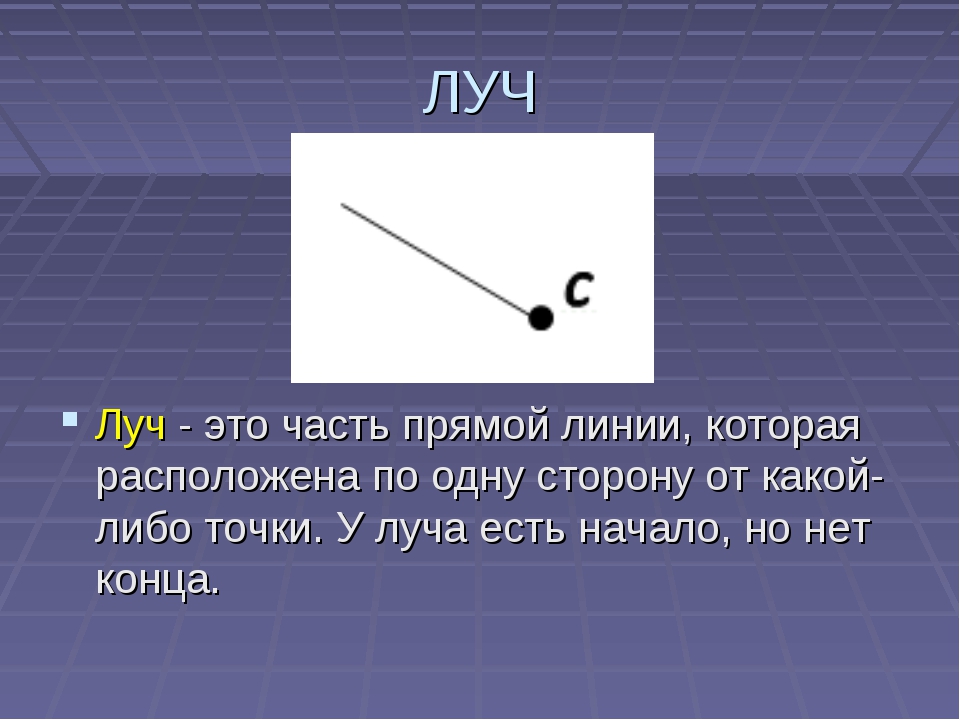 Сколько человек едут в двух вагонах?
Сколько человек едут в двух вагонах?
Решение
- 46 — 18 = 28
- 46 + 28 = 74
- Ответ:74 человека.
Задача 7
- Что надо поставить вместо знака вопроса? Назови взаимно обратные операции.
Решение
- а) Заменить букву о на букву и. Заменить букву и на букву о.
- б) 1м 5см выразить в сантиметрах. 105см выразить в метрах и сантиметрах.
Задача 8
Реши задачу, а затем составь и реши обратную задачу:
«В ларёк привезли 180 кг винограда и продали его за 3 дня. В первый день продали 56 кг, а во второй — на 8 кг больше. Сколько килограммов винограда продали в третий день?»
Решение
- 1) 56 + 8 = 64
- 2) 64 + 56 = 120
- 3) 180 — 120 = 60
- 60кг продали в 3 день.

Задача 9
Найди закономерность и вставь пропущенные числа. Кто быстрее назовёт все числа этого ряда?
Решение Каждое последующее число больше предыдущего на 3.
3 6 9 12 15 18 21 24 27 30
На странице использован материал из книги Л. Г. Петерсон «Математика второй класс. Часть2».
Ссылка на сайт автора:
www.sch3000.ru
Составные задачи
Простые задачи
Урок математики в 5 классе «Прямая. Луч. Отрезок»
Разработка урока математики в 5 классе
Прямая.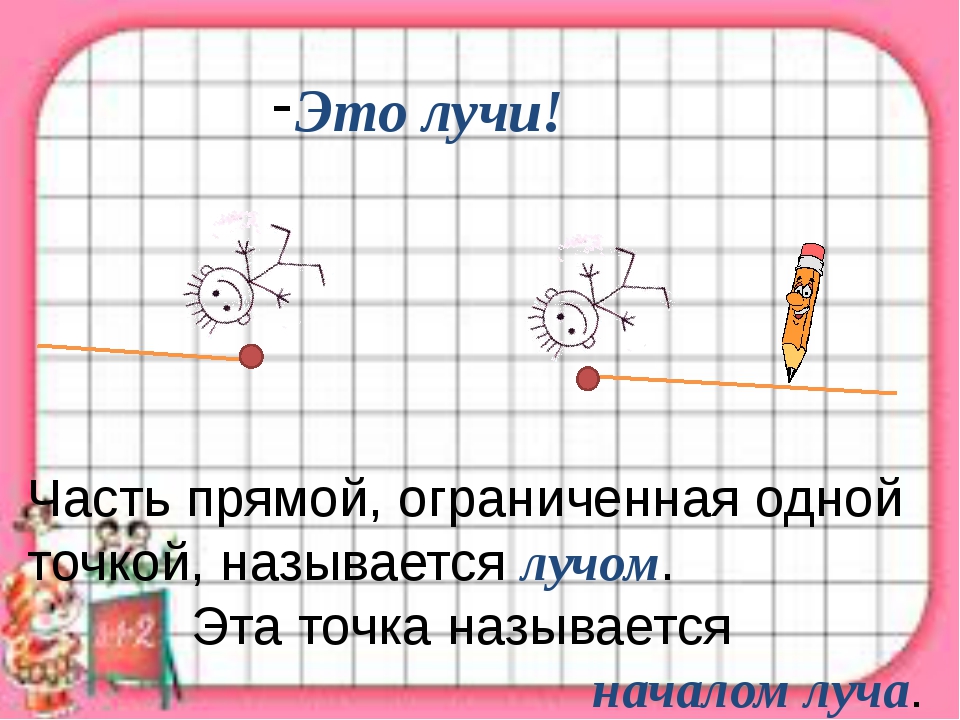 Луч. Отрезок
Луч. Отрезок
Цель: Учить школьников различать прямую, луч, отрезок. Познакомить с общепринятыми обозначениями. Развивать мыслительные операции, математические способности, логическое мышление, чертежные навыки. Воспитывать ответственность, дружелюбие.
Ход урока
1. Организационный момент
Ну-ка, проверь дружок!
Готов ли ты начать урок?
Все ли на месте? Все ль в порядке?
Книжка, ручка и тетрадка…
Проверили? Вот здорово!
К уроку все готово!
2. Актуализация знаний учащихся
Учитель: Геометрия – наука о фигурах.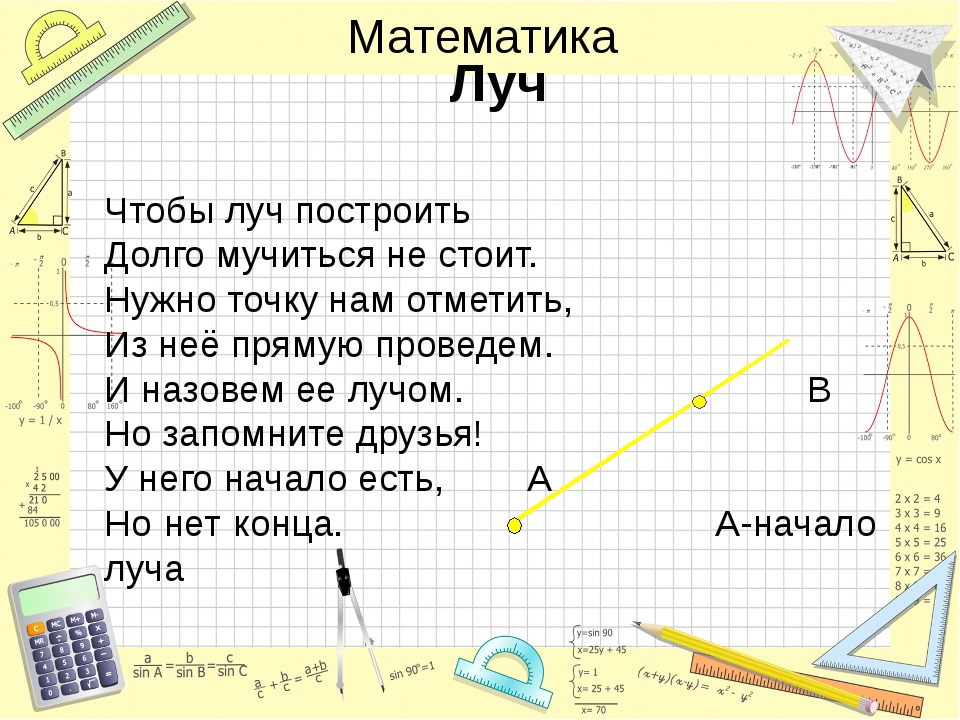 Верным помощником на нашем сегодняшнем уроке будет простейшая геометрическая фигура – точка.
Верным помощником на нашем сегодняшнем уроке будет простейшая геометрическая фигура – точка.
Слайд 1
1.1. Вычислите устно, записав ответы через строчку в тетрадь.
Слайд 2
1.2. Анаграммы (расшифровать слова)
Слайд 3
Слайд 4
1. 3. Вопросы классу:
3. Вопросы классу:
— Все ли расшифрованные слова знакомы?
— На каких уроках мы с ними встречались?
— Какое слово и почему лишнее?
3. Сообщение темы урока
Слайд 5
4. Изучение нового материала
4.1. Вступительное слово о плоскости
Слайд 6
4. 2. Прямая
2. Прямая
l
B
A
Прямая – прямая линия, которая не имеет ни начала, ни конца.
Обозначение: прямая АВ, прямая l
Свойства:
а) если две прямые на плоскости пересекаются, то они имеет одну общую точку
m F – точка пересечения прямых m и l
l F (общая точка)
б) через две точки на плоскости можно провести только одну прямую
М
Д
в) через одну точку на плоскости можно провести бесконечно много прямых
г) если прямые на плоскости не пересекаются, то они не имеют общих точек
m l
Прямые m и l называются параллельные прямые
Вывод:
Без начала и без края линия прямая.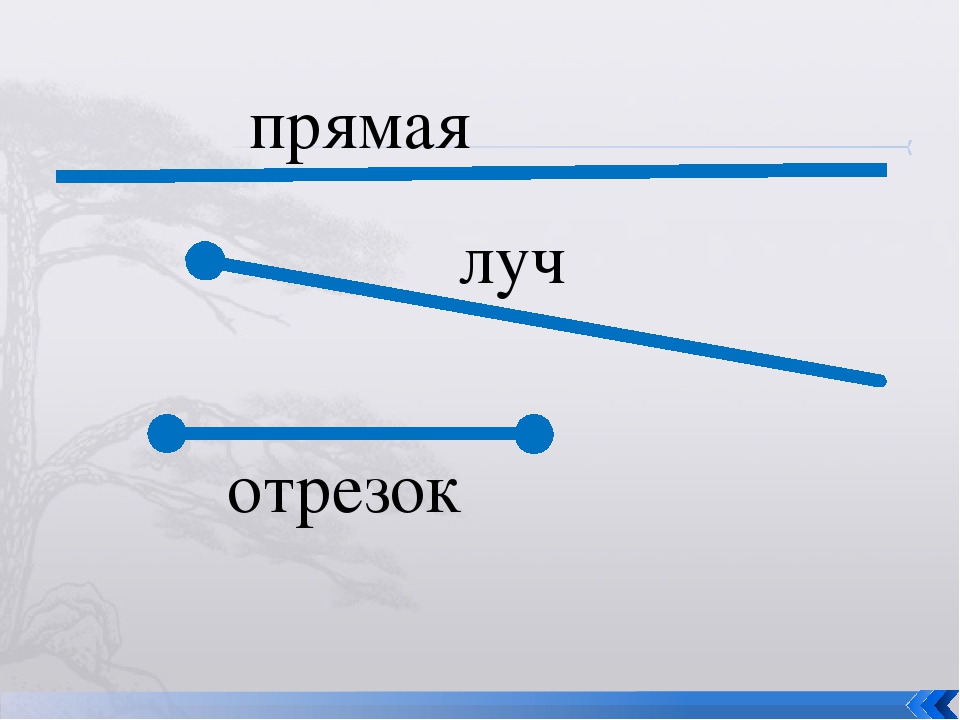
Хоть 100 лет по ней идти,
Не найдешь конца пути.
4.3. Луч
Учитель: А теперь мысленно разрежьте прямую и к месту разреза прикрепите солнышко. Что получилось? На что похоже?
Слайд 7 (луч солнца)
О новой фигуре разносится весть.
Конца пусть в ней нет,
Но начало-то есть!
И солнце, тихонько взойдя из-за тучь,
Сказало: «Друзья, назовем его ЛУЧ!»
О
К
Определение: Луч – часть прямой, которая имеет начало, но не имеет конца
Обозначение: луч ОК (т.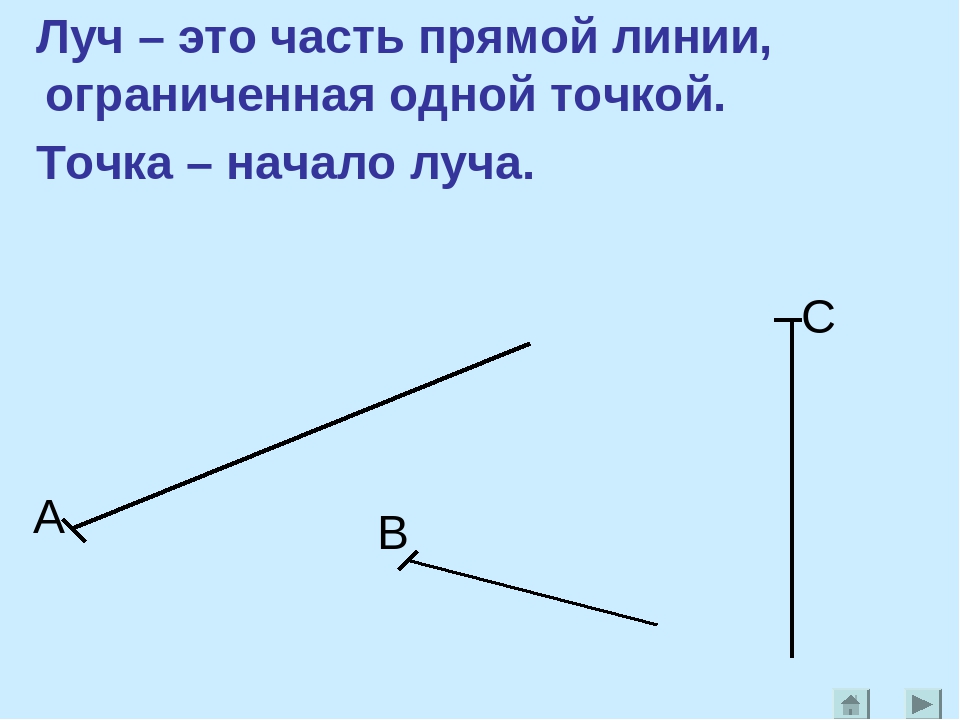 О – начало луча)
О – начало луча)
Свойства:
Из одной точки можно провести бесконечно много лучей
Физкультминутка: Слайд 8:
Раз, два, три, четыре, пять, -
Все умеем мы считать.
Отдыхать умеем тоже,
Руки за спину заложим,
Голову поднимем выше
И легко-легко подышим.
Раз – подняться, потянуться,
Два – согнуться, разогнуться.
Три – в ладоши три хлопка,
На четыре – руки шире,
Пять – руками помахать,
Шесть – за парту тихо сесть.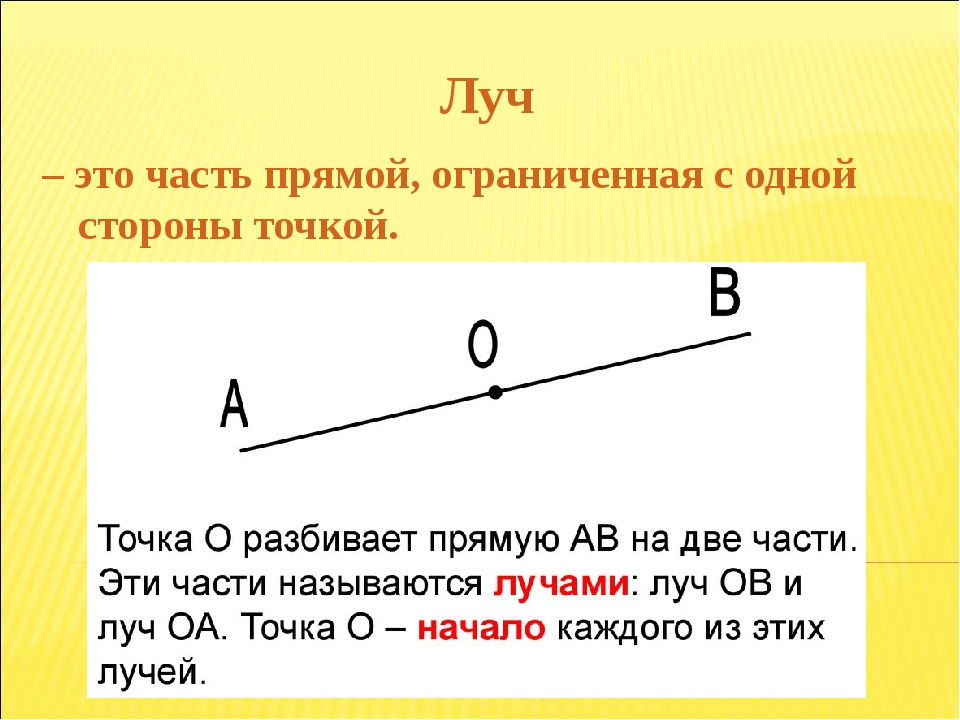
4.4. Отрезок
Точки две поставь в тетради,
Чтоб потом нарисовать между ними
Под линеечку – прямую.
И окажется, мой друг,
Что отрезок вышел вдруг.
А В
Определение: Отрезок – часть прямой, ограниченная точками.
Обозначение: отрезок АВ (т. А – начало отрезка, т. В – конец отрезка)
5. Закрепление изученного:
№ 341 – устно
№ 343 – работа в парах с последующей проверкой
6. Подведение итогов работы . Домашнее задание
Объясните что такое луч как обозначаются лучи в математике и геометрии
Содержание
- Геометрия
- Световой луч
Чаще всего этот вопрос задают в школах, на уроках геометрии, а также понятие достаточно популярно в оптике. Однако, как это часто бывает, слово имеет довольно много значений. Стоит подробнее остановиться на самых ключевых.
Однако, как это часто бывает, слово имеет довольно много значений. Стоит подробнее остановиться на самых ключевых.
Геометрия
Для того, чтобы понять, что такое луч с точки зрения геометрии, нужно рассмотреть одно из фундаментальных понятий этой науки, а именно – прямую.
Дать определение этому термину достаточно трудно, так как оно является одним из исходных, и именно с помощью прямой объясняются другие различные слова. Существует довольно мало аксиом в этом вопросе. Тем не менее, прямую можно трактовать как линию, находящуюся между двумя точками.
Прямая имеет свои свойства, согласно евклидовой геометрии.
- Через любую точку можно провести сколько угодно прямых, а вот через две несовпадающие точки – лишь одну.
- Прямые могут находиться лишь в трех состояниях – они могут пересекаться, быть параллельными друг другу, а также могут скрещиваться.
- Существует линейное уравнение, задающее прямую на плоскости.
Итак, стоит вернуться к понятию луча. Он является частью прямой. Если на такой линии поставить точку, то автоматически получится два луча, при этом они не будут иметь второй ограничивающей их точки.
Он является частью прямой. Если на такой линии поставить точку, то автоматически получится два луча, при этом они не будут иметь второй ограничивающей их точки.
Таким образом, луч – это часть прямой, имеющая начало, но не имеющая конца.
Световой луч
Геометрическая оптика рассматривает понятие светового луча довольно схожим образом. Здесь он тоже будет являться линией, однако она будет использоваться световой энергией. Иначе говоря, световой луч – это небольшой пучок света.
Как и понятие прямой в геометрии, так и понятие луча в оптике является довольно базовым явлением. Однако, в отличие от геометрического луча, световой не имеет какого-то четкого направления, так как происходит дифракция. Однако, если свет очень большой, то расходимостью принято пренебрегать. В этом случае можно выделить четкое направление.
Помимо базовых терминов в точных науках, этим словом обозначают самые разнообразные объекты. Например, около семи спортивных клубов носили такое название, а некоторые из них существуют до сих пор.
Множество деревень, поселков и хуторов на территории России, Украины и Белоруссии тоже называются Лучами. От них не отстают и суда – причем в этом случае Луч является маркой пассажирских судов, а также целым классом яхт.
Эти яхты являются одноместными и используются для гонок. Часто их применяют в качестве обучающего снаряда для детей, однако на нем проводятся и соревнования.
Существуют и другие значения:
- Этим словом называются три российских спутника-ретранслятора.
- В Удмуртии и Предуралье выходит журнал с таким названием.
- Лучом назвали и объединение атомной промышленности.
- С таким названием есть часовой завод и обувная фабрика в Минске.
- Луч – это псевдоним чувашского писателя, официальное имя которого Григорий Васильевич Васильев.
Презентация — Математика 1 класс «Линии: кривая, прямая. Луч — Отрезок
Слайды и текст этой презентации
Слайд 1
2014 год,
13 октября,
понедельник.
Слайд 2
К задуманному числу прибавили 1 и получили 5. Какое число задумали?
Какое число при счёте следует за числом 6?
Число на 1 меньше, чем 8.
Какое число имеет соседей 3 и 4?
Какое число предшествует числу 7?
Слайд 3
1
2
3
4
5
6
7
8
9
10
Слайд 4
Ежик по лесу шел,
На обед грибы нашел:
Два — под березой,
Один — у осины,
Сколько их будет
В плетеной корзине?
2+1=3
Слайд 5
Три ромашки-желтоглазки,
Два веселых василька
Подарили маме дети.
Сколько же цветов в букете?
3+2=5
Слайд 6
1
1
2
Слайд 7
Слайд 8
Слайд 9
Слайд 10
Отдыхай-ка
Слайд 11
Слайд 12
.Линии: кривая, прямая.
Луч. Отрезок.
Точка.
Слайд 13
На какие две группы можно разделить эти
линии?
Сколько прямых линий?
Сколько кривых линий?
Каких линий больше?
Слайд 14
Сказка
В стране Геометрии жила-была точка.
Она была маленькой. Её оставил карандаш, когда наступил на лист тетради, и никто её не замечал. Так и жила она, пока не попала в гости к линиям.
Слайд 15
Прямая линия начала хвастаться: «Я самая длинная
У меня ни начала, ни конца! Я бесконечная!»
Очень интересно стало точке посмотреть на неё.
Сама-то она малюсенькая. Вышла она да так
увлеклась, что не заметила и наступила на прямую
линию. И вдруг исчезла прямая линия. На её месте
появился луч.
Слайд 16
Он тоже был длинный, но всё же не такой, как
прямая линия. У него появилось начало.
Испугалась точка: «Что же я наделала!» Хотела она
убежать, да как назло наступила опять на луч.
И на месте луча появился отрезок. Он не хвастался,
какой он большой, у него уже были и начало и конец.
Слайд 17
Вот так маленькая точка смогла изменить жизнь
больших линий.
Слайд 18
Слайд 19
Слайд 20
! Прямую линию мы проводим по линейке.
Слайд 21
Сколько линий можно провести через одну точку?
Слайд 22
Сколько линий можно провести через две точки?
Слайд 23
Отдыхай-ка
Слайд 24
Слайд 25
С.15
Слайд 26
Слайд 27
Что мы узнали?
Что повторили?
Слайд 28
Оцени свою работу на уроке.
Слайд 29
Наше настроение
Конспект урока математики по теме «Прямая. Луч.Отрезок.»
Тема: «Прямая. Луч. Отрезок».
Основные цели:
1) Сформировать умение распознавать луч, прямую и отрезок на основе использования их существенных признаков, умение обозначать и называть прямую, луч, отрезок.
2) Тренировать умения считать тройками, решать текстовые задачи.
Мыслительные операции, необходимые на этапе проектирования: анализ, сравнение, классификация, обобщение.
Демонстрационный материал:
1) изображение гномика:
2) эталоны обозначения прямой,
отрезка, луча:
3) карточка с названием темы: ПРЯМАЯ. ЛУЧ. ОТРЕЗОК;
4) две катушки ниток (клубков), незаметно соединённых
концами;
5) маленькая настоящая корзинка;
6) изображение маленького солнышка: .
Раздаточный материал:
1) карточка для этапа актуализации:
2) карточка с заданием для пробного действия:
3) карточка для работы групп:
Ход урока:
1. Мотивация к учебной деятельности.
Цель:
1) создать условия для возникновения внутренней потребности включения в учебную деятельность на уроке посредством введения героя урока, не имеющего некоторых знаний по математике;
2) актуализировать требования к ученику со стороны учебной деятельности;
3) установить тематические рамки урока: работа с прямыми.
Организация учебного процесса на этапе 1:
Открыть на доске «Здравствуйте, ребята!». Запись сделана по неровной линии, некрасиво, с разной высотой букв.
– Посмотрите на доску. Кто-то написал на ней приветствие для вас. Кто же это?.. А…, он, наверное, спрятался. Как вы думаете, почему? (…Вероятно, он застеснялся того, что запись у него получилась кривой, неровной…)
– Я тоже так думаю. Почему же у нашего гостя получилась такая неровная запись, ведь он так старался для вас? Что ему надо было сделать, прежде чем писать? (Сначала надо было начертить строчку по линейке.)
– А чем является строчка с точки зрения математики? (Прямой.)
– Как же помочь нашему таинственному гостю? (Надо начертить ему строчку-прямую, …)
Открыть на доске изображение гномика.
– Ах, вот и он! Это же гномик. Не волнуйся, мы тебе поможем! Начертите прямую в тетради.
1 ребёнок чертит на доске, остальные в тетради.
– Итак, вы начертили прямую. Чему же будет посвящён сегодняшний урок? (Прямым.)
– Вы правы, а ещё вы узнаете что-то новое о прямых линиях, а знание о прямой вам в этом поможет. А как вы будете узнавать новое? (Сначала повторим необходимые знания, потом выполним задание для пробного действия. Скорее всего, не получится. Тогда постараемся понять причину затруднения, поставим цель, …)
– Итак, начинаем с … (Повторения необходимого.)
2. Актуализация и пробное учебное действие.
Цель:
1) актуализировать представления о прямой и отрезке, тренировать умения обозначать и называть прямую и отрезок с помощью букв латинского алфавита;
2) активизировать мыслительные операции: анализ, сравнение, классификацию;
3) мотивировать учащихся к выполнению пробного действия;
4) организовать самостоятельное выполнение учащимися индивидуального задания на применение нового знания, запланированного для изучения на данном уроке;
5) организовать фиксацию учащимися возникшего затруднения в обосновании правильности полученного результата.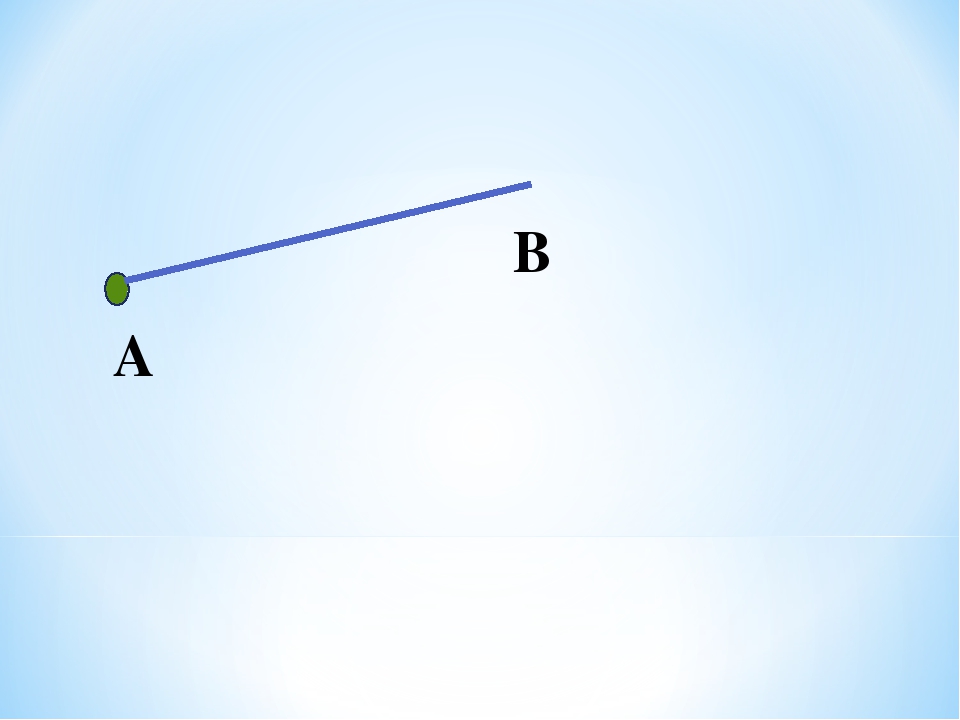
Организация учебного процесса на этапе 2:
1) Актуализация представлений о прямой и отрезке.
– Для начала надо убедиться, что вы действительно начертили прямую. Для этого вспомните всё, что вы о ней знаете. (Прямая – это прямая линия, не имеющая ни начала, ни конца. Её можно продолжать в любую сторону до бесконечности.)
Открыть на доске изображение отрезка.
– Посмотрите на эту фигуру. Знакома она вам? (Да, это отрезок.)
– Что вы знаете об отрезке? (Отрезок – это прямая линия, ограниченная с двух сторон. Отрезок нельзя продолжить.)
Раздать листы с заданием для этапа актуализации.
Открыть это же задание на доске.
– Вы хорошо разбираетесь в линиях, поэтому выполните следующее задание самостоятельно. Посмотрите на листы, которые я вам раздала. На какие группы надо разделить все изображённые линии? (На прямые, отрезки и другие линии.)
– Выполните это задание, записав номера линий в кружок под карточкой с соответствующим названием.
– Проверим. Под какими номерами вы видите прямые? (Под номерами 2 и 4.)
– Докажите. (Это прямые, так как их можно продолжить в любую сторону до бесконечности.)
– Вспомните, а как можно обозначить прямые? (Одной маленькой латинской буквой или двумя большими латинскими буквами.)
Открыть на доске эталон обозначения прямой:
– Обозначьте обе прямые по-разному и назовите их.
Учитель обозначает прямые на доске со слов детей, учащиеся – на листах.
– Молодцы! Что вам необходимо было знать, чтобы найти прямые? (Надо было знать, что это за линии, их признаки…)
– Под какими номерами вы видите отрезки? (Под номером 1.)
– Докажите. (Отрезок – это прямая линия, у которой два конца.)
– Как обозначают отрезки? (Двумя заглавными латинскими буквами.)
Открыть на доске эталон обозначения отрезка:
– Обозначьте отрезок на ваших карточках и назовите его.
Учитель обозначает отрезок на доске со слов детей, учащиеся – на листах.
– Что вам необходимо было знать, чтобы найти отрезок? (Надо было знать, что это за линия, её признаки…)
2) Введение термина «луч». Обобщение.
– В геометрии есть ещё линии, которые называют «луч». Именно с этим видом линий будет связано задание для пробного действия. А пока обобщите, что мной было выбрано для повторения. (Что такое прямая и отрезок, как они обозначаются.)
– Какой ещё вид линий есть в геометрии? (Лучи.)
– Этап повторения закончен. Что дальше? (Задание для пробного действия.)
– В чём особенность этого задания? (В нём обязательно есть что-то для нас новое.)
3) Задание для пробного действия.
Раздать листы с заданием для пробного действия:
– Рассмотрите лист с заданием для пробного действия. Я предлагаю вам распределить все изображённые линии на две группы: лучи и другие линии и записать номера линий в кружок под карточкой с соответствующим названием. Что в этом задании для вас ново? (Нам не приходилось определять, какие линии можно назвать лучами. )
)
– Что вы будете делать? (Мы попробуем выполнить задание.)
– Пробуйте.
– Проверим. Как вы считаете, под какими номерами изображены лучи? (Под номерами 3, 4, 6; …)
Учитель фиксирует на доске все варианты ответов детей.
– Что видите? (Выполнили задание по-разному.)
– Поднимите руку, кто уверен, что его ответ верен.
– Вы не подняли рук, значит, у вас есть трудность. В чём? (Мы не уверены, что правильно определили среди линий лучи.)
– Вы зафиксировали трудность. Что думаете делать дальше? (Надо понять причину возникшей трудности.)
3. Выявление места и причины затруднения.
Цель:
1) создать условия для проведения учащимися анализа своих действий;
2) организовать выявление и фиксацию учащимися причины затруднения: неизвестны существенные признаки луча.
Организация учебного процесса на этапе 3:
– Давайте думать. Какое задание надо было выполнить? (Надо было определить, какие из линий являются лучами, и записать номер в кружок под соответствующей карточкой.)
Какое задание надо было выполнить? (Надо было определить, какие из линий являются лучами, и записать номер в кружок под соответствующей карточкой.)
– На какие знания вы опирались, когда среди линий находили прямые и отрезки? (На знания существенных признаков этих линий.)
– А как вы рассуждали, определяя, какие из линий являются лучами? (…)
– В чём же причина вашего затруднения? (Нам неизвестны существенные признаки луча.)
– Вы поняли причину своего затруднения. Что сделаете дальше? (Поставим перед собой цель.)
4. Построение проекта выхода из затруднения.
Цель:
1) создать условия для формулирования учащимися конкретной цели будущих учебных действий;
2) согласовать тему урока;
3) организовать выбор учащимися средств для построения нового знания.
Организация учебного процесса на этапе 4:
– Сформулируйте цель своих дальнейших действий. (Выявить существенные признаки луча.)
(Выявить существенные признаки луча.)
– От себя добавлю, что ещё вам предстоит узнать, как обозначают и называют лучи.
– Как бы вы назвали урок? (Луч.)
– Учитывая, что вам помогут знания об отрезке и прямой, назовём урок «Прямая. Луч. Отрезок».
Открыть название темы на доске.
– Итак, в качестве средств, знания о каких линиях вам будут необходимы? (Знания о прямой и отрезке.)
Учитель берёт в руки корзинку, в которой лежат два незаметно соединённых между собой клубка.
– Гномик сказал мне только что, что он шёл через одну из областей математики – геометрию, и ему передали для вас какие-то странные предметы, которые, как ему сказали, помогут вам узнать новое. Давайте посмотрим, что в корзинке.
Достать из корзинки два клубка.
– Клубки! Предположите, чем же они вам могут помочь? (…)
– Вы всё как следует обдумали, теперь начинаем действовать.
5. Реализация построенного проекта.
Цель:
1) организовать построение нового знания, используя предметные действия с клубками;
2) организовать фиксацию нового знания в речи и в виде эталона;
3) организовать применение нового знания для выполнения задания, вызвавшего затруднение;
4) зафиксировать преодоление возникшего ранее затруднения.
Организация учебного процесса на этапе 5:
Вызвать к доске двух учеников.
– Ребята, попробуйте размотать клубки, натягивая нитку. На что похожа натянутая нитка? (На прямую, так как её можно продолжать, разматывая клубки.)
– Какая разница между клубками и прямой? (Нитка в клубках закончится, а прямая – нет.)
– Действительно: Без конца без края линия прямая,
Хоть сто лет по ней иди, не найдёшь конца пути.
– Теперь я разрежу прямую ножницами.
Учитель разрезает и прикрепляет к месту разреза солнышко.
– На что похожа линия? (На солнечный луч.)
– Именно луч вы сейчас видите перед собой. Можно ли продолжить луч со стороны разреза? (Нет.)
– А в другую сторону? (А в другую сторону можно.)
– Какие же существенные признаки луча вы только что выяснили? (Луч – это часть прямой, ограниченная с одной стороны.)
– Сравните луч и прямую. (Прямую можно продолжить в любую сторону, а луч только в одну. Луч имеет начало.)
– Можно ли изобразить луч на доске и в тетради? Начертите.
1 у доски, остальные в тетради.
– Давайте вернёмся к заданию для пробного действия. Под какими номерами изображены лучи? Докажите. (3; 4 и 6, так как это прямые линии, которые можно продолжить только в одну сторону. )
)
– Молодцы! Осталось определить, как люди договорились обозначать и называть лучи. Этот вывод вы сделаете в группах, используя карточки, которые я для вас подготовила. Спланируйте свою работу по этим карточкам. (Мы посмотрим, как обозначены все лучи, найдём общее и сделаем вывод.)
Раздать карточки для работы групп:
– Как же в математике принято обозначать лучи? (Двумя заглавными буквами. Первой называют ту букву, которая обозначает начало луча.)
Открыть на доске эталон обозначения луча:
– Вы достигли цели? Докажите. (Да, мы узнали существенные признаки луча и выяснили, как обозначают и называют лучи.)
– Какую следующую цель перед собой поставите? (Надо потренироваться в нахождении лучей среди других линий, в их обозначении и назывании.)
6. Первичное закрепление с проговариванием во внешней речи.
Цель:
создать условия для выполнения учащимися нескольких типовых заданий на применение изученного знания с проговариванием во внешней речи.
Организация учебного процесса на этапе 6:
1) – Вы начертили в тетради и на доске луч. Обозначьте и назовите его. (Например, луч SK.)
1 у доски с объяснением, остальные – в тетради.
2) – Скажите, а если ли я у луча отрежу ту часть, которую можно продолжать до бесконечности, какую фигуру получим? (Отрезок.)
При необходимости учитель может проделать эти действия у доски.
– Сравните луч и отрезок. (Луч имеет начало и не имеет конца, у отрезка есть начало и конец, его нельзя продолжить ни в какую сторону.)
– Предлагаю вам отработать каждое из понятий: прямая, луч, отрезок, выполнив № 3 (а) на стр. 7.
По 1 с места с объяснением.
– Объясните, почему именно с этой карточкой соединили прямую АВ? (Эту линию можно продолжить в оба конца до бесконечности. )
)
– Как по-другому можно назвать прямую? (ВА.) и т.д.
3) – Теперь выполните № 2 на стр. 7. Прочитайте задание.
– Докажите, что на рисунке изображены лучи. (Это прямые линии, ограниченные с одной стороны.)
– С какой целью вы будете выполнять это задание? (Потренироваться в обозначении и назывании лучей.)
– Выполняйте.
По 1 с места с объяснением.
4) – И чтобы окончательно закрепить ваши представления о луче, выполните № 4 на стр. 7. Прочитайте задание.
По 1 с места с доказательством.
– Как вы можете узнать, научились вы различать прямые, отрезки и лучи или нет? (Надо поработать самостоятельно.)
7. Самостоятельная работа с самопроверкой по эталону.
Цель:
1) организовать самостоятельное выполнение учащимися типовых заданий на применение нового знания;
2) организовать самопроверку учащимися своих работ по эталону для самопроверки;
3) создать (по возможности) ситуацию успеха для каждого ребёнка.
Организация учебного процесса на этапе 7:
– Выполните самостоятельно № 6 на стр. 8.
– Проверьте.
Открыть на доске эталон:
– Какие были затруднения? В чём их причина?
– Что осталось непонятным?
– У кого всё верно? Поставьте «+».
8. Включение в систему знаний и повторение.
Цель:
повторить счёт тройками, решение текстовых задач.
Организация учебного процесса на этапе 8:
1) Счёт тройками.
– Давайте немного отдохнём от линий и поработаем с числами. Вспомните счёт тройками. Считаем хором.
– Теперь запишите счёт тройками в тетрадь за 30 секунд.
– Проверим, ещё раз посчитав хором.
– Молодцы!
2) Решение текстовых задач.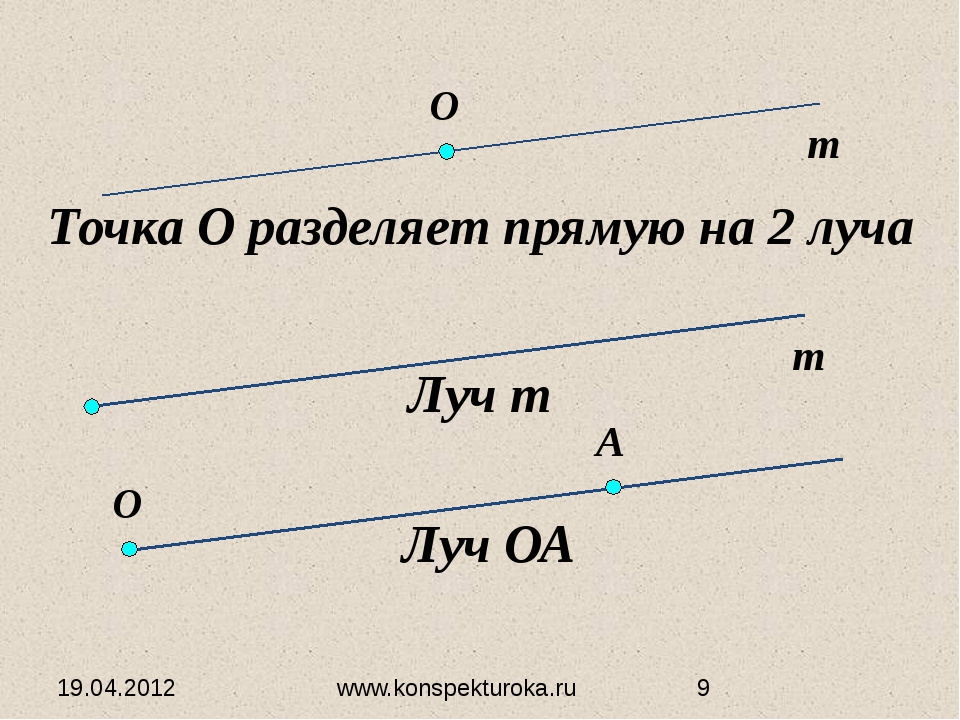
– Сейчас вы будете работать с задачами. Какая из линий, которую вы изучали сегодня на уроке, вам понадобится? (Отрезок, чтобы начертить схему.)
– Из каких двух частей состоит любая задача? (Из условия и вопроса.)
– Прочитайте условие задачи из № 7 на стр. 8.
– Можно решать задачу? (Нет, не хватает во-
проса.)
– Выберите из данных вопросов те, которые
можно поставить к задаче. (2 и 4.)
По 1 с места с обоснованием.
– Выберите схему ко второму вопросу. Обос-
нуйте.
– Решите задачу устно.
С места с доказательством.
– Какая схема соответствует четвёртому вопросу? (Последняя, так как …)
– Запишите решение и ответ этой задачи.
1 у доски выполняет анализ и записывает решение, остальные – в тетради.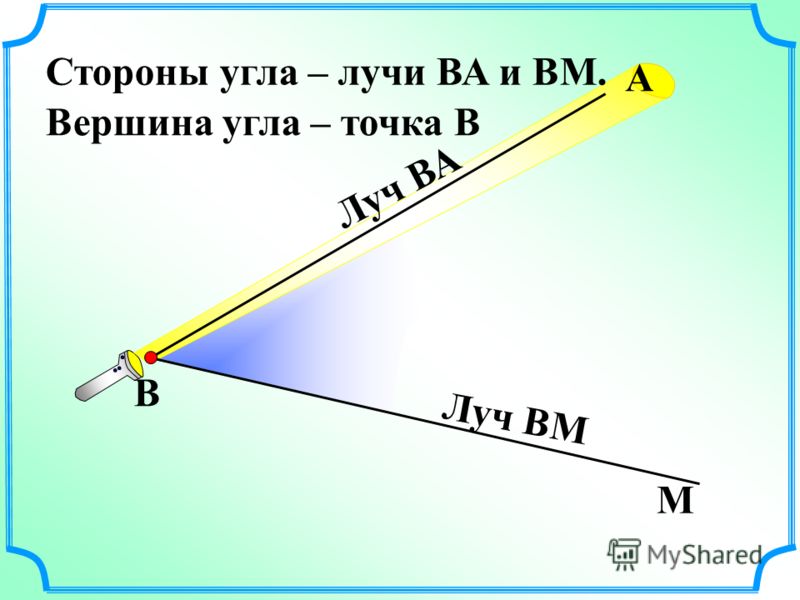
9. Рефлексия учебной деятельности на уроке.
Цель:
1) организовать фиксацию учащимися степени соответствия поставленной цели и полученного результата учебной деятельности;
2) создать условия для фиксации учащимися в речи нового знания, изученного на уроке: что такое прямая, луч, отрезок;
3) организовать самооценку учениками собственной учебной деятельности на уроке;
4) согласовать домашнее задание.
Организация учебного процесса на этапе 9:
– С какими линиями вы работали сегодня на уроке? (С прямой, лучом и отрезком.)
– Что было для вас новым? (Что такое луч, как его обозначают и называют.)
– Достигли вы поставленной цели? Докажите.
– Что вы узнали о луче?
– Что вы знаете о прямой, об отрезке?
– Какое средство, принесённое гномиком, помогло вам понять отличие между этими линиями? (Клубок, нить.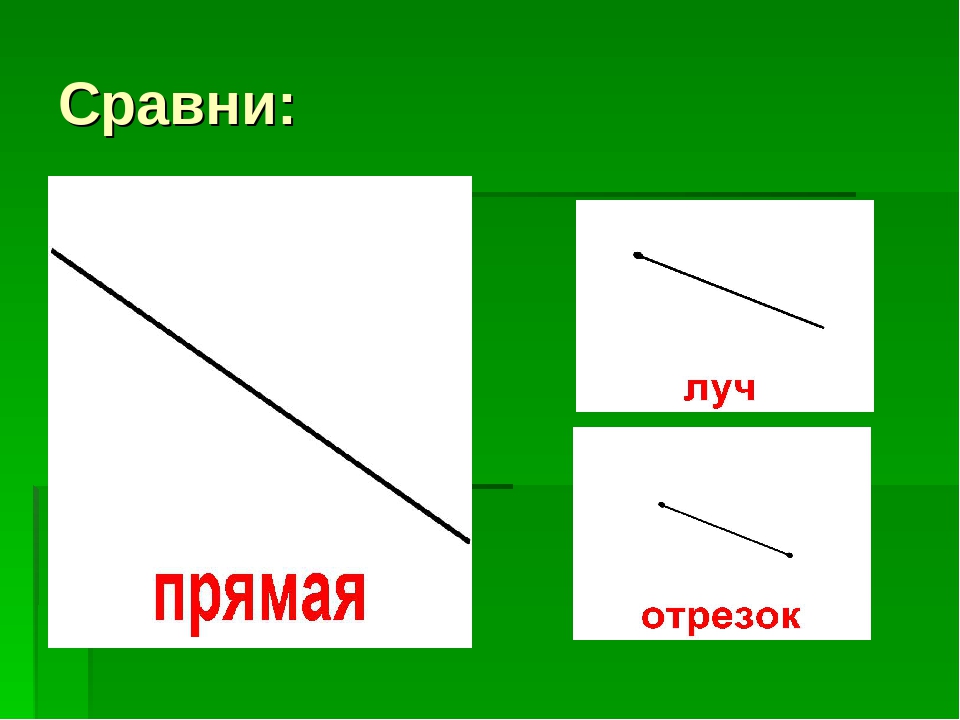 )
)
– Оцените свою работу как работу ученика.
– Наш гость тоже кое-чему научился. Он сначала провёл прямую и по ней ровно и красиво написал… Прочитайте хором.
Открыть на доске: Спасибо за помощь!
7
Урок математики » Луч и его обозначение » 2 класс УМК 21 век | Учебно-методический материал по математике (2 класс) на тему:
Конспект урока математики 2 класс
Тема: Луч и его обозначение
Тип урока: ОНЗ (открытие новых знаний), урок в технологии деятельностного метода
Цель урока:
- Познакомить учащихся с понятием луча как бесконечной фигуры.
- Учить показывать луч с помощью указки.
Задачи урока:
- Познакомить с геометрической фигурой луч.
- Обозначать луч.
- Научится отличать луч от других геометрических фигур.
- Чертить ( строить) луч.
Оборудование:
Учебник: Математика: 2 класс: часть 1, В. Н. Рудницкая, Е.Э. Кочурова, О.А. Рыдзе. М.: Вентана Граф, 2012, Начальная школа XXI века;
Н. Рудницкая, Е.Э. Кочурова, О.А. Рыдзе. М.: Вентана Граф, 2012, Начальная школа XXI века;
Рабочая тетрадь: 2 класс: часть 1, В.Н.Рудницкая, Т.В. Юдачева. М.: Вентана Граф, 2012, Начальная школа XXI века.
Ход урока:
I Орг .момент
-Ребята, как прошла у вас перемена ?
У нашей совы Веры тоже хорошо! (Вера веселилась, играла в подвижные игры)
Посмотрите , что она с клубком сделала?
А теперь стала спокойная , как вы думаете почему? ( начался урок математики)
Давайте сделаем так, пока я буду сматывать клубок , вы должны успеть перечислить , что нам понадобится на уроке? ( учебник)
А для чего нам нужен учебник ? ( в нем важная информация), тетрадь, линейка, ручка, карандаш, пенал .
И всё? Подумайте?( смекалка, трудолюбие, взаимопомощь, дружба).
Всё я клубок смотала.
Ну, что приступаем к работе. Вместе с Верой « Вперёд к знаниям».
II Освоение нового знания
1)Подведение к теме урока ( практическая работа)
-Итак, что у меня в руке? ( клубок)
-Хорошо
-На что он похож? Какую геометрическую фигуру напоминает? ( точку , ставлю на доске)
— Что я сделала?( чуть-чуть отмотала)
— Я могу это изобразить графически ? ( показать на доску)
Как? ( взять линейку и от точки провести прямую)
((Если скажут ,что это луч ( какое интересное слово Луч) )
— На что похоже? ( на луч солнца)
-Посмотрите была точка, а появилась новая геометрическая фигура.
Давайте дадим ей название? Предлагайте?
2) Формулирование темы урока и постановка задач
— Так, что мы сегодня будем изучать? ( новую геометрическую фигуру)
— Какую фигуру? (луч) на боковой доске, посередине креплю тему урока « Луч»
-Что бы вы хотели узнать о луче?
С 1 класса мы задаём вопросы Что? Как? Почему?
— Когда мы знакомимся с новой фигурой, то спрашиваем Что это такое ?
А сегодня работая с новой геометрической фигурой луч ?
Какой зададим вопрос ? ( Что такое луч?) Цепляю на боковую доску 1 вопрос
-Хорошо
-Что ещё мы можем узнать о луче?
-Как чертить? Цепляю на боковую доску 2 вопрос
Как обозначать? Цепляю на боковую доску 3 вопрос
3) Практическая работа
— Давайте попытаемся ответить на 1 вопрос, что такое луч? Ваше мнение? ( тишина)
— Прежде всего что это? Что такое овал, квадрат, прямоугольник?( это геометрические фигуры)
— Луч тоже геометрическая фигура.
-Давайте посмотрим, что в ней особенного( зову 2 детей Карину и Рому)
— Подойдите пожалуйста ко мне ( даю клубок одному ребёнку ) .
Что Карина держит в руке? ( начало клубка)
-Значит, начало есть. Продлеваем наш луч. Карина отматывает, Рома двигайся в сторону
-А как вы думаете, как долго может длиться наш луч ? ( пока клубок не закончится)
— Давайте представим, что наш клубок размером с планету или вселенную, тогда как будет длиться наш луч ( бесконечно).
А если там внутри паук бесконечно плетёт их или вечный двигатель ( механизм), который постоянно плетёт нити , то как будет длиться наш луч (бесконечно).
III Первичное закрепление
-В каком направлении может двигаться луч, сразу в две стороны или только в одну?
Правильно. От точки начала луч движется только в одном направлении.
В нашем случае в каком направлении? (вправо)
Хорошо. Ребята дайте мне клубок. А может в любом другом направлении? ( я показываю на клубке с ниткой вверх, вниз, влево и вправо.
Конечно может.
— Давайте сделаем вывод что же такое луч? ( Луч- это геометрическая фигура, которая имеет начало , но не имеет конца)
— Мы ответили на 1 наш вопрос? ( ставлю + на доске возле 1 вопроса)
4) Учебный диалог , обозначение луча ( работа с информацией)
Ребята работаем с учебником.
— Кто уже открыл?
-На какой странице?
— Почему? ( потому что тема урока «Луч и его обозначение»)
-Скажите ,а тема нашего урока относится к каким знаниям?
-Может быть к арифметике, алгебре или информатике, а может к геометрии?
-Хорошо
-Посмотрите на 2 рисунка, как видят авторы учебника луч?
-С чем его сравнивают?( с солнечными лучами)
— А мы с чем сравнивали? ( клубок и нитки)
-Значит мы думаем также , как и авторы учебника. Молодцы
-Найдите в учебнике значок важная информация .
-Все нашли? Кто не нашёл? Соседи покажите.
— Ребята поработайте с этой статьёй самостоятельно, прочтите про себя ( молча) и постарайтесь понять ( советую 2 раза) . Пожалуйста работайте ( даю 2-3 минуты)
— Сколько раз успели прочитать?
-На какой из этих вопросов отвечает статья учебника ? ( показываю на боковую доску ,2 вопрос)
— Хорошо.
-Что о луче вы для себя узнали? ( включаю интерактивную доску уч.с.19)
— Кто обозначит наш луч? Ещё что поняли? (Точка А- начало луча),
-Всё? ( Буква В- может обозначать любую точку на луче).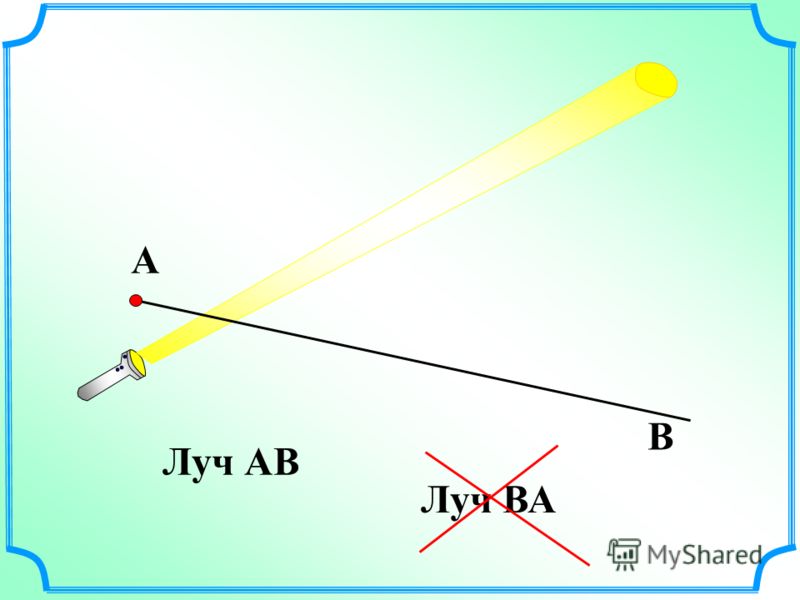
— Да , конечно, это очень важно, писать буквы надо строго в определённом порядке: первой пишется буква над точкой , которая обозначает начало луча, вторая буква пишется ближе к концу нарисованной части луча.
— Вся информация? ( читают так АВ)
— Как читается ? ( читается от начала луча)
— Давайте прочитаем хором ( АВ)
— Всё? ( Конца у луча нет)
— В этом мы с вами убедились.
Мы с вами ответили на 2 вопрос? Как обозначать? ( ставлю + на доске возле 2 вопроса)
5)Первичное закрепление
Найдите в учебнике задания, которые проверяют , как мы поняли что такое луч и его обозначение (№ 2)
Почему? ( т.к. в задании №2 сказано прочитай название луча)
Хорошо, работаем по заданию.
Чем являются лучи для богатыря? (дорогами) . а из текста задание возьмите нужное слово? ( направлением )
Кто прочитает и укажет первое направление?( луч АМ ). А почему не МА?
Найдите доказательство учебнике (рубрика обрати внимание).Вызываю 2 и 3 человека .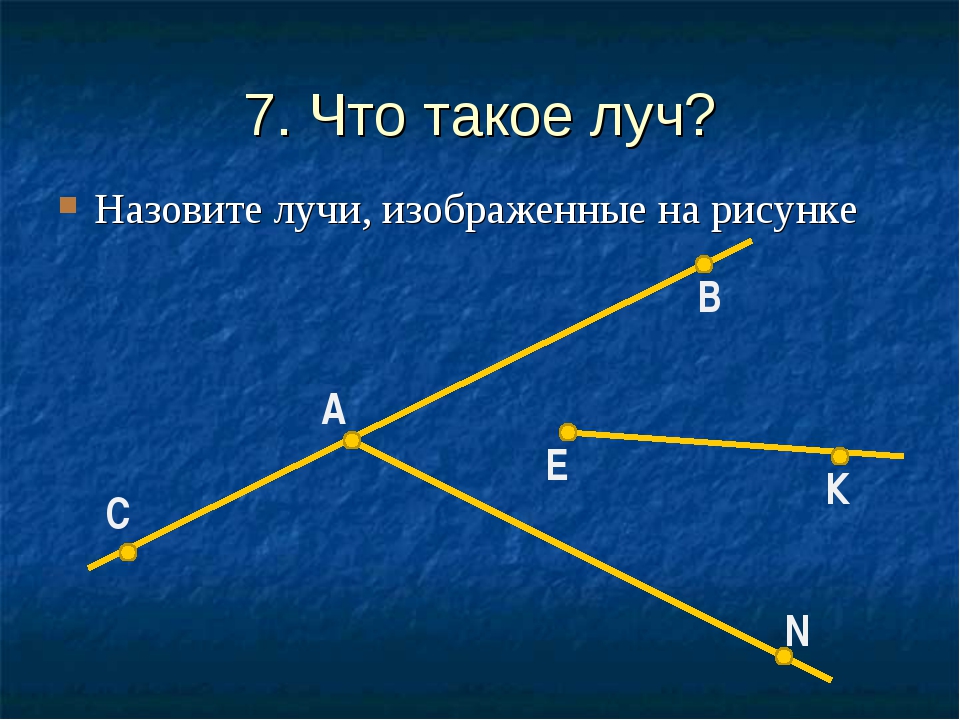
Сколько здесь направлений ? (3). Могло быть больше? (да)
Есть ещё задание, чтобы проверить наши полученные знания? (да) № 3
Полина прочитай задание ( ребёнок читает вслух)
Чем отличается это задание от предыдущего? ( найти только луч, а здесь и отрезки)
Тогда, что нам нужно учесть выполняя это задание?
Какие знания нам понадобятся( что такое отрезок и что такое луч)
Хорошо . Кто найдёт и назовёт лучи ( вызываю к доске детей ).
Кто хочет показать и назвать отрезки?
Если ребёнок ошибётся — Ты уверен? Подумай ещё? Поможем Паше?
Ты понял в чём ошибка?)
Так чем отличается луч от отрезка?
Физминутка ( рисуем фигуры – круг, овал и квадрат)
6) Составление алгоритма построения луча.
На какой вопрос нам осталось ответить? ( как чертить)
Хорошо. А как бы вы построили луч?
Давайте продумаем с вами все действия по порядку построения луча( Поставим точку-это начало луча ).
Дальше? ( возьмём линейку, приложим к началу луча и проведём прямую линию)
Все действия перечислили?( нет, надо ещё обозначить наш луч)
Хорошо. Всё? ( да)
Всё? ( да)
Найдите, пожалуйста в учебнике № 4, который нас учит, как построить луч.
Давайте сверим. ( на интерактиве учебник с алгоритмом)
Какой первый шаг? ( прошу прочитать 3 детей).
Что вы можете сказать, наши предположения совпадают или отличаются ? ( совпадают)
7) Построение луча. Практическое задание.(№ 5)
Над какой темой мы работаем ? (луч)
Хорошо.
Давайте потренируемся, в № 5 нам предлагают начертить 2 луча.
Прочитайте название лучей, назовите начало первого луча? ( точка М )
Почему ? ( она стоит первая в названии луча)
Хорошо. А как вы думаете где мы будем чертить луч ? ( в тетради под сегодняшней датой).
А я изображу наш луч на доске.
Я выбираю направление луча вверх , а вы ?
Только давайте договоримся, если у вашего луча будет направление вниз- то, чтобы сэкономить место в тетради отступите одну клеточку от классной работы, у кого луч будет направлен в сторону влево или вправо – отступите небольшое расстояние , у кого вверх- давайте отступим 6 клеток, посмотрите в учебнике небольшие лучи изображены, чтобы не тратить много бумаги- в этом проявляется бережное отношение к природе и нашим лесам).
Давайте попробуем начертить наш луч МК (проговариваем алгоритм построения луча, я выполняю –на доске).
Попробуйте начертить самостоятельно второй луч.
Назовите его начало, почему вы так решили?
Кто хочет это сделать на доске? ( ребёнок выполняет задание на доске, я смотрю тетради у других детей )
( несколько работ показываю через документ-камеру, Маша выполнила так задание) .
Поднимите вверх и покажите друг другу , как вы справились с этим заданием.
IV Учебная рефлексия( самостоятельная работа на листах)
Сейчас мне бы очень хотелось посмотреть как вы усвоили этот материал.
У каждого из вас на парте лист приступайте к выполнению заданий , даю вам 5 минут.
8) Самопроверка.
Время выполнения работы закончилось.
Я надеюсь, что все справились.
Возьмите в руки красный карандаш.
Давайте проверять, обратите внимание на доску и исправляйте , если это нужно.
Кто полностью справился, поставьте на полях плюс. Кто нашёл у себя ошибку,
Кто нашёл у себя ошибку,
поделитесь ? ( показать на интерактивной доске)
V Итог урока.
А) рефлексия ( технология рюкзак знаний).
Передаю рюкзак каждому ребёнку , он должен ответить , что нового узнал?
Чему научился? Что понял?
Сдайте пожалуйста тетради на проверку.
Завтра на уроке математики мы узнаем ещё много интересного и важного о луче.
б) Д/З.
Ваше задание на дом будет таким — на индивидуальном листе ксерокопии выполнить
№ 1,2,3.
И задание от нашей Веры по желанию: нарисовать рисунок из нашей жизни,
где могут прятаться лучи в разных предметах или объектах.
лучей — Концепция — Геометрия Видео от Brightstorm
Луч является частью линии, имеет одну фиксированную конечную точку и бесконечно проходит вдоль линии от конечной точки. Противоположные математические лучи — лучи с общей конечной точкой, проходящие в противоположных направлениях и образующие линию.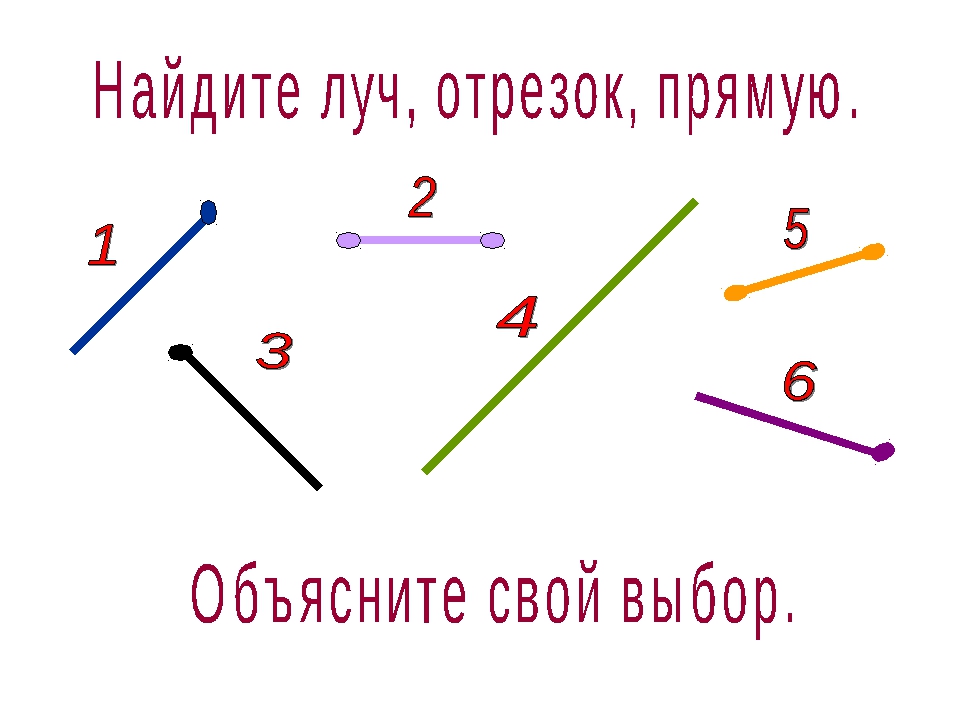
Если бы у нас была линия, которая бесконечно продолжалась
в любом направлении, и я где-то выбрал конечную точку
и стер все
, выходящие за пределы этой конечной точки
, то я создал только
луч.
Итак, у луча одна конечная точка, и он бесконечно простирается на
от этой конечной точки.
Но как обозначить луч?
Ну, вы начинаете с того, что говорите
, какова ваша конечная точка?
Моя конечная точка этого луча — A, потому что это
, где он начинается, и он простирается от
до точки B. Итак, я собираюсь обозначить этот луч
как линию, но
у меня только одна стрелка.
Итак, стрелка
проходит над B.
Поскольку моя конечная точка — A и обратите внимание, что у меня
нет стрелки над A, которая
сообщает ученику-геометру или учителю геометрии
, что этот луч начинается с
.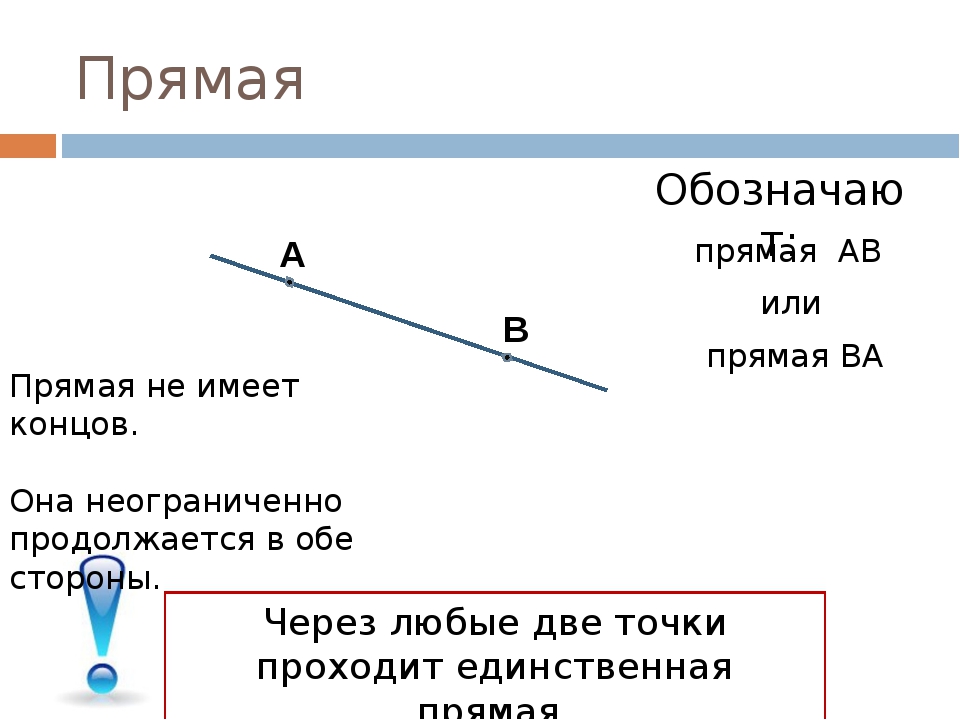 А и проходит через Б.
А и проходит через Б.
Теперь у вас также могут быть противоположные лучи,
и противоположные лучи имеют общую конечную точку
.
Итак, если вы посмотрите на эту строку прямо здесь,
содержит X, Y и Z, где X, Y и
Z все коллинеарны.
У нас есть противоположные лучи
, если я выберу точку Y.
Итак, я мог бы сказать, что луч Y, Z — так что снова
, я говорю от точки Y до точки
Z. Итак, идите YZ и обратите внимание, как
я выравниваю. здесь стрелка находится на
над Z, потому что она начинается с Y и
, противоположной будет луч
, начинающийся с Y, проходящий с
через X.
Так что я могу обозначить это как луч YX.
Таким образом, противоположные лучи имеют общую конечную точку, а
лучей в целом имеют одну конечную точку, а
бесконечно продолжаются от
этой конечной точки.
Что такое луч в геометрии? | Определение и примеры (видео)
Найдите светодиодный фонарик. Войдите в темную комнату и включите фонарик. Вы только что смоделировали луч, плоскую фигуру в геометрии, которая имеет одну конечную точку, но вечно продолжается в другом направлении.Лучи и реальные примеры лучей есть повсюду.
Войдите в темную комнату и включите фонарик. Вы только что смоделировали луч, плоскую фигуру в геометрии, которая имеет одну конечную точку, но вечно продолжается в другом направлении.Лучи и реальные примеры лучей есть повсюду.
Содержание
- Видео
- Определение луча в геометрии
- Как нарисовать луч по математике
- Символ и этикетка Ray
- Луч в примерах геометрии
Определение луча в геометрии
Луч можно рассматривать как фрагмент или сегмент линии. В плоской геометрии луч легко построить по двум точкам. Один будет конечной точкой, началом луча.Другой момент — это просто указатель, способ дать лучу имя. Линия, соединяющая две точки, тянется бесконечно только в одном направлении:
Вместо того, чтобы позволить обоим концам линии длиться вечно, мы отрезаем одну сторону в заданной точке. Теперь у нас есть луч.
Как нарисовать луч по математике
Чтобы нарисовать луч, поместите две точки на лист бумаги. Обозначьте обе точки заглавными буквами. Выберите одну точку в качестве конечной. Используйте линейку, чтобы нарисовать линию, начиная с конечной точки и продолжая через вторую точку.Нарисуйте одну стрелку на открытом конце вашей линии (тот, который находится напротив конечной точки). Там! У вас есть луч:
Обозначьте обе точки заглавными буквами. Выберите одну точку в качестве конечной. Используйте линейку, чтобы нарисовать линию, начиная с конечной точки и продолжая через вторую точку.Нарисуйте одну стрелку на открытом конце вашей линии (тот, который находится напротив конечной точки). Там! У вас есть луч:
Символ и этикетка Ray
Чтобы обозначить и обозначить луч, нам нужно идентифицировать эту конечную точку. Нам также понадобится еще одна точка на односторонней линии. Затем мы записываем конечную точку и другую точку вместе заглавными буквами, ограниченными крошечной односторонней стрелкой (указывающей вправо):
Это символ Рэя Р.Н. →, названного в честь квотербека НФЛ, который может бросать футбольный мяч, который движется почти как луч.Гравитация тянет мяч вниз, но скорость и сила рук квотербэков могут сделать короткие передачи похожими на прямые лучи. Он конечная точка; Путешествующий футбол — это линия с односторонним движением.
Луч в примерах геометрии
Луч солнечного света есть луч. Он берет начало у нашей звезды, Солнца, и движется в одном направлении, ударяясь о Землю примерно через восемь минут после того, как покинул свою «конечную точку», Солнце.
Он берет начало у нашей звезды, Солнца, и движется в одном направлении, ударяясь о Землю примерно через восемь минут после того, как покинул свою «конечную точку», Солнце.
Профессиональный теннисист Рафаэль Надаль, как известно, подает теннисные мячи со скоростью около 217 км / ч (135 миль / ч), которая так хорошо сопротивляется силе гравитации, что кажется, будто летит по прямой, как луч.
Луч света от классного ЖК-проектора представляет собой луч; так же свет от кинопроектора в вашем местном кинотеатре.
Путь, по которому стрела идет из лука, является лучом и имеет дополнительное преимущество в том, что он имеет форму стрелы.
Лазеры являются прекрасным примером лучей, потому что в отличие от спортивных мячей на них не сильно влияет земная гравитация, поэтому они светят ровными прямыми односторонними линиями от своего источника.
Слово предостережения
Поскольку носители английского языка, читатели и писатели двигают глазами слева направо, почти все лучи, которые вы видите в математических символах, будут иметь левые концы и стрелки вправо. Однако имейте в виду, что геометрия — это чистая наука . Лучи могут идти в любом направлении, например, вверх, вниз, влево, вправо и по диагонали.
Однако имейте в виду, что геометрия — это чистая наука . Лучи могут идти в любом направлении, например, вверх, вниз, влево, вправо и по диагонали.
Следующий урок:
Что такое прямая линия?
Линий, лучей и углов — бесплатный урок геометрии с упражнениями
На этом уроке геометрии для четвертого класса изучаются определения линии, луча, угла, острого угла, прямого угла и тупого угла. Мы также изучаем, как размер угла определяется ТОЛЬКО тем, насколько он «раскрылся» по сравнению со всем кругом.Урок содержит множество разнообразных упражнений для студентов.
| ||||||||||
Линия не имеет начальной или конечной точки. Представьте, что это продолжается
бесконечно в обоих направлениях. Мы можем назвать линию, используя две точки на ней.Это строка EF или строка
(обратите внимание на стрелки). | ||||||||||
| ||||||||||
Что
угол? Много людей
думаю, что угол — это какая-то наклонная линия Это
точка называется вершиной , а два луча называются сторон Чтобы назвать
угол, мы используем три точки, перечисляя вершину посередине. |
1. Напишите, является ли каждая фигура линией, лучом, отрезком линии,
или угол, и назовите его.
Напишите, является ли каждая фигура линией, лучом, отрезком линии,
или угол, и назовите его.
а. _______________________ | б. _______________________ | г. _______________________ |
г. _______________________ | е. _______________________ | ф. _______________________ |
2. а. Найдите угол, образованный лучами DE и DF.
Как мы это называем?
г. Найдите образованный угол
лучами CA и CE.
Как мы это назовем?
г. Что такое BD? (линия,
отрезок или луч)?
3. а. Нарисуйте две точки, D и E. Затем нарисуйте
линия DE.
а. Нарисуйте две точки, D и E. Затем нарисуйте
линия DE.
г. Точка вытяжки Q не на линия.
г. Нарисуйте лучи DQ и EQ.
г. Найдите углы EDQ и DEQ в вашем Рисунок.
| |||||
Если угол открывается до полный | Этот угол составляет половину полного круга, Ваши два карандаша (лучи)
лежа | Это четверть от Это называется справа | |||
На каждой из этих картинок ракурс раскрывается больше и больше и держит становится все больше. Дуга круга больше. Эти углы острые углы , что означает, что они меньше чем право угол (менее 90 °). Думайте об острых углах как о острых углах.Если кто-то зарезал у вас острие острого угла, он будет ощущаться острым. | Угол открыт даже Думайте о тупых углах как о | ||||
Вот еще один способ мышления об углах.Представьте себе восход солнца над горизонтом, постепенно поднимающийся выше, и путешествуя по небу по дуге круг. |
| Насколько велик угол? Неважно, какой длины стороны угла находятся. Помните, что это лучи, и лучи продолжаются бесконечно. Но когда мы рисуем их на бумаге, мы должны рисовать их где-то концами. Стороны
может даже показаться, что угол имеет разную длину. Это не
тоже имеет значение. Размер уголка определяется ТОЛЬКО , как
сильно он «раскрылся» по сравнению с целым кругом . | ||||||||||||
|
4.Какой угол больше?
5. а. Три разных эскиза
острый
углы.
г. Три разных эскиза
тупые углы.
г. Набросок под прямым углом
и
прямой угол.
6. Обозначьте углы как острые, прямые, тупые или прямые. К
помогите, сделайте эти углы двумя карандашами,
проверка, сколько тебе нужно
чтобы открыть угол.
7. У треугольника три угла. В Фактически, слово трехугольник означает трехугольную форму.
| Какой из треугольников a, b или c имеет один тупой угол? | а. | б. | г. |
8.(Необязательно) Сделайте тетрадь геометрии где записываешь каждый новый термин и рисуешь картинку
или
картинки, иллюстрирующие
срок. Используйте цвета и аккуратный текст. Это похоже на ваш
персональная геометрия
толковый словарь. Вы также можете решать любые задачи с рисованием из
уроки в нем. Рисование и письмо
себя вместо
просто прочтите, это поможет вам лучше запомнить термины!
| Новые условия | ||
|
Этот урок взят из книги Марии Миллер Math Mammoth Geometry 1 и размещен на сайте www. HomeschoolMath.net с разрешения автора. Авторские права © Мария Миллер.
HomeschoolMath.net с разрешения автора. Авторские права © Мария Миллер.
линий, сегментов линий и лучей — математика для 3-го класса
Узнайте о линиях, сегментах линий и лучах
Вы знаете, что такое геометрия?
Геометрия — это математика форм и пространств.
😃 В geometry мы работаем с различными формами.
(Вы можете назвать каждую из этих форм? Попробуйте! 🤗)
В геометрии мы также работаем с более простыми вещами, такими как точек, линий, отрезков линий, и лучей .
Это строительных блоков геометрии.
В этом уроке давайте узнаем о каждом из них.
Что такое очки?
🤓 Посмотрите на эти точки.
Каждая из этих точек называется точкой .
точка — это любое место в космосе. Он не имеет длины, высоты или ширины .
👉 Очки обозначаются одиночными заглавными буквами .
Например, это точка А.
👉 Кончик карандаша можно рассматривать как острие.
👉 Каждое место на фигуре представляет собой точку.
Что такое линии?
😃 Посмотрите на это изображение. Он показывает горизонт.
Можете ли вы сказать, где заканчивается горизонт с обеих сторон? 🤔
Нет, не можем. 🤓
Это потому, что горизонт продолжает идти с обеих сторон. Это никогда не заканчивается. Это называется линия .
Это никогда не заканчивается. Это называется линия .
Линия — это прямой путь точек, который вечно продолжается в обоих направлениях.
В геометрии рисуется линия со стрелками на обоих концах.
Как вы думаете, мы можем измерить длину линии? 🤔
Нет! 😁 Мы не можем.
✅ Поскольку линия никогда не заканчивается, мы не можем измерить ее длину .
👉 Чтобы назвать линию, используйте любые две точки на ней.
Например, чтобы назвать эту линию, мы используем две точки на ней, A и B, и называем ее Line AB или Line BA.
При написании имени поместите двустороннюю стрелку поверх этикетки.
Что такое линейные сегменты?
🤓 Посмотрите на края этой шахматной доски.
Каждое ребро представляет собой линейный сегмент .
Линейный сегмент — это прямой путь с двумя конечными точками.
Отрезок линии с точками на каждом конце.
Можете ли вы измерить длину отрезка? 🤔
Да! Вы можете! 🤗
✅ Это потому, что в определенный момент отрезок линии заканчивается .
👉 Чтобы назвать сегмент линии , используйте его конечные точки.
Например, этот линейный сегмент может называться Линейный сегмент AB или Линейный сегмент BA .
При написании имени поставьте строку поверх этикетки.
Что такое лучи?
Посмотрите на эти лучи света. 🌞
🌞
Мы знаем, где начинаются лучи.
Но вы можете сказать, где кончаются эти лучи? 🤔
Нет! Мы не можем.
Это потому, что луч начинается в одной точке и всегда движется в обратном направлении.
Луч — это прямой путь из точек, который начинается в одной точке и продолжается в одном направлении вечно.
✅ У луча одна конечная точка.
Рисуется луч с точкой на одном конце и стрелкой на другом.
Можете ли вы измерить длину луча? 🤔
Нет! 😎 Вы не можете.
✅ Это потому, что луч, как и линия, никогда не заканчивается.
👉 Чтобы назвать луч , начните с его конечной точки и закончите в любой точке на другой стороне.
✅ Помните! Существует только один способ назвать луч , который начинается с его конечной точки.
Например, этот луч можно назвать Ray XY (но не Ray YX).
При написании имени поместите одностороннюю стрелку поверх этикетки.
Смотри и учись
Поздравляем! 👏 Теперь вы знаете, что такое прямые, отрезки и лучи. Начните свою практику ниже.
Что такое линии, сегменты линии, лучи и противоположные лучи
Что такое линия в геометрии?
Определение линии: Линия не имеет начальной или конечной точки.Это просто продолжается бесконечно в обоих направлениях. Линия имеет только одно измерение: длину. Линия обычно имеет 2 точки, но может иметь много точек.
Вы можете позвонить по номеру Line XY или Line a, a всегда будет написано маленькой буквой .
Что нужно помнить О линии:
- Нет начальной или конечной точки
- Линия A продолжается бесконечно в обоих направлениях
Вы можете нарисовать много линий, используя одну точку, но если есть только две точки, вы можете нарисовать только одну линию.
Что такое линейный сегмент?
Сегмент линии — это просто часть линии, имеющая 2 конечные точки. В приведенном ниже примере MN — это линейный сегмент для первой линии, а CD — это линейный сегмент для второй линии.
Итак, если вы хотите нарисовать отрезок линии MN и CD, он будет выглядеть следующим образом:
Что такое луч в геометрии?
У луча есть начальная точка, и он бесконечно продолжается только в одном направлении. Он не может расширяться в обоих направлениях, как Line. Возьмем, к примеру, луч факела. Начальная точка — факел, но конечная точка не определена, и она освещает все, к чему прикасается. Даже если вы переместите резак, начальная точка никогда не изменится.
Он не может расширяться в обоих направлениях, как Line. Возьмем, к примеру, луч факела. Начальная точка — факел, но конечная точка не определена, и она освещает все, к чему прикасается. Даже если вы переместите резак, начальная точка никогда не изменится.
Вот еще один пример Ray XY :
Что нужно помнить о лучах
- Луч имеет начальную точку и бесконечно продолжается только в одном направлении.
- Вы всегда будете определять первую точку луча в начале (точно так же, как красное пятно на изображении выше с началом X).Конечная точка может быть указана где-нибудь рядом с наконечником стрелки, но не на наконечнике стрелки.
Видео, поясняющее линию, луч и линейный сегмент
Что такое противоположные лучи в геометрии?
Противоположные Лучи — это те 2 луча, которые начинаются точно из одной точки, но продолжаются в противоположном направлении. Возьмите пример противоположных лучей ниже:
Возьмите пример противоположных лучей ниже:
Начальная точка для лучей ZX и ZY — это Z, , а затем они оба идут в противоположном направлении, образуя 2 противоположных луча: ZX и ZY.
Что нужно помнить о противоположных лучах
- Оба луча должны начинаться из одной точки
- Необходимо ехать в обратном направлении
- Должен образовать линию
Идентификация противоположных лучей (видео)
Линии, лучи, отрезки | Параллельные линии | Перпендикулярные линии
В геометрии часто бывает ошибкой говорить, что сегмент и линия — это одно и то же.
Отрезок имеет определенное начало и определенный конец, причем каждый конец представлен точкой.
Примеры сегментов: длина стола, расстояние до прямой дороги и т. Д.
С другой стороны, линия не имеет определенного начала или конца.
Сегмент является частью линии, но линия не является частью сегмента.
Мы можем видеть так много примеров прямых линий вокруг нас, края здания, дороги, по которым мы путешествуем.
Разберемся с линиями подробнее.
Линия — это фигура, образованная, когда две точки соединены с минимальным расстоянием между ними, а оба конца вытянуты в бесконечность.
Хотя линии не имеют определенного начала или конца, они представлены в нашей повседневной жизни такими примерами, как железнодорожные пути или автострады.
Луч — это часть линии, которая имеет только одну фиксированную точку, а другая точка не имеет конца.
Хотя лучи имеют фиксированное начало и не имеют определенного конца, они представлены в нашей повседневной жизни такими примерами, как солнечный свет или свет факела.
Сегмент — это часть линии, имеющая фиксированную длину, или мы можем сказать, что оба конца сегмента фиксированы.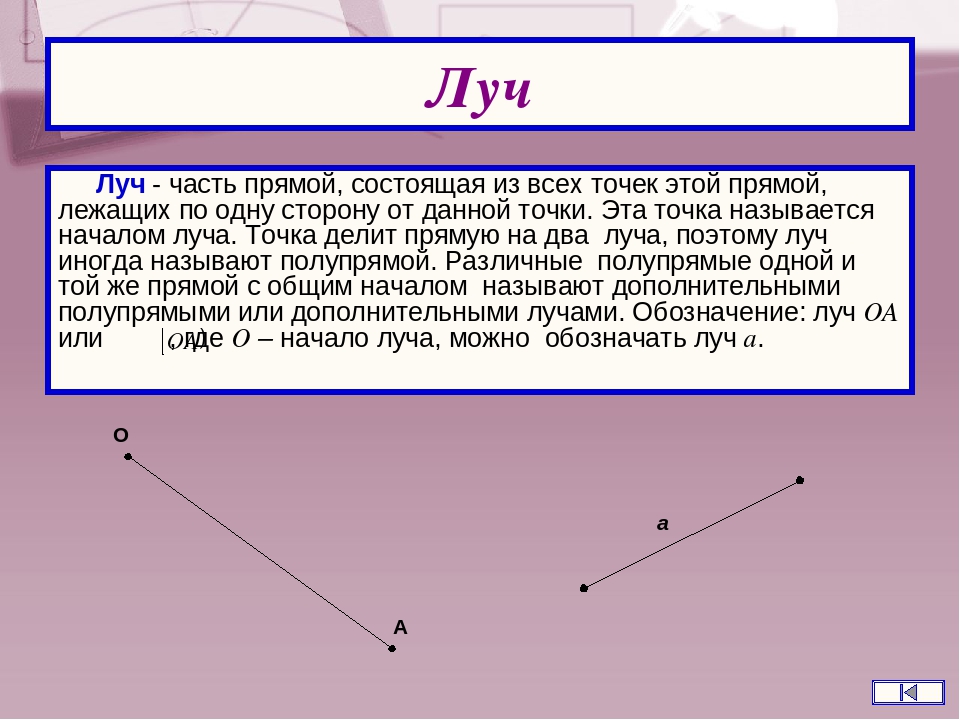 Сегменты, иногда также называемые линейными сегментами.
Сегменты, иногда также называемые линейными сегментами.
Хотя линейные сегменты имеют оба фиксированных конца, в нашей повседневной жизни они представлены такими примерами, как край стола, провод или столб.
Аналитический центр
- Предположим, вы привязали веревку к одной точке на Земле и начали идти, держа другой конец веревки в руке. Вы идете по прямой, спустя столько месяцев вам каким-то образом удалось вернуться в ту же точку, с которой вы начали.Один из ваших друзей отмечает, что когда вы двигались по веревке, фигура, полученная с помощью веревки, не была линией. Какой ответ вы дадите своему другу?
Две прямые называются параллельными, если они лежат в одной плоскости и никогда не пересекаются.
Или мы можем сказать, что если две прямые не имеют точки пересечения, они называются параллельными линиями.
Пересекающиеся линии Если две линии пересекаются в одной точке, они считаются интересными линиями. {\ circ} \), то они перпендикулярны друг другу.
{\ circ} \), то они перпендикулярны друг другу.
Изучите типы линий в приведенном ниже моделировании.
Горизонтальные и вертикальные линии
Линии классифицируются на основе их расположения.
Горизонтальные линииЛинии, нарисованные горизонтально, называются горизонтальными линиями.
Вертикальные линииВертикальные линии называются вертикальными линиями.
Косая или наклонная линия
Линии, которые нарисованы в наклонном положении или образуют угол, отличный от 0, 90, 180, 270, 360 градусов с горизонтальными или вертикальными линиями, называются наклонными или наклонными линиями.
Важные примечания
- Линия не имеет конечных точек.
- Луч имеет только одну фиксированную точку.
- Сегмент линии — это часть линии фиксированной длины.

- Перпендикулярные линии имеют угол между ними 90 градусов.
- Параллельные линии не пересекаются.
Сэм хочет найти фигуры, состоящие только из отрезков линий. Помогите ему выбрать правильные цифры из следующего.
Решение
Давайте обсудим каждый вариант по порядку:
Вариант А состоит из 5 линейных сегментов.
Вариант B состоит из 3 отрезков линии и изогнутой части.
Вариант C представляет собой круг, поскольку он состоит только из изогнутых частей.
Вариант D состоит из 4 линейных сегментов.
\ (\ следовательно \) Опции A и D верны. |
Найдите правильные типы линий на рисунке ниже.
Решение
Вариант А — пара параллельных линий
Вариант B — это пара непараллельных линий или линий пересечения.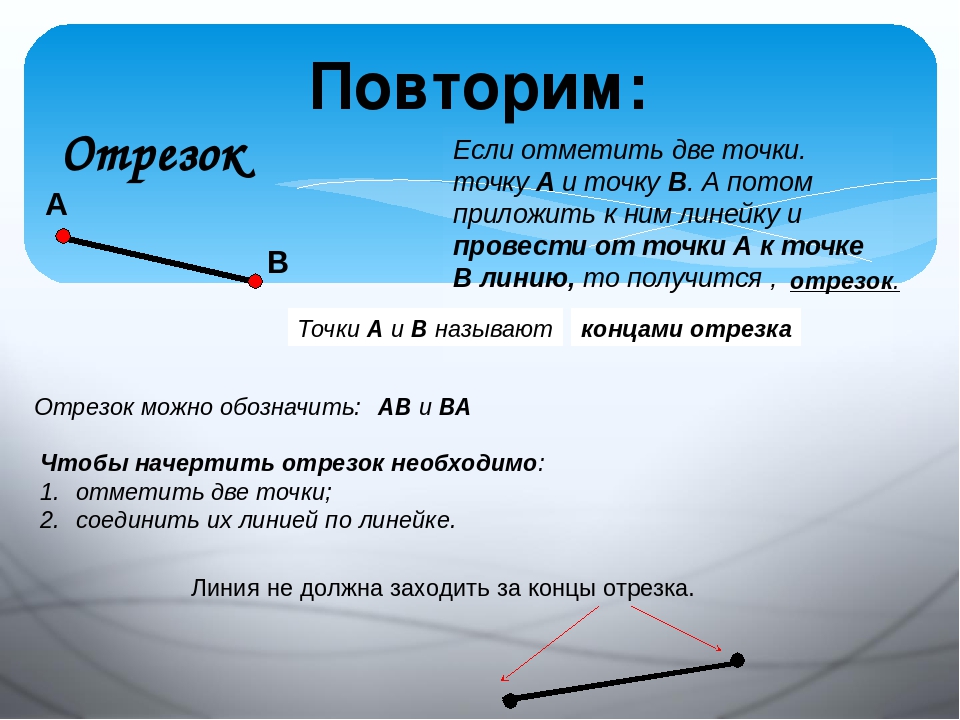
Вариант C — это пример перпендикулярных линий.
Том выбирает точки пересечения линий, показанных на рисунке ниже, он заметил, что есть 5 точек пересечения. Он прав?
Решение
Точки пересечения любой из этих линий: \ (\ text {A, B, C, D, E, F} \)
Следовательно, всего 6 точек пересечения.
| \ (\ следовательно \) Том не прав |
Интерактивные вопросы
Вот несколько занятий для вас.
Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Подведем итоги
Надеемся, вам понравилось узнать о линиях с интерактивными вопросами. Теперь вы сможете легко решать проблемы в режиме онлайн.
В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу «обучение-обучение-обучение» учителя исследуют тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, мы в Cuemath верим в логическое мышление и интеллектуальный подход к обучению.
Часто задаваемые вопросы по линиям
1. Что такое уравнение прямой?
Общее уравнение прямой может быть записано как \ (ax + by + c = 0 \).
Где \ (a, b, c \) — константы, а \ (x, y \) — переменные.
2. Какой угол между двумя перпендикулярными линиями?
Угол между двумя перпендикулярными линиями составляет 90 градусов.
3. Что такое секущая?
Секущая — это линия, пересекающаяся в двух точках с кругом.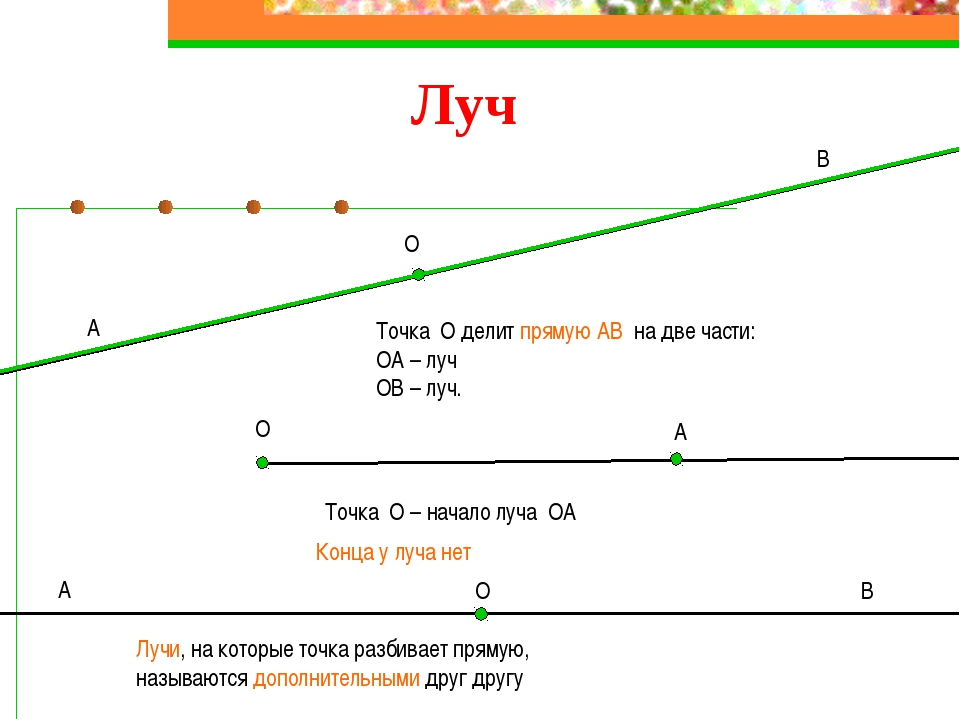
Прямая AB — секущая к окружности.
4. Что такое касательная?
Касательная — это линия, которая касается окружности в одной точке.
Прямая \ (L \) касается окружности в точке \ (P \).
5. Какие параллельные прямые?
Две прямые называются параллельными, если они лежат в одной плоскости и никогда не пересекаются.
геометрических терминов — бесплатная справка по математике
Балл:
Точка показывает местоположение и не имеет размера или размера. Точка обозначается точкой и обычно обозначается выбранной буквой. На рисунке ниже точки помечены ближайшей буквой.
Строка:
Линия — это набор точек, проходящих в двух противоположных направлениях без конца. Линия одномерная и не имеет ширины. Он идентифицируется путем обозначения двух точек на линии или написания выбранной строчной буквы после строки.
Обозначение, например, AB (написанное символом линии <---> над буквами), читается как «линия AB» и относится к линии, имеющей точки A и B.
Самолет:
Плоскость — это плоская поверхность без толщины, продолжающаяся без конца во ВСЕХ направлениях. Это двухмерный объект. Плоскость представлена параллелограммом и может быть названа заглавной буквой выбора в одном из углов. Я подробно расскажу, что такое параллелограмм, в будущих уроках.А пока подумайте о параллелограмме как о «оконном стекле». Для простоты вы можете представить себе плоскость как бесконечно большой лист бумаги.
На схеме ниже показаны три точки, линия и плоскость.
Сегмент линии:
Линейный сегмент — это часть линии, имеющая две точки, называемые конечными точками. У него также есть точки между конечными точками. Сегмент линии не имеет набора НЕПРЕРЫВНЫХ точек, как линия. Конечная точка означает, что линия имеет начало и конец.Обозначение отрезка линии на полосе над любой буквой по выбору. Скажем, AB имеет полосу над ним, вы бы прочитали это как «отрезок AB».
Луч:
Луч — это часть линии, имеющая одну конечную точку и набор всех точек с одной стороны от конечной точки. Луч всегда обозначается двумя буквами по выбору. Первая буква должна быть конечной точкой. Над буквами рисуем стрелку с конечной точкой.
Луч всегда обозначается двумя буквами по выбору. Первая буква должна быть конечной точкой. Над буквами рисуем стрелку с конечной точкой.
Угол:
Угол — это объединение двух лучей, имеющих одинаковую конечную точку.Конечная точка угла называется вершиной; лучи называются сторонами угла.
Есть несколько дополнительных терминов в геометрии, которые также необходимо понимать. Они определяют отношения между геометрическими объектами:
Коллинеарные точки: точки, лежащие на одной линии.
Копланарные точки: точки, лежащие в одной плоскости.
Противоположные лучи: 2 луча, лежащих на одной линии, с общей конечной точкой и не имеющей других общих точек.Противоположные лучи образуют прямую линию и / или прямой угол, равный 180 °.
Параллельные линии: две копланарные прямые, которые не пересекаются.
.
 Тогда луч нужно обозначить, как луч «АВ». Чтобы было понятнее, читать можно так: вторая точка В – это точка, через которую проходит луч.
Тогда луч нужно обозначить, как луч «АВ». Чтобы было понятнее, читать можно так: вторая точка В – это точка, через которую проходит луч. От них не отстают и суда – причем в этом случае Луч является маркой пассажирских судов, а также целым классом яхт.
От них не отстают и суда – причем в этом случае Луч является маркой пассажирских судов, а также целым классом яхт.
 Множество деревень, поселков и хуторов на территории России, Украины и Белоруссии тоже называются Лучами. От них не отстают и суда – причем в этом случае Луч является маркой пассажирских судов, а также целым классом яхт.
Множество деревень, поселков и хуторов на территории России, Украины и Белоруссии тоже называются Лучами. От них не отстают и суда – причем в этом случае Луч является маркой пассажирских судов, а также целым классом яхт.
 Подумайте о солнечных лучах:
Подумайте о солнечных лучах: 
 Это тупой
Это тупой  Подумайте, насколько велика дуга круга
стороны нарисованы по сравнению с целым кругом.
Подумайте, насколько велика дуга круга
стороны нарисованы по сравнению с целым кругом.