Урок 3. что такое симметрия? — Технология — 2 класс
Технология. 2 класс
Урок № 3 «Что такое симметрия?»
Вопросы:
- Что такое симметрия?
- Что такое ось симметрии?
- Как проверить и получить симметрично изображение?
Ключевые слова: Симметрия, композиция, ось симметрии
Основная и дополнительная литература по теме урока: Е.А. Лутцева, Т.П. Зуева. Технология 2 класс. Учебник для общеобразовательных организаций – 5-е издание – 2017. М.: «Просвещение» — С. 26-29
Открытые электронные ресурсы по теме урока: Сайт центра технологического образования АО Издательство «Просвещение» (http://technology.prosv.ru)
Теоретический материал для самостоятельного изучения:
И в искусстве, и в природе присутствуют такие понятия, как симметрия и асимметрия. Их мы наблюдаем повседневно в окружающем нас мире. И каждому субъекту присущи одно из или оба этих понятия.
Симметрия – это соразмерность, пропорциональность, одинаковость в расположении частей.
Симметрией обладают не только геометрические фигуры или вещи, сделанные рукой человека, но и многие творения природы (бабочки, стрекозы, листья, морские звезды, снежинки). Особенно разнообразны свойства симметрии кристаллов… Одни из них более симметричны, другие — менее.
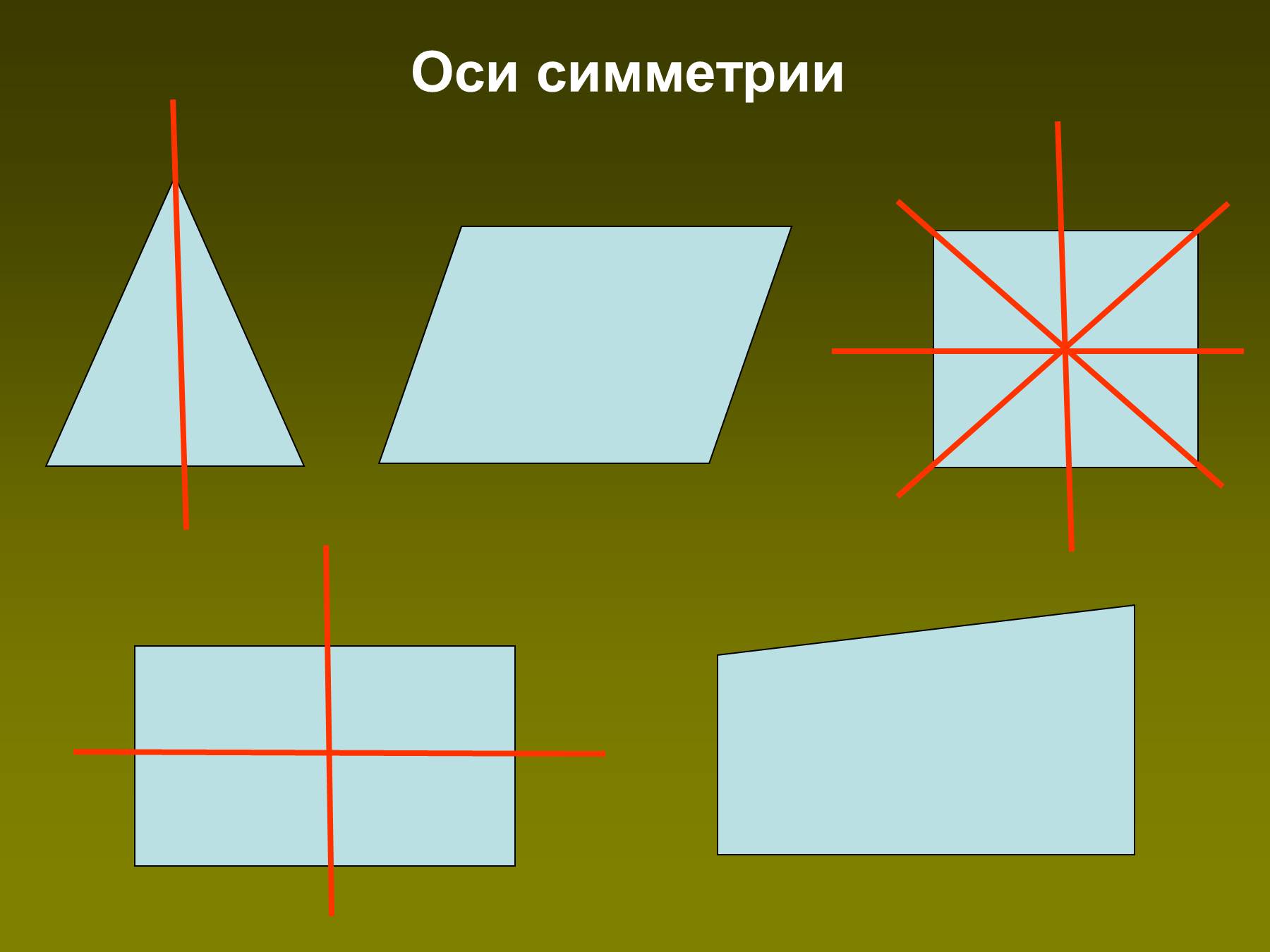
Плоскость симметрии, разумеется, воображаема, но именно она делит фигуру на две равные друг другу части. Она может проходить через одну или несколько сторон, быть параллельной ей, а может делить их. Для одной и той же фигуры может существовать сразу несколько плоскостей.
Но, пожалуй, наиболее часто встречается то, что называют «оси симметрии».
Воображаемая линия сгиба в симметричных изображениях называется осью симметрии.
Различают несколько основных типов симметрии, из которых наиболее часто встречаются три: Зеркальная – наблюдается относительно одной или нескольких плоскостей. Также термин употребляется для обозначения типа симметрии, когда используется такое преобразование, как отражение.
Лучевая, радиальная или осевая, в общем смысле – симметрия относительно прямой. Может рассматриваться как частный случай вращательной разновидности.
Центральная – наблюдается симметричность относительно некой точки.
Художественное вырезание из бумаги – уникальный вид искусства. Существует два метода вырезания — ножницами и ножом. В разных странах искусство вырезания называется примерно одинаково, в переводах — как «бумажная картинка», «бумажный цветок», «вырезка из бумаги», «вырезка ножницами», «силуэтное вырезание», «вытынанка» и т. д. Современные работы, выполненные в технике художественного вырезания из бумаги, называют прорезными изображениями, бумажной графикой, ажурным (филигранным) вырезанием. В этой технике можно делать много красивых вещей: картины (панно), открытки, украшения на окна и многое другое.
Одним из интересных, но сложных по технике выполнения является симметричное вырезание.
Симметричное вырезание заключается в том, что у изображаемого предмета одна часть симметрична другой, воображаемая плоскость делит предмет пополам, на две одинаковые зеркальные половины (лист дерева, само дерево, цветок тюльпана или василька, ваза, бокал, человек и т. п.).
п.).
Наиболее простыми для передачи в аппликации являются листья. Большинство из них построено по принципу зеркальной симметрии. Несмотря на многообразие формы листовой пластины (простые, простые рассеченные, сложные), различие по протяженности, относительной величине, строению краев, по окраске, все они (кроме неравнобоких) характеризуются общим распределением боковых сторон равномерно справа и слева.
Поэтому при вырезании листьев целесообразно применять прием предварительного складывания заготовок пополам (для передачи в аппликации зеркального соответствия боковых сторон) и одновременного прорезания обоих слоев бумаги по воображаемому контуру половины фигуры относительно сгиба. Изменение формы заготовки, ее соотношения по ширине и длине, величине и окраске позволяет изобразить многообразие и многоцветие листьев, особенно осенних.
При вырезании листьев путем сгибания заготовки пополам следует учитывать особенности строения исходной фигуры, соотношение ее величины и формы.
Для вырезания цветков из бумаги можно применить описанный выше прием складывания заготовки пополам, чтобы отобразить в аппликации равенство противоположных частей симметричной фигуры. После складывания бумаги вырезают половину формы цветка. При этом изменение очертаний контура, окраски и величины бумажной заготовки позволяет получить различные изображения колокольчиков, ландышей, ирисов, лилий.
Из заготовки бумаги, разделенной путем сложения на двенадцать равных частей, также можно вырезать разнообразные формы снежинок.
Сегодня на уроке вы познакомились с таким понятием как симметрия, с видами симметрии и таким видом техники, как симметричное вырезание.
Разбор типового тренировочного задания
Понятие «симметрия»
Впишите в текст пропущенное слово.
Соразмерность, пропорциональность, одинаковость в расположении частей – это …
Решение:
Симметрия
Выберите из списка правильный ответ.
Воображаемая линия сгиба в симметричных изображениях называется ….
Варианты ответов:
- Черта симметрии
- Ось симметрии
- Линия симметрии
- Центр симметрии
Решение:
Ось симметрии
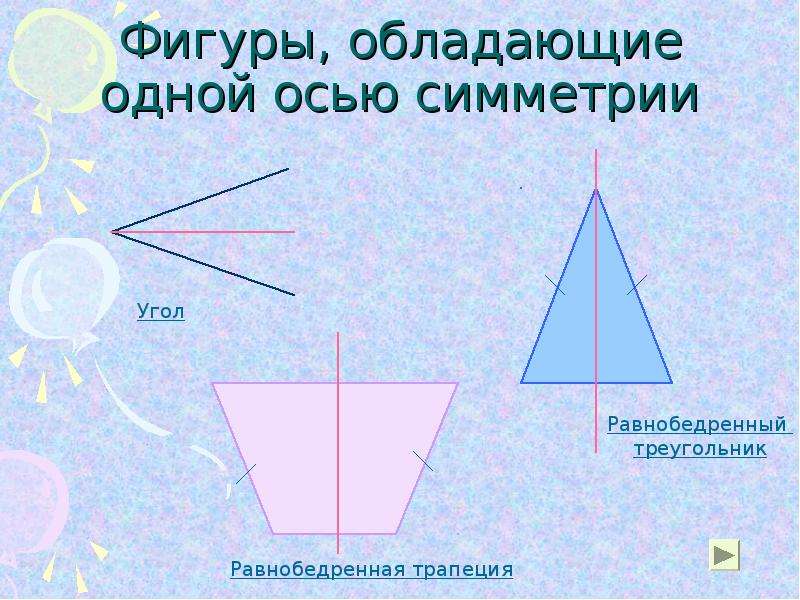
Прямоугольник. Ось симметрии фигуры
Технологическая карта урока – Прямоугольник. Ось симметрии фигуры.
Предмет: математика
Класс: 5
Тип урока: комбинированный
УМК: А.М. Мерзляк
Учитель: Санаева И.В.
Цели урока:
Предметные: закрепить навыки распознавания, построения прямоугольника и квадрата, нахождение их периметров, научить учащихся находить на рисунках фигуры, имеющие ось симметрии, и в окружающем мире объекты, имеющие ось симметрии.

Личностные: формировать умение корректировать свои действия в соответствии с изменяющейся ситуацией.
Метапредметные: развивать познавательный интерес к математике, умение использовать приобретенные знания в практической деятельности.
Образовательные ресурсы: учебники, мультимедийная презентация, раздаточный материал
Применяемая технология: технология системно-деятельностного метода обучения
Методы обучения:
— словесные методы (беседа, чтение),
— наглядные (демонстрация презентации),
— проблемно-поисковый,
— метод рефлексивной самоорганизации (деятельностный метод).
Средства обучения:
— компьютерная презентация,
— карточки с заданиями,
— карточки оценки работы на уроке,
— карточки с практическими заданиями по новой теме.
Формы организации познавательной деятельности:
— групповая,
— коллективная (фронтальная),
— индивидуальная.
Технологическая карта урока:
ПриветствиеНачинается урок
Он пройдёт ребятам впрок
Постарайтесь всё понять
Учитесь тайны открывать
Ответы полные давайте
И на уроке не зевайте.
Мы сегодня будем снова на раскрывать тайны математики
Готовы?
А какое открытие сделает каждый из вас сегодня, поделитесь в конце урока!.
Приветствует обучающихся, проверяет их готовность к уроку
Приветствуют учителя проверяют свою готовность к уроку
2. Актуализация знаний.
(5-7 мин)
постановка темы урока
1. Устный счет:
-Что изучали на прошлом уроке? (вопросы по теме «Прямоугольник, квадрат»)
-Вопросы по домашней работе?
А если фигура будет уже дана, как найти площадь и периметр?
(конверт)
Возьмём прямоугольник соединим его противоположные вершины, свернём. Что получим?
Что получим?
Соединим его середины противоположных сторон. Что получим?
Такие фигуры называют симметричными, а прямую, разъединяющую фигуры – осью симметрии. Если согнуть лист по этой прямой, то эти фигуры полностью совпадут, и мы будем видеть одну фигуру (продемонстрировать данное утверждение).
*перегиб листа, вырезание нарисованной на одной стороне фигуры;
*разглаживание линии сгиба и демонстрация всем, что получилось
*как расположились фигуры относительно линии сгиба
Итак, тема нашего урока: Прямоугольник . Симметричные фигуры. Ось симметрии фугуры.
Давайте подумаем, о чем будет наш урок?
-Какую цель мы поставим?
-Сегодня мы будем работать по плану.
(составление плана)
Что такое симметрия.
Что такое ось симметрии
Где встречается симметрия в окружающем нас мире.
В древности слово «симметрия» употреблялось как «красота», «гармония». Термин «гармония» в переводе с греческого означает «соразмерность, одинаковость в расположении частей». Известный немецкий математик нашего столетия Герман Вейль дал определение симметрии таким образом: «Симметрия является той идеей, с помощью которой человек веками пытается объяснить и создать порядок, красоту и совершенство».
Термин «гармония» в переводе с греческого означает «соразмерность, одинаковость в расположении частей». Известный немецкий математик нашего столетия Герман Вейль дал определение симметрии таким образом: «Симметрия является той идеей, с помощью которой человек веками пытается объяснить и создать порядок, красоту и совершенство».
Активизировать мыслительные операции, внимание, память и т.д., стимулировать к активной работе
Учитель цитирует слова великого математика
-актуализируют знания прошлых уроков
-работают над понятиями
Учащиеся осмысливают сказанное
3. «Открытие» нового знания
(8 мин)
Посмотрим внимательно на рисунки (рис. 1 и 2). Что вы на них увидели?
Такие фигуры называют симметричными, а прямую, разъединяющую фигуры – осью симметрии. Если согнуть лист по этой прямой, то эти фигуры полностью совпадут, и мы будем видеть одну фигуру (продемонстрировать данное утверждение).
*перегиб листа,вырезание нарисованной на одной стороне фигуры;
*разглаживание линии сгиба и демонстрация всем, что получилось
*как расположились фигуры относительно линии сгиба
Построить процесс осознанного представления об осевой симметрии
— перегибают лист бумаги,вырезают-3
-наблюдение над фигурами относительно линии сгиба
Исследовательская работа
— У вас на столе лежат конверты №1.
Достаньте квадрат. Давайте попробуем найти у него оси симметрии.
— Сложим его пополам и четко обозначим линию сгиба.
— Что мы получили? Покажите!
— Обведём цветным карандашом получившуюся прямую. Это 1 ось симметрии.
— Давайте попробуем сложить квадрат вновь пополам, но по-другому.
— Что получили?
— Покажите!
— Как еще можно сложить квадрат?
— Так сколько же осей симметрии у квадрата? (4)
Комментирует , привлекает учащихся найти ось симметрии
Активная работа н уроке 1 бал
Находят ось симметрии
4. Первичное закрепление
Практическая работа.
Цель: усвоение нового способа действий
Практическая работа
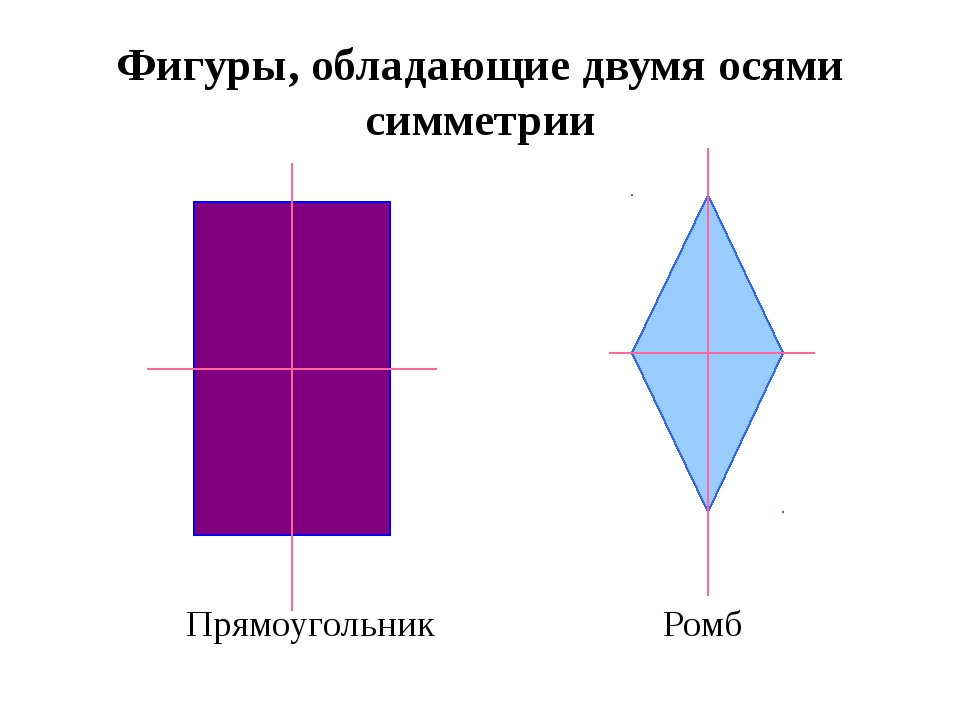
Найти у фигур оси симметрии и заполнить таблицу (на столах лежат конверты(прямоугольник, квадрат, круг, равнобедренный и разносторонний треугольники, семиугольник)
-сколько осей симметрии могут иметь разные фигуры ?
Контролирует выполнение работы, оказывает помощь
Все правильно – 3 бала
Есть 2- 3 ошибки – 2 бала
Есть 4-5 ошибок – 1 бал
работают в парах, извлекают информацию
-принимают решение о возможности или невозможности проведения оси симметрии
-заполняют таблицу
5.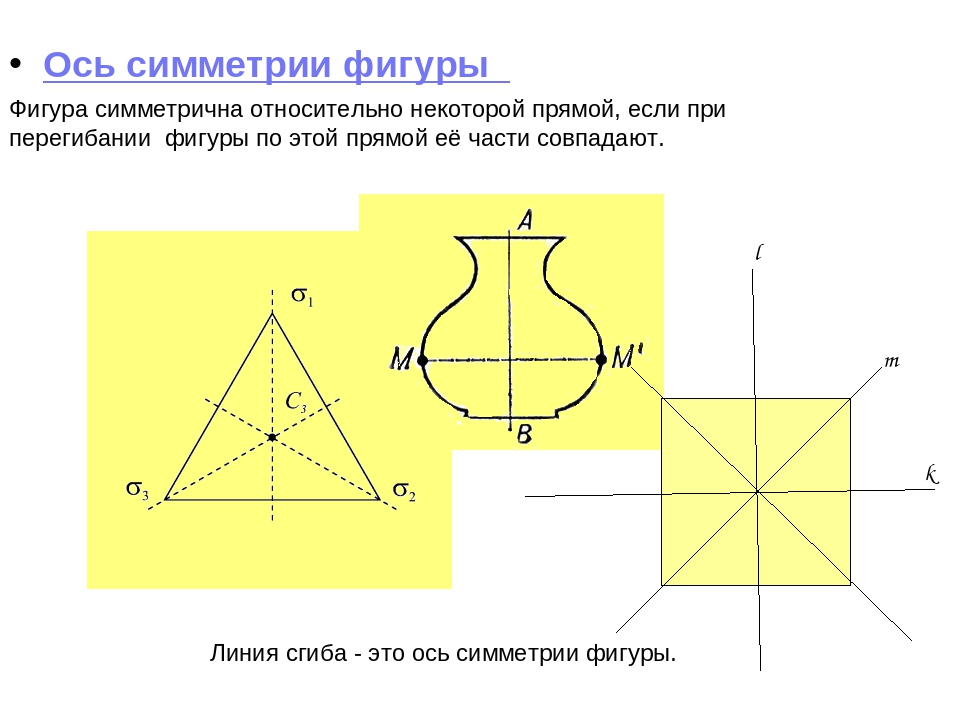 Включение в систему знаний и повторение
Включение в систему знаний и повторение
Цель: включение «открытия» в систему знаний, повторения и закрепление ранее изученного
— Мы выяснили, что симметрия в математике существует, но не у всех фигур.
Только ли в этой науке она может быть?
Увас на столах имеются конверты. Вам нужно провести исследование каждой группе — в своей области. Доказать, или опровергнуть наличие симметричности и, конечно же, сделать выводы о проделанной работе.
ВЫВОД:
Симметрия может встречаться не только в указанных группах, но и в другой окружающей нас действительности.
Просмотр видео
— Оказывается, все в мире построено по принципу симметрии. Продолжим нашу исследовательскую работу.
—Посмотрите, сколько областей жизни, и где только не встречается симметрия!
Знакомство с симметрией вокруг нас.
Организует исследовательскую работу
бала – работал активнее всех, предлагал интересные идеи.
2 бала – принимал активное участие в группе
1 бал – работал по мере необходимости
По ходу работы учитель составляет таблицу на доске:
(прикрепляют возле стрелочек свои проекты, некоторые стрелочки остаются пустыми.)
-Давайте сделаем вывод (по таблице).
-выполнение задания, основанного на ранее изученном
Выполняют исследовательскую работу в группе.
6.Самостоятельная работа
РТ № 161
Покажите ребята свои рисунки. Итак, ребята, оцените себя:
3 бала – достроили все рисунки
2 бала- достроено 4 рисунка
1 бал – достроено 2 рисунка.
Создает ситуации успеха
3бала – работа оригинальная, аккуратная
2 бала – работа аккуратная, но рисунок простой
1 бал – работа не аккуратная
-взаимопроверка
8. Рефлексия
(2 мин)
1.на уроке я работал…. активно/пассивно
2.своей работой на уроке я доволен /не доволен
3. Урок для меня показался… интересен/скучен
Урок для меня показался… интересен/скучен
4.За урок я… не устал/устал
5.мое настроение… стало лучше/ хуже
6.материал урока мне был… понятен/не понятен
Мотивирует рефлексии.
-учащиеся оценивают свою деятельность
-обозначают проблемные места
9.Домашнее задание
П. 15, №364, нарисовать фигуры имеющие ось симметрии (1,2 и более)
Поясняет д.з.
Слушают, записывают
10.Итоги урока
Какое открытие мы сделали на уроке?
— На следующем уроке мы будем учиться строить с вами симметричные геометрические фигуры относительно оси симметрии при помощи чертежных инструментов.
Что сегодня нового вы узнали? Что такое ось симметрии?
Сколько осей симметрии может иметь фигура?
Выставление оценок.
8-9 балов – оценка 5
6-7 балов – оценка 4
4-5 балов оценка 3
Задает вопросы, корректирует ответы
8-9 балов – оценка 5
6-7 балов – оценка 4
4-5 балов оценка 3
Отвечают на вопросы
НАБОР ГЕОМЕТРИЧЕСКИХ ФИГУР
Маршрутный лист
1 группа. Симметрия в мире животных.
Симметрия в мире животных.
На белой бумаге перед вами – контур бабочки. Проведите ось симметрии, раскрасьте бабочку в соответствии с правилами симметрии.
Определить оси симметрии у данных животных.
Правила работы в группе
1.Соответствует ли результат теме проекта.
2. Сотрудничество.
3. Аккуратность выполнения.
4. Защита проекта (умение донести информацию до аудитории).
Маршрутный лист
2 группа. Симметрия в мире растений.
Перед вами – одна половинка известного всем растения, вторая его половинка рассыпалась в виде мозаики. Склейте растение и проведите оси симметрии.
Определить оси симметрии у данных растений.
Правила работы в группе
1.Соответствует ли результат теме проекта.
2. Сотрудничество.
3. Аккуратность выполнения.
4. Защита проекта (умение донести информацию до аудитории).
Маршрутный лист
3 группа. Симметрия в мире архитектуры.
Построить с учетом воображаемой линии симметрии необычный замок, в котором вам хотелось бы жить.
Определить оси симметрии у данных памятников архитектуры.
Правила работы в группе
Конспект открытого урока по математике 1 класс «Оси симметрии»
МКОУ СОШ
с. Ивановка
Открытый урок в 1 классе
«Ось симметрии»
Тукало С.А.
Тема урока: Ось симметрии.
Цель урока: создать условия для формирования представления обучающихся о фигурах, имеющих одну или несколько осей симметрии.
Задачи урока:
-научиться проверять практическим путем, имеет ли данная фигура ось симметрии,
-отработка вычислительных навыков,
-развитие логического мышления,
-формирование у учащихся навыки контроля и самоконтроля.
Ход урока
1. Организационный момент.
Прозвенел звонок, урок начинается. Я улыбнусь вам, и вы улыбнитесь друг другу и подумайте, как хорошо, что, что мы сегодня все вместе. Мы спокойны, добры, приветливы, ласковы. Мы все здоровы. Забудьте об обидах. Вдохните в себя свежесть весеннего утра, тепло солнечных лучей, чистоту рек. Я желаю вам хорошего настроения и бережного отношения друг к другу.
2. Разминка ума.
1) Математический диктант.
Сумма чисел 10 и 8.
Разность чисел16 и 7.
5 увеличить на 6.
20 уменьшить на 8.
По 2 взять 4 раза.
Самопроверка. На доске ответы: 18, 9, 11, 12, 8.
2) Решить примеры
( 6+8) – 4; (12-7) +6; (5 ? 2) +8;
(6+8) – 10; (12 –6) +7; (6:3) ? 4.
3) Игра.
Цель: закрепить знание свойств геометрических фигур, развивать логическое мышление.
У каждого учащегося на парте набор геометрических фигур. Это 16 маленьких и 16 больших геометрических фигур (круг, квадрат, треугольник, прямоугольник) четырех видов и четырех цветов.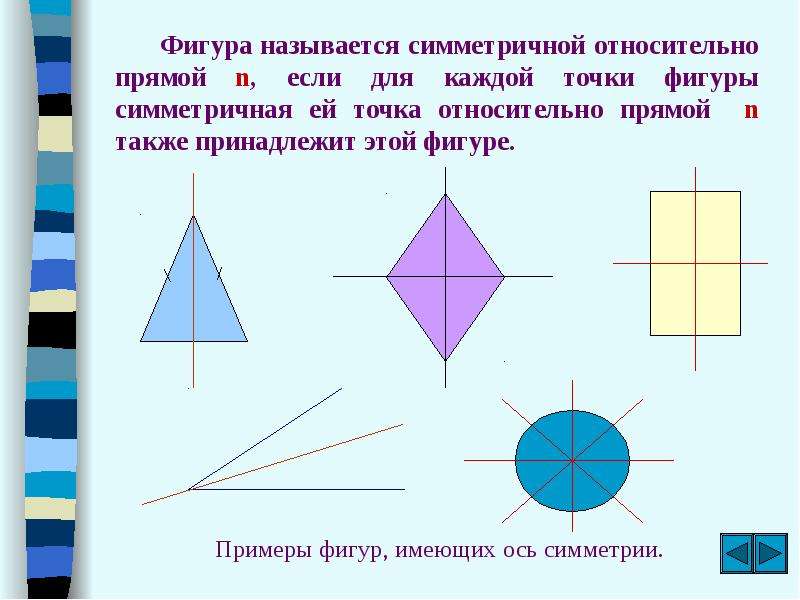
Игра строится по типу домино. У доски 2 ученика. Один кладет на стол любую фигуру, второй должен положить фигуру, отличающуюся от нее только одним признаком. В случае неправильного хода, у игрока забирают фигуру. Проигрывает тот, кто останется без фигур.
3. Сообщение темы урока.
Сегодня научимся проверять практическим путем, имеет ли данная фигура ось симметрии, дорисовывать симметричную часть данной фигуры.
4. Работа над темой урока.
1) Практическая работа 1
Возьмите лист бумаги и перегните его пополам. Хорошо разгладьте линию сгиба и отметьте на линии сгиба две точки. Не раскрывая листа бумаги, вырежьте какой-либо узор так, чтобы не перерезать линию сгиба на отрезке, ограниченном этими точками. Расправьте лист бумаги. Какую фигуру вы получили? Вы видите, что фигуры, расположенные по разные стороны от линии сгиба, совершенно одинаковы – они совпадут, если лист снова перегнуть около этой линии. Укажите ось симметрии.
Рассмотрите предметы или их части, находящиеся в классе. Укажите, какие из них имеют одну (или несколько) ось симметрии.
Укажите, какие из них имеют одну (или несколько) ось симметрии.
2) Практическая работа 2.
а) Докажи, сгибая рисунки по осям, что красный треугольник имеет одну ось симметрии, а желтый четырехугольник – две.
(Перегибая фигуру по той или иной оси, ученик увидит, что части этой фигуры совместились.)
б) Сколько осей симметрии имеет квадрат? Перегните его сначала по одной диагонали, потом еще по одной, затем по линиям, проходящим через середины противоположных сторон.
(Учащиеся убеждаются, что квадрат имеет 4 оси симметрии)
в) Сколько осей симметрии имеет пятиугольник?
(Имеет 5 осей симметрии. Каждая из них проходит через его вершину и середину противолежащей стороны.
г) Сколько осей симметрии имеет круг? Перегни его по какой-нибудь из осей.
д) работа в тетради №4 с.55. Является ли прямая на рисунке осью симметрии прямоугольника?
3) Демонстрация рисунков на больших ватманах бумаги.
а) Сколько осей симметрии имеет звезда? (5 осей симметрии)
б) Назовите времена года.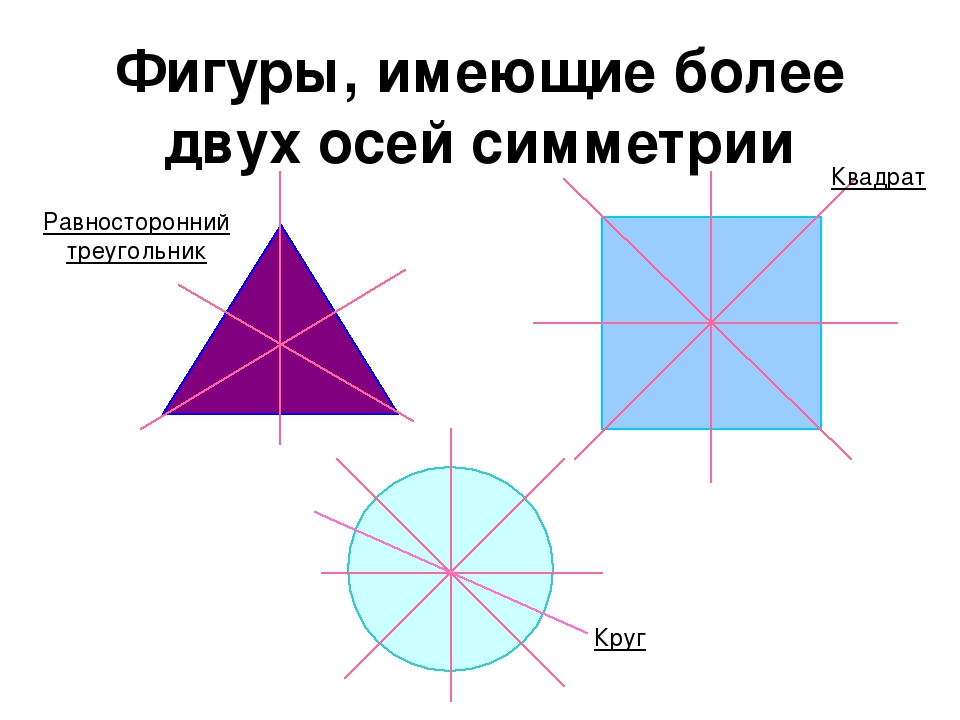 Давайте закроем глаза и представим, что мы идем по осеннему лесу, а под ногами разноцветный ковер. Глядите – красный фонарик, поднимаете – это листок уронила осинка; а у пруда милая ивушка рассыпала золотистые рыбки – листочки – узкие, длинные, тонкие; дальше – желтая звездочка – подарил ее клен. Давайте поднимем листочек клена.
Давайте закроем глаза и представим, что мы идем по осеннему лесу, а под ногами разноцветный ковер. Глядите – красный фонарик, поднимаете – это листок уронила осинка; а у пруда милая ивушка рассыпала золотистые рыбки – листочки – узкие, длинные, тонкие; дальше – желтая звездочка – подарил ее клен. Давайте поднимем листочек клена.
(Показ осеннего листа клена)
Говорят, что кленовый лист симметричен – имеет единственную ось симметрии. Если его перегнуть по этой оси, то обе части листа совпадут.(Показ)
Назовите еще растения, листья которых имеют ось симметрии.
в) А теперь побываем в зимнем лесу. Зима…Кругом белым-бело. Вот подул ветер, и с неба посыпались снежинки. Кружатся в воздухе и падают на землю – одна красивее другой! Вот цветок с шестью лепестками, вот звездочка с шестью лучами, вот тончайшая пластинка с шестью гранями! Беззвучно летят они в тихом воздухе над землей и падают вниз. Снежинки плывут, покачиваются, отыскивая себе дорогу на землю, так как им мешает невидимый воздух. Хорошо прогуляться зимним днем в лесу!
Хорошо прогуляться зимним днем в лесу!
Посмотрите на эту снежинку.
Сколько осей симметрии имеет снежинка на рисунке?
5) Физкультминутка
Загадка.
Я раскрываю почки, в зеленые листочки.
Деревья одеваю, посевы поливаю,
Движения полна,
Зовут меня …(весна)
Сейчас время года весна. Назовите, какой сейчас месяц.
6) Работа по учебнику
№6,№7
Имеют ли ось симметрии изображенные на рисунке предметы?
8) Работа в тетради №1 ,№2 с.54
Работа с зеркалом.
Назовите еще буквы русского алфавита, изображения которых имеют оси симметрии.
№7 с.57
5. Итог урока.
Чем занимались на уроке?
Как проверить имеет ли данная фигура ось симметрии?
Урок математики в 3 классе «Симметрия на бумаге в клетку. Повторение изученного материала».
Разработка урока математики в 3 классе 2 четверть
Тема: Симметрия на бумаге в клетку. Повторение изученного материала.
Повторение изученного материала.
Тип урока: комбинированный.
Цель: закрепить у обучающихся понимание понятия симметричные фигуры с осью симметрии.
Задачи:
Образовательные:
— формировать понятие о “симметричных фигурах”;
— формировать способность проводить ось симметрии в симметричных фигурах;
— формировать способность определять симметричные фигуры в окружающем мире.
Развивающие:
— развивать логическое мышление;
— коммуникативные качества;
— практические умения;
— навыки рефлексии (самоанализ деятельности).
Воспитательные:
— прививать доброе отношение друг к другу и окружающим;
— расширять эстетические представления о мире (понятие красоты, совершенства, гармонии).
Методические приёмы:
-словесный;
-наглядный;
-практический
Ожидаемые результаты:
1. Освоение программного материала по теме урока: обучающиеся должны уметь определять симметричные фигуры, проводить ось симметрии.
2. Расширение кругозора, представления о мире.
3. Развитие коммуникативных качеств.
Оборудование: магнитная доска, магниты в форме геометрических фигур, листы в клетку на каждого обучающегося, линейки, карандаши, циркуль.
- Организационный момент.
Математика пришла.
Занимай свои места!
Математика сложна,
Но скажу с почтением:
Математика нужна
Всем без исключения.
- Проверка домашнего задания (р.т. с. 49 №173, №174, № 175)
Учитель:
— Ребята, о чём мы с вами говорили на прошлом уроке? — Какое домашнее задание выполняли?
— Прошу вас обменяться тетрадями и проверить домашнюю работу друг у друга. Оцените работу одноклассника (поставить отметку на полях). В конце урока я соберу тетради и оценю выполнение вашей домашней работы и то, как вы оценили работу одноклассника.
3. Повторение ранее изученного материала.
а) Графический диктант.
— Ребята, слушайте внимательно команды, выполняйте их в своих тетрадях и у вас получится графическое изображение задуманного мною предмета.
— Прошу вас отступить вниз три клеточки от вашей последней записи и поставить точку посередине страницы.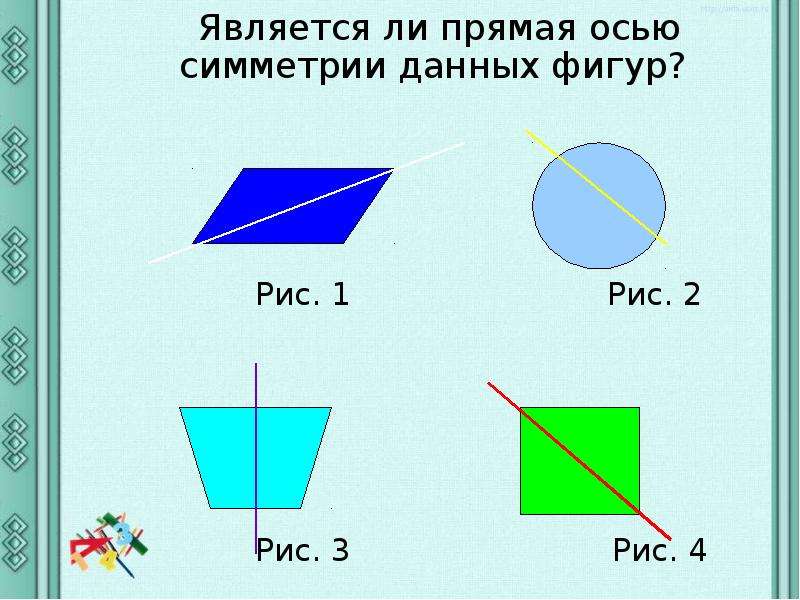
Команды: 1 клетка вправо,1 клетка вверх, 1 клетка вправо,1 клетка вверх, 3 клетки вправо, 1 клетка вниз, 1 клетка вправо, 1 клетка вниз, 1 клетка вправо, 1 клетка вниз, 1 клетка вправо, 3 клетки вниз, 1 клетка влево, 1 клетка вниз, 1 клетка влево, 1 клетка вниз, 1 клетка влево, 1 клетка вниз, 1 клетка влево, 1 клетка вниз, 1 клетка влево, 1 клетка вниз, 1 клетка влево, 1 клетка вниз, 1 клетка влево, 1 клетка вниз, 2 клетки влево,1 клетка вверх, 1 клетка влево, 1 клетка вверх, 1 клетка влево,1 клетка вверх, 1 клетка влево, 1 клетка вверх, 1 клетка влево, 1 клетка вверх, 1 клетка влево, 1 клетка вверх, 1 клетка влево, 1 клетка вверх, 1 клетка влево, 3 клетки вверх, 1 клетка вправо,1 клетка вверх, 1 клетка вправо,1 клетка вверх, 1 клетка вправо, 1 клетка вверх, 3 клетки вправо, 1 клетка вниз, 1 клетка вправо, 1 клетка вниз, 1 клетка вправо.
-Что изображено на вашем рисунке? (сердечко)
— Что символизирует данное изображение?
— В свою очередь я хочу вам сказать, что этот рисунок я выбрала не случайно. Это моё признание в том, что вы мои любимые ученики, вы – молодцы, и у вас сегодня на уроке всё получится. (собираю тетради)
Это моё признание в том, что вы мои любимые ученики, вы – молодцы, и у вас сегодня на уроке всё получится. (собираю тетради)
Учитель:
— Посмотрите на магнитную доску и скажите, под какими номерами фигуры являются симметричными? (ответы 1.2,5)
Учитель:
—Посмотрите на изображение. Скажите, какие оси симметрии существуют? (вертикаль, горизонталь) Сколько осей симметрии имеет каждая фигура?
Ответы:
№1
1,2,5
№2
2 оси симметрии 1 ось симметрии 1 ось симметрии 2 оси симметрии
1 ось симметрии 2 оси симметрии
б) Закрепление понятий «горизонтальная ось симметрии», «вертикальная ось симметрии».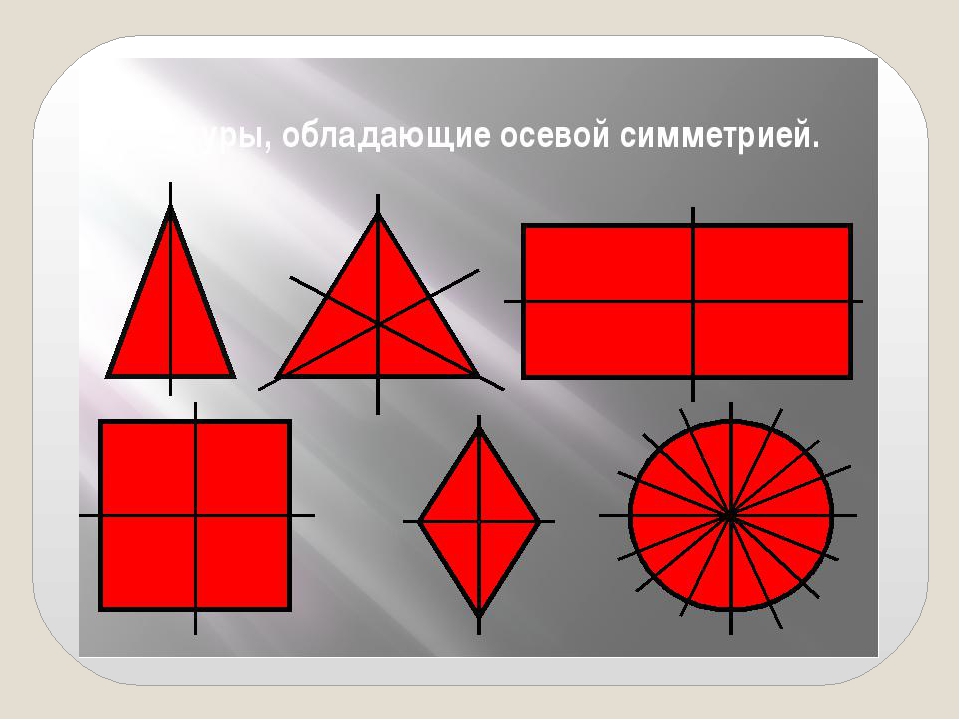
Учитель:
— Скажите, ребята, а если бы я дала вам задание начертить симметричные фигуры и предложила на выбор три листа (демонстрация): белый, в клетку, в линию. Какой бы выбрали?
Ребята:
— В клетку.
Учитель:
— Объясните, почему. (Ответы детей)
в) Практическая работа:
Учитель:
— У вас на столах лежат листы в клетку. Сложите их пополам. Сгиб — это у нас что? (ось симметрии). Отсчитайте относительно оси влево 10 клеток. Поставьте точку. Теперь отобразите точку, симметричную данной. Теперь от каждой из этих точек вниз проведите отрезок длиной 10 см. Что получилось? (два параллельных отрезка).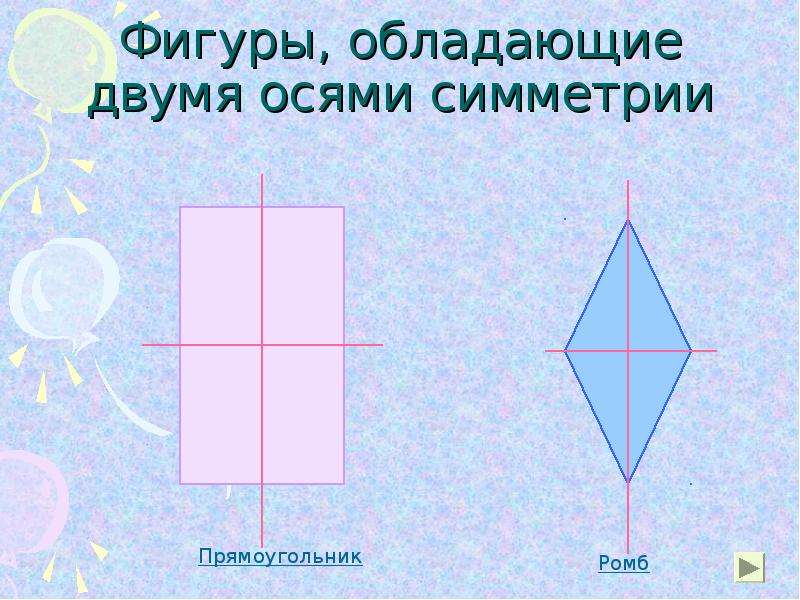 Соедините их посередине отрезком. Что видите? (Букву Н). Что скажете про неё с математической точки зрения? (Она симметрична).
Соедините их посередине отрезком. Что видите? (Букву Н). Что скажете про неё с математической точки зрения? (Она симметрична).
Учитель:
— Давайте перевернём лист на другую сторону и напишем ещё одну букву. Чтобы узнать, какую букву напишем, ответьте на вопрос:
— Без чего человек не сможет жить на Земле? (без воды, без воздуха). А на какую букву начинаются эти слова? (на букву В).
— Напишем букву В. Нам подойдёт эта ось симметрии? (Да)
На оси ставим точку. Вниз от точки ведём отрезок длиной 10 см. Делим его пополам. Ставим посередине точку. Из верхней точки до середины ведём полуовал. Затем из середины вниз другой. Чтобы была абсолютная точность, что необходимо? (циркуль)
Учитель:
— А какие ещё симметричные печатные буквы алфавита вы знаете?
Обучающиеся: А, В, Д, Е, Ж, 3, К, Л, М, О, П. , С, Т, Ф, Ю, X, Ш, Э.(Уточняем, что ось симметрии бывает как вертикальная, так и горизонтальная)
, С, Т, Ф, Ю, X, Ш, Э.(Уточняем, что ось симметрии бывает как вертикальная, так и горизонтальная)
Учитель:
— У нас получилась карточка с буквами В и Н. Что в математике означают эти буквы? (верно-неверно). Молодцы, ребята.
-Давайте с помощью этой карточки поиграем в “Верно-неверно”.
- Устный счёт:
- больше 7 в 5 раз (Н)
В году 365 дней (В)
1 час равен 100 мин (Н)
- больше суммы 27 и 4 (В)
10 составляет треть числа 30 (В)
В 1 дм- 20 см (Н)
Ширина прямоугольника 7 см, а длина- 3 см. Периметр равен 10 см (Н) Учитель:
Периметр равен 10 см (Н) Учитель:
— Вот видите, как много мы повторили при помощи сделанных карточек. — Помогла нам симметрия? (Да).
А теперь давайте немного отдохнём.
- Физминутка:
Симметричен человек,
И увидеть можно
Уха два и глаза два
И ноги две точно!
Две руки и две ноздри,
Губы улыбаются.
Симметричен человек —
Это всех касается!
Учитель:
— А что, по вашим наблюдениям, ребята, симметрично в природе ещё, кроме нас с вами? (Ребята связывают симметрию со своими знаниями окружающего мира: листья, животные, предметы, изготовленные человеком)
-
Закрепление изученного материала.

(Запись числа в рабочей тетради)
а) Выполнение творческого задания.
Учитель:
—Ребята, а сейчас предлагаю вам выполнить творческое задание: самостоятельно постройте какую — либо фигуру относительно оси
симметрии (горизонтальной или вертикальной). Затем передайте тетрадь соседу для того, чтобы он нарисовал фигуру симметричную данной.
б) Работа по учебнику.
Учитель:
а) Решение выражений с объяснением у доски (с. 103 №6)
б) Решение задачи с использованием рисунка — схемы (с. 104 №8)
- Подведение итогов урока:
— Итак, ребята, время урока подходит к концу. Поделитесь своими впечатлениями от сегодняшнего урока.
Поделитесь своими впечатлениями от сегодняшнего урока.
— Продолжите предложения:
— Теперь я знаю… .
— Теперь я умею… .
- Домашнее задание:
Р.т. с.50 №176, с.51 №178
Математика. 2 класс. Рабочая тетрадь. М. И. Моро, С. И. Волкова — «Сплошные РЕБУСЫ и ЗАГАДКИ. Как будто не математикой для 2 класса занимаешься, а IQ тесты проходишь!»
…:::★☆★ Всем привет! ★☆★:::…
Решила я тут написать свои мысли по поводу рабочей тетради по математике для 2 класса (М.И. Моро, С.И. Волкова)
Я, кстати, понятия не имею, сколько такая тетрадочка стоит, так как нам бесплатно выдают эти учебные пособия в школе. Но дело не в этом, дело совсем в другом
Итак, почему вдруг я решила написать отзыв на такую тему?
Да потому что это так забавно, что вот я, взрослый человек с высшим образованием (правда оно у меня гуманитарное, но это не важно), иной раз теряюсь перед заданиями из этого учебного пособия по математике для детей 2(!!!) класса
Ну вот реально, бывает, перечитываешь по 2-3 раза, чтобы понять о чем тут автор вообще спрашивает
Просто мне иногда кажется, что в министерстве образования слабо себе представляют, как в 7-8 лет выглядят дети. А меж тем мне хотелось бы напомнить, что некоторые в этом возрасте еще читать толком не умеют. Я имею в виду именно читают по-русски с трудом Просто благодаря дистанционке я имела честь поприсутствовать на он-лайн уроке и поняла, что реально пол класса с трудом «Колобка» по слогам читает.
А меж тем мне хотелось бы напомнить, что некоторые в этом возрасте еще читать толком не умеют. Я имею в виду именно читают по-русски с трудом Просто благодаря дистанционке я имела честь поприсутствовать на он-лайн уроке и поняла, что реально пол класса с трудом «Колобка» по слогам читает.
А им надо въехать, например, вот в такое задание к задачке №27. Я понимаю, что задание само по себе примитивное, но вы зацените формулировку
Из двух задач составь одну, которая решается в два действия, а лишние слова в приведённом тексте зачеркни.
А что это за такие «обратные» задачи в номере 68?… Нет, ну реально это ребусы какие-то. Это не математика.
Обведи кружком номера двух задач, обратных задаче 1. Запиши выражения для решения каждой из данных задач.
Я уж молчу про то что, чтобы заниматься по этой тетрадочке второклассник уже должен быть в курсе того, что такое ось симметрии, шестиугольники, дециметры, метры, периметр, ломаные, уравнение (!) и прочие заумные словечки.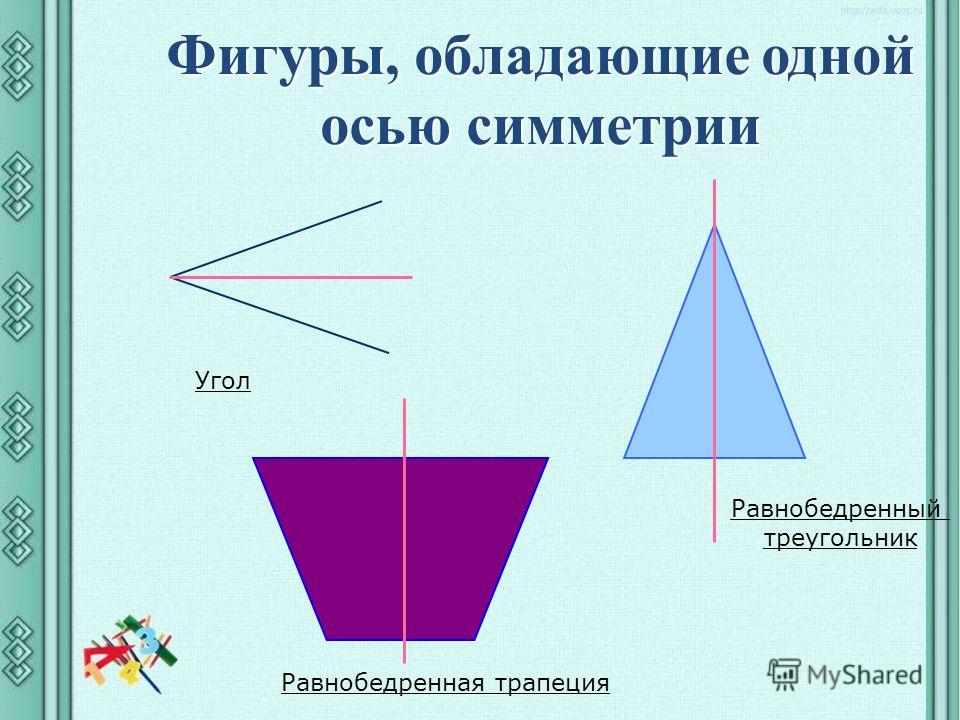
Задание №44
Начерти еще два таких шестиугольника.
1. Проведи в первой фигуре две оси симметрии.
2. Проведи во второй и третьей фигурах по одному отрезку так, чтобы второй шестиугольник был разделен на два четырехугольника, а третий — на два пятиугольника.
А сейчас будет вообще мое самое любимое
Так уж получилось, что в тот день муж был занят и домашнее задание по математике с ребенком делала я (хотя обычно у нас с мужем разграничение полномочий — математика это его сфера деятельности, я же делаю с ребенком все остальное )
Так вот задание №30 на странице 14.
Половина родительского чата обсуждало, как правильно решить эту задачку И как потом еще ребенку объяснить, что такое число десятков и число единиц.
Попробуйте и Вы проверить свои знания в «начальной» математике
Решите задание № 30
Честное слово, в качестве эксперимента я просила уже многих взрослых решить эту задачку. Правильно отвечают единицы. И в основном это мужчины
Правильно отвечают единицы. И в основном это мужчины
●•●•●•●•●•●•●•●•●•●•●•●•●•●•●•●•●•●•●•●•●•●•●•●•●•●•●•●•●•●•●•●•●•●•●•●•●•●•●•●•●•●•●•●•●•
🌸💗🌸 ВЫВОД 🌸💗🌸
Я даже не знаю, что сказать про вот всю эту программу…
Вроде бы она такая вся из себя веселая и в какой-то степени не «занудная», с нормальными иллюстрациями и иногда весьма занимательными задачками. Но в целом формулировка заданий явно не для второго класса (в первом классе была аналогичная ситуация с этими учебными пособиями Моро).
Плюс, все как-то так хаотично изложено, темы скачут.
В общем, хорошо, что у меня есть муж, который знает математику, и что немаловажно обладает определенным талантом и достаточной выдержкой, чтобы объяснить моему сыну, что в этих ребусах спрашивается.
Я не могу сказать, что я не рекомендую учебник Моро и эту вот рабочую тетрадь…
Но только заниматься по таким программам можно исключительно при наличии у ребенка умных и не особо занятых родители, которые могут ему вовремя что-то подсказать и объяснить.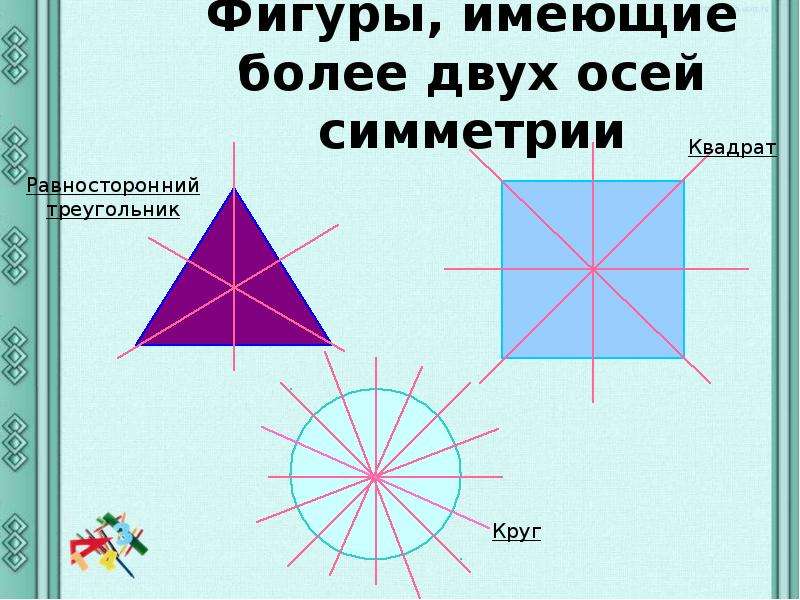 Ну или еще вариант – репетиторов нанимать. Ибо самостоятельно заниматься по такому учебному пособию второклассник в принципе не может.
Ну или еще вариант – репетиторов нанимать. Ибо самостоятельно заниматься по такому учебному пособию второклассник в принципе не может.
P.S.
И еще вот что хочу добавить…
Мой сын является одним из лучших учеников в классе. Недавно у них был брейн ринг в школе и из 32 учеников нашего класса в команду взяли только 6 самых одаренных и смышленых (мой сын как раз в команду попал, и даже был ее капитаном). Но я это говорю не к тому, чтобы рассказать, что мой ребенок весь из себя такой умный и расчудесный.
Я просто хочу донести до Вас мысль, что с учебой у нас все нормально, мы явно не «отстающие». И тем не менее, я считаю что этот учебник математики и эта рабочая тетрадь слишком «заумные» для второго класса!
Деятельность учителя | Деятельность учащихся |
1. (Слайд 1) Легко отыскать примеры прекрасного, но как трудно объяснить, почему они прекрасны. (Платон ) – Сегодня на уроке мы попытаемся разобраться в некоторых особенностях создания прекрасного! А работать мы сегодня будем в группах. | Дети заранее распределились на 4 группы. |
2. Этап актуализация опорных знаний – Посмотрите на кленовый лист, снежинку, бабочку. (Слайд 2) Что их объединяет? – Напомните мне, пожалуйста, что же означает слово «симметрия». — Какой вид симметрии мы уже рассмотрели? — Определите, симметричны ли фигуры относительно прямой? (слайд 3) | — Они симметричны относительно оси. — «Симметрия» по-гречески означает «соразмерность, пропорциональность, одинаковость в расположении частей». Мы рассмотрели осевую и зеркальную симметрию. Симметричны только на 1 рисунке. Если согнуть лист по этой прямой, то эти фигуры полностью совпадут. |
3.Этап целеполагания. — Ребята, симметричными могут быть не только 2 фигуры, в некоторых фигурах тоже можно провести ось симметрии. Говорят, что такие фигуры обладают осевой симметрией. (слайд 4) — Как определить имеет ли фигура ось симметрии? — Как вы думаете, какова тема сегодняшнего урока? (слайд 5) — Какую цель вы поставите перед собой. — Сегодня на уроке будем находить оси симметрии в различных геометрических фигурах и предметах окружающей действительности. | — Можно согнуть фигуру, если левая и правая части совпадут, то фигуры симметричны. Научится определять ось симметрии фигур. |
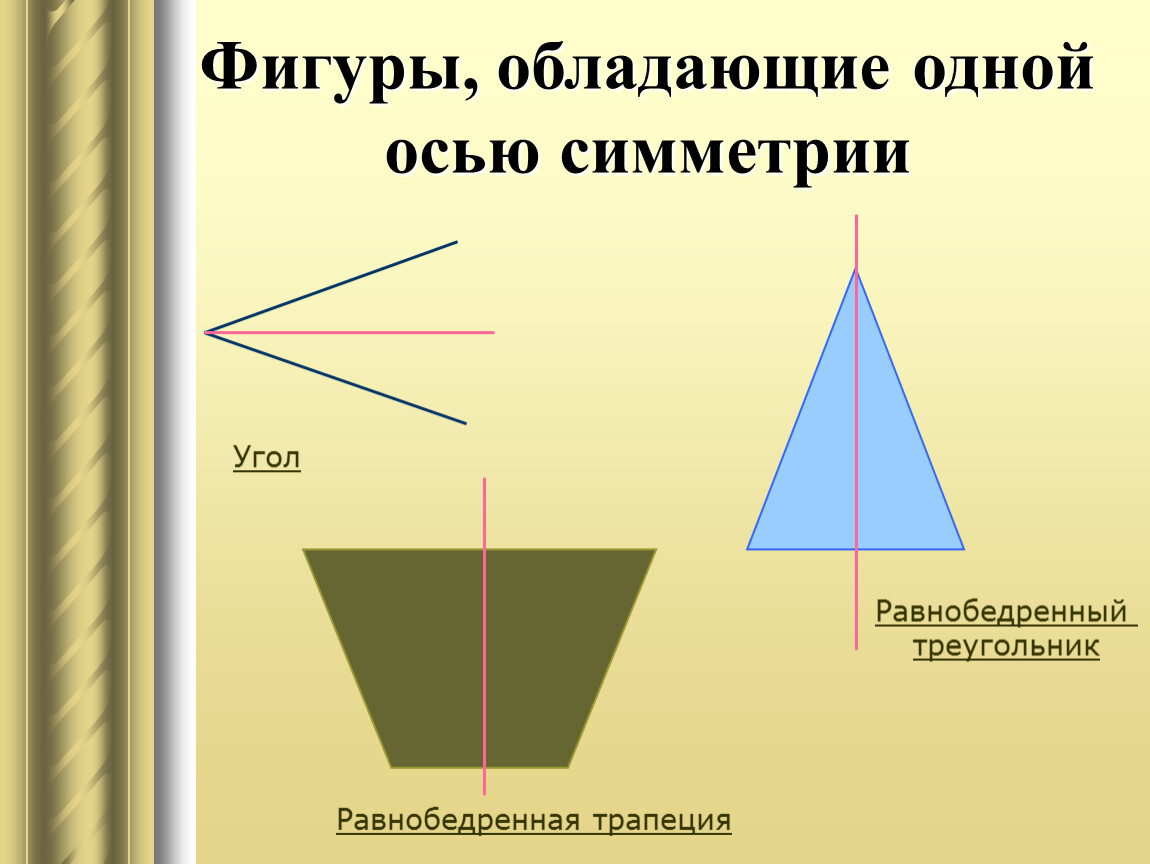
4. Этап открытия нового знания — Сколько осей симметрии может иметь фигура. Каждой группе выдается набор различных геометрических тел. Сейчас я буду называть геометрические фигуры, вы их должны найти и показать. Ваша задача самостоятельно определить, сколько осей симметрии имеет каждая фигура, определить самую симметричную и самую несимметричную фигуру. Проверим, что у нас получилось. 1 группа назовёт фигуры имеющие 1 ось симметрии (угол, равнобедренный треугольник, трапеция). (слайд 6) 2 группа назовёт фигуры, имеющие две оси симметрии (прямоугольник, ромб) (слайд 7) 3 группа назовёт фигуры имеющие более двух осей симметрии (равносторонний треугольник, квадрат, круг). (слайд 8) Многоугольник у которого равны все стороны и все углы называется правильным. Можно ли равносторонний треугольник и квадрат назвать правильными многоугольниками? 4 группа назовёт фигуры не имеющие осей симметрии (разносторонний треугольник, параллелограмм, неправильный многоугольник). (слайд 9) Какая из данных фигур самая симметричная и самая несимметричная? | Находят и показывают фигуры. Предполагают. Находят оси симметрии у различных геометрических фигур (угол, равносторонний треугольник, равнобедренный треугольник, разносторонний треугольник, прямоугольник, ромб, квадрат, трапеция, параллелограмм, круг, неправильный многоугольник) Отчет групп. |
5. Этап первичного закрепления. А сейчас следующее задание. (слайд 10) Используя перегибания листа, вырезать из листа бумаги фигуру, которая имеет:
При выполнении этого задания соблюдай те правила ТБ при работе с ножницами. Принципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке. Симметрично практически все транспортные средства, предметы домашнего обихода (мебель, посуда), некоторые музыкальные инструменты. — А мы с вами обладаем симметрией? (слайд 11) Красота человеческого тела обусловлена пропорциональностью и симметрией. Строение внутренних органов – не симметрично. | Выполняют задание. Слушаем, как выполнялось задание. Лучшие фигуры каждой группы вывешиваем на доске. Называют по очереди. |
6. Физкультминутка (слайд 12) Раз – подняться, потянуться, | |
7. Осмысление учебного материала. Буквы русского языка тоже можно рассмотреть с точки зрения симметрии. шалаш, казак, радар, Алла, Анна, кок, поп. Могут быть палиндромическими и предложения. Написаны тысячи таких предложений. А роза упала на лапу Азора. Я иду с мечем судия. Составьте слова, имеющие вертикальную ось симметрии и вертикальную. | Высказывают предположения. Проверяют свои предположения по слайду. Воспринимают информацию. Составляют слова, озвучивают их. |
8. Самостоятельная работа. Тест. Часть урока вы работали в группе. Пришло время проверить, как каждый из вас усвоил новый материал. А сейчас поменяйтесь тетрадями и проверьте работу по готовым ответам, поставьте оценку в соответствии с критериями. ( слайд 16) Встаньте те, кто выполнил работу на пять. Работа с учебником. ( при наличии времени) С. 578, № 578: Среди фигур, изображенных на рисунке, найдите симметричные. Перерисуйте их в тетрадь и проведите оси симметрии. Осуществляется фронтальная проверка. — под какими номерами изображены симметричные фигуры. — сколько осей симметрии у ромба? — сколько осей симметрии у трапеции? — сколько осей симметрии у вогнутого четырёхугольника? С. 153, № 587(практическая ситуация – восстановить симметричное панно) |
Работают самостоятельно. Вариант 1
1) Б 2) Г 3) Б 4) А 5) В
Вариант 2 1) Б,В 2) Б 3) Б 4) Г 5) Г Оценивание выполненной работы по соответствующим критериям: «5» – 5 заданий; Осуществляют самопроверку. — 1,2, 4 — у ромба 2 оси; — у трапеции 1 ось; — у четырёхугольника 1 ось. Проверку осуществляет учитель. |
9. Подведение итогов. Рефлексия. – Подходит к концу наш урок, но знакомство с симметрией продолжается. На протяжении всего урока мы выполняли разнообразные задания. — Определите, является ли прямая осью симметрии фигуры.(слайд 17) — Какая фигура лишняя? (слайд 18) Мы выполнили поставленные цели? — Какое задание вам показалось самым трудным? — Что нового «открыли» вы для себя на уроке? -Как вы думаете, над чем, каждому из вас следует потрудиться? | Ось симметрии фигуры. Рис. 1,2 – нет; рис. 3,4 – да. Фигура № 3 – нет оси симметрии. Научится определять ось симметрии фигур. Да. |
10. Домашнее задание. Чтобы научиться думать, надо научиться придумывать. Дж. Родари (слайд 19) | Записывают в дневники. П. 7.2, № 586 Попытайтесь придумать палиндромы. Придумайте рисунок, иллюстрирующий осевую симметрию и изобразите его на отдельном листе. |
11. Заключение. – Ребята, спасибо вам за работу! Без помощи и поддержке друг друга мы не смогли бы достичь цели. Я очень довольна вашей работой на уроке. |
Актуализация знаний. Устный счёт (5 мин ) | 1.Индивидуальная работа. Карточки. 11 – 45 + 512 – 814 – 5 7 + 912 – 913 – 59 + 0 6 + 82 + 96 + 918 – 10 17 – 815 – 913 – 611 – 2 2. а) У Ани 14 тетрадей: 8 из них в клетку, а остальные – в линию. Сколько тетрадей в линейку? (6: 14 – 8 =6.) б) Почтальон за день разнес 17 телеграмм, 9 из них – срочные, а остальные – простые. Сколько простых телеграмм? (8. 17 – 9 = 8.) 3. Проверка индивидуальных работ. | Решают, самопроверка | Предлагает выполнить задание с использованием ИКТ Организует самоконтроль учащихся | Познавательные (общеучебные, логические) | Открытие нового знания. Практическая работа (4 мин) | – Возьмем лист бумаги, сложим его пополам и вырежем какую-нибудь фигурку. Но сначала вспомним правила работы с ножницами. СЛАЙД Теперь развернем лист и посмотрим на линию сгиба. — Какую функцию выполняет эта линия? ( Эта линия делит фигуру пополам.) -Как расположены все точки фигуры на двух получившихся половинках? (Все точки половинок находятся на равном расстоянии от линии сгиба и на одном уровне. – Значит, линия сгиба делит фигурку пополам так, что 1 половинка является копией 2 половинки, т.е. эта линия непростая, она обладает замечательным свойством (все точки относительно ее находятся на одинаковом расстоянии), эта линия – ось симметрии. | Складывают, вырезают, отвечают, высказывают предположения | Контроль за деятельностью детей | Преобразование практической задачи в познавательную. Познавательные 1).Постановка и формулирование проблемы 2).Применение изученных правил в решении практической задачи. общеучебные: умение структурировать знания, контроль и оценка процесса и результатов деятельности; логические: анализ, синтез, выбор оснований для сравнения. Коммуникативные Умение составлять вопросы, вести устный диалог | 2. | Сообщение темы урока. (2 мин.) | — Вы помните девочку Алису из мультфильма и её приключения в Зазеркалье? На этом уроке мы тоже будем смотреть в зеркало, чтобы разобраться в новой теме «Симметричные фигуры». Сформулируйте вопрос на который мы будем искать ответ. — Какие фигуры называются симметричными? — Что такое ось симметрии? | Отвечают, определяют умения, которые будут сформированы | Познавательные (общеучебные, логические) | 4. | Реализация построенного проекта. Первичное закрепление. (15 мин) Физкульт- минутка (1 мин) | А) Учитель подносит к зеркалу различные предметы: тетрадь, ручку, кубик кружок. — Что вы видите в зеркале? Если посмотреть на зеркало сбоку, то мы увидим прямую. — Кто знает и помнит как она называется? (Ось симметрии) — Какие предметы по обе стороны её? По обе стороны её совершенно одинаковые предметы. Они называются симметричными Б) Работа в учебнике с. 64 № 5 №1 С явлениями симметрии, с симметричными фигурами мы встречаемся буквально на каждом шагу. — А люди каких профессий постоянно сталкиваются с симметрией? (строители, конструкторы, …) Симметрия есть и в творениях природы (животные, растении, кристаллы…) и в творениях человеческих рук. Посмотрите вокруг. Нельзя не восхищаться порхающей бабочкой, ярким цветком, загадочной снежинкой. Об этих и других предметах можно сказать, что они красивы. И в основе их красоты лежит симметрия. Но симметрия – это не только красота. Симметричность фигуры необходима рыбе, чтобы плавать, птице, чтобы летать. СЛАЙД -Сейчас будем исследовать геометрические фигуры. — Как вы думаете, сколько осей симметрии они могут иметь? — Подтвердились ваши предположения? -Сколько же осей симметрии могут иметь фигуры? СЛАЙД Симметричен человек, И увидеть можно: Глаза два, и уха два, И руки две – точно! Две ноги и две ноздри, Щёчки улыбаются. Симметричен человек, Это всех касается! Музыкальная физкультминутка. | Отвечают. Высказывают предположения. (помогут ответить на вопрос) Читают слово с помощью зеркальца Рассматривают, сравнивают, делают вывод практическая работа. Высказывают предположения Выполняют физические упражнения, связанные с нагрузкой разных мышц тела и рук | Запись на доске (1, 2, несколько — круг) Отбирает упражнения для физкультминутки и проводит её | Познавательные (общеучебные, логические) Коммуникативные Проявлять активность во взаимодействии для решения задач Формулировать собственное мнение Регулятивные (контроль, прогнозирование) |
Что такое линия симметрии?
Игры «Линия симметрии»
Линии симметрии Если вы сложите фигуру по линии симметрии, две половинки точно сложатся друг над другом. Отметьте линии симметрии на множестве замкнутых фигур.
Учитесь с помощью полной программы обучения математике K-5
Что такое линия симметрии?
Мы часто находим симметрию в вещах вокруг нас.
Мы говорим о симметрии, когда создается точное отражение или зеркальное отображение линии, формы или объекта.
Линия симметрии может быть определена как ось или воображаемая линия, которая проходит через центр формы или объекта и делит его на идентичные половины.
Учитесь с помощью полной программы обучения математике K-5
Вот, например, если свернуть вырезанную точно по центру фигурку вертикально, то ее половинки будут совпадать. Линия сгиба — это линия симметрии.
Фигуры или формы, которые имеют точное сходство с другой его частью, при разделении на две или более равных части называются симметричными.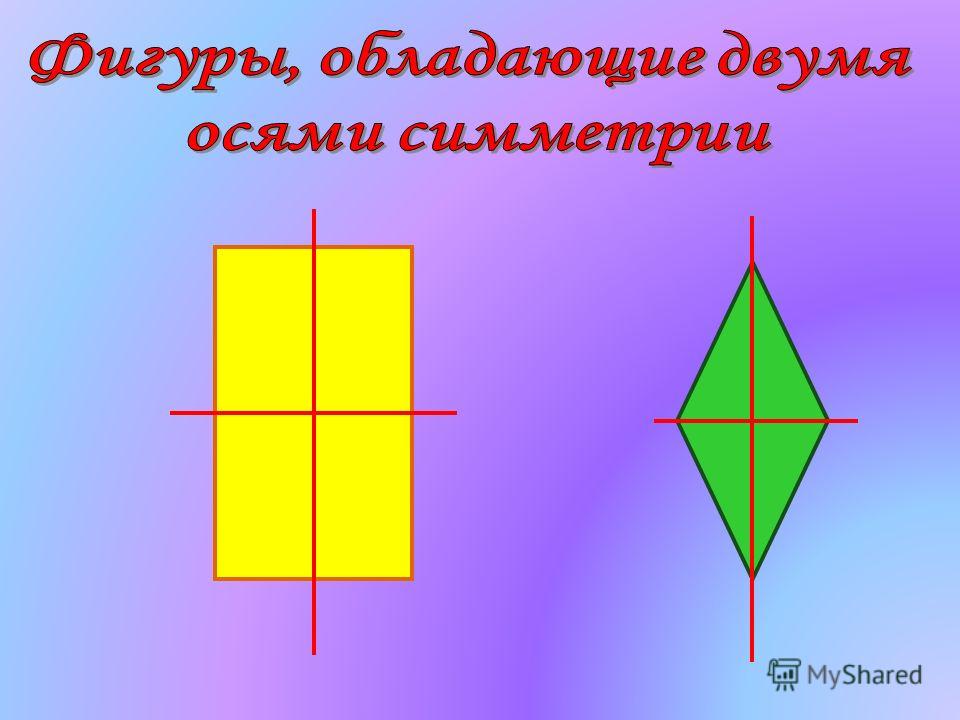
Фигуры и объекты, которые не похожи друг на друга при разделении на две части, называются асимметричными.
Линии симметрии могут быть вертикальными, горизонтальными или диагональными.
Линия симметрии дает совпадающие отражения.Вот как формы и объекты могут иметь несколько линий симметрии.
Интересные факты
|
Давай сделаем это!
Вместо того, чтобы раздавать своим детям листы математики с линиями симметрии, попросите их наблюдать объекты в их окружении, которые являются симметричными и могут быть разделены линиями симметрии, такими как улей, цветок.
Связанный математический словарь
Ось симметрии параболы
График
квадратичная функция
это парабола. Ось симметрии параболы — это вертикальная линия, разделяющая параболу на две совпадающие половины. Ось симметрии всегда проходит через
вершина параболы
. В
Икс
-координата вершины — уравнение оси симметрии параболы.
Ось симметрии параболы — это вертикальная линия, разделяющая параболу на две совпадающие половины. Ось симметрии всегда проходит через
вершина параболы
. В
Икс
-координата вершины — уравнение оси симметрии параболы.
Для квадратичной функции в стандартной форме у знак равно а Икс 2 + б Икс + c ось симметрии — вертикальная линия Икс знак равно — б 2 а .
Пример 1:
Найдите ось симметрии показанной параболы.
В Икс -координата вершины — уравнение оси симметрии параболы.
Вершина параболы равна ( 2 , 1 ) .
Итак, осью симметрии является линия
Икс
знак равно
2
.
Пример 2:
Найдите ось симметрии графика у знак равно Икс 2 — 6 Икс + 5 по формуле.
Для квадратичной функции в стандартной форме у знак равно а Икс 2 + б Икс + c ось симметрии — вертикальная линия Икс знак равно — б 2 а .
Вот, а знак равно 1 , б знак равно — 6 и c знак равно 5 .
Замена.
Икс знак равно — — 6 2 ( 1 )
Упрощать.
Икс знак равно 6 2 знак равно 3
Следовательно, ось симметрии Икс знак равно 3 .
Симметрия — Элементарная математика
Несмотря на то, что существует много видов симметрии, в начальной школе обычно используется только отражательная симметрия (или «зеркальная симметрия»). В результате в школьных материалах слово «симметрия» используется так, как будто оно имеет только одно значение. В этой статье мы сосредоточимся на одном значении, но также проиллюстрируем другие.
На этой фотографии показан простой снимок с зеркалом, расположенным по линии симметрии. Видимый результат — половина оригинала и зеркальное отображение этой половины — точно соответствует исходному рисунку.Мы говорим, что исходная фигура «симметрична» относительно зеркала; он обладает отражающей симметрией.
Отражательная симметрия и «линия симметрии»
Зеркально-симметричные объекты имеют по крайней мере одну линию симметрии , линию, вдоль которой фигура может быть сложена на две точно совпадающие части, части, которые являются зеркальным отображением друг друга.
Эта фигура имеет две линии симметрии: горизонтальная линия симметрии разрезает фигуру на верхнюю и нижнюю части, которые являются зеркальным отображением друг друга; вертикальная линия симметрии разрезает фигуру на левую и правую части, которые являются зеркальным отображением друг друга.У звезды ниже 5 линий симметрии, пять линий, по которым ее можно сложить так, чтобы обе стороны идеально совпадали.
Распространенное заблуждение , встречающееся даже во многих глоссариях и текстах: не все линии, разделяющие фигуру на две конгруэнтные части, являются линиями симметрии. Например, диагональ (не квадратного) прямоугольника не является линией симметрии.
Когда зеркало помещается по диагонали прямоугольника, результат не будет таким же, как исходный прямоугольник, поэтому диагональ не является линией симметрии. Эта новая форма — комбинация треугольной половины исходного прямоугольника и его изображения в зеркале — называется воздушным змеем.
Эта новая форма — комбинация треугольной половины исходного прямоугольника и его изображения в зеркале — называется воздушным змеем.
Mirror Play
Задолго до того, как дети начнут какое-либо формальное изучение симметрии, игра с зеркалами — возможно, с конструкциями Узорных блоков, которые они строят, — развивает опыт и интуицию, которые могут служить как их геометрическому мышлению, так и их художественным идеям. Красочный дизайн выше имеет только вертикальные и горизонтальные линии симметрии, но размещение зеркала под другим углом может создать красивый новый дизайн.
Первый рисунок ниже показывает, что буква А имеет вертикальную линию симметрии, но это скорее «ручная» игра. Более смелые эксперименты дают и другие интересные результаты.
То же самое и с буквой М.
Такие буквы, как B и D, имеют горизонтальную линию симметрии: их верхняя и нижняя части совпадают.
Некоторые буквы, например X, H и O, имеют как вертикальные, так и горизонтальные линии симметрии.
А некоторые, такие как P, R и N, не имеют линий симметрии.
Вращательная симметрия
Еще одна симметрия, которую дети иногда используют в своих конструкциях с узорами, — это «симметрия вращения». Фигура имеет вращательную симметрию, если некоторое вращение (кроме полного поворота на 360 °) дает ту же фигуру. Например, эти фигуры при повороте на нужную величину — 360 ° / 3 для изображения «имя» и 360 ° / 5 для звезды — выглядят точно так же, как и до вращения.
Буквы N, Z и S также разделяют это свойство.
Обратите внимание, что некоторые фигуры, такие как звезда и красочная капля в верхней части страницы, но не буквы N, Z или S, обладают как отражательной, так и вращательной симметрией .
Самая симметричная форма
У окружности бесконечно много линий симметрии: любой диаметр лежит на линии симметрии, проходящей через центр круга. Любое вращение на любую величину вокруг центра круга также оставляет круг без изменений.
Книги для детей
- Сделайте лужу побольше Сделайте червя поменьше , Марион Уолтер
- Для детей старшего возраста, от 2 класса:
- Книга-головоломка «Зеркало» , Марион Уолтер,
Что одним словом?
«Метрия» в симметрии и геометрия и метрика относится к измерению.
Иллюстративная математика
Задача
Ниже представлены изображения четырех треугольников с заданной длиной сторон:
Для каждого треугольника найдите и нарисуйте все линии симметрии.
Комментарий IM
Можно представить себе деление треугольников на разносторонние, равнобедренные и равносторонние.
из линий симметрии. Разносторонний треугольник — это треугольник без
линии симметрии, в то время как равнобедренный треугольник имеет хотя бы одну линию симметрии
а равносторонний треугольник имеет три линии симметрии.Эта деятельность обеспечивает
учащимся предоставляется возможность распознавать эти отличительные черты различных типов треугольников до того, как будет введен технический язык.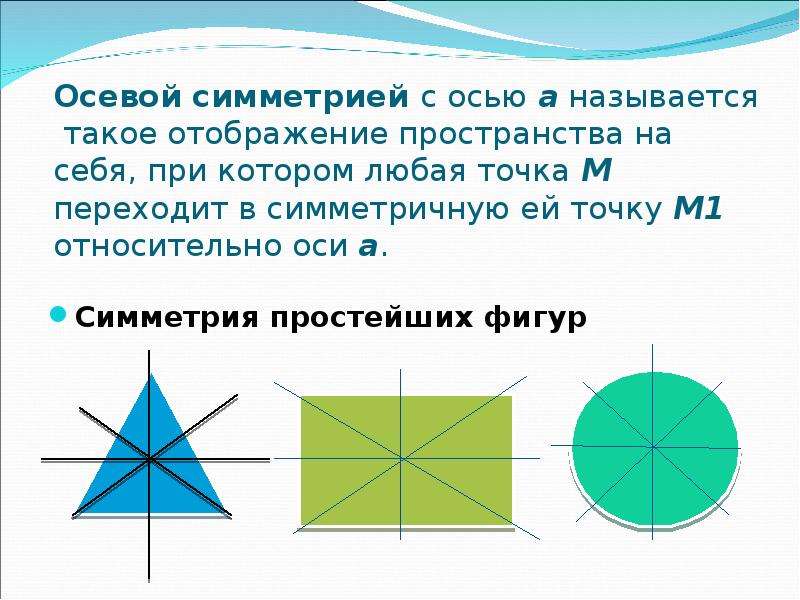 Для
найдя линии симметрии, вырезанные модели четырех треугольников будут
полезно, чтобы ученики могли сложить их, чтобы найти линии.
Для
найдя линии симметрии, вырезанные модели четырех треугольников будут
полезно, чтобы ученики могли сложить их, чтобы найти линии.
Это задание предназначено для обучения, предоставления студентам с возможностью экспериментировать с физическими моделями треугольников, получая пространственные интуиция, выполняя размышления.В конце решения было добавлено слово о том, почему для этих треугольников нет других линий симметрии: это было вставлено на тот случай, если эта тема поднимется в ходе обсуждения в классе, но основное внимание должно быть уделено определению правильных линий симметрии .
Решение
На рисунке показаны линии симметрии четырех треугольников. ниже:
Линия симметрии треугольника должна проходить через одну вершину. Две стороны, встречающиеся в этой вершине, должны быть одинаковой длины, чтобы существовала линия симметрии.Когда две стороны, встречающиеся в вершине, действительно имеют одинаковую длину, линия симметрии, проходящая через эту вершину, проходит через середину противоположной стороны. Для треугольника с длинами сторон 4,4,3 единственная возможность — это сложить так, чтобы две стороны длины 4 совпали, так что линия симметрии проходит через вершину, где встречаются эти две стороны. Для треугольника, все стороны которого имеют длину 3, правильный сгиб через любую вершину может служить линией симметрии, поэтому существует три возможных прямых. Треугольник с длинами сторон 2,4,5 не может иметь никаких линий симметрии, поскольку все стороны имеют разные длины.Наконец, треугольник с длинами сторон 3,5,5 имеет одну линию симметрии, проходящую через вершину, где встречаются две стороны длиной 5.
Для треугольника с длинами сторон 4,4,3 единственная возможность — это сложить так, чтобы две стороны длины 4 совпали, так что линия симметрии проходит через вершину, где встречаются эти две стороны. Для треугольника, все стороны которого имеют длину 3, правильный сгиб через любую вершину может служить линией симметрии, поэтому существует три возможных прямых. Треугольник с длинами сторон 2,4,5 не может иметь никаких линий симметрии, поскольку все стороны имеют разные длины.Наконец, треугольник с длинами сторон 3,5,5 имеет одну линию симметрии, проходящую через вершину, где встречаются две стороны длиной 5.
Чтобы понять, почему для этих треугольников нет других линий симметрии, обратите внимание, что линия симметрии должна проходить через вершину треугольника: если линия разрезает треугольник на два многоугольника, но не проходит через вершину, то одна из этих линий polygons — это треугольник, а другой — четырехугольник. После выбора вершины треугольника остается только одна возможная линия симметрии для треугольника, проходящая через эту вершину, а именно та, которая проходит через середину противоположной стороны.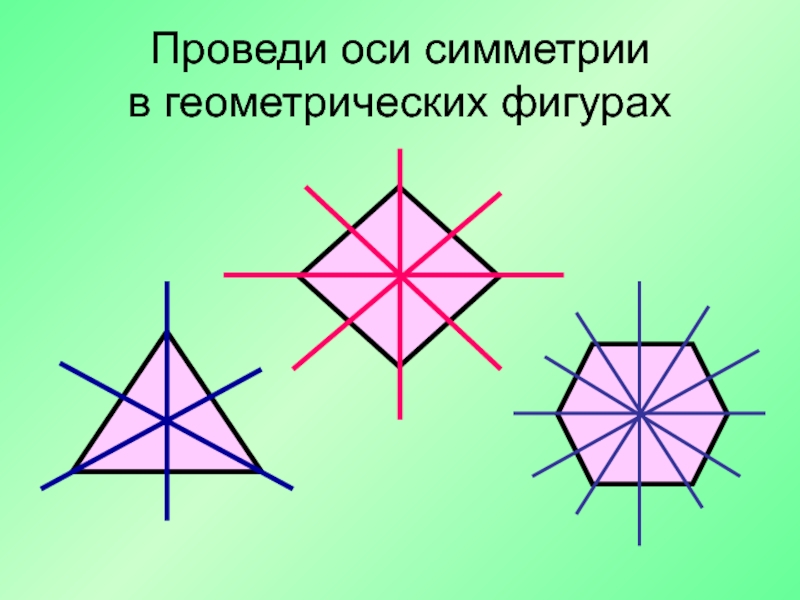
Ось симметрии — Cuemath
Посмотрите на изображение шестиугольника ниже.
Это симметрично?
Как определить симметричность?
Есть ли у этого шестиугольника ось симметрии?
Возможно, вы слышали эти термины раньше, но задумывались ли вы, что они означают?
В этом уроке вы узнаете в основном об оси симметрии и других вопросах, связанных с ней.
Посмотрите интерактивные симуляции, чтобы узнать больше об уроке, и попробуйте свои силы в решении нескольких интересных практических вопросов в конце страницы.
План урока
Определение оси симметрии
Ось симметрии — это прямая линия, разделяющая объект на две равные половины.
Ось симметрии создает зеркальное отображение с другой стороны.
Если мы складываем и раскладываем объект вдоль оси симметрии, две стороны должны быть одинаковыми.
Ось симметрии может быть горизонтальной, вертикальной или боковой. {2} + b x + c \ end {уравнение} \)
{2} + b x + c \ end {уравнение} \)
где a, b — коэффициенты при «x»
c — постоянная форма.{2} + k \ end {Equation} \)
где (h, k) — вершина параболы.
В форме вершины мы можем сказать, что x = h, поскольку ось симметрии и вершина лежат на одной прямой.
| \ (\ begin {уравнение} h = \ frac {-b} {2a} \ end {уравнение} \) |
Вывод параболического уравнения обсуждается на следующем занятии ниже.
Калькулятор осей симметрии
Ось симметрии и вычислитель вершин показаны ниже.
Использование
Это поможет вам рассчитать положение оси симметрии с использованием уравнения стандартной формы.
Калькулятор области симметрии помогает найти фактическое положение параболы.
Примеры осей симметрии
Мы можем видеть эту ось симметрии даже в природе, такой как цветы, берег реки, здания и т. Д.
Д.
Мы можем наблюдать ось симметрии в Тадж-Махале, культовом мраморном сооружении Индии.
Некоторые из примеров оси симметрии в природе перечислены ниже.
Вывести ось симметрии параболы
Формула оси симметрии для параболы: \ [\ begin {equal} x = \ frac {-b} {2a} \ end {equal} \]
Почему ось симметрии находится в \ (\ begin {equal} x = \ frac {-b} {2a} \ end {equal} \)?
Вот как это.
По определению оси симметрии параболы, это вертикальная линия, разделяющая параболу на две идентичные половины.{2} + b x = 0 \ end {уравнение} \]
\ [\ begin {уравнение} x (ax + b) = 0 \ end {уравнение} \]
\ [\ begin {уравнение} (ax + b) = 0 \ end {уравнение} \] (поскольку взятие \ (\ begin {уравнение} x \ end {уравнение} \) с другой стороны)
\ [\ begin {уравнение} x = \ frac {-b} {a} \ end {уравнение} \]
Следовательно, два значения x равны \ (\ begin {формула} 0, \ frac {-b} {a} \ end {уравнение} \)
Формула средней точки: \ begin {уравнение} x = \ frac {x_ {1} + x_ {2}} {2} \ end {уравнение}
\ [\ begin {уравнение} x = \ frac {0+ \ left (\ frac {-b} {a} \ right)} {2} \ end {уравнение} \]
| \ (\ begin {align} \ поэтому x = \ frac {-b} {2a} \ end {align} \) |
Ось симметрии горизонтальной параболы
Парабола может быть двух видов.
Может быть горизонтальным или вертикальным, но это основано на оси симметрии.
Если ось симметрии вертикальна, то парабола вертикальна.
Если ось симметрии горизонтальна, то парабола горизонтальна.
Поскольку ось симметрии лежит на оси x, мы берем точку пересечения с y.
| \ (\ begin {align} \ поэтому y = \ frac {-b} {2a} \ end {align} \) |
Определить ось симметрии по графику
Пример 1 .{2} + b y + c \ end {Equation} \]
Следовательно, a = 4, b = 5 и c = 3
Мы знаем, что \ [\ begin {уравнение} y = \ frac {-b} {2a} \ end {уравнение} \]
\ [\ begin {уравнение} y = \ frac {-5} {2 (4)} \ end {уравнение} \]
\ [\ begin {уравнение} \, следовательно, y = -0,625 \ end {уравнение} \]
Решенные примеры
1. Помогите Анне определить форму, которая удовлетворяет определению оси симметрии.
Помогите Анне определить форму, которая удовлетворяет определению оси симметрии.
Решение
Определение оси симметрии утверждает, что это прямая линия, разделяющая объект на две идентичные половины.
Ось симметрии должна создавать зеркальное отображение.
Это форма, симметричная как по горизонтали, так и по вертикали.
Ось симметрии образует две идентичные половинки.
| \ (\ следовательно \) Определение оси симметрии выполнено. |
Мистер Джейд призывает своего ученика Джорджа провести ось симметрии на графике вдоль оси x.
Помогите Джорджу нарисовать ось симметрии.
Подсказка: a = 3, b = -12 & c = 5
Решение
Мы знаем, что \ [\ begin {equal} x = \ frac {-b} {2a} \ end {equal} \]
Применение значений a и b.
\ [\ begin {уравнение} x = \ frac {- (- 12)} {2 (3)} \ end {уравнение} \]
\ [\ begin {уравнение} \ поэтому x = 2 \ end {уравнение} \]
| \ (\ следовательно \) Ось симметрии нарисована. |
1. Симметрична ли парабола относительно оси x или оси y?
2. Каково уравнение оси симметрии этой параболы?
Интерактивные вопросы
Вот несколько занятий для вас.
Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Какая форма имеет бесконечные линии (или) ось симметрии?
Подведем итоги
Мини-урок был посвящен увлекательной концепции оси симметрии. Математическое путешествие вокруг оси симметрии начинается с того, что ученик уже знает, и переходит к творческому созданию новой концепции в молодых умах.Сделано таким образом, чтобы не только было понятно и легко понять, но и навсегда осталось с ними. В этом и заключается магия Куэмат.
Математическое путешествие вокруг оси симметрии начинается с того, что ученик уже знает, и переходит к творческому созданию новой концепции в молодых умах.Сделано таким образом, чтобы не только было понятно и легко понять, но и навсегда осталось с ними. В этом и заключается магия Куэмат.
О компании Cuemath
В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу «обучение-обучение-обучение» учителя исследуют тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, это логическое мышление и интеллектуальный подход к обучению, в которые мы в Cuemath верим.{2} + b x + c \ end {Equation} \)
Формула оси симметрии: \ [\ begin {уравнение} x = \ frac {-b} {2a} \ end {уравнение} \]
Урок в девятом классе Ось симметрии и форма вершины
Теперь, когда у нас есть корни для каждой из этих функций, мы можем повторить то, что мы видели два дня назад: ось симметрии и вершина находятся на полпути между ними. два корня. На втором слайде заметок к уроку учащимся предлагается найти ось симметрии и вершину для каждой из трех функций в открывателе.Конечно, когда мы это делаем, мы видим — что вы знаете? — что ось симметрии у всех одинакова.
два корня. На втором слайде заметок к уроку учащимся предлагается найти ось симметрии и вершину для каждой из трех функций в открывателе.Конечно, когда мы это делаем, мы видим — что вы знаете? — что ось симметрии у всех одинакова.
Я распространяю по мере того, как студенты приступают к работе, а затем устанавливаю таблицу на боковой доске, которую мы можем использовать для отслеживания того, что мы находим. Когда мы подходим к заполнению первых трех строк диаграммы, становится ясно, что разделяют эти три функции. В этот момент дети могут начать подозревать, что действительно существует связь между средним коэффициентом и осью симметрии. Если они начнут говорить об этом, я могу вслух задаться вопросом о соотношении между 8 и -4.
На третьем слайде нам предлагается повторить процесс поиска корней, оси симметрии и вершины еще для трех квадратичных функций, и вы увидите, что я сделал снимок прилагаемой диаграммы в середине этой работы. Цель этих трех функций — предоставить студентам дополнительные доказательства того, что ось симметрии тесно связана со средним коэффициентом, и, надеюсь, любой, у кого есть предположение, сможет сделать здесь некоторые прогнозы.
На четвертом слайде спрашивается: Что общего между d, e и f? На первый взгляд это может быть трудно сказать, но после выполнения задачи должно быть ясно, что вершина каждого из них имеет координату y, равную -9.Это дает трамплин для размышлений о форме вершин, что делает эту связь еще более ясной. Когда мы дойдем до этого (как подсказывают нам слайды 5 и 6), я мог бы спросить: «Что мне нужно добавить к каждой из этих функций, чтобы завершить квадрат?»
Отсюда может начаться обсуждение того, как вершина появляется в представлении формы вершины каждой функции. Обратите внимание, что я использовал ту же модифицированную версию формы вершины — со знаком плюс внутри круглых скобок — что я использовал в действии Квадратичные функции в трех формах.2 + к
с вершиной в (h, k), когда это их идея сделать эту настройку.
Симметрия: определение, типы, упражнения и примеры
Сегодня вы узнаете, что такое симметрия, и мы увидим некоторые упражнения на симметрию, которые дети выполняют во время своих сессий Smartick, и типичные ошибки, которые обычно допускаются.
Что такое симметрия?
Симметрия — это одно из математических понятий, которое учащиеся начинают изучать вне школы. Тем не менее, они все еще изучают его в дошкольном образовании и строят симметричные фигуры, не прибегая к строгому определению.
Как мы увидим ниже, существуют различные типы симметрии. Мы собираемся начать с наиболее известной симметрии относительно прямой или осевой симметрии . Давайте начнем с рисования прямой линии на плоскости, в данном случае это может быть лист бумаги с сеткой, как показано на рисунке ниже:
Линия нарисована вертикально, но может быть горизонтальной или иметь любое другое направление.Мы говорим, что фигура симметрична относительно линии, когда каждая точка на одной стороне этой линии имеет другую точку на другой стороне и на том же расстоянии от этой линии.
Если мы хотим знать, симметрично ли изображение относительно линии и есть ли оно на листе бумаги, нам просто нужно сложить бумагу вдоль линии.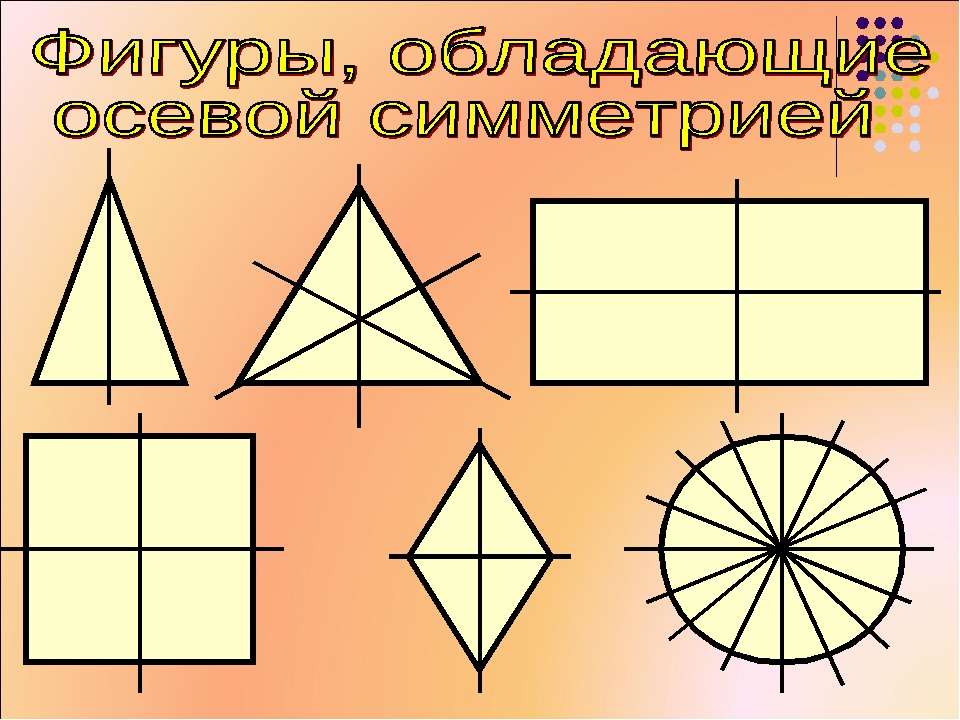 Если, когда мы складываем бумагу, фигуры совпадают друг с другом, это потому, что они симметричны относительно линии. Если они не совпадают, значит, они не симметричны.
Если, когда мы складываем бумагу, фигуры совпадают друг с другом, это потому, что они симметричны относительно линии. Если они не совпадают, значит, они не симметричны.
Если мы хотим создать симметричное изображение на бумаге, мы начинаем с того, что складываем бумагу и, используя маркер, который будет слегка растекаться сквозь бумагу, рисуем желаемую фигуру.Затем разворачиваем бумагу. Маркер просочился на другую сторону и создал две фигуры, симметричные относительно линии, которую мы сложили. Когда бумага сложена, они точно совпадают. Вместо маркера можно было бы использовать ножницы.
Видео: симметричные фигуры и оси симметрии
Чтобы лучше понять, что такое симметрия с относительно оси , взгляните на это видео одного из наших интерактивных руководств. Он больше не интерактивен, но у вас есть то преимущество, что вы можете смотреть его столько раз, сколько необходимо, и делиться им с другими.Если вы хотите получить доступ к настоящим интерактивным обучающим материалам, зарегистрируйтесь в Smartick, онлайн-методе обучения математике для детей от 4 до 14 лет.
В этом видео мы представляем семинар по симметрии, посмотрите:
Что такое ось симметрии?
Симметричная фигура может иметь одну или несколько осей симметрии, которые могут быть прямыми линиями или линиями, разделяющими фигуру на две симметричные части.
На изображении, взятом из видео, у звезды четыре оси симметрии, а у рук только одна — вертикальная прямая.
Типы симметрии
Существует много типов симметрии, но мы собираемся сосредоточиться на этих трех, которые можно увидеть в школе:
- Во-первых, осевая симметрия или симметрия относительно линии, — это тот, который делит объект или фигуру пополам, используя прямую линию , другими словами, осью симметрии.
 Этот тип симметрии может напоминать, когда мы смотрим в зеркало и видим в нем свое отражение.
Этот тип симметрии может напоминать, когда мы смотрим в зеркало и видим в нем свое отражение. - Мы говорим, что одна или несколько фигур имеют симметрию вращения , когда они не изменяются при повороте на определенный угол.Четырехконечная звезда на предыдущем изображении имеет симметрию вращения, потому что если вы повернете ее на 90 ° (или любое кратное 90 °), оно будет таким же.
- Третий тип симметрии на плоскости — это симметрия относительно точки или центральная симметрия . Две точки симметричны относительно точки, которую мы называем центром симметрии, если они находятся на одинаковом расстоянии от нее и на одной линии. Центральная симметрия дает тот же эффект, что и поворот на 180 °.
Упражнения по симметрии в Smartick
В посте о новом контенте Smartick мы привели примеры последовательности действий симметрии. Сложность зависит от формы фигур и ориентации оси симметрии. Сложность постепенно увеличивается, облегчая изучение и понимание этой концепции. Эти упражнения способствуют развитию пространственного видения и геометрического мышления.
Сложность зависит от формы фигур и ориентации оси симметрии. Сложность постепенно увеличивается, облегчая изучение и понимание этой концепции. Эти упражнения способствуют развитию пространственного видения и геометрического мышления.
- У нас есть упражнения, в которых дети должны проанализировать, симметричны ли две фигуры:
- В других они должны построить симметричные фигуры:
- Или разместите ряд точек симметрично на наклонной оси:
Типичные ошибки
Эти две фигуры симметричны относительно оси? Столкнувшись с этим вопросом, студенты часто допускают две ошибки.
- Подумайте, идентичны ли фигуры, если они симметричны:
Чтобы исправить эту ошибку (как мы упоминали ранее), полезно думать о сетке как о бумаге, которую можно сложить по оси симметрии.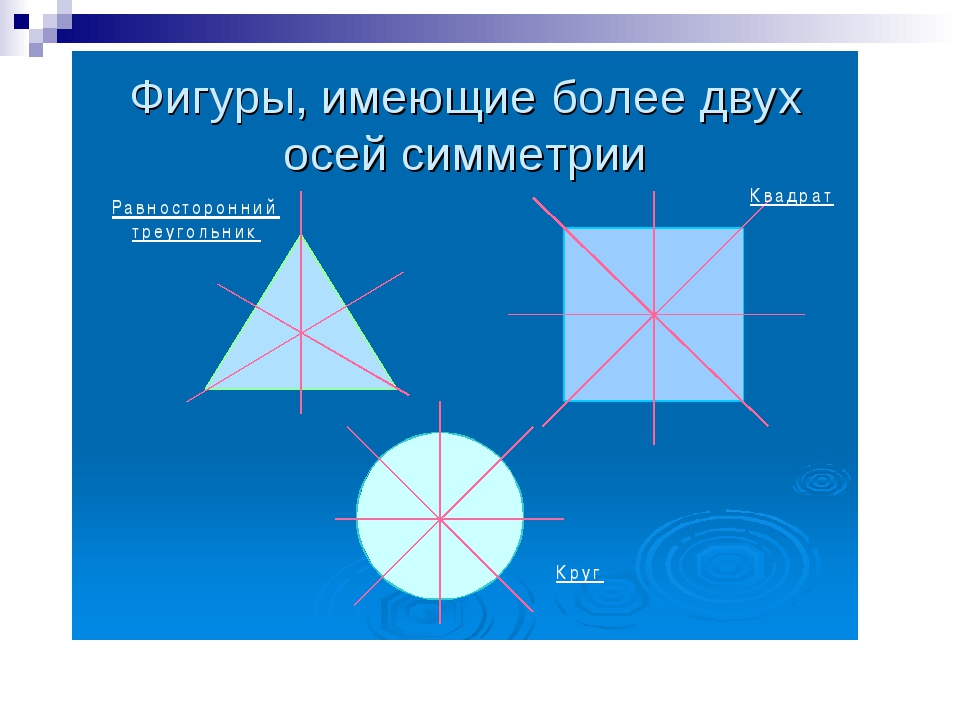 Если в сложенном виде фигуры не совпадают, то это потому, что они не симметричны.Другой способ — представить ось как зеркало. Если одна фигура не является отражением фигуры, которая проецировалась бы в зеркало, тогда они не симметричны.
Если в сложенном виде фигуры не совпадают, то это потому, что они не симметричны.Другой способ — представить ось как зеркало. Если одна фигура не является отражением фигуры, которая проецировалась бы в зеркало, тогда они не симметричны.
- Другая распространенная ошибка — думать, что если одна фигура является зеркальным отражением другой, то они симметричны независимо от их положения относительно оси симметрии:
Мы можем использовать те же стратегии, что и раньше, чтобы исправить эту ошибку. Если сложить бумагу по оси симметрии, фигуры не совпадают.И одна фигура не является отражением другой в осевом зеркале. Следовательно, эти две фигуры не симметричны относительно оси.
Симметрия вне математики
Симметрия нас окружает:
- В зеркале или отражении на поверхности воды. Отраженное изображение симметрично реальному изображению.
- В нас самих: у нас есть правая рука и левая рука, правое ухо и левое ухо, и каждая пара симметрична.
 Наше тело разделено на две симметричные части, правую и левую, относительно оси, идущей от макушки головы до пальцев ног.
Наше тело разделено на две симметричные части, правую и левую, относительно оси, идущей от макушки головы до пальцев ног. - Большинство домов и построек имеют фасады, симметричные относительно вертикальной оси.
- Машины, тостеры, сотовые телефоны, стакан, тарелка, бутылка, телевизор, диван… большинство повседневных предметов имеют одну или несколько осей симметрии.
- Мы также можем найти симметрию в искусстве. Художники используют симметрию в живописи, скульптуре, музыке и множестве других дисциплин.
- В природе тоже. Большинство животных и растений имеют тот или иной тип симметрии: двустороннюю, радиальную…
Если вы хотите узнать больше о геометрии и математике в начальной школе, зарегистрируйтесь в Smartick и попробуйте бесплатно.
Подробнее:
степень бакалавра коммуникативных расстройств и степень бакалавра испанского языка Университета Род-Айленда.
Степень магистра международного образования Университета Алькала — Instituto Franklin.

 Организационный момент.
Организационный момент.

 Выступает один представитель от группы. Остальные группы слушают, высказывают своё мнение, проверяют себя с опорой на слайд.
Выступает один представитель от группы. Остальные группы слушают, высказывают своё мнение, проверяют себя с опорой на слайд.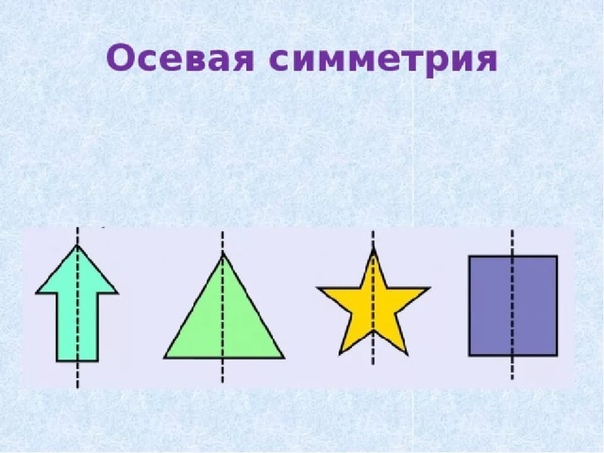 Однако человеческая фигура может быть асимметричной. Одним из таких примеров является сколиоз – искривление позвоночника, приобретенное в том числе неправильной осанкой. Одна из главных причин – неправильная поза во время учебных занятий, из за которой возникает неравномерная нагрузка на позвоночник и мышцы. Предотвратим это заболевание – проведем физкультминутку.
Однако человеческая фигура может быть асимметричной. Одним из таких примеров является сколиоз – искривление позвоночника, приобретенное в том числе неправильной осанкой. Одна из главных причин – неправильная поза во время учебных занятий, из за которой возникает неравномерная нагрузка на позвоночник и мышцы. Предотвратим это заболевание – проведем физкультминутку.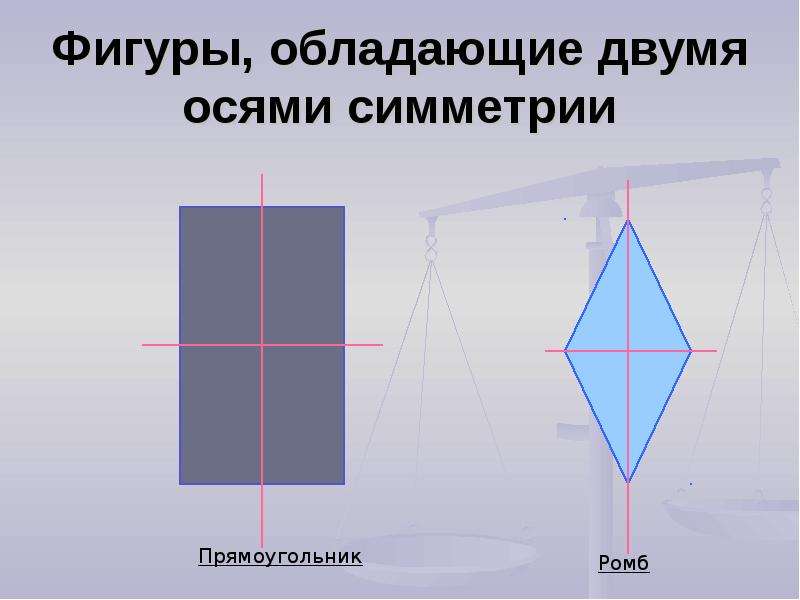 (Слайд 13)
(Слайд 13) Займите, пожалуйста, свои места. Сейчас вам будет предложен тест. Подпишите в тетрадях вариант. Ответы на вопросы пишем в тетради. (слайд 15)
Займите, пожалуйста, свои места. Сейчас вам будет предложен тест. Подпишите в тетрадях вариант. Ответы на вопросы пишем в тетради. (слайд 15) Осуществляют взаимоконтроль.
Осуществляют взаимоконтроль.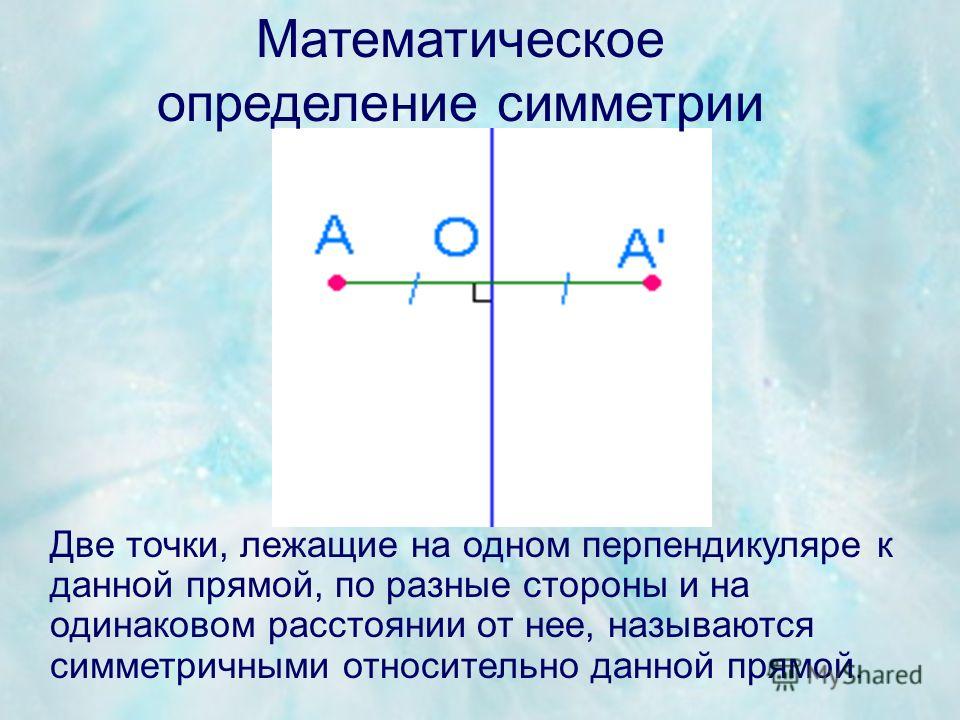
 Решение задач. Слайд
Решение задач. Слайд )
)
 — Где вы встречались в жизни с симметрией? (дома, автомобили, самолеты, мебель, посуда…)
— Где вы встречались в жизни с симметрией? (дома, автомобили, самолеты, мебель, посуда…)
 Этот тип симметрии может напоминать, когда мы смотрим в зеркало и видим в нем свое отражение.
Этот тип симметрии может напоминать, когда мы смотрим в зеркало и видим в нем свое отражение. Наше тело разделено на две симметричные части, правую и левую, относительно оси, идущей от макушки головы до пальцев ног.
Наше тело разделено на две симметричные части, правую и левую, относительно оси, идущей от макушки головы до пальцев ног.