Разряды для начинающих

Наш первый урок назывался числа. Мы рассмотрели лишь малую часть этой темы. На самом деле тема чисел достаточно обширна. В ней много тонкостей и нюансов, много хитростей и интересных фишек.

Сегодня мы продолжим тему чисел, но опять же не будем рассматривать её всю, чтобы не затруднять обучение лишней информацией, которая на первых порах не особо то и нужна. Мы поговорим о разрядах.

Что такое разряд?

Если говорить простым языком, то разряд это позиция цифры в числе или место, где располагается цифра. Возьмём для примера число 635. Это число состоит из трёх цифр: 6, 3 и 5.

Разряды надо читать справа налево. В числе 635 на первой позиции располагается цифра 5, на второй позиции – цифра 3, на третьей позиции – цифра 6.

Позиция, где располагается цифра 5, называется разрядом единиц

Позиция, где располагается цифра 3, называется разрядом десятков

Позиция, где располагается цифра 6, называется разрядом сотен

Каждый из нас слышал со школы такие вещи как «единицы», «десятки», «сотни». Разряды помимо того, что играют роль позиции цифры в числе, сообщают нам некоторую информацию о самом числе. В частности, разряды сообщают нам вес числа. Они сообщают сколько в числе единиц, сколько десятков и сколько сотен.

Вернёмся к нашему числу 635. В разряде единиц располагается пятёрка. О чём это говорит? А говорит это о том, что разряд единиц содержит пять единичек. Выглядит это так:

В разряде десятков располагается тройка. Это говорит о том, что разряд десятков содержит три десятка. Выглядит это так:

В разряде сотен располагается шестёрка. Это говорит о том, что в разряде сотен располагаются шесть сотен. Выглядит это так:

Если сложить число получившихся единиц, число десятков и число сотен, то получим наше изначальное число 635

Существуют и более старшие разряды такие как разряд тысяч, разряд десятков тысяч, разряд сотен тысяч,  разряд миллионов и так далее. Такие большие числа мы будем рассматривать редко, но тем не менее о них тоже желательно знать.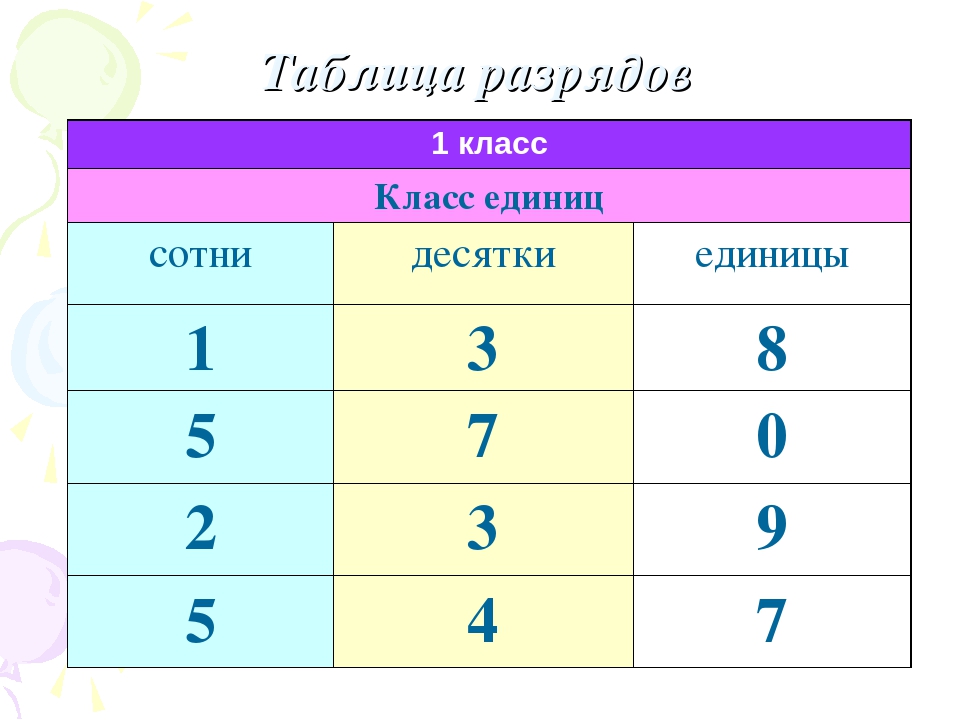

Например, в числе 1 645 832 разряд единиц содержит 2 единицы, разряд десятков — 3 десятка, разряд сотен — 8 сотен, разряд тысяч — 5 тысяч, разряд десятков тысяч — 4 десятка тысяч, разряд сотен тысяч — 6 сотен тысяч, разряд миллионов — 1 миллион.

На первых этапах изучения разрядов желательно разбираться сколько единиц, десятков, сотен содержит то или иное число. К примеру, число 9 содержит 9 единиц. Число 12 содержит две единицы и один десяток. Число 123 содержит три единицы, два десятка и одну сотню.

---

Группировка предметов

После подсчета каких-нибудь предметов, разряды можно использовать для группировки этих предметов. К примеру, если мы насчитали во дворе 35 кирпичей, то можно использовать разряды для группировки этих кирпичей. В случае группировки предметов, разряды можно читать слева направо. Так, цифра 3 в числе 35 будет говорить о том, что в числе 35 содержатся три десятка. А это значит, что 35 кирпичей можно сгруппировать три раза по десять штук.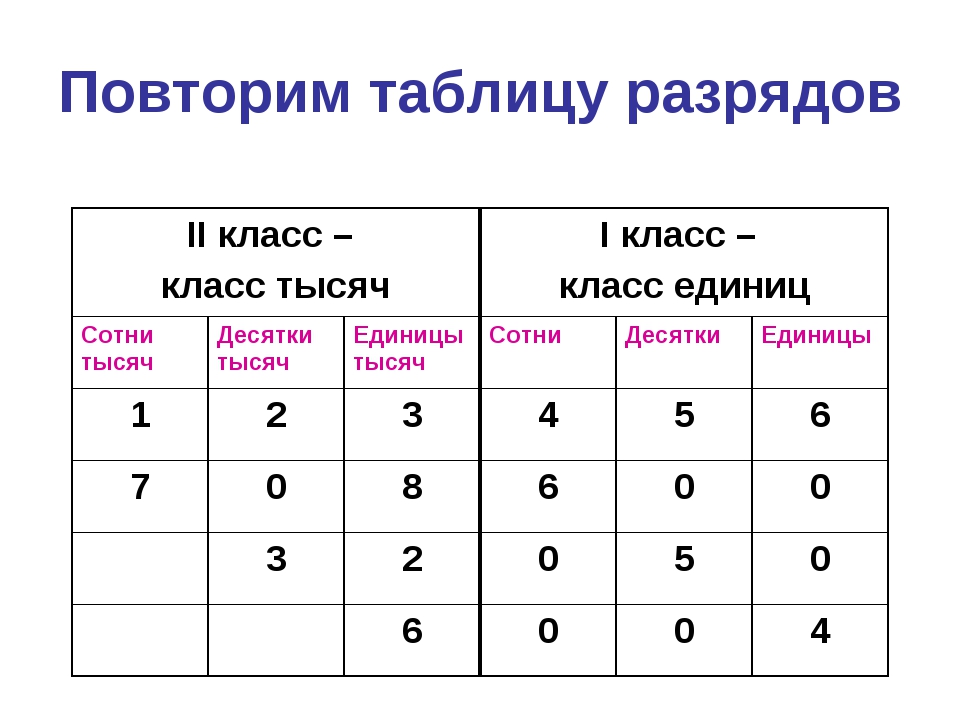

Итак, сгруппируем кирпичи три раза по десять штук:

Получилось тридцать кирпичей. Но осталось еще пять единиц кирпичей. Их мы назовем как «пять единиц»

Получилось три десятка и пять единиц кирпичей.

А если бы мы не стали группировать кирпичи на десятки и единицы, то можно было бы сказать, что число 35 содержит тридцать пять единиц. Такая группировка тоже была бы допустимой:

Аналогично можно рассуждать и про другие числа. К примеру, о числе 123. Ранее мы сказали, что это число содержит три единицы, два десятка и одну сотню. Но можно ещё сказать, что это число  содержит 123 единицы. Более того, можно сгруппировать это число и другим образом, сказав что оно содержит 12 десятков и 3 единицы.

Слова единицы, десятки, сотни, заменяют собой множимые 1, 10 и 100. К примеру, в разряде единиц числа 123 располагается цифра 3. С помощью множимого 1 можно записать, что эта единица содержится в разряде единиц три раза:

1 × 3 = 3

Далее в разряде десятков числа 123 располагается цифра 2.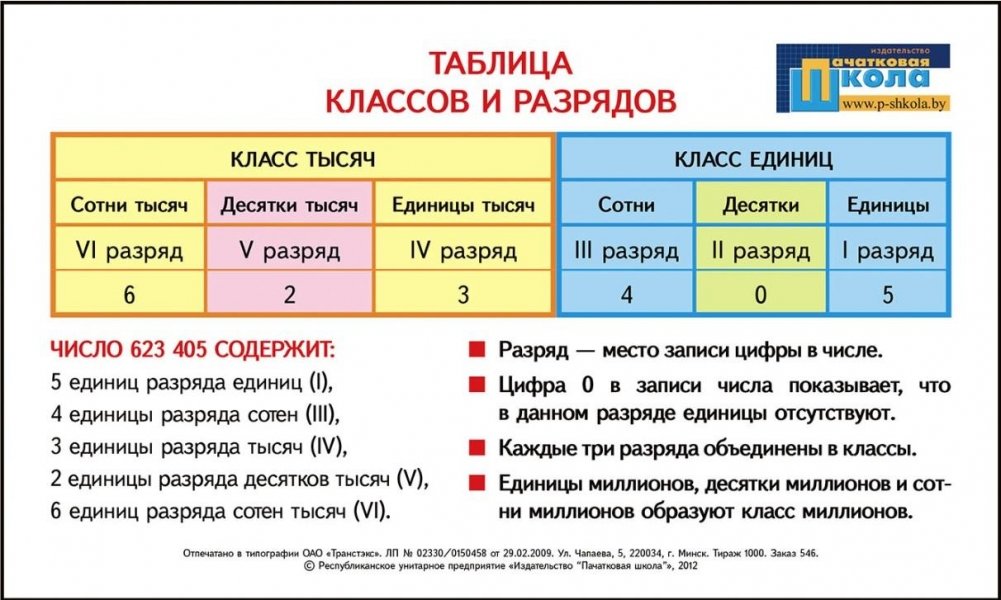

С помощью множимого 10 можно записать, что эта десятка содержится в разряде десятков два раза:

10 × 2 = 20

Далее в разряде сотен числа 123 располагается цифра 1. С помощью множимого 100 можно записать, что эта сотня содержится в разряде сотен один раз:

100 × 1 = 100

Если сложить полученные результаты 3, 20 и 100, то получим число 123

3 + 20 + 100 = 123

То же самое будет происходить если мы скажем, что число 123 содержит 12 десятков и 3 единицы. Другими словами, десятки будут сгруппированы 12 раз:

10 × 12 = 120

А единицы три раза:

1 × 3 = 3

Это можно понять на следующем примере. Если имеется 123 яблока, то можно сгруппировать первые 120 яблок 12 раз по 10 штук:

Получилось сто двадцать яблок. Но осталось еще три яблока. Их мы назовем как «три единицы»

Если сложить полученные результаты 120 и 3, снова получим число 123

120 + 3 = 123

Ещё можно сгруппировать 123 яблока на одну сотню, два десятка и три единицы.

Сгруппируем сотню:

Сгруппируем два десятка:

Сгруппируем три единицы:

Если сложить полученные результаты 100, 20 и 3, снова получим число 123

100 + 20 + 3 = 123

Ну и наконец, рассмотрим последнюю возможную группировку, где яблоки не будут распределяться на десятки и сотни, а будут собраны вместе. В таком случае число 123 будет читаться как

«сто двадцать три единицы». Такая группировка тоже будет допустимой:

1 × 123 = 123

---

Пример 3. Прочитать число 523 всеми возможными способами.

Число 523 можно прочесть, как 3 единицы, 2 десятка и 5 сотен:

1 × 3 = 3 (три единицы)

10 × 2 = 20 (два десятка)

100 × 5 = 500 (пять сотен)

3 + 20 + 500 = 523

Ещё  можно прочесть, как 3 единицы 52 десятка:

1 × 3 = 3 (три единицы)

10 × 52 = 520 (пятьдесят два десятка)

3 + 520 = 523

Ещё число 523 можно прочесть, как 523 единицы:

1 × 523 = 523 (пятьсот двадцать три единицы)

---

Где применить разряды?

Разряды существенно облегчают некоторые вычисления. Представьте, что вы у доски и решаете задачу. Вы почти закончили задачу, осталось только вычислить последнее выражение и получить ответ. Выражение, которое надо вычислить, выглядит следующим образом:

Калькулятора под рукой нет, а хочется быстро записать ответ и удивить всех скоростью своих вычислений. Всё просто, если отдельно сложить единицы, отдельно десятки и отдельно сотни. Начинать нужно с разряда единиц. В первую очередь после знака равно (=) необходимо мысленно поставить три точки. Вместо этих точек будет располагаться новое число (наш ответ):

Теперь начинаем складывать. В разряде единиц числа 632 располагается цифра 2, а в разряде единиц числа 264 — цифра 4. Это означает, разряд единиц числа 632 содержит две единицы, а разряд единиц числа 264 содержит четыре единицы. Складываем 2 и 4 единицы — получаем 6 единиц. Записываем цифру 6 в разряде единиц нового числа (нашего ответа):

Далее складываем десятки. В разряде десятков числа 632 располагается цифра 3, а в разряде десятков числа 264 — цифра 6.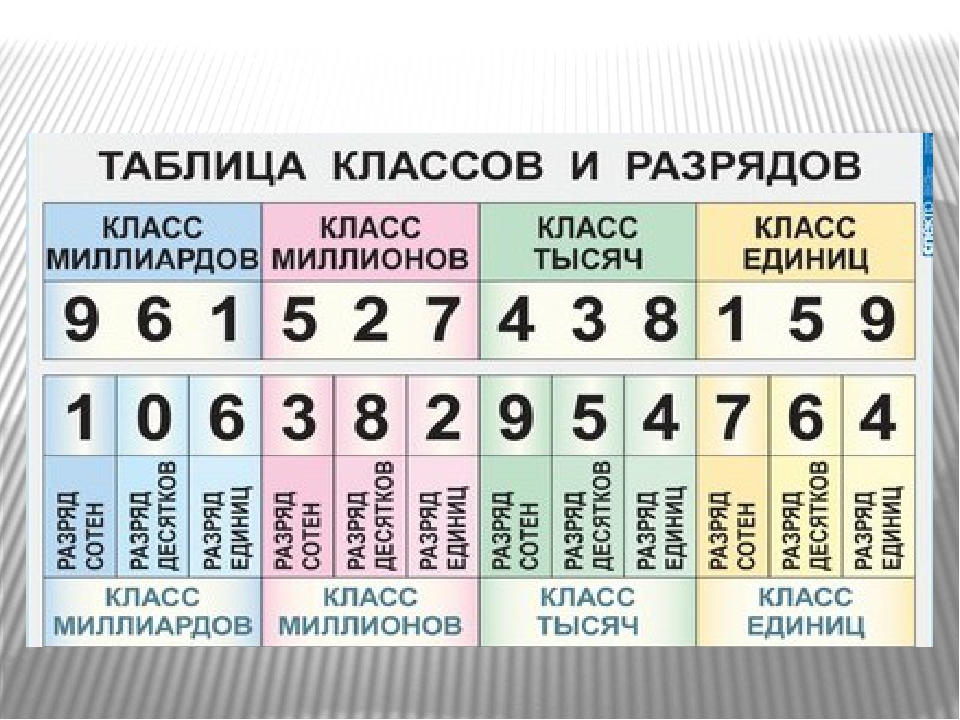  Это означает, что разряд десятков числа 632 содержит три десятка, а разряд десятков числа 264 содержит шесть десятков. Складываем 3 и 6 десятков — получаем 9 десятков. Записываем цифру 9 в разряде десятков нового числа (нашего ответа):

Ну и в завершении складываем отдельно сотни. В разряде сотен числа 632 располагается цифра 6, а в разряде сотен числа 264 — цифра 2. Это означает, что разряд сотен числа 632 содержит шесть сотен, а разряд сотен числа 264 содержит две сотни. Складываем 6 и 2 сотни, получаем 8 сотен. Записываем цифру 8 в разряде сотен нового числа (нашего ответа):

Таким образом, если к числу 632 прибавить 264, получается 896. Конечно, вы вычислите подобное выражение быстрее и окружающие начнут удивляться вашим способностям. Они будут думать, что вы быстро вычисляете большие числа, а на самом деле вы вычисляли маленькие. Согласитесь, что маленькие числа вычислять легче, чем большие.

---

Переполнение разряда

Разряд характеризуется одной цифрой от 0 до 9. Но иногда при вычислении числового выражения в середине решения может произойти переполнение разряда.

Например, при сложении чисел 32 и 14 переполнения не происходит. Сложение единиц этих чисел даст 6 единиц в новом числе. А сложение десятков этих чисел даст 4 десятка в новом числе. Получится ответ 46 или шесть единиц и четыре десятка.

А вот при сложении чисел 29 и 13 произойдёт переполнение. Сложение единиц этих чисел даёт 12 единиц, а сложение десятков 3 десятка. Если в новом числе в разряде единиц записать полученные 12 единиц, а в разряде десятков записать полученные 3 десятка, то получится ошибка:

Значение выражения 29 + 13 равно 42, а не 312. Как же следует поступать при переполнении? В нашем случае переполнение случилось в разряде единиц нового числа. При сложении девяти и трёх единиц у нас получилось 12 единиц. А в разряд единиц можно записывать только цифры в диапазоне от 0 до 9.

Дело в том, что 12 единиц это не просто «двенадцать единиц».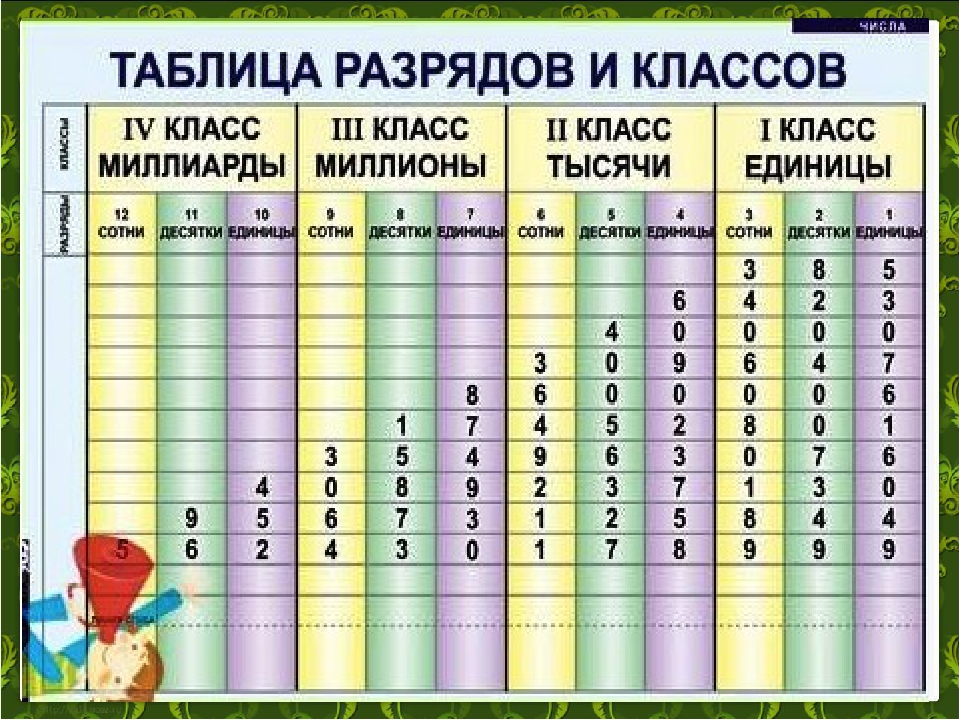 По другому это число можно прочитать как «две единицы и один десяток». Разряд единиц предназначен только для единиц. Десяткам там не место. Здесь и заключается наша ошибка. Сложив 9 единиц и 3 единицы мы получили 12 единиц, которые по-другому можно назвать двумя единицами и одним десятком. Записав две единицы и один десяток в одном разряде, мы допустили ошибку, которая в итоге привела к неправильному ответу.

Чтобы исправить ситуацию, две единицы нужно записать в разряде единиц нового числа, а оставшийся десяток перенести на следующий разряд десятков. После сложения десятков в примере 29 + 13, мы прибавим к полученному результату тот десяток, который остался при сложении единиц.

Итак, из 12 единиц две единицы запишем в разряде единиц нового числа, а один десяток перенесем на следующий разряд

Как видно на рисунке, 12 единиц мы представили как 1 десяток и 2 единицы. Две единицы мы записали в разряде единиц нового числа. А один десяток перенесли к разрядам десятков.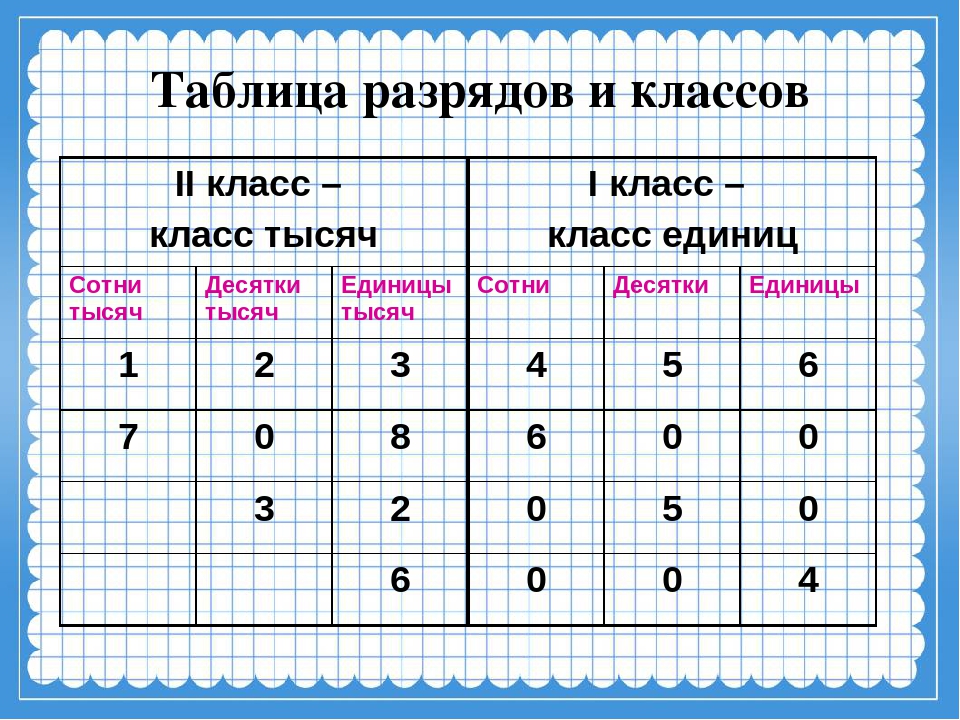 Этот десяток мы прибавим к результату сложения десятков чисел 29 и 13. Чтобы не забыть о нем, мы надписали его над десятками числа 29.

Теперь складываем десятки. Два десятка плюс один десяток будет три десятка, плюс один десяток, который остался от предыдущего сложения. В результате в разряде десятков получаем четыре десятка:

---

Пример 2. Сложить по разрядам числа 862 и 372.

Начинаем с разряда единиц. В разряде единиц числа 862 располагается цифра 2, в разряде единиц числа 372 — также цифра 2. Это означает, что разряд единиц числа 862 содержит две единицы, и разряд единиц числа 372 также содержит две единицы. Складываем 2 единицы плюс 2 единицы — получаем 4 единицы. Записываем цифру 4 в разряде единиц нового числа:

Далее складываем десятки. В разряде десятков числа 862 располагается цифра 6, а в разряде десятков числа 372 — число 7. Это означает, что разряд десятков числа 862 содержит шесть десятков, а разряд десятков числа 372 содержит семь десятков. Складываем 6 десятков и 7 десятков — получаем 13 десятков. Произошло переполнение разряда. 13 десятков это десятка повторенная 13 раз. А если повторить десятку 13 раз, то получится число 130

10 × 13 = 130

Число 130 состоит из трех десятков и одной сотни. Три десятка мы запишем в разряде десятков нового числа, а одну сотню отправим на следующий разряд:

Как видно на рисунке, 13 десятков (число 130) мы представили как 1 сотню и 3 десятка. Три десятка мы записали в разряде десятков нового числа. А одну сотню перенесли к разрядам сотен. Эту сотню мы прибавим к результату сложения сотен чисел 862 и 372. Чтобы не забыть о ней, мы надписали её над сотнями числа 862.

Теперь складываем сотни. Восемь сотен плюс три сотни будет одиннадцать сотен плюс одна сотня, которая осталась от предыдущего сложения. В результате в разряде сотен получаем двенадцать сотен:

Здесь также происходит переполнение разряда сотен, но это не приводит к ошибке, поскольку решение завершено. При желании с 12 сотнями можно провести те же действия, что мы провели с 13 десятками.

12 сотен это сотня, повторенная 12 раз. А если повторить сотню 12 раз, то получится 1200

100 × 12 = 1200

В числе 1200 две сотни и одна тысяча. Две сотни записываются в разряд сотен нового числа, а одна тысяча перенеслась к разряду тысяч.

---

Теперь рассмотрим примеры на вычитание. Для начала вспомним, что такое вычитание. Это операция, которая позволяет от одного числа вычесть другое. Вычитание состоит из трёх параметров: уменьшаемого, вычитаемого и разности. Вычитать тоже нужно по разрядам.

Пример 3. Вычесть из числа 65 число 12.

Начинаем с разряда единиц. В разряде единиц числа 65 располагается цифра 5, а в разряде единиц числа 12 — цифра 2. Это означает, что разряд единиц числа 65 содержит пять единиц, а разряд единиц числа 12 содержит две единицы. Вычтем из пяти единиц две единицы, получим три единицы. Записываем цифру 3 в разряде единиц нового числа:

Теперь вычитаем десятки.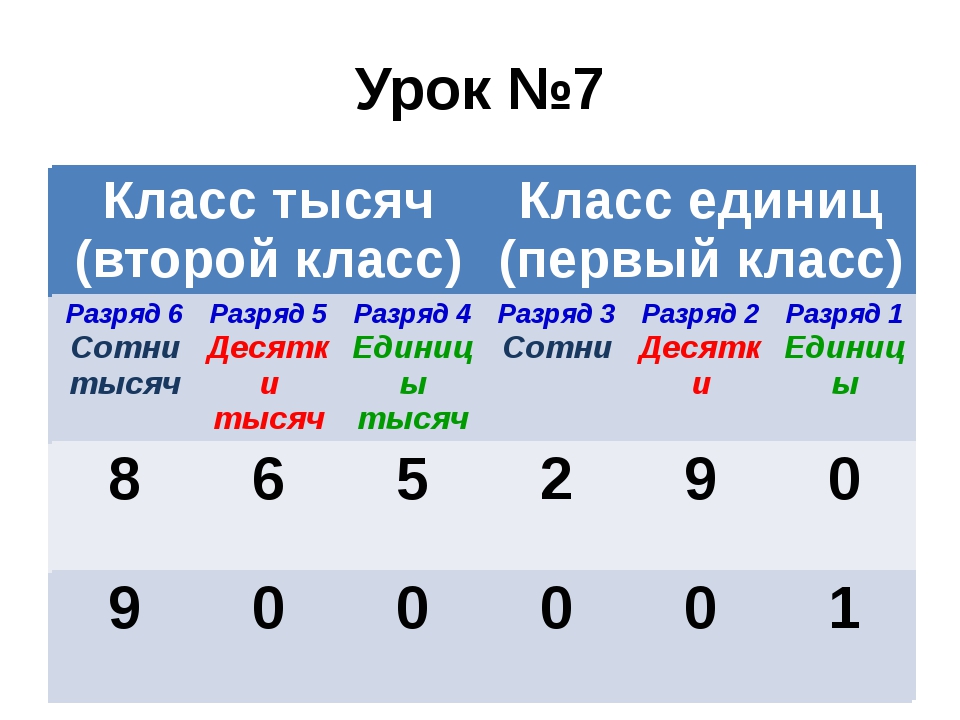 В разряде десятков числа 65 располагается цифра 6, а в разряде десятков числа 12 — цифра 1. Это означает, что разряд десятков числа 65 содержит шесть десятков, а разряд десятков числа 12 содержит один десяток. Вычтем из шести десятков один десяток, получим пять десятков. Записываем цифру 5 в разряде десятков нового числа:

---

Пример 4. Вычесть из числа 32 число 15

В разряде единиц числа 32 содержится две единицы, а в разряде единиц числа 15 — пять единиц. От двух единиц не вычесть пять единиц, поскольку две единицы меньше, чем пять единиц.

Сгруппируем 32 яблока так, чтобы в первой группе было три десятка яблок, а во второй — оставшиеся две единицы яблок:

Итак, нам нужно из этих 32 яблок вычесть 15 яблок, то есть вычесть пять единиц и один десяток яблок. Причем вычесть по разрядам.

От двух единиц яблок нельзя вычесть пять единиц яблок. Чтобы выполнить вычитание, две единицы должны взять несколько яблок у соседней группы (разряда десятков).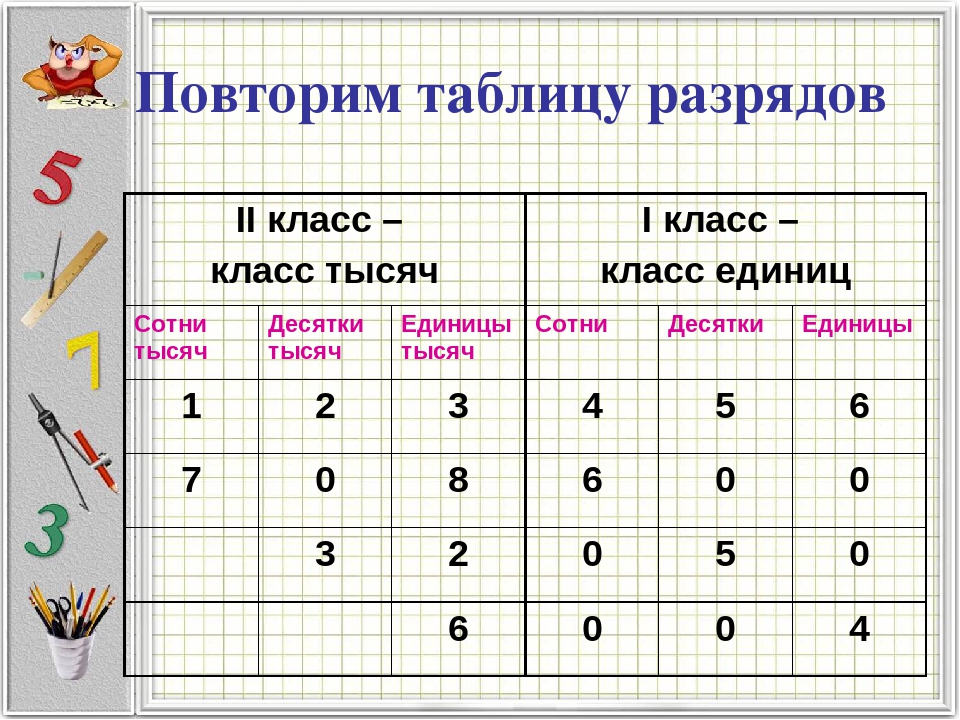 Но нельзя брать сколько хочется, поскольку десятки строго упорядочены по десять штук. Разряд десятков может дать двум единицам только один целый десяток.

Итак, берём один десяток из разряда десятков и отдаём его двум единицам:

К двум единицам яблок теперь присоединился один десяток яблок. Получается 12 единиц яблок. А от двенадцати можно вычесть пять, получится семь. Записываем цифру 7 в разряде единиц нового числа:

Теперь вычитаем десятки. Поскольку разряд десятков отдал единицам один десяток, сейчас он имеет не три, а два десятка. Поэтому вычитаем из двух десятков один десяток. Останется один десяток. Записываем цифру 1 в разряде десятков нового числа:

Чтобы не забывать, что в каком-то разряде был взят один десяток (либо сотня либо тысяча), над этим разрядом принято ставить точку.

---

Пример 5. Вычесть из числа 653 число 286

В разряде единиц числа 653 содержится три единицы, а в разряде единиц числа 286 — шесть единиц.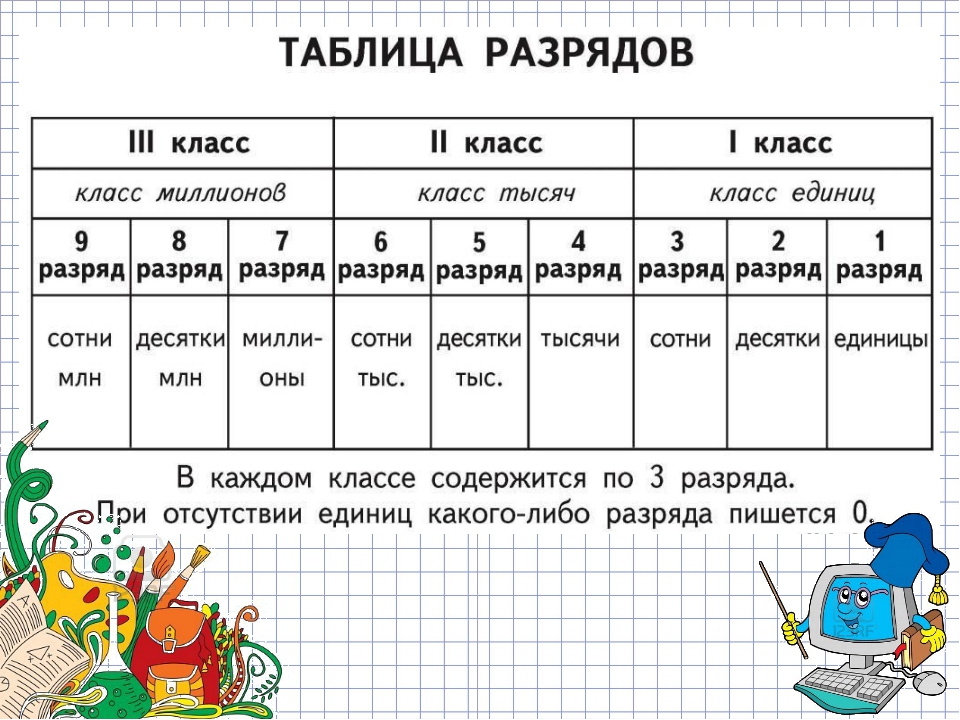 От трёх единиц не вычесть шесть единиц, поэтому берем один десяток у разряда десятков. Ставим точку над разрядом десятков, чтобы помнить о том, что мы взяли оттуда один десяток:

Взятый один десяток и три единицы вместе образуют тринадцать единиц. От тринадцати единиц можно вычесть шесть единиц, получится семь единиц. Записываем цифру 7 в разряде единиц нового числа:

Теперь вычитаем десятки. Раньше разряд десятков числа 653 содержал пять десятков, но мы взяли с него один десяток, и теперь в разряде десятков содержатся четыре десятка. Из четырех десятков не вычесть восемь десятков, поэтому берем одну сотню у разряда сотен. Ставим точку над разрядом сотен, чтобы помнить о том, что мы взяли оттуда одну сотню:

Взятая одна сотня и четыре десятка вместе образуют четырнадцать десятков. От четырнадцати десятков можно вычесть восемь десятков, получится шесть десятков. Записываем цифру 6 в разряде десятков нового числа:

Теперь вычитаем сотни. Раньше разряд сотен числа 653 содержал шесть сотен, но мы взяли с него одну сотню, и теперь в разряде сотен содержатся пять сотен. Из пяти сотен можно вычесть две сотни, получается три сотни. Записываем цифру 3 в разряде сотен нового числа:

Намного сложнее вычитать из чисел вида 100, 200, 300, 1000, 10000. То есть числа, у которых на конце нули. Чтобы выполнить вычитание, каждому разряду приходится занимать десятки/сотни/ тысячи у следующего разряда. Давайте посмотрим, как это происходит.

Пример 6. Вычесть из числа 200 число 84

В разряде единиц числа 200 содержится ноль единиц, а в разряде единиц числа 84 — четыре единицы. От нуля не вычесть четыре единицы, поэтому берем один десяток у разряда десятков. Ставим точку над разрядом десятков, чтобы помнить о том, что мы взяли оттуда один десяток:

Но в разряде десятков нет десятков, которые мы могли бы взять, поскольку там тоже ноль. Чтобы разряд десятков смог дать нам один десяток, мы должны взять для него одну сотню у разряда сотен. Ставим точку над разрядом сотен, чтобы помнить о том, что мы взяли оттуда одну сотню для разряда десятков:

Взятая одна сотня это десять десятков. От этих десяти десятков мы берём один десяток и отдаём его единицам. Этот взятый один десяток и прежние ноль единиц вместе образуют десять единиц. От десяти единиц можно вычесть четыре единицы, получится шесть единиц. Записываем цифру 6 в разряде единиц нового числа:

Теперь вычитаем десятки. Чтобы вычесть единицы мы обратились к разряду десятков за одним десятком, но на тот момент этот разряд был пуст. Чтобы разряд десятков смог дать нам один десяток, мы взяли одну сотню у разряда сотен. Эту одну сотню мы назвали «десять десятков». Один десяток мы отдали единицам. Значит на данный момент в разряде десятков содержатся не десять, а девять десятков. От девяти десятков можно вычесть восемь десятков, получится один десяток. Записываем цифру 1 в разряде десятков нового числа:

Теперь вычитаем сотни. Для разряда десятков мы брали у разряда сотен одну сотню. Значит сейчас в разряде сотен содержатся не две сотни, а одна. Поскольку в вычитаемом разряд сотен отсутствует, мы переносим эту одну сотню в разряд сотен нового числа:

Получили окончательный ответ 116.

Естественно, выполнять вычитание таким традиционным методом довольно сложно, особенно на первых порах. Поняв сам принцип вычитания, можно воспользоваться нестандартными способами.

Первый способ заключается в том, чтобы уменьшить число, у которого на конце нули на одну единицу. Далее из полученного результата вычесть вычитаемое и к полученной разности прибавить единицу, которую изначально вычли из уменьшаемого. Давайте решим предыдущий пример этим способом:

Уменьшаемое здесь это число 200. Уменьшим это число на единицу. Если от 200 вычесть 1 получится 199. Теперь в примере 200 − 84 вместо числа 200 записываем число 199 и решаем пример 199 − 84. А решение этого примера не составляет особого труда.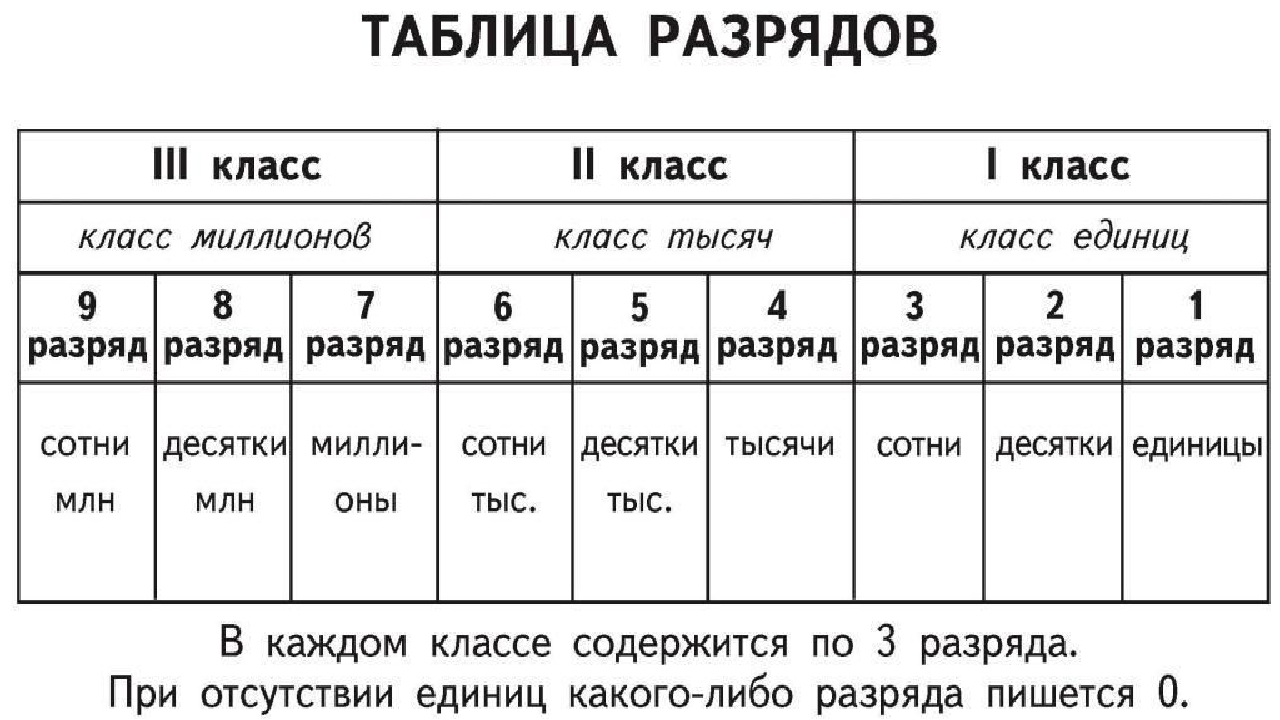 Единицы вычтем из единиц, десятки из десятков, а сотню просто перенесем к новому числу, поскольку в числе 84 нет сотен:

Получили ответ 115. Теперь к этому ответу прибавляем единицу, которую мы изначально вычли из числа 200

Получили окончательный ответ 116.

---

Пример 7. Вычесть из числа 100000 число 91899

Вычтем из 100000 единицу, получим 99999

Теперь из 99999 вычитаем 91899

К полученному результату 8100 прибавим единицу, которую мы вычли из 100000

Получили окончательный ответ 8101.

---

Второй способ вычитания заключается в том, чтобы рассматривать цифру, находящуюся в разряде, как самостоятельное число. Решим несколько примеров этим способом.

Пример 8. Вычесть из числа 75 число 36

Будем считать, что каждая цифра в разряде это самостоятельное число.

Итак, в разряде единиц числа 75 располагается число 5, а в разряде единиц числа 36 располагается число 6. Из пяти не вычесть шести, поэтому берем одну единицу у следующего числа, находящегося в разряде десятков.

В разряде десятков располагается число 7. Берем от этого числа одну единицу и мысленно дописываем её слева от числа 5

А поскольку от числа 7 взята одна единица, это число уменьшится на одну единицу и обратится в число 6

Теперь в разряде единиц числа 75 располагается число 15, а в разряде единиц числа 36 число 6. Из 15 можно вычесть 6, получится 9. Записываем число 9 в разряде единиц нового числа:

Переходим к следующему числу, находящемуся в разряде десятков. Раньше там располагалось число 7, но мы взяли с этого числа одну единицу, поэтому сейчас там располагается число 6. А в разряде десятков числа 36 располагается число 3. Из 6 можно вычесть 3, получится 3. Записываем число 3 в разряде десятков нового числа:

---

Пример 9. Вычесть из числа 200 число 84

Будем считать, что каждая цифра в разряде это самостоятельно число.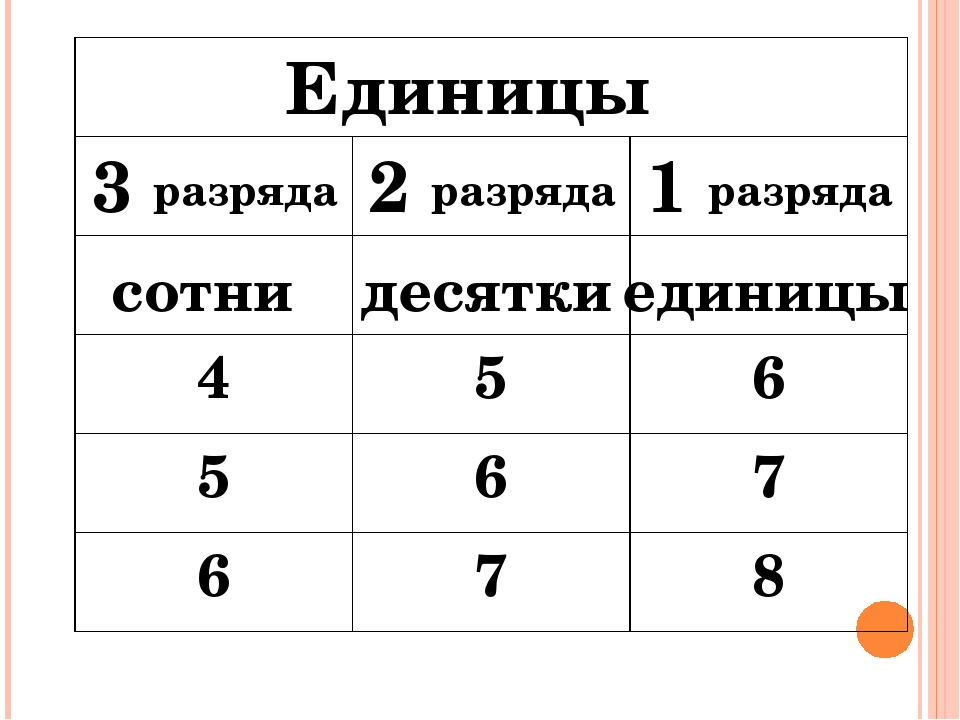

Итак, в разряде единиц числа 200 располагается ноль, а в разряде единиц числа 84 — располагается четыре. От нуля не вычесть четыре, поэтому берем одну единицу у следующего числа, находящегося в разряде десятков. Но в разряде десятков тоже ноль. Ноль не сможет дать нам единицу. В таком случае за следующее принимаем число 20.

Берём одну единицу от числа 20 и мысленно дописываем её слева от нуля, располагающегося в разряде единиц. А поскольку от числа 20 взята одна единица, это число обратится в число 19

Теперь в разряде единиц располагается число 10. Десять минус четыре равно шесть. Записываем число 6 в разряде единиц нового числа:

Переходим к следующему числу, находящемуся в разряде десятков. Раньше там располагался ноль, но этот ноль вместе со следующей цифрой 2 образовал число 20, от которого мы брали одну единицу. В результате число 20 обратилось в число 19. Получается, что теперь в разряде десятков числа 200 располагается число 9, а в разряде десятков числа 84 располагается число 8.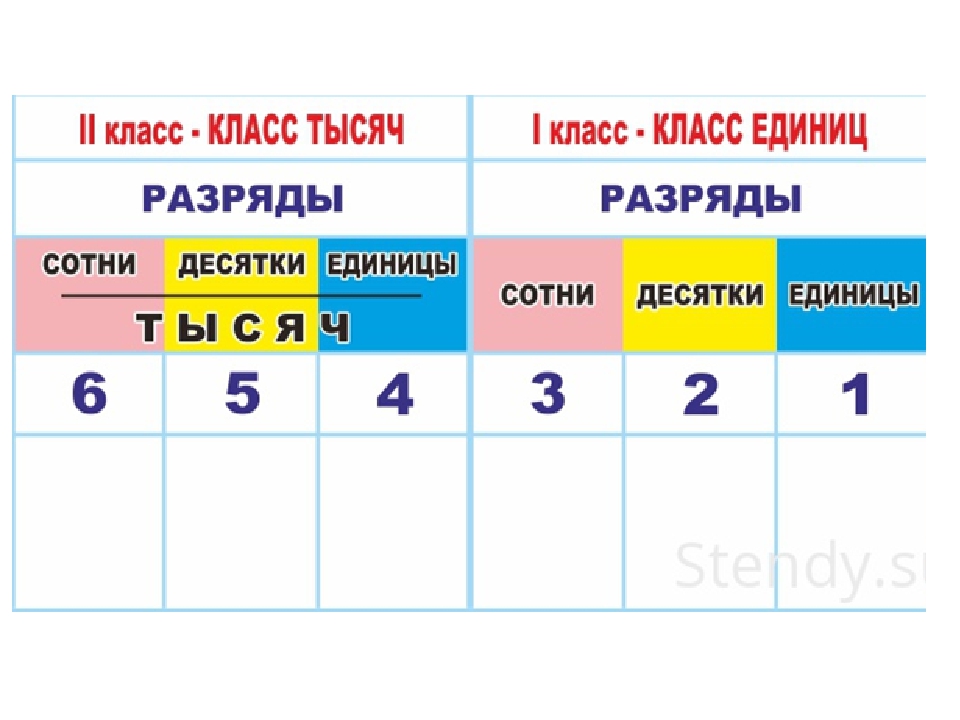 Девять минус восемь равно одному. Записываем число 1 в разряде десятков нашего ответа:

Переходим к следующему числу, находящемуся к разряду сотен. Раньше там располагалось число 2, но это число вместе с цифрой 0 мы приняли за число 20, от которого взяли одну единицу. В результате число 20 обратилось в число 19. Получается, что теперь в разряде сотен числа 200 располагается число 1, а в числе 84 разряд сотен пустой, поэтому мы переносим эту единицу к новому числу:

Этот метод поначалу кажется сложным и лишенным всякого смысла, но на деле он самый лёгкий. В основном мы будем им пользоваться при сложении и вычитании чисел в столбик.

---

Сложение в столбик

Сложение в столбик это школьная операция, которую помнят многие, но не мешает вспомнить её ещё раз. Сложение в столбик происходит по разрядам — единицы складываются с единицами, десятки с десятками, сотни с сотнями, тысячи с тысячами.

Рассмотрим несколько примеров.

Пример 1.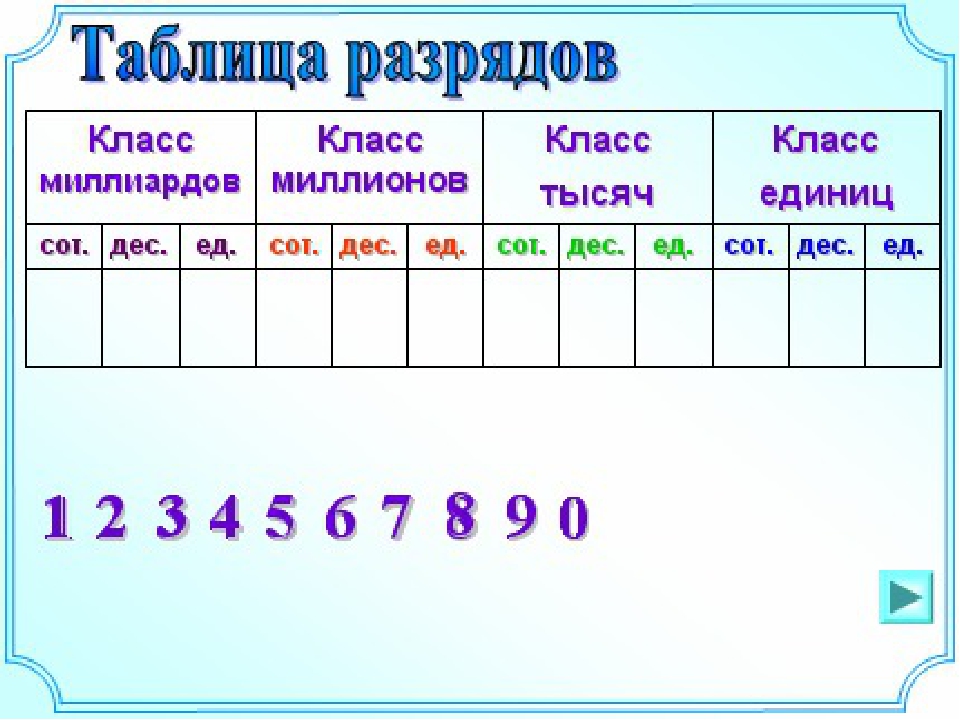 Сложить 61 и 23.

Сначала записываем первое число, а под ним второе число так, чтобы единицы и десятки второго числа оказались под единицами и десятками первого числа. Всё это соединяем знаком сложения (+) по вертикали:

Теперь единицы первого числа складываем с единицами второго числа, а десятки первого числа складываем с десятками второго числа:

Получили 61 + 23 = 84.

---

Пример 2. Сложить 108 и 60

Записываем числа в столбик. Единицы под единицами, десятки под десятками:

Теперь складываем единицы первого числа с единицами второго числа, десятки первого числа с десятками второго числа, сотни первого числа с сотнями второго числа. Но сотня есть только у первого числа 108. В этом случае цифра 1 из разряда сотен добавляется к новому числу (нашему ответу). Как говорили в школе «сносится»:

Видно, что мы снесли цифру 1 к нашему ответу.

Когда речь идёт о сложении, нет разницы в каком порядке записывать числа.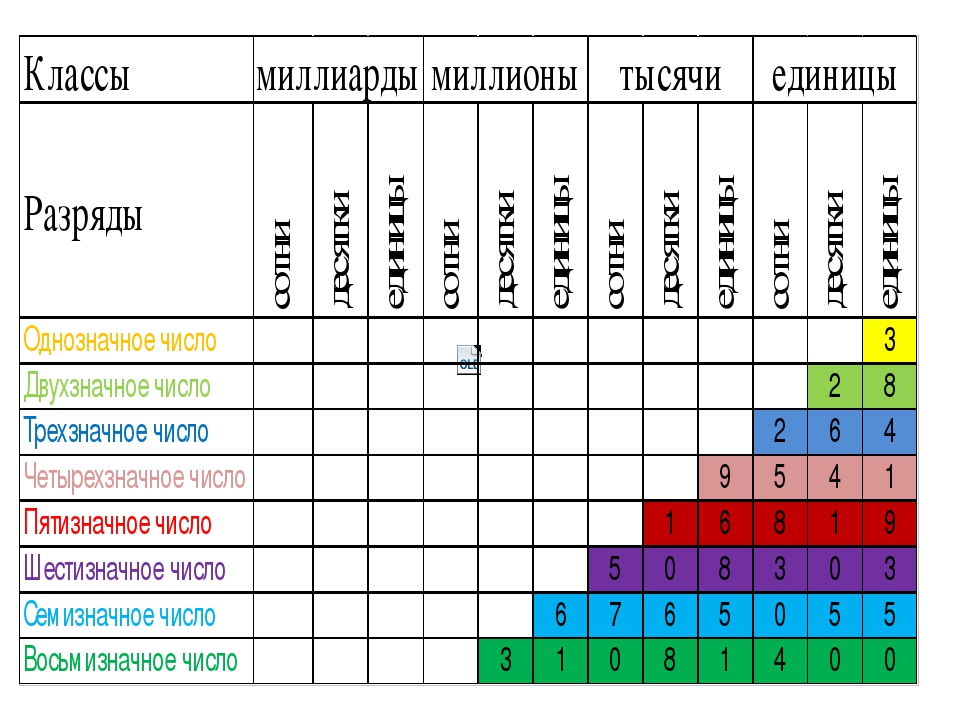 Наш пример вполне можно было записать и так:

Первая запись, где число 108 было наверху, более удобнее для вычисления. Человек вправе выбирать любую запись, но обязательно нужно помнить, что единицы надо записывать строго под единицами, десятки под десятками, сотни под сотнями. Другими словами, следующие записи будут неправильными:

Если вдруг при сложении соответствующих разрядов получится число, которое не помещается в разряд нового числа, то необходимо записать одну цифру из младшего разряда, а оставшуюся перенести на следующий разряд.

Речь в данном случае идет о переполнении разряда, о котором мы говорили ранее. Например, при сложении 26 и 98 получается 124. Давайте посмотрим, как это получилось.

Записываем числа в столбик. Единицы под единицами, десятки под десятками:

Складываем единицы первого числа с единицами второго числа: 6+8=14. Получили число 14, которое не вместится в разряд единиц нашего ответа. В таких случаях мы сначала вытаскиваем из 14 цифру, находящуюся в разряде единиц и записываем её в разряде единиц нашего ответа.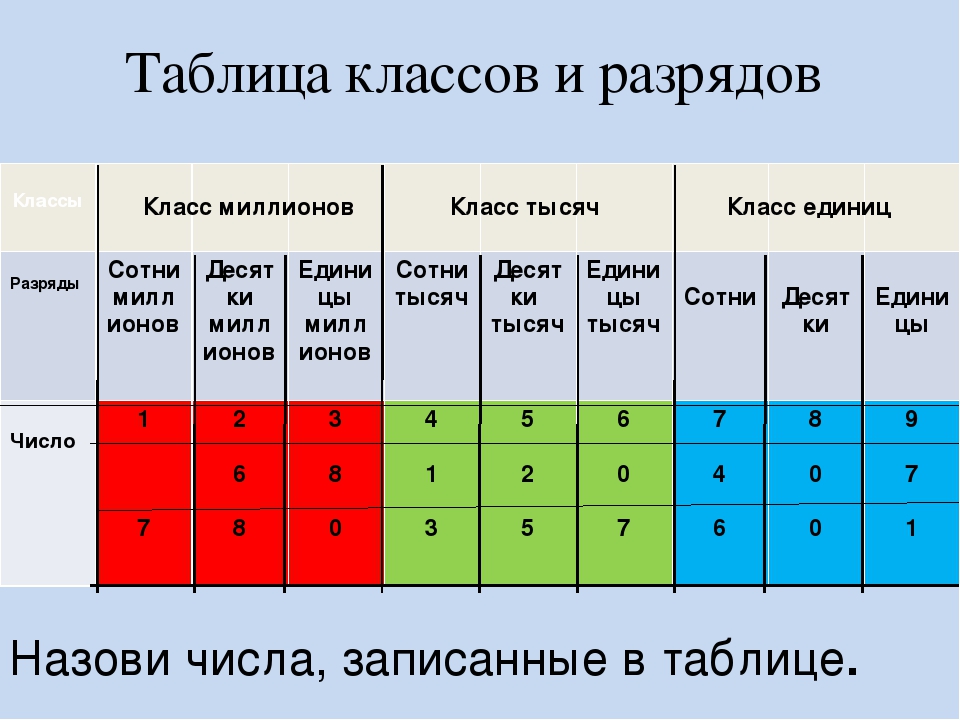 В разряде единиц числа 14 располагается цифра 4. Записываем эту цифру в разряде единиц нашего ответа:

А куда девать цифру 1 из числа 14? Здесь начинается самое интересное. Эту единицу мы переносим на следующий разряд. Она будет добавлена к разряду десятков нашего ответа.

Складываем десятки с десятками. 2 плюс 9 равно 11, плюс добавляем единицу, которая досталась нам от числа 14. Добавив к 11 нашу единицу, мы получим число 12, которое и запишем в разряде десятков нашего ответа. Поскольку это конец решения, здесь уже не стоит вопрос о том, вместится ли полученный ответ в разряд десятков. 12 мы записываем целиком, образуя окончательный ответ.

Получили ответ 124.

Говоря традиционным методом сложения, при сложении 6 и 8 единиц получилось 14 единиц. 14 единиц это 4 единицы и 1 десяток. Четыре единицы мы записали в разряде единиц, а один десяток отправили на следующий разряд (к разрядам десятков). Затем сложив 2 десятка и 9 десятков, мы получили 11 десятков, плюс добавили 1 десяток, который остался при сложении единиц. В результате получили 12 десятков. Эти двенадцать десятков мы записали целиком, образуя окончательный ответ 124.

Этот простенький пример демонстрирует школьную ситуацию, в которой говорят «четыре пишем, один в уме». Если вы будете решать примеры и у вас после сложения разрядов останется цифра, которую надо держать в уме, запишите её над тем разрядом, куда она будет потом добавлена. Это позволит вам не забыть о ней:

---

Пример 2. Сложить числа 784 и 548

Записываем числа в столбик. Единицы под единицами, десятки под десятками, сотни под сотнями:

Складываем единицы первого числа с единицами второго числа: 4+8=12. Число 12 не вмещается в разряд единиц нашего ответа, поэтому мы из 12 вынимаем цифру 2 из разряда единиц и записываем её в разряд единиц нашего ответа. А цифру 1 переносим на следующий разряд:

Теперь складываем десятки. Складываем 8 и 4 плюс единица, которая осталась от предыдущей операции (единица осталась от 12, на рисунке она выделена синим цветом). Складываем 8+4+1=13. Число 13 не вместится в разряд десятков нашего ответа, поэтому мы запишем цифру 3 в разряде десятков, а единицу перенесём на следующий разряд:

Теперь складываем сотни. Складываем 7 и 5 плюс единица, которая осталась от предыдущей операции: 7+5+1=13. Записываем число 13 в разряд сотен:

---

Вычитание в столбик

Пример 1. Вычтем из числа 69 число 53.

Запишем числа в столбик. Единицы под единицами, десятки под десятками. Затем вычитаем по разрядам. Из единиц первого числа вычитаем единицы второго числа. Из десятков первого числа вычитаем десятки второго числа:

Получили ответ 16.

---

Пример 2. Найти значение выражения 95 − 26

Записываем в столбик данное выражение:

Разряд единиц числа 95 содержит 5 единиц, а разряд единиц числа 26 содержит 6 единиц. От пяти единиц нельзя вычесть шесть единиц, поэтому берем один десяток у разряда десятков. Этот десяток и имеющиеся пять единиц вместе составляют 15 единиц. Из 15 единиц можно вычесть 6 единиц, получится 9 единиц. Записываем цифру 9 в разряде единиц нашего ответа:

Теперь вычитаем десятки. Разряд десятков числа 95 раньше содержал 9 десятков, но мы взяли с этого разряда один десяток, и сейчас он содержит 8 десятков. А разряд десятков числа 26 содержит 2 десятка. Из восьми десятков можно вычесть два десятка, получится шесть десятков. Записываем цифру 6 в разряде десятков нашего ответа:

Воспользуемся нестандартным способом вычитания при котором каждая цифра, входящая в число, рассматривается как отдельное число. При вычитании больших чисел в столбик этот способ очень удобен.

В разряде единиц уменьшаемого располагается число 5. А в разряде единиц вычитаемого число 6. Из пятёрки не вычесть шестёрку. Поэтому берем одну единицу у числа 9. Взятая единица мысленно дописывается слева от пятёрки. А поскольку у числа 9 мы взяли одну единицу, это число уменьшится на одну единицу:

В результате пятёрка обращается в число 15.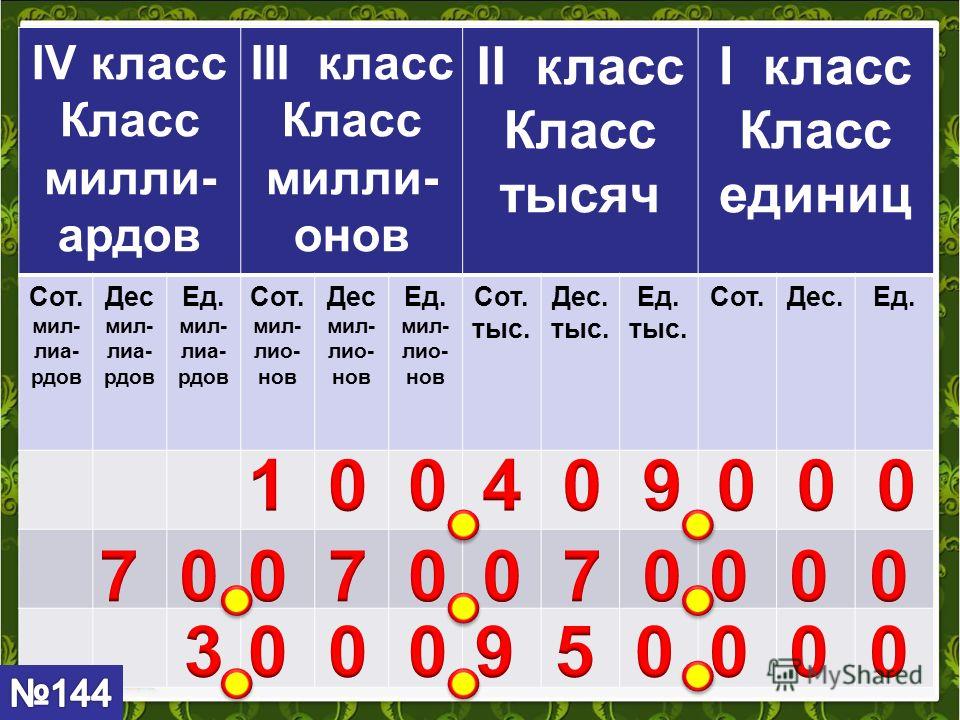 Теперь можно из 15 вычесть 6. Получается 9. Записываем число 9 в разряде единиц нашего ответа:

Переходим к разряду десятков. Раньше там располагалось число 9, но поскольку мы взяли у него одну единицу оно обратилось в число 8. В разряде десятков второго числа располагается число 2. Восемь минус два будет шесть. Записываем число 6 в разряде десятков нашего ответа:

---

Пример 3. Найдем значение выражения 2412 − 2317

Записываем в столбик данное выражение:

В разряде единиц числа 2412 располагается число 2, а в разряде единиц числа 2317 располагается число 7. Из двойки не вычесть семёрку, поэтому берем единицу у следующего числа 1. Взятую единицу мысленно дописываем слева от двойки:

В результате двойка обращается в число 12. Теперь можно из 12 вычесть 7. Получается 5. Записываем цифру 5 в разряде единиц нашего ответа:

Переходим к десяткам. В разряде десятков числа 2412 раньше располагалось число 1, но поскольку мы взяли у него одну единицу, оно обратилось в 0. А в разряде десятков числа 2317 располагается число 1. Из нуля не вычесть единицу. Поэтому берем одну единицу у следующего числа 4. Взятую единицу мысленно дописываем слева от нуля. А поскольку у числа 4 мы взяли одну единицу, это число уменьшится на одну единицу:

В результате ноль обращается в число 10. Теперь можно из 10 вычесть 1. Получается 9. Записываем цифру 9 в разряде десятков нашего ответа:

В разряде сотен числа 2412 раньше располагалось число 4, но сейчас там располагается число 3. В разряде сотен числа 2317 также располагается число 3. Три минус три равно нулю. То же самое и с разрядами тысяч в обоих числах. Два минус два равно нулю. А если разность старших разрядов равна нулю, то этот ноль не записывают. Поэтому окончательным ответом будет число 95.

---

Пример 4. Найти значение выражения 600 − 8

Запишем в столбик данное выражение:

В разряде единиц числа 600 располагается ноль, а в разряде единиц числа 8 само это число.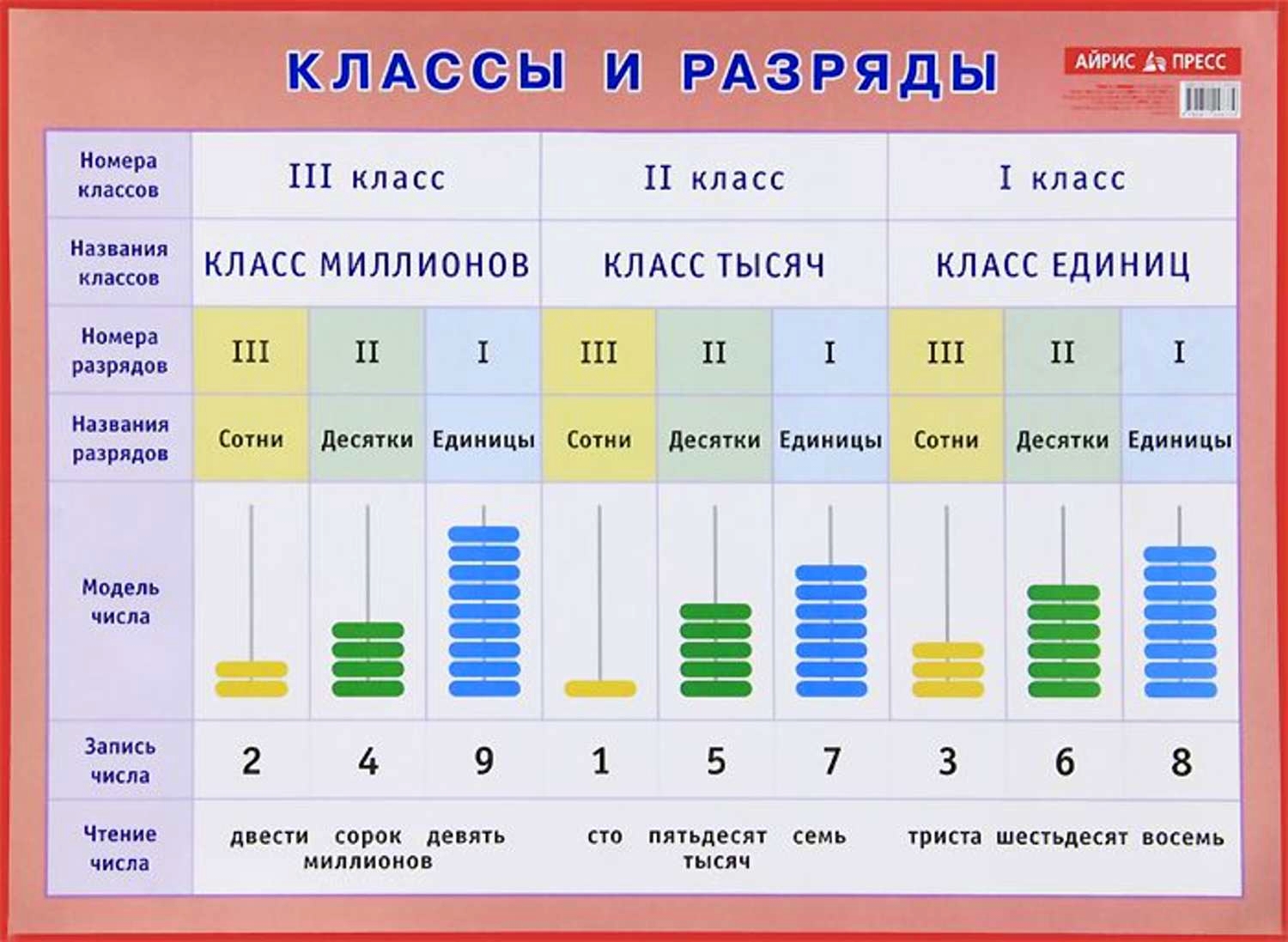 Из нуля не вычесть восьмерку, поэтому берем единицу у следующего числа. Но следующее число это тоже ноль. Тогда за следующее число принимаем число 60. Берем одну единицу у этого числа и мысленно дописываем её слева от нуля. А поскольку у числа 60 мы взяли одну единицу, это число уменьшится на одну единицу:

Теперь в разряде единиц располагается число 10. Из 10  можно вычесть 8, получится 2. Записываем число 2 в разряде единиц нового числа:

Переходим к следующему числу, находящемуся в разряде десятков. В разряде десятков раньше располагался ноль, но сейчас там располагается число 9, а во втором числе разряд десятков отсутствует. Поэтому число 9 переносится к новому числу:

Переходим к следующему числу, находящемуся в разряде сотен. В разряде сотен раньше располагалось число 6, но сейчас там располагается число 5, а во втором числе разряд сотен отсутствует. Поэтому число 5 переносится к новому числу:

---

Пример 5. Найти значение выражения 10000 − 999

Запишем в столбик данное выражение:

В разряде единиц числа 10000 располагается 0, а в разряде единиц числа 999 располагается число 9. Из нуля не вычесть девятку, поэтому берем одну единицу у следующего числа, находящегося в разряде десятков. Но в следующем разряде тоже ноль. Тогда за следующее число принимаем 1000 и берем от этого числа единицу:

Следующее число в данном случае было 1000. Взяв у него единицу, мы обратили его в число 999. А взятую единицу дописали слева от нуля.

Дальнейшее вычисление не составило особого труда. Десять минус девять равно одному. Вычитание чисел, находящихся в разряде десятков обоих чисел дало ноль. Вычитание чисел, находящихся в разряде сотен обоих чисел тоже дало ноль. А девятка из разряда тысяч была перенесена к новому числу:

---

Пример 6. Найти значение выражения 12301­ − 9046

Запишем в столбик данное выражение:

В разряде единиц числа 12301 располагается число 1, а в разряде единиц числа 9046 располагается число 6. Из единицы не вычесть шесть, поэтому берем одну единицу у следующего числа, находящегося в разряде десятков. Но в следующем разряде располагается ноль. Ноль ничего нам дать не сможет. Тогда за следующее число принимаем 1230 и берем от этого числа единицу:

Следующее число в данном случае было 1230. Взяв у него единицу, мы обратили его в число 1229. А взятую единицу мысленно дописали слева от единицы, находящейся в разряде единиц.

Дальнейшее вычисление не составило особого труда. Одиннадцать минус шесть равно пять. Вычитание чисел, находящихся в разряде десятков обоих чисел дало число 5. Вычитание чисел, находящихся в разряде сотен обоих чисел дало число 2. Вычитание чисел, находящихся в разряде тысяч обоих чисел дало число 3.

---

Задания для самостоятельного решения

Задание 1. Выполните сложение:

Решение:

Задание 2. Выполните сложение:

Решение:

Задание 3. Выполните сложение:

Решение:

Задание 4. Выполните сложение:

Решение:

Задание 5. Выполните сложение:

Решение:

Задание 6.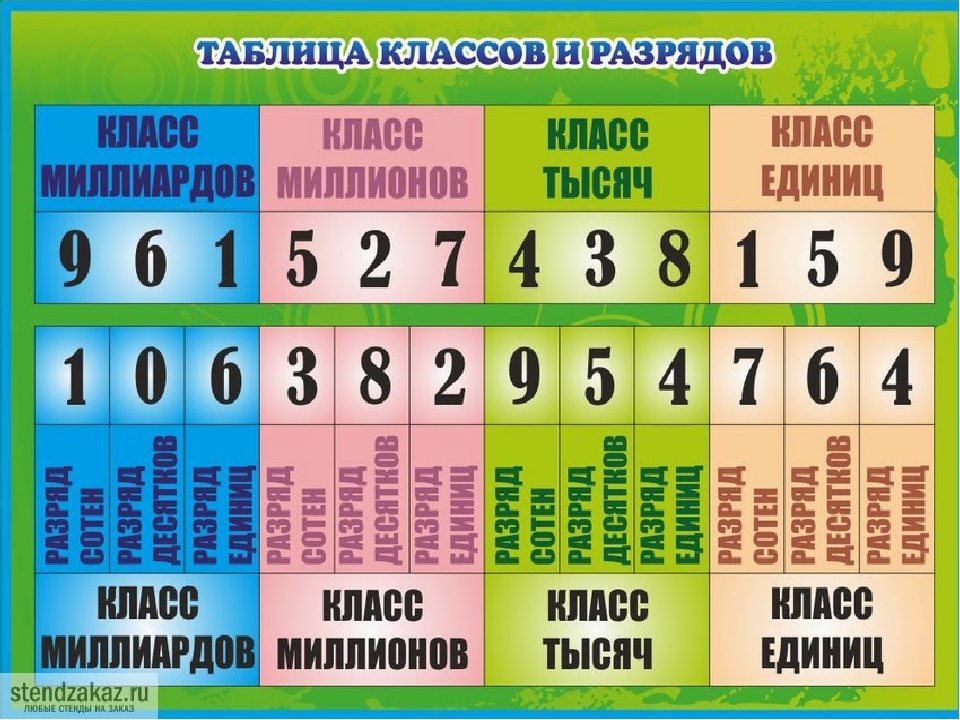 Выполните сложение:

Решение:

Задание 7. Выполните сложение:

Решение:

Задание 8. Выполните вычитание:

Решение:

Задание 9. Выполните вычитание:

Решение:

Задание 10. Выполните вычитание:

Решение:

Задание 11. Выполните вычитание:

Решение:

Задание 12. Выполните вычитание:

Решение:

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Разряды и классы чисел по математике

В начальных классах дети изучают «Разряды и классы чисел», однако эта тема вызывает много вопросов у родителей.

В этой статье Вы сможете «освежить» свои знания и объяснить ребенку эту тему.

Числа и цифры

ЧИСЛА — это единицы счёта. С помощью чисел можно сосчитать количество предметов и определить различные величины (длину, ширину, высоту и т. д.).
Для записи чисел используются специальные знаки — ЦИФРЫ.
Цифр десять: 1 2 3 4 5 6 7 8 9 0

Натуральные числа

НАТУРАЛЬНЫЕ ЧИСЛА — это числа, которые используются при счёте.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …,
1 — самое маленькое число, а самого большого числа не существует.
Число 0 (нуль) обозначает отсутствие предмета.  Нуль НЕ является натуральным числом.

 

Разряды и классы  натуральных чисел

Для записи чисел используется ДЕСЯТИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ. В десятичной системе счисления пользуются единицами, десятками единиц, десятками десятков — сотнями и т. д.
Каждая новая единица счёта больше предыдущей ровно в 10 раз:

Десятичная система счисления — позиционная. В этой системе счисления значение каждой цифры в записи числа зависит от её позиции (места).

Позиция (место) цифры в записи числа называется РАЗРЯДОМ. Самый младший разряд — ЕДИНИЦЫ. Затем следуют ДЕСЯТКИ, СОТНИ, ТЫСЯЧИ и т. д.

Каждые три разряда натуральных чисел образуют КЛАСС.

Плакат «Сделай уроки сам!» 3-4 класс  https://делайурокисам.рф

Основной вопрос, который родители часто задают: зачем ребенку эти знания? Ответ на этот вопрос очень простой — после изучения этого материала, дети переходят к таким темам как сложение и вычитание в столбик, где обязательно необходимо знать разряды числа, чтобы правильно вычислить примеры.

И если ребенок не освоит эту тему, тогда он не сможет правильно решать в столбик.

Складываем и вычитаем через разряды

Сложение столбиком

    А) Складываем единицы: 4 + 3 = 7.
          Записываем под единицами.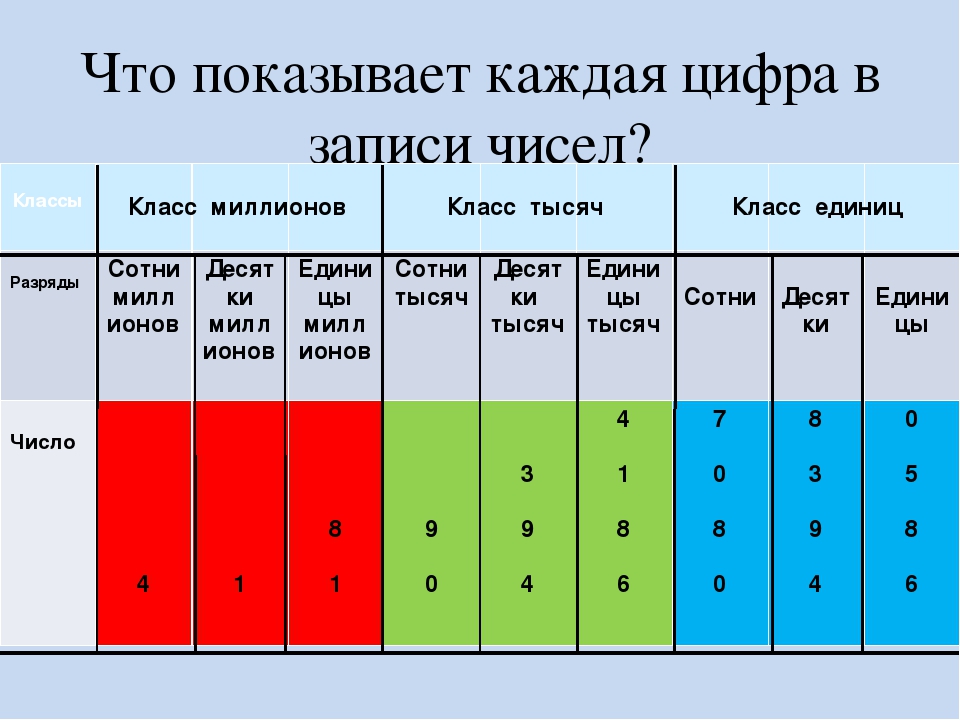
     Б) Складываем десятки: 4 + 3 = 7.
           Записываем под десятками.
     В) Складываем сотни: 4 + 3 = 7.
           Записываем под сотнями.
                                                 Ответ: 777

Вычитание столбиком

        А) Вычитаем единицы: 9 – 3 = 6.
              Записываем под единицами.
        Б) Вычитаем десятки: 0 меньше,
             чем 2, занимаем в сотнях (тысячах).

            10 – 2 = 8. Записываем под десятками.
                                           В) Вычитаем сотни: 9 – 4 = 5.
                                                Записываем под сотнями.
                                                Ответ: 586

Опубликовано: 10.03.2018

Стыд включает в себя множество негативных эмоций. Это и боязнь, и гнев, и недовольство собой, когда ты как личность обесцениваешься.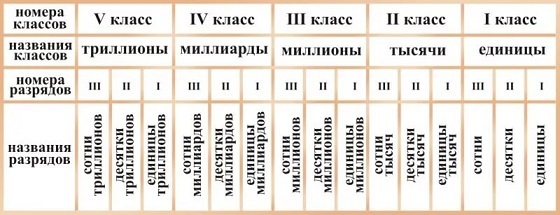 Читать далее

нет комментариев

Опубликовано: 14.02.2018

 Родители и учителя ломают головы, как доступно объяснить ребенку падежи, но поначалу для юного школьника это бывает сущим мучением.Читать далее

нет комментариев

Опубликовано: 13.03.2018

Появление у ребенка друзей-невидимок, как правило, связано с работой детского подсознания, ведь продумывая в голове и проигрывая в лицах различные жизненные ситуации маленький человек учится контактировать с окружающими и внешним миром, где ему предстоит еще найти свое место.Читать далее

нет комментариев

Опубликовано: 22.05.2018

В статье рассмотрены 7 приложений, которые помогают учиться школьникам и студентам.Читать далее

нет комментариев

Опубликовано: 18. 04.2018

В статье даны советы, как организовать общение с детьми, оградить от вредного влияния среды и виртуального мира. Эти советы позволят сохранить не только здоровье детей, но и доверительные отношения на долгие годы.Читать далее

нет комментариев

Многозначные числа. Единицы разрядов и классов. Сумма разрядных слагаемых.

Многозначные числа.

Существуют в математике огромное количество натуральных чисел. Они все разные. Например, 2, 67, 354, 1009. Рассмотрим подробно эти числа.
Натуральное число 2 состоит из одной цифры, поэтому такое число называют, однозначным числом. Еще пример однозначных чисел: 3, 5, 8.
Натуральное число 67 состоит из двух цифр, поэтому такое число называют, двузначным числом. Пример двузначных чисел: 12, 35, 99.
Трехзначные числа состоят из трех цифр, например: 354, 444, 780.
Четырехзначные числа состоят из четырёх цифр, например: 1009, 2600, 5732.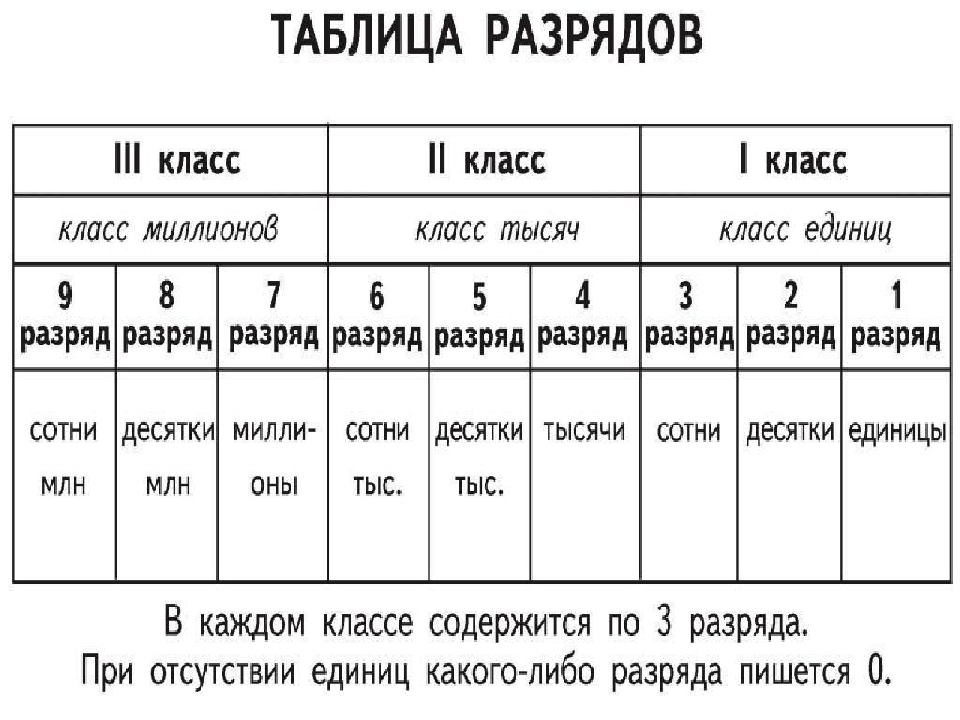

Двузначные, трехзначные, четырехзначные, пятизначные, шестизначные и т.д. числа, называются, многозначными числами.

Разряды чисел.

Рассмотрим число 134. У каждой цифры этого числа есть свое место. Такие места, называются, разрядами.

Цифра 4 занимает место или разряд единиц. Так же цифру 4 можно назвать цифрой первого разряда.
Цифра 3 занимает место или разряд десятков. Или цифру 3 можно назвать цифрой второго разряда.
И цифра 1 занимает разряд сотен. По-другому, цифру 1 можно назвать цифрой третьего разряда. Цифра 1 является последней цифрой слава числа 134, поэтому цифру 1 можно назвать, цифрой высшего разряда. Цифра высшего разряда всегда больше 0.

Каждые 10 единиц любого разряда образуют новую единицу более высокого разряда.  10 единиц образуют один разряд десяток, 10 десятков образуют один разряд сотен, десять сотен образуют разряд тысяч и т.д.
Если нет какого-то разряда, то вместо него будет стоять 0.

Например: число 208.
Цифра 8 – первый разряд единиц.
Цифра 0 – второй разряд десятков. 0 означает в математике ничего. Из записи следует, что десятков у данного числа нет.
Цифра 2 –  третий разряд сотен.

Такой разбор числа называется разрядным составом числа.

Классы.

Многозначные числа разбивают на группы по три цифры справа налево. Такие группы цифр называют классам. Первый класс справа называется классом единиц, второй называется классом тысяч,  третий – классом миллионов, четвёртый – классом  миллиардов, пятый – классом триллионов, шестой – классом квадриллионов, седьмой – классом квинтиллионов, восьмой – классом секстиллионов.

Класс единиц – первый класс справа с конца три цифры состоит из разряда единиц, разряда десятков и разряда сотен.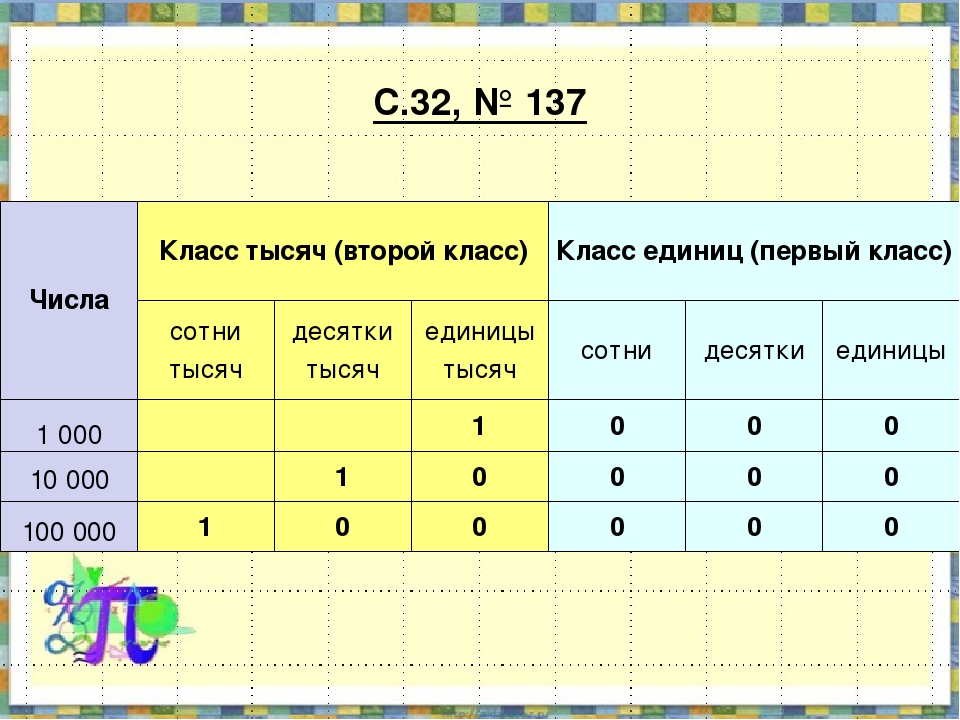
Класс тысяч – второй класс состоит из разряда: единиц тысяч, десятков тысяч и сотен тысяч.
Класс миллионов – третий класс состоит из разряда: единиц миллионов, десятков миллионов и сотен миллионов.

Разберем пример:
У нас есть число 13 562 006 891.
Это число имеет 891 единиц в классе единиц, 6 единиц в классе тысяч, 562 единиц в классе миллионов и 13 единиц в классе миллиардов.

Таблица разрядов и классов.

Чтобы прочитать натуральное число 13562006891 нужно справа отметить по три цифры класса 13 562 006 891  и прочитать число единиц каждого класса слева направо:

13 миллиардов 562 миллионов 6 тысяч 891.

Сумма разрядных слагаемых.

Любое натурально число имеющее различные разряды можно разложить на сумму разрядных слагаемых. Рассмотрим пример:
Число 4062 распишем на разряды.

4 тысяч 0 сотен 6 десятков 2 единиц или по-другому можно записать

4062=4 ⋅1000+0 ⋅100+6 ⋅10+2

Следующий пример:
26490=2 ⋅10000+6 ⋅1000+4 ⋅100+9 ⋅10+0

Вопросы по теме:

Назовите первые четыре класса в записи натуральных чисел?
Ответ: класс единиц, класс тысяч, класс миллионов, класс миллиардов.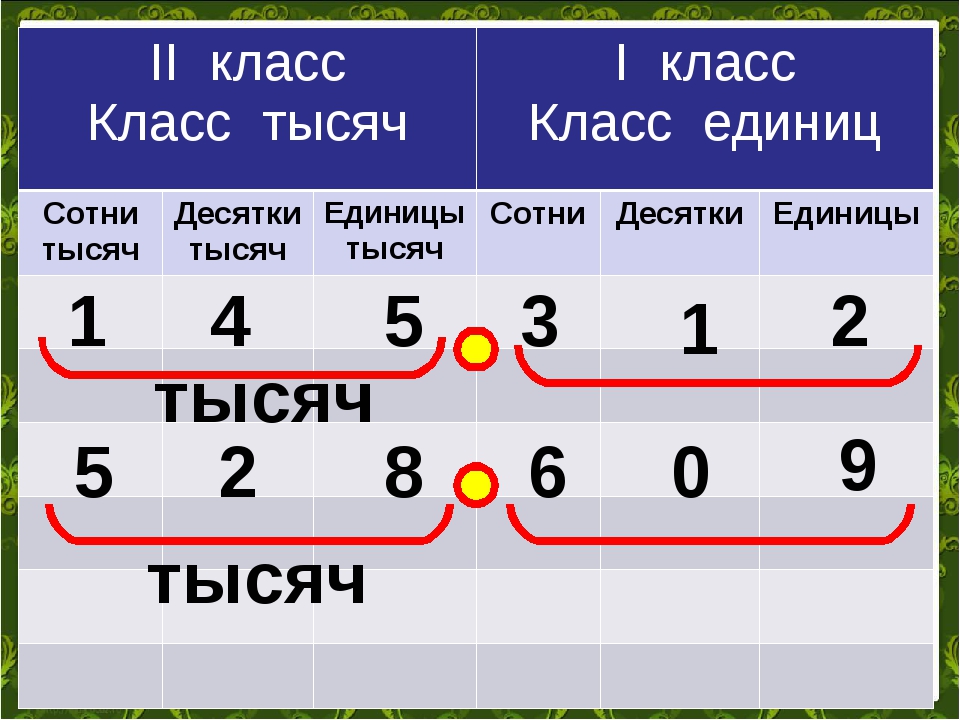

Как читают многозначные числа?
Ответ: многозначные числа читают слева направо. Разбивают число по 3 цифры с конца на классы, называют все цифры, кроме нуля. Цифра 0 в записи  числа означают отсутствие разряда.

Какие цифры могут стоять в любом разряде числа, кроме высшего?
Ответ: 0, 1, 2, 3, 4. 5, 6, 7, 8, 9.

Какие цифры могут стоять в высшем разряде числа?
Ответ: 1, 2, 3, 4. 5, 6, 7, 8, 9.

Что такое сумма разрядных слагаемых?
Ответ: Это разложение натурального числа на разряды и суммирование их.

Сколько десятков в сотне?
Ответ: в сотне 10 десятков.(10+10+10+10+10+10+10+10+10+10=100)

Сколько сотен в тысячи?
Ответ: в тысячи 10 сотен. (100+100+100+100+100+100+100+100+100+100=1000)

Сколько десятков в тысячи?
Ответ: в тысячи 100 десятков.

Сколько тысяч в миллионе?
Ответ: в миллионе 1000 тысяч.

Примеры на задачи.

Пример №1:
Запишите и прочитайте число: а) пятизначное б) шестизначное.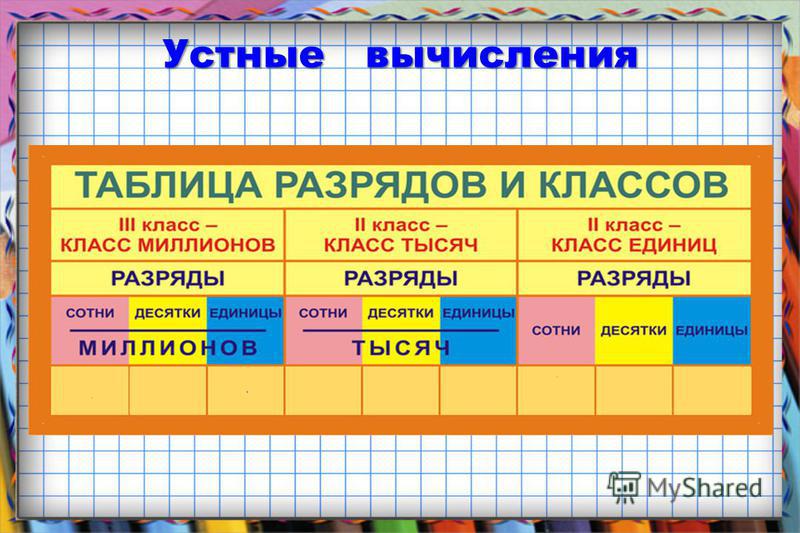
Ответ: а) 35 100 (тридцать пять тысяч сто) б) 803 273 (восемьсот три тысячи двести семьдесят три)

Пример №2:
Сколько натуральных чисел: а) однозначных б) двузначных?
Ответ: а) однозначных натуральных чисел 10 (0, 1, 2, 3, 4. 5, 6, 7, 8, 9), б) двузначных натуральных чисел 90 (10, 11, 12, …,99)

Пример №3:
В записи числа 10398 назовите цифры разрядов единиц, десятков, сотен, тысяч, десятков тысяч, …
Ответ: 8 – разряд единиц, 9 – разряд десятков, 3 – разряд сотен, 0 – разряд тысяч, 1 – разряд десятков тысяч.

Пример №4:
Напишите наименьшее трехзначное число и наибольшее пятизначное число.
Ответ: 100 и 99999.

Пример №5:
Запишите число 56976 в виде суммы разрядных слагаемых:
Ответ: 56976=50000+6000+900+70+6=5⋅10000+6⋅1000+9⋅100+7⋅10+6

Классы и разряды. Состав числа. Сравнение чисел.

1. Главная
2. Справочники
3. Справочник по математике для начальной школы
4. Числа больше 1000
5. Классы и разряды. Состав числа. Сравнение чисел.

Классы и разряды

Чтобы прочесть многозначное число, его необходимо разбить справа налево на группы по три цифры в каждой. Крайняя левая группа может состоять из одной или двух цифр.

Эти группы называют классами.

Три первые цифры спра­ва ‒ это класс единиц, три следующие — класс тысяч, затем класс миллионов, класс миллиардов и т. д.

Место, занимаемое цифрой в записи числа, назы­вают разрядом.

Если считать справа налево, то первое место в за­писи числа называют разрядом единиц, второе — разрядом десятков, третье — разрядом сотен и т. д.

Представленное на рисунке число читают так: 192 миллиарда 412 миллионов 163 тысячи 829. Записывают так: 192 412 163 829.

---

1) Если в числе отсутствуют единицы какого-либо разряда, то на месте этого разряда в записи числа ставят цифру 0. Например, 4 млрд 130 млн 150 тыс. 405 записывают так:

4 130 150 405

---

2) Если в числе отсутствуют единицы какого-либо класса, то в записи на месте этого класса будет три нуля. При чтении название этого класса не произносится. Например, число 5 000 430 800 читается так:

5 миллиардов 430 тысяч 800.

---

Число 30 000 014 читается так: 30 миллионов 14.

---

Любое число, имеющее разряды, можно разложить на сумму разрядных слагаемых.

Например:

3043 = 3 • 1000 + 0 • 100 + 4 • 10 + 3

43271 = 4 • 10000 + 3 • 1000 + 2 • 100 + 7 • 10 + 1

---

Сравнение чисел

Числа можно сравнить так:

1) по месту, которое они занимают при счёте.

Например:

7 < 10, так как 7 встречается при счёте раньше, чем 10;

2) поразрядно, начиная сравнение с высших разрядов.

Например:

1547 < 3987, так как 1 тыс. < 3 тыс.

8457 > 8256, так как 4 сот. > 2 сот.

1345 > 875, так как высший разряд в числе 1345 — единицы тысяч, а в числе 875 — сотни.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Сложение

Вычитание

Умножение

Деление

Числа больше 1000

Правило встречается в следующих упражнениях:

4 класс

Страница 23, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 26, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 55, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 16, Моро, Волкова, Рабочая тетрадь, часть 1

Страница 16. Вариант 1. Проверочная работа 1, Моро, Волкова, Проверочные работы

Страница 23. Вариант 2. Тест 2, Моро, Волкова, Проверочные работы

Страница 77. Тест. Вариант 2, Моро, Волкова, Проверочные работы

Страница 26, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 103, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 115, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

5 класс

Упражнение 562, Мерзляк, Полонский, Якир, Учебник

Упражнение 846, Мерзляк, Полонский, Якир, Учебник

Упражнение 847, Мерзляк, Полонский, Якир, Учебник

Упражнение 852, Мерзляк, Полонский, Якир, Учебник

Упражнение 853, Мерзляк, Полонский, Якир, Учебник

Упражнение 856, Мерзляк, Полонский, Якир, Учебник

Упражнение 857, Мерзляк, Полонский, Якир, Учебник

Упражнение 858, Мерзляк, Полонский, Якир, Учебник

Упражнение 6, Мерзляк, Полонский, Якир, Учебник

Упражнение 1, Мерзляк, Полонский, Якир, Учебник

---

© budu5.com, 2020

Пользовательское соглашение

Copyright

Классы, разряды и чтение чисел

Классы и разряды

Для того, чтобы было удобно записывать, читать и использовать числа, каждая цифра в числе относится к определённому классу и разряду.

Разрядов всего три:

• Единицы
• Десятки
• Сотни

Классов же, бесконечное множество:

• Единицы
• Тысячи
• Миллионы
• Миллиарды
• Триллионы
• и т.д.

Каждый из классов содержит все три разряда: разряд единиц, разряд десятков и разряд сотен.

Чтение и запись чисел

Отсчитывать к какому классу и разряду принадлежат цифры в числе надо справа налево. То есть не так как при чтении текста, а наоборот (номера разрядов указаны в нижнем ряду).

Чтобы правильно написать или прочитать число надо знать, к какому классу и разряду относится каждая из цифр числа. Для того, чтобы удобно определять классы и разряды, цифры в длинных числах обычно пишут группами по три знака, отсчитывая с правой стороны:

• 1 643 — число начинается с единиц 4 разряда
• 268 490 — число начинается с единиц 6 разряда
• 5 489 657 — число начинается с единиц 7 разряда
• 58 261 754 458 — число начинается с единиц 11 разряда

Затем последовательно определяются и количество единиц в других разрядах.

Пример 1:

В числе 786 325 274 358 будет:

• 7 — сотен миллиардов (единиц 12 разряда)
• 8 — десятков миллиардов (единиц 11 разряда)
• 6 — миллиардов (единиц 10 разряда)
• 3 — сотни миллионов (единиц 9 разряда)
• 2 — десятка миллионов (единиц 8 разряда)
• 5 — миллионов (единиц 7 разряда)
• 2 — сотни тысяч (единиц 6 разряда)
• 7 — десятков тысяч (единиц 5 разряда)
• 4 — тысячи (единиц 4 разряда)
• 3 — сотни (единиц 3 разряда)
• 5 — десятков (единиц 2 разряда)
• 8 — единиц (единиц 1 разряда)

Это число прочитаем: семьсот восемьдесят шесть миллиардов триста двадцать пять миллионов двести семьдесят четыре тысячи триста пятьдесят восемь.

Пример 2:

В числе 5 143 будет:

• 5 тысяч (единицы 4 разряда)
• 1 сотня (единицы 3 разряда)
• 4 десятка (единицы 2 разряда)
• 3 единицы (единицы 1 разряда)

Читается число 5 143 так: пять тысяч сто сорок три.

Внимание! При чтении названия классов называются только после всех названий разрядов этого класса, слово «десятки» заменяется на «-десят», а слово «единиц» вообще не произносится:

• 105 000 000 — сто пять миллионов
• 356 218 — триста пятьдесят шесть тысяч двести восемнадцать.

Если в числе отсутствуют единицы какого-либо разряда, то в записи числа на этот месте ставят 0.

Если отсутствуют единицы целого класса, то в записи на этом месте ставят 000 и при чтении числа класс не произносится.

Пример 3:

В числе 600 050 будет:

• 6 — сотен тысяч (единицы 6 разряда)
• 5 — десятков (единицы 2 разряда)

А вместо всех остальных разрядов стоят нули. Число читается: шестьсот тысяч пятьдесят.

Пример 4:

В числе 4 000 100 будет:

• 4 миллиона (единицы 7 разряда)
• 1 сотня (единицы 3 разряда)

Число читается: четыре миллиона сто.

Урок 11: Единицы измерения — 100urokov.ru

План урока:

Луч, угол, отрезок

Измерение отрезков. Сантиметр. Дециметр

Геометрические фигуры. Треугольник. Четырехугольник. Многоугольники

Килограмм

Литр

 

Начинаем наш урок

Пусть тебе пойдет он впрок.

Будем вместе рассуждать,

Наблюдать и измерять.

Наверное, каждый ребенок мечтает быть изобретателем или исследователем. Надеюсь, ты тоже, ведь наш урок мы проведем в лаборатории.

Там мы будем моделировать, проводить разные опыты и измерения. Ты узнаешь много нового, познакомишься с различными измерительными инструментами. Я научу тебя как нужно ими пользоваться. Итак, приступим.

 

Луч, угол, отрезок

Давай вспомним материал из нашего первого урока. Мы знакомились с некоторыми геометрическими понятиями и выучили названия основных геометрических фигур. Посмотри на картинку и попробуй назвать, что здесь изображено.

Проверь, все ли ты правильно вспомнил.

Замечательно. А теперь мы приступим к изучению нового. Начнем с самого простого.

Это луч.

Как ты думаешь, почему его так называют?

Если присмотреться, то мы можем представить, что точка – это солнышко. Оно испускает лучи.

Обрати внимание, что все лучи исходят из центра солнца. У них общее начало.

Мы возьмем только два луча, которые исходят из одной точки.

Теперь давай поэкспериментируем. Сделаем модель угла. Нужно две палочки. Это могут быть счетные палочки, палочки для мороженого или обычные зубочистки.

Теперь поучимся чертить угол в тетради. Для этого нам понадобится линейка и карандаш.

Нужно положить линейку на лист и крепко прижать ее левой рукой. Поставь карандаш возле ее верхнего края.

У нас получился отрезок. Это часть прямой, которая с двух сторон ограничена точками. Значит, у отрезка должно быть две точки.

Создадим модель отрезка. Сделай два шарика из пластилина и прикрепи их с обеих сторон палочки.

Готово. Правда, это было легко?

Чертить отрезок в тетради тоже не сложно. Действуем так же, как и при черчении луча.

После того как проведем под линейку прямую линию, отметим точками начало и конец отрезка.

Длина отрезка может быть разной. Его можно начертить совсем маленьким или продлить на всю страничку и даже выйти за нее. Потренируйся чертить разные отрезки в разном направлении.

Скажи, ты можешь определить, какой отрезок больше? Какой самый маленький? Есть ли здесь равные отрезки? На сколько один отрезок больше, чем другой? Как начертить отрезок, который будет заданной длины?

На все эти вопросы мы ответим после работы в нашей лаборатории.

 

Измерение отрезков. Сантиметр. Дециметр

Чтобы сравнивать, нам нужно научиться измерять отрезки. Это можно делать и с помощью обычной палочки. Найди себе подходящую палочку, и мы вместе проведем измерения.

Следует приложить ее начало к началу отрезка и отметить на палочке конец отрезка.

Теперь эту же палочку приложим к другому отрезку, тоже соединив их начало. И отметим конец этого отрезка.

Мы получили на палочке две отметки. Чья отметка находится дальше, тот отрезок и больше по длине.

Мы можем с помощью этой палочки чертить равные отрезки. Нужно только приложить ее к листу тетради и провести вдоль нее линию от начала и до нужной отметки.

Попробовал? Мы получили точно такой же отрезок, как и тот, что измеряли первым и отметили его длину красной черточкой.

Однако, измеряя отрезки палочкой мы получаем о них очень мало информации, которую нельзя никому передать или записать. Например, как ты расскажешь своему другу о своих измерениях в нашей лаборатории? Какой длины оказались твои отрезки? Кусочек палочки?

Это похоже на то, как герои мультфильма пытались измерить длину удава, считая ее шагами, попугаями и даже мартышками.

Но мы с тобой занимаемся научными исследованиями, а значит, все измерения должны быть точными и правильно записанными. Поэтому сейчас познакомимся с инструментами и единицами измерения, необходимыми для определения длины отрезков.

Ты уже знаком с линейкой. Возьми ее и положи перед собой.

Мы ее использовали для проведения прямых линий. Но линейка является измерительным инструментом. Рассмотри ее. На ней нанесены штрихи и цифры. Обрати внимание, что штрихи разной длины, а цифры написаны только возле самых длинных черточек.

Это шкала измерений. Начало отсчета обозначено числом 0, а дальше идут числа по порядку, как в числовом ряду, который тебе уже знаком.

Особенность шкалы заключается в том, что расстояние между схожими штрихами одинаковое. Сегодня мы будем изучать только длинные черточки. Часть шкалы от одной длинной черточки до соседней длинной черточки называется сантиметр. Отметим на рисунке 1 сантиметр.

Сантиметр – это единица измерения длины отрезков. Вся шкала на линейке разделена на сантиметры.

Давай посчитаем каждый сантиметр на линейке. Например, здесь мы отметили пять сантиметров и остановились на числе 5.

Числа указывают сколько сантиметров отсчитано от числа 0. Поэтому мы, начиная измерять или чертить отрезок, обязательно совмещаем его начало с черточкой возле числа 0.

Например, выполним измерение отрезка. Приставим к точке, которая отмечает начало отрезка, черточку возле числа 0. Линейку нужно положить ровно вдоль линии.

После такого совмещения посмотрим на точку, которая отмечает конец отрезка. Она находится возле черточки, внизу которой написано число 7. Значит длина этого отрезка составляет 7 сантиметров.

Все довольно просто. Главное – соблюдать точность.

Чтобы записать длину отрезка будем использовать короткую запись см. Пишем так:

7 см

Сейчас мы используем полученные навыки для проведения опыта. Нам нужно найти равные отрезки.

Глядя на отрезки, нельзя сразу сказать, какие из них одинаковые. Чтобы найти равные отрезки, нужно провести их измерения. Посмотри, как мы это сделали.

Определи размеры каждого отрезка в сантиметрах.

Я тоже это сделала. У меня получилось так.

Итак, мы опытным путем установили, что здесь два одинаковых отрезка, длина которых 12 см.

Никаких сомнений быть не может – все точно.

Потренируйся проводить самостоятельные измерения. Попроси кого-то из взрослых начертить тебе несколько отрезков, а ты измерь их длину.

А сейчас ты и сам научишься чертить отрезки. Это тоже легко. Например, начертим отрезок длиной 4 см.

Приложим линейку. Поставим точку напротив числа 0.

Не сдвигая линейку, поставим точку напротив числа, соответствующего длине отрезка. В нашем случае это число 4.

Теперь крепко прижмем линейку. Убедимся, что обе точки находятся непосредственно у верхнего края линейки. Поставим карандаш на первую точку и плавно проведем линию до второй точки.

Теперь линейку можно убирать. Отрезок готов.

Теперь твоя очередь. Выполни аналогичные действия в такой же последовательности, чтобы начертить отрезок длиной 6 см.

А теперь взгляни на рисунок и скажи, сколько сантиметров составляет длина этого отрезка.

Итак, мы установили, что длину отрезка можно записать, как 13 см, а можно, как 1 дм 3 см. Это можно делать с любым отрезком, если его длина выражена двузначным числом. Подумай, как можно еще записать длину отрезка, если мы определили, что она составляет 17 см.

Правильно, это будет 1 дм 7 см.

Замечательно. Ты усвоил много новой информации об угле, отрезке и единицах измерения длины. Дальше будет проще, потому что основное ты уже знаешь.

 

Геометрические фигуры. Треугольник.  Четырехугольник. Многоугольники

Давай вернемся к нашей модели угла.

Такие замкнутые ломаные линии являются геометрическими фигурами. Мы уже с тобой посчитали, что в этой фигуре три угла. Каждый угол имеет вершину – точку, в которой соединяются две стороны угла. Значит вершин тоже три. А теперь посчитай, сколько палочек мы использовали.

И палочек тоже три, т.е. у фигуры три стороны.

Такая фигура называется треугольник. Ты уже знаешь это название и знаешь, как выглядит треугольник. Сегодня мы выучили основные характеристики этой фигуры. Треугольники бывают разные и по размеру, и по виду.

Главное, что у треугольника три угла, три вершины и три стороны. Наверное, и название у него такое, потому что у него всего по три.

Вокруг нас есть много предметов, которые имеют треугольную форму. Например, крыши домов.

Убедись, что это треугольник – посчитай стороны крыши. Их три, значит, красная фигура является треугольником.

Вспомни, что еще похоже на треугольник.

А сейчас давай продолжим моделировать. Разъедини две палочки и сделай их все отрезками.

Посчитай углы каждого четырехугольника.

Убедился? Любая фигура, у которой есть четыре угла, является четырехугольником. Мы знаем очень много предметов, которые имеют четырехугольную форму. Например, тетрадь и книга.

Все эти предметы имеют по четыре стороны, а значит они четырехугольники.

Надеюсь, ты уже понял связь между названием и строением фигуры. Подумай, какую фигуру называют пятиугольником?

Правильно, это фигура, у которой пять углов, пять вершин и пять сторон. Знаешь, как его смоделировать?

Сначала разъединим любые две палочки.

Посчитай углы и стороны каждого многоугольника и назови их. Найди среди этих фигур четырехугольники.

Обрати внимание, что сторонами фигур являются отрезки. Значит, их можно измерять. Для этого нужна линейка. Ты уже знаешь, как ею пользоваться.

Давай измерим каждую сторону треугольника.

Длина третей стороны 13 см. Это тоже можно записать в другом виде: 1 дм 3 см.

Мы отлично справились. Наша работа не прошла в пустую. Теперь ты можешь правильно назвать почти любую геометрическую фигуру.А с помощью линейки сумеешь измерить стороны у любой фигуры.

 

Килограмм

Продолжим. Будем снова измерять. Только уже совсем по-другому. Нам нужно сравнить два предмета.

Что ты можешь сказать? Чем они отличаются?

Конечно, они отличаются по цвету, но ведь мы изучаем математические понятия. Поэтому поговорим о других параметрах.

Ты уже, наверное, догадался, о чем речь. Арбуз тяжелый, а мяч легкий. Это значит, что у них разная масса. Итак, мы поговорим о том, что у предметов можно измерять массу, т.е. узнавать, сколько они весят. Какой измерительный инструмент нам нужен для определения массы?

Это весы. Они бывают разных видов.

Есть весы с чашами. Они называются механическими.

На одну чашу нужно положить сам предмет, а на другую чашу ставят гири. Следует подобрать такие гири, чтобы чаши весов оказались на одном уровне.

А сколько весит арбуз? Определи общее количество килограммов на гирях.

Правильно, 5 и 2 будет 7. Значит, арбуз весит 7 кг.

Все очень просто и интересно. Попроси родителей купить себе такой набор и потренируйся взвешивать разные предметы, которые есть в твоей комнате.

Запомни, что их масса измеряется в килограммах.

 

Литр

А теперь нам нужно измерить молоко. Как мы будем наливать его на чашу весов? Что произойдет?

Верно, если лить молоко, то оно разольется по столу и ничего измерить не получится. Молоко нужно лить в посуду: бутылку, стакан, банку.

Как же измерить, сколько молока вместилось в бидон или кувшин? Для этого есть еще одна единица измерения – литр. Она нужна для измерения вместимости. При этом используется специальная мерная посуда, на которой нанесена шкала.

Чтобы определить, сколько литров молока находится в кувшине, надо перелить его в мерную посуду и посмотреть какой метки достигнет его уровень.Таким образом, мы можем измерить не только количество молока, но и любой другой жидкости.

Есть емкости, которые имеют определенный объем. Например, вот посуда, которая вмещает 1 литр.

Записывается так:

1 литр – 1 л

Вот мы и закончили наш урок. Ты узнал много нового. Теперь ты знаешь, как начертить многоугольник.

А главное, мы выучили единицы измерения. Вот что ты должен запомнить.

Сегодня мы сделали только первый шаг в деле исследования. Надеюсь, тебе понравилось проводить опыты, моделировать и ты продолжишь это делать самостоятельно.А сейчас выполни несколько проверочных заданий.

 

Какие есть примеры рычагов 1-го, 2-го и 3-го класса?

Физика

Наука

• Анатомия и физиология
• Астрономия
• Астрофизика
• Биология
• Химия
• науки о Земле
• Наука об окружающей среде
• Органическая химия
• Физика

Математика

• Алгебра
• Исчисление
• Геометрия
• Предалгебра
• Precalculus
• Статистика

China High Speed ​​Rail First Class vs.Второй класс, что лучше

Сиденья первого и второго класса — наиболее часто используемые типы кресел на высокоскоростных железных дорогах Китая. Но какой выбрать?

Если вы заботитесь о комфорте больше, чем о деньгах, или вы деловой человек, которому нужно хорошо отдохнуть во время поездки, или если вы крупный человек, мы рекомендуем место в первом классе. Когда места во втором классе распроданы, лучшим выбором будет место первого класса.

Если вы путешествуете с ограниченным бюджетом или путешествуете с семьей или друзьями, вам рекомендуются места второго класса из-за их более низкой цены на билеты; они также удобны по сравнению с эконом-классом в самолете.

Сиденья второго класса стоят дешевле, чем места первого класса.

В зависимости от расстояния, стоимость билета на место первого класса китайского высокоскоростного поезда обычно на 20-40% выше, чем на место второго класса.

Вагон первого класса обеспечивает более широкие сиденья и пространство для перемещения.

В вагонах первого класса четыре сиденья расположены в ряд, в вагонах второго класса по пять сидений в каждом ряду.Это приводит к чуть более узким сиденьям и проходам в вагонах второго класса. Кроме того, пространство для ног между двумя рядами в вагонах первого класса шире, в то время как место второго класса с более коротким пространством для ног может вызывать дискомфорт у высоких пассажиров. См. Информацию о размерах ниже:

	Сиденье первого класса	Сиденье второго класса
Ширина сиденья	47 см (19 дюймов)	42 см (17 дюймов)
Пространство для ног	40- 50 см (16-20 дюймов)	40 см (16 дюймов)
Ширина прохода	60 см (24 дюйма)	45 см (18 дюймов)

Напоминание: даже сиденье и подвижное пространство в вагоне второго класса уже, чем в вагоне первого класса, оно шире, чем в эконом-классе самолета.Если вы можете путешествовать экономическим классом самолета, место второго класса в китайском сверхскоростном экспрессе никогда не будет проблемой.

Подножка и подушка спинки предусмотрены в вагонах первого класса.

Пассажиры могут ставить ноги на подставку для ног при посадке в места первого класса. К спинке сиденья также прикреплена подушка спинки, чтобы пассажиры чувствовали себя комфортно.

Складные столы в вагоне первого класса более удобны для пассажиров.

Сиденья первого и второго класса могут поворачиваться, что позволяет пассажирам сидеть в направлении движения поезда или лицом к лицу, если они хотят.Однако складной столик в вагонах первого класса устанавливается независимо внутри подлокотника с правой стороны пассажира, в то время как стол в вагоне второго класса крепится к опоре впереди. Когда пассажиры в группе сидят лицом к лицу в вагоне второго класса, они не смогут пользоваться столиками.

Пассажиры, сидящие лицом к лицу, могут также использовать складные столы в вагоне первого класса.

Складной столик крепится к спинке переднего сиденья в вагоне второго класса.

Вагоны первого класса обычно тише, чем вагоны второго класса.

С одной стороны, вагоны первого класса вмещают меньше пассажиров, чем вагоны второго класса; с другой стороны, вагоны первого класса обычно менее загружены, следовательно, тише и менее многолюдно.Если не повезет, в вагонах второго класса дети могут плакать или играть, а взрослые громко болтают, не обращая внимания на других пассажиров.

Туалет в вагоне второго класса меньше, чем в вагоне первого класса.

Условно говоря, туалет в вагоне первого класса просторнее и светлее. Также предусмотрены удобства для инвалидов. Некоторые даже оснащены складными столиками для смены подгузников. В вагоне второго класса туалет относительно меньше, но все основные удобства оборудованы.

Пассажирам первого класса может быть предоставлено бесплатное питание.

Это не универсальный случай, но пассажиры мест второго класса всегда должны платить за еду или напитки на борту. Общее представление о китайских высокоскоростных поездах: высокоскоростные железнодорожные линии между крупными городами:

— Последнее изменение 20 апреля 2020 г.-

Рычажные системы в биомеханике — 1-й класс, 2-й класс, 3-й класс в спорте

Рычажная система — это жесткий стержень, который перемещается в фиксированной точке, называемой точкой опоры, когда к ней прилагается сила.В человеческом теле движение стало возможным благодаря рычажным системам, которые образованы нашими мышцами и суставами, работающими вместе. Понимание рычагов в теле помогает нам понять, как возможно движение.

Рычаги в биомеханике

Мышцы прикреплены к костям с помощью сухожилий, а кости скелета действуют как рычаги, на которые мышцы тянут, чтобы создать движение. Система рычагов состоит из трех частей; усилие, нагрузка и точка опоры. В человеческом теле усилие обеспечивается мышцей (точка приложения / приложения мышц), нагрузка — это вес тела и любое дополнительное сопротивление, а точкой опоры является сам сустав.

---

Типы рычага

В теле есть три типа, каждый из которых определяется относительным положением точки опоры (F), усилием (E) и нагрузкой (L). Полезный способ определения различных типов рычажных систем, действующих во время определенного движения, — это запомнить следующую рифму.

«Для 1, 2, 3 подумайте F, L, E». ​​Эта рифма помогает нам определить средний компонент каждой системы.

• Для первоклассного рычага F — средний компонент.
• Для рычага второго класса L — средний компонент.
• Для рычага третьего класса E — средний компонент.

---

---

Функции рычажной системы

Рычажные системы выполняют две основные функции; во-первых, чтобы увеличить сопротивление движению заданной силы, а во-вторых, чтобы увеличить скорость, с которой движется тело. Кроме того, разные типы допускают разные диапазоны движения. Это означает, что одни эффективны при преодолении сопротивления, в то время как другие способны развивать скорость.

---

Первоклассная рычажная система

В первоклассном рычаге точка опоры является средним компонентом и находится между усилием и нагрузкой. Примеры первоклассного рычага в теле редки, поскольку в некоторых упражнениях используется первоклассная рычажная система, хотя разгибание (выпрямление) в локте является одним из примеров. Разгибание в локте можно увидеть во время броска или теннисного удара.

На изображении ниже трицепс — это усилие, точка опоры — это локтевой сустав, а нагрузка — это вес руки и копья.Первоклассные рычаги увеличивают как эффект усилия, так и скорость тела.

Иногда на стыке задействовано несколько рычагов. Локтевой сустав — один из примеров. Во время разгибания локтя усилие создается трицепсом через точку его прикрепления к локтевой кости, поэтому это первоклассный рычаг. Однако при сгибании в локтевом суставе, как и при сгибании рук на бицепс, усилие исходит от точки прикрепления двуглавой мышцы к лучевой кости, это пример системы третьего класса.

---

Рычажная система второго класса

В системе рычагов второго класса нагрузка является средней составляющей и находится между точкой опоры и усилием. Упражнения, включающие подошвенное сгибание в голеностопном суставе (подъем на пальцы ног), относятся к рычажным системам второго класса, например, подъем на икры или прыжок вверх во время простоя в баскетболе. Системы рычагов второго класса имеют тенденцию только увеличивать действие силы усилия, другими словами, они эффективны при преодолении сопротивления, а не для создания скорости.

В примере подошвенного сгибания голеностопного сустава подушечка стопы и пальцы ног являются точкой опоры, вес тела является нагрузкой, а усилие прилагается икроножной мышцей.

---

Рычажная система третьего класса

Большинство движений человеческого тела относятся к рычажным системам третьего класса. В рычажной системе третьего класса усилие является средним компонентом и находится между точкой опоры и грузом.

Существует множество примеров рычажных систем третьего класса, включая сгибание и разгибание в коленном суставе.Эти движения связаны с бегом, прыжками и ударами ногами. Во время сгибания в колене точка прикрепления подколенных сухожилий к большеберцовой кости — это усилие, коленный сустав — точка опоры, а вес ноги — нагрузка. Рычажные системы третьего класса используются для увеличения скорости тела и обеспечения широкого диапазона движений.

---

Сопутствующие тесты

---

ФГ принять в качестве учителей выпускников 1-го и 2-го классов

— Федеральное правительство хочет привлечь к профессии учителя только лучшие умы

— Новая политика, гарантирующая, что это уже осуществляется на федеральном уровне

— Только люди второго класса, высшего и первого класса впредь будет допущен к профессии.

ОБРАТИТЕ ВНИМАНИЕ: Выиграйте приз в размере N115,000, N75000 или N38000: примите участие в конкурсе на независимость Big Naija от Legit.ng

Федеральное правительство заявляет, что начнет ограничивать точку входа в обучение только для лиц с разделениями второго класса, высшего и первого класса.

Об этом сообщил постоянный секретарь федерального министерства образования Сонни Эчоно в субботу, 14 ноября.

Эчноно сказал, что учителя, не имеющие необходимой квалификации, компетенций и лицензии на практику, в настоящее время переводятся из Нигерийской педагогической службы.

Президент Бухари ранее заявил, что только лучшим должно быть позволено учить.Фото: @MBuhari
Источник: Twitter

ОБРАТИТЕ ВНИМАНИЕ: Получайте последние новости Нигерии в любом месте 24/7. Тратьте меньше в Интернете!

Его слова:

«К 2021 году мы не будем привлекать учителей, если они не будут соответствовать определенному порогу, теперь мы ограничиваем точку входа в обучение только для лучших, которые имеют квалификацию, мы будем привлекать людей со вторым классом. высшие и первоклассные подразделения ».

Нгиге: Если ASUU отменит забастовку, другие профсоюзы могут начать свою, мы должны их продолжить.

Эчоно сделал комментарий в Абудже, наблюдая за проведением профессиональных квалификационных экзаменов для учителей диетической партии B в октябре 2020 года (PQE).

Он добавил:

«Мы организуем программы конверсии для людей, у которых есть эти категории результатов из других областей, им необходимо изучить педагогику, методологию через NTI и TRCN, и они будут проходить специальные программы, которые даст им возможность учить ».

Он утверждал, что начальный уровень будет выше, и они получат лучшее вознаграждение с особыми надбавками, добавив, что соответствующие образовательные учреждения завершают цифры с национальными доходами и заработной платой.

Федеральное правительство, по его словам, больше заинтересовано в результатах обучения, и что до конца ноября 2020 года будет открыт Национальный комитет по осуществлению плана оздоровления / реанимации учителей.

Он сказал:

«Мы должны обеспечить выполнение директивы г-на президента о том, что в наши классы допускаются только квалифицированные учителя. Профессиональные квалификационные экзамены проходят гладко в 34 штатах, и отзывы были положительными.

Okowa клянется бороться с безработицей, поскольку правительство Delta начинает программу приобретения навыков

Legit.ng ранее сообщал, что учителя по всей Нигерии без квалификации, предусмотренной Советом регистрации учителей Нигерии (TRCN), будут показаны путь к двери скоро.

Об этом сообщил регистратор TRCN, профессор Джосайя Олусегун Аджибойе, который сказал, что цель федерального правительства — сделать будущих лидеров нигерийских детей путем повышения уровня образования.

Он также сказал, что отныне преподавание станет завидной профессией в стране, которая будет утверждена Национальным советом по образованию для учителей «Карьерный путь».

Ненавижу, когда меня жалели, — говорит учитель математики с физическими недостатками | Legit TV

Советы по преподаванию комбинированных классов / многоуровневых классов

Если вы преподаете в раздельном классе (многоуровневом или комбинированном классе) и вам нужен совет по организации и организации работы в классе, вы пришли в в нужном месте! Вы найдете практические советы от учителей, которые преподавали в многоуровневых классах и комбинированных классах на всех уровнях обучения.

Советы учителей общеобразовательных школ

Я пригласила учителя-блоггера Мэри Мюллер из Guided-Math, чтобы рассказать больше о своем опыте преподавания в раздельных классах. Спасибо, Мэри, за подсказки!

Вы только что узнали, что преподаете в раздельном / комбинированном / разновозрастном классе? Вы находитесь в состоянии паники, пытаясь понять, как вы собираетесь справиться с двумя (а иногда и более) уровнями обучения одновременно?

Десять лет назад моя педагогическая карьера началась в раздельном классе в очень большом школьном округе в Иллинойсе.Во-первых, не могу поверить, что я всего десять лет писал! Во-вторых, теперь, когда я считаю, я не могу поверить, что семь из этих лет я провел в комбинированных классах! Все эти вопросы и моменты паники пронеслись в моей голове, когда я узнал о моем первом назначении. Тогда я и представить себе не мог, что первый год, разделенный на 1/2, поставит меня на путь большего разделения классных комнат и поможет положительно сформировать то, кем я являюсь сегодня как учитель.

Вначале я рассматривал комбинированное обучение как долгожданный вызов.Это был вызов, который я не собирался терпеть. Я всегда смотрел на то, что я делал, и выяснял, как я могу улучшить структуру как для моих учеников, так и для меня.

За годы, которые я провел в разделении на 1/2, 2/3, 3/4 и три года в 4-м классе, я понял, что разделенное обучение ничем не отличается от обычного класса. Я обнаружил, что не изменил способ преподавания или структуру дня в раздельном классе по сравнению с обычным классом.

Вот некоторые вещи, о которых следует подумать при планировании комбинированного класса.

1. Поговорите со своим администратором, чтобы узнать, что от вас требуется. Вы должны преподавать по двум отдельным учебным программам? Какие предметы можно сочетать? Как товарищи по команде могут вас поддержать?
2. Думайте о своем классе как о диапазоне способностей, а не о двух разных уровнях обучения. Реальность такова, что у обычных классов могут быть только большие возможности, чем у комбинированных классов.
3. Я рекомендую сбалансированный формат грамотности. Проведите уроки чтения и письма всей группой, а затем разбейте их на небольшие группы для чтения с гидом или индивидуальных конференций.Здесь вы сможете удовлетворить потребности своих студентов.
4. Обычно вам придется преподавать по двум отдельным учебным программам по математике. Я настоятельно рекомендую вам взглянуть на формат управляемой математики. Это решит, как преподавать две программы математики, и даст вам возможность индивидуализировать обучение математике.
5. Подготовьтесь к началу учебного года с информацией для родителей. Когда эти списки классов поднимутся, у вас обязательно появятся вопросы от родителей. Если вы будете готовы показать им, как вы собираетесь эффективно справляться с двумя оценками, их страхи уменьшатся.Создайте брошюру или информационный бюллетень с указанием вашего расписания обучения, учебной программы, которую вы собираетесь охватить, и подробностей о том, как вы собираетесь удовлетворить потребности своих студентов.
6. Оставайся позитивным !! Помните, что это будет отличный опыт не только для студентов, но и для вас!

Удачи вам в обучении в комбинированном классе! Я знаю, что у вас все получится! Чтобы получить дополнительную информацию и узнать больше о том, как я структурирую свой математический или разновозрастный класс, посетите мой веб-сайт Guided-Math.

Вопросы о разделенных классах и общих классах

Следующие вопросы были заданы мне как часть серии сообщений в блоге «Спроси Анжелу о чем угодно». Вы можете отправить любой вопрос, связанный с преподаванием, анонимно, чтобы сохранить конфиденциальность и конфиденциальность учащихся. Я включил два вопроса ниже здесь, на этой странице, а не в столбец, чтобы учителям комбинированных классов было легче находить ответы в одном месте.

Я преподаю в 2/3 классах.Я слышал, что один уровень назывался юниорами, а другой — старшими. Мое чутье подсказывает мне не начинать день с разговора о втором или третьем, но неизбежно ли это? Как лучше всего управлять классом, чтобы создать команду, соблюдая при этом свой класс? Я не хочу, чтобы кто-то из моих третьеклассников чувствовал, что они все еще второклассники.
-Джейн

Привет, Джейн! Бывают моменты, когда вам нужно будет ссылаться на них по уровням обучения, и тогда лично я бы назвал их второклассниками и третьеклассниками.Но вы также можете позволить каждому классу выбрать себе имя, которое отражает их уникальную идентичность как класса внутри класса. Это может быть часть вашей первой недели школьных занятий, как некоторые учителя делают с группами чтения. Я думаю, что это был бы хороший способ создать чувство общности и дать детям право владеть классом. Они также могут создать имя класса, чтобы у них была одна связная идентичность. Например, весь ваш класс может состоять из китов, второклассники могут быть косатками, а третьеклассники — белухами.Расскажите детям о своей дилемме, как их называть, и попросите их мнение! Бьюсь об заклад, они придумают что-нибудь получше, чем мы могли придумать.

Я подал заявление о приеме на работу в комбинированном классе 4/5 и у меня есть хорошие шансы пройти собеседование. У меня нет опыта работы с многоуровневыми комнатами, я даже не знаю, какие вопросы задавать, и, хотя я вижу, как книга Cornerstone может помочь в этом типе класса, есть ли что-нибудь, что в вашей книге не упоминается, чтобы помочь мне организовать этот тип комнаты?
-J.

Я могу представить, что ученики 4 и 5 классов будут вместе работать над множеством заданий; вы сможете дифференцировать свои инструкции и занятия по уровню способностей, а не только по классу. Судя по тому, что я вижу в последних образовательных тенденциях, наверное, так бы и хотелось директору. Если бы вы учили так, то, вероятно, было бы полезно — при подготовке к собеседованию — придумать несколько конкретных примеров того, как вы бы это сделали. Что касается организации, вам может потребоваться хранить некоторые вещи отдельно (возможно, разные ящики, чтобы они могли сдавать свои бумаги и т.), но по большей части я не думаю, что разделение классов сильно повлияет на планировку комнаты.

Мультиклассирование — 5-е издание SRD

Multiclassing позволяет вам получать уровни в нескольких классах. Это позволяет вам смешивать способности этих классов для реализации концепции персонажа, которая может не отражаться в одном из стандартных вариантов класса.
С этим правилом у вас есть возможность получить уровень в новом классе всякий раз, когда вы продвигаетесь по уровню, вместо получения уровня в вашем текущем классе.Ваши уровни во всех ваших классах суммируются, чтобы определить уровень вашего персонажа. Например, если у вас три уровня волшебника и два уровня бойца, вы персонаж 5-го уровня.
По мере того, как вы продвигаетесь по уровням, вы можете в первую очередь оставаться членом своего исходного класса, имея всего несколько уровней в другом классе, или вы можете полностью изменить курс, никогда не оглядываясь на оставленный вами класс. Вы даже можете начать прогресс в третьем или четвертом классе. По сравнению с персонажем одного класса того же уровня, вы пожертвуете некоторой концентрацией в обмен на универсальность.

Предварительные требования

Чтобы претендовать на новый класс, вы должны соответствовать предварительным требованиям для оценки способностей как для вашего текущего, так и для нового класса, как показано в таблице требований для мультиклассирования. Например, варвар, который решает перейти в класс друида, должен иметь как Сила, так и Мудрость 13 или выше. Без полной подготовки, которую получает начинающий персонаж, вы должны быстро учиться в своем новом классе, обладая естественными способностями, которые отражаются в показателях способностей выше среднего.

Класс	Минимум очков способностей
Варвар	Прочность 13
Бард	Харизма 13
Клерик	мудрость 13
Друид	мудрость 13
Истребитель	Сила 13 или Ловкость 13
Монах	Ловкость 13 и Мудрость 13
Паладин	Сила 13 и Харизма 13
Рейнджер	Ловкость 13 и Мудрость 13
Разбойник	Ловкость 13
Колдун	Харизма 13
Чернокнижник	Харизма 13
Мастер	Разведка 13

Очки опыта

Стоимость в очках опыта для получения уровня всегда зависит от общего уровня вашего персонажа, как показано в таблице развития персонажа, а не от вашего уровня в конкретном классе.Итак, если вы клерик 6 / боец ​​1, вы должны набрать достаточно опыта, чтобы достичь 8-го уровня, прежде чем вы сможете перейти на второй уровень как боец ​​или седьмой уровень как клерик.

Здоровье и Hit Dice

Вы получаете очки жизни от вашего нового класса, как описано для уровней после 1-го. Вы получаете очки жизни 1-го уровня для класса, только если вы персонаж 1-го уровня.
Вы складываете Hit Dice, предоставленные всеми вашими классами, чтобы сформировать пул Hit Dice. Если Hit Dice принадлежат к одному типу, вы можете просто объединить их вместе.Например, и боец, и паладин имеют d10, поэтому, если вы паладин 5 / боец ​​5, у вас есть десять Hit Dice d10. Если ваши классы дают вам Hit Dice разных типов, отслеживайте их отдельно. Например, если вы паладин 5 / священник 5, у вас есть пять Hit Dice d10 и пять Hit Dice d8.

Бонус к умению

Ваш бонус мастерства всегда зависит от вашего общего уровня персонажа, а не от вашего уровня в конкретном классе. Например, если вы боец ​​3 / разбойник 2, у вас есть бонус мастерства персонажа 5-го уровня, который равен +3.

Уровень владения

Когда вы получаете свой первый уровень в классе, отличном от вашего начального класса, вы получаете только некоторые из начальных навыков нового класса, как показано в таблице «Мультиклассовые навыки».

Мультиклассирование

Класс	Полученных навыков
Варвар	Щиты, простое оружие, боевое оружие
Бард	Легкая броня, один навык на ваш выбор, один музыкальный инструмент на ваш выбор
Клерик	Легкая броня, средняя броня, щиты
Друид	Легкая броня, средняя броня, щиты (друиды не будут носить броню и использовать металлические щиты)
Истребитель	Легкая броня, средняя броня, щиты, простое оружие, боевое оружие
Монах	Простое оружие, короткие мечи
Паладин	Легкая броня, средняя броня, щиты, простое оружие, боевое оружие
Рейнджер	Легкая броня, средняя броня, щиты, простое оружие, боевое оружие, один навык из списка навыков класса
Разбойник	Легкая броня, один навык из списка навыков класса, воровские инструменты
Колдун	–
Чернокнижник	Легкая броня, простое оружие
Мастер	–

Характеристики класса

Когда вы получаете новый уровень в классе, вы получаете его возможности для этого уровня.Однако вы не получаете стартовое снаряжение класса, и некоторые функции имеют дополнительные правила, когда вы мультиклассируете: Божественность канала, Дополнительная атака, Защита без брони и Колдовство.

Канал Divinity

Если у вас уже есть функция Божественного канала и вы получаете уровень в классе, который также предоставляет эту функцию, вы получаете эффекты Божественности канала, предоставляемые этим классом, но повторное получение этой функции не дает вам дополнительного использования ее. Вы получаете дополнительные возможности использования только тогда, когда достигнете уровня класса, который явно предоставляет их вам.Например, если вы клерик 6 / паладин 4, вы можете использовать Божественный канал дважды между отдыхами, потому что у вас достаточно высокий уровень в классе клерика, чтобы иметь больше применений. Всякий раз, когда вы используете эту функцию, вы можете выбрать любой из доступных вам эффектов Channel Divinity из ваших двух классов.

Если вы получаете возможность класса Extra Attack от более чем одного класса, эти функции не складываются. Вы не можете совершить более двух атак с этой функцией, если она не говорит, что вы делаете (как это делает боевая версия Extra Attack).Точно так же жуткий призыв чернокнижника Thirsting Blade не дает вам дополнительных атак, если у вас также есть Extra Attack.

Небронированная защита

Если у вас уже есть функция защиты без брони, вы не можете получить ее снова от другого класса.

Колдовство

Ваша способность к колдовству частично зависит от ваших объединенных уровней во всех ваших колдовских классах и частично от ваших индивидуальных уровней в этих классах. Если у вас есть возможность заклинания более чем одного класса, используйте правила ниже.Если вы мультиклассируете, но имеете возможность заклинания только от одного класса, вы следуете правилам, описанным для этого класса.
Известные и подготовленные заклинания. Вы определяете, какие заклинания вы знаете, и можете подготовить для каждого класса индивидуально, как если бы вы были членом одного класса этого класса. Если вы, например, рейнджер 4 / волшебник 3, вы знаете три заклинания рейнджера 1-го уровня в зависимости от ваших уровней в классе рейнджера. Как волшебник 3-го уровня, вы знаете три заклинания волшебника, и ваша книга заклинаний содержит десять заклинаний волшебника, два из которых (два, которые вы получили, когда достигли 3-го уровня как волшебник) могут быть заклинаниями 2-го уровня.Если ваш Интеллект равен 16, вы можете приготовить шесть заклинаний волшебника из своей книги заклинаний.
Каждое заклинание, которое вы знаете и готовите, связано с одним из ваших классов, и вы используете колдовскую способность этого класса, когда произносите заклинание. Точно так же фокус колдовства, такой как святой символ, может использоваться только для заклинаний из класса, связанного с этим фокусом.
Слоты для заклинаний. Вы определяете свои доступные ячейки заклинаний, складывая вместе все свои уровни в классах бардов, клериков, друидов, колдунов и волшебников, и половину своих уровней (с округлением в меньшую сторону) в классах паладинов и рейнджеров.Используйте это количество, чтобы определить свои ячейки заклинаний, сверяясь с таблицей Multiclass Spellcaster.
Если у вас более одного класса колдовства, эта таблица может дать вам ячейки заклинаний уровня выше, чем заклинания, которые вы знаете или можете подготовить. Вы можете использовать эти ячейки, но только для сотворения заклинаний более низкого уровня. Если сотворенное вами заклинание более низкого уровня, такое как горящие руки , имеет усиленный эффект при использовании слотом более высокого уровня, вы можете использовать усиленный эффект, даже если у вас нет заклинаний более высокого уровня. уровень.
Например, если вы вышеупомянутый рейнджер 4 / волшебник 3, вы учитываетесь как персонаж 5-го уровня при определении своих слотов заклинаний: у вас есть четыре слота 1-го уровня, три слота 2-го уровня и два слота 3-го уровня. Однако вы не знаете ни заклинаний 3-го уровня, ни заклинаний рейнджера 2-го уровня. Вы можете использовать ячейки заклинаний этих уровней, чтобы произносить заклинания, которые вы знаете, и потенциально усиливать их эффекты.
Пакт Магии. Если у вас есть и функция класса Колдовство, и функция класса Магия пакта из класса чернокнижника, вы можете использовать ячейки заклинаний, которые вы получаете от функции Магия Пакта, чтобы произносить заклинания, которые вы знаете или подготовили из классов с функцией класса Колдовство, вы можете использовать ячейки заклинаний, которые вы получаете от функции класса Spellcasting, чтобы читать заклинания чернокнижника, которые вы знаете.

Multiclass Spellcaster: количество ячеек для заклинаний на уровень заклинания

Уровень	1-й	2-я	3-й	4-я	5-й	6-я	7-й	8-й	9-я
1-й	2	–	–	–	–	–	–	–	–
2-я	3	–	–	–	–	–	–	–	–
3-й	4	2	–	–	–	–	–	–	–
4-я	4	3	–	–	–	–	–	–	–
5-я	4	3	2	–	–	–	–	–	–
6-я	4	3	3	–	–	–	–	–	–
7-я	4	3	3	1	–	–	–	–	–
8-я	4	3	3	2	–	–	–	–	–
9-я	4	3	3	3	1	–	–	–	–
10-я	4	3	3	3	2	–	–	–	–
11-я	4	3	3	3	2	1	–	–	–
12-я	4	3	3	3	2	1	–	–	–
13-я	4	3	3	3	2	1	1	–	–
14-я	4	3	3	3	2	1	1	–	–
15-я	4	3	3	3	2	1	1	1	–
16-я	4	3	3	3	2	1	1	1	–
17-я	4	3	3	3	2	1	1	1	1
18-я	4	3	3	3	3	1	1	1	1
19	4	3	3	3	3	2	1	1	1
20-й	4	3	3	3	3	2	2	1	1

.