Разработка проекта на тему «Как рисование по клеточкам помогает нам в математике» (1 класс)

Государственное бюджетное общеобразовательное учреждение города Москвы «Школа № 118»

Проектная работа на тему:

«Как рисование по клеточкам помогло нам в математике?»

Работу выполнили ученицы 1 «Г» класса

Коноваленко Елизавета и Гарманова Софья

Руководитель проекта:

Учитель начальных классов

Павлыго Екатерина Александровна

2017 год

Введение

Обоснование выбора темы состоит в следующем: ещё в сентябре учитель на уроках математики показал нам интересные задания, которые называются графические диктанты. Мы приходили в восторг, когда после выполнения команд учителя «две клетки вверх, одну вправо…» у нас получались интересные картинки.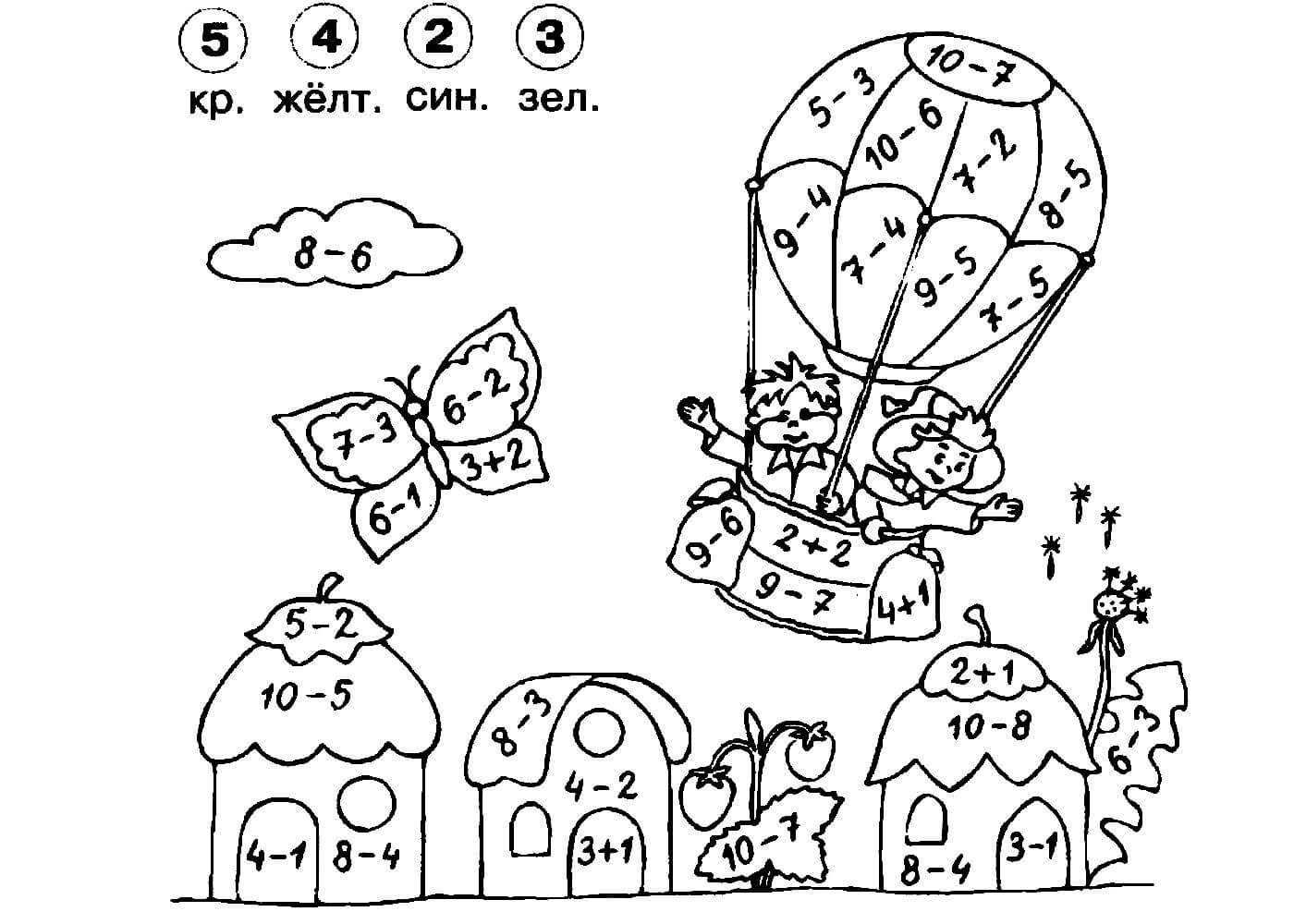

На переменах мы стали сами придумывать такие рисунки по клеточкам, скоро это увлечение переросло в наше хобби.

Позже в интернете мы увидели цветные рисунки, выполненные по клеточкам, и стали перерисовывать их в свои тетрадки. Нашим одноклассникам понравилась эта затея, и многие подключились к нам.

После этого мы стали дополнять простенькие картинки своими рисунками по клеточкам, начали сами придумывать рисунки. Вот что у нас получилось:

Мы заметили, что нам стало проще справляться с заданиями по математике, где нужно быстро сосчитать количество предметов, сложить числа или найти определённое место на листе бумаги (например, подписать работу в правом верхнем углу).

Новизна нашей работы состоит в том, что мы создали серию рисунков по клеточкам, которые могут быть использованы как в качестве графического диктанта, так и для перерисовывания детьми дошкольного и младшего школьного возраста.

Цель нашего исследования — определить, как графические диктанты и рисунки по клеточкам помогают ученикам в математике, ответить для себя на вопрос: «Зачем учитель даёт нам такие задания? Неужели просто, чтобы мы отдохнули от сложных примеров?»

Задачи нашей работы следующие:

1. Собрать имеющуюся в литературе и на интернет-сайтах информацию о ценности графических диктантов в начальной школе.

2. Опросить учеников нашего класса, любят ли они графические диктанты и занимаются ли ими в свое свободное время.

3. Сравнить уровень развития математических способностей у учеников, увлекающихся и регулярно занимающихся графическими диктантами, с теми, кто их не любит или выполняет очень редко.

4. Сделать вывод о значимости графических диктантов и рисования по клеточкам для учеников первых классов и дошкольников.

5. Создать серию своих собственных графических диктантов для дошкольников.

Гипотеза исследования в том, что рисование по клеточкам помогает нам лучше запомнить понятия «право», «лево», «вверх», «вниз», а также учит нас быстро и без ошибок считать.

Этапы работы:

1. Беседа с учителем о важности графических диктантов.

2. Изучение информации о рисовании по клеточкам на разных сайтах и в журналах.

3. Опрос и тестирование первоклассников нашей школы.

4. Анализ результатов и подведение итогов.

Глава I. Ценность графических диктантов в обучении

Графический диктант – это рисование по клеточкам по определенным командам.

Многим детям графические диктанты кажутся развлечением, но у многих они в то же время вызывают трудности. И преодолевая эти трудности ребенок учится, запоминает такие понятия, как право и лево, верх и низ, и закрепляет эти понятия на практике.

Всего парочка таких графических диктантов в неделю всего за пару месяцев позволит дошкольнику уже не путаться в названиях, а ориентироваться точно. Диктант заключается в рисовании по клеточкам, соответственно, под диктовку взрослого. Поэтому еще одно важное умение развивают в ребенке диктанты, и в частности графический диктант — он учит слушать и слышать, сосредоточиться на том, что говорит учитель, а это практически самое важное для школы умение.

Простые графические диктанты прекрасно помогают родителям и учителям предотвратить многие сложности на начальном этапе учебы в школе. Это рассеянность, неумение сконцентрироваться, неусидчивость, невнимательность. Регулярные короткие занятия с графическими диктантами развивают у ученика пространственное воображение и мышление, внимательность, координацию движений, мелкую моторику пальцев и многое другое.

Рисование по клеточкам – очень увлекательное и полезное занятие для детей. Это игровой способ развития у ребенка пространственного воображения, мелкой моторики пальцев рук, координации движений, усидчивости. Графические диктанты могут с успехом применяться для детей от 5 до 10 лет.

Графические диктанты, помогают подготовить руку ребенка к письму, развить пространственное воображение, научить ребенка ловкости при обращении с ручкой и карандашом и точности в движениях руки, что дает возможность заложить правильную основу для формирования каллиграфически правильного письма.

Глава II. Экспериментальная часть

Из беседы с нашим учителем и после изучения информации на детских сайтах, где предлагаются разные графические диктанты, мы выяснили, что письмо по клеточкам не только помогает отработать умение ориентироваться на листе бумаги (лево, право, верх, низ), но и учит нас быть более внимательными, усидчивыми, подолгу слушать учителя, считать нужное количество клеток, развивает мелкую моторику рук, помогает сосредотачиваться на одном задании.

Для проверки нашей гипотезы мы провели тестирование среди учеников нашего класса. Мы просили их нарисовать разные символы в разных частях листа (в центре, в правом верхнем углу и т.д.), затем проверяли умение долго сосредотачиваться на одном задании при выполнении однообразной работы (был проведен долгий графический диктант), а затем просили придумать и выполнить свои собственные рисунки по клеточкам.

Результаты были следующими: те дети, которые не любят графические диктанты и не занимаются ими в свободное время, не всегда с легкостью могут ориентироваться на листе бумаги. Эти дети имеют трудности даже на уроках изобразительного искусства, когда нужно найти центр листа или отступить какое-то расстояние от края листа.

У детей, которые вместе с нами стали выполнять эту интересную работу, правильнее и быстрее получается пересчитывать предметы, такие ученики дольше могут выполнять сложные задания на уроках, когда нужно подолгу прописывать слова, цифры или считать примеры.

А ещё у таких детей улучшился почерк, потому что рисование по клеточкам развивает мелкую моторику!

Кроме этого, мы заметили, что дети, увлекающиеся рисованием по клеточкам, смогли самостоятельно нарисовать более сложные и интересные рисунки, то есть у них лучше развито воображение.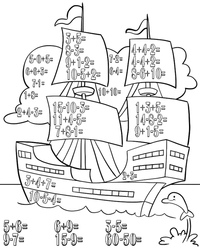

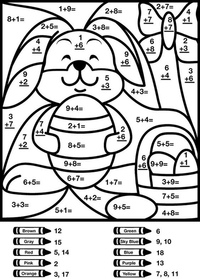
Для сравнения представляем рисунки, выполненные детьми, не занимающимися графическими диктантами:

И рисунки, выполненные за то же время детьми, которые увлекаются рисованием по клеточкам и регулярно выполняют графические диктанты:

Глава

III. Разработка собственных графических диктантов и рисунков по клеточкам

Теперь, когда мы увидели, что наше хобби не только доставляет нам удовольствие, но ещё и является таким полезным, мы начали создавать свои собственные графические диктанты для дошкольников, чтобы дети интересно проводили время и готовились к школе, стали внимательными и научились считать!

Глава IV. Выводы

Рисование по клеточкам, действительно, помогает ученикам первых классов в математике и других науках, ведь оно:

• Развивает мелкую моторику, поэтому цифры в тетрадках будут красивыми!

• Помогает дольше не отвлекаться на уроках, поэтому ученики услышат и запомнят больше важной информации!

• Учит пересчитывать предметы и клетки без ошибок!

• Развивает воображение, поэтому многие из нас смогут стать художниками или писателями!

В результате проведённого исследования наша гипотеза подтвердилась.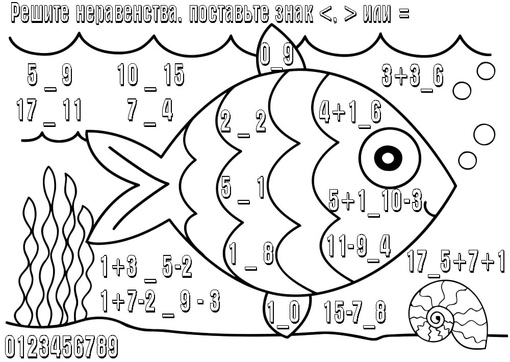

Использованная литература и интернет-ресурсы:

http://www.kindergenii.ru/grdiktant.htm

http://www.7gy.ru/rebenok/podgotovka-k-shkole/765-graficheskie-diktanty-po-kletochkam-dlya-doshkolnikov.html

http://bebiklad.ru/loqicheskie-zadachi/graficheskie-diktantyi

полезные сайты для детей начальной школы

Сайт «Верные слова»

«Верные слова» — это развивающий сайт для первоклассников и не только. Используется для проверки знаний по русскому языку. Помимо практических заданий, есть и теория — не нужно искать в другом месте. На сайте легко отслеживать прогресс. Первому классу подойдёт курс «Легче лёгкого» — отличное дополнение к основному образовательному процессу.

Приложение «Сказбука»

Полезный сайт для учеников начальной школы — здесь малыш сможет учиться чтению, математике и английскому. Интерфейс не напрягает глаза, а задания разделены по возрастной шкале. Преимущество в удобной функции: с помощью лимита можно ограничить время, которое ребёнок проводит в приложении.

Приложение для первоклассников доступно для iOS и Android.

Приложение «Математика и логика для детей»

Это приложение для детей начальной школы разработано совместно с педагогами и психологами. Включает в себя небольшие игры, которые нацелены на развитие мышления, логики, геометрического воображения и навыков счёта. То, что нужно первоклассникам! Доступно для iOS. 

Приложение «Намби»

В приложении есть больше тысячи увлекательных математических задач, которые соответствуют школьной программе первого класса. Нужно купать монстриков, помогать ламе забраться на скалу, запускать таксу в воздух и кормить птиц печеньем — параллельно изучая математику. Приложение для первоклассников доступно для iOS. 

Приложение Bubl Draw

Необычное приложение, которое разовьёт творческие способности малыша: здесь можно одновременно рисовать и сочинять музыку. Каждый цвет звучит по-своему и меняет тональность в зависимости от формы рисунка. Возможно, это облегчит родителям задачу по выбору дополнительной секции — вы узнаете, что больше нравится ребёнку. Доступно для iOS. 

Сайт Learn English Kids

Этот развивающий сайт для занятий первоклассников и всех детей, начинающих путь в английском, разработан Британским Советом — международной организацией, представляющей Великобританию в области культуры и образования. На сайте малыши могут слушать песни, смотреть мультфильмы, играть в обучающие игры и многое другое. 

Приложение Memory Trainer

Приложение для всех, кто хочет тренировать память. Нужно запоминать картинки и выбирать их из множества других. С каждым шагом количество картинок растёт, и игра усложняется.

Это образовательное приложение подходит для Android. 

Начальная школа «Фоксфорда»

Хорошо, когда есть отдельные образовательные ресурсы и приложения для первоклассников — они помогают отработать конкретные предметы и заполнить пробелы. Но если первокласснику нужно комплексное онлайн-обучение, на помощь придёт «Фоксфорд»!

Начальная школа «Фоксфорда» — это интерактивное онлайн-обучение для 1-4 классов. Ребёнок сможет осваивать школьную программу в режиме реального времени: в назначенный час ученики собираются на платформе и смотрят вебинар. Не нужно никуда ехать и тратить время на дорогу!

В 1-2 классе родители присутствуют на уроках вместе с детьми, чтобы сразу получить методические рекомендации и помочь юному ученику написать свой вопрос в чат. А в 3-4 классе ребята уже могут взаимодействовать с преподавателями сами, а для родителей проводятся отдельные методические вебинары.

<<Блок перелинковки>>

Обучение включает в себя все необходимые в начальных классах предметы:

• русский язык и литературное чтение (в 1-2 классе эти предметы объединены в один — обучение грамоте),
• математика,
• окружающий мир,
• английский язык,
• алгоритмика.  

Занятия ведут преподаватели, чей средний педагогический стаж составляет 15 лет. Они знают, как заинтересовать детей и найти подход к каждому.

Ученикам и родителям предоставляются материалы, необходимые для успешной учёбы. Также на помощь малышам и родителям всегда готов прийти классный руководитель. А в течение учебного года психолог, логопед и другие квалифицированные специалисты проводят вебинары для родителей, где можно задать вопросы и получить рекомендации. 

Кому подойдёт начальная школа «Фоксфорда» 

• Тем, кто готов присутствовать на уроках в первом и втором классе вместе с детьми. 
• Тем, кто хочет с первого класса выстраивать для ребёнка индивидуальный маршрут обучения и учиться тому, что интересно. 
• Семьям, которые часто переезжают или проживают за границей, но хотят, чтобы у детей был российский аттестат. 
• Тем, у кого слабое здоровье или травмирующий опыт учёбы в обычной школе. 

Пользуйтесь онлайн-ресурсами, чтобы сделать учебный процесс современней и эффективней. А за полноценным обучением приходите в начальную школу «Фоксфорда».

4 класс. Моро. Учебник №1. Ответы к стр. 78

Числа от 1 до 1000

Умножение и деление

Умножение на однозначное число

Ответы к стр. 78

Вспомни правила умножения с числами 0 и 1 (с. 107 — 108). Вычисли:

1 • 8 = 8     312 • 1 = 312     0 • 35 = 0
1 • 1 = 1     703 • 1 = 703     0 • 100 = 0

918 • 0 = 0    10 • 1 = 10
617 • 0 = 0    10 • 0 = 0

340. (Устно.)

0 дес. • 5 + 3 дес. = 3 дес.
0 тыс. • 7 + 4 тыс. = 4 тыс.
0 сот. • 3 + 2 сот. = 2 сот.
0 сот. • 1 + 1 сот. = 1 сот.

341. 803 • 5     50801 • 4     41008 • 6
      4019 • 7     90048 • 7     70032 •  8

_× 803     _× 50801     _× 41008
      5               4               6
 4015     203204      246048

_× 4019     _× 90048     _× 70032
        7               7               8
 28133      630336      560256

342.  Начерти три отрезка. Длина первого 8 см 5 мм, что на 7 мм больше длины второго и на 1 см 5 мм меньше длины третьего отрезка.

1) 8 см 5 мм − 7 мм = 7 см 8 мм — длина второго отрезка
2) 8 см 5 мм + 1 см 5 мм = 10 см — длина третьего отрезка

343. Комбайнер убирал 9 дней пшеницу на двух полях. На первом поле он собрал 400 т пшеницы, а на втором − 320 т. Сколько тонн зерна убирал комбайнер за 1 день, если ежедневная выработка была одинаковой?

1) 400 + 320 = 720 (т) − собрал с двух полей
2) 720 : 9 = 80 (т) − убирал за 1 день
О т в е т: за 1 день комбайнер убирал 80 т зерна.

344. На мельницу отправили пшеницу на 10 машинах, по 42 ц на каждой, а ячменя в 3 раза меньше, чем пшеницы. На сколько центнеров больше отправили пшеницы, чем ячменя?

1) 10 • 42 = 420 (ц) − пшеницы отправили на мельницу
2) 420 : 3 = 140 (ц) − ячменя отправили на мельницу
3) 420 − 140 = 280 (ц) − пшеницы больше, чем ячменя
О т в е т: пшеницы отправили на 280 ц больше, чем ячменя.

345. Запиши выражения и вычисли их значения.
1) Произведение чисел 8 и 3125 уменьшить на 5186.
2) Наименьшее шестизначное число увеличить в 10 раз, а результат уменьшить в 1000 раз.
3) Частное чисел 872 и 8 увеличить в 7 раз.

1) 8 • 3125 − 5186 = 25000 − 5186 = 19814
_×3125      _— 25000
       8          5186
25000        19814

2) 100000 • 10 : 1000 = 1000000 : 1000 = 1000
3) 872 : 8 • 7 = 109 • 7 = 763
_— 872|8          _×109
   8    |109           7
 _—072               763  
     72                   
       0                   

346. Рассмотри рисунки и объясни, чем похожи и чем различаются рисунки 1 и 2, 2 и 3, 3 и 4, 1 и 4.

Рисунки 1 и 2 схожи тем, что на них изображены окружности, большая и маленькая, большая голубая, а маленькая розовая. Отличие рисунков в том, что на первом рисунке окружности находятся рядом друг с другом и не имеют общих точек соприкосновения, а на втором они касаются друг друга и имеют одну общую точку соприкосновения.
Рисунки 2 и 3 сходи тем, что на них изображены окружности, большая и маленькая, большая голубая, а маленькая розовая. Отличие рисунков в том, что на втором рисунке окружности касаются друг друга и имеют одну общую точку соприкосновения, а на третьем они пересекаются и имеют 2 общих точки пересечения.
Рисунки 3 и 4 схожи тем, что на них изображены окружности, большая и маленькая, большая голубая, а маленькая розовая. Отличие рисунков в том, что на третьем рисунке окружности пересекаются и имеют 2 общих точки пересечения, а на 4 одна окружность находится внутри другой и общих точек соприкосновения или пересечния у них нет.
Рисунки 1 и 4 схожи тем, что на них изображены окружности, большая и маленькая, большая голубая, а маленькая розовая, в обоих случаях общих точек соприкосновения или пересечения у окружностей нет. Отличие рисунков в том, что на первом рисунке окружности находятся рядом друг с другом, а на четвертом одна окружность находится внутри другой.

347. Сколько в числе 15400 десятков? сотен? тысяч? Сколько единиц в числе, содержащем 208 дес.? 32 сот.?

В числе 15400 содержится 1540 десятков, 154 сотни и 15 тысяч.
В числе, содержащем 208 десятков, содержится 2080 единиц.
В числе, содержащем 32 сотни, содержится 3200 единиц.

348. 45010 − (3908 + 17613)     6008 • 9     97168 • 6
         60000 − 2407 + 5849      91005 • 3     7 • 23844

45010 − (3908 + 17613) = 45010 − 21521 = 23489
₊ 3908     _— 45010
 17613       21512
 21521       23489

60000 − 2407 + 5849 = 57593 + 5849 = 63442
_— 60000      ₊ 57593
    2407          5849
  57593        63442

_× 6008     _× 91005
        9               3
 54072      273015

_× 97168      _× 23844
          6                7
 583008       166908

349.  Переставляя карточки с цифрами, сделай равенство верным.
[6] [2] : [3] [1] = [3] 

[6][3] : [2][1] = [3]
[3][6] : [1][2] = [3]
[6][3] : [3] = [2][1]
[3][6] : [3] = [1][2]

---

Вычисли.
609 • 7   32009 • 3

_× 609     _× 32009
      7               3
 4263       96027

ЗАДАНИЕ НА ПОЛЯХ
Ребус

_× 739
      9
 6651

ГДЗ по математике. Учебник. 4 класс. Часть 1. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.

Математика. 4 класс

4 класс. Моро. Учебник №1. Ответы к стр. 78

4.1 (82.63%) от 76 голосующих

Прописи — Учимся писать цифры, страница 1.

8333333333333

Коллекция авторских раскрасок для детей всех возрастов. На данный момент насчитывает 14.365 картинок. -Азбуки (Русская, Украинская, English) -Для малышей -Зарубежные мультфильмы -Отечественные мультфильмы -Мандалы

Флеш-раскраски для ваших малышей. Огромный выбор интересных картинок.

Интересные и необычные факты обо всем на свете.

Новый раздел ТРАФАРЕТЫ поможет в оформлении праздников. К новому году добавлены тафареты Ёлочки, Игрушки, Олени, Снеговички, Снежинки. Раздел регулярно пополняется, Следите за новинками.

Игры различных жанров для девочек и мальчиков всех возрастов.

Большая коллекция картинок для развития детей. Ребусы, азбуки, цифры, животные, растения.

Фотографии интересных мест, детей, животных. Все самое интересное в фотографиях.

Стенгазеты ко всевозможным праздникам создадут необходимую атмосферу. -Стенгазеты «С днем рождения» -Стенгазеты «С новым годом» -Стенгазеты «Времена года» -Стенгазеты «С юбилеем» -Стенгазеты «C 8 марта» и много других.

Самые разнообразные лабиринты различной степени сложности.

Интересное и смешное видео с участием детей и животных. Мастер классы.

Детские песни для детей к Новому году и другим праздникам.

Аудио-сказки для детей.

Открытки к праздникам. С Новым годом, 14 февраля — День влюбленных, День Святого Валентина, Деньзащитника отечества-23 февраля, 8 марта, День Победы, 1 мая, Ретро открытки, советские открытки, авторские.

Огромная коллекция смайликов, на данный момент содержит 7371 смайликов.

Всевозможные анимированнные картинки и аватарки для соцсетей.

Детские анекдоты на различные темы: Из жизни животных, Объявления, Отцы и дети, Про Вовочку, Про рыбалку, Школа. Коллекция анекдотов регулярно пополняется, следите за обновлениями.

Веселые истории из жизни с детьми и о них.

Загадки для детей на разные темы

Статьи для родителей о воспитании детей, здоровье детей и их досуге.

Поделки с детьми и для детей. Поделки из бумаги, природных материалов, соленое тесто, лепка из глины и пластилина.

Узнай стоимость своей работы Бесплатная оценка заказа!

1С:Школа

Для наполнения электронной библиотеки системы «1С:Образование» можно использовать электронные учебные пособия серии «1С:Школа», которые охватывают все ступени общего образования – от дошкольного до старшей школы.

Учебные пособия «1С:Школа» выпускаются издательством «1С-Паблишинг». Издательство «1С-Паблишинг» входит в перечень организаций, выпускающих учебные пособия, которые допускаются к использованию при реализации образовательных программ общего образования, имеющих государственную аккредитацию (см. Приказ Минобрнауки РФ № 699 от 09.06.2016, строка 8 Приложения).

Учебные пособия «1С:Школа» помогут сделать урок ярким и динамичным. Интерактивные и анимированные рисунки, карты и схемы повысят наглядность на уроках изучения нового материала, интерактивные модели и динамические чертежи позволят провести учебное исследование, эксперимент или лабораторную работу, интерактивные практические задания, тренажеры и тесты – закрепить полученные знания или проверить результаты обучения.

Перечень учебных пособий

Дошкольное образование

1С:Школа. Дошкольное образование, 6-7 лет

Начальная школа

1С:Школа. Математика, 1 класс. 1 часть

1С:Школа. Математика, 1 класс. 2 часть

1С:Школа. Математика, 2 класс.

1С:Школа. Математика, 3 класс.

1С:Школа. Математика, 4 класс.  

1С:Школа. Математика, 1-4 класс. Тесты.

1С:Школа. Азбука.

1С:Школа. Русский язык, 1 класс.

1С:Школа. Русский язык, 3 класс.

1С:Школа. Русский язык, 4 класс.

1С:Школа. Литературное чтение, 1 класс.

1С:Школа. Литературное чтение, 2 класс.

1С:Школа. Литературное чтение, 3 класс.

1С:Школа. Литературное чтение, 4 класс.

1С:Школа. Развитие речи, 1–4 класс. Тесты.

1С:Школа. Окружающий мир, 1 класс.

1С:Школа. Окружающий мир, 2 класс.

1С:Школа. Окружающий мир, 3 класс.

1С:Школа. Окружающий мир, 4 класс.

1С:Школа. Окружающий мир, 1-4 класс. Тесты.

1С:Школа. Тайны времени и пространства, 1-4 класс.

Окружающий мир. Интерактивные карты, 1-4 класс.

1С:Школа. Игры и задачи, 1–4 класс.

1С:Школа. Студия лепки. Животные.

Русский язык

1С:Школа. Русский язык, 5–6 класс. Морфемика. Словообразование

1С:Школа. Русский язык, 5–6 класс. Лексикология.

1С:Школа. Русский язык, 5 класс.

1С:Школа. Русский язык, 6 класс.

1С:Школа. Русский язык, 7 класс.

1С:Школа. Русский язык, 8 класс.

1С:Школа. Русский язык, 9 класс.

1С:Школа. Тесты по пунктуации, 9–11 класс.

Математика, алгебра, геометрия, информатика и ИКТ

1С:Школа. Математика, 5 класс.

1С:Школа. Математика, 6 класс.

1С:Школа. Алгебра, 7–9 класс.

1С:Школа. Алгебраические задачи с параметрами, 9–11 класс.

1С:Школа. Геометрия, 7 класс.

1С:Школа. Геометрия, 8 класс.

1С:Школа. Геометрия, 9 класс.

1С:Школа. Геометрия. Интерактивные задания на построение на плоскости, 7–10 класс.

1С:Школа. Геометрия. Интерактивные задания на построение в пространстве, 10-11 класс.

Математика. Коллекция интерактивных моделей, 5-11 класс.

1С:Школа. Информатика, 10 класс.

1С:Школа. Информатика, 11 класс.

Естествознание и биология

1С:Школа. Введение в естественнонаучные предметы, 5 класс.

1С:Школа. Биология, 6 класс.

1С:Школа. Биология, 7 класс.

1С:Школа. Биология, 8 класс.

1С:Школа. Биология, 9 класс.

1С:Школа. Биология, 10 класс.

1С:Школа. Биология, 11 класс.

1С:Школа. Биология, 6-9 класс. Дыхание

1С:Школа. Биология. Коллекция наглядных материалов. 5-11 классы

Биология. Коллекция интерактивных моделей, 9-11 класс.

География

1С:Школа. География, 7-11 класс. Библиотека наглядных пособий (готовится к выпуску).

География. Интерактивные карты, 6-10 класс.

Физика

1С:Школа. Физика, 7 класс.

1С:Школа. Физика, 8 класс.

1С:Школа. Физика, 9 класс.

1С:Школа. Физика, 10 класс.

1С:Школа. Физика. Практикум. 7-11 классы.

Химия

1С:Школа. Химия, 8 класс.

1С:Школа. Химия, 9 класс.

1С:Школа. Химия, 10 класс.

1С:Школа. Химия. Коллекция наглядных материалов. 8-11 классы.

История

1С:Школа. История Древнего мира, 5 класс.

1С:Школа. История Средних веков, 6 класс.

1С:Школа. Российская и всеобщая история, 6 класс.

1С:Школа. Новейшая история зарубежных стран, 9 класс.

Всеобщая история. Интерактивные карты, 5-9 класс.

1С:Школа. История России. Часть 1. С древнейших времен до начала XVI века

1С:Школа. История России. Часть 2. С середины XVI до конца XVIII века

1С:Школа. История России. Часть 3. С конца XVIII по 90-e годы XIX века

1С:Школа. История России. Часть 4. XX век.

1С:Школа. История России, 6–9 класс. Библиотека наглядных пособий.

1С:Школа. История 10–11 класс. Подготовка к ЕГЭ.

Экономика и обществознание

1С:Школа. Обществознание, 10–11 класс.

1С:Школа. Экономика, 9-11 класс.

самых неправильно понятых математических стандартов в 1 классе

Я был так взволнован, написав этот пост, потому что более половины своей 23-летней педагогической карьеры я провел в 1 ^{-м классе} . Мне нравится этот класс, и мне особенно нравится богатый математический материал, который студенты получают в течение года обучения!

Как я уже говорил в своем последнем посте, обучение математике в начальных классах невероятно сложное, и стандарты могут быть легко неправильно поняты. Вот почему я изучал согласованные материалы, учился у Core Advocates и постоянно углубляю собственное понимание математического содержания.Давайте рассмотрим несколько примеров!

Инструкция Инструкция Инструкция

Стандартный	Общая инструкция смещения
1.OA.A.1 Используйте сложение и вычитание в пределах 20 для решения задач со словами, включающих ситуации сложения, взятия из, сложения, разборки и сравнения с неизвестными во всех позициях, например, с использованием объектов, рисунков , и уравнения с символом для неизвестного числа, чтобы представить проблему.	Инструкция не включает все типы задач из таблицы сложения и вычитания *. Инструкция по типам задач подчеркивает одни ситуации больше, чем другие, и рассматривает сложение как более важное значение, чем вычитание. Инструкция включает приемы получения ответов, такие как обучение ключевым словам, вместо поддержки математического мышления и осмысления. * Типичные ситуации сложения и вычитания можно найти здесь .
1.OA.B.3 Применяйте свойства операций как стратегии сложения и вычитания.* Примеры: Если известно 8 + 3 = 11, то также известно 3 + 8 = 11. (Коммутативное свойство сложения.) Чтобы сложить 2 + 6 + 4, можно сложить вторые два числа, чтобы получилась десятка, так что 2 + 6 + 4 = 2 + 10 = 12. (Ассоциативное свойство сложения.) * Студентам не нужно использовать формальные термины для этих свойств.	фокусируется на процедурном обучении свойствам операций, а не на построении понимания свойств, почему они работают математически и как их можно использовать при сложении и вычитании. Инструкция делает упор на изучение словарного запаса, обучение только терминам и их определениям вместо понимания математических концепций и идей, лежащих в основе терминологии. Примечание. Использование точного математического языка важно, но учащимся не нужно запоминать или запоминать термины. Акцент делается на понимание и использование свойств операций.
1.OA.D.7 Поймите значение знака равенства и определите, верны или ложны уравнения, включающие сложение и вычитание.Например, какие из следующих уравнений верны, а какие нет? 6 = 6, 7 = 8-1, 5 + 2 = 2 = 5, 4 + 1 = 5 + 2.	Инструкция упрощает значение знака равенства путем процедурной обработки операций вместо того, чтобы дать учащимся понимание того, что знак равенства означает одинаковость величин по обе стороны от знака равенства в уравнении (независимо от того, присутствует ли число или выражение). Инструкция фокусируется на том, чтобы всегда решать каждую сторону знака равенства, вместо того, чтобы иногда использовать стратегии или математические рассуждения, чтобы определить, когда уравнение истинно или ложно.
1.NBT.B.3 Сравнивать двузначные числа на основе значений разряда десятков и единиц, записывая результаты сравнений с помощью символов>, = и <.	не связывает разряды с пониманием того, что две цифры в двузначных числах представляют собой десятки и единицы, используемые при сравнении. Инструкция фокусируется на процедурах сравнения чисел, а не на понимании количества двузначных чисел.
1.NBT.C.4 Сложение в пределах 100, включая двузначное число и однозначное число, и добавление двузначного числа и числа, кратного 10, с использованием конкретных моделей или чертежей и стратегий, основанных на разряде, свойствах операций и / или взаимосвязь между сложением и вычитанием, свяжите стратегию с письменным методом и объясните используемую аргументацию. Поймите, что при сложении двузначных чисел добавляются десятки и десятки, единицы и единицы; а иногда нужно составить десятку.	Инструкции и задачи, которые предоставляются учащимся, ограничиваются задачами, в которых одно из двух дополнений всегда является однозначным числом или десятичным числом. Инструкция приближается к стандартному алгоритму и не связывает конкретные и графические представления, основанные на понимании числовых значений.
1.MD.A.2 Выразите длину объекта как целое число единиц длины, положив несколько копий более короткого объекта (единицы длины) встык; поймите, что измерение длины объекта — это количество единиц длины одинакового размера, которые охватывают его без зазоров или перекрытий. Ограничение контекстами, в которых измеряемый объект охватывает целое число единиц длины без пропусков или перекрытий.	фокусируется на процедурах измерения вместо построения понимания повторяющихся единиц длины при измерении (используйте одну единицу многократно, от начала до конца, без пробелов, начиная с одной конечной точки). Инструкция включает измерения с использованием стандартных единиц измерения или стандартных измерительных инструментов, таких как линейки.

Давайте подробнее рассмотрим два ключевых стандарта: 1.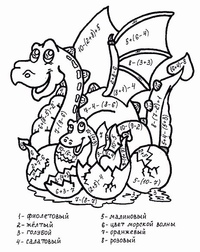 OA.D.7 и 1.NBT.C.4. Оба эти стандарта представляют собой основную работу для 1 класса и играют важную роль в последовательном продвижении обучения математике в начальной школе.Как учитель, я много изучал эти стандарты!

1.OA.D.7

Поймите значение знака равенства и определите, верны ли уравнения, включающие сложение и вычитание. Например, какие из следующих уравнений верны, а какие нет? 6 = 6, 7 = 8 — 1, 5 + 2 = 2 = 5, 4 + 1 = 5 + 2.

В моем классе, когда я ставил истинные / ложные задачи с выражением по обе стороны от знака равенства, я учил студентов всегда сначала решать обе стороны.Я бы последовал за этим сравнением количеств: если количества были одинаковыми, то это было верно, а если не одинаково, это было ложно. Беседуя с коллегами и посещая другие классы, я обнаружил, что многие учителя используют тот же метод. Узнав больше об этом стандарте, я понял, что превратил это обучение в процедуру, и в итоге студенты не смогли лучше понять знак равенства.

Аспектом Rigor, предусмотренным в этом стандарте, является концептуальное понимание.Задача математического обучения состоит в том, чтобы учащиеся поняли , что величины по обе стороны от знака равенства должны быть одинаковыми, в противном случае уравнение не имеет математического смысла. Знак равенства не означает получение ответа, а означает нечто гораздо более глубокое! Это показывает, что количества одинаковы или равны.

Я не только систематизировал то, что должно было быть концептуальным обучением, я также упустил возможность сделать упор на рассуждение и математическое мышление, основанное на числах и операциях.Например, в задаче 4 + 4 = 3 + 9 учащимся не нужно ничего добавлять. Они должны уметь рассуждать, что 4 + 4 не больше 9, а 3 + 9 должно быть больше 9, поэтому без добавления чего-либо (кроме известного факта 4 + 4) это уравнение должно быть ложным. Каждый раз, когда мы можем сделать упор на математическом осмыслении в наших инструкциях, мы должны использовать эту возможность !!

1.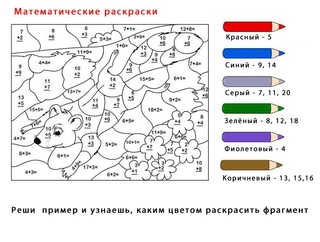 NBT.C.4.

Сложить в пределах 100, включая двузначное число и однозначное число, и добавить двузначное число и число, кратное 10, с использованием конкретных моделей или чертежей и стратегий, основанных на разряде, свойствах операций и / или взаимосвязь между сложением и вычитанием, свяжите стратегию с письменным методом и объясните используемую аргументацию.Поймите, что при сложении двузначных чисел добавляются десятки и десятки, единицы и единицы; а иногда нужно составить десятку.

Я выбрал этот стандарт, потому что его неправильно понимал как учитель первого класса, пока у меня не появилась возможность углубить свое понимание, углубившись в учебную программу, соответствующую стандартам. Я думал, что стандарт требует, чтобы все задачи, над которыми работают студенты, выглядели примерно так: 23 + 6 , 42 + 4 и 38 + 3 или 23 + 60 , 42 + 40 и . 38 + 30 .Во всех этих примерах одно из слагаемых всегда является однозначным числом или кратным десяти. Как оказалось, я неправильно понял этот стандарт!

Изучая в качестве учителя учебную программу, соответствующую стандартам, я столкнулся со многими проблемами, такими как 23 + 36, 42 + 54 и 38 + 27. Итак, как эти двузначные дополнения могут соответствовать этому стандарту и способствовать работе, которая будет выполняться в 2 ^ой класс? Я также задавался вопросом, как избежать процедурных инструкций и вместо этого сосредоточить внимание на понимании ценности операции сложения.Давайте посмотрим на 23 + 36 и воспользуемся примерами студенческих работ ниже:

Как вы можете видеть, в одном примере ученик разложил 36 на 30 и 6, затем сложил 23 + 6 в качестве первого шага, добавив единицы и единицы. Затем ученик сложил 29 + 30, добавив десятки и десятки, чтобы найти всю сумму. Этот метод соответствует стандарту.

В другом примере ученик разложил оба числа в развернутую форму, затем сложил единицы и десятки отдельно (20 + 30 и 3 + 6), а затем сложил 50 + 9. В этом случае студент использовал графическое представление и связал его с записанными уравнениями. Этот метод также соответствует стандарту.

Другая часть этого стандарта предполагает понимание того, что «иногда необходимо составить десятку». Как первоклассник может решить этот тип задачи (например, 38 + 27), при этом соблюдая стандарт? Опять же, давайте посмотрим на образцы студенческих работ ниже:

Как видите, один студент разложил 27 на 25 и 2, затем сложил 38 + 2, получив эквивалентную задачу 40 + 25.Этот ученик знал, что 2 необходимо, чтобы сделать следующую декаду числом 40, и был способен разложить 27, чтобы получить 2. С помощью этого метода ученик составил новую десятку.

Другой ученик добавил единицы к единицам, составив новую десятку, а затем добавил десятки к десяткам, используя графическое представление на основе разряда. Затем ученик решил, сложив 50 + 15. Оба метода входят в сферу применения стандарта.

Мне нравится гибкость, допускаемая в этих задачах, которая создает основу для различных методов решения и различных типов мышления учащихся. Все методы решения основаны на разрядах и построены на плавном добавлении в пределах 100 и сложении трехзначных чисел в 2 ^и классах и являются основополагающими для глубокого понимания будущих алгоритмов.

Я надеюсь, что этот пост помог вам по-другому взглянуть на сложное изучение математики, которое происходит в первом классе! Я хотел бы прочитать ваши комментарии или услышать от вас в Twitter! (@ mrsmillergrade1). С этой серией блогов я также опускаюсь в оценки, так что следите за обновлениями моего поста о детском саду, который выйдет в ближайшее время!

Как решить математический рисунок фруктов

• Пользователи Twitter не могут разгадать домашнее задание первоклассника по математике.
• Передовая педагогика стремится выявить у детей различные идеи (буквально!), Чтобы понять, как они думают.
• Развитие критического мышления и повседневной математической грамотности помогает учащимся более устойчиво изучать математику.
  

---

На прошлой неделе The N ew Yorker Хелен Рознер поделилась тупо написанной детской математической задачей, и Интернет ответил соответствующим образом:

Этот контент импортирован из Twitter. Вы можете найти то же содержимое в другом формате или найти дополнительную информацию на их веб-сайте.

Предположения сильно различались.

(Бен прав, но это сложно объяснить одним твитом.)


Этот контент импортирован из Twitter. Вы можете найти то же содержимое в другом формате или найти дополнительную информацию на их веб-сайте.

Прав ли Билл Шиллито из Университета Оглторпа? W hat Означает ли эта математическая задача?

➗ Вы любите числа. И мы тоже. Давайте вместе разберемся с числами.

Общая задача следует общей формуле с обновленными математическими педагогиками разных видов. Родитель, который не читал или просто не получил нужных материалов для понимания педагогики, вырывает отрывок из контекста и смеется над тем, что это кажется чепухой. В этом случае в домашнем задании используется язык, который студенты, вероятно, выучили в классе.

Этот контент импортирован из {embed-name}. Вы можете найти то же содержимое в другом формате или найти дополнительную информацию на их веб-сайте.

Математический рисунок — это отрендеренная ребенком версия того, как они в реальной жизни считают такие объекты, как блоки или даже пальцы. Например, они рисуют круги, которые соответствуют количеству объектов в вопросе. Затем они также рисуют взаимосвязи, обводя некоторые объекты, вычеркивая некоторые из них, помещая их в разные группы и т. Д.

Если это звучит довольно изощренно, это так, и это не так — дети тянутся к такому типу мышления, но для взрослых за пределами таких областей, как комбинаторика или теория множеств, это можно найти почти исключительно в инфографике.

---

📚

Лучшие книги по математике

Бесконечные силы: как расчеты раскрывают тайны Вселенной

Zero: Биография опасной идеи

Искусство статистики: как учиться на данных

The Joy of x: A Guided Tour of Math, from One to Infinity

---

Давайте рассмотрим, что такое математические рисунки и почему такой вид педагогики набирает популярность в математике. Математика, в частности, уязвима для множества болевых точек в образовании. Тревожные по математике учителя начальной школы сообщают об этом беспокойстве ученикам и влияют на их результаты, и это еще до того, как чему-то научат.

В книге 2005 года « Как ученики учатся: математика в классе », которая является продолжением некоторых других хорошо известных книг по психологии об обучении, эксперты сосредотачиваются на способах взаимодействия со студентами по математике, чтобы показать, как они ‘ думаешь о проблемах.Дети приобретают числа более осязаемым образом, например, видят количество вещей, поставленных на прилавок, или считают по пальцам.

Поскольку взаимосвязь между реальной, счетной и удерживаемой вещью и числами, которые вы начинаете писать в своем домашнем задании по математике, не всегда ясна, эксперты говорят, что некоторые ученики оказываются в затруднительном положении, просто пытаясь поделиться своими мыслями о том, как решать задачи.

Детей старшего возраста поощряют показывать свои работы, хотя честно, это больше похоже на способ выявить обман, а не исследовать, как они думают.Математическая педагогика утверждает, что говорение младшим детям через их мысли также является большим подспорьем. «Такое сообщение о математическом мышлении может помочь каждому в классе понять данную концепцию или метод, потому что оно проливает свет на противоположные подходы, некоторые из которых ошибочны, но часто по интересным причинам», — пишут авторы в книге How Student Learn .

Это ключевая точка . Если вы когда-нибудь проходили Princeton Review или другой курс подготовки к экзаменам, вы знаете, что один из основных способов, с помощью которых писатели ловят тестируемых на неправильные ответы, — это предлагать что-то почти правильных.Если вы допустили одну распространенную и ключевую ошибку, ваша работа приведет вас к отвлекающим маневрам. А понимание различных распространенных ошибок в мышлении — отличный способ помочь детям обдумать свои варианты в среде, которая не наказывает их за обдумывание.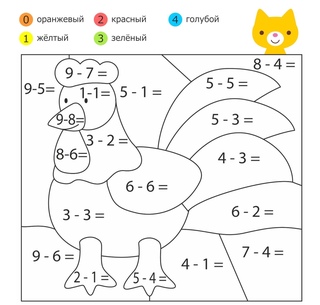 Здесь, в Popular Mechanics , мы участвуем в командном математическом рисовании.

Итак, теперь, когда вы освоили математические рисунки и счетные вещи, взгляните на проблему еще раз. Как бы вы ее решили?
Расскажите в комментариях.💬 ⬇


Этот контент создается и поддерживается третьей стороной и импортируется на эту страницу, чтобы помочь пользователям указать свои адреса электронной почты. Вы можете найти дополнительную информацию об этом и подобном контенте на сайте piano.io.

уроков в классе | Математические решения

Черил начала урок с чтения Спагетти и Фрикадельки для всех! вслух в класс. По сюжету мистер и миссис Комфорт приглашают 32 члена семьи и друзей на встречу и устанавливают восемь квадратных столов, чтобы разместить по четыре человека за каждым, по одному сбоку.По мере того, как гости приходят, у всех есть свои идеи о том, как переставить столы, чтобы группы разного размера могли сидеть вместе.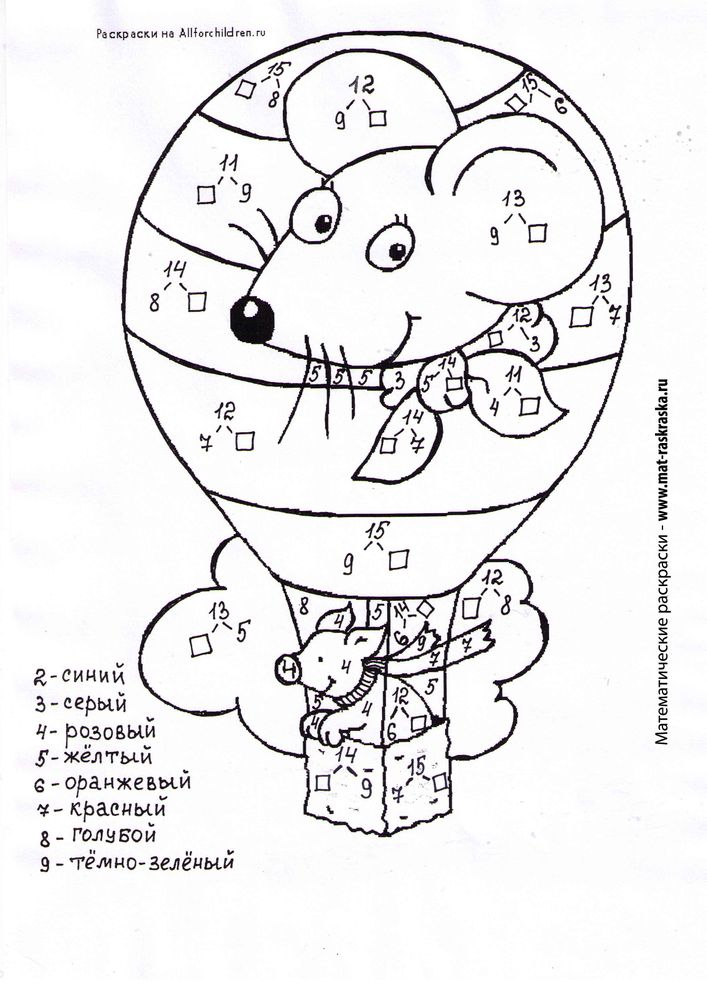 Миссис Комфорт протестует, зная, что позже возникнут проблемы с сиденьями, но ее протесты игнорируются. Вечеринка превращается в веселую смесь переставленных столов, стульев, тарелок, стаканов и еды. Однако, в конце концов, все работает, когда миссис Комфорт оказалась права.

Когда Шерил закончила читать рассказ, она спросила класс: «Что это была за миссис Хьюстон?Беспокоитесь о комфорте?

Николь сначала ответила: «Здесь не будет достаточно места, потому что, когда вы складываете столы вместе, вы теряете стулья», — сказала она.

«Что ты имеешь в виду?» — спросила Черил.

«Это как если вы сложите два стола вместе, вы потеряете места там, где они соприкасаются. Это трудно объяснить.» Николь нарисовала в воздухе два стола, указывая на стороны, где они встретились. Черил нарисовала на доске два квадрата, начертив стрелку в местах соприкосновения сторон. «Вы имеете в виду потерять стулья здесь?» она спросила.Николь кивнула. (См. Рисунок 1).

Выслушав идеи других студентов по поводу проблемы миссис Комфорт, Черил сказала: «Давайте использовать цветные плитки, чтобы изучить различные способы расставить всего четыре стола. Начнем всего с четырех столов ».

Черил дала классным указаниям по расстановке квадратных «столов». «Когда плитки соприкасаются, — сказала она, — они должны касаться всей стороны. Соприкосновение частей сторон или только углов — недопустимо ». Она продемонстрировала на диапроекторе.(См. Рисунок 2.)

Шерил также разместила плитки так, чтобы не следовать ее правилу, и попросила учеников объяснить, почему. (См. Рисунок 3.)

Затем она выполнила инструкции. «В своей группе поделитесь плитками, которые я положил на ваш стол, и найдите разные способы расставить четыре плитки. Обязательно следуй моему правилу ». Черил разложила около 70 плиток для каждой группы из четырех студентов.

Пока ученики работали, Шерил ходила по классу, наблюдая за учениками и отвечая на вопросы по мере необходимости.Когда у всех была возможность поработать над проблемой, она прервала студентов и попросила их внимания.

«Что вы сделали?» — спросила Черил. «Кто бы хотел описать расположение, чтобы я мог построить его из плитки наверху?»

«Можно провести прямую линию», — сообщил Брэндон.

«Как это?» — спросила Черил, складывая четыре плитки в прямоугольник размером 1 на 4. Брэндон кивнул.

«Сделайте квадрат со всеми четырьмя из них», — сказала Рахиль. Черил построила квадрат из четырех плиток.

«Я сделала тройку и одну», — сказала Николь.

«Что ты имеешь в виду?» — спросила Черил.

«Один маленький столик, как у Натана, — объяснила Николь, — а потом столик 1 на 3».

«Вы можете сделать четыре отдельных стола», — сказал Натан.

«Ты мог бы поставить Т», — сказал Зак. «Положите три в ряд и один под средним».

«Я тоже сделал это, но моя перевернутая», — сказал Эрик.

Черил построила аранжировку Эрика под руководством Зака ​​и указала классу, что когда вы можете перевернуть, повернуть или сдвинуть фигуру, чтобы она точно соответствовала другой фигуре, фигуры совпадают. «Мы будем считать конгруэнтные формы одинаковыми», — пояснила она.

Когда расстановки студентов заполнили накладные расходы, Черил спросила: «Что, если бы мы использовали только отдельные прямоугольные столы, сделанные из четырех плиток? Какие формы мы должны удалить? »

«Я предложил четыре отдельные таблицы, — сказал Натан.

Рифка добавил: «И тот, который похож на букву Т.»

«Вы также должны снять мою», — сказала Николь. «Это не один прямоугольник».

Когда Малкия предложила убрать квадрат, разгорелся разговор.Некоторые ученики помнили, что квадрат есть прямоугольник, а другие — нет. Черил пояснила: «Квадрат — это особый вид прямоугольника, потому что все его стороны имеют одинаковую длину. Но, как и прямоугольник, квадрат по-прежнему имеет четыре угла в 90 градусов, а противоположные стороны параллельны ».

Шерил хотела убедиться, что у учеников есть способ пометить построенные ими прямоугольники. Она нарисовала на доске прямоугольник размером 1 на 4. «Я могу записать это двумя способами», — сказала она и записала под прямоугольником:

Затем Черил нарисовала квадрат 2 на 2 и пометила его.

Черил указала на квадратный стол 2 на 2 и спросила: «Если один человек сидит сбоку от небольшого квадратного стола, и никто не сидит в углах или в щелях между столами, сколько людей может сидеть здесь? ”

«Легко, восемь», — ответила Николь. «Просто сосчитайте по два человека с каждой стороны, умноженные на четыре».

«Когда вы подсчитываете количество людей, которые могут сесть за стол, вы фактически находите его периметр», — объяснила Шерил. «Это потому, что каждый человек сидит по одну сторону от меньшего квадрата и занимает одну единицу длины.Таким образом, периметр прямоугольника 2 на 2 составляет 8 единиц ».

«Периметр стола размером 1 на 4 равен 10», — заметил Эрик.

Шерил попросила остальных проверить показания Эрика, а также изобразить периметр нескольких других прямоугольников. Затем она представила еще одну проблему.

— Давайте вспомним вечеринку мистера и миссис Комфорт, — начала Черил. «Предположим, миссис Комфорт решила, что все 32 человека должны сесть за один большой массивный прямоугольный стол, и она хотела выяснить, сколько маленьких квадратных столов можно арендовать.Посмотрим, сможете ли вы найти все возможные прямоугольные столы разных размеров и форм, на которых могут разместиться 32 человека ».

«Должен ли каждый стол соответствовать ровно 32?» JT хотел знать.

«Да», — ответила Черил.

«Сколько плиток мы используем?» — спросила Малкия.

«Это будет зависеть от столов, которые вы построите», — ответила Черил.

«Можем ли мы работать с партнером?» — спросила Николь.

«Да, — ответила Черил, — но веди свои записи».

Больше вопросов не было.Черил дала последнее указание. «Используйте плитки, но нарисуйте свои решения на листе бумаги. Обязательно запишите размеры каждого стола и количество людей, за которыми он может разместиться ».

Наблюдая за детьми

Остаток урока Черил наблюдала за учениками за работой и при необходимости оказывала помощь.

Она наблюдала, как Кэтлин составляла прямоугольник 16 на 2. «Хм, — громко сказала Кэтлин, работая, — давайте посмотрим, 32 человека. Это должно сработать, потому что 16 умножить на 2 равно 32.Кэтлин сосредоточенно нахмурилась, считая стороны квадратов. Затем она с удивлением посмотрела на Шерил.

«Я не понимаю», — сказала она. «Я насчитал 36 мест. Но в этом нет смысла, потому что 16 умножить на 2 равно 32. Может, я неправильно посчитал ». Она снова сосчитала стороны.

«Еще 36. Ага». Кэтлин пожала плечами, перемешала 16 плиток обратно в стопку в центре стола и начала строить еще один прямоугольник.

«Что ты делаешь?» — спросила ее Шерил.

«Ну, я, должно быть, напортачила, потому что первая, которую я сделал, не сработала, поэтому я попробую что-нибудь еще», — ответила Кэтлин.

«Что ты собираешься попробовать?» — спросила Черил.

«Не знаю. Я просто собираюсь поваляться и посмотреть, что будет, — сказала она.

Черил наблюдала, как Кэтлин начала складывать плитки в длинный ряд шириной в один квадрат. Она продолжала считать стороны одну за другой каждый раз, когда добавляла новую плитку. Наконец она улыбнулась.

«Это работает! Этот вмещает 32 человека. Это 1 на 15. А теперь записать. Кэтлин начала рисовать прямоугольник на бумаге.

Алекс сидел напротив Кэтлин.«Я тоже нашел это», — сказал он. «Теперь я пробую что-то вдвое».

«О», — ответила Кэтлин и начала строить прямоугольник шириной четыре квадрата.

Натан подошел к Шерил. «Я не рисую на бумаге прямоугольники, как все, — сказал он. «Вместо этого я решил использовать Xs. Но Люк сказал мне, что это неправильно. Разве я не могу нарисовать крестики, если захочу? » Натан показал Шерил свою газету.

Черил попросила Натана объяснить, что он сделал. Удовлетворенная тем, что он понимает, что делает, Шерил сказала: «То, что вы сделали, имеет для меня смысл. ”

Натан вернулся к Люку. «Я сказал вам, что она сказала, что все в порядке», — сказал он.

Черил пошла по классу. К концу периода она увидела, что все студенты нашли некоторые прямоугольники, а некоторые нашли их все. Она попросила детей убрать плитку и собрала их бумаги. Шерил планировала продолжить урок на следующий день.

На следующий день

На следующее утро Черил дала классу возможность подумать над расширением. «Какой самый дешевый способ разместить 32 человека за одним большим прямоугольным столом? А какой самый дорогой способ? Чтобы ответить, некоторым из вас потребуется найти больше расстановок столов.”

Примерно через 10 минут Черил прервала учеников, чтобы начать обсуждение в классе. «Какие варианты есть у Comforts для размещения всех 32 человек за одним столом?» — спросила Черил. Руки студентов вскинулись.

«У них будет группа, точнее восемь», — сказала Рэйчел. Большинство студентов кивнули или пробормотали свое согласие.

«Может ли кто-нибудь описать размеры таблиц, которые будут работать?» — спросила Черил. «Я запишу их на доске».

Эрик сообщил: «Один раз-15, 2-раз-14, 3-раз-13, 4-раз-12, 5-раз-11, 6-раз-10, 7-раз-9 и-8-раз-8. .После того, как Шерил записала размеры, она вернулась и зарисовала каждый соответствующий прямоугольник.

«О, я вижу закономерность!» — сказала Анферни. «Могу я показать это?» Черил кивнула, и Анферни подошла к доске. Она сказала, указывая: «Сверху вниз идет 1, затем 2, затем 3, затем 4, затем 5 и так далее, вплоть до 8».

«А другая сторона идет вниз», — добавила Анн Мария.

«О да, я этого не видела», — сказал Анферни. «Да, 15, 14, 13, и так далее». Он снова сел.

«Разве список не должен продолжаться?» — спросила Черил.»Разве не должен быть прямоугольник 9 на 7?» (См. Рисунок 6.)

«Он у тебя уже есть», — сказала Малкия.

«Да, 9 на 7 и 7 на 9 — одно и то же, — добавила Николь.

«Все числа после 8-умножить на 8 — это повторения, — сказала Кирстен, — поэтому вы не можете их сосчитать».

«Давайте подумаем, сколько квадратных столов придется арендовать мистеру и миссис Комфорт на каждый большой прямоугольник», — сказала Шерил. «Сколько им придется арендовать за стол размером 15 на 1?»

«Пятнадцать.Легко, — ответили несколько студентов.

«А как насчет 2х14?» Черил продолжила. «Сколько столов придется арендовать Комфортс для такой договоренности?»

«Двадцать восемь», — звали многие дети.

«А как насчет расположения 3х13?» — спросила Черил. Класс быстро понял, чем занимается Шерил.

«Вы просто размножаетесь», — сказала Рифка. «Просто сделай это для всех — 28, 39, 48, 55, 60, 63 и 64».

«Что вы заметили в форме столов?» Затем спросила Черил.

Малкия сказала: «Размер 8 на 8 — квадрат, а все остальные — прямоугольники».

«Но ведь размер 8 на 8 тоже прямоугольник, помнишь?» Эрин напомнила Малкию.

«Смотрите, — сказал Брэндон. «Если они устроят длинный узкий прямоугольник на 32 человека, то они смогут сделать это всего с 15 столами. Так дешевле всего.

«И они также сэкономили бы место, поскольку 1-умноженный на 15 занимает меньше всего места», — добавил Шарнет.

«Но вам понадобится длинная комната, — добавила Николь, — как для королевского банкета.”

Затем Шерил остановила беседу и дала письменное задание оценить мышление каждого ученика. Она написала на доске три вопроса, чтобы дети могли ответить:

1. Какие шаблоны вам пригодились в работе?
2. Какие расстановки столов наиболее и наименее экономичны?
3. Что вы заметили в областях и периметрах выполненных вами мероприятий?

Учащиеся работали над заданием на остальной класс.

Учебный план начальной математики | Учебная программа по математике для 1-го класса | Учебная программа по математике для 2 класса

2 класс

Обзор

Ученики уделяют особое внимание четырем важнейшим областям, указанным в Общих государственных стандартах математики для второго класса:

• Расширение понимания системы десятичных чисел
• Развитие навыков сложения и вычитания
• Использование стандартных единиц линейного измерения
• Описание и анализ форм

Первый блок повторяет и расширяет сложение и вычитание в пределах 20, помогая обеспечить, чтобы второклассники работали с пониманием и беглостью фактов с начала учебного года.

Блоки 2, 3, 5 и части блока 7 посвящены разряду и сложению и вычитанию многозначных чисел. Во время этих блоков учащиеся учатся считать на пять, десятки и сотни, десятки и единицы; читать, писать и сравнивать числа с 1000; и развивать свободное владение сложением и вычитанием до 100, решая и ставя самые разные задачи со словами. Позднее в этом году дети используют конкретные модели и наброски, а также стратегии, основанные на разряде, свойствах операций и соотношении между сложением и вычитанием, чтобы складывать и вычитать до 1000.

Раздел 6 вращается вокруг геометрии, построения основ для понимания площади, объема, конгруэнтности, сходства и симметрии, когда учащиеся исследуют, описывают, строят, рисуют, комбинируют, разлагают и анализируют двух- и трехмерные формы.

Раздел 4 и первая часть Раздела 7 посвящены линейным измерениям, поскольку учащиеся конструируют свои собственные линейки; оценивать и измерять в дюймах, футах, ярдах, сантиметрах и метрах; и решать задачи, связанные с сложением, вычитанием и сравнением длин.

Модуль 8 пересматривает линейные измерения в контексте науки и техники, поскольку студенты изготавливают и тестируют картонные пандусы различных типов, чтобы исследовать некоторые факторы, которые заставляют шарики катиться все дальше и быстрее. В процессе они генерируют данные, многократно измеряя расстояния между мраморными роликами, объединяют свои данные и вводят их на линейных графиках, чтобы лучше видеть, понимать и анализировать, как манипулирование различными переменными влияет на результаты.

Структура содержимого

Блок 1 Изложение фактов

• Сортировка и построение графиков
• Числовые факты с помощью числовой стойки
• Введение в стратегии сложения и вычитания
• Свободное владение с добавлением фактов к двадцати

Единица 2-местная стоимость и измерение с бобовыми стеблями Джека

• Подсчет и моделирование двух- и трехзначных чисел
• Измерение гигантских бобов Джека с помощью десятков
• Добавление открытой числовой строки
• Мыслить двоими

Блок 3 Сложение и вычитание в пределах ста

Блок 4 Измерение

• дюймов и футов
• дюймов, футов и ярдов
• Пропорции и доли с гигантом
• Мыслить тройками

Разрядная стоимость единицы 5 до одной тысячи и

Блок 6 Геометрия

• Атрибуты двумерных форм
• Исследование области и массивов
• Составление и разложение фигур для пэчворка
• Фракции пэчворк

Блок 7 Измерение, дроби и многозначные вычисления с голодными муравьями

Блок 8 Измерение, данные и многозначные вычисления с мраморными валками

Номер угол

• Сетка календаря
• Сборщик календарей
• Ежедневный прямоугольник
• Беглость вычислений
• Номерная строка
Подробнее о Number Corner

Весь Интернет зашел в тупик из-за математической задачи этого первоклассника

С тех пор, как я учился в школе, скажем так, , много лет назад, способ преподавания математики резко изменился.Не знаю, почему. Похоже, они поняли, что есть лучший способ привить детям математические принципы, чем опрашивать их по их таблицам умножения, пока они не выучат их наизусть.

Продолжение статьи под рекламой

Но поскольку математика сейчас преподается по-другому, или, возможно, потому что учителя математики не умеют писать задачи со словами, я чувствую, что появляется все больше и больше математических задач школьного уровня, которые ставят в тупик не только детей, но и родители тоже. Возьмем, к примеру, последнюю вирусную математическую задачу, которая входила в рабочую тетрадь первоклассника.

Мой друг только что прислал мне это фото из учебника по математике своего первоклассника, и ни он, ни я не имеем ни малейшего представления о том, что ребенок должен делать здесь pic.twitter.com/Xz2wP6P9j1

— Хелен Р. (@hels) 6 октября, 2020

Продолжение статьи под рекламным объявлением

Друг Хелен — выпускник Массачусетского технологического института, как она позже выясняет, не мог, хоть убей, понять, что означает эта проблема. И Хелен тоже. Поэтому она поделилась этим с Twitterverse, чтобы узнать, есть ли у тех, кто есть в Интернете, какие-нибудь яркие идеи.

У меня … очень много вопросов по этой проблеме. Прежде всего, что такое «математический рисунок»? Это не тот термин, который я слышал раньше за всю свою жизнь. Похоже, что сначала нужно уравнять картинки, используя «математические рисунки», а затем соединить их знаком равенства, чтобы составить «числовые предложения».

Продолжение статьи ниже рекламного объявления

Якобы первое и второе изображения должны совпадать настолько, чтобы между ними был поставлен знак равенства. Но кроме этого, я просто не понимаю.И люди Твиттера тоже.

«Ты … должен рисовать точно такие же фрукты во второй корзине ?????» спрашивает один человек. «Чтобы сделать их« равными »????? Я чувствую, что это психологический эксперимент, а не математическая задача». Я согласен с оценкой этого человека, хотя не думаю, что она использовала достаточно вопросительных знаков.

Продолжение статьи ниже рекламы

вычтите фрукты, чтобы показать, как вы попадаете из полной корзины в пустую, цель состоит в том, чтобы укрепить связь между абстрактной математикой и физическим миром

— Бен (@BenMahtin) 6 октября, 2020

Бен казался уверенным в своем ответе, приведенном выше, но для большинства других людей он не имел особого смысла.«Что?» — ответила Хелен на его теорию. Проблема в рисовании. Вы не можете вынуть фрукт из корзины, потому что он уже там. Чернилами. На бумаге.

Продолжение статьи под рекламой

В обновлении своего исходного твита Хелен написала: «Хорошо, после глубокого чтения мы склоняемся к идее, что каждый отдельный фрукт представляет собой один (1)« математический рисунок », поэтому рисуем пять фруктов будет «математические рисунки» множественного числа «. Это … шаг. Но это все еще кажется немного не таким.

Если один фрукт — это математический рисунок, и вам нужно уравнять оба рисунка с математическими рисунками, вы просто должны … точно скопировать рисунок? Я не уверен, чему это учит.

Продолжение статьи под рекламным объявлением

Но кто-то другой столкнулся с подобной проблемой и поделился ею с объяснением, которое казалось наиболее реалистичным.

Продолжение статьи под рекламным объявлением

Так что, возможно, вам нужно нарисовать одинаковое количество фруктов, но они могут быть разных видов и сгруппированы по-разному.Вы знаете, что действительно помогло бы с этим листом? Пример задачи, где вам показали, как это сделать! Потому что то, что Кейт показывает и описывает, кажется, имеет смысл!

Преподаватель математики из колледжа поделился своими мыслями и немного рассказал о вероятной цели задания: «Преподаватель математики из колледжа. Моя мысль: убедитесь, что в обеих корзинах есть одинаковое количество фруктов. добавив три апельсина и два банана справа, но вы также можете добавить ЧЕТЫРЕ апельсина и два банана, а затем еще один апельсин слева!

Продолжение статьи под рекламой

«У меня такое чувство, что здесь важно заставить учеников думать о знаке ‘=’ не только как о значении ‘ответ есть’ — это то, что заставляет детей думать, что такие утверждения, как 7 = 2 + 5 или 6 = 6, неверны — а скорее означают, что вещи с обеих сторон равны * друг другу.* «

С таким объяснением это имеет смысл. Я понимаю, что вы хотите научить детей тому, что» = «не просто означает» вот ответ «, а что две стороны уравнения на самом деле равны Однако эта проблема сформулирована крайне неудачно.

15 способов интегрировать математику и искусство в начальных классах

Математика и искусство идут рука об руку, как арахисовое масло и желе! Просто нужно знать, где искать, и быть мало творческого в создании уроков, значимых для обеих областей содержания.Вы никогда не захотите жертвовать навыками и процессами в любой области при создании интеграции искусств или урока STEAM.

Хотя на первый взгляд объединение математики и искусства может показаться попыткой смешать масло и воду, существует множество полезных способов объединения этих двух предметов. Дети могут использовать цвета и формы, чтобы улучшить свое понимание математики. Они также могут применять теорию математики к изображениям и объектам. Если думать о математике не только с точки зрения арифметики, но также с точки зрения решения задач, геометрии и визуализации, идеи начнут воплощаться в интегрированные планы уроков.Вот список художественных проектов, которые достоверно связаны с математическими идеями и концепциями.

15 идей математического художественного проекта

1. Изучите симметрию через гобелены

Радиальная симметрия присутствует везде в старых гобеленах, особенно в исламском искусстве. Просмотрите некоторые из этих примеров гобеленов и определите представленную симметрию. Затем попросите учащихся создать свой собственный план проекта радиальной симметрии, используя числовые правила. Назначьте разным учащимся разные числовые правила (+ 3, + 4, + 5).Затем учащиеся могут использовать круг из 10 точек, линейку или линейку и карандаш, чтобы создавать свои собственные рисунки фигур, используя свои правила чисел.

2. Задание на определение времени

Учащиеся рисуют часы и раскрашивают их двумя кружками по окружности часов. Сделайте внутренний круг синим. Это соответствует часам на часах. Сделайте внешний круг красным. Это соответствует минутам. Не пишите числами. Просто напишите демаркационные линии вместо минутных стрелок.Постройте часовую и минутную стрелки, раскрасьте их в соответствующие синий и красный цвета и прикрепите их к центральным часам, чтобы они могли свободно вращаться. Этот урок помогает студентам визуализировать воображаемые числа на часах. Спросите учащихся о том, какие числа соответствуют расположению стрелок на часах, и попросите их сосчитать по 5 до 60.

3. Вырежьте геометрические фигуры разной формы для коллажей

Создайте коллаж из папиросной бумаги абстрактное искусство с использованием разных размеров одной и той же формы.Попросите учащихся вырезать все прямоугольники или квадраты разных размеров. Затем они могут создать коллаж из одной из фигур. После склеивания попросите учащихся измерить каждую из фигур на бумаге, которые расположены рядом или наложены друг на друга (соединенные части). Для каждой соединенной формы попросите учащихся приклеить этикетку, соединяющую две части, и записать разницу между длинами обеих соединенных фигур.

4. Составные фигуры

Учащиеся могут создавать составные фигуры, используя геометрические формы в стиле средневековых витражей.Используя карандаши и макулатуру, создайте треугольник, квадрат или прямоугольник, используя только меньшие треугольники, прямоугольники и квадраты. Используя черный маркер, нарисуйте большую геометрическую фигуру посередине страницы. Затем нарисуйте меньшие геометрические фигуры, которые составляют или составляют эту большую форму. Раскрасьте фигуры маркерами разного цвета.

5. Графическое изображение

Ссылайтесь на работы Мондриана и попросите учащихся создать свои собственные сеточные работы. Укажите координаты и попросите учащихся нанести их на сетку.Затем раскрасьте каждый раздел в зависимости от того, где находятся координаты. Например, если координаты попадают в правый верхний квадрант, ученики могут выбрать теплый цвет.

6. Выполните измерения

Подчеркните измерения, которые учащиеся выполняют с помощью линейок для измерения сеток или вырезают рамки для художественных проектов. Кроме того, учащиеся могут брать линейки и измерять различные предметы в классе, такие как бумага, мелки, классная доска, книги, кисти и стол.Студенты также могут сортировать свои художественные материалы по размеру.

7. Определите соотношение для смешивания красок

При смешивании и смешивании цветов научите учащихся соотношениям, используемым при смешивании, например «2 части синего + одна часть зеленого» и «4 части белого + 1 часть серого».

8. От части к целому со струнным искусством

Изучите некоторые примеры современного струнного искусства. Предложите учащимся обсудить, что они замечают в произведении искусства и художественном процессе. Раздайте учащимся квадратный кусок картона, несколько веревок разного цвета и ножницы.Студенты должны сделать надрезы длиной в дюйм по периметру пластины с равным интервалом (им нужно будет это измерить). Затем протяните один кусок пряжи от одного надреза к другому на другой стороне доски и завяжите его сзади, пока пряжа не станет натянутой. Это числовая линия. Обозначьте одну сторону как 0, а другую как 100. Затем попросите учащихся определить, где 25 будет на их числовой строке. Попросите их продеть еще один кусок пряжи вдоль этого места и прикрепить на концах выемки. Обозначьте каждый конец как «25».Продолжайте через различные интервалы через числовую линию. Затем положите кусок оловянной фольги поперек доски и натяните нить и раскрасьте естественные пересечения.

9. Решите неизвестное с помощью оп-арта

Изучите формы оп-арта и то, как они используются для создания оптических иллюзий. Затем раздайте всем учащимся листы цветной бумаги и обрывки бумажных лент. Дайте каждому ученику наполовину заполненное уравнение, например: 8 x? = 48. Студенты должны выяснить, какое число использовать для того, сколько всего блоков им нужно создать, а также сколько строк и сколько столбцов им нужно будет создать.Затем следуйте этим инструкциям по созданию плетения из бумаги в стиле оп-арт.

10. Создайте фрагмент фрактального искусства

Предложите учащимся рассмотреть примеры фракталов и фрактального искусства. Изучите идею о том, что фрактал — это меньшая часть всего оригинала. Например, вы можете начать с треугольника, а затем
нарисовать перевернутый треугольник внутри оригинала. Это будет четверть исходного треугольника, но все той же формы. Затем вы можете создать еще один треугольник внутри вашего 2-го треугольника, который будет еще на 1/4 (или 1/8 от оригинала).Создайте кусок фрактального искусства, выбрав форму, а затем измерив фракталы той же формы на других листах бумаги и вырезав их. Обозначьте каждый фрактал как соответствующую фракцию исходной формы. Затем создайте произведение искусства, используя исходную форму и ее фракталы.

Фрактал слов Фибоначчи. Автор Самуэль Монье.

11. Мозаика в виде массива

Создайте мозаику из прямоугольных массивов до 100 штук. Дайте каждому ученику однозначное число и лист сетки.Попросите их заштриховать массив на своей сетке, который будет представлять это число, умноженное на 10. Например, если число 6, они могут заполнить 60 блоков. Спросите студентов, как они использовали свое понимание массивов, чтобы помочь им в этом. Затем
ученика могут набросать дизайн, используя только закрашенные блоки. Наконец, они могут создавать мозаику из плиток на основе своих рисунков массива сетки. Они могут использовать столько плиток, сколько сумма их уравнения умножения, и каждая плитка может содержать только один предмет и / или цвет.

12. Мозаика, вдохновленная Эшером

Раздайте каждому ученику разные печатные копии Эшера. Попросите их измерить, как раньше, и определить, сколько квадратных единиц на их отпечатке. Затем создайте собственный мозаичный принт в стиле Эшера. Выберите объект для облицовки плиткой. Затем измерьте его квадратную единицу. Создайте плитку, не содержащую промежутков и использующую цвет для контрастирования узора.

13. 100-дневная мозаика из плитки аборигенов

Совместите празднование 100-летия школьного праздника с изучением десятой основы.Создайте мозаику из плитки аборигенов из 100 точек. Раздайте каждому ученику по одной плитке. Студенты изучают искусство аборигенов, а затем разрабатывают изображение, которое они хотели бы создать (например, черепаху или реку). Разделите картинку на 10 равных частей. Решите, какую часть большого искусства представляет каждая плитка. Студенты должны создать эту часть художественного произведения на своей собственной плитке. Каждая плитка содержит всего 10 точек. Объедините 10 плиток, чтобы создать мозаику.

14. Интерпретируйте умножение как масштабирование с помощью теней

Создайте трассировку тени.Поместите объект (например, блок Lego) на лист бумаги, а затем посветите на него светом, чтобы он создавал тень. Сравните размер тени с размером объекта (он больше исходного объекта). Затем измерьте размер тени по длине и ширине. Учитель даст каждому ученику дробь больше 1, например 20/5 или 16/4. Учащемуся нужно будет создать тень от трассировки тени, которая будет представлять их исходную длину и ширину x полученную долю.Например, если размер моей тени составлял 3 дюйма x 1 дюйм, и я получил дробь 20/5, моя новая тень моего рисунка тени должна быть 3 дюйма x 20/5 (12 дюймов) на 1 дюйм x 20/5 ( 4 ”).

15. Классифицируйте двумерные фигуры с помощью Кандинского

Используя работы Кандинского, измерьте различные формы, которые он использовал в своей работе. Сравните все атрибуты и сделайте выводы о 2D-фигурах в каждой подкатегории, представленной в работе. Затем создайте произведение искусства в стиле Кандинского, которое поддерживает эти отличительные атрибуты, и пометьте каждую область произведения назначенными атрибутами.

Василий Кандинский, «Желто-красно-синий» (1925), холст, масло (Национальный музей современного искусства, Центр Жоржа Помпиду, Париж, через WikiArt)

Есть много забавных и познавательных способов объединить математику и искусство для учеников начальной школы. Если вы ищете способ вдохнуть новую жизнь в свой класс, интеграция искусств — прекрасный способ заинтересовать учеников и пробудить в них собственное творчество!

Дополнительные источники:

Math Activities Home

ArtClass Curator’s 13 художественных и математических проектов

6 способов соединить математику и искусство в начальном классе

« Создание математических связей. »Одна эта фраза покалывает многих учителей изобразительного искусства. Сочетание красок, страсти и азарта художественного класса с черно-белым миром математики может привести всех нас в замешательство.

Такая реакция объяснима, учитывая, что многие учителя рисования выбрали искусство вместо математики не просто так. Тем не менее, связи между двумя предметами неопровержимы и неотъемлемы. Одно без другого не существует. Фактически, при небольшом планировании связи возможны в любом уроке или проекте, особенно на начальном уровне.

Вот 6 способов, не вызывающих беспокойства, связать математику и искусство в вашем классе.

1. Выведите правителей

Не оставляйте линейку знакомств с классными учителями. Линейки — это повседневный инструмент художников. Покажите своим ученикам, как вы используете линейки. Попросите их сделать соответствующие возрасту измерения и порезаться. Это может быть дополнительный шаг или немного больше времени, однако измерение и резка — важный навык. Это улучшит их навыки пространственного мышления и приведет к более осознанному творческому выбору.

2. Введение в архитектуру

Архитектура — это одна большая творческая математическая головоломка. Художники веками создавали конструкции. Создавая свой собственный стиль в городах, культовых сооружениях и правительственных структурах, архитекторы создали не только здания, но и произведения искусства. Поделитесь этими подвигами человеческой изобретательности со своими учениками. Работы таких художников, как Антони Гауди, Фрэнк Ллойд Райт и мастера Микеланджело, являются основными примерами магии математики и искусства.

В результате каждый раз, когда учащиеся строят что-либо или собирают трехмерную скульптуру, они используют математические и творческие навыки. Поощряйте учеников, которые не любят математику, напоминая им, хороши ли они в строительстве; они также могут преуспеть в академической математике. Сделайте для них связь. Вы можете видеть, как вращаются их мозговые колеса, когда они принимают решение о том, куда положить части или элементы. Используйте эту статью как трамплин для примеров. Или создайте архитектурный центр как постоянную часть вашего класса.Напоследок разработать проект здания в стиле известного архитектора.

3. Используйте математический словарь и язык

Слова имеют значение, а математика — больше, чем числа. Язык, на котором вы разговариваете со своими учениками, может соединить искусство и математику без каких-либо специальных материалов или проектов. Скорее всего, в вашем округе есть стандарты словарного запаса по математике по классам. Исследуйте концепции и термины, которые ваши ученики изучают по математике, вместе с их классными учителями. Вот полезный пример.Затем убедитесь, что вы используете одни и те же слова, когда инструктируете студентов и говорите об их произведениях.

4. Примеры обмена

Покажите своим ученикам, сколько математики вы используете в качестве учителя. Вы можете быть приятно удивлены их любопытством. Разбейте для них свой бюджет на материалы. Сколько вы тратите на одного студента в год? Расскажите им, сколько глины вы планируете и покупаете в учебном году и почему. Покажите им, какое соотношение воды и муки вы используете для изготовления папье-маше. Опишите им, сколько минут творческого времени они имеют в учебном году по сравнению с переменой.Используйте ежедневную математику в качестве инструмента защиты их художественного образования!

5. Выберите художников, которые используют математику

Используйте других визуальных художников как блестящие примеры творческих и математических связей. Очевидный архетип математического и творческого гения Леонардо Да Винчи — отличное место для начала. Выделите его летающие изобретения и его любопытную природу. Он был очарован искусством И математикой.

Каждый раз, когда вы обсуждаете узор, форму, форму, симметрию и архитектуру, показывайте пример М.Точная, головоломная работа К. Эшера. Наконец, существует множество современных художников, которые используют математику для реализации своих творческих увлечений. Например, Вирсавия Гроссман — первопроходец. Она использует искусство и трехмерные принтеры для создания уникальных скульптур, которых раньше не было. Кристин Фарр — еще одна интересная художница.

6. Продолжайте говорить о форме и форме

Студенты начального уровня (и выше) постоянно развивают свой пространственный интеллект.Каждый день небольшой урок геометрии. Пока ученики рисуют, вырезают, раскрашивают, раскрашивают, конструируют, формируют и лепят формы, они изучают пространственные отношения. Когда учащиеся могут визуализировать формы «мысленным взором», у них появляется больше свободы в работе с произведениями искусства и другими предметами. Короче говоря, продолжайте в том же духе работать со своими учениками и формой. Он уже приносит огромную пользу математическим связям.

Стереотипно, те, кто занимается изобразительным искусством, не являются математиками.На самом деле, многие преподаватели искусства обеспокоены этим предметом. (Мы могли бы даже избежать этого больше, чем просто блеска.) Но на самом деле вы используете математику больше, чем думаете. Каждый раз, когда вы управляете принадлежностями для рисования, организуете художественную выставку или просите ученика сложить лист бумаги пополам, вы включаете математику. Вуаля! Более того, ваши ученики не должны этого делать только потому, что вы можете чувствовать себя неловко, когда дело касается математики.

Как вы устанавливаете математические связи в классе?

Любите ли вы математику или ненавидите ее? Почему?

.

No related posts.