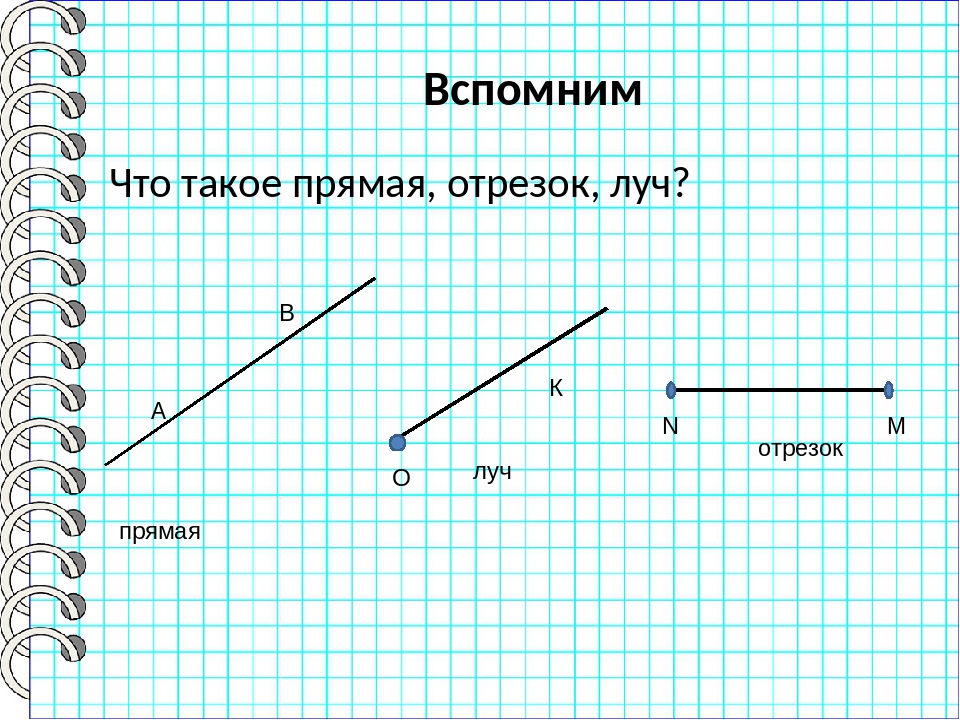
Точка, отрезок, луч, прямая — числовая прямая

 

Мы рассмотрим каждую из тем, а в конце будут даны тесты по темам.

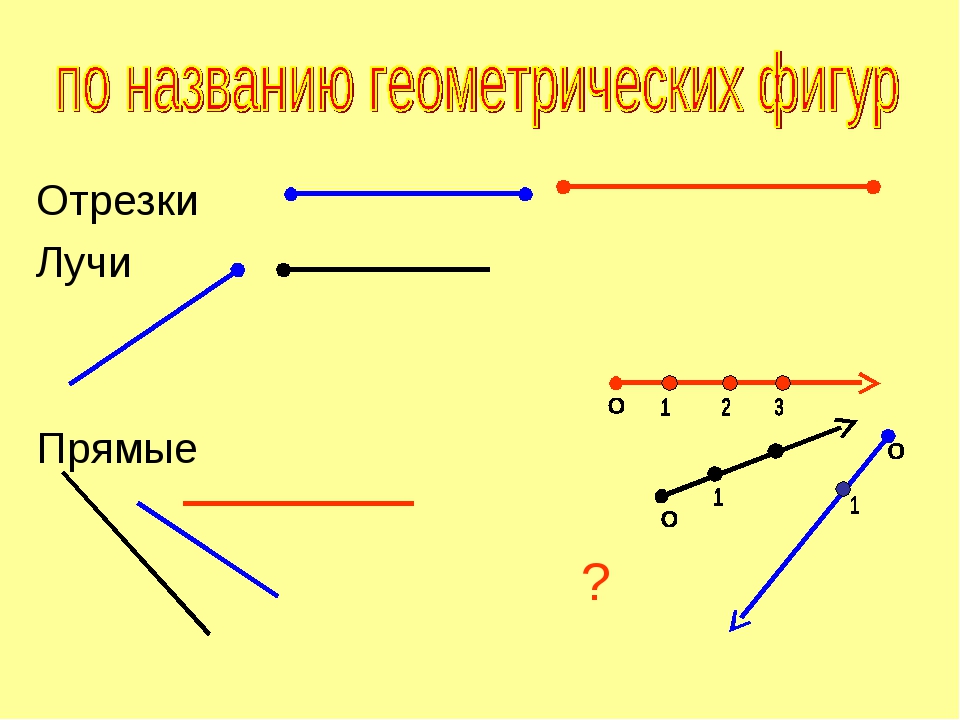
Точка в математике

Что такое точка в математике? Математическая точка не имеет размеров и обозначается заглавными латинскими буквами: A, B, C, D, F и т.д.

На рисунке можно видеть изображение точек A, B, C, D, F, E, M, T, S.

Отрезок в математике

Что такое отрезок в математике? На уроках математики можно услышать следующее объяснение: математический отрезок имеет длину и концы. Отрезок в математике — это совокупность всех точек, лежащих на прямой между концами отрезка. Концы отрезка — две граничные точки.

На рисунке мы видим следующее: отрезки [A;C],[C;D],[D;M],[M;F],[F;E] и [E;T], а также две точки B и S.

Прямая в математике

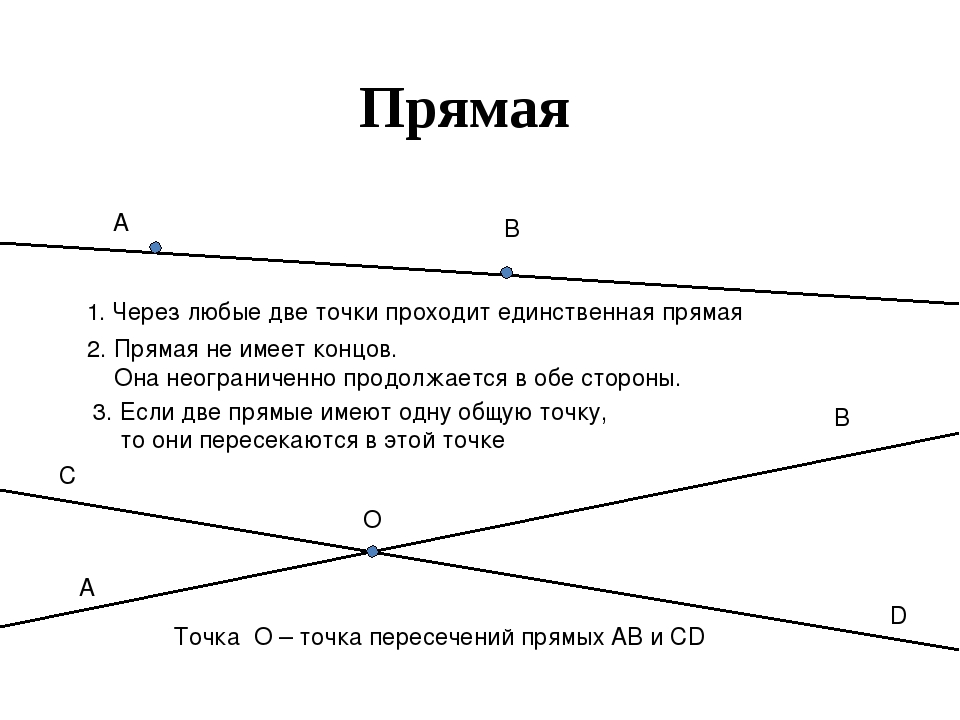
Что такое прямая в математике? Определение прямой в математике: прямая не имеет концов и может продолжаться в обе стороны до бесконечности. Прямая в математике обозначается двумя любыми точками прямой.

Для объяснения понятия прямой ученику можно сказать, что прямая — это отрезок, который не имеет двух концов.

На рисунке изображены две прямые: CD и EF.

Луч в математике

Что же такое луч? Определение луча в математике: луч — часть прямой, которая имеет начало и не имеет конца. В названии луча присутствуют две буквы, например, DC. Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.

На рисунке изображены лучи: DC, KC, EF, MT, MS. Лучи KC и KD — один луч, т.к. у них общее начало.

Числовая прямая в математике

Определение числовой прямой в математике: прямая, точки которой отмечают числа, называют числовой прямой.

На рисунке изображена числовая прямая, а также луч OD и ED

Нужна помощь в учебе?

Предыдущая тема: Сложение и вычитание дробей с одинаковыми знаменателями: ПРИМЕРЫ
Следующая тема:&nbsp&nbsp&nbspЧтение и запись больших натуральных чисел: разряды, классы + ПРИМЕР

5 класс — прямая, плоскость и луч в 5 классе, урок по математике, презентация

Дата публикации: 08 апреля 2017.

Что такое плоскость? Определение, примеры

Вокруг нас множество примеров плоскостей, например, оконное стекло

Поверхность озера

Лист бумаги

Но все плоскости, о которых мы говорим, имеют границы. В математике же плоскость бесконечна, то есть не имеет границ.

Запомните!
У математической плоскости НЕТ границ. Она простирается безгранично далеко во всех направлениях.

Прямая и её особенности

Нарисуем две точки А и В и соединим их. У нас получился отрезок АВ или ВА (кому как нравится). Продолжим отрезок АВ в оба направлениях. Мы получим прямую АВ или ВА. Запомните!
Прямая не имеет начала и конца. Только границы тетрадного листа или экрана заставляют нас рисовать прямую, как отрезок, на самом деле она бесконечна. Рисуя прямую, нужно мысленно продлевать ее бесконечно.
Принято говорить, что точки А и В лежат на прямой.

В математике прямую обозначают двумя способами.

1. «Прямая АВ»

2. «Прямая с» (маленькая буква)

Рассмотрим особенности прямой.
1. Если две прямые пересекаются в какой-либо точке, то эта точка является точкой пересечения прямых. В нашем примере прямые а и в пересекаются в точке О. Точка О делит каждую прямую на две части. 2. Через любые две точки можно провести одну единственную прямую.

Луч, Особенности

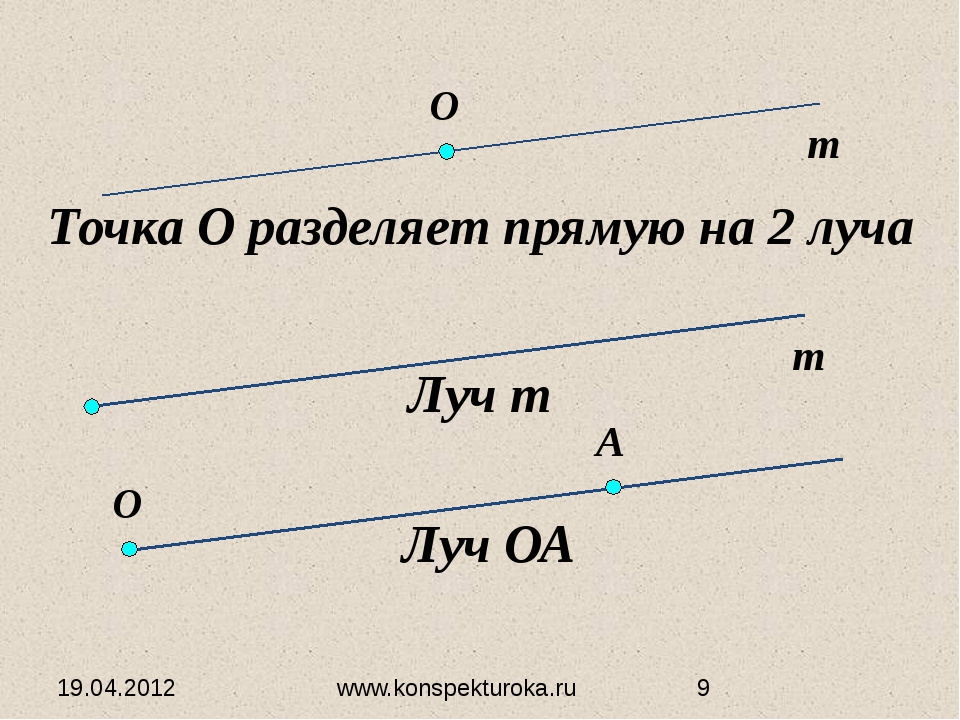
Если мы отметим на прямой точку, например, точку А, то эта точка разделит прямую на две части или на два луча.

Запомните!
Луч имеет начало, но не имеет конца. Это как луч света от какого-либо источника, который начинается от самого источник света (точки) и уходит в бесконечность.

В нашем примере точка О делит прямую АВ на два луча: луч ОА и луч ОВ. Соответственно, оба луча имеют начало в точке О, но не имеют конца. Они продолжаются до бесконечности.
Переставлять буквы в названии луча нельзя. Первой буквой всегда обозначается начало луча.

Плоскость. Прямая. Луч

На этом уроке мы познакомимся с понятиями «отрезок», «прямая», «луч» и «плоскость».

Рассмотрим расположение точек, отрезков, прямых и лучей в плоскости.

На прошлом уроке мы разобрались, как строить отрезок. Мы уже знаем, что отрезок – это прямая линия, ограниченная двумя точками.

Определение

Давайте начертим отрезок MN. Если продлить этот отрезок неограниченно за точку N, то мы получим новую фигуру, которая называется луч. У нас получился луч MN.

Точку М называют началом луча.

Если бы мы продлевали отрезок MN неограниченно за точку М, то у нас бы получился луч NМ, у которого точка N – начало луча.

Заметьте: обозначается луч большими заглавными буквами латинского алфавита, первой буквой записывают его начало, а затем букву, обозначающую какую-либо другую точку луча.

Обратите внимание, что луч имеет начало, но не имеет конца, т. е. он бесконечен в одну сторону.

Для того чтобы представить луч в окружающей среде, достаточно сфотографировать след от самолёта в безоблачном небе, где сам самолёт – это начальная точка, а след, оставленный на небе, – это прямая линия, которая бесконечна.

Либо солнечный луч, где начальная точка – это солнце, а конечной точки нет.

Определение

Если отрезок MN неограниченно продлевать в обе стороны – как за точку М, так и за точку N, то у нас получится фигура, которая называется прямой.

На рисунке у нас получилась прямая MN, также её можно назвать и прямая NМ. Как кому больше нравится!

Заметьте, что прямая не имеет ни начала, ни конца.

Любая точка прямой разделяет её на 2 луча.

В нашем случае точка О разделяет прямую MN на луч ОМ и луч ОN. Лучи, на которые точка разбивает прямую, называют

дополнительными друг другу.

Представление о прямой можно получить, если сложить лист бумаги (линия, которая получилась при сгибе, и будет прямой) или туго натянуть верёвку.

В математике прямая представляется идеально ровной и бесконечной в обе стороны.

Прямую можно обозначить двумя вариантами.

1-й вариант: двумя заглавными буквами латинского алфавита, например MN. В таком случае говорят: «Прямая MN».

2-й вариант: прямую обозначают одной малой буквой, например m, и говорят: «

Прямая m».

Давайте попробуем провести ещё одну прямую через эти же две точки.

У нас это не получится. Через любые две точки можно провести только одну прямую!

Точки, отрезки, лучи и прямые располагаются в плоскости. Примеры плоскостей в жизни мы встречаем каждый день. Представление о плоскости дают поверхности стола, оконного стекла или замёрзшего водоёма.

Только эти поверхности имеют границы, а плоскость в математике безгранична во всех направлениях.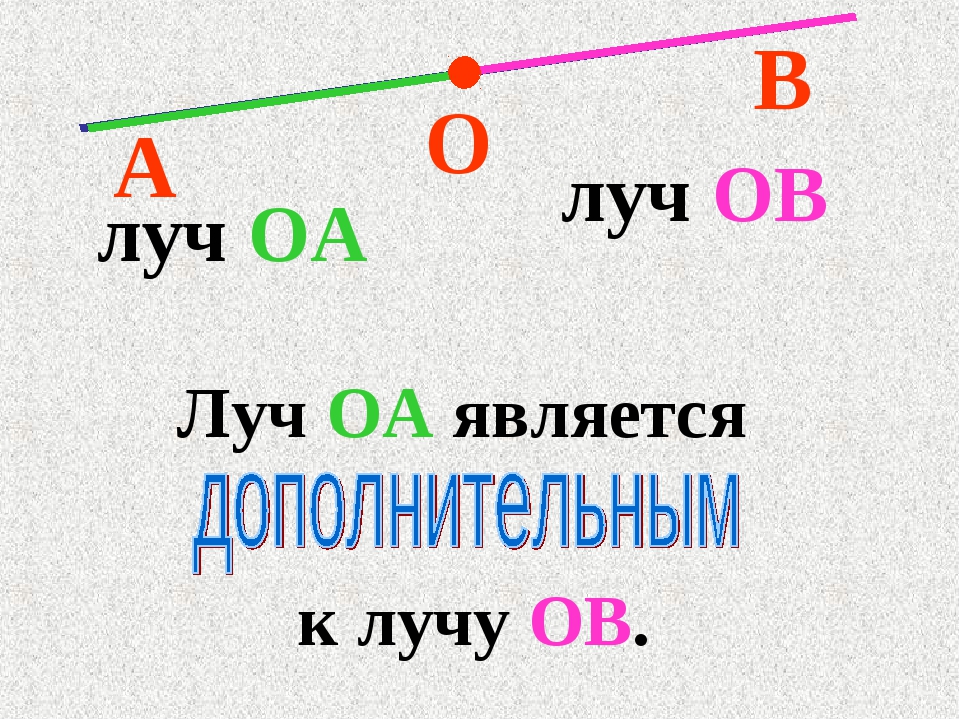 Мы рисуем фигуры на «кусках» плоскости, например в тетрадном листе или на школьной доске.

Теперь давайте рассмотрим расположение точек, отрезков, прямых и лучей в плоскости.

На рисунке изображены прямая EF и точки А, L, P и T. Точки А, E, F лежат на отрезке EF, а точки L, P, T не лежат на этом отрезке. Посмотрите, как это записывается.

Точки А, E, F лежат на луче EF, а точки А, E, F, Т лежат на луче FЕ. Посмотрите запись этих утверждений.

Точки А, E, F, Т лежат на прямой EF, а точки А, P, L – на прямой PL.

Обозначается это так:

Точка А лежит между точками Е и F. Точка L не лежит между точками Е и F, она находится вне отрезка EF. Точка Е лежит между точками А и Т, а точка А – между точками P и L.

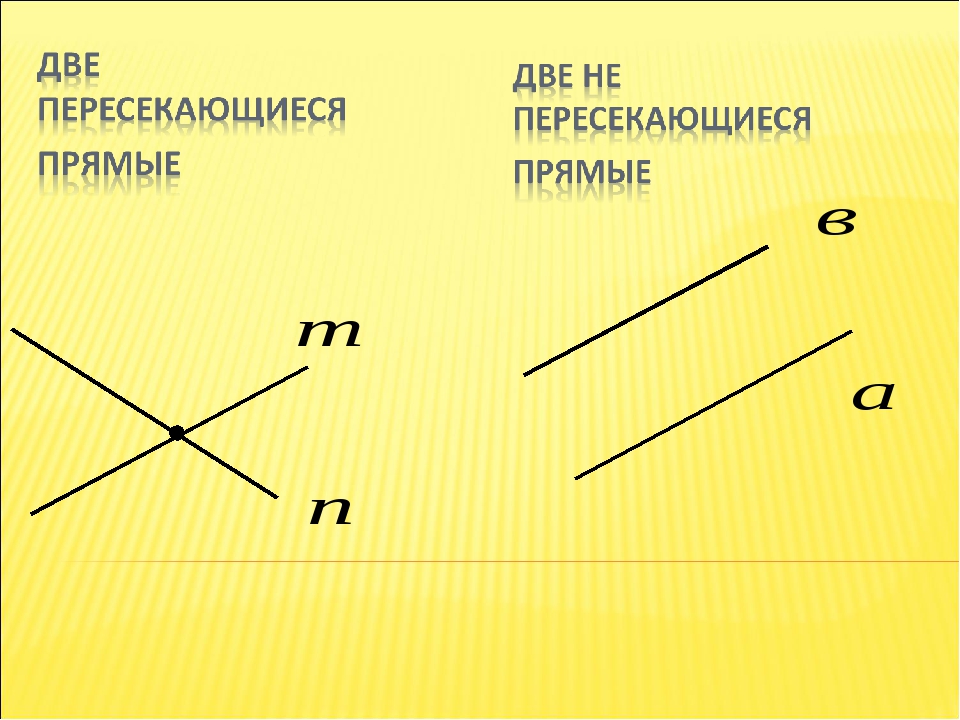
На следующем рисунке изображены прямая a и прямая b.

Если две прямые имеют одну общую точку, то говорят, что они пересекаются в этой точке. В нашем примере прямые а и b пересекаются в точке О. Точка О делит каждую прямую на две части. Точка О – точка пересечения прямых.

Посмотрите на взаимное расположение прямых m и n:

Они не имеют общих точек. Если прямые не имеют общих точек, то говорят, что они параллельны.

Запомните!

·                    Прямая бесконечна.

·                    Отрезок ограничен.

·                    Луч имеет начало, но не имеет конца.

·                    Плоскость бесконечна.

Итоги

Итак, на уроке мы с вами разобрались в отличиях понятий «отрезок», «прямая», «луч». Научились их строить. Узнали, что такое плоскость, а также рассмотрели расположение точек, отрезков, прямых и лучей в плоскости.

 

Математика 5 СР-04 Прямая. Луч. Шкала

СР-04 Прямая. Луч.  Шкала — это цитаты самостоятельных работ из пособия для учащихся «Математика 5 класс. Дидактические материалы / Мерзляк и др.», которое используется в комплекте с учебником «Математика 5 класс» авторов: Мерзляк и др. Цитаты из пособия указаны в учебных целях.

Математика 5 класс. Самостоятельная работа № 4

Прямая. Луч. Шкала. Координатный луч

Для увеличения изображения — нажмите на картинку !
Чтобы скачать работу — нажмите на правую кнопку мыши и выберите «Сохранить изображение как …»

---

 

Прямая. Луч. Шкала. Вариант 1

---

 

Прямая. Луч. Шкала. Вариант 2

---

Текстовые варианты самостоятельной

Смотреть Вариант 1

Вариант 1.

19. Пересекаются ли изображённые на рисунке 4:
1) прямая MN и отрезок AR;
2) луч ОТ и отрезок AR;
3) луч ОТ и прямая MN7

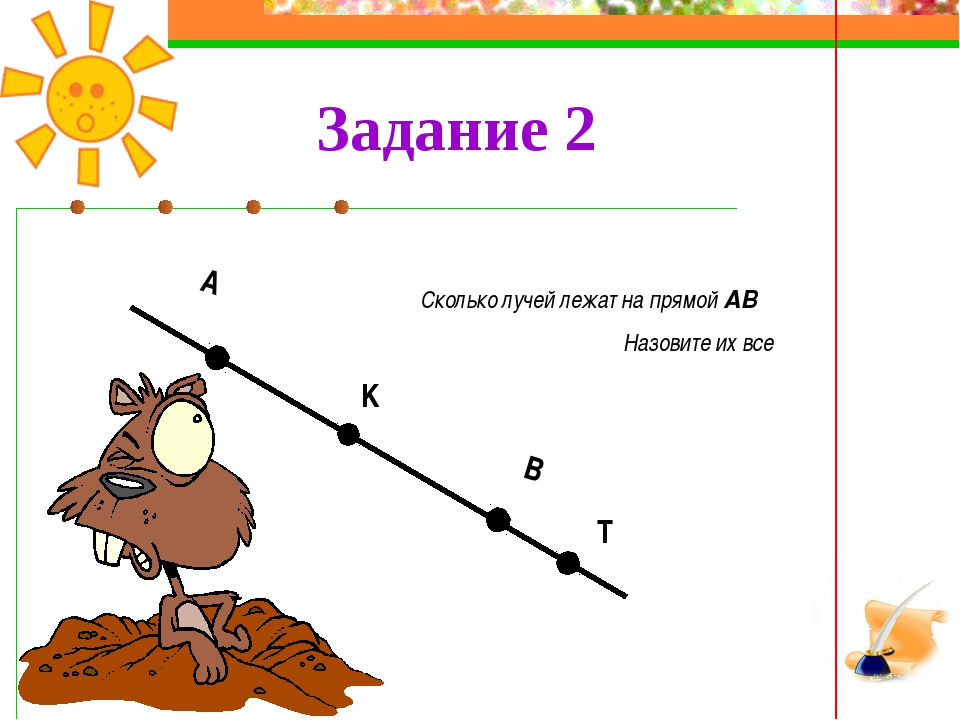
20. Запишите все отрезки, прямые и лучи, изображённые на рисунке 5.
21. Найдите координаты точек N, М, Р, Е, К на рисунке 6.
22. Найдите координаты точек А, В, С, D, Е на рисунке 7.
23. Начертите координатный луч и отметьте на нём точки, изображающие числа: 0, 1,3, 7, 8.
24. Начертите координатный луч и отметьте на нём все натуральные числа, которые больше 3 и меньше 8.

25. Начертите координатный луч и отметьте на нём точки, удалённые от точки М (6) на:
1) восемь единичных отрезков;
2) четыре единичных отрезка.
26. Начертите отрезок длиной 12 см. Над одним концом отрезка напишите число 0, а над другим — 24. Разделите отрезок на 6 равных частей. Назовите числа, которые соответствуют каждому штриху деления. Отметьте на полученной шкале числа 2, 10, 15, 18, 21.

Вариант 1.

19. Пересекаются ли изображённые на рисунке 4:
1) прямая MN и отрезок AR;
2) луч ОТ и отрезок AR;
3) луч ОТ и прямая MN7

20. Запишите все отрезки, прямые и лучи, изображённые на рисунке 5.
21. Найдите координаты точек N, М, Р, Е, К на рисунке 6.
22. Найдите координаты точек А, В, С, D, Е на рисунке 7.
23. Начертите координатный луч и отметьте на нём точки, изображающие числа: 0, 1,3, 7, 8.
24. Начертите координатный луч и отметьте на нём все натуральные числа, которые больше 3 и меньше 8.

25. Начертите координатный луч и отметьте на нём точки, удалённые от точки М (6) на:
1) восемь единичных отрезков;
2) четыре единичных отрезка.
26. Начертите отрезок длиной 12 см. Над одним концом отрезка напишите число 0, а над другим — 24. Разделите отрезок на 6 равных частей. Назовите числа, которые соответствуют каждому штриху деления. Отметьте на полученной шкале числа 2, 10, 15, 18, 21.

Смотреть Вариант 2

Вариант 2.

19. Пересекаются ли изображённые на рисунке 25:
1) прямая ЕМ и отрезок КР;
2) прямая ЕМ и луч ОА;
3) луч ОА и отрезок КР?

20. Запишите все отрезки, прямые и лучи, изображённые на рисунке 26.
21. Найдите координаты точек В, А, Е, С, D на рисунке 27.
22. Найдите координаты точек М, N, Р, К, Е на рисунке 28.
23. Начертите координатный луч и отметьте на нём точки, изображающие числа: 0, 1, 2, 6, 9.
24. Начертите координатный луч и отметьте на нём все натуральные числа, которые больше 2 и меньше 7.

25. Начертите координатный луч и отметьте на нём точки, удалённые от точки Р (5) на:
1) шесть единичных отрезков;
2) три единичных отрезка.
26. Начертите отрезок длиной 10 см. Над одним концом отрезка напишите число 0, а над другим — 20. Разделите отрезок на 5 равных частей. Назовите числа, которые соответствуют каждому штриху деления. Отметьте на полученной шкале числа 3, 7, 12, 17, 19.

Вариант 2.

19. Пересекаются ли изображённые на рисунке 25:
1) прямая ЕМ и отрезок КР;
2) прямая ЕМ и луч ОА;
3) луч ОА и отрезок КР?

20. Запишите все отрезки, прямые и лучи, изображённые на рисунке 26.
21. Найдите координаты точек В, А, Е, С, D на рисунке 27.
22. Найдите координаты точек М, N, Р, К, Е на рисунке 28.
23. Начертите координатный луч и отметьте на нём точки, изображающие числа: 0, 1, 2, 6, 9.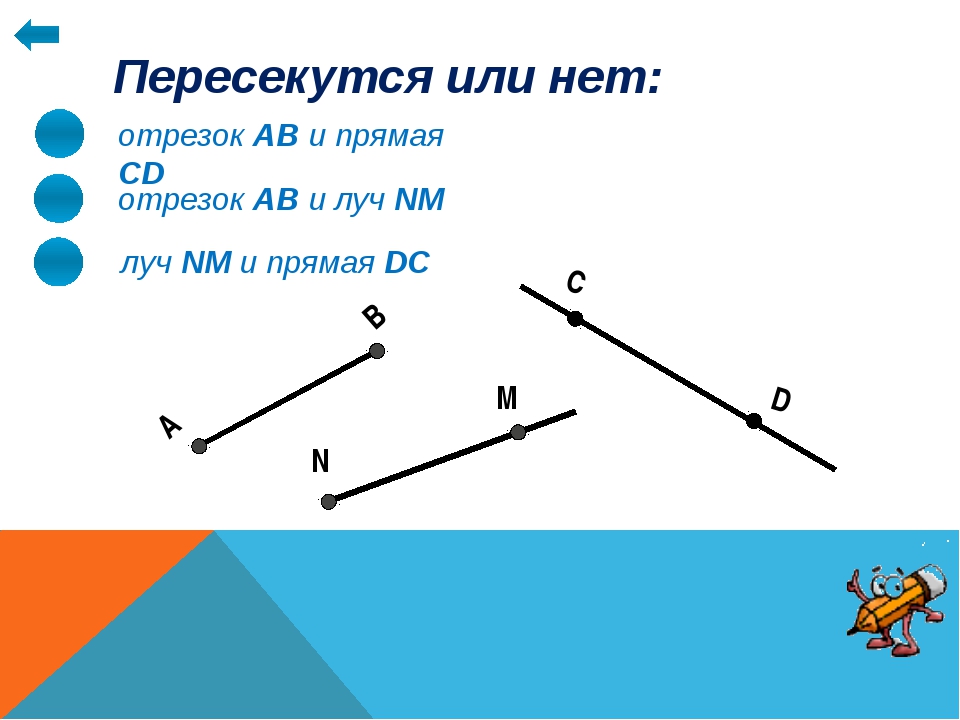
24. Начертите координатный луч и отметьте на нём все натуральные числа, которые больше 2 и меньше 7.

25. Начертите координатный луч и отметьте на нём точки, удалённые от точки Р (5) на:
1) шесть единичных отрезков;
2) три единичных отрезка.
26. Начертите отрезок длиной 10 см. Над одним концом отрезка напишите число 0, а над другим — 20. Разделите отрезок на 5 равных частей. Назовите числа, которые соответствуют каждому штриху деления. Отметьте на полученной шкале числа 3, 7, 12, 17, 19.

Смотреть Вариант 3

Вариант 3.

19. Пересекаются ли изображённые на рисунке 46:
1) прямая ЕВ и отрезок ЕТ;
2) прямая FB и луч ОА;
3) луч ОА и отрезок ЕТ?

20. Запишите все отрезки, прямые и лучи, изображённые на рисунке 47.
21. Найдите координаты точек
22. Найдите координаты точек Р, К, F, Г, А на рисунке 49.
23. Начертите координатный луч и отметьте на нём точки, изображающие числа: 0, 1,4, 8, 10.
24. Начертите координатный луч и отметьте на нём все натуральные числа, которые больше 4 и меньше 9.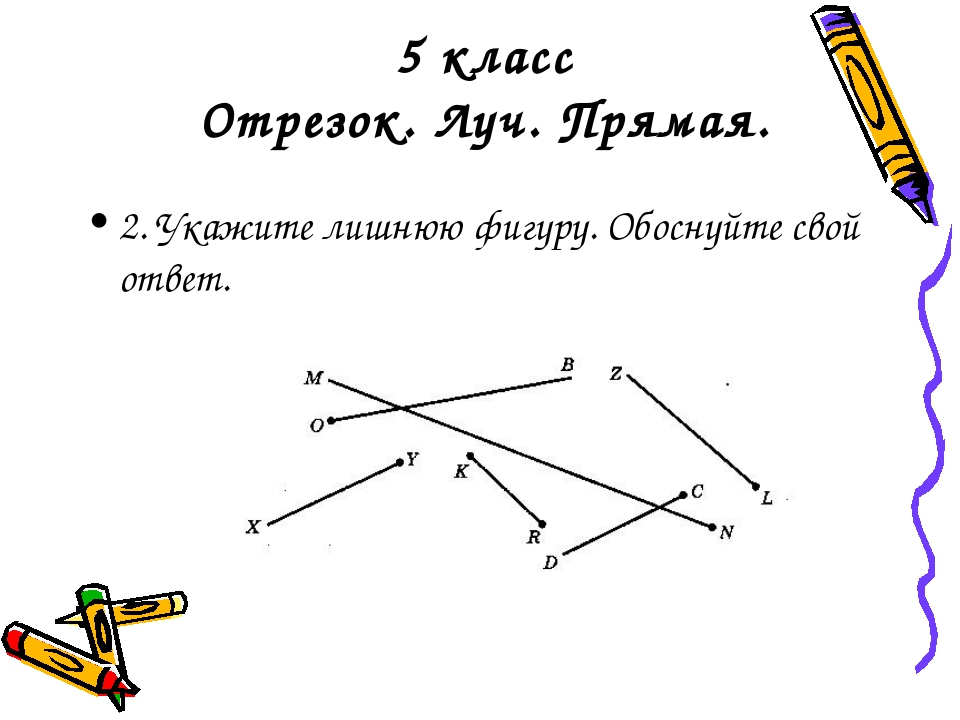

25. Начертите координатный луч и отметьте на нём точки, удалённые от точки D (4): 1) на семь единичных отрезков; 2) два единичных отрезка.
26. Начертите отрезок длиной 9 см. Над одним концом отрезка напишите число 0, а над другим — 18. Разделите отрезок на 6 равных частей. Назовите числа, которые соответствуют каждому штриху деления. Отметьте на полученной шкале числа 4, 8, 11, 15, 17.

Вариант 3.

19. Пересекаются ли изображённые на рисунке 46:
1) прямая ЕВ и отрезок ЕТ;
2) прямая FB и луч ОА;
3) луч ОА и отрезок ЕТ?

20. Запишите все отрезки, прямые и лучи, изображённые на рисунке 47.
21. Найдите координаты точек
22. Найдите координаты точек Р, К, F, Г, А на рисунке 49.
23. Начертите координатный луч и отметьте на нём точки, изображающие числа: 0, 1,4, 8, 10.
24. Начертите координатный луч и отметьте на нём все натуральные числа, которые больше 4 и меньше 9.

25. Начертите координатный луч и отметьте на нём точки, удалённые от точки D (4): 1) на семь единичных отрезков; 2) два единичных отрезка.
26. Начертите отрезок длиной 9 см. Над одним концом отрезка напишите число 0, а над другим — 18. Разделите отрезок на 6 равных частей. Назовите числа, которые соответствуют каждому штриху деления. Отметьте на полученной шкале числа 4, 8, 11, 15, 17.

Смотреть Вариант 4

Вариант 4.

19. Пересекаются ли изображённые на рисунке 67:
1) луч СЕ и отрезок А К;
2) луч СЕ и прямая MN;
3) прямая MN и отрезок АК ?

20. Запишите все отрезки, прямые и лучи, изображённые на рисунке 68.
21. Найдите координаты точек С, Е, D, А, В на рисунке 69.
22. Найдите координаты точек D, F, Я, К, Р на рисунке 70.
23. Начертите координатный луч и отметьте на нём точки, изображающие числа: 0, 1, 6, 7, 11.
24. Начертите координатный луч и отметьте на нём все натуральные числа, которые больше 5 и меньше 11.

25. Начертите координатный луч и отметьте на нём точки, удалённые от точки Т (7) на:
1) девять единичных отрезков;
2) три единичных отрезка.
26. Начертите отрезок длиной 8 см. Над одним концом отрезка напишите число 0, а над другим — 16. Разделите отрезок на 4 равные части. Назовите числа, которые соответствуют каждому штриху деления. Отметьте на полученной шкале числа 3, 6, 10, 13, 15.

Вариант 4.

19. Пересекаются ли изображённые на рисунке 67:
1) луч СЕ и отрезок А К;
2) луч СЕ и прямая MN;
3) прямая MN и отрезок АК ?

20. Запишите все отрезки, прямые и лучи, изображённые на рисунке 68.
21. Найдите координаты точек С, Е, D, А, В на рисунке 69.
22. Найдите координаты точек D, F, Я, К, Р на рисунке 70.
23. Начертите координатный луч и отметьте на нём точки, изображающие числа: 0, 1, 6, 7, 11.
24. Начертите координатный луч и отметьте на нём все натуральные числа, которые больше 5 и меньше 11.

25. Начертите координатный луч и отметьте на нём точки, удалённые от точки Т (7) на:
1) девять единичных отрезков;
2) три единичных отрезка.
26. Начертите отрезок длиной 8 см. Над одним концом отрезка напишите число 0, а над другим — 16. Разделите отрезок на 4 равные части. Назовите числа, которые соответствуют каждому штриху деления. Отметьте на полученной шкале числа 3, 6, 10, 13, 15.

---

 

ОТВЕТЫ на самостоятельную работу

Вариант 1.

№ 19. 1) да, 2) нет, 3) да.
№ 20. Отрезки: АВ, ВС, АС. Прямые: DK. Лучи: АЕ, AF, BD, ВК, CD, СК, BE, KF.
№ 21. N(3), M(5), P(6), E(7), K(9).
№ 22. A(10), B(60), C(75), D(110), E(160).

Вариант 2.

№ 19. 1) нет, 2) да, 3) да.
№ 20. Отрезки: АВ, ВС, АС, AD, BD, CD. Прямые: FE. Лучи: АЕ, AF, АК, ВК, CF, СЕ.
№ 21. В(1), А(3), Е(5), С(6), D(8).
№ 22. М(10), N(50), P(100), K(110), E(130).

Вариант 3.

№ 19. 1) да, 2) нет, 3) да.
№ 20. Отрезки: МО, МК, МР, КР, OP, ОК. Прямые: нет. Лучи: ML, PL, ОЕ, РЕ.
№ 21. А(1), В(3), С(5), D(6), E(8).
№ 22. Р(5), К(25), F(4О), T(55), N(65).

Вариант 4.

№ 19. 1) да, 2) да, 3) нет.
№ 20. Отрезки: МС, MN, CN. Прямые: АВ. Лучи: СО, МО, СТ, NT, МА, MB, NA, NB.
№ 21. С(1), Е(2), D(4), A(5), B(8).
№ 22. D(20), F(80), H(140), К(190), Р(210).

 

Полную версию ответов на самостоятельные работы смотрите на сайте: «Все Контрольные»

 

---

Вы смотрели страницу «Самостоятельная работа СР-04 Прямая. Луч. Шкала». Цитаты самостоятельных работ из пособия для учащихся «Математика 5 класс. Дидактические материалы / Мерзляк и др.», которое используется в комплекте с учебником Математика 5 класс Мерзляк.

Вернуться к Списку самостоятельных работ по математике в 5 классе (УМК Мерзляк)

Урок математики 5 класс Координатный луч Учитель Пестрикова А.В. ГБОУ СОШ им.

А.А.Каргина

5 класс математика Тема: Координатный луч

Цели: сформировать понятие координатного луча, научить строить координатный луч, находить координаты точек и строить точки по заданным координатам. Личностные УУД: Формировать учебную мотивацию, адекватную самооценку, необходимость приобретения новых знаний.

Метапредметные УУД:

Регулятивные:

• понимать учебную задачу урока, осуществлять решение учебной задачи под руководством учителя, определять цель учебного задания, контролировать свои действия в процессе его выполнения, обнаруживать и исправлять ошибки, отвечать на итоговые вопросы и оценивать свои достижения

Познавательные:

• формировать навыки изображения прямой и её частей, а также ломаной; знать общие и отличительные особенности изучаемых линий; познакомить с разными способами обозначения прямой и луча; научить правильно обозначать прямую, её части и ломаную линию; формировать умение применять полученные знания при решении практических задач.

Коммуникативные:

• воспитывать любовь к математике, коллективизм, уважение друг к другу, умение слушать, дисциплинированность, самостоятельность мышления.

Оборудование: плакат с координатным лучом, сигнальные карточки (одна сторона зеленая, другая – красная).

Ход урока

I. Устные упражнения «Математическая разминка».

1. Вот задача не для робких!

    Вычитай, дели и множь,

    Плюсы ставь, а также скобки!

    Верим – к финишу придешь!

5   5   5   5 = 30 (Ответ: 5 + 5 × 5 + 5 = 30)

5   5   5   5 = 55 (Ответ: 5 × (5 + 5) + 5 = 55)

5   5   5   5 = 120 (Ответ: 5 × 5 × 5 – 5 = 120).

2. Если математическое утверждение верно, то показывается карточка зеленого цвета, если нет – то красного:

а) Две точки можно соединить двумя отрезками.

б) В одном сантиметре 10 дециметров.

в) Прямая не имеет концов.

г) Точка разбивает прямую на два луча.

д) Лучи АМ и AN – дополнительные лучи.

е) В одной тонне 100 кг.

3. № 122, 123.

4. Класс делится на две команды. К доске приглашается с учебником по 1 человеку от каждой команды.

Кому присвоить звание «Лучший счетчик»? Нужно устно сосчитать и записать на доске только ответ.

№ 126 (а, в)                                       № 126 (б, г)

II. Изучение нового материала.

1. Объясняется новая тема урока.

2. Учитель объясняет в соответствии с текстом, а учащиеся выполняют соответствующие чертежи. Во время объяснения обращается внимание на новые математические термины, которые записываются отдельно на доске (единичный отрезок, координатный луч, координаты), а также нежно сказать о том, что координатный луч называют ещё «числовым лучом». Почему?

Примечание: такую работу можно проводить на каждом уроке: дома учащиеся записывают определение новых терминов, и к концу обучения в школе, у каждого ученика будет свой математический словарь.

III. Физкультминутка для глаз.

Не поворачивая головы, делать движения глазами: вправо – влево; вверх – вниз; «восьмерка». На вытянутой руке держать ручку или карандаш, зафиксировать взгляд на карандаше, приближая и отодвигая его.

IV. Закрепление.

1. На доске начерчен луч с началом в точке О.

Беседа  по  вопросам:  Является   ли  этот  луч  координатным  лучом? (Нет.) Почему? (Не выбран единичный отрезок.) Как обозначается единичный отрезок? Почему он так называется? Как понимать запись: В(3)? Как называется число 3? Сколько точек В(3) можно отметить на координатном луче? (Одну.)

2. № 118 (а), 119, 121 (устно).

V. Самостоятельная работа (ДМ варианты 2, 3).

Вариант I	Вариант II
1. Напишите координаты точек D, Е, Т и К, отмеченных на координатном луче. 2. Начертите координатный луч и отметьте на нем точки А(8), К(12), Р(1), М(9), N(6),S(3).	1. Напишите координаты точек М, N, С и Р, отмеченных на координатном луче. 2. Начертите координатный луч и отметьте на нем точки А(6), В(5), С(3), D(10), Е(2), F(1).
3. Выразите в граммах:
5 кг 750 г; 2 кг 60 г	5 кг 200 г; 1 кг 5 г
Выразите в килограммах:
3 т 180 кг; 4 ц 3 кг	3 т 60 кг; 8 ц 70 кг
Выразите в килограммах и граммах:
4370 г; 1030 г	6840 г; 3090 г
Выразите в тоннах и центнерах:
853 ц; 205 ц	556 кг; 4350 кг.

VI. Итог урока.

Ответить на вопросы п. 4.

VII. Домашнее задание: п. 4, повторить п. 3, № 138, 141, 143. В математический словарь занести: единичный отрезок, координатный луч, координаты.

Двумя прямыми линиями разделить треугольник на два треугольника, четырехугольник и пятиугольник.

  Поиск Поиск

• Школьный помощник
  • математика 5 класс
  • математика 6 класс
  • алгебра 7 класс
  • алгебра 8 класс
  • геометрия 7 класс
  • русский язык 5 класс
  • русский язык 6 класс
  • русский язык 7 класс
• математика
• алгебра
• геометрия
• русский язык

«»

следующая предыдущая вернуться на предыдущую страницу

Такой страницы нет !!!

• Популярные запросы
  • Обстоятельство
  • Дополнение
  • Определение
  • Деление дробей
  • Русский язык 7 класс
  • Математика 6 класс
  • Русский язык 6 класс
  • Русский язык 5 класс
  • Алгебра 7 класс
  • Математика 5 класс
  • Алгебра 8 класс
  • Наименьшее общее кратное
  • Буквы о и а в корнях -кос- / -кас-; -гор- / — гар-; -клан- / -клон-; -зар- / -зор-
  • Наибольший общий делитель. Взаимно простые числа
  • Буквы о и а в корнях -кос- / -кас-; -гор- / — гар-; -клан- / -клон-; -зар- / -зор-
  • Деление и дроби
  • Доли. Обыкновенные дроби
  • Квадратный корень из неотрицательного числа
  • Окружность и круг
  • Антонимы. Синонимы
  • Десятичная запись дробных чисел
  • Буквы о – а в корнях -лаг- / -лож-, -рос- / -раст- (-ращ-)

Методическая разработка урока математики 5 класса «Координатный луч»

Тема урока:				Координатный луч
Цели обучения, которые достигаются на данном уроке:
-знать различные единицы длины и понимать, что такое единичный отрезок на координатном луче; -изображать натуральные числа на координатном луче; -сравнивать натуральные числа, в том числе с помощью координатного луча; -записывать результат сравнения натуральных чисел с помощью знаков ; -исследовать ситуацию, требующую сравнения и упорядочивания натуральных чисел;
Цели урока:		сформировать понятие координатного луча, научить строить координатный луч, находить координаты точек и строить точки по заданным координатам; развивать умения анализировать, сравнивать, обобщать, делать выводы,
Критерии успеха		развивать познавательный интерес через игровые моменты взаимоконтроля, взаимопроверки, способствовать пониманию необходимости интеллектуальных усилий для успешного обучения, положительного эффекта настойчивости для достижения цел.
Привитие ценностей		Ценности, основанные на национальной идее «Мәңгілік ел»: казахстанский патриотизм и гражданская ответственность; уважение; сотрудничество; труд и творчество; открытость; образование в течение всей жизни.
Межпредметные связи		Взаимосвязь с предметами: информатика и география
Навыки использования ИКТ		На данном уроке учащиеся используют наборное полотно, которое можно загрузить на планшет или мобильный телефон через QR-код
Ход урока
Этапы урока	Запланированная деятельность на уроке					Ресурсы
Начало урока	приветствует учащихся, проверяет их готовность к уроку. — У каждого из вас на столах лежат карточки самооценивания (приложение 1). Подпишите их. В течение урока мы с вами будем выполнять различные задания. По окончанию решения каждого задания, вы должны оценить свою работу: «+» — справился без затруднений, «±» — справился, но возникали сложности, «-» — не справился с заданием. Организация устного счета и повторения основных типов задач. Устные упражнения «Математическая разминка». 1. Вот задача не для робких! Вычитай, дели и множь, Плюсы ставь, а также скобки! Верим – к финишу придешь! 5 5 5 5 = 30 (Ответ: 5 + 5  5 + 5 = 30) 5 5 5 5 = 55 (Ответ: 5  (5 + 5) + 5 = 55) 5 5 5 5 = 120 (Ответ: 5  5  5 – 5 = 120). 2. Если математическое утверждение верно, то показывается карточка зеленого цвета, если нет – то красного: а) Две точки можно соединить двумя отрезками. б) В одном сантиметре 10 дециметров. в) Прямая не имеет концов. г) Точка разбивает прямую на два луча. д) Лучи АМ и AN – дополнительные лучи. е) В одной тонне 100 кг.					Касса с геометрическими фигурами
Критерии успеха	Учащиеся высказывают свои мнения. Учащиеся сдают карточки самооценивания.
Середина урока	Плакат с координатным лучом. Определение координатного луча. Постройте в тетради координатный луч с единичным отрезком 1 клеточка. На своем луче проставьте буквы, соответствующие числам данного ключа, и прочитайте получившееся слово. 21 9 27 3 0 24 15 12 6 18 а р а о к т и д о н Итак, появляется новое понятие – «координата». Самостоятельная работас проверкой на уроке. Группа I Группа II 1. Напишите координаты точек D, Е, Т и К, отмеченных на координатном луче. 2. Начертите координатный луч и отметьте на нем точки А(8), К(12), Р(1), М(9), N(6), S(3). 1. Напишите координаты точек М, N, С и Р, отмеченных на координатном луче. 2. Начертите координатный луч и отметьте на нем точки А(6), В(5), С(3), D(10), Е(2), F(1). 3. Выразите в граммах: 5 кг 750 г; 2 кг 60 г 5 кг 200 г; 1 кг 5 г Выразите в килограммах: 3 т 180 кг; 4 ц 3 кг 3 т 60 кг; 8 ц 70 кг Выразите в килограммах и граммах: 4370 г; 1030 г 6840 г; 3090 г Выразите в тоннах и центнерах: 853 ц; 205 ц 556 кг; 4350 кг.					линейка
Конец урока	Реши.П 1) Какие числа называются натуральными? 2) Сколько цифр используется для записи натуральных чисел? Назвать эти цифры. 3) Для чего употребляется цифра «нуль»?
Дифференциация Каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?			Оценивание Как Вы планируете проверить уровень усвоения материала учащимися? Используйте данный раздел для записи методов, которые Вы будете использовать для оценивания того, чему учащиеся научились во время урока.		Здоровье и соблюдение техники безопасности Здоровьесберегающие технологии. Используемые физминутки и активные виды деятельности.
Дополнительное задание, выполняется на компьютере, планшете или на мобильном устройстве http://files.school-collection.edu.ru/dlrstore/fa31707f-d302-4070-897f-6d1bbe3a648e/%5BNS-MATH_1-01-06%5D_%5BIM_005%5D.html			К концу урока учащиеся научатся: чертить кортинатный луч знают как заисывать чило в координатный луч		№1: Руки в стороны — в полёт Отправляем самолёт. Правое крыло вперёд, Левое крыло вперёд. Раз, два, три, четыре — Полетел наш самолёт. №2 На носочках ходят мыши. Так, чтоб кот их не услышал.

Математика 5 класса — Начальная школа Бернис Рэй

Математика 5 класса — Начальная школа Бернис Рэй

Решение проблем

• Изучите и изучите дополнительные стратегии решения проблем
• Используйте простые задачи, чтобы предлагать более сложные решения
• Решайте многоэтапные задачи
• развивайте уверенность, настойчивость и настойчивость в решении проблем (независимо и в группах)

Рассуждение

• Используйте модели, факты, свойства и отношения для объяснения мышления
• сравните и сопоставьте двухмерные геометрические фигуры
• с учетом проблемы, определите одну или несколько стратегий для решения проблемы

Связь

• сделать и проверять предположения об отношениях
• рисовать диаграммы и использовать объекты для иллюстрации концепций
• использовать таблицы, диаграммы, графики и математический символизм

Связи

• обнаруживать взаимосвязи и закономерности в наборе целых чисел
• изучать закономерности и r увлечения в геометрии
• использовать математические темы в других дисциплинах
• применять математику в повседневных жизненных ситуациях
• изучить взаимосвязь между +, -, x, ÷ с целыми числами
• соединить операции с целыми числами с дробями и десятичными числами

Число Смысл и нумерация

• название места значение от тысячных долей до миллионов
• круглых чисел для оценки и мысленных вычислений
• заказ набора рациональных чисел
• чтение и наименование чисел с показателями целых чисел
• изучение простых, квадратных и составных чисел

Операции с целыми числами

• раскрыть значение + — x ÷ с дробями
• изучить концепцию +, — для целых, десятичных и дробных чисел
• изучить x для целых, десятичных и дробных чисел
• основные факты — все операции
• + — x ÷ целые числа разумного размера
• используйте калькуляторы по мере необходимости

Geometry

• исследуйте и описывайте свойства общих двумерных фигур

Spatial Sense

• идентифицируйте совпадающие или похожие фигуры

измерения

• используйте стандарт для измерения длины
• используйте стандарт и найти область общих цифр
• изучить и подготовить формулы для площадей прямоугольника и треугольника
• изучить стандартные и нестандартные единицы измерения объема, вместимости, веса и температуры
• определить сумму изменения с момента покупки

Анализ данных и вероятность

• построение и интерпретация графических изображений, столбцов, кругов и линий
• количественная оценка эмпирической вероятности простых событий

Функции и отношения

• распознавать, описывать, анализировать, расширять и создавать разнообразие выкройки по моделям, таблицам, графику s, простые правила и манипуляторы

Алгебра

• писать и решать открытые предложения
• наносить точки на числовую линию и в прямоугольную систему координат

Бесплатные стандартизированные тесты Флэш-карточки по математике PSSA

две прямые, отрезки или лучи, которые пересекаются и образуют прямые углы 9 0141 четырехугольник

Вопрос	Ответ
время на часах с часовой и минутной стрелками (не цифровое)	аналоговое
прямоугольное тело с 6 равными квадратными гранями	куб
математическое предложение, показывающее, что одно выражение равно другому	уравнение
число (или любая комбинация чисел и символов), которое показывает математическую связь	выражение
плоская поверхность (или плоскость), которая является одной стороной твердой фигуры	грань
число, которое равномерно делится на другое число	фактор
таблица ввода / вывода, в которой правило заставляет каждое «входящее значение» иметь уникальное «выходное значение»	функция
многоугольник с 6 сторон	шестигранник
прямой путь, идущий в обоих направлениях без конечных точек	линия
линия, разделяющая фигуру на две половины, которые являются зеркальным отображением друг друга	линия симметрии
часть линии с двумя конечными точками	сегмент линии
произведение одного числа на другое число	кратное
математическое уравнение с числами	числовое предложение
многоугольник с 8 сторонами	восьмиугольник
пара чисел, используемая для определения точки на координатной сетке	упорядоченная пара
прямые, которые никогда не пересекаются и всегда находятся на одинаковом расстоянии	параллельные прямые
четырехугольник, противоположные стороны которого параллельны и конгруэнтны	параллелограмм
многоугольник с 5 сторонами	пятиугольник	перпендикулярные линии
график, который использует изображения для отображения и сравнения информации	пиктограмма
сплошная фигура с основанием многоугольника и треугольными сторонами, которые встречаются в одной точке	пирамида
часть линия, которая имеет одну конечную точку и продолжается в другом направлении вечно	луч
параллелограмм с 4 равными сторонами	ромб
сплошная фигура, все точки которой находятся на одинаковом расстоянии от центра	сфера
таблица, в которой используются метки подсчета для записи данных	таблица подсчетов
четырехугольник с одной парой параллельных сторон	трапеция
угол, который составляет 90 градусов и образует «квадратный» угол	правый угол
точка пересечения двух или более прямых, лучей или отрезков s	пересечение
плоская форма с 4 или более сторонами	многоугольник
трехмерная форма с длиной, шириной и высотой	сплошная
угол менее 90 градусов	острый
число, которое добавляется	добавление
мера (в квадратных единицах) внутренней части плоской фигуры (длина, умноженная на ширину)	площадь
прямоугольное расположение объекты в равных строках или столбцах	массив
группа элементов, в которой порядок не имеет значения	комбинация
сплошная фигура с круглым основанием и одной вершиной	конус
сплошная фигура с двумя параллельными и конгруэнтными круглыми основаниями	цилиндр
отрезок прямой, где 2 fa точки сплошной фигуры соответствуют	ребру
, имеющему то же значение	эквивалент
набор связанных уравнений сложения / вычитания или умножения / деления, в которых используются одинаковые числа	семейство фактов
a математическое предложение, которое содержит символ, показывающий, что члены с обеих сторон не равны	неравенство
число, полученное путем деления суммы списка чисел на количество слагаемых (также называемое средним)	среднее значение
среднее число в списке упорядоченных чисел	медиана
число (а), которое чаще всего встречается в списке данных	режим
угол, который больше 90 градусов	тупой
расстояние вокруг фигуры	периметр
многоугольник с 4 сторонами
треугольник с углом 90 градусов	прямоугольный треугольник
точка, где встречаются линии, лучи, стороны или края (также называется углом)	вершина
количество пространство (в кубических единицах), которое может содержать сплошная фигура (длина, ширина, высота)	объем
целое число, которое имеет более двух факторов	составное число
способ записи чисел который показывает значение каждой цифры	расширенное обозначение
наименьшее число (отличное от нуля), которое является общим кратным двух или более других чисел	наименьшее общее кратное (НОК)
плоская поверхность, которая продолжается бесконечно во всех направлениях	плоскость
целое число, которое имеет ровно два множителя: 1 и само	простое число
разница между наибольшим и наименьшим числами в наборе данных	диапазон
перемещение фигуры в новое положение путем сдвига (перемещения), переворота (отражения) или поворота (вращения)	преобразование
любое из счетных чисел	целое число
перемещение фигуры без поворота или переворачивания (скольжение)	перемещение
перемещение фигуры путем поворота ее вокруг фиксированной точки (поворот)	поворот
перемещение фигуры для отображения ее зеркального отображения (переворот)	отражение
расстояние по окружности	окружность
фигурки того же размера и формы	конгруэнтные
фигурки с такими же форма, но не обязательно того же размера	аналогично

точек рисования, линий, сегментов и лучей: Урок для детей — Обучающие видео для детей

Точки, отрезки линий и лучи

Пираты, закапывающие сокровища, используют крестик, чтобы отметить место, где было захоронено сокровище.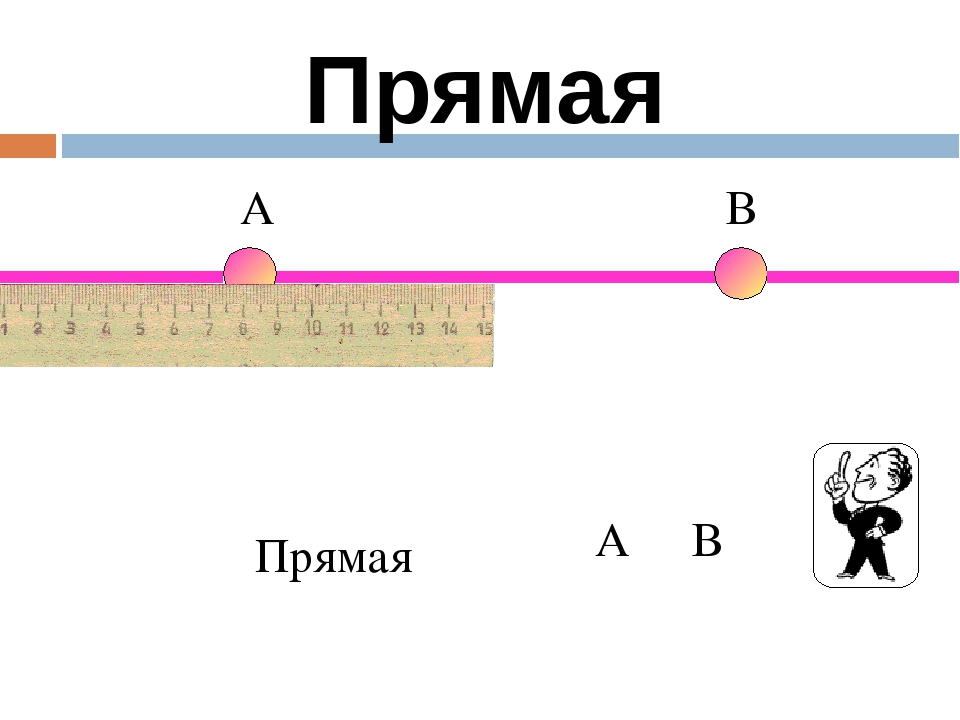 Точно так же точка используется для обозначения точного местоположения. Вы рисуете точку с помощью точки и обозначаете ее буквой, например «Точка А» или даже «Точка X».

Когда вы завершаете тест с заполнением пропусков, вы заполняете сегмент линии. Сегмент линии — это кусок линии. Вы рисуете его, рисуя прямую линию и добавляя точки к ее концам. Это показывает, что это отрезок линии с определенными начальной и конечной точками.

Подобно солнечным лучам, которые исходят от Солнца и навсегда уходят в космос, луч начинается как единственная точка и навсегда уходит в одном направлении.Чтобы нарисовать луч, вы рисуете точку, а затем проводите прямую линию, выходящую из нее в одном направлении. В конце строки вы добавляете стрелку, чтобы показать, что это продолжается вечно.

Строки

Во время конги люди выстраиваются в очередь и танцуют по комнате, как поезд. Линия состоит из бесконечного количества точек, идущих в прямой ряд, как и люди в линии конги.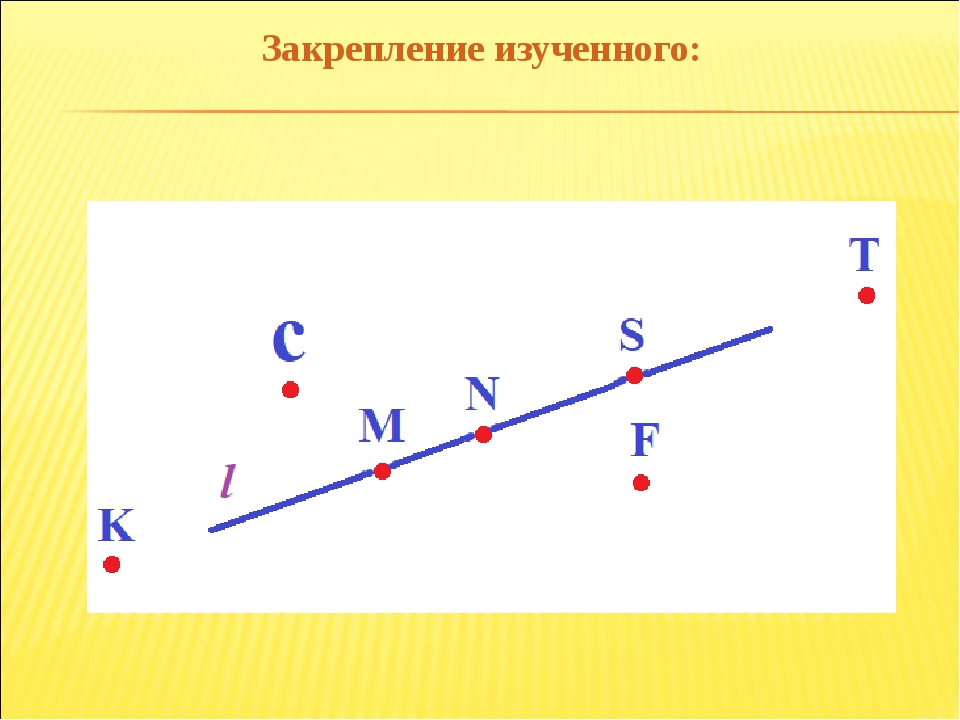 Строки продолжаются бесконечно, и подсчитать все точки на самом деле невозможно. Вы, вероятно, не захотели бы так долго оставаться в линии конги!

Вы можете нарисовать линию, нарисовав прямую линию на бумаге и добавив стрелки на каждом конце, чтобы показать, что линия продолжается бесконечно.

В отличие от точек, отрезков и лучей, существует не только один тип линий. Линии можно описать по направлению, в котором они движутся, и по тому, как они выглядят с другими линиями. Давайте посмотрим на несколько примеров.

Если вы видели восход солнца, значит, солнце поднимается за горизонт. Точно так же, как горизонт рассматривается как линия между землей и небом, горизонтальные линии проходят слева направо или с востока на запад. Они плоские, как столешница или пол. С другой стороны, вертикальные линии идут вверх и вниз или с севера на юг.Вертикальные линии напоминают флагшток или памятник Вашингтону.

Пересекающиеся линии — это линии, которые пересекают друг друга в любой точке. Вы можете нарисовать их, нарисовав линию, а затем другую линию, пересекающую ее в какой-то момент. Перпендикулярные линии — это линии, которые пересекаются, образуя четыре угла в 90 градусов. Линии на доске для крестиков-ноликов перпендикулярны. Чтобы нарисовать эти линии, вы рисуете горизонтальную линию, а затем проходящую через нее вертикальную линию. Параллельные линии — это линии, которые находятся на одинаковом расстоянии друг от друга и никогда не соприкасаются.Подумайте о брусьях в гимнастике. Вы рисуете параллельные линии, рисуя линию, а затем рисуя другую линию, которая идентична ей, но на заданном расстоянии от нее.

Сводка урока

Точки, линии, отрезки линий и луча (которые начинаются как отдельные точки и уходят вечно в отдельных направлениях) — все это геометрические фигуры. Линии можно нарисовать по горизонтали, (слева направо) или по вертикали, (вверх и вниз). Линии , которые продолжаются бесконечно, также могут быть описаны как пересекающиеся линии , которые являются линиями, пересекающими друг друга в любой точке; перпендикулярные линии , которые пересекаются, образуя четыре угла в 90 градусов; или, наконец, параллельные линии , которые находятся на одинаковом расстоянии друг от друга и никогда не соприкасаются. Там много точек, форм и линий, поэтому некоторые из них могут быть непростыми. Но теперь, когда вы узнали обо всех из них, у вас не должно возникнуть никаких проблем!

бесплатных онлайн-видео о геометрии, часть 1: 4–5 классы

Наслаждайтесь бесплатными онлайн-видео по математике по этим темам геометрии примерно для 4-5 классов. Я также поддерживаю более полную страницу, на которой перечислены все мои видео по геометрии для 1-7 классов. На этой странице размещены видео по геометрии для 4-5 классов. Выберите тему ниже:

Вы можете использовать эти видео…

• … чтобы самому изучить эти темы (например, если вы студент или взрослый, нуждающийся в переподготовке)
• … как планы уроков по преподаванию этих тем. Часто одно видео снизу можно превратить в несколько уроков с учениками.

Видео на этой странице соответствуют урокам из моей книги «Математическая геометрия мамонта 1» (книга «Голубая серия») или урокам из главы 6 учебной программы для 4-В классов (серия «Голубая серия»). В любой из книг вы получите ГОРАЗДО больше практических упражнений, задач со словами и головоломок, чем показано в видеороликах, а также некоторые уроки, которые не включены в этот набор видеороликов.

Линии, лучи и углы

Сначала я объясню разницу между линией и лучом в геометрии. Затем угол определяется как два луча, исходящие из одной и той же точки, называемой вершиной угла.

Я обсуждаю размер угла и то, как он не зависит от сторон угла. Я показываю воображаемую дугу окружности, которая рисуется, когда угол открывается все дальше и дальше. Наконец, я делаю несколько упражнений о том, какой угол больше.

---

Как использовать транспортир для измерения и рисования углов

Я объясняю, что такое угловая мера, как измерять углы с помощью транспортира и как рисовать углы с помощью транспортира.

Когда угол «открывается», он рисует дугу окружности, и мы сравниваем эту дугу с полным кругом, равным 360 градусам.

Использовать транспортир довольно просто. Вы выравниваете одну сторону своего угла с «нулевой линией» транспортира и помещаете среднюю точку транспортира в вершину угла. Затем вы считываете угол, где другая сторона угла касается полукруга транспортира. Но транспортир нужно разместить правильно.

---

Расчетные углы

Оценка угловых мер основана на сравнении их с некоторыми приблизительными углами, такими как прямой угол, угол 45 ° и угол 30 ° (который представляет собой угол между двумя последовательными числами на циферблате).

Во-первых, я прикинул несколько углов. Затем я рисую несколько углов, оценивая их (не измеряя), а потом проверяю.

Наконец, в этом видео я объясняю концепцию поворота на определенный угол, например поворот на угол 30 °.

---

Как нарисовать прямой угол (перпендикулярную линию) и прямоугольник

Я показываю, как вы можете нарисовать прямой угол (или перпендикулярную линию к данной линии), используя транспортир или треугольную линейку. Я также показываю линию, перпендикулярную данной линии, проведенную через точку на линии или проведенную через точку не на линии.

Наконец, я рисую прямоугольник с заданной длиной сторон, используя транспортир для создания прямых углов и обычную линейку для измерения сторон.

Этот урок рассчитан на 3 или 4 класс.

---

Параллелограммы

Что такое параллелограмм? В определении говорится, что это фигура, окруженная двумя наборами параллельных линий, и именно с этого мы начнем. ОПРЕДЕЛЕНИЕ ничего не говорит о длине сторон или углах. Эти вещи ученики могут заметить или узнать сами, нарисовав и измерив.

Я также рисую увеличенную копию данного ромба, что является очень хорошим упражнением для студентов и даю идеи для решения других задач рисования на базовом уровне.

---

Острый, тупой и прямоугольный треугольники

Этот урок является отправной точкой для классификации треугольников по их углам. Прямоугольный треугольник имеет один прямой угол.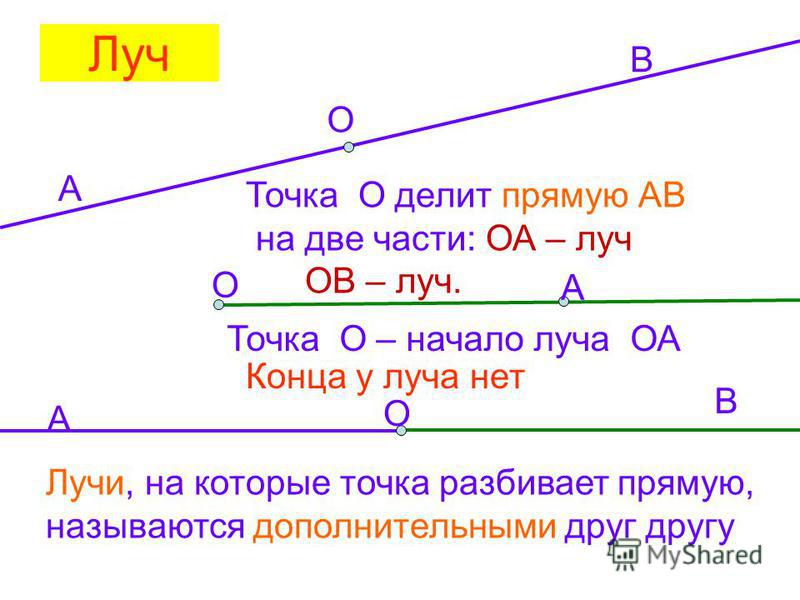 (А как насчет двух других углов? Мы узнаем.) У тупого треугольника один тупой угол. (А как насчет двух других углов? Мы узнаем.) У острого треугольника ТРИ острых угла.

---

Круги

Что такое круг? Это фигура, в которой расстояние от центральной точки до любой точки внешней линии (окружности) одинаково. Вот почему овал не классифицируется как круг.

Студентам необходимо попрактиковаться в рисовании кругов различных размеров с помощью циркуля. Рисование концентрических кругов — забавное упражнение для них.

Я показываю два других упражнения по рисованию: нарисовать круг внутри квадрата, а затем скопировать простой рисунок круга.

---

Полигоны — введение

Это введение в полигоны для начальной школы — примерно 4-го класса.

Мне нравится давать студентам упражнения по рисованию на бумаге случайным образом 4, 5, 6, 7 или 8 точек и соединению их для получения многоугольника.

Я также показываю упражнения, в которых мы делим многоугольники на новые или складываем многоугольники, чтобы получить новые.

---

Периметр — концепция и различные упражнения

Концепция периметра проста: это как обойти фигуру и проверить, на какое расстояние вы прошли. Находим периметр, складывая длины сторон. Трудно вспомнить, что означает это слово.Я решаю несколько разных задач, связанных с периметром, в том числе те, где указан периметр и задаются длины сторон. Этот урок рассчитан на 4 класс и выше.

---

Площадь прямоугольников — различные задачи

Я работаю над различными задачами, связанными с областью прямоугольников — не стесняйтесь использовать их со своими учениками на уроке геометрии. Подходит для 3-5 классов.

---

Площадь по сравнению с периметром

Мы рассмотрим геометрические задачи, которые связаны как с площадью, так и по периметру прямоугольников.Например, задается площадь квадрата и задается периметр. Или наоборот: задается периметр квадрата и задается площадь. Затем я решаю две задачи, в которых указывается некоторая длина сторон и другая информация, а также задается периметр или площадь. Наконец, мы рассмотрим эту открытую проблему: если площадь прямоугольника составляет 18 квадратных сантиметров, каков может быть его периметр?

---

Объем прямоугольной призмы и кубические единицы

Объем измеряется в кубических единицах или «кубиках».Если стороны вашего «кубика» равны 1 см, то это 1 кубический сантиметр. Точно так же, если стороны вашего «маленького куба» равны 1 дюйму, то это 1 кубический дюйм.

Я демонстрирую с помощью детских блоков, как найти объем прямоугольных призм. Затем решаем несколько словесных задач с объемом прямоугольных призм (ящиков).

---

Следующие видео являются более старыми и не HD. Последний не принадлежит книге Math Mammoth Geometry 1.

Сумма углов треугольника — 180 градусов — Видео

Простое доказательство того, что сумма углов треугольника составляет 180 градусов, доступная для учеников средней школы и даже младше.(Эта тема предназначена для учеников средней школы.)

---

Углы в параллелограмме

Начиная с двух параллельных линий и линии, пересекающей их обе, я показываю, что противоположные углы в параллелограмме равны, а сумма углов равна 360 градусам.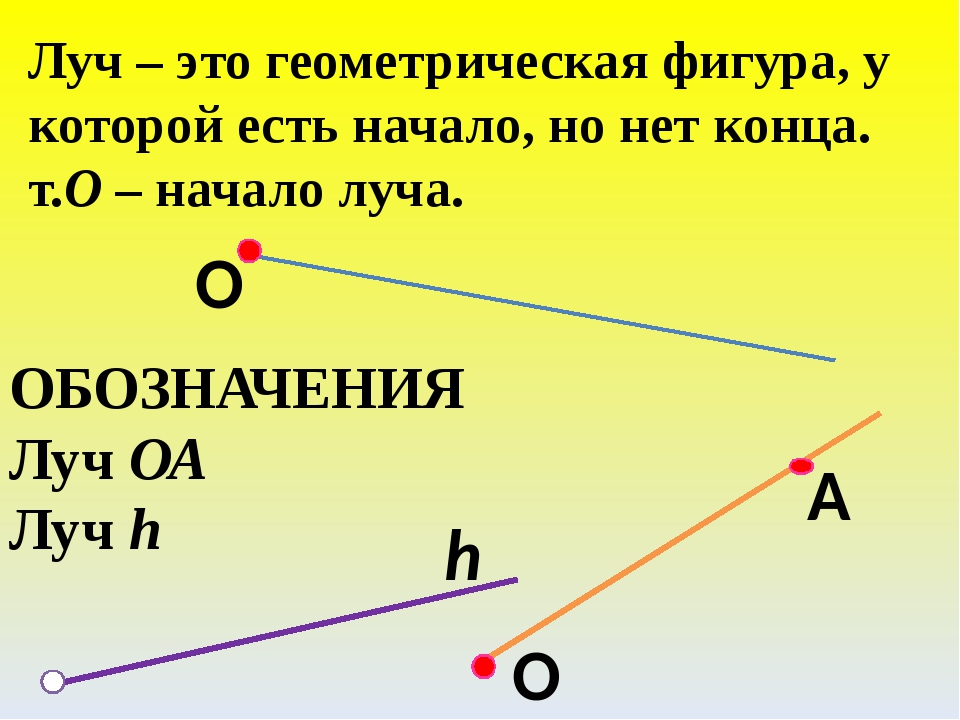 (Эта тема предназначена для средней школы, о 7 классе.)

---

Вертикальные углы — доказательство на видео

Краткое и простое доказательство того, что вертикальные углы равны. (Эта тема предназначена для средней школы, около 7 класса.)

---

Большинство видеороликов на этой странице соответствуют урокам из моей книги «Математическая геометрия мамонта 1» (книга «Голубая серия») или урокам в главах геометрии 4-го и 5-го классов серии «Голубой». В книгах вы найдете гораздо больше практических упражнений, задач со словами и головоломок, чем показано в видеороликах, а также некоторые уроки, которые не включены в этот набор видеороликов.

Мария Миллер

5-й класс по математике | Бесплатные онлайн-математические игры

1 класс

2 класс

3 класс

4 класс

5 класс

6 класс

Веселые игры для детей

Математические игры для 5-го класса

Обзор игры: Десятичные дроби в погоне за щенками

Реклама | Без рекламы

Операции и алгебраическое мышление

Конфеты Вызов

Загадка глубоководной математики

Four Wheel Fracas

Марсианские ховерборды

Блоки мышления

Музыкальный микс

Показатели

Сделайте число

Shuttle Mission Jr

Monster Mischief

PEMDAS Экспонат

Один продукт

Math Hop

Удаленные функции

Пазлы с числами

Shuttle Mission Pro

Сопряжение факторов

Применить умножение

Дивизион Дерби

Умножение следов

Человек-математик

Блоки умножения

Pony Pull Division

Tug Team Multiplication

Умножение Гран-при

10 Маха, кратное

Demolition Derby

Космическая гонка

Дивизион дрэг-рейсинга

Блоки продуктов

Мозг

Выдры

Алгебраическое мышление

Быстрый расчет

Число и оперативная база десять

Визуальный отдел

Умножение недостающих цифр

Дивизион отсутствующих цифр

Коммутативное видео

Ассоциативное видео

Распределительное видео

Добавление недостающих цифр

Вычитание отсутствующих цифр

Число и операции с дробями

Десятичные образцы

Десятичные дроби для щенков

Десятичные

Дроби на прогулке с монстрами

Десятичные числа для построителя мостов

Задачи с дробными словами

Сложение дробей

Добавление дробей Pro

Добавление дробей Введение

Фракции строителя мостов

Galaxy Pals Fractions

Дроби

Пицца Панды

Столбцы фракций

Математические дроби превосходят

Galaxy Pals Decimals

Десятичные

Умножение дробей

Decention Jr

Дроби

процентов

Пропорции велосипеда для грязи

Процент превосходства по математике

Пазлы с десятичными числами

Сложить дроби

Измерения и данные

Кубическая перспектива

Инопланетные углы

Линейные графики Видео

Ракетные углы

Геометрия

Космический граф

(un) Земляные черви

Географическая доска

Узорчатые блоки

Спасательная миссия

Код чертежа

Художник с отражением

Художник вращения

Area Snatch Pro

Perimeter Snatch Pro

Искусство уравнения

Игры на логику и решение задач

Cookie Trail

Утиная жизнь 4

Ледяные супер слайды

Кролик Самурай 2

Duck Life Space

Ледяная пурпурная голова 2

Лазерная ловушка

Кролик Самурай

Красный блок возвращается

3

Красный блок возвращается

2

Красный блок возвращается

Пурпурный крот Moley

Fox Journey

Доктор Желудь 3

Обрушение лабиринта

3

Обрушение лабиринта

2

Обрушение лабиринта

Острова роботов PLUS

Гольф Энди

Острова Роботов

Коробки Zippy

Лампочка

Ловушка для мыши

Парковка

Зеленая миссия

Пространственное спасение

Лампочка 3

Приключения Том

Fox Adventurer

Острова существ

Распоряжение 2

Джелли Дудс

Тренажер для мозга

Лучи света

Джон Лайтнинг

Время ClickPLAY 6

Ромб

Распоряжение

Клоки

Синий ящик

В штучной упаковке

Без точки

Суммы перекрытия

Наполнение

Филлтреки

Суммарные стеки

Шахматы

Лампочка 2

Двойная доставка

Переверните диски

Шашки

Джемпер Peg

Манкала

Наконечник для метчика

Склад

Четыре в ряд

Игры в слова

Spelling Bees

Двойные гласные

Правописание слов

Времена глаголов

Sky Chase Typing

Giraffe Karts — Грамматика

Части речи

Антонимы и синонимы

Форсунки для набора слов

Синонимы

Бампер Boat Bash

Octo Feed — омофоны

Яростные лягушки — Антонимы

Орфография

Набор текста

География Игры

Штаты I

Штаты II

Страны I

Страны II

МАТЕМАТИЧЕСКАЯ ИГРОВАЯ ПЛОЩАДКА
Игры для 1-го класса
Игры для 2-го класса
Игры для 3-го класса
Игры для 4-го класса
Игры для 5-го класса
Игры для 6-го класса
Блоки мышления
Видео по математике МАТЕМАТИЧЕСКИЕ ИГРЫ
Игры на сложение
Игры на вычитание
Игры на умножение
Игры на деление
Игры на дроби
Игры на соотношение
Игры на предварительную алгебру
Игры на геометрию ОБУЧАЮЩИЕ ИГРЫ
Логические игры
Классические игры
Орфографические игры
Грамматические игры
Игры с набором текста
Географические игры
Математические головоломки
Пространственное мышление
ДЕТСКИЕ ИГРЫ
Веселые игры
Приключенческие игры
Автомобильные игры
Спортивные игры
Endless Runner
Perfect Timing
Многопользовательские игры
Все игры Реклама | Без рекламы

---

О нас Политика конфиденциальности Условия использования Условия оплаты Получить помощь

Авторские права © ООО «Математическая площадка, 2021» • Все права защищены.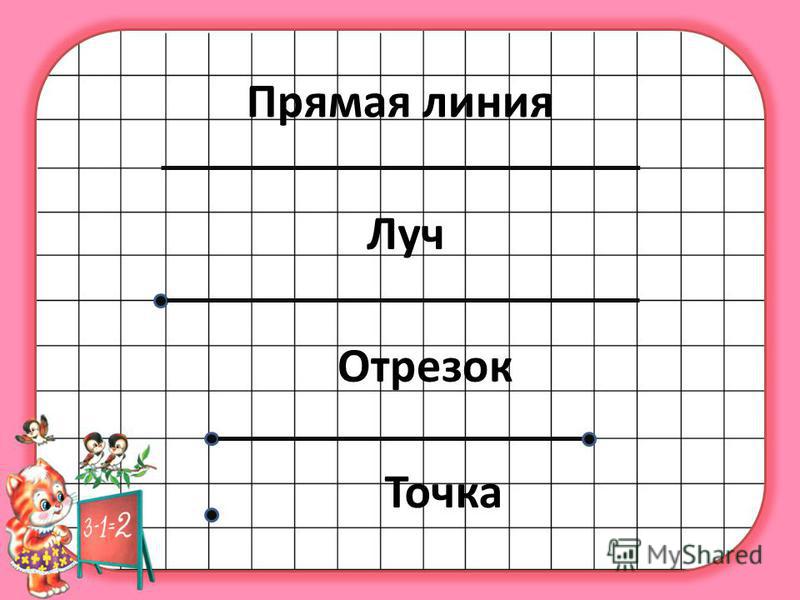

GRADE 5 Классные бесплатные онлайн-математические игры для детей

Найдите фрукт, который весит больше всего, в этой простой игре с неограниченным взвешиванием.Играть может быть просто, но некоторые из верхних уровней могут быть сложными. К счастью, есть видео, которое поможет.

MathPup не боится призраков, но пылесосы, ловцы собак, грозы и ванны заставляют MathPup немного нервничать. Так что используйте свои навыки умножения, чтобы помочь MathPup отогнать их!

Используйте свои навыки умножения, чтобы безопасно провести танк через минное поле. Нужно больше времени, чтобы решить задачу умножения? Нет проблем, просто нажмите на свой танк, чтобы поставить его на паузу!

MathPup ведет перетягивание каната на своем снегоходе.Найдите ответ на задачи умножения, чтобы дать снегоходу MathPup дополнительную тяговую мощность. Тебе нужно действовать быстро, ведь его противники сильны!

MathPup ищет кошку-грабителя. Решите задачу умножения, чтобы помочь MathPup поймать грабителя. 3 режима сложности на выбор.

Воспользуйтесь рентгеновским аппаратом, чтобы увидеть в коробке задачу умножения. Решите проблему, а затем перетащите поле в поле правильного ответа.

Воспользуйтесь рентгеновским аппаратом, чтобы увидеть проблему разделения в коробке.Выясните ответ на проблему, а затем перетащите поле в поле правильного ответа.

Соберите эти летающие тарелки и избавьтесь от них до того, как они приземлятся, округлив их числа до ближайшего 10. Игра типа Space Invaders с округлением чисел.

Воспользуйтесь рентгеновским аппаратом, чтобы увидеть вопрос округления в рамке. Округлите число, а затем перетащите рамку в поле ответа, содержащее округленное число.

Делите числа, чтобы ваш танк благополучно прошел через минное поле.Нужно больше времени, чтобы решить проблему разделения? Нет проблем, просто нажмите на свой танк, чтобы поставить его на паузу!

MathPup ведет перетягивание каната на своем снегоходе. Найдите решение проблем с разделением, чтобы дать снегоходу MathPup дополнительную тяговую мощность. Тебе нужно действовать быстро, ведь его противники сильны!

MathPup ищет кошку-грабителя. Решите задачу деления, чтобы помочь MathPup поймать грабителя. 3 режима сложности на выбор.

Стреляйте десятичными снежками в снежных ноидов, чтобы они не захватили форт MathPup.Правильно ответьте на задачи сложения, вычитания, умножения и деления, чтобы выбить Ноиды с экрана!

Найдите средства с цифрами, чтобы безопасно провести танк через минное поле. Нужно больше времени, чтобы найти среднее значение? Нет проблем, просто нажмите на свой танк, чтобы поставить его на паузу!

Найдите эквивалентные дроби, чтобы безопасно провести танк через минное поле. Нужно больше времени, чтобы найти эквивалентную дробь? Нет проблем, просто нажмите на свой танк, чтобы поставить его на паузу!

Сделайте рентгеновский снимок коробки, чтобы увидеть фракцию внутри нее. Затем перетащите его на эквивалентную дробь в поле ответа. Вы можете не торопиться, так как эта игра не имеет времени.

Mathpup пробует свои навыки рыбной ловли и математики, чтобы поймать рыбу. Помогите MathPup поймать рыбу, содержащую дробь, эквивалентную его дроби. Никаких ограничений по времени и много рыбы!

Mathpup пробует свои навыки рыбной ловли и сложения дробей, чтобы поймать рыбу. Помогите MathPup поймать рыбу, которая правильно отвечает на задачу сложения дробей.И вы можете не торопиться, так как ограничений по времени нет.

Игра в жанре «три в ряд» с математическим уклоном. Практикуйте свои навыки сложения десятичных дробей в этой увлекательной математической игре «три в ряд». Неограниченная игра с 3 уровнями сложности на выбор.

Игра в жанре «три в ряд» с математическим уклоном. Практикуйте свои навыки десятичного вычитания в этой увлекательной математической игре в жанре «три в ряд». Неограниченная игра с 3 уровнями сложности на выбор.

Игра в жанре «три в ряд» с математическим уклоном.Практикуйте свои навыки десятичного умножения в этой увлекательной математической игре в жанре «три в ряд». Неограниченная игра с 3 уровнями сложности на выбор.

Игра в жанре «три в ряд» с математическим уклоном. Практикуйте свои навыки десятичного деления в этой веселой математической игре в жанре «три в ряд». Неограниченная игра с 3 уровнями сложности на выбор.

Проезжайте сквозь пробки, чтобы узнать, как далеко вы можете проехать, прежде чем разбиться или закончится топливо. Вам нужно будет правильно решать задачи сложения десятичных дробей, чтобы ваш гоночный автомобиль был заправлен топливом.

Проезжайте сквозь пробки, чтобы узнать, как далеко вы можете проехать, прежде чем разбиться или закончится топливо. Вам нужно будет правильно решить задачи на вычитание десятичной дроби, чтобы гоночная машина оставалась заправленной топливом.

Проезжайте сквозь пробки, чтобы узнать, как далеко вы можете проехать, прежде чем разбиться или закончится топливо. Вам нужно будет правильно решить задачи десятичного умножения, чтобы ваша гоночная машина была заправлена ​​топливом.

Проезжайте сквозь пробки, чтобы узнать, как далеко вы можете проехать, прежде чем разбиться или закончится топливо.Вам нужно будет правильно решить задачи с десятичным делением, чтобы ваша гоночная машина была заправлена ​​топливом.

Сделайте рентгеновский снимок коробки, чтобы увидеть внутри нее десятичную дробь. Затем перетащите его в нужное поле ответа. Начинается с задач сложения десятичных дробей, в то время как на более поздних уровнях возникают дополнительные проблемы и возникают проблемы с десятичным вычитанием, умножением и делением. Вы можете не торопиться, так как эта игра не имеет времени.

Стреляйте десятичными снежками в снежных ноидов, чтобы они не захватили форт MathPup.Стреляйте в Ноид с десятичной дробью, которая составляет 1 при добавлении к номеру Ноида. Это выбьет Ноид с экрана!

Mathpup пробует свои навыки рыбной ловли, чтобы поймать рыбу с десятичным числом. Помогите MathPup поймать рыбу, содержащую десятичную дробь. Не торопитесь, рыбы много и нет ограничений по времени.

Mathpup пробует свои навыки рыбной ловли, чтобы поймать рыбу с десятичным числом. Помогите MathPup поймать рыбу, содержащую ответ на десятичную задачу (сложение или вычитание).Не торопитесь, рыбы много и нет ограничений по времени.

Стреляйте водой в бомбу, расположенную в правильной паре координат x, y, чтобы обезвредить ее, прежде чем она взорвется. Не стреляйте водой не в ту бомбу, иначе она взорвется!

Безопасно проведите кита к финишу. Вам нужно будет планировать заранее, так как как только вы нажмете кнопку «Переместить», кит не остановится, пока не достигнет финишной черты или не столкнется с препятствием!

Помогите пчелам доставить мед в нужное место в улье, используя их упорядоченную пару.

Очистите квадранты, удалив злодеев, определив упорядоченную пару, связанную с их местоположением. Выберите для игры в обычном или временном режиме в квадранте 1 или во всех 4 квадрантах.

Версия 2 игры с координатной сеткой Rocket Down с улучшенной графикой и игровым процессом. Выберите для игры следующие режимы: Untimed, Beginner, Advanced и Expert

.

Fly MathPup, чтобы получить кости, используя пару координат, которую дает вам MathPup. Избегайте столкновений с астероидами и не позволяйте инопланетянам украсть все кости MathPup..

Возьмите топливные баки, расположенные на координатной сетке, чтобы замедлить ракету для безопасной посадки. Слишком тяжело приземлиться, и игра окончена!

CCSS: 5.G.A.1, 5.G.A.2
Перемещайтесь по координатам x, y, чтобы вовремя добраться до финиша, собирая монеты и избегая препятствий. Прочтите внутриигровые инструкции или посмотрите видео с советами и инструкциями: Видео с координатами лодки

CCSS: 5.G.A.1, 6.NS.C.6c
Управляйте своей лодкой, чтобы получить флаг на координатной сетке, избегая препятствий.

Перетащите жемчужину числа, содержащую ответ, в банку с решением.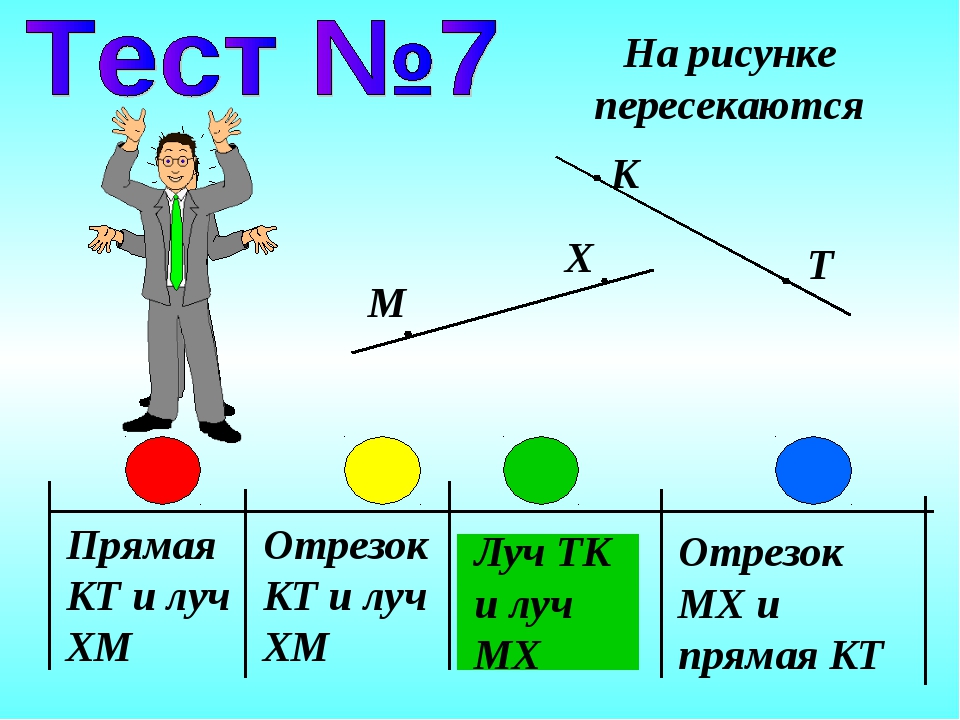 Выберите, чтобы попрактиковаться в поиске решений задач наименьшего общего кратного (НОК), наибольшего общего множителя (НОК), квадратного корня или экспоненты.

Помогите MathPup очистить поле в этой игре с геометрическими совпадениями, где вам нужно будет сопоставить геометрические объекты с их именами. 3 уровня навыков на выбор.

Получите MathPup его кости, вычислив угол между костями и MathPup К счастью, у вас есть транспортир на экране для определения углов.

Помогите MathPup выиграть кости, стреляя пузырями под заданным углом. Транспортира нет, поэтому вам нужно оценить угол, и чем ближе вы приблизитесь, тем больше костей выиграет MathPup.

Еще больше спрятанных костей для MathPup! Помогите MathPup, остановив угол расширения, когда он достигнет целевого угла.

Нажмите на карточки MathPup, чтобы увидеть, что под ними! Чтобы получилась спичка, переверните два одинаковых угла. Сопоставьте все карты, чтобы пройти уровень.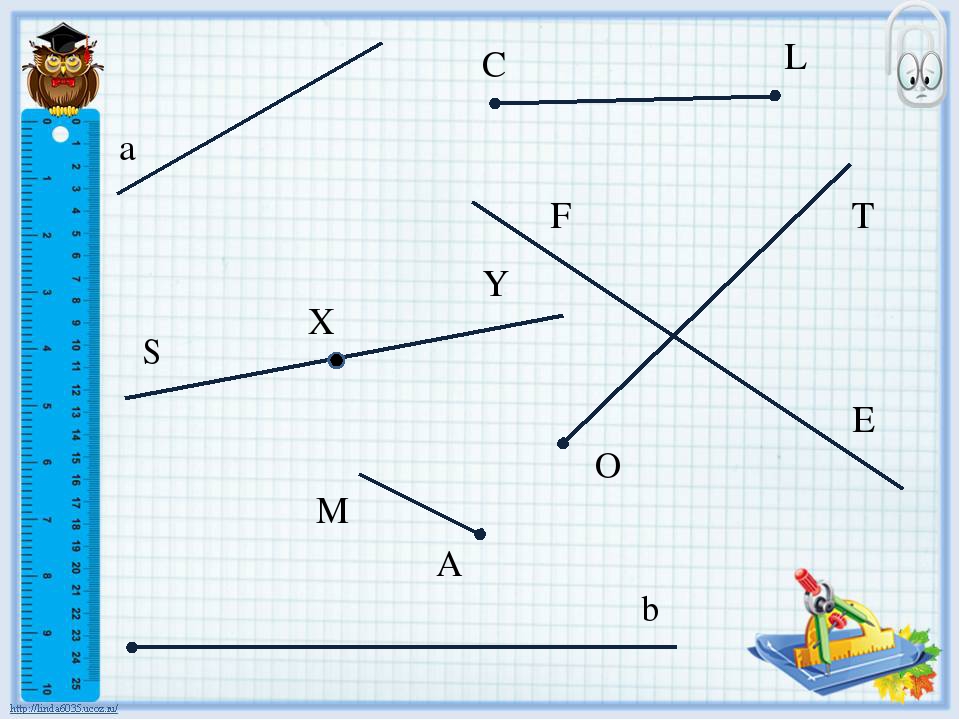

Нажмите на карточки MathPup, чтобы увидеть, что под ними! Составьте совпадение, соединив угол с его количеством градусов. Сопоставьте все карты, чтобы пройти уровень.

Уничтожайте вражеские танки, но выбирайте количество, чтобы стрелять с умом, чтобы не стрелять в собственные танки. Чтобы преуспеть, вам нужно знать факторные пары чисел. Играйте против другого игрока или против компьютера.

Определите, является ли утверждение о факторах верным или ложным, чтобы найти совпадения в этой игре «три в ряд» с математическим уклоном.3 уровня сложности на выбор.

Найдите множители данного числа, чтобы ваш танк благополучно прошел через минное поле. Нужно больше времени, чтобы выяснить, какая мина содержит фактор? Нет проблем, просто нажмите на свой танк, чтобы поставить его на паузу!

Догони свой мотоцикл до финиша. Соревнуйтесь с некоторыми сильными соперниками и попытайтесь победить их всех, определяя числовые коэффициенты.

Вождение автомобиля для MathPup — непростая задача, и что еще сложнее, так это выбрать правильный пункт взимания платы за проезд.Помогите MathPup выбрать плату за проезд, которая содержит коэффициент целевого числа.

Просто перетащите камень ответов в банку. 4 навыка на выбор: LCM, GCF, Exponents или Square Roots. & Nbps; Вы можете играть по расписанию или без него, и есть 3 уровня сложности на выбор.

Бесплатная программа обучения математике на дому — Жизнь в ботанике

---

Учебная программа начальной математики (классы K-5)

---

Обычный и не такой простой
С сайта: Я верю в то, что могу делиться плодами своего труда и хочу, чтобы любой родитель, который не может позволить себе учебную программу, мог обучать своего ребенка дома.Это будет стоить вам чернил для принтера и бумаги, вот и все !!!

Бесплатная математическая программа
Бесплатная математическая программа — это исключительно высококачественная математическая программа, охватывающая все математические навыки, которым следует обучать в 1–5 классах.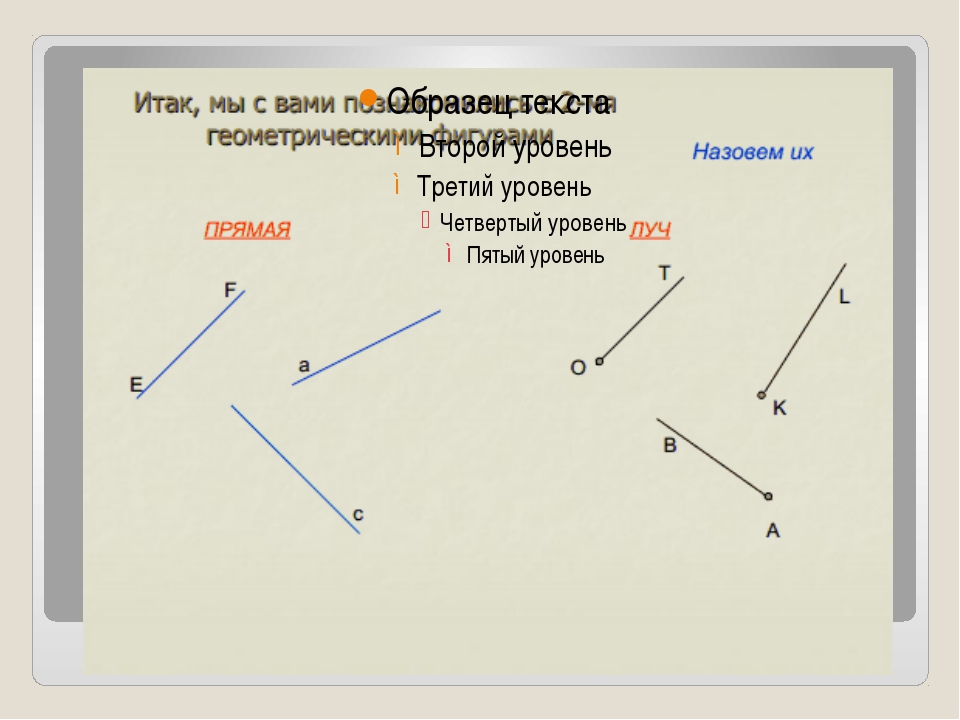 Эта программа была разработана путем проведения полного анализа учебников математики из различных источников (включая учебники по математике из школьного округа Флориды, получившего наивысшие баллы). На основе этой информации они смогли составить подробный список определенных математических навыков, которым следует обучать в каждом начальном классе.

Easy Peasy All-in-One Homeschool
Онлайн-курс совершенно бесплатный, с бесплатными рабочими листами для печати. Если вы предпочитаете не печатать или не можете печатать, вы можете заказать рабочую книгу с печатными формами, прилагаемую к онлайн-курсу, или рабочую тетрадь и руководство для родителей, составляющие автономный курс. Я привязал к каждому из них для вашего удобства.

Little House Kindergarten Math
180 дней для печати Учебная программа для детского сада по математике, созданная бывшей классной учительницей, которая стала мамой, работающей на дому.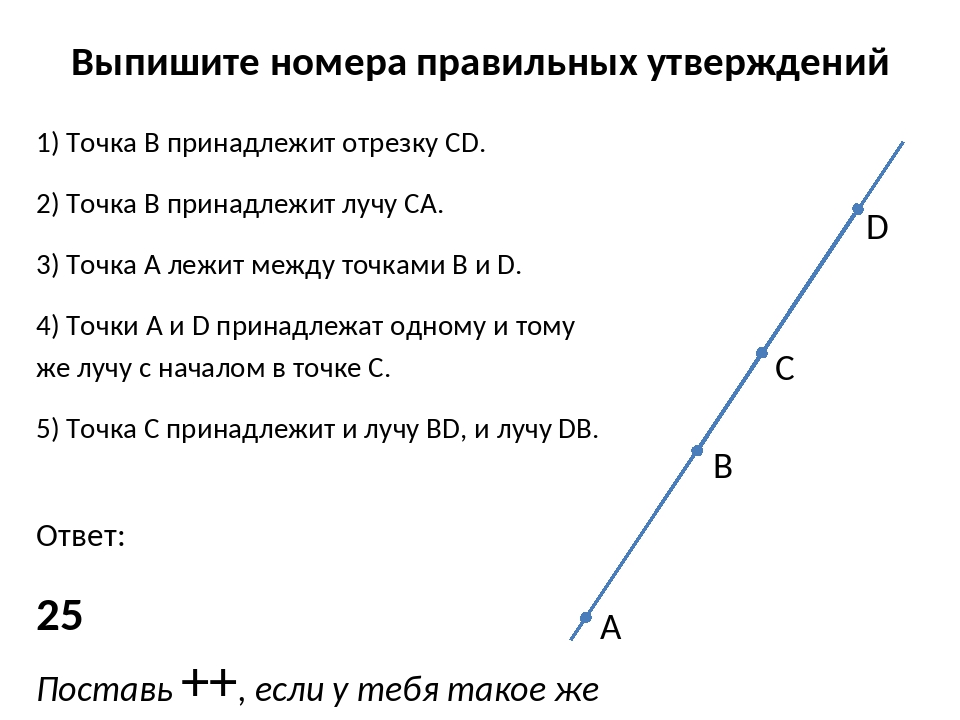

Miniature Masterminds
Полная 36-недельная печатная рабочая тетрадь по математике для детей от детского сада до второго класса.

Программа по математике для общеобразовательной школы
CSMP был разработан Национальным институтом образования в качестве образцовой учебной программы для других. Несмотря на то, что многие пьесы были адаптированы, примерно тридцать лет спустя есть несколько программ, которые можно сравнить. Каждая оценка включает файлы уроков, рабочие листы, мастера Blackline, сборники рассказов и учебники рассказов.

cK -12 Элементарная математика — 1–5 классы
CK-12 Программы по математике состоят из интерактивных уроков, видео, практических занятий и рабочих листов. Эта программа согласована с Common Core.

Центр инноваций в преподавании математики — Программа совершенствования математики
Каждый год есть учебники, подробные планы уроков и копии мастер-классов, которые будут использоваться на уроках, а также общая информация о проекте Primary MEP.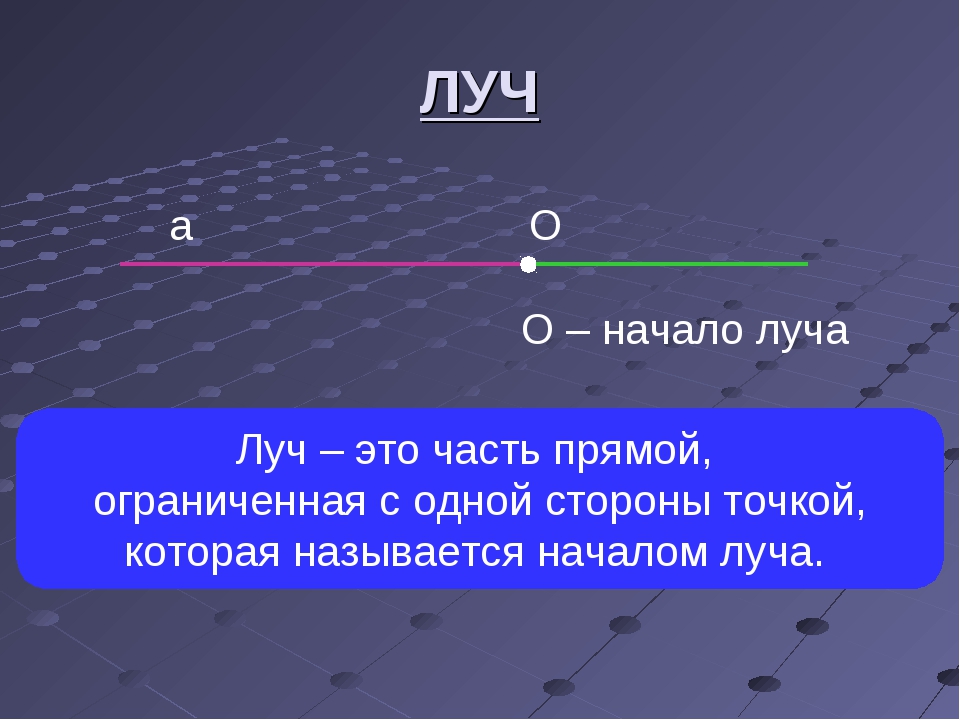

Match Fishtank
Цель наших программ по математике — дать нашим ученикам навыки и знания, которые потребуются им для успешной учебы в колледже и за его пределами. В Match мы стремимся вдохновить наших учеников на прохождение углубленных курсов математики и даем им основы, которые потребуются им для успешного изучения математики на высшем уровне.

Арифметика Рэя — включая выпуски для учителей для 3-5 классов
Полностью бесплатные учебники и руководство для учителей по Арифметике Рэя, старой программе, которая находится в свободном доступе.

Под домом
Эта учебная программа вдохновлена ​​Шарлоттой Мейсон и охватывает все предметы в классе K-4, включая математику. 5 класс сейчас в процессе.

.

No related posts.