метр — это… Что такое метр?
метр — метр, а … Русский орфографический словарь
МЕТР — (греч. мера). 1) стопа в стихе, а также размер ритмического движения в музыке. 2) французская мера длины, десятимиллионная часть четверти земной окружности = 1 арш. и 2,5 верш. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А … Словарь иностранных слов русского языка
МЕТР — (греч. metron мера) 1) основная единица длины СИ.2) мера длины, воспроизводящая единицу длины метр. Согласно определению, принятому 17 й Генеральной конференцией по мерам и весам (1983), метр длина пути, проходимого светом в вакууме за 1/299 792… … Большой Энциклопедический словарь
МЕТР — 1. МЕТР1, метра, муж. (греч. metron мера). Международная единица длины, равная одной сорокамиллионной части меридиана. Метр равен 1,4061 аршина. Метр содержит сто сантиметров. Кубический метр.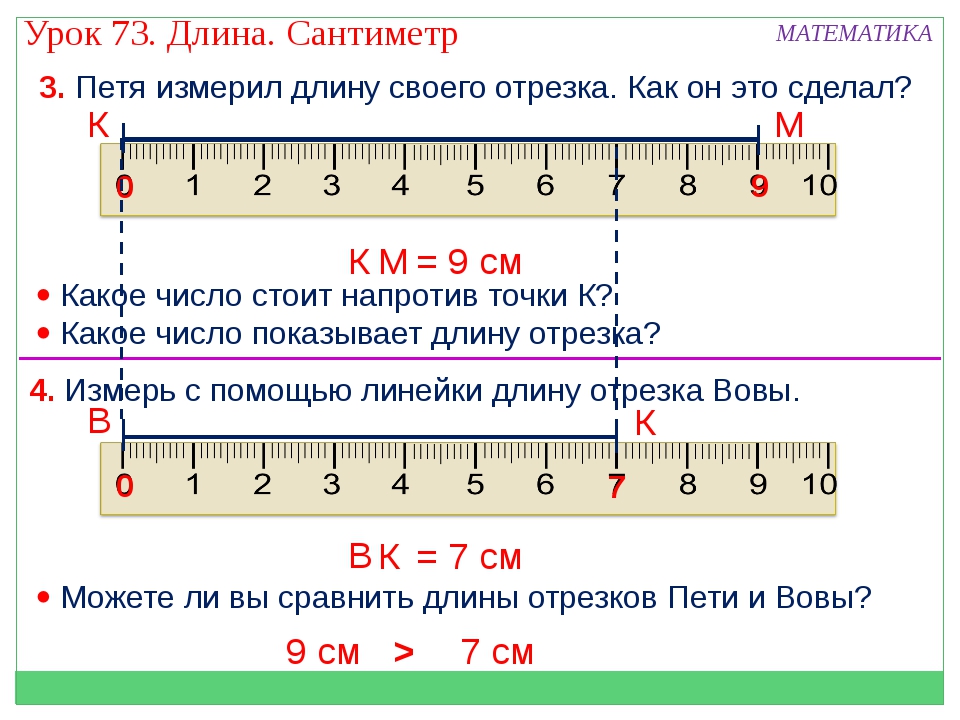
МЕТР — 1. МЕТР1, метра, муж. (греч. metron мера). Международная единица длины, равная одной сорокамиллионной части меридиана. Метр равен 1,4061 аршина. Метр содержит сто сантиметров. Кубический метр. Комната в 10 квадратных метров. || Металлическая,… … Толковый словарь Ушакова
МЕТР — 1. МЕТР1, метра, муж. (греч. metron мера). Международная единица длины, равная одной сорокамиллионной части меридиана. Метр равен 1,4061 аршина. Метр содержит сто сантиметров. Кубический метр. Комната в 10 квадратных метров. || Металлическая,… … Толковый словарь Ушакова
метр — 1. МЕТР1, метра, муж. (греч. metron мера). Международная единица длины, равная одной сорокамиллионной части меридиана. Метр равен 1,4061 аршина. Метр содержит сто сантиметров. Кубический метр. Комната в 10 квадратных метров. || Металлическая,… … Толковый словарь Ушакова
метр — 1.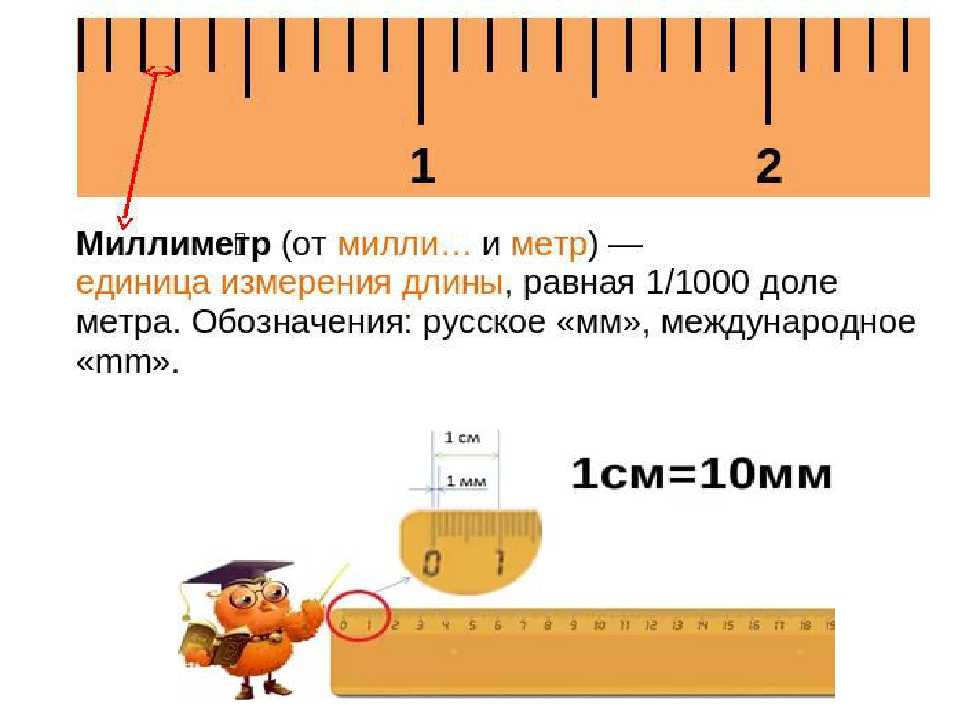 МЕТР1, метра, муж. (греч. metron мера). Международная единица длины, равная одной сорокамиллионной части меридиана. Метр равен 1,4061 аршина. Метр содержит сто сантиметров. Кубический метр. Комната в 10 квадратных метров. || Металлическая,… … Толковый словарь Ушакова
МЕТР1, метра, муж. (греч. metron мера). Международная единица длины, равная одной сорокамиллионной части меридиана. Метр равен 1,4061 аршина. Метр содержит сто сантиметров. Кубический метр. Комната в 10 квадратных метров. || Металлическая,… … Толковый словарь Ушакова
метр — 1. МЕТР1, метра, муж. (греч. metron мера). Международная единица длины, равная одной сорокамиллионной части меридиана. Метр равен 1,4061 аршина. Метр содержит сто сантиметров. Кубический метр. Комната в 10 квадратных метров. || Металлическая,… … Толковый словарь Ушакова
МЕТР — 1. МЕТР1, метра, муж. (греч. metron мера). Международная единица длины, равная одной сорокамиллионной части меридиана. Метр равен 1,4061 аршина. Метр содержит сто сантиметров. Кубический метр. Комната в 10 квадратных метров. || Металлическая,… … Толковый словарь Ушакова
Величина в математике — это что такое
Величина рассматривается как одна из основ математики, в частности одного из ее разделов — геометрии. Это понятие уходит глубоко в прошлое. Оно было описано в III веке до н. э. древнегреческим математиком Евклидом в его труде «Начала». Люди применяли величины на протяжении более двух тысяч лет, пока они не подверглись ряду обобщений.
Это понятие уходит глубоко в прошлое. Оно было описано в III веке до н. э. древнегреческим математиком Евклидом в его труде «Начала». Люди применяли величины на протяжении более двух тысяч лет, пока они не подверглись ряду обобщений.
Величина в математике — это очень важная тема для изучения в школе. Фактически из понимания детьми величины строится дальнейшее обучение от простого к все более сложному. Измеряя линейкой различные отрезки и площадь, взвешивая на весах массу, определяя скорость, исходя из расстояния и времени, ребенок постепенно учится постигать материальный мир и строит свою картину восприятия, а также определяет для себя роль математики в окружающем мире.
Понятие величины в математике
Величина в математике — это свойство объектов, которое поддается измерению путем сопоставления с единицей измерения, относящейся к величине этого рода. Выделяют длину, массу, объем, скорость, площадь и время. Говоря простым языком, это то, что можно измерить и выразить числом.
Данный раздел математики ученики проходят еще в начальной школе, и все измерения на этом этапе производятся натуральными числами величины. В математике младших классов такой числовой ряд представляет собой последовательность чисел от 1 и до бесконечности. В старших классах для расчетов величины используются также числа и с отрицательным значением.
Исторический очерк
В древних цивилизациях, в основном в связи с обширным развитием торговли, возникла потребность в измерениях товаров, определении расстояния, времени, расчете посевных площадей и прочего. Сначала люди измеряли предметы при помощи сравнения их с человеком или животным. Но все эти меры были довольно относительными, ведь у каждого свои пропорции тела, а величина в математике — это в первую очередь точность. Поэтому со временем возникла необходимость в создании единого эталона системы величин.
Так, во Франции в 1791 году во время Великой революции единицей измерения длины было принято считать метр, который составлял одну сорокамиллионную часть земного меридиана, пересекающего Париж. Кроме метра была установлена такая величина, как килограмм. Он был равен одному кубическому дециметру воды при температуре 4 °С. А также ар как мера площади, литр и грамм.
Кроме метра была установлена такая величина, как килограмм. Он был равен одному кубическому дециметру воды при температуре 4 °С. А также ар как мера площади, литр и грамм.
Так как в основе новых величин был метр, то и система измерения стала называться метрической. В Национальном архиве Франции до сих пор лежат платиновые эталоны метра в виде линейки со штрихами на концах и килограмма в виде цилиндрической гири.
Русская система измерения
С Древней Руси до принятия в Российской империи метрической системы мер принято было производить замеры с помощью длины локтя, ширины ладони, длины стопы — фут. Расстояние от кончика вытянутой вверх руки до пятки противоположной ноги называлось сажень, расстояние между вытянутыми руками — маховая сажень и т. д. Для измерения расстояния брали, например, слышимость петушиного крика или способность лошади без отдыха добраться из пункта А в пункт Б. Так люди измеряли дальность проложенного маршрута.
Даже сейчас в пословицах и поговорках мы можем встретить напоминания о существовании старинных величин. Об этом свидетельствую такие выражения, как «слышать за версту», «косая сажень в плечах», «мерить на свой аршин» и другие крылатые фразы.
Об этом свидетельствую такие выражения, как «слышать за версту», «косая сажень в плечах», «мерить на свой аршин» и другие крылатые фразы.
В 1899 году, 4 июня была принята единая метрическая система, которая являлась необязательной. Обязательной она стала 14 сентября 1918 года уже при советской власти, практически сразу после Великой октябрьской революции.
Основные математические величины
Дети в школе, изучая величины в математике, к 4 классу уже имеют широкое представление о таких значениях, как длина, масса, объем, площадь, скорость и время.
- Под длиной предмета принято понимать характеристику линейного размера. Ее измеряют в миллиметрах, сантиметрах, дециметрах, метрах и километрах. Эту тему в школе дети проходят, начиная с первого класса.
- Масса предмета — еще одна физическая величина, измеряемая в основном граммами и килограммами. А также объем тел, который исчисляется литрами и миллилитрами. Однако не стоит вводить ребенка в заблуждение и считать массу и вес равными понятиями.
 Масса — это постоянная величина в математике, в то время как вес зависит от силы и скорости притяжения объекта к земле.
Масса — это постоянная величина в математике, в то время как вес зависит от силы и скорости притяжения объекта к земле. - Под площадью геометрической фигуры принято понимать занимаемое ею пространство на плоскости, которое исчисляется в мм2, см2, дм2, м2 и км2.
- Время — понятие довольно относительное и для человека связано с его ощущениями, его нельзя увидеть, но можно почувствовать в смене дня, ночи и времен года. Поэтому для знакомства детей с понятием времени используют точные приборы, такие как песочные часы и часы со стрелкой. Время исчисляется секундами, минутами, часами, днями, годами и так далее.
- На основании пройденной темы о времени и длине дети изучают понятие скорости. По сути, скорость — это отрезок пути, пройденный за некоторое время.
Бесконечная величина измерения в математике
В старших классах школьниками изучается тема бесконечно малых и больших чисел. Это те числовые значения, которые либо стремятся к нулю, либо к бесконечности.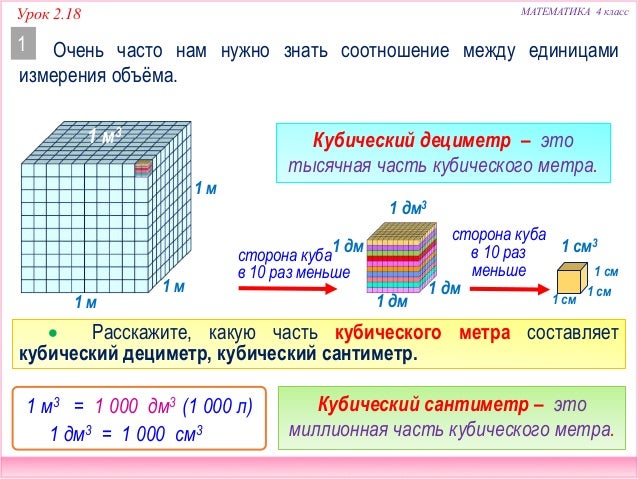 Масса дрейфующей льдины в океане, которая находится в процессе таяния, будет относиться к бесконечной малой величине. Ведь под воздействием беспрерывного тепла лед растает, и масса глыбы будет равна нулю. Противоположным процессом с точки зрения физики является расширение Вселенной. Она стремится к бесконечно большой величине, расширяя свои пределы.
Масса дрейфующей льдины в океане, которая находится в процессе таяния, будет относиться к бесконечной малой величине. Ведь под воздействием беспрерывного тепла лед растает, и масса глыбы будет равна нулю. Противоположным процессом с точки зрения физики является расширение Вселенной. Она стремится к бесконечно большой величине, расширяя свои пределы.
Постоянная и переменная величина
В процессе развития математики величины были разделены на два класса: постоянные и переменные.
Постоянная величина, или так называемая научным языком константа, остается неизменной, то есть при любых условиях она сохраняет свое значение. Например, для расчета длины окружности используется постоянная величина «Пи» = 3,14. Константа Пифагора √2=1,41, используемая в математике, также неизменна. Постоянная величина является частным случаем и рассматривается как переменная величина с одинаковым значением.
Переменная величина в математике — это обратный процесс, который по различным причинам меняет свое числовое значение.
Погонный метр Википедия
Метр
Согласно действующему определению, метр есть длина пути, проходимого светом в вакууме за интервал времени 1/299 792 458 секунды
Определение метра
Современное определение метра в терминах времени и скорости света было принято XVII Генеральной конференцией по мерам и весам (ГКМВ) в 1983 году[2][3].
Метр — длина пути, проходимого светом в вакууме за интервал времени 1/299 792 458 секунды.
Из этого определения следует, что в СИ скорость света в вакууме принята равной в точности 299 792 458 м/с. Таким образом, определение метра, как и два столетия назад, вновь привязано к секунде, но на этот раз с помощью универсальной мировой константы.
Изменения определений основных единиц СИ 2018—2019 годов не затронуло метр с содержательной точки зрения, однако из стилистических соображений было принято формально новое определение, полностью эквивалентное предыдущему[4]:
Метр, обозначение м, является единицей длины в СИ; его величина устанавливается фиксацией численного значения скорости света в вакууме c{\displaystyle c} равным в точности 299 792 458, когда она выражена единицей СИ м·с−1, где секунда определена через частоту перехода в цезии ΔνCs{\displaystyle \Delta \nu _{\text{Cs}}}.
Кратные и дольные единицы
В соответствии с полным официальным описанием СИ, содержащемся в действующей редакции Брошюры СИ (фр.
| Кратные | Дольные | ||||||
|---|---|---|---|---|---|---|---|
| величина | название | обозначение | величина | название | обозначение | ||
| 101 м | декаметр | дам | dam | 10−1 м | дециметр | дм | dm |
| 102 м | гектометр | гм | hm | 10−2 м | сантиметр | см | cm |
| 103 м | километр | км | km | 10−3 м | миллиметр | мм | mm |
| 106 м | мегаметр | Мм | Mm | 10−6 м | микрометр | мкм | µm |
| 109 м | гигаметр | Гм | Gm | 10−9 м | нанометр | нм | nm |
| 1012 м | тераметр | Тм | Tm | 10−12 м | пикометр | пм | pm |
| 1015 м | петаметр | Пм | Pm | 10−15 м | фемтометр | фм | fm |
| 1018 м | эксаметр | Эм | Em | 10−18 м | аттометр | ам | am |
| 1021 м | зеттаметр | Зм | Zm | 10−21 м | зептометр | зм | zm |
| 1024 м | иоттаметр | Им | Ym | 10−24 м | иоктометр | им | ym |
| применять не рекомендуется не применяются или редко применяются на практике | |||||||
Соотношение с другими единицами длины
| Метрическая единица, выраженная через единицу, не входящую в СИ | Единица, не входящая в СИ, выраженная через метрическую единицу | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 метр | ≈ | 39,37 | дюйма | 1 дюйм | ≡ | 0,0254 | метра | ||
| 1 сантиметр | ≈ | 0,3937 | дюйма | 1 дюйм | ≡ | 2,54 | сантиметра | ||
| 1 миллиметр | ≈ | 0,03937 | дюйма | 1 дюйм | ≡ | 25,4 | миллиметра | ||
| 1 метр | ≡ | 1⋅1010 | ангстрем | 1 ангстрем | ≡ | 1⋅10−10 | метра | ||
| 1 нанометр | ≡ | 10 | ангстрем | 1 ангстрем | ≡ | 100 | пикометров | ||
История
Один из публичных эталонов метра, установленных на улицах Парижа в 1795—1796 гг.
В Европе со времён распада империи Карла Великого не существовало общих стандартных мер длины: они могли быть стандартизированы в пределах одной юрисдикции (которая зачастую имела размеры одного торгового городка), но единых мер не было, и каждый регион мог иметь свои собственные. Причиной этого служило в какой-то мере то, что меры длины использовались в налогообложении (налог, например, мог измеряться в определённой длине полотна), а поскольку каждый местный правитель вводил свои налоги, то для соответствующей местности законами устанавливались свои единицы измерений[8].
С развитием науки в XVII веке стали раздаваться призывы к введению «универсальной меры» (universal measure
Метр — длина маятника
Идея Уилкинса заключалась в том, чтобы выбрать для единицы длины длину маятника с полупериодом колебаний, равным 1 с. Подобные маятники были незадолго до этого продемонстрированы Христианом Гюйгенсом, и их длина была весьма близка к длине современного метра (так же, как к единицам длины, использовавшимся в те времена, например, ярду). Однако вскоре было обнаружено, что длина, измеренная таким способом, различается в зависимости от места измерений. Французский астроном Жан Рише во время экспедиции в Южную Америку (1671—1673) обнаружил увеличение периода колебаний секундного маятника по сравнению с тем, который наблюдался в Париже. Выверенный в Париже маятник в процессе наблюдений им был сокращён на 1,25 французской линии (~ 2,81 мм), дабы избежать отставания во времени на 2 минуты в день. Это было первое прямое доказательство уменьшения силы тяжести по мере приближения к экватору, и это дало разницу в 0,3 % длины между Кайенной (во французской Гвиане) и Парижем[11].
Вплоть до французской революции 1789 года в вопросе установления «универсальной меры» не было никакого прогресса. Франция была озабочена вопросом распространения единиц измерений длины, необходимость реформы в этой области поддерживали самые различные политические силы. Талейран возродил идею о секундном маятнике и предложил её Учредительному собранию в 1790 году, с тем уточнением, что эталон длины будет измерен на широте 45° N (примерно между Бордо и Греноблем). Таким образом, метр получал следующее определение: метр — это длина маятника с полупериодом колебаний на широте 45°, равным 1 с (в единицах СИ эта длина равна g/π² · (1 с)2 ≈ 0,994 м).
Первоначально за основу было принято это определение (8 мая 1790, Французское Национальное собрание). Но несмотря на поддержку собрания, а также поддержку Великобритании и новообразованных Соединённых Штатов, предложение Талейрана так и не было осуществлено[12][Комм. 2].
Метр — часть Парижского меридиана
Крепость Монжуик — южный конец дуги меридианаВопрос реформы единиц измерения был отдан на рассмотрение Французской академии наук, которая создала специальную комиссию, возглавляемую инженером и математиком Жаном-Шарлем де Борда. Борда был ярым приверженцем перехода на десятичную систему исчисления: он усовершенствовал лимб повторительного теодолита, который позволял намного улучшить точность измерения углов на местности, и настаивал, чтобы инструмент калибровался в градах (1⁄100 четверти круга), а не в градусах, чтобы град делился на 100 минут, а минута — на 100 секунд[13]. Для Борда метод секундного маятника был неудовлетворительным решением, поскольку он основывался на существовавшей в то время секунде — недесятичной единице, которая не подходила для предлагавшейся к внедрению системы десятичного времени — системе, когда в одних сутках 10 часов, в часе 100 минут, а в минуте 100 секунд.
Борда был ярым приверженцем перехода на десятичную систему исчисления: он усовершенствовал лимб повторительного теодолита, который позволял намного улучшить точность измерения углов на местности, и настаивал, чтобы инструмент калибровался в градах (1⁄100 четверти круга), а не в градусах, чтобы град делился на 100 минут, а минута — на 100 секунд[13]. Для Борда метод секундного маятника был неудовлетворительным решением, поскольку он основывался на существовавшей в то время секунде — недесятичной единице, которая не подходила для предлагавшейся к внедрению системы десятичного времени — системе, когда в одних сутках 10 часов, в часе 100 минут, а в минуте 100 секунд.
Вместо метода секундного маятника комиссия — среди членов которой были Жозеф Луи Лагранж, Пьер-Симон Лаплас, Гаспар Монж и Кондорсе — решила, что новая единица измерения должна быть равна одной десятимиллионной расстояния от Северного полюса до экватора (четверть земной окружности), измеренного вдоль меридиана, проходящего через Париж[12]. Помимо той выгоды, что это решение давало лёгкий доступ для французских геодезистов, существовало такое важное достоинство, что часть расстояния от Дюнкерка до Барселоны (около 1000 км, то есть одна десятая от общего расстояния) могла быть проложена от начальных и конечных точек, расположенных на уровне моря, а как раз эта часть находилась в середине четверти окружности, где влияние формы Земли, которая не является правильным шаром, а сплюснута, было бы наибольшим[12].
Помимо той выгоды, что это решение давало лёгкий доступ для французских геодезистов, существовало такое важное достоинство, что часть расстояния от Дюнкерка до Барселоны (около 1000 км, то есть одна десятая от общего расстояния) могла быть проложена от начальных и конечных точек, расположенных на уровне моря, а как раз эта часть находилась в середине четверти окружности, где влияние формы Земли, которая не является правильным шаром, а сплюснута, было бы наибольшим[12].
30 марта 1791 предложение определить метр через длину меридиана было принято следующим: одна сорокамиллионная часть Парижского меридиана (то есть одна десятимиллионная часть расстояния от северного полюса до экватора по поверхности земного эллипсоида на долготе Парижа). Интересно, что в современных единицах это 11,00000000005{\displaystyle {\frac {1}{1{,}000\,000\,000\,05}}} метра. Идея привязать единицу измерения длины к меридиану Земли была не нова: аналогичным образом ранее были определены морская миля и лье.
Вновь определённая единица получила наименование «метр подлинный и окончательный» (фр. metre vrai et définitif)[1].
7 апреля 1795 Национальный Конвент принял закон о введении метрической системы во Франции и поручил комиссарам, в число которых входили Ш. О. Кулон, Ж. Л. Лагранж, П.-С. Лаплас и другие учёные, выполнить работы по экспериментальному определению единиц длины и массы. В 1792—1797 годах по решению революционного Конвента французские учёные Деламбр (1749—1822) и Мешен (1744—1804) за 6 лет измерили дугу парижского меридиана длиной в 9°40′ от Дюнкерка до Барселоны, проложив цепь из 115 треугольников через всю Францию и часть Испании. Впоследствии, однако, выяснилось, что из-за неправильного учёта полюсного сжатия Земли эталон оказался короче на 0,2 мм; таким образом, длина меридиана лишь приблизительно равна 40 000 км.
Первый прототип эталона метра был изготовлен из латуни в 1795 году.
Следует отметить, что единица массы (килограмм, определение которого было основано на массе 1 дм³ воды), тоже была привязана к определению метра.
В 1799 году был изготовлен из платины эталон метра, длина которого соответствовала одной сорокамиллионной части Парижского меридиана[14].
Во время правления Наполеона метрическая система распространилась по многим странам Европы. Выгода от её применения была столь очевидна, что и после отстранения Наполеона от власти принятие метрических единиц продолжалось[15]:
- 1816 — Бельгия и Голландия;
- 1832 — Португалия;
- 1849 — Испания и Греция;
- 1870 — Германия;
- 1873 — Австрия;
- 1875 — Швейцария.
К концу XIX века из крупных стран только в Великобритании (и её колониях), США, России, Китае и Османской империи остались традиционные меры длины.
На метре как единице длины и килограмме как единице массы была основана метрическая система, которая была введена «Метрической конвенцией», принятой на Международной дипломатической конференции 17 государств (Россия, Франция, Великобритания, США, Германия, Италия и др. ) 20 мая 1875 года[16].
) 20 мая 1875 года[16].
В 1889 году был изготовлен более точный международный эталон метра. Этот эталон изготовлен из сплава 90 % платины и 10 % иридия[17] и имеет поперечное сечение в виде буквы «X». Его копии были переданы на хранение в страны, в которых метр был признан в качестве стандартной единицы длины.
Дальнейшее развитие
В 1960 было решено отказаться от использования изготовленного людьми предмета в качестве эталона метра, и с этого времени по 1983 год метр определялся как число 1 650 763,73, умноженное на длину волны оранжевой линии (6 056 Å) спектра, излучаемого изотопом криптона 86Kr в вакууме. После принятия нового определения платино-иридиевый прототип метра продолжают хранить в Международном бюро мер и весов в тех условиях, что были определены в 1889 году. Однако теперь его статус стал иным: длина прототипа перестала считаться в точности равной 1 м и её фактическое значение должно определяться экспериментально. По своему первоначальному назначению прототип больше не используется.
К середине 1970-х годов был достигнут значительный прогресс в определении скорости света. Достаточно сказать, что если в 1926 году погрешность наиболее точных на то время измерений, выполненных А. Майкельсоном, составляла 4000 м/с[18], то в 1972 году сообщалось о снижении погрешности вплоть до 1,1 м/с[19]. После многократной проверки полученного результата в различных лабораториях XV Генеральная конференция по мерам и весам в 1975 году рекомендовала использовать в качестве значения скорости света в вакууме величину, равную 299 792 458 м/с с относительной погрешностью 4·10−9, что соответствует абсолютной погрешности 1,2 м/с[20]. Впоследствии в 1983 году именно это значение XVII Генеральная конференция по мерам и весам положила в основу нового определения метра[2].
| Основа | Дата | Абсолютная погрешность | Относительная погрешность |
|---|---|---|---|
| 1⁄10,000,000 часть четверти Парижского меридиана, определённая по результатам измерений, проведённых Деламбром и Мешеном | 1795 | 0,5—0,1 мм | 10−4 |
| Первый эталон Metre des Archives из платины | 1799 | 0,05—0,01 мм | 10−5 |
| Платино-иридиевый профиль при температуре таяния льда (1-я ГКМВ) | 1889 | 0,2—0,1 мкм | 10−7 |
| Платино-иридиевый профиль при температуре таяния льда и атмосферном давлении, поддерживаемый двумя роликами (VII ГКМВ) | 1927 | неизв. | неизв. |
| 1 650 763,73 длины волны оранжевой линии (6056 Å) спектра, излучаемого изотопом криптона 86Kr в вакууме (XI ГКМВ) | 1960 | 4 нм | 4·10−9[2] |
| Длина пути, проходимого светом в вакууме за (1/299 792 458) секунды (XVII ГКМВ) | 1983 | 0,1 нм | 10−10 |
Погонный метр
Погонный метр — единица измерения количества длинномерных объектов (так называемых погонажных изделий, материалов и т. п.), соответствующая куску или участку длиной 1 метр. Погонный метр ничем не отличается от обычного метра, это единица, которой измеряют длину материала независимо от ширины. Погонным метром могут, например, измерять кабельные каналы, доски, листы металла, трубы, плинтусы, оконные уплотнители, ткани. Хотя для тканей правильнее было бы измерять их площадь, но если ширина ткани подразумевается известной и постоянной — используется понятие «погонный метр» (как правило, ширина ткани составляет 1,4 м, и, таким образом, погонный метр ткани является куском 1,0×1,4 м). Говоря строго, в быту чаще используется понятие именно погонного метра, информация о ширине или высоте предметов подразумевается известной или не важной. Наименование погонного метра выделяется в специальной литературе либо для создания различной экспрессивной окраски речи.
Говоря строго, в быту чаще используется понятие именно погонного метра, информация о ширине или высоте предметов подразумевается известной или не важной. Наименование погонного метра выделяется в специальной литературе либо для создания различной экспрессивной окраски речи.
Метрологическая литература не рекомендует использовать термин «погонный метр». Общее правило заключается в том, что в случае необходимости поясняющие слова должны входить в наименование физической величины, а не в наименование единицы измерения. Поэтому, например, следует писать «погонная длина равна 10 м», а не «длина равна 10 пог. м»[22].
Примечания
- Комментарии
- ↑ metro cattolico (lit. «catholic [в значении „универсальная“] мера»), заимствовано из греческого μέτρον καθολικόν (métron katholikón)
- ↑ Идея секундного маятника для назначения стандартной длины тем не менее окончательно не умерла, и такой стандарт был использован для определения длины ярда в Великобритании в период 1843—1878 годов.

- Источники
- ↑ 1 2 Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 77—82. — 240 с. — ISBN 5-7050-0118-5.
- ↑ 1 2 3 4 Определение метра (англ.) Резолюция 1 XVII Генеральной конференции по мерам и весам (1983)
- ↑ 1 2 Положение о единицах величин, допускаемых к применению в Российской Федерации. Основные единицы Международной системы единиц (СИ) (неопр.) (недоступная ссылка). Федеральный информационный фонд по обеспечению единства измерений. Росстандарт. Дата обращения: 28 февраля 2018. Архивировано 18 сентября 2017 года.
- ↑ SI base units (неопр.) (недоступная ссылка). BIPM. Дата обращения: 22 июня 2019.
 Архивировано 23 декабря 2018 года.
Архивировано 23 декабря 2018 года. - ↑ SI brochure Официальное описание СИ на сайте Международного бюро мер и весов
- ↑ Положение о единицах величин, допускаемых к применению в Российской Федерации. Десятичные множители, приставки и обозначения приставок… (неопр.) (недоступная ссылка). Федеральный информационный фонд по обеспечению единства измерений. Росстандарт. Дата обращения: 28 февраля 2018. Архивировано 18 сентября 2017 года.
- ↑ Окунь Л. Б. Слабое взаимодействие // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга — Робертсона — Стримеры. — С. 552—556. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
- ↑ Nelson, Robert A. (1981), Foundations of the international system of units (SI), Phys. Teacher: 596–613, <http://plato.if.usp.br/1-2009/fmt0159n/PDFFiles/ThePhysTeacher_FoundationsOfTheSI.
 pdf> Архивная копия от 6 июля 2011 на Wayback Machine.
pdf> Архивная копия от 6 июля 2011 на Wayback Machine. - ↑ Wilkins, John (1668), An Essay Towards a Real Character, And a Philosophical Language, London: Gillibrand, <http://www.metricationmatters.com/docs/WilkinsTranslationLong.pdf> .
- ↑ Misura Universale, 1675 .
- ↑ Poynting, John Henry & Thompson, Joseph John (1907), A Textbook of Physics: Properties of Matter (4th ed.), London: Charles Griffin, с. 20, <https://books.google.com/books?id=TL4KAAAAIAAJ&pg=PA20> .
- ↑ 1 2 3 Grand dictionnaire universel du XIXe siècle, Paris: Pierre Larousse, 1866—1877, p. 163—164.
- ↑ Jean Charles de Borda, MacTutor, <http://www-history.mcs.st-andrews.ac.uk/Biographies/Borda.html>. Проверено 13 августа 2010. .
- ↑ Brief history of the SI (англ.). International Bureau of Weights and Measures. Дата обращения: 12 июля 2010.
 Архивировано 21 августа 2011 года.
Архивировано 21 августа 2011 года. - ↑ Гевара И., Карлес П. Измерение мира. Календари, меры длины и математика.. — М.: Де Агостини, 2014. — С. 125—126. — 160 с. — (Мир математики: в 45 томах, том 38). — ISBN 978-5-9774-0733-5.
- ↑ Метрическая система мер (неопр.) (недоступная ссылка). История измерений. Дата обращения: 12 июля 2010. Архивировано 27 октября 2011 года.
- ↑ ПЛАТИНА — статья из энциклопедии «Кругосвет»
- ↑ Ландсберг Г. С. Оптика. — М.: Физматлит, 2003. — С. 387. — ISBN 5-9221-0314-8.
- ↑ Evenson K. M., Wells J. S., Petersen F. R., Danielson B. L., Day G. W. Speed of Light from Direct Frequency and Wavelength Measurements of the Methane-Stabilized Laser (англ.) // Phys. Rev. Lett.. — 1972. — Vol. 29, no. 19. — P. 1346—1349. — doi:10.1103/PhysRevLett.29.1346.
- ↑ Рекомендованное значение скорости света (англ.
 ) Резолюция 2 XV Генеральной конференции по мерам и весам (1975)
) Резолюция 2 XV Генеральной конференции по мерам и весам (1975) - ↑ Encydopaedia of scientific units, weights, and measures: their SI equivalences and origins. — Springer, 2004. — P. 5. — ISBN 1-85233-682-X.
- ↑ Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 78. — 240 с. — ISBN 5-7050-0118-5.
Литература
- Cardarelli, Francois (2003). Encydopaedia of scientific units, weights, and measures: their SI equivalences and origins, Springer-Verlag London Limited, ISBN 1-85233-682-X, page 5, table 2.1, data from Giacomo, P., Du platine a la lumiere, Bull. Bur. Nat. Metrologie, 102 (1995) 5-14.
- Humerfelt, Sigurd. (26 October 2010).
- Layer, H.P. (2008). Length—Evolution from Measurement Standard to a Fundamental Constant. Gaithersburg, MD: National Institute of Standards and Technology. Retrieved 18 August 2008.
- Mohr, P.
 , Taylor, B.N., and David B. Newell, D. (13 November 2012). CODATA Recommended Values of the Fundamental Physical Constants: 2010. Gaithersburg, MD: National Institute of Standards and Technology.
, Taylor, B.N., and David B. Newell, D. (13 November 2012). CODATA Recommended Values of the Fundamental Physical Constants: 2010. Gaithersburg, MD: National Institute of Standards and Technology. - National Institute of Standards and Technology. (December 2003). The NIST Reference on Constants, Units, and Uncertainty: International System of Units (SI) (web site):
- National Institute of Standards and Technology. (27 June 2011). NIST-F1 Cesium Fountain Atomic Clock. Author.
- National Physical Laboratory. (25 March 2010). Iodine-Stabilised Lasers. Author.
- Naughtin, Pat. (2008). Spelling metre or meter. Author.
- Taylor, B.N. and Thompson, A. (Eds.). (2008a). The International System of Units (SI). United States version of the English text of the eighth edition (2006) of the International Bureau of Weights and Measures publication Le Système International d’ Unités (SI) (Special Publication 330). Gaithersburg, MD: National Institute of Standards and Technology. Retrieved 18 August 2008.
- Taylor, B.N. and Thompson, A. (2008b). Guide for the Use of the International System of Units (Special Publication 811). Gaithersburg, MD: National Institute of Standards and Technology. Retrieved 23 August 2008.
- Tibo Qorl. (2005) The History of the Meter (Translated by Sibille Rouzaud). Retrieved 18 August 2008.
- Zagar, B.G. (1999). Laser interferometer displacement sensors in J.G. Webster (ed.). The Measurement, Instrumentation, and Sensors Handbook. CRC Press. isbn=0-8493-8347-1.
- Белобров В. А. (2019). История метра (короткая версия), История метра (полная версия)
Ссылки
1 п м это сколько метров: в чем измеряется ткань
» Трубы
Что такое погонный метр трубы
Погонный метр — это сколько? Как его используют для кухонь? Какие изделия отмериваются погонной системой?
Тот, кто не имеет дело со швейным или мебельным производством, часто задается вопросом: 1 погонный метр – это сколько? На самом деле это та же единица измерения, с которой все привыкли сталкиваться каждый день. Чаще всего такую меру применяют для ориентации в длине материалов, чаще всего именно ткани.
Способ измерения погонным метром
Погонный метр – это сколько? Для того чтобы ответить на этот вопрос, следует знать, что такая мера имеет те же самые 100 см. Единственное, что если ее применяют для счета ткани, то учитывается только длина, при этом ширину не берут в расчет.
Кстати, то же самое касается и покупки труб или электрического кабеля. Учитывается непосредственная длина изделия, без учета диаметра или сечения. Та же система может применяться и для стройматериалов, например линолеума или плинтуса. То есть погонный метр используется тогда, когда другие показатели значения не имеют, например для рулонов.
Но вот тут часто можно встретить на ценниках, что тот же самый уплотнитель или утеплитель имеет стоимость за 1 квадратный, а не погонный метр. Это сколько же тогда выходит? Рассмотрим разницу между ними.
Пару слов о квадратной мере
Квадратным метром называют площадь, например, земельного участка, помещения, строительных и иных материалов размером 100 х 100 см. Если площадь имеет разные цифровые значения сторон, то показатели длины и ширины умножают друг на друга и получают измерение, которое обозначается квадратными метрами.
Данную систему измерений чаще всего используют именно для жилплощади, так как комнаты редко когда имеют равные стороны. Закупка облицовочного материала для пола или потолка, да и для стен тоже, идет по расчету из квадратных метров.
Чем отличаются погонный и квадратный метр?
Квадратный и погонный метр — это сколько в сантиметрах? На самом деле общий момент в таких измерениях — только длина, которая равна 100 см, а далее идут отличия. Дело в том, что квадратная величина предназначена для вычисления площади, в то время как погонная затрагивает только длину, без учета остальных сторон материала.
Перевести одну единицу в другую можно только в том случае, если есть значение ширины. Тогда, к примеру, если ткань имеет длину 1 погонный метр (это сколько в сантиметрах? — 100), а ширину – 2 метра, то две эти цифры необходимо между собой перемножить. В результате получится площадь такого куска материи.
Измерение для кухонных помещений
Что касается кухни, то тут также применяется данная система. Погонный метр кухни – это сколько? И что же можно там мерить? В данном случае мера применима не к самой площади помещения, а к мебельному гарнитуру.
В данном случае в учет берутся все элементы, которые располагаются вдоль стен, например стол или полка, разделочная поверхность или тумба, ну и прочие модули. Цена указывается с расчетом за весь комплект, с тем, сколько он будет занимать места в погонных метрах. Но может быть стоимость и отдельной единицы, тогда в этом случае цифра умножается на количество элементов в гарнитуре, и получается конечная стоимость.
Сразу стоит оговорить тот момент, что не все продавцы указывают полную цену.
Поэтому сразу следует уточнить, входит ли мебельная фурнитура в указанную стоимость, иначе можно не рассчитать свои финансы.
Мера для трубчатых материалов
Погонный метр трубы – это сколько получится? В данном варианте часто используется вес изделий, поэтому и ценник имеет соответствующие обозначения. На самом деле немногие интересуются, почему идет именно такая система измерений.
В зависимости от предназначения, каждая труба может иметь свое сечение и толщину стенок, к тому же и сам материал выполнения бывает разным. Но если взять две одинаковых трубы с одинаковой окружностью, длиной по одному метру, но с разной толщиной стен, то получится, что весить они будут по-разному. Обычно весовую категорию назначают согласно ГОСТу. Но редко когда у продавца имеются такие документы.
Логично, что возникает вопрос: Для труб погонный метр – это сколько? Поможет ли эта информация вычислить вес? Для этого есть формула:
— От диаметра изделия вычитают толщину его стенок, затем данную величину умножают опять же на толщину стенок, а после — на 0,025 кг, в результате станет известна масса 1-го погонного метра.
Для вычислений линейные измерения производятся в миллиметрах.
Система измерения арматуры
Арматура служит для создания более надежной конструкции, особенно что касается загородных домов. Ее тоже рассчитывают при помощи погонной системы.
Для этого все необходимые стержни измеряются по длине (если они разные) и полученную сумму умножают на массу 1-го погонного метра. Для определения этого значения есть специальная таблица, которая позволит рассчитать, в каком процентном соотношении будет проармирована постройка. Для самостоятельных вычислений используется формула: 1 м х (0,785 х диаметр х диаметр) = объем арматуры. Цифры обозначают геометрическую площадь круга.
Погонный метр это сколько? Что такое погонный метр
Диаметр берется в метрах. Полученное значение затем нужно умножить на удельный вес арматуры, который равен 7850 кг/м 3 .
что такое погонный метр трубы в Липецке
Компания City Metall г. Липецк
Однако даже триста лет назад Россия имела довольно высокие показатели в производстве металлопроката. Вспомните из школьного курса истории — ведь именно тогда царь Петр начал осваивать уральские залежи железной руды.
Специалисты различают следующие основные разновидности этих изделий: — черный металлопрокат. Этот вид представлен различными изделиями из стали разных сортов, а также из чугуна. — цветной металлопрокат. В этом направлении все изделия изготовлены из цветных металлов (медь, алюминий, цинк и т.д.) или из их сплавов.
Кроме такой классификации, основанной на происхождении , различают также следующие виды металлопроката.
- трубный. Само название говорит за себя — все изделия из этой группы представляют собой различный по форме и размерам трубы.
- сортовой. Этот вид металлопроката представлен разными по форме изделиями, начиная от катанки и заканчивая шестигранником.
- фасонный. Здесь можно выделить такие изделия, как уголок или швеллер.
- листовой — представлен листами различного металла.
Кроме труб и стальных листов, мы предлагаем листы оцинкованные, разнообразную арматуру, проволоку, дорожную сетки и много другой продукции металлопроката. Если необходима нарезка металла, то мы сделаем это на нашем складе в соответствии с требованиями клиента.
Что такое погонный метр?
Все мы привыкли считать единицей измерения расстояния или длины — метр. Тогда что такое погонный метр? Чем он отличается от обычного? Да, по сути, ничем. В погонных метрах принято измерять длину любого материала. При этом ширина его, либо высота, в расчет не берутся. Они или стандартные, или же, при измерении, существенного значения не имеют.
Что измеряют в погонных метрах
В погонных метрах вам, обычно, отмеряют ткань в магазине. При ширине 1,5 м погонным метром будет считаться кусок ткани 1 м на 1,5 м. Если вы покупаете трубы, то, независимо от их толщины, длина трубы будет измеряться в погонных метрах. Так же и электрический кабель. Совершенно не важно, какое у него сечение, толстый он или тонкий, цена на него указывается за метр погонный. Та же ситуация и с плинтусами, линолеумом, различными утеплителями и уплотнителями, и т.п. А когда стоимость кухни рассчитывается в погонных метрах, что имеется в виду?
Что такое погонный метр кухни
В этом контексте погонный метр используется, скорее, как величина условная. Для удобства расчетов принято считать, что погонный метр кухни – это та мебель, которая устанавливается вдоль стены длиной 1 м от пола до потолка, согласно дизайнерскому проекту. Это могут быть столы, полки, тумбы и другие модули. Обычно, стоимость кухни так и указывается – за погонный метр. Так удобно сразу рассчитать ее приблизительную цену, умножив длину стены, вдоль которой она будет располагаться на стоимость одного погонного метра кухни.
Источники: http://www.syl.ru/article/177075/new_pogonnyiy-metr—eto-skolko-kak-ego-ispolzuyut-dlya-kuhon-kakie-izdeliya-otmerivayutsya-pogonnoy-sistemoy, http://orsha-citi.ru/new/novosibirsk-city-metall/6060-chto-takoe-pogonnyj-metr-truby.html, http://elhow.ru/ucheba/opredelenija/p/chto-takoe-pogonnyj-metr
Комментариев пока нет!
119 Работа по математике — Академические должности
Спонсируемый 15 докторских стипендийСеть инновационного обучения Марии Склодовской-Кюри: экономическая политика в сложных средах (EPOC) EPOC ищет 15 высокомотивированных докторантов для участия в передовых междисциплинарных исследованиях в сочетании со структурированной учебной программой…
Спонсируемый Стипендии 4 PhD в разных областяхТемы: по телефону предлагается до 4 вакансий для аспирантов в следующих областях: Ядро прикладной математики: анализ Фурье, алгебраическая геометрия и теория сингулярностей, дискретная математика, обратные задачи, УЧП, математическая физика, …
Спонсируемый 1-2 постдокторант в области науки о данных и психиатрической геномикиВы хотите внести свой вклад в высококачественные медицинские исследования? Мы ищем нового постдока, который будет работать в KI-Psychiatric Genomics Institute (KI-PGI) под руководством профессора Патрика Салливана.KI-PGI — это исследовательская программа в рамках Департамента медицинской эпидемиологии и биостатистики …
Спонсируемый Программа стипендиатовПрограмма стипендиатов на 2021 год — это программа с постоянным проживанием, рассчитанная на макс. 8 исследователей из сторонних организаций CY Initiative на период от 4 месяцев до одного года. Эта программа направлена на продвижение междисциплинарных обменов, международного сотрудничества и на…
Спонсируемый Программа докторских стипендий INPhINIT «la Caixa»Программа докторских стипендий INPhINIT «la Caixa» предназначена для привлечения талантливых начинающих исследователей любой национальности, желающих получить докторскую степень на территории Испании или Португалии. Спонсируемый фондом «La Caixa», он направлен на поддержку…
6 часов назад | Закрытие 31 октября Кандидатская диссертация — Квантовые вычисления для оптимизации на компьютерах NISQ.SL-DRT-21-0400 ОБЛАСТЬ ИССЛЕДОВАНИЙ Новые вычислительные парадигмы, схемы и технологии, в т.ч. квант АННОТАЦИЯ Сегодняшние квантовые компьютеры все еще далеки от идеального сценария, который, по мнению первых участников квантовых вычислений, по-прежнему существует…
Mathway | Решение основных математических задач
Хотя мы рассматриваем очень широкий круг проблем, в настоящее время мы не можем помочь с этой конкретной проблемой. Я разговаривал со своей командой, и мы учтем это для будущих тренировок. Есть ли другая проблема, для решения которой вам нужна дополнительная помощь?
Mathway в настоящее время не поддерживает эту тему.Мы более чем рады ответить на любой математический вопрос, который может у вас возникнуть по этой проблеме.
Mathway в настоящее время не поддерживает «Спросите эксперта в прямом эфире по химии». Если это то, что вы искали, обратитесь в службу поддержки.
Mathway в настоящее время вычисляет только линейные регрессии.
Мы здесь, чтобы помочь вам с математическими вопросами. Если у вас возникнут проблемы с вводом ответов в онлайн-задание, вам потребуется помощь вашей школы.
Поддержка по телефону доступна с понедельника по пятницу с 9:00 до 22:00 по восточному времени.Вы можете поговорить с членом нашей службы поддержки клиентов по телефону 1-800-876-1799.
Математический журнал | Hindawi
Research Article
07 Dec 2020
Управление в скользящем режиме с комплексным обучением нелинейных систем, подверженных сбоям привода
Сяньминь Хоу | Songyu Wang
Эта статья посвящена управлению нелинейными системами с одним входом и одним выходом (SISO) с отказами исполнительного механизма с помощью скользящего режима управления (SMC) и SMC с композитным обучением (CLSMC).В конструкции SMC предлагается скользящая поверхность целого порядка и построен адаптивный закон для обновления оценки параметров при отказе привода. Метод SMC может достигать ошибки отслеживания, приближающейся к нулю, если выполняется условие строгого постоянного возбуждения (PE). Чтобы смягчить это требование, используя все данные, записанные во время работы контроллера, мы конструируем ошибки прогнозирования, которые используются для создания составного адаптивного закона обучения. Затем предлагаемый метод CLSMC не только сводит ошибку отслеживания к нулю, но также реализует точную оценку несогласованного неизвестного параметра при отказе исполнительного механизма.Кроме того, в предлагаемом методе CLSMC нам нужно только удовлетворять условию интервального возбуждения (IE). Результаты моделирования представлены, чтобы указать на достоверность наших методов.
Исследовательская статья
07 дек 2020
В дискретном времени Wilson Systems
Тина Кохли | Суман Панвар | S. K. Kaushik
В этой статье мы определяем фрейм Вильсона с дискретным временем (фрейм DTW) и обсуждаем некоторые свойства фреймов Вильсона с дискретным временем. Кроме того, мы даем взаимодействие между кадрами DTW и кадрами Габора с дискретным временем.Кроме того, даны необходимые и достаточные условия для кадра DTW с точки зрения преобразования Зака. Кроме того, получается оператор кадра для кадра DTW. Наконец, мы обсуждаем двойственную пару фреймов для дискретных систем Вильсона и даем достаточное условие их существования.
Исследовательская статья
07 дек 2020
Новая модификация метода Хойна на основе контрагармонического среднего для решения задач с начальным значением с высокой эффективностью
Абушет Хаялу Ворки
В этой статье предлагается небольшая модификация усовершенствованного метода Эйлера (метод Хойна) для повышения эффективности решения обыкновенных дифференциальных уравнений с начальным условием путем принятия тангенциального наклона как среднего арифметического среднего и противоположного. -гармоническое среднее.Чтобы подтвердить вывод, были оценены стабильность, согласованность и точность системы и представлены численные результаты, и было признано, что предложенный метод является более стабильным, последовательным и точным с высокими характеристиками.
Исследовательская статья
04 декабря 2020
Девяносто шесть различных вещественных матриц для представления кватернионного числа
W. E. Ahmed
В этой статье мы исследуем количество всех возможных вещественных матриц, представляющих кватернионное число в виде трех кососимметричных матриц плюс единичную матрицу четвертого порядка, а также способы определения этих матриц.Мы устанавливаем, что существует 96 различных вещественных матриц, обладающих этим свойством, и с помощью операций со строками матрицы мы получаем эти матрицы.
Research Article
03 Dec 2020
Аналитическое решение системы интегральных уравнений Вольтерра с использованием OHAM
Мухаммад Акбар | Рашид Наваз | … | Kottakkaran Sooppy Nisar
В этой работе используется надежный метод решения системы интегральных уравнений Вольтерра (VIE), называемый асимптотическим методом оптимальной гомотопии (OHAM).Предложенная методика успешно применяется для решения различных задач, и проводится сравнение с расслабленным методом Монто Карло (RMCM) и методом базисных функций шляпы (HBFM). Сравнение показывает, что данная методика является более подходящей и надежной для решения системы VIE. В представленной методике используется вспомогательная функция, содержащая вспомогательные константы, контролирующие сходимость. Более того, OHAM не требует дискретизации, как другие численные методы, а также не содержит малых или больших параметров.
Исследовательская статья
02 дек 2020
Неприводимость полинома, сдвинутого на степень другого полинома
Артурас Дубицкас
В этой заметке мы показываем, что для любого и любого простого числа существует, для которого многочлен неприводим над.
 Масса — это постоянная величина в математике, в то время как вес зависит от силы и скорости притяжения объекта к земле.
Масса — это постоянная величина в математике, в то время как вес зависит от силы и скорости притяжения объекта к земле.
 Архивировано 23 декабря 2018 года.
Архивировано 23 декабря 2018 года. pdf> Архивная копия от 6 июля 2011 на Wayback Machine.
pdf> Архивная копия от 6 июля 2011 на Wayback Machine. Архивировано 21 августа 2011 года.
Архивировано 21 августа 2011 года. ) Резолюция 2 XV Генеральной конференции по мерам и весам (1975)
) Резолюция 2 XV Генеральной конференции по мерам и весам (1975) , Taylor, B.N., and David B. Newell, D. (13 November 2012). CODATA Recommended Values of the Fundamental Physical Constants: 2010. Gaithersburg, MD: National Institute of Standards and Technology.
, Taylor, B.N., and David B. Newell, D. (13 November 2012). CODATA Recommended Values of the Fundamental Physical Constants: 2010. Gaithersburg, MD: National Institute of Standards and Technology.