«Решение неравенств». 10-й класс

Цели:

1. Систематизировать, обобщить, расширить знания и умения учащихся, связанные с применением методов решения рациональных неравенств.
2. Содействовать развитию математического мышления учащихся,умению комментировать,тренировать память.
3. Воспитание ответственного отношения к учебному труду,чувства товарищества и взаимопомощи.

Оборудование: интерактивная доска, раздаточный материал(разноуровневые карточки с практическими заданиями).

Структура урока:

1. Сообщение темы и цели урока (1 мин.)
2. Проверка домашнего задания (5 мин.)
3. Систематизация знаний и умений по пройденному материалу (10 мин.)
4. Инструктирование по выполнению заданий в группах (3 мин.)
5. Выполнение заданий в группах (15 мин.)
6. Проверка и обсуждение полученных результатов (8 мин. )
7. Постановка домашнего задания (2 мин.)
8. Подведение итогов урока (1 мин.)

Ход урока

I. Сообщение темы и цели урока.

Сегодня на уроке мы будем решать неравенства методом интервалов и методом замены переменных. Эпиграфом к сегодняшнему уроку будут слова Ньютона:“При изучении наукпримеры не менее поучительны,нежели правила” и слова Ломоносова: “Примеры учат больше,чем теория”.

II. Проверка домашнего задания.

На дом были даны неравенства. Проверьте ваше решение по интерактивной доске.

Слайд №1

№1.

Отметим на числовой оси корни числителя и знаменателя.

Ответ: Є (-3; 1]

№2.

Ответ: x Є [1; 2] U (3; +∞)

№3.

Ответ: x Є (-6; 1)

№4.

≥

Социальное неравенство — понятие, виды и причины расслоения общества

Исторический аспект

Люди отличаются между собой по внешности, этнической принадлежности, полу, уровню интеллекта, талантливости и другим признакам, которые носят определение естественных и могут проявляться в виде разных форм личностной дискриминации. Если различия порождены такими факторами, как уклад жизни, социальная роль, разделение труда и другими, ведущими к различиям в статусе, обладании собственностью и властью, то они становятся основой для возникновения разных видов социального неравенства (СН).

На всех этапах эволюции человеческого общества встречаются признаки СН. В общинах собирателей и охотников некоторыми незначительными преимуществами пользовались только главы общин, и особого расслоения общества или стратификации, не наблюдалось. Страты — это отдельные группы, состоящие из людей, которые занимают разное социальное положение в общественной структуре.

Примеры социального неравенства из истории: рабство, сословия, классы. Через них в разное время прошли многие народы. Еще один вид — касты — существует только на территории Индии.

Выраженное расслоение населения на массовые группы началось, когда возникли и развились аграрные культуры и появилась частная собственность. Самые успешные собственники получили управленческие права и стремились закрепить их за своей семьей. Таким образом возникла идея наследования имущественных и должностных обязанностей. Свою роль в разнообразной природе страт сыграли войны завоевательного характера и развитие религии, в результате чего сформировались такие группы, как рабы и священнослужители.

Причины появления

Разные ученые и исследователи задавались вопросом возможности существования человеческих сообществ вне какой-либо иерархии. Существует несколько интерпретаций понятия социального неравенства и причин его возникновения. Основные из них:

• Функционализм.
• Статусность.
• Экономические факторы.

Функционализм основывается на существующем многообразии социальных функций, присущих разным слоям и стратам. Общественные отношения могут развиваться и функционировать только в условиях разделения труда. В этом случае на каждую социальную группу возлагается осуществление определенных задач, которые важны для всего социума. Одна часть людских ресурсов направлена на производство материальных благ, другая занимается созданием духовных ценностей. Необходимость контроля за их деятельностью вытекает в создание третьего слоя — управляющего.

Чтобы общество благополучно существовало и было жизнеспособно, необходимо пропорциональное сочетание трех составляющих человеческой деятельности, при этом некоторые из них оказываются более важными, другие же — менее значимыми. Таким образом, иерархия функционирования выражается в разделении на соответствующие классы и слои населения.

Статусное объяснение СН основывается на действиях и поведении конкретных членов социума. Каждый индивид занимает конкретное положение в обществе и, следовательно, имеет определенный статус, поэтому можно считать, что СН — это неравенство статусов. Для выполнения своей роли человеку нужно иметь способности к ней и возможности для самореализации, что в итоге позволит ему занять определенное положение в социуме. К способностям обычно относятся знания и умения, полученные во время обучения профессии, а также личные склонности и качества, способствующие успешной карьере в выбранной сфере.

Возможностями считаются происхождение человека, например, из обеспеченной или известной семьи, владение собственностью и капиталами, принадлежность к влиятельным политическим силам. Сущность экономической точки зрения на причины возникновения СН заключается в неравномерном распределении материальных благ между членами социума и их неравного отношения к собственности, что ведет к стратификации общества на антагонистические классы.

Критерии и формы

В каждом обществе есть механизмы, которые поддерживают его стратификационную структуру.

Традиционному была присуща сословная иерархия, жестко регулирующая отношения между представителями разных слоев и устанавливающая права и обязанности каждого сословия, обойти которые было крайне затруднительно.

Для индустриального общества характерно декларирование равноправия всех граждан, но неравенство при этом не исчезает. Богатства скапливаются в руках небольшой группы людей за счет обнищания другой, что может привести к социальным взрывам. С другой стороны, неравенство — стимулирующий развитие фактор, в отличие от уравнивания в доходах. В современном обществе огромное значение имеет наличие сдерживающей прослойки между полюсами богатства и бедности — среднего класса. Чем он больше, тем сильнее его влияние на политику государства и формирование системы общественных ценностей.

Теория социологии считает, что экономических признаков для объяснения явлений СН недостаточно, и вводит еще один — социальный престиж, под которым понимается обретенный по рождению или благодаря личностным свойствам социальный статус. Современное общество структурируется по таким критериям, как:

• Доход, который измеряется в деньгах и может быть получен как личным трудом, так и от владения собственностью.
• Власть — характеризуется количеством людей, на которых, независимо от их желания, распространяются влияние и решения одного человека.
• Образование — количество лет, затраченных на учебу, и значимость полученных знаний и умений.
• Престиж, который показывает уважение к социальному статусу индивида.

Для традиционного социума характерна форма пирамиды, вершина которой отображает небольшую прослойку очень богатых людей, а основание — широкий слой бедноты. Развитое общество можно изобразить в форме ромба, две противоположные вершины которого символизируют противоположные состояния абсолютного богатства и бедности, а центральная часть — многочисленный средний класс.

Функции и задачи

СН запускает в социуме сложные процессы и, кроме основной, стратификационной, выполняет и другие функции. Регулирующая, или нормирующая, заключается в выработке некоторых норм, которые социум вынужден создавать для каждого слоя или класса. Они должны обязательно выполняться и служат для сохранения структуры внутреннего баланса общества.

В длительной перспективе при формировании новых классов на СН ложится функция перераспределения и реорганизации социальной энергии и культурных ресурсов социума в ответ на изменение условий внешней среды или снятия ограничений, наложенных предыдущими поколениями. Этим СН помогает адаптации социума к каждому новому витку развития общественных отношений, возникающему под воздействием процессов, зависящих или не поддающихся влиянию человека.

Функции, присущие СН, относятся не только ко всему обществу в целом, но и выполняют задачи, касающиеся каждого индивида отдельно. Например, стимулируют личностный или профессиональный рост, для чего человеку нужно проявить индивидуальные способности и таланты по максимуму. К задачам СН относится и упорядочивание экономической сферы: владельцы капитала создают рабочие места, а те, кто не имеет материальных ресурсов, трудятся, чтобы подняться над чертой бедности.

Социальная мобильность

Важным показателем развития общественной сферы, позволяющим несколько уменьшить уровень неравенства, является социальная мобильность — перемещение членов социума из одного слоя в другой. Для ее существования имеется две причины:

• Изменение обществ приводит к видоизменению разделения труда и появлению новых статусов, в то время как старые утрачивают свою значимость.
• Даже полная монополизация элитами доступа к образованию не может контролировать естественное появление талантливых людей, которые пополняют высшие слои, переходя в них из низших.

Мобильность может быть нисходящей или восходящей по вертикали, а также горизонтальной. Для групповой мобильности возможно снижение или престижности некоторых профессий под действием объективных факторов, или утрата влияния политическими партиями, что приводит к перемещению представителей таких групп в социальный слой более низкого статуса.

У индивидов нисходящая мобильность проявляется выталкиванием с рынка менее удачливых коллег в конкурентной борьбе. Путем получения хорошего образования или при наличии предпринимательских способностей человек может приобрести восходящую мобильность. Перемещения внутри классового слоя относятся к горизонтальной мобильности и не приводят к изменению статуса.

Основные проблемы

Социальное неравенство очень сильно распространено во всем мире, в том числе в России, и как любое другое общественное явление сталкивается с рядом затруднений. Особенность современного СН состоит в том, что неодинаковый доступ к ресурсам является как одной из его причин, так и следствием, а проблемы одновременно затрагивают две самые развитые области социума — общественную и экономическую. Осложнения возникают на почве нарушения принципов социальной справедливости и выражаются в таких проявлениях, как:

• неуверенность не только в будущем, но даже в устойчивости той позиции, в которой индивид находится сейчас;
• недовольство одних слоев населения приводит к приостановке производства и недостатку продукции для другой части социума;
• невозможность переместиться по социальной лестнице из-за отсутствия выполняющих свою функцию социальных лифтов;
• психологическое давление из-за непредсказуемости будущего, которое особенно сильно сказывается на незащищенных слоях населения.

Все эти явления могут вызвать рост социальной напряженности и в особо острых случаях привести к беспорядкам и конфликтам как между гражданскими лицами, так и между гражданами и государственными силовыми структурами. Проблемы СН в экономической сфере возникают из-за несправедливости в распределении доходов — меньше всего получают те, кто реально работает, расходуя свои физические силы, а больше всего имеют владельцы промышленных и финансовых ресурсов.

Снижение напряженности в обществе

История не знает времени, когда СН отсутствовало совершенно, но чтобы общество было меньше подвержено его влиянию, требуется соблюдать баланс между власть имущим классом и другими слоями населения. Этому способствует правильная политика государств, направленная на создание условий для экономического роста, что позволяет финансировать различные социальные программы. К ним можно отнести все виды помощи малоимущим гражданам, доступность бесплатного качественного образования и медицинского обслуживания, отсутствие дискриминации при приеме на работу по половому или национальному признаку.

Особое значение имеет государственная помощь людям, занимающимся индивидуальным предпринимательством, которые не только повышают свой социальный статус, но и создают рабочие места для других, т. е. дают возможность преодолеть черту бедности безработным. Таким образом во многих странах постепенно формировался средний класс, который позднее стал основой стабильного развития экономики и снижения уровня СН. Этот слой населения незаменим и в условиях экономических кризисов, так как его мобильность позволяет быстро перестраиваться с учетом новых условий.

Последствия социального неравенства сказываются на развитии многих стран. Нарастание социального напряжения приводит к конфликтам, которые, к сожалению, нередки в современном мире.

Урок 23. показательные неравенства — Алгебра и начала математического анализа — 10 класс

Алгебра и начала математического анализа, 10 класс

Урок №23.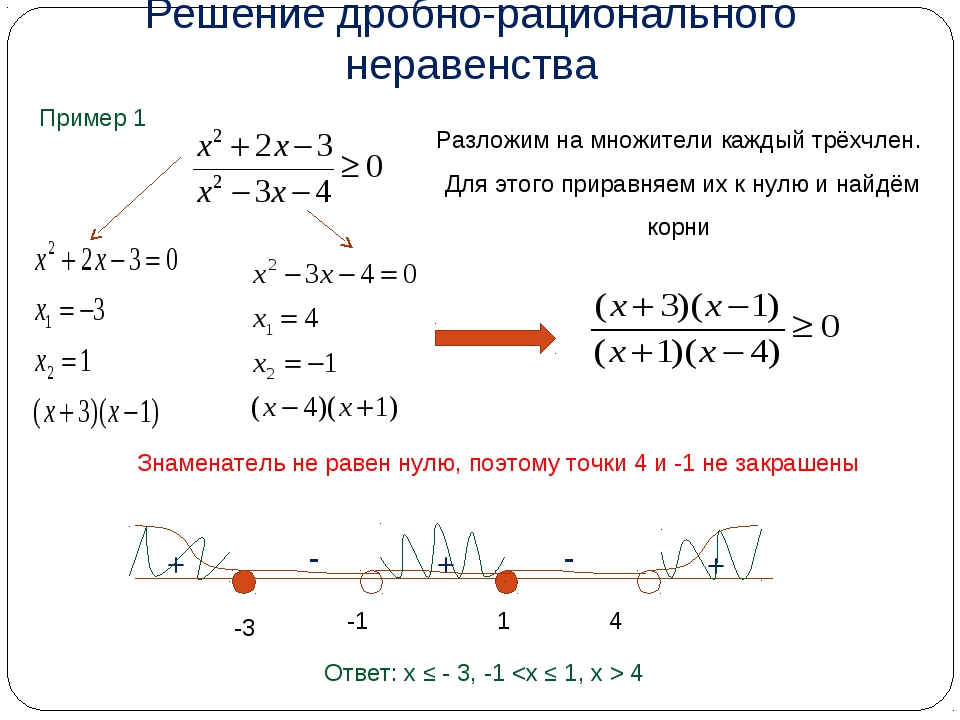 Показательные неравенства.

Перечень вопросов, рассматриваемых в теме

• простейшие показательные неравенства;
• решение показательных неравенств замена переменной, разложение на множители;
• метод рационализации при решении показательных неравенств;
• метод интервалов при решении показательных неравенств;
• графический метод решения показательных неравенств.

Глоссарий по теме

Показательным называется неравенство, в котором переменная входит только в показатели степеней, при постоянном основании.

Неравенства вида , называются простейшими показательными неравенствами.

Метод рационализации для решения показательных неравенств – переход от неравенства, содержащего показательные выражения, к равносильному рациональному неравенству (или равносильной системе рациональных неравенств).

Основная литература:

Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е.,  Шабунин М.И. под ред. Жижченко А.Б. Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. учреждений: базовый и профил. Уровни – 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-025401-4, сс. 216—220, 223-230.

Дополнительная литература:

Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 11 класса: Учеб. пособие для учащихся шк. и классов с углубл. изуч. математики — 4-е изд. — М.: Просвещение, 1995. — 288 с.: ил. — ISBN 5-09-0066565-9, сс. 70-74.

Открытые электронные ресурсы:

https://ege.sdamgia.ru/ — решу ЕГЭ образовательный портал для подготовки к экзаменам

http://fcior.edu.ru/ — Федеральный центр информационно-образовательных ресурсов

http://school-collection.edu.ru/ — Единая коллекция цифровых образовательных ресурсов

Теоретический материал для самостоятельного изучения

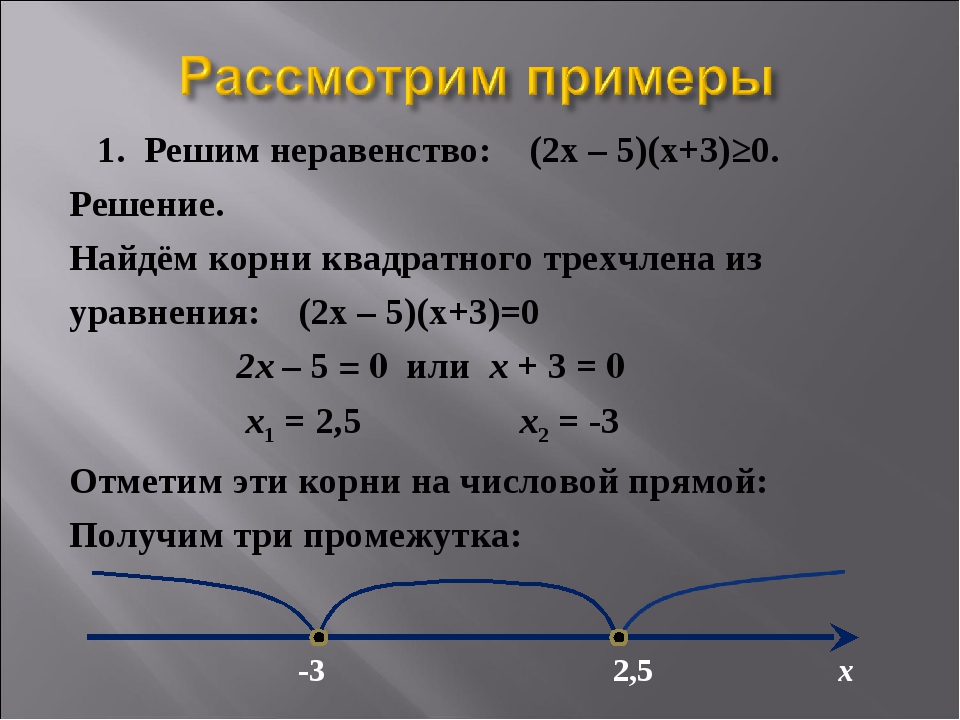
1. Рассмотрим показательные неравенства.

Показательным называется неравенство, в котором переменная входит только в показатели степеней, при постоянном основании.

Неравенства вида , называются простейшими показательными неравенствами.

В самом простом случае неравенство принимает вид: . Очевидно, что знак неравенства может быть любым (<, >, , ).

Множество решения неравенства будет зависеть и от знака неравенства, и от основания степени, и от значения b.

Так как множество значений показательной функции – множество положительных чисел, то при неравенства: и решений не имеют, независимо от значения основания а. В то же время множеством решения неравенств и является все множество действительных чисел, независимо от значения основания а (см. Рисунок 1).

Рисунок 1 – иллюстрация решения простейшего показательного неравенства при b<0

Теперь рассмотрим случай b>0, a>1.

В том случае, когда основание степени a>1, то при переходе от исходного неравенства к неравенству с показателями знак неравенства не изменяется (см. Рисунки 2 и 3).

Рисунок 2 – иллюстрация решения простейшего показательного неравенства или при b>0, a>1.

Рисунок 3 – иллюстрация решения простейшего показательного неравенства или при b>0, a>1.

Теперь рассмотрим случай b>0, 0<a<1.

В том случае, когда основание степени 0<a<1, то при переходе от исходного неравенства к неравенству с показателями знак неравенства изменяется на противоположный (см. Рисунки 4 и 5).

Рисунок 4 – иллюстрация решения простейшего показательного неравенства или при b>0, 0<a<1.

Рисунок 5 – иллюстрация решения простейшего показательного неравенства илипри b>0, 0<a<1.

Для того чтобы решить простейшее показательное неравенство , нужно число b представить в виде степени числа a.

Рассмотрим пример: .

Представим в виде степени числа 5: .

Теперь перепишем данное неравенство в виде: .

Так как основание степени больше 1, то при переходе к показателям знак неравенства сохраняется, поэтому x>3/7.

Ответ: x>3/7.

Рассмотрим еще один пример: .

Перепишем его в виде

.

Так как основание степени меньше 1, то при переходе к показателям знак неравенства изменяется на противоположный:

,

,

.

Ответ: .

2. Теперь перейдем к решению более сложных показательных неравенств.

2.1) Рассмотрим пример: .

Преобразуем показатель первого слагаемого: .

Теперь в левой части вынесем за скобку общий множитель: .

Разделим обе части неравенства на 4: . Получили простейшее показательное неравенство. Так как основание степени больше 1, то при переходе к показателям знак неравенства сохраняется, получаем: . Решение этого неравенства является полуинтервал (0; 1].

Ответ: (0; 1].

2.2) Рассмотрим еще один пример: .

Заметим, что , поэтому введем новую переменную . Получим вспомогательное неравенство: .

Решим его:

.

Вернемся к исходной переменной:

, .

Так как основание степени меньше 1, то при переходе к показателям знак неравенства изменится на противоположный:

.

Ответ: .

2.3) Рассмотрим еще одной показательное неравенство, которое решается методом замены переменной.

.

Видим, что неравенство зависит от выражения , поэтому введем новую переменную и запишем вспомогательное неравенство: .

Преобразуем полученное неравенство к виду: F(t)<0.

, приведем левую часть к общему знаменателю:

, . Так как , то , поэтому решение полученного неравенства сводится к: , то есть .

Вернемся к исходной переменной: , то есть x<0.

Ответ:

Примеры и разбор решения заданий тренировочного модуля

1. .

Решение:

Введем новую переменную .

Запишем вспомогательное неравенство: .

1) Если , то решением неравенства является любое значение t, которое удовлетворяет области определения: .

Решив систему: , получаем: .

2) Если (), возведем обе части неравенства в квадрат:

.

Решим его: ,

,

,

0<t<9.

Учитывая условие , получаем: . ((x+5)/(x+2))

Решение:

Используем метод рационализации и перепишем неравенство в виде:

,

.

Получили неравенство: .

Упростим его и решим методом интервалов:

,

.

Запишем ответ: .

Ответ: .

Определение социального неравенства Типы и примеры

Определение социального неравенства

Когда в обществе существуют неравные возможности или вознаграждения для людей с другим социальным статусом или положением, это называется социальным неравенством. Неравенство имеет разные измерения, и каждое государство имеет разные измерения.

Принято считать, что люди, живущие в Америке, живут лучше, чем большинство людей, живущих в других частях мира.В некоторой степени это правда, но страна не свободна от социального неравенства. Почему это так? Это можно объяснить двумя способами. Первый обвиняет бедных. Эта концепция предполагает, что бедные несут ответственность за свою бедность. Они не работают, потому что у них нет необходимых навыков, мотивации или образования, чтобы найти работу. Вторая возможность — обвинять общество. Это говорит о том, что общество несет ответственность за бедность. Не хватает возможностей для работы, чтобы содержать семьи.

Виды социального неравенства

В основном, существует 5 типов социального неравенства. Они перечислены ниже:

1. Политическое неравенство : Неравенство, при котором нет гражданского равенства перед законом.
2. Неравенство доходов и богатства : Это результат или результат, который в основном связан с заработками людей.
3. Неравенство в жизни : Это относится к неравенству возможностей, если они предоставляются, и могут улучшить качество жизни.
4. Неравенство обращения и ответственности : Хотя эта идея менее изучена, но она порождает проблемы в отношении свободы действий и ответственности.
5. Неравенство членства : Это существует в членстве веры, семьи и нации.

Примеры социального неравенства

Я могу привести массу примеров социального неравенства в Америке. Многие рабочие места в стране зависят от социального неравенства, такого как доход, пол, образование и расовое неравенство как на региональном, так и на национальном уровне.

Самый распространенный пример — разрыв в доходах в Америке между черными и белыми. Разница в среднем доходе домохозяйств между чернокожими и белыми составляла 19 000 долларов в 1967 году, но в 2012 году она достигла 27 000 долларов и постоянно увеличивается.

Гендерное неравенство — еще один распространенный пример. Женщины недостаточно представлены в своих ролях, процессах принятия решений и политической деятельности. Нет сомнений в том, что участие женщин в различных областях и отраслях во всем мире увеличивается, но они по-прежнему сталкиваются с различиями в заработной плате. Их заработная плата ниже, чем у мужчин.

Не каждый человек имеет доступ к одинаковому типу медицинских услуг. Существует неравенство по признаку расы, пола, экономических условий. Не все граждане имеют доступ к медицинским учреждениям одного типа. Более обеспеченные группы могут быть легко замечены врачами и получат лекарства по сравнению с теми, кто их не лечит.

Сегодня доступны средства для сбора и анализа данных, относящихся к экономике различных стран по всему миру, и можно проводить исследования социального расслоения и неравенства.Между самыми богатыми и беднейшими людьми существует большой разрыв, который необходимо устранить. Существует множество способов решения проблемы социального неравенства. Вот некоторые из них:

1. Убедитесь, что высококачественные медицинские услуги доступны и доступны по цене для всех.
2. Решите проблему поляризованной заработной платы. Кажется, что средняя реальная заработная плата снижается, а зарплата руководителей растет. Пора устранить это неравенство.
3. Наряду с лучшими рабочими местами должны быть предоставлены возможности обучения для развития новых навыков.
4. По всей стране должно создаваться все больше и больше рабочих мест для всех.
5. И последнее, но не менее важное: следует взимать справедливые налоги. Должна быть оказана помощь малообеспеченным слоям населения.

Даже маленькие шаги могут время от времени приводить к огромным изменениям в восстановлении социального благополучия людей.

Алгебра — линейные неравенства

Онлайн-заметки Павла

Примечания Быстрая навигация Скачать

• Перейти к
• Примечания
• Проблемы с практикой
• Проблемы с назначением
• Показать / Скрыть
• «> Показать все решения / шаги / и т. Д.
• Скрыть все решения / шаги / и т. Д.

• Разделы
• Уравнения с радикалами
• Полиномиальные неравенства
• Разделы
• Предварительные испытания
• Графики и функции
• Классы
• Алгебра
• Исчисление I
• Исчисление II
• Исчисление III
• Дифференциальные уравнения
• Дополнительно
• Алгебра и триггерный обзор
• Распространенные математические ошибки
• Праймер для комплексных чисел
• Как изучать математику

Сложные неравенства и отличие от простых неравенств

Составное неравенство Неравенство , иногда называемое комбинированным неравенством , представляет собой неравенство, которое объединяет два или более простых неравенства, объединенных вместе с или или и .

Чтобы быть решением неравенства или , значение должно делать только одну часть неравенства истинной. Это означает, что окончательным решением будет объединение решений отдельных неравенств. Чтобы быть решением неравенства и , оно должно сделать обе части истинными. Неравенства, условия которых ограничены числами и , не являются независимыми друг от друга. Это означает, что окончательным решением будет пересечение решений отдельных неравенств.

Помните:

или $ \ Rightarrow $ union

и пересечение $ \ Rightarrow $

Пример с неравенством или

$ x <5 $ или $ x> 9 $ В примере задается следующий вопрос: какие числа можно подставить вместо $ x $, чтобы выполнялось одно из неравенств?

$ x <5 \ Rightarrow x \ in \ left <- \ infty, 5 \ right> $

$ x> 9 \ Rightarrow x \ in \ left <9, \ infty \ right> $

Ответ — все числа меньше 5 и все числа больше 9, поэтому решение представляет собой объединение двух интервалов $ \ left <- \ infty, 5 \ right> \ cup \ left <9, \ infty \ right> $ .

Пример с неравенствами и

$ x> 4 $ и $ x <7 $

Этот оператор эквивалентен $ 4

$ x> 4 \ Rightarrow x \ in \ left <4, \ infty \ right> $

$ x <7 \ Rightarrow x \ in \ left <- \ infty, 7 \ right> $

Решение представляет собой пересечение двух интервалов $ \ left <- \ infty, 7 \ right> \ cap \ left <4, \ infty \ right> $, что является интервалом $ \ left <4, 7 \ right> $ .

Пример 1:

$ 2 + 2x \ leq x <5 + x $ Эту проблему можно решить двумя способами.

I.

Задача делится на два неравенства, которые затем решаются отдельно . Решение — пересечение индивидуальных решений.

$ 2 + 2x \ leqslant x $ и $ x <5 + x $$ 2 + 2x \ leqslant x \ Rightarrow 2 \ leq -x \ Rightarrow x \ leq - 2 \ Rightarrow x \ in \ left <- \ infty, - 2 \ right] $$ x <5 + x \ Rightarrow 0 <5 $ Из второго неравенства следует утверждение $ 0

Если случай был другим и утверждение неверно, например $ 5 <0 $, то неравенство не будет решений. Например, неравенство $ x

Решением неравенства из примера 1 является множество $ \ left <- \ infty, - 2 \ right] $.

II.

При работе с уравнениями можно складывать, вычитать, умножать и делить выражение, но то, что изменяется с одной стороны, также должно быть изменено таким же образом с другой. То же самое и при работе с неравенством. Если вы складываете, вычитаете, умножаете или делите, вы должны делать это для каждой части неравенства.

В нашем примере мы можем вычесть 2x $.

$ 2 + 2x \ leqslant x <5 + x

$ $ 2 \ leqslant — x <5 - x $
$ — x

Пример 2:

$ 1 + 58x <55x <57x + 10 $ 90 248 Из каждой части неравенства вычитается $ 57x $:

$ 1 + x <- 2x <10 $

$ 1 + x <- 2x $ и - 2x <10 $

Когда выражение $ — 2x <10 $ делится на $ -2 $, знак неравенства меняется.

$ 3x <- 1 $ и $ x> — 5 $

$ x <- \ frac {1} {3} $ и $ x> — 5 $

Окончательное решение — это набор $ \ left <- 5, - \ frac {1} {3} \ right> $.

В случае, если перекресток пуст, решений нет.

Например, если $ x> 5 $ и $ x <- 7 $, то пересечение множеств $ \ left <5, \ infty \ right> $ и $ \ left <- \ infty, -7 \ right> $ пусто, следовательно, неравенство не имеет решений.

Пример 3:

$ 5> x> 2 $

$ 5> x $ и $ x> 2 \ Rightarrow x \ in \ left <2, 5 \ right> $

Пример 4:

$ — 6 2 $

$ x> — 6 $ и $ x> 2 \ Rightarrow x \ in \ left <2, + \ infty \ right> $

Пример 5:

$ 2x> 4 $ или $ -x> 7 $
$ 2x> 4 \ Rightarrow x> 2 $$ — x> 7 \ Rightarrow x <- 7 $

Решение первого неравенства устанавливается $ \ left <2, \ infty \ right> $ и решение второго неравенства устанавливается $ \ left <- \ infty, - 7 \ right> $.

Окончательное решение — объединение этих двух наборов: $ \ left <- \ infty, - 7 \ right> \ cup \ left <2, \ infty \ right> $.

Пример 6:

$ \ frac {x} {2}> 3 $ или $ x \ geqslant — 3 $
$ x> 6 $ или $ x \ geqslant- 3 $ В таком случае нет необходимости записывать объединение двух наборы, поскольку одно является подмножеством другого. Решением является просто больший набор, в данном случае $ \ left [- 3, + \ infty \ right> $.

Рабочие листы для комплексного неравенства

Целые числа (946.4 КиБ, 967 обращений)

Десятичные числа (1,0 МБ, 593 обращений)

Дроби (1,2 МБ, 583 обращений)

Как записать линейные неравенства в форме пересечения наклона

Запись линейных неравенств из графика — это процесс, обратный построению линейных неравенств.

Прежде чем научиться писать линейные неравенства, мы должны знать информацию о двух прямых линиях, показанных ниже.

Чтобы найти линейные неравенства по двум переменным из графиков, сначала мы должны найти две информации из графика.

(i) Наклон

(ii) y-точка пересечения

Используя две вышеупомянутые информации, мы можем легко получить линейное линейное уравнение в форме y = mx + b.

Здесь m обозначает наклон, а b обозначает точку пересечения с y.

Теперь мы должны заметить, является ли данная линия сплошной линией или пунктирной линией.

• Если на графике есть пунктирная линия, то нужно использовать один из знаков <или>.
• Если график содержит сплошную линию, то нужно использовать один из знаков ≤ или ≥.

Примеры

Пример 1:

Запишите неравенство для приведенного ниже графика.

Решение:

Из приведенного выше графика сначала давайте найдем наклон и точку пересечения по оси Y.

Rise = — 3 and Run = 1

Slope = — 3/1 = — 3

Y-intercept = 4

Итак, уравнение данной линии:

y = — 3x + 4

Но , нам нужно использовать неравенство, удовлетворяющее заштрихованной области.

Поскольку график содержит сплошную линию, мы должны использовать один из знаков ≤ или ≥.

Чтобы найти правильный знак, возьмем точку из заштрихованной области.

Возьмите точку (2, 1) и подставьте в уравнение прямой.

y = — 3x + 4

То есть

1 = — 3 (2) + 4 ?

1 = — 6 + 4 ?

1 = — 2 ?

Здесь 1 больше -2. Итак, мы должны выбрать знак ≥ вместо знака равенства в уравнении y = -3x + 4

Следовательно, необходимое неравенство составляет

y ≥ — 3x + 4.

Пример 2:

Запишите неравенство для графика, приведенного ниже.

Решение:

Из приведенного выше графика сначала давайте найдем наклон и точку пересечения по оси Y.

Rise = 3 and Run = 5

Slope = 3/5

Y-intercept = — 5

Итак, уравнение данной линии:

y = (3/5) x + 4

y = 3x / 5 + 4

Но нам нужно использовать неравенство, удовлетворяющее заштрихованной области.

Поскольку график содержит сплошную линию, мы должны использовать один из знаков ≤ или ≥.

Возьмите точку (5, -3) и подставьте в уравнение прямой.

y = 3x / 5 + 4

-3 = 3 (5) / 5 + 4 ?

-3 = 3 + 4 ?

-3 = 7 ?

Здесь (-3) меньше 7. Итак, мы должны выбрать знак ≤ вместо знака равенства в уравнении y = 3x / 5 + 4.

Следовательно, необходимое неравенство:

y ≤ 3x / 5 + 4.

Пример 3:

Запишите неравенство для приведенного ниже графика.

Решение:

Из приведенного выше графика сначала давайте найдем наклон и точку пересечения по оси Y.

Rise = — 2 and Run = 2

Slope = — 2/2 = — 1

Y-intercept = — 5

Итак, уравнение данной прямой

y = — x — 5

Но нам нужно использовать неравенство, которое удовлетворяет заштрихованной области.

Поскольку график содержит пунктирную линию, мы должны использовать один из знаков <или>.

Возьмите точку (0, 0) и подставьте в уравнение прямой.

y = — x — 5

0 = 0 — 5 ?

0 = — 5 ?

Здесь 0 больше (-5). Итак, мы должны выбрать знак <вместо знака равенства в уравнении

y = — x — 5

Следовательно, требуемое неравенство:

y> -x — 5

Кроме того, что описано в этом разделе, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.

Если у вас есть какие-либо отзывы о нашей математической информации, напишите нам:

[email protected]

Мы всегда ценим ваши отзывы.

Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.

ЗАДАЧИ СО СЛОВАМИ

Задачи со словами HCF и LCM

Задачи со словами на простых уравнениях

Задачи со словами на линейных уравнениях

Проблемы со словами на квадратные уравнения

Проблемы со словами в поездах

Проблемы со словами по площади и периметру

Проблемы со словами по прямой и обратной вариациям

Проблемы со словами по цене за единицу

Проблемы со словами по скорости за единицу

задачи по сравнению ставок

Преобразование обычных единиц словесные задачи

Преобразование метрических единиц в текстовые задачи

Word задачи по простому проценту

Word задачи по сложным процентам

ngles

Проблемы с дополнительными и дополнительными углами в словах

Проблемы со словами с двойными фактами

Проблемы со словами тригонометрии

Проблемы со словами в процентах

Проблемы со словами в виде прибыли и убытка 9667 00066 Задачи

Задачи с десятичными словами

Задачи со словами о дробях

Задачи со словами о смешанных фракциях

Одношаговые задачи с уравнениями со словами

Проблемы со словами с линейным неравенством

66 Задачи со словами

Проблемы со временем и рабочими словами

Задачи со словами на множествах и диаграммах Венна

Проблемы со словами на возрастах

Проблемы со словами из теоремы Пифагора

Процент числового слова проблемы

Проблемы со словами при постоянной скорости

Проблемы со словами при средней скорости

Проблемы со словами на сумме углов треугольника 180 градусов

ДРУГИЕ ТЕМЫ

Сокращения прибыли и убытков

Сокращение в процентах

Сокращение в таблице времен

Сокращение времени, скорости и расстояния

Сокращение соотношения и пропорции

Домен и диапазон рациональных функций 9 9667 функции с отверстиями

Графики рациональных функций

Графики рациональных функций с отверстиями

Преобразование повторяющихся десятичных знаков в дроби

Десятичное представление рациональных чисел

видение

Л. Метод CM для решения задач времени и работы

Преобразование задач со словами в алгебраические выражения

Остаток при делении 2 в степени 256 на 17

Остаток при делении в степени 17 на 16

Сумма всех трехзначных чисел, делимых на 6

Сумма всех трехзначных чисел, делимых на 7

Сумма всех трехзначных чисел, делимых на 8

Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4

Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами

Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3

Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6

.

No related posts.