Урок 7. осевая и центральная симметрия — Геометрия — 8 класс
КонспектРассмотрим прямую a и точку, не принадлежащую ей.
Точки А и А1 называются симметричными относительно прямой а, если:
— эта прямая проходит через середину отрезка АА1
— а ⊥ АА1.
Прямая a называется осью симметрии. Если точка принадлежит прямой а, то она симметрична сама себе.
Составим алгоритм построения точки, симметричной данной.
Алгоритм построения
• Провести прямую b перпендикулярную прямой а
• Отложить от точки О на прямой b расстояние, равное ОА
• Получить точку А1
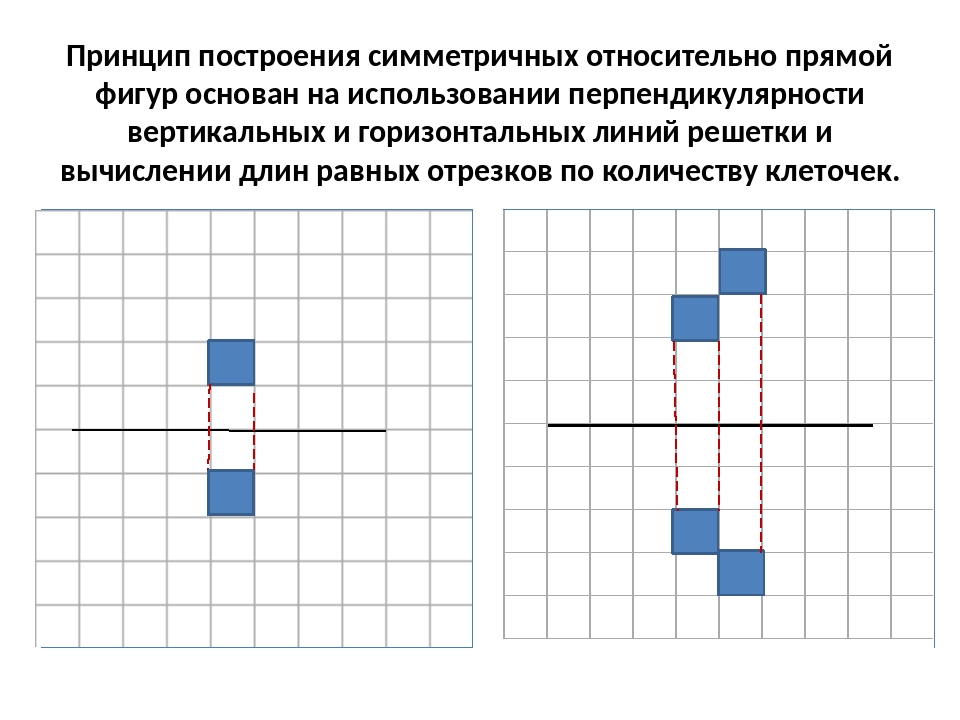
Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая а называется осью симметрии фигуры.
(Цвет линий и букв черный)
Равносторонний треугольник имеет три оси симметрии.
Подумайте, какие из данных фигур имеют ось симметрии и сколько?
Рассмотрим симметрию относительно точки.
Симметрия относительно точки
Две точки А и А1 называются симметричными относительно точки О, если О – середина отрезка АА1.
Составим алгоритм построения точки, симметричной данной относительно точки О.
Алгоритм построения
• Соединить точку А и точку О прямой и продолжить прямую за точку О
• От точки О отложить расстояние равное ОА
Фигура называется симметричной относительно центра, если для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре.
Центр симметрии имеет круг, квадрат.
Подумайте, какие из данных фигур имеют центр симметрии?
Слово «симметрия» греческое (συμμετρία), оно означает «соразмерность, пропорциональность, одинаковость в расположении частей», неизменность при каких-либо преобразованиях.
В словаре С.И. Ожегова симметрия – это соразмерность, пропорциональность частей чего-нибудь, расположенных по обе стороны от середины, центра.
Симметрией обладают некоторые буквы латинского и русского алфавита. Например, буква М обладает осевой симметрией, а буква Х – центральной симметрией.
Многие дорожные знаки обладают осевой или центральной симметрией. Гуляя по городу, приглядитесь к знакам. Найдите такие, которые имеют несколько осей симметрии и такие, которые не имеют осей симметрии.
Есть ось симметрии, центра симметрии нет Есть центр симметрии и 4 оси симметрии
Урок 7. осевая и центральная симметрия — Геометрия — 8 класс
осевая и центральная симметрия — Геометрия — 8 класс
КонспектРассмотрим прямую a и точку, не принадлежащую ей.
Точки А и А1 называются симметричными относительно прямой а, если:
— эта прямая проходит через середину отрезка АА1
— а ⊥ АА1.
Прямая a называется осью симметрии. Если точка принадлежит прямой а, то она симметрична сама себе.
Составим алгоритм построения точки, симметричной данной.
Алгоритм построения
• Провести прямую b перпендикулярную прямой
• Отложить от точки О на прямой b расстояние, равное ОА
• Получить точку А1
Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая а называется осью симметрии фигуры.
(Цвет линий и букв черный)
Равносторонний треугольник имеет три оси симметрии.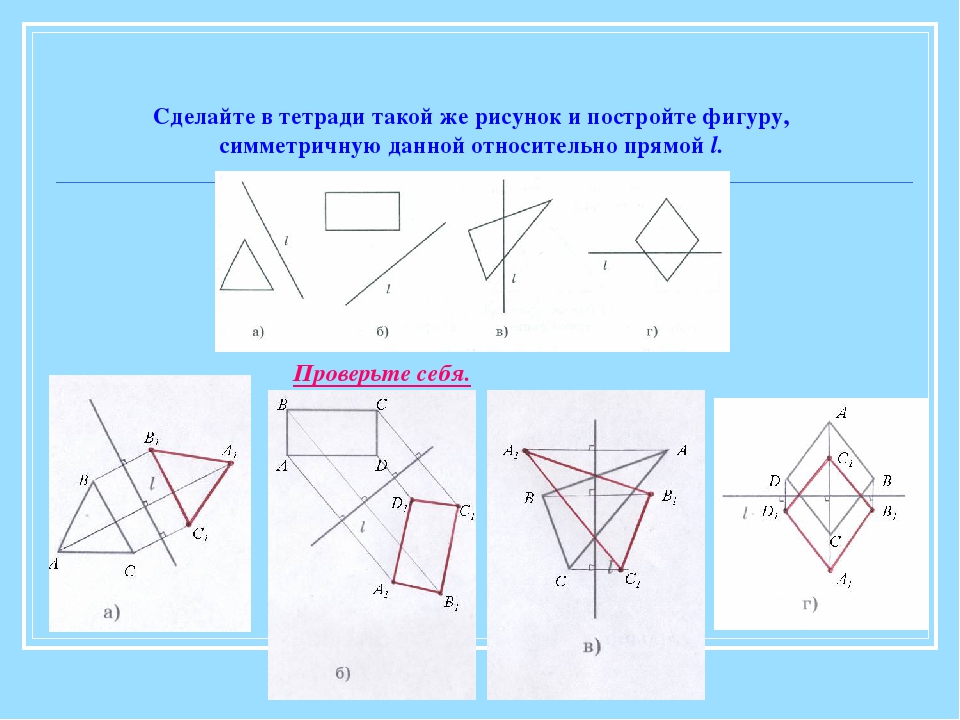 Неразвернутый угол имеет одну ось симметрии – прямую, содержащую биссектрису угла.
Неразвернутый угол имеет одну ось симметрии – прямую, содержащую биссектрису угла.
Подумайте, какие из данных фигур имеют ось симметрии и сколько?
Рассмотрим симметрию относительно точки.
Две точки А и А1 называются симметричными относительно точки О, если О – середина отрезка АА1.
Составим алгоритм построения точки, симметричной данной относительно точки О.
Алгоритм построения
• Соединить точку А и точку О прямой и продолжить прямую за точку О
• От точки О отложить расстояние равное ОА
• Получить точку А1
Фигура называется симметричной относительно центра, если для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре.
Центр симметрии имеет круг, квадрат.
Подумайте, какие из данных фигур имеют центр симметрии?
Слово «симметрия» греческое (συμμετρία), оно означает «соразмерность, пропорциональность, одинаковость в расположении частей», неизменность при каких-либо преобразованиях.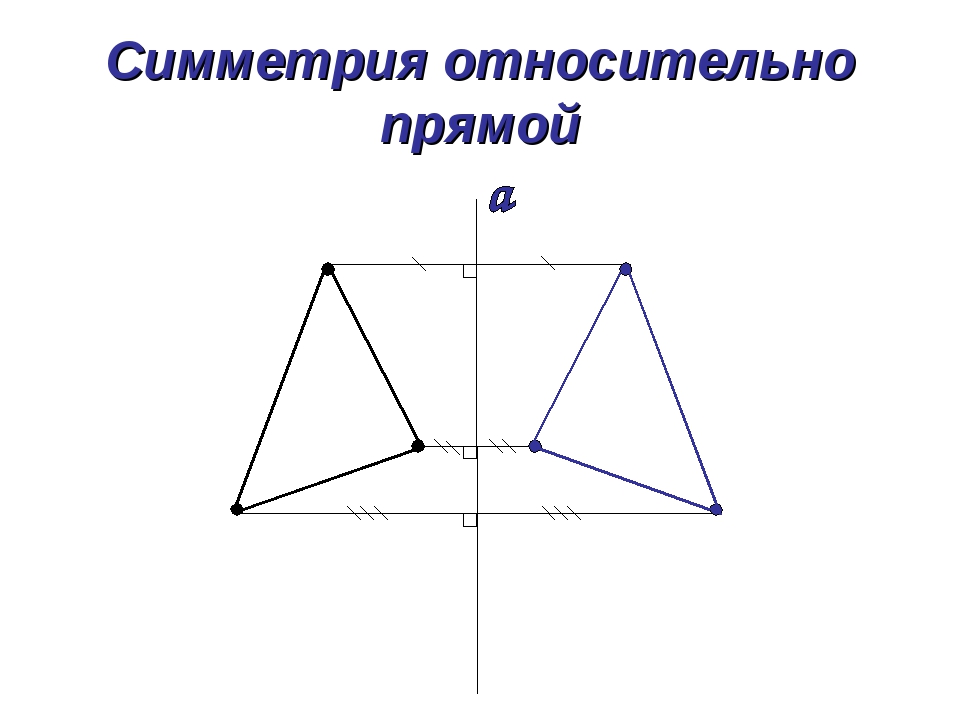
В словаре С.И. Ожегова симметрия – это соразмерность, пропорциональность частей чего-нибудь, расположенных по обе стороны от середины, центра.
С симметрией мы часто встречаемся в природе, архитектуре, искусстве, технике и быту. Симметрия в одежде – это символ строгости. Симметрия в архитектуре – это признак красоты и надежности. Некоторые люди утверждают, что симметрия – это совершенство.
Симметрией обладают некоторые буквы латинского и русского алфавита. Например, буква М обладает осевой симметрией, а буква Х – центральной симметрией.
Есть ось симметрии, центра симметрии нет Есть центр симметрии и 4 оси симметрии
Геометрия, 7-9: учеб. для общеобразоват. учреждений/ [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.]. – М.: Просвещение, 2017.
Симмерия относительно прямой | Образовательная социальная сеть
Слайд 1
Симметрия относительно прямой Выполнил : Хомяк Вадим 8 “Б”Слайд 2
Симметрия относительно прямой А А 1 a Точки А и А 1 называются симметричными относительно прямой (ось симметрии), если прямая проходит через середину отрезка АА 1 и перпендикулярна к этому отрезку.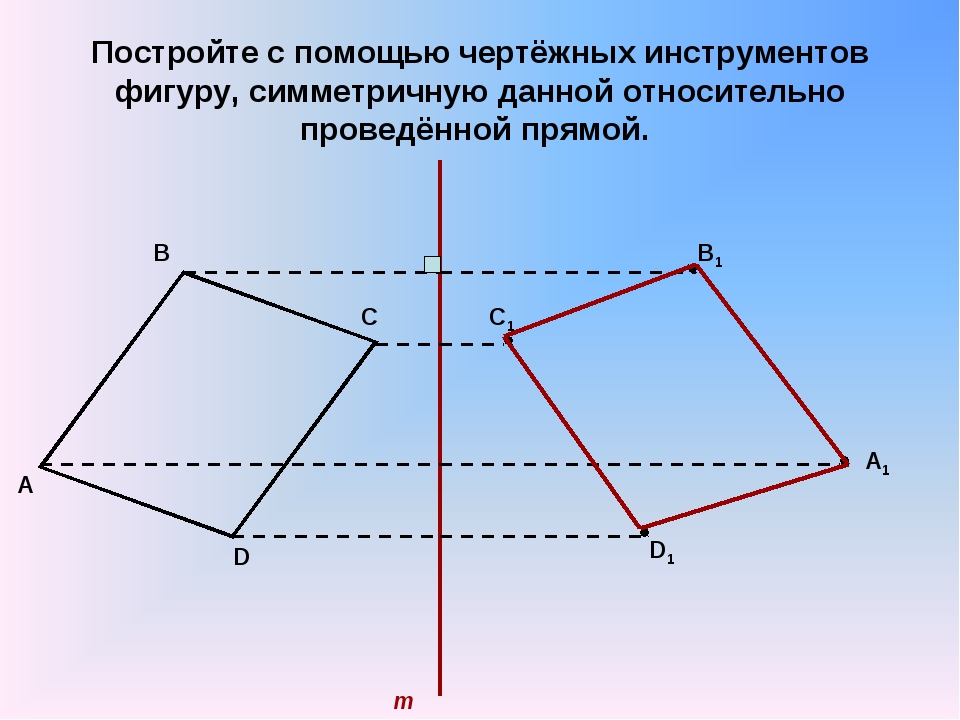 Каждая точка прямой считается симметричной самой себе. a a a Симметрия относительно прямой называется осевой симметрией
Каждая точка прямой считается симметричной самой себе. a a a Симметрия относительно прямой называется осевой симметрией
Слайд 3
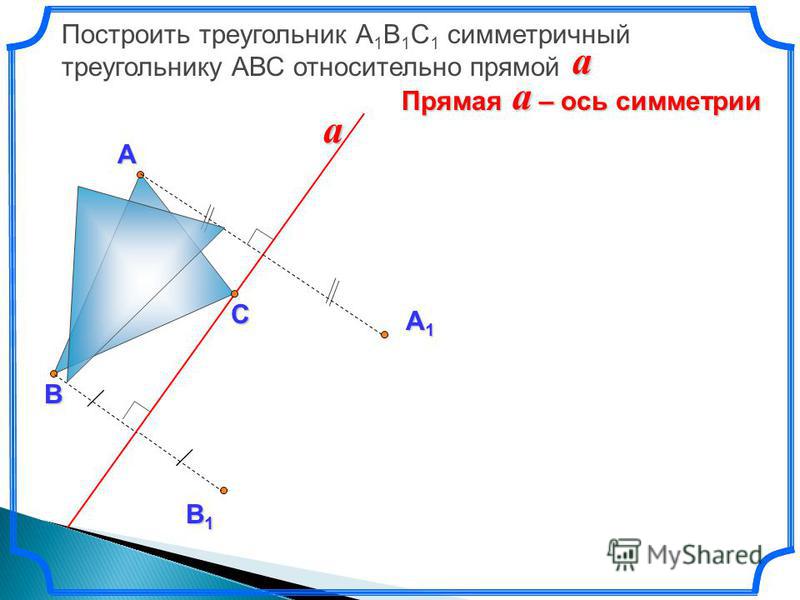
А Построить отрезок А 1 В 1 симметричный отрезку АВ относительно прямой В a А 1 В 1 a Прямая – ось симметрии a
Слайд 4
Построить отрезок А 1 В 1 симметричный отрезку АВ относительно прямой В a А a А 1 В 1 Прямая – ось симметрии a
Слайд 5
Построить треугольник А 1 В 1 С 1 симметричный треугольнику АВС относительно прямой a Прямая – ось симметрии a А С В А 1 С 1 В 1 a
Слайд 6
Построить треугольник А 1 В 1 С 1 симметричный треугольнику АВС относительно прямой a Прямая – ось симметрии a А В a А 1 С В 1
Слайд 7
Построить треугольник А 1 В 1 С 1 симметричный треугольнику АВС относительно прямой a Прямая – ось симметрии a А В a В 1 С
Слайд 8
Прямая – ось симметрии a А В a А 1 В 1 С С 1
Слайд 9
Если фигура имеет ось симметрии, то говорят, что она обладает осевой симметрией. Фигура может иметь одну или несколько осей симметрии.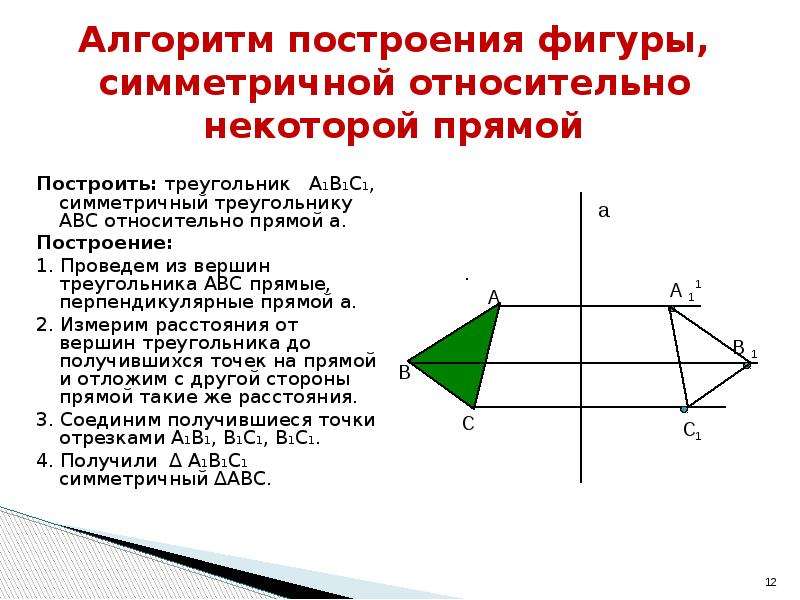 Фигура называется симметричной относительно оси , если для каждой точки фигуры симметричная ей точка относительно прямой также принадлежит этой фигуре. a a
Фигура называется симметричной относительно оси , если для каждой точки фигуры симметричная ей точка относительно прямой также принадлежит этой фигуре. a a
Слайд 10
Правильный треугольник Равнобедренный треугольник Отрезок Прямоугольник Сколько осей симметрии имеет каждая фигура? Равнобедренная трапеция
Слайд 11
прямая Луч Правильный шестиугольник Параллелограмм Угол Сколько осей симметрии имеет каждая фигура?
Слайд 12
Какие буквы имеют ось симметрии? А Б Г Ж Э Ю Н Ш 0 П Ф
Слайд 13
W U D R Y S V Какие буквы имеют ось симметрии? Х С М В
Слайд 16
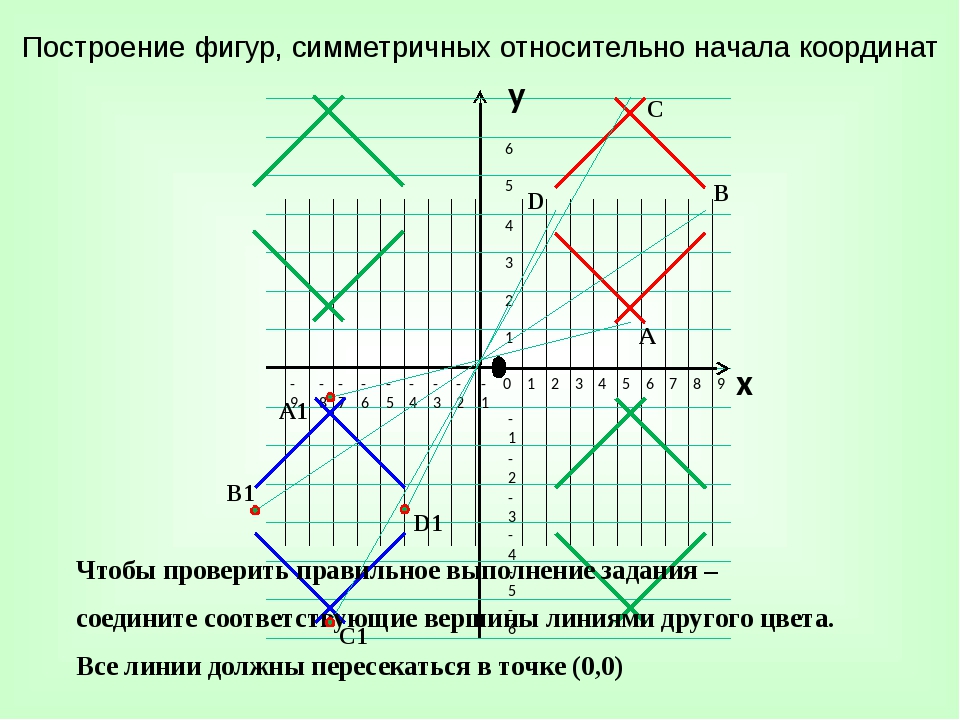
1 2 3 4 5 6 7 х -7 -6 -5 -4 -3 -2 -1 7 6 5 4 3 2 1 -1 -2 -3 -4 -5 -6 -7 у Симметрия на координатной плоскости Центральная симметрия
Слайд 17
1 2 3 4 5 6 7 х -7 -6 -5 -4 -3 -2 -1 7 6 5 4 3 2 1 -1 -2 -3 -4 -5 -6 -7 у Осевая симметрия Симметрия на координатной плоскости
Осевая симметрия | Образовательная социальная сеть
Слайд 1
Презентация Предмет: Геометрия Тема: Осевая симметрия Создатель: Павел ЩЕГЛОВ Дата: 15 февраля 2010 год.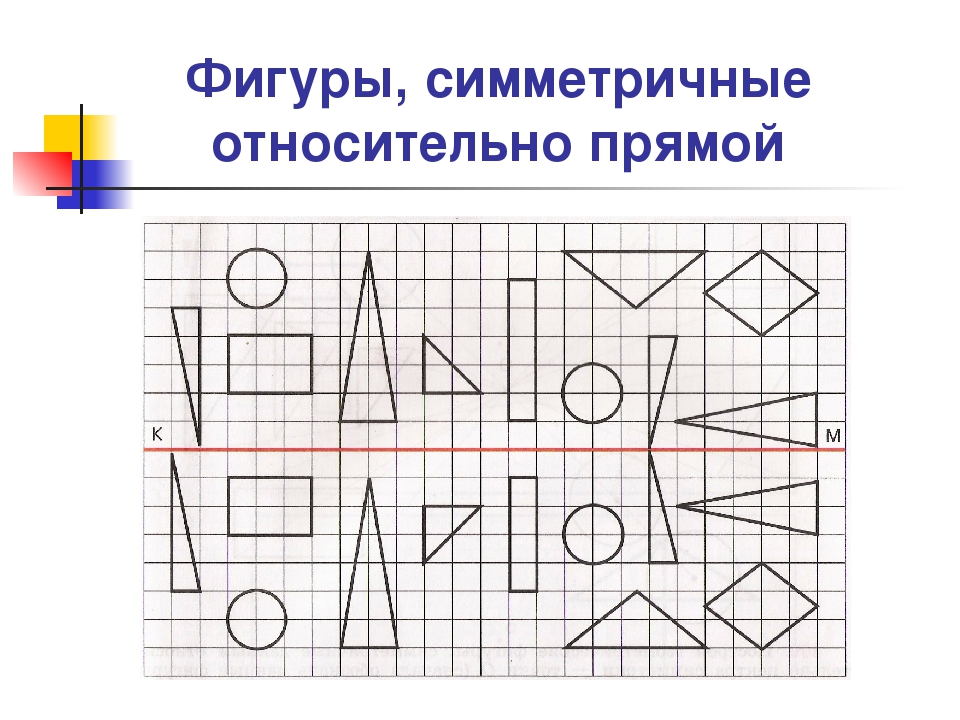
Слайд 2
Определение: Симметрия – это соразмерность, одинаковость в расположении частей чего-нибудь по противоположным сторонам от точки, прямой или плоскости. Осевая симметрия
Слайд 3
Симметричность точек относительно прямой A A 1 a Т AO = OA 1 Определение: Две точки А и А 1 называются симметричными относительно прямой а , если эта прямая проходит через середину отрезка АА 1 и перпендикулярна к нему. Каждая точка прямой а считается симметричной самой себе. A A 1 a О Г
Слайд 4
Симметричность фигуры относительно прямой Определение: Фигура называется симметричной относительно прямой , если для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре. Прямая а называется осью симметрии фигуры. Говорят также, что фигура обладает осевой симметрией. А D B C a
Слайд 5
Построение точки, симметричной данной А с А 1 1 . АО с О 2. АО=ОА1
Слайд 6
построение отрезка, симметричного данному А с А1 В В1 O O 1 АА1 с, АО=ОА1. ВВ1 с, ВО1=О1В1. 3. А1В1 – искомый отрезок.
3. А1В1 – искомый отрезок.
Слайд 7
Алгоритм построения осевой симметрии От всех точек данной фигуры, отложить отрезки перпендикулярно прямой так, чтобы прямая делила их пополам. Соединить концы отрезков. А B D C А 1 B1 C1 D1 Г Г
Слайд 8
Примеры осевой симметрии. У неразвёрнутого угла одна ось симметрии — прямая, на которой расположена биссектриса угла. Равнобедренный (но не равносторонний) треугольник имеет также одну ось симметрии. А равносторонний треугольник — три основные симметрии Прямоугольник и ромб , не являющиеся квадратами имеют по две оси симметрии, а квадрат — четыре оси симметрии.
Слайд 9
У окружности их бесконечно много — любая прямая, проходящая через её центр, является осью симметрии. Имеются фигуры, у которых нет ни одной оси симметрии. К таким фигурам относятся параллелограмм, отличный от прямоугольника, разносторонний треугольник.
Слайд 10
y x A B (4;3) C y x A 1 B 1 B C C 1 (-4;3) (4;-3) Симметричность на координатной плоскости A
Слайд 11
y y x x A B C D A 1 B 1 C 1 D 1 M K K 1 M 1
Слайд 12
Осевая симметрия в природе
Слайд 13
Осевая симметрия в Архитектуре
Слайд 15
Осевая симметрия в Технике
Слайд 16
Осевая симметрия в искусстве И так далее…
Слайд 17
Конец!!!
Слайд 18
Конец!!!
Слайд 19
Конец!!!
6. 7.3. Осевая симметрия.
7.3. Осевая симметрия.
- Две точки А и А1 называются симметричными друг другу относительно прямой m
- При сгибании плоскости чертежа по прямой m – оси симметрии симметричные фигуры совместятся.
- Прямоугольник имеет две оси симметрии.
- Квадрат имеет четыре оси симметрии.
- Любая прямая, проходящая через центр окружности, является ее осью симметрии. Окружность имеет бесконечное множество осей симметрии.
Точки А и А1 симметричны относительно прямой m, так как прямая m перпендикулярна отрезку АА
m – ось симметрии.
Прямоугольник ABCD имеет две оси симметрии: прямые m и l.
Если чертеж перегнуть по прямой m или по прямой l, то обе части чертежа совпадут.
Квадрат ABCD имеет четыре оси симметрии: прямые m, l, k и s.
Если квадрат перегнуть по какой-либо из прямых: m, l, k
Окружность с центром в точке О и радиусом ОА имеет бесчисленное количество осей симметрии. Это прямые: m, m1, m2, m3 …
Задание. Построить точку А1, симметричную точке А(-4; 2) относительно оси Ох.
Построить точку А2, симметричную точке А(-4; 2) относительно оси Оy.
Точка А1(-4; -2) симметрична точке А(-4; 2) относительно оси Ох, так как ось Ох перпендикулярна отрезку АА1 и проходит через его середину.
У точек, симметричных относительно оси Ох абсциссы совпадают, а ординаты являются противоположными числами.
Точка А2(4; -2) симметрична точке А(-4; 2) относительно оси Оy, так как ось Оу перпендикулярна отрезку АА2 и проходит через его середину.
У точек, симметричных относительно оси Оу ординаты совпадают, а абсциссы являются противоположными числами.
Симметрия фигур в пространстве
Центральная симметрия
Две фигуры называются симметричными относительно какой-либо точки О пространства, если каждой точке А одной фигуры соответствует в другой фигуре точка А, расположенная на прямой ОА по другую сторону от точки О, на расстоянии, равном расстоянию точки А от точки О (черт. 114). Точка О называется центром симметрии фигур.
Пример таких симметричных фигур в пространстве мы уже встречали (§ 53), когда, продолжая за вершину рёбра и грани многогранного угла, получали многогранный угол, симметричный данному. Соответственные отрезки и углы, входящие в состав двух симметричных фигур, равны между собой. Тем не менее фигуры в целом не могут быть названы равными: их нельзя совместить одну с другой вследствие того, что порядок расположения частей в одной фигуре иной, чем в другой, как это мы видели на примере симметричных многогранных углов.
Соответственные отрезки и углы, входящие в состав двух симметричных фигур, равны между собой. Тем не менее фигуры в целом не могут быть названы равными: их нельзя совместить одну с другой вследствие того, что порядок расположения частей в одной фигуре иной, чем в другой, как это мы видели на примере симметричных многогранных углов.
В отдельных случаях симметричные фигуры могут совмещаться, но при этом будут совпадать несоответственные их части. Например, возьмём прямой трёхгранный угол (черт. 115) с вершиной в точке О и рёбрами ОХ, OY, OZ.
Построим ему симметричный угол ОХYZ. Угол OXYZ можно совместить с OXYZ так, чтобы ребро ОХ совпало с OY, а ребро OY c OX. Если же совместить соответственные рёбра ОХ с ОХ и OY с OY, то рёбра OZ и OZ окажутся направленными в противоположные стороны.
Если симметричные фигуры составляют в совокупности одно геометрическое тело, то говорят, что это геометрическое тело имеет центр симметрии. Таким образом, если данное тело имеет центр симметрии, то всякой точке, принадлежащей этому телу, соответствует симметричная точка, тоже принадлежащая данному телу. Из рассмотренных нами геометрических тел центр симметрии имеют, например:
Из рассмотренных нами геометрических тел центр симметрии имеют, например:
- параллелепипед,
- призма, имеющая в основании правильный многоугольник с чётным числом сторон.
Правильный тетраэдр не имеет центра симметрии.
Симметрия относительно плоскости
Две пространственные фигуры называются симметричными относительно плоскости Р, если каждой точке А в одной фигуре соответствует в другой точка А, причём отрезок АА перпендикулярен к плоскости Р и в точке пересечения с этой плоскостью делится пополам.
Теорема. Всякие два соответственных отрезка в двух симметричных фигурах равны между собой.
Пусть даны две фигуры, симметричные относительно плоскости Р. Выделим две какие-нибудь точки А и В первой фигуры, пусть А и В — соответствующие им точки второй фигуры (черт. 116, на чертеже фигуры не изображены).
Пусть далее С — точка пересечения отрезка АА с плоскостью Р, D — точка пересечения отрезка ВВ с той же плоскостью.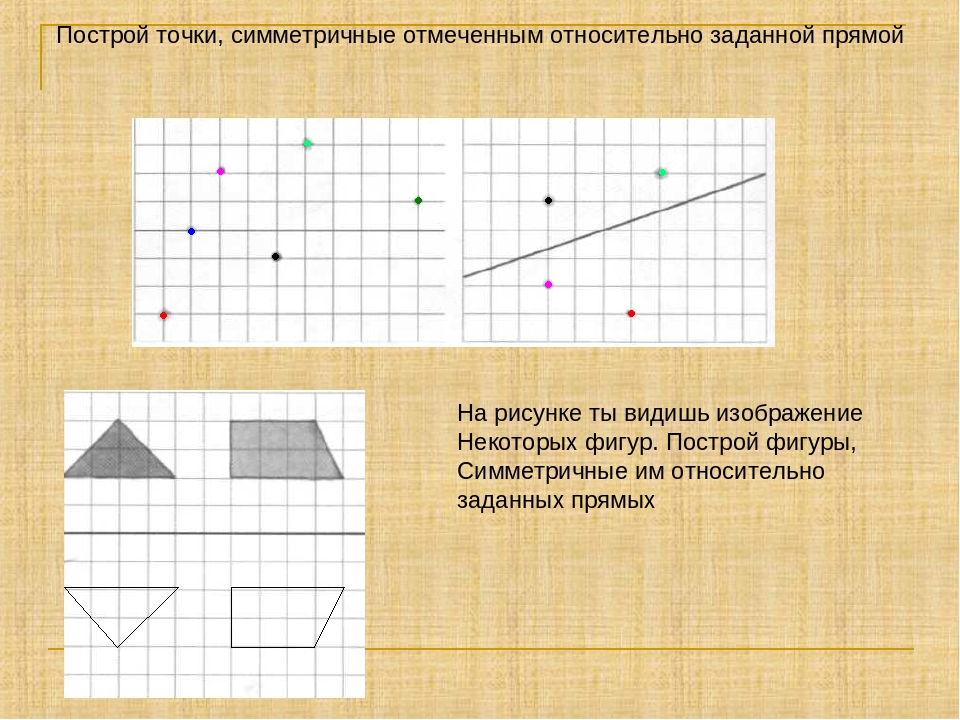 Соединив прямолинейным отрезком точки С и D, получим два четырёхугольника ABDC и ABDC. Так как AС = AС, BD = BD и
Соединив прямолинейным отрезком точки С и D, получим два четырёхугольника ABDC и ABDC. Так как AС = AС, BD = BD и
∠ACD = ∠ACD, ∠BDC = ∠ВDC, как прямые углы, то эти четырёхугольники равны (в чём легко убеждаемся наложением). Следовательно, АВ = АВ. Из этой теоремы непосредственно вытекает, что соответствующие плоские и двугранные углы двух фигур, симметричных относительно плоскости, равны между собой. Тем не менее совместить эти две фигуры одну с другой так, чтобы совместились их соответственные части, невозможно, так как порядок расположения частей в одной фигуре обратный тому, котoрый имеет место в другой. Простейшим примером двух фигур, симметричных относительно плоскости, являются: любой предмет и его отражение в плоском зеркале; всякая фигура, симметрична со своим зеркальным отражением относительно плоскости зеркала.
Если какое-либо геометрическое тело можно разбить на две части, симметричные относительно некоторой плоскости, то эта плоскость называется плоскостью симметрии данного тела.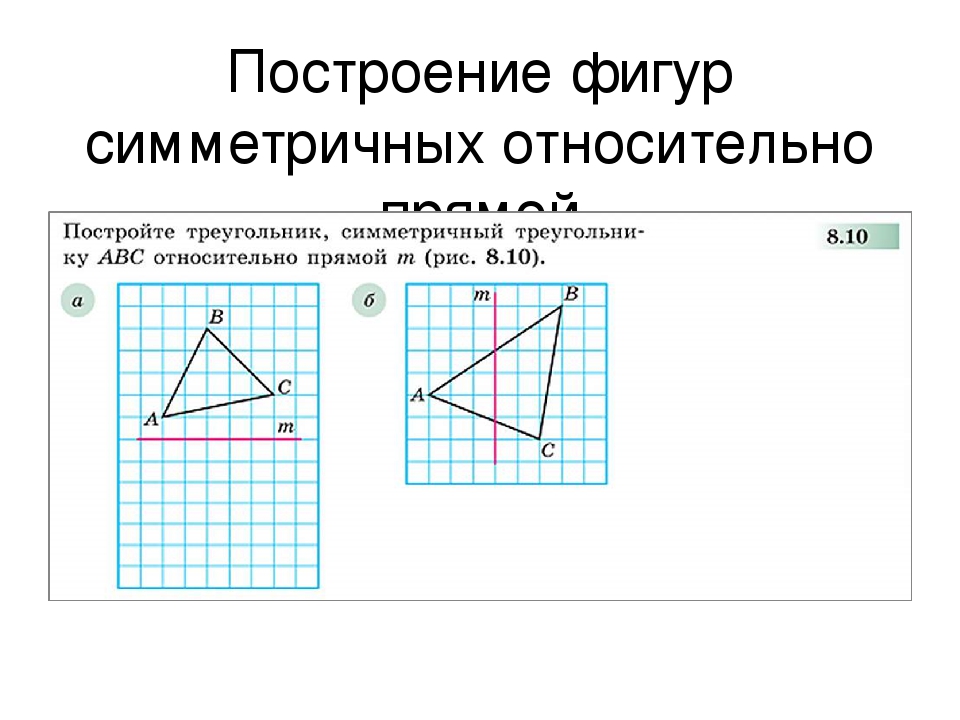
Геометрические тела, имеющие плоскость симметрии, чрезвычайно распространены в природе и в обыденной жизни. Тело человека и животного имеет плоскость симметрии, разделяющую его на правую и левую части.
На этом примере особенно ясно видно, что симметричные фигуры нельзя совместить. Так, кисти правой и левой рук симметричны, но совместить их нельзя, что можно видеть хотя бы из того, что одна и та же перчатка не может подходить и к правой и к левой руке. Большое число предметов домашнего обихода имеет плоскость симметрии: стул, обеденный стол, книжный шкаф, диван и др. Некоторые, как например обеденный стол, имеют даже не одну, а две плоскости симметрии (черт. 117).
Обычно, рассматривая предмет, имеющий плоскость симметрии, мы стремимся занять по отношению к нему такое положение, чтобы плоскость симметрии нашего тела, или по крайней мере нашей головы, совпала с плоскостью симметрии самого предмета. В этом случае симметричная форма предмета становится особенно заметной.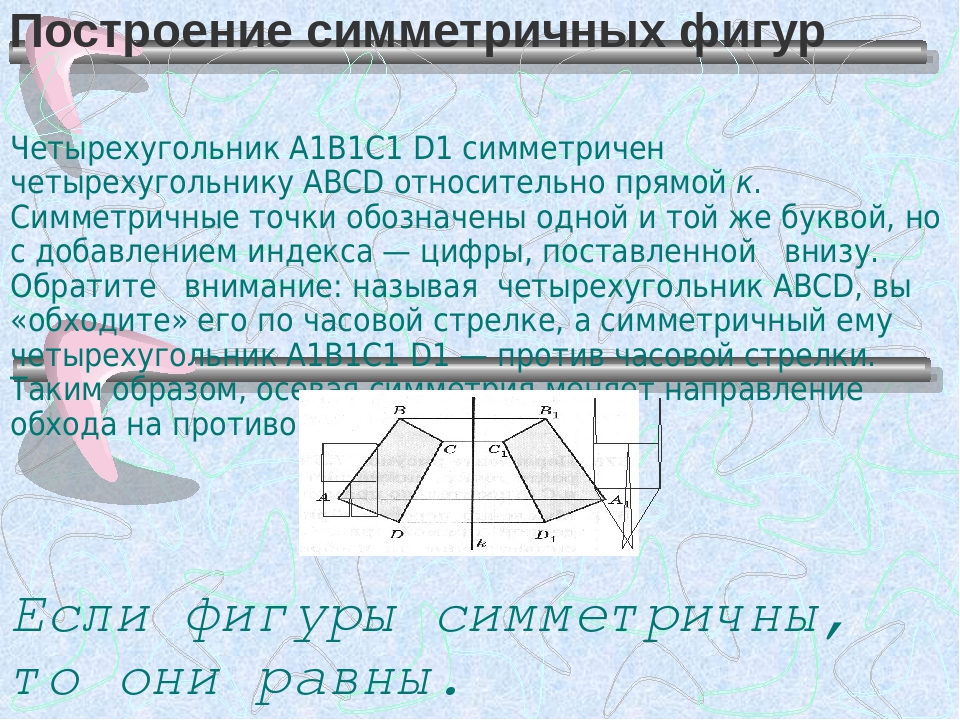
Симметрия относительно оси. Ось симметрии второго порядка.
Две фигуры называются симметричными относительно оси l (ось-прямая линия), если каждой точке А первой фигуры соответствует точка А второй фигуры, так что отрезок АА перпендикулярен к оси l, пересекается с нею и в точке пересечения делится пополам. Сама ось l называется осью симметрии второго порядка.Из этого определения непосредственно следует, что если два геометрических тела, симметричных относительно какой-либо оси, пересечь плоскостью, перпендикулярной к этой оси, то в сечении получатся две плоские фигуры, симметричные относительно точки пересечения плоскости с осью симметрии тел.
Отсюда далее легко вывести, что два тела, симметричных относительно оси, можно совместить одно с другим, вращая одно из них на 180° вокруг оси симметрии. В самом деле, вообразим все возможные плоскости, перпендикулярные к оси симметрии.
Каждая такая плоскость, пересекающая оба тела, содержит фигуры, симметричные относительно точки встречи плоскости с осью симметрии тел.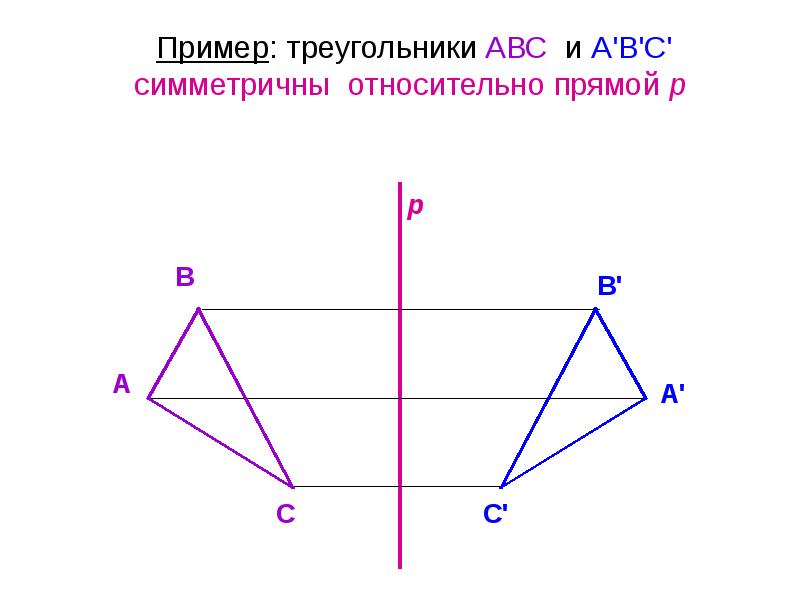 Если заставить скользить секущую плоскость саму по себе, вращая её вокруг оси симметрии тела на 180°, то первая фигура совпадает со второй.
Если заставить скользить секущую плоскость саму по себе, вращая её вокруг оси симметрии тела на 180°, то первая фигура совпадает со второй.
Это справедливо для любой секущей плоскости. Вращение же всех сечений тела на 180° равносильно повороту всего тела на 180° вокруг оси симметрии. Отсюда и вытекает справедливость нашего утверждения.
Если после вращения пространственной фигуры вокруг некоторой прямой на 180° она совпадает сама с собой, то говорят, что фигура имеет эту прямую своею осью симметрии второго порядка.
Название «ось симметрии второго порядка » объясняется тем, что при полном обороте вокруг этой оси тело будет в процессе вращения дважды принимать положение, совпадающее с исходным (считая и исходное). Примерами геометрических тел, имеющих ось симметрии второго порядка, могут служить:
1) правильная пирамида с чётным числом боковых граней; осью её симметрии служит её высота;
2) прямоугольный параллелепипед; он имеет три оси симметрии: прямые, соединяющие центры его противоположных граней;
3) правильная призма с чётным числом боковых граней. Осью её симметрии служит каждая прямая, соединяющая центры любой пары её противоположных граней (боковых граней и двух оснований призмы). Если число боковых граней призмы 2k, то число таких осей симметрии будет k + 1. Кроме того, осью симметрии для такой призмы служит каждая прямая, соединяющая середины её противоположных боковых рёбер. Таких осей симметрии призма имеет А.
Осью её симметрии служит каждая прямая, соединяющая центры любой пары её противоположных граней (боковых граней и двух оснований призмы). Если число боковых граней призмы 2k, то число таких осей симметрии будет k + 1. Кроме того, осью симметрии для такой призмы служит каждая прямая, соединяющая середины её противоположных боковых рёбер. Таких осей симметрии призма имеет А.
Таким образом, правильная 2k-гранная призма имеет 2k+1 осей, симметрии.
Зависимость между различными видами симметрии в пространстве.
Между различными видами симметрии в пространстве — осевой, плоскостной и центральной — существует зависимость, выражаемая следующей теоремой.Теорема. Если фигура F симметрична с фигурой F относительно плоскости Р и в то же время симметрична с фигурой F» относительно точки О, лежащей в плоскости Р, то фигуры F и F» симметричны относительно оси, проходящей через точку О и перпендикулярной к плоскости Р.
Возьмём какую-нибудь точку А фигуры F (черт.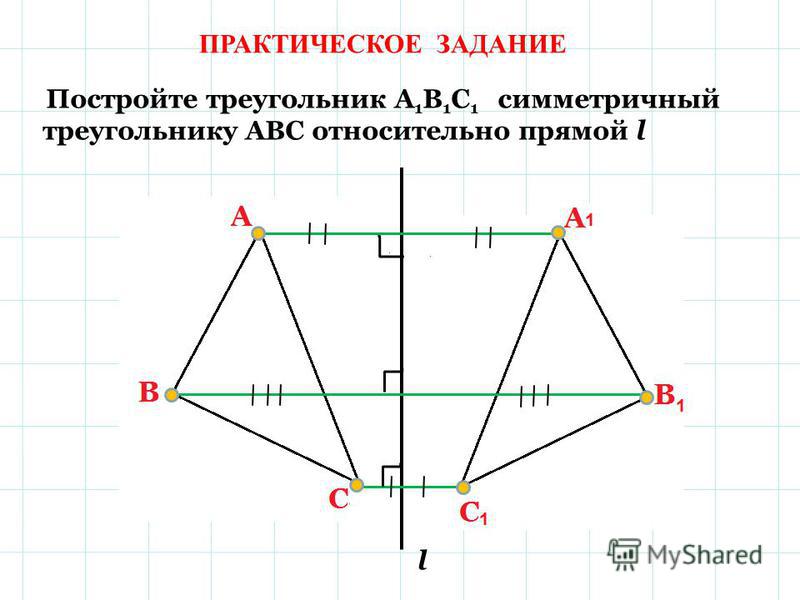 118). Ей соответствует точка А фигуры F и точка А» фигуры F» (сами фигуры F, F и F» на чертеже не изображены).
118). Ей соответствует точка А фигуры F и точка А» фигуры F» (сами фигуры F, F и F» на чертеже не изображены).
Пусть B — точка пересечения отрезка АА с плоскостью Р. Проведeм плоскость через точки А, А и О. Эта плоскость будет перпендикулярна к плоскости Р, так как проходит через прямую АА, перпендикулярную к этой плоскости. В плоскости ААО проведём прямую ОН, перпендикулярную к ОВ. Эта прямая ОН будет перпендикулярна и к плоскости Р. Пусть далее С-точка пересечения прямых АА» и ОН.
B треугольнике ААА» отрезок ВО соединяет середины сторон АА и АА», следовательно, ВО || АА», но ВО⊥ОН, значит, АА»⊥ОН. Далее, так как О — середина стороны АA», и СО || АА, то АС = А»С. Отсюда заключаем, что точки А и А» симметричны относительно оси ОН. То же самое справедливо и для всех других точек фигуры. Значит, наша теорема доказана. Из этой теоремы непосредственно следует, что две фигуры, симметричные относительно плоскости, не могут быть совмещены так, чтобы совместились их соответственные части. В самом деле, фигура F совмещается с F» путём вращения вокруг оси ОН на 180°. Но фигуры F» и F не могут быть совмещены как симметричные относительно точки, следовательно, фигуры F и F также не могут быть совмещены.
В самом деле, фигура F совмещается с F» путём вращения вокруг оси ОН на 180°. Но фигуры F» и F не могут быть совмещены как симметричные относительно точки, следовательно, фигуры F и F также не могут быть совмещены.
Оси симметрии высших порядков
Фигура, имеющая ось симметрии, совмещается сама с собой после поворота вокруг оси симметрии на угол в 180°. Но возможны случаи, когда фигура приходит к совмещению с исходным положением после поворота вокруг некоторой оси на угол, меньший 180°. Таким образом, если тело сделает полный оборот вокруг этой оси, то в процессе вращения оно несколько раз совместится со своим первоначальным положением. Такая ось вращения называется осью симметрии высшего порядка, причём число положений тела, совпадающих с первоначальным, называется порядком оси симметрии. Эта ось может и не совпадать с осью симметрии второго порядка. Так, правильная треугольная пирамида не имеет оси симметрии второго порядка, но её высота служит для неё осью симметрии третьего порядка.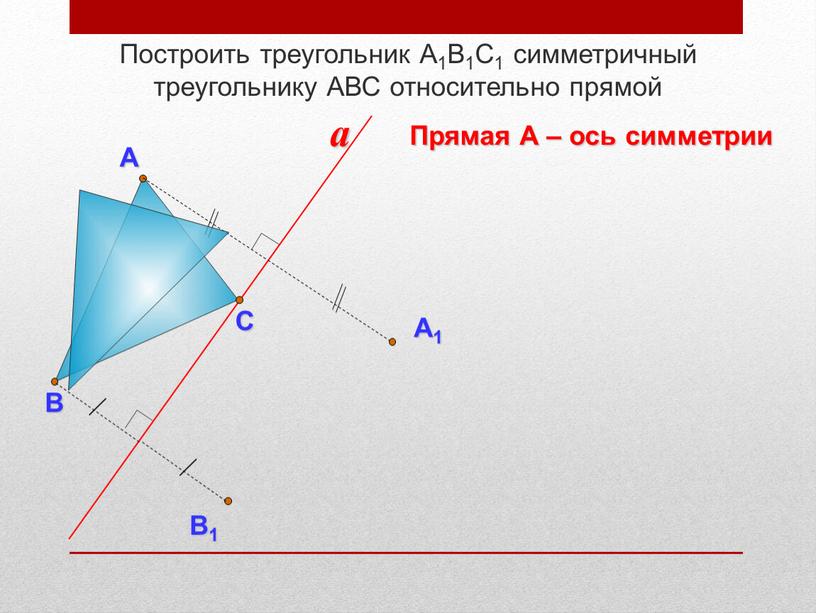 В самом деле, после поворота этой пирамиды вокруг высоты на угол в 120° она совмещается сама с собой (черт. 119).
В самом деле, после поворота этой пирамиды вокруг высоты на угол в 120° она совмещается сама с собой (черт. 119).
При вращении пирамиды вокруг высоты она может занимать три положения, совпадающие с исходным, считая и исходное. Легко заметить, что всякая ось симметрии чётного порядка есть в то же время ось симметрии второго порядка.
Примеры осей симметрии высших порядков:
1) Правильная n-угольная пирамида имеет ось симметрии n-го порядка. Этой осью служит высота пирамиды.
2) Правильная n-угольная призма имеет ось симметрии n-го порядка. Этой осью служит прямая, соединяющая центры оснований призмы.
Симметрия куба.
Как и для всякого параллелепипеда, точка пересечения диагоналей куба есть центр его симметрии.Куб имеет девять плоскостей симметрии: шесть диагональных плоскостей и три плоскости, проходящие через середины каждой четвёрки его параллельных рёбер.
Куб имеет девять осей симметрии второго порядка: шесть прямых, соединяющих середины его противоположных рёбер, и три прямые, соединяющие центры противоположных граней (черт.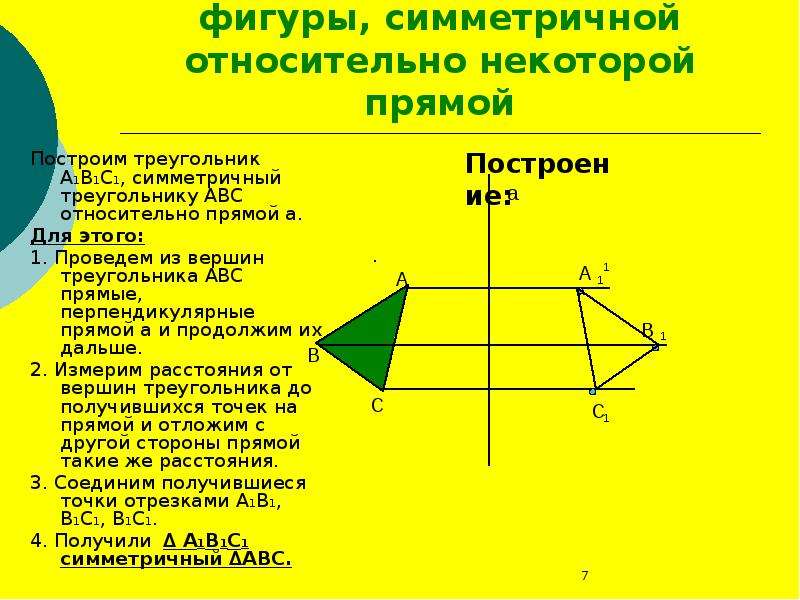 120).
120).
Эти последние прямые являются осями симметрии четвёртого порядка. Кроме того, куб имеет четыре оси симметрии третьего порядка, которые являются его диагоналями. В самом деле, диагональ куба АG (черт. 120), очевидно, одинаково наклонена к рeбрам АВ, АD и АЕ, а эти рёбра одинаково наклонены одно к другому. Ecли соединить точки В, D и Е, то получим правильную треугольную пирамиду АDВЕ, для которой диагональ куба AG служит высотой. Когда при вращении вокруг высоты эта пирамида будет совмещаться сама с собой, весь куб будет совмещаться со своим исходным положением. Других осей симметрии, как нетрудно убедиться, куб не имеет. Посмотрим, сколькими различными способами куб может быть совмещён сам с собой. Вращение вокруг обыкновенной оси симметрии даёт одно положение куба, отличное от исходного, при котором куб в целом совмещается сам с собой.
Вращение вокруг оси третьего порядка даёт два таких положения, и вращение вокруг оси четвёртого порядка — три таких положения.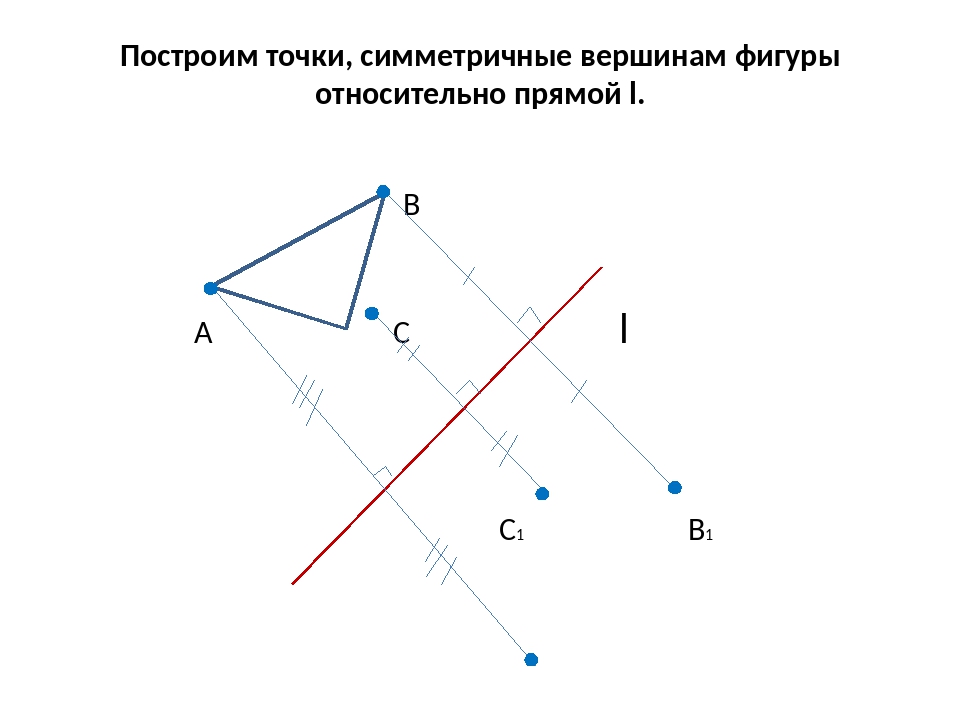 Так как куб имеет шесть осей второго порядка (это обыкновенные оси симметрии), четыре оси третьего порядка и три оси четвёртого порядка, то имеются 6•1 + 4•2 + 3•3 = 23 положения куба, отличные от исходного, при которых он совмещается сам с собой.
Так как куб имеет шесть осей второго порядка (это обыкновенные оси симметрии), четыре оси третьего порядка и три оси четвёртого порядка, то имеются 6•1 + 4•2 + 3•3 = 23 положения куба, отличные от исходного, при которых он совмещается сам с собой.
Легко убедиться непосредственно, что все эти положения отличны одно от другого, а также и от исходного положения куба. Вместе с исходным положением они составляют 24 способа совмещения куба с самим собой.
Straight Line — Положение точки относительно линии
Здравствуйте. Этот урок будет иметь дело с относительно простой концепцией по сравнению с недавно рассмотренным параметрическим уравнением, чтобы вы немного расслабились.
Основное внимание будет уделено определению относительного положения двух (или более) точек по отношению к заданной линии. То есть, лежат ли две заданные точки по одну сторону от заданной линии или напротив.
Пусть L — заданная прямая ax + by + c = 0, а P (x 1 , y 1 ) и Q (x 2 , y 2 ) — две точки.
Пусть R (x, y) будет точкой на прямой L, такой, что P, Q и R лежат на одной прямой, и пусть эта точка R делит PQ в соотношении m: n.
Теперь координаты R (используя формулу сечения) будут \ ((\ frac {mx_2 + nx_1} {m + n}, \ frac {my_2 + ny_1} {m + n}) \)
Поскольку точка также лежит на прямой ax + by + c = 0, его координаты будут удовлетворять уравнению.
Следовательно, мы имеем a (mx 2 + nx 1 ) + b (my 2 + ny 1 ) + c (m + n) = 0 или \ (\ frac {m} { n} = — \ frac {ax_1 + by_1 + c} {ax_2 + by_2 + c} \) [1]
Теперь вот как мы определим относительное положение двух точек.
Если ax 1 + на 1 + c и ax 2 + на 2 + c имеют противоположный знак (т.е. один положительный, а другой отрицательный), то правая часть [1] будет положительный, что делает m / n положительным, подразумевая, что R делит PQ в соотношении m: n внутри .
И это может произойти только тогда, когда R лежит между P и Q, или P и Q лежат на противоположных сторонах данной линии.
С другой стороны, если ax 1 + на 1 + c и ax 2 + by 2 + c имеют одинаковый знак (т.е.е. оба положительные или оба отрицательные), тогда правая часть [1] будет отрицательной, что делает m / n отрицательным, подразумевая, что R делит PQ в соотношении m: n внешне .
И это может произойти только в том случае, если R лежит за пределами сегмента линии PQ, или P и Q лежат на той же стороне R или данной линии.
Вот и все!
Может быть случай, когда на данной прямой нет такой точки R, что P, Q и R лежат на одной прямой. Это произойдет, когда PQ параллельна данной линии, что означает, что P и Q лежат на одной стороне линии.(Вам не нужно беспокоиться об этом случае отдельно.)
Краткое содержание урока
- Две заданные точки P (x 1 , y 1 ) и Q (x 2 , y 2 ) будут лежать на то же сторона линии ax + by + c = 0, если ax 1 + by 1 + c и ax 2 + by 2 + c будет иметь одинаковых знаков.

- С другой стороны, P (x 1 , y 1 ) и Q (x 2 , y 2 ) будут лежать на , противоположных сторонам линии ax + by + c = 0 если ax 1 + на 1 + c и ax 2 + на 2 + c будет иметь напротив знаков.
Увидимся на следующем уроке с несколькими примерами.
обработка изображений — Как найти отрезки прямой, ближайший к отрезку прямой?
Переполнение стека- Около
- Товары
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- Вакансии Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- Реклама Обратитесь к разработчикам и технологам со всего мира
- О компании
Линейные функции и прямые
6. 2 — Линейные функции и прямые линии
2 — Линейные функции и прямые линии6.2 — Линейные функции и прямые
Линейные функции
Щелкните здесь, чтобы просмотреть функции. Линейные функции — самые простые из всех типов функций. Линейная функция принимает на вход число x и возвращает число m x + b как выход: m и b — постоянные. Проще говоря, x умножается на м (это называется масштабированием на коэффициент м ) а затем добавляется b (это называется смещением на величину b ).Используя обозначение функции, линейная функция выглядит так:f ( x ) = м x + b .Если мы положим y = f ( x ), то это будет выглядеть так:
y = м x + b .Это называется уравнением прямой линии , потому что если мы построим точки, которые удовлетворить это уравнение на графике y против x , тогда, как мы увидим ниже, все точки лежат на прямой линии.
Типичное использование линейной функции — преобразование одного набора единиц в другой. Простой пример: i — это расстояние в дюймах, а c — то же самое. расстояние в сантиметрах; тогда c = 2,54 i . Это просто масштабирование. Более сложный пример: если c — температура измеряется в градусах Цельсия и f то же самое температура измеряется в градусах Фаренгейта; тогда f = 1.8 с + 32. Это масштабирование и сдвиг.
Уравнение прямой
В разделе 6.1 мы ввели декартову плоскость с осью x , нарисованной горизонтально, и осью y , нарисованной вертикально. Предположим, что m и b — постоянные. Мы хотим построить график линейной функции:y = м x + b ,на этой плоскости и покажите, что график представляет собой прямую линию.Для этого составляем следующую таблицу значений y (то есть выражения м x + b ) по сравнению с x :
Обратите внимание на следующее:
- Каждая строка таблицы показывает точку на графике.

- В одной из строк указано, что если x = 0, тогда y = b . Таким образом, точка (0, b ) это точка на графике. Поскольку эта точка лежит на оси y , число b называется точкой пересечения y .
- При переходе от одной строки таблицы к следующей, значение x увеличивается на 1, а значение y увеличивается на m . Потому что увеличение устойчиво, точки должны лежать на прямой , а не на какой-то другой кривой.
- Более крупный м , тем быстрее увеличивается y . Если m отрицательное, то значение y фактически уменьшается .Номер м известен как склон .
- x не обязательно должно быть целым числом — это может быть любое действительное число. Так как вещественные числа плотные, точки на графике бесконечно близко друг к другу и образуют сплошную линию (т.е. без зазоров).
| Вывод: Уравнение y = м x + b ,где m и b — константы, это уравнение прямой .  м называется уклоном, а b называется
перехват y . Эта форма уравнения называется пересечением наклона форма . Возможны и другие формы; Нажмите здесь, чтобы увидеть их. м называется уклоном, а b называется
перехват y . Эта форма уравнения называется пересечением наклона форма . Возможны и другие формы; Нажмите здесь, чтобы увидеть их. |
Нахождение уравнения прямой
Учитывая график прямой, есть несколько способов найти ее уравнение.
Метод 1: Этот метод работает, только если видна точка пересечения y .
- Найдите любые две точки, ( x 1 , y 1 ) и ( x 2 , y 2 ), на линии и подставьте их координаты в следующую формулу, чтобы получить м :
- Получите b из просмотра точки пересечения y графика.
- Подставьте полученные числа для m и b в уравнение y = m x + b .
Метод 2: Этот метод работает, даже если точка пересечения y не видна.

- Как и в методе 1, найдите любые две точки, ( x 1 , y 1 ) и ( x 2 , y 2 ), на линии и подставьте их координаты в следующую формулу, чтобы получить м :
- Замените полученное вами число м на
уравнение y = m x + b .Также возьмите одну из точек, скажем ( x 1 , y 1 ),
и подставляем его координаты в уравнение. Это дает:
y 1 = m x 1 + b
- Возможно, это не так, но это уравнение имеет только одну переменную, b , и вы легко можете решить эту проблему.
- Подставьте полученные числа для m и b в уравнение y = m x + b .
Метод 3: Этот метод имеет то преимущество, что он использует только алгебру, а не геометрию, и может применяться к любому типу функции, а не только к прямой линии:
- Найдите две точки,
( x 1 , y 1 ) и
( x 2 , y 2 ), которые находятся на линии.
 Возьмите первую точку ( x 1 , y 1 ) и
подставляем его в уравнение прямой, y = м x + b .Это дает:
Возьмите первую точку ( x 1 , y 1 ) и
подставляем его в уравнение прямой, y = м x + b .Это дает:y 1 = m x 1 + b
Аналогичным образом возьмем вторую точку ( x 2 , y 2 ) и подставляем его в уравнение прямой, y = м x + b . Это дает:y 2 = м x 2 + b
- Вместе эти два уравнения составляют систему двух уравнений с двумя неизвестными: m и b .Мы можем решить их для m и b , используя метод исключения.
Чтобы быть конкретным, если мы вычтем первое уравнение из второго, то b будет
исключили, и мы получаем уравнение:
y 2 — y 1 = м x 2 — м x 1 ,
которое при решении для м дает то же уравнение, что и в двух других методах, а именно: - Найти b обратной подстановкой.
 Чтобы быть конкретным, замените номер, который вы
полученное для м в одно уравнение системы уравнений, скажем в y 1 = m x 1 + b .
Это может не выглядеть так, но это уравнение имеет только одну переменную, b ,
и вы легко можете решить эту проблему.
Чтобы быть конкретным, замените номер, который вы
полученное для м в одно уравнение системы уравнений, скажем в y 1 = m x 1 + b .
Это может не выглядеть так, но это уравнение имеет только одну переменную, b ,
и вы легко можете решить эту проблему.
Пример: Воспользуйтесь методом 1, чтобы найти уравнение прямой на графике справа.
Решение: Две точки на этой линии: ( x 1 , y 1 ) = (0, 15) и ( x 2 , y 2 ) = (3, 0). Подставляя эти координаты в формулу наклона, получаем
= -5.При осмотре перехватчик y
b = 15.Подставляя эти два значения для m и b в уравнение прямой линии, y = m x + b , дает
y = −5 x + 15.
Пример: Используйте метод 3, чтобы найти уравнение прямой линии на графике справа.
Решение: Две точки на этой линии — это (7, 15) и (1, 3). Подставляем координаты точки (7, 15) в уравнение прямой, y = m x + b , а затем проделайте то же самое с точкой (1, 3). Это дает систему двух уравнений с двумя неизвестными: m и b .Неизвестный b можно исключить, вычитая уравнения:
Решение относительно m дает m = 2. Подставляя назад m = 2, скажем, в первое уравнение, дает 15 = 7 · 2 + b , что легко решается и дает b = 1. Подставляя эти два значения для m и b в уравнение прямой линии, y = m x + b , даетy = 2 x + 1.
Если вы нашли эту страницу в веб-поиске, вы не увидите
Оглавление в рамке слева.
Щелкните здесь, чтобы отобразить его.
Исчисление III — Уравнения линий
Онлайн-заметки ПавлаПримечания Быстрая навигация Скачать
- Перейти к
- Примечания
- Проблемы с практикой
- Проблемы с назначением
- Показать / Скрыть
- Показать все решения / шаги / и т. Д.
- Скрыть все решения / шаги / и т. Д.
- Разделы
- Трехмерная система координат
- Уравнения плоскостей
- Разделы
- Частные производные инструменты
- Классы
- Алгебра
- Исчисление I
- Исчисление II
- Исчисление III
- Дифференциальные уравнения
- Дополнительно
- Алгебра и триггерный обзор
- Распространенные математические ошибки
- Праймер для комплексных чисел
- Как изучать математику
- Шпаргалки и таблицы
- Разное
- Свяжитесь со мной
- Справка и настройка MathJax
- Мои студенты
- Заметки Загрузки
- Полная книга
- Текущая глава
- Текущий раздел
- Practice Problems Загрузок
- Полная книга — Только проблемы
- Полная книга — Решения
- Текущая глава — Только проблемы
- Текущая глава — Решения
- Текущий раздел — Только проблемы
- Текущий раздел — Решения
- Проблемы с назначением Загрузок
- Полная книга
- Текущая глава
- Текущий раздел
- Прочие товары
- Получить URL для загружаемых элементов
- Распечатать страницу в текущем виде (по умолчанию)
- Показать все решения / шаги и распечатать страницу
- Скрыть все решения / шаги и распечатать страницу
- Дом
- Классы
- Алгебра
- Предварительные мероприятия
- Целочисленные экспоненты
- Рациональные экспоненты
- Радикалы
- Полиномы
- Факторинговые многочлены
- Рациональные выражения
- Комплексные числа
- Решение уравнений и неравенств
- Решения и наборы решений
- Линейные уравнения
- Приложения линейных уравнений
- Уравнения с более чем одной переменной
- Квадратные уравнения — Часть I
- Квадратные уравнения — Часть II
- Квадратные уравнения: сумма
- Предварительные мероприятия
Типы баланса в искусстве и дизайне (и зачем они вам нужны)
Люди естественным образом стремятся к симметрии, и, согласно гештальт-психологии, мы склонны воспринимать объекты как симметричные формы, которые образуются вокруг центральной точки.Вот почему баланс — один из ключевых принципов дизайна.
Визуальный баланс важен, потому что он обеспечивает чувство единства, порядка и равновесия. Ваш дизайн должен визуально «держаться вместе», чтобы казаться законченным и гармоничным. Но чтобы было ясно, баланс не означает, что все должно быть идеально симметричным. Это просто означает, что визуальный вес объектов, пространства и цвета равномерно распределяется по странице. Без баланса дизайн кажется нестандартным, непоследовательным и тревожным.
Прочтите, чтобы открыть для себя четыре типа баланса в искусстве и дизайне и узнать, как достичь их в своей работе.
1. Симметричные весы
ноги на трамплине от Алекса Эмануэля КохаПри симметричном балансе вы можете провести линию вниз (или поперек) середины проекта, чтобы создать зеркальное отражение. Эта идеальная двусторонняя симметрия выглядит элегантно, формально и консервативно.
Симметричное изображение 2 фламинго с отраженными в воде шеями от SmileusModern Симметричный туннель в футуристическом интерьере с бетонными арками в перспективе от telesniukИзображения выше иллюстрируют, насколько визуально вес очень ровный и аккуратный с каждой стороны.Приглашения на свадьбу, театральные программы и стихи часто приводят в качестве примеров использования симметричного баланса (например, текст с выравниванием по центру и симметричные макеты).
Однако чистый симметричный баланс может показаться скучным, унылым и скованным, поэтому попробуйте смешать его и с другими типами баланса.
2. Асимметричные весы
Слон и собака сидят на летнем пляже. Фотобанк, галереяАсимметричный баланс создает напряжение за счет контраста и намного интереснее визуально.Поскольку это абстрактно, симметрии нет; идеальных зеркальных изображений не существует. Вместо этого вы располагаете элементы с разной визуальной массой таким образом, чтобы каждая сторона оставалась сбалансированной. «Более тяжелые» элементы будут прыгать вперед и бросаться в глаза больше, чем «более легкие», которые отступают.
Этот тип баланса кажется более непринужденным, свободным и энергичным. Чтобы выровнять вес по всему дизайну, вы можете поиграть с этими различными факторами, которые влияют на визуальный вес:
- Размер: большие предметы кажутся тяжелее маленьких.
- Значение: Темные предметы кажутся тяжелее легких.
- Цвет: Теплые яркие цвета привлекают больше внимания, чем холодные или нейтральные приглушенные. Красный считается самым тяжелым, а желтый — самым светлым. (Для получения дополнительной информации ознакомьтесь с нашим сообщением об основах цветовой температуры!)
- Текстура: Объекты с текстурой кажутся трехмерными и кажутся физически тяжелее, чем объекты без текстуры.
- Количество: Несколько маленьких объектов могут уравновесить один большой объект.
- Ориентация: диагональные элементы тяжелее вертикальных и горизонтальных.
3. Радиальный баланс
Фон «Колесо корабля» от РедчанкиВ радиальном балансе элементы расходятся (в форме круга) из одной главной центральной точки. Если вы хотите создать сильную точку фокусировки, радиальный баланс — эффективный метод, потому что ваши глаза естественным образом направлены внутрь к центру.
Секция раковины наутилуса от aaltairВеликолепная лестница в Санто-Доминго-де-Бонаваль.Сантьяго-де-Компостела, Испания. Автор: Хосе Игнасио СотоЗавитки раковины наутилуса и винтовая лестница не только создают визуальный интерес, но и естественным образом направляют ваш взгляд прямо в центр изображения.
4. Кристаллографические весы
красочная стена от Just2shutterЭтот тип баланса, также называемый мозаикой или «сплошным» балансом, основан на повторении. На первый взгляд изображения, использующие кристаллографический баланс, могут показаться случайными и хаотичными; это может выглядеть как визуальный шум, поскольку вы не можете сразу определить четкую фокусную точку или визуальную иерархию.Но хотите верьте, хотите нет, это работает.
Текстура цветных карандашей от Луисмы ТапиаПомните, что повторение и последовательность являются основными принципами дизайна, и за счет равномерного повторения элементов с равным весом во всем дизайне это фактически создает ощущение баланса. Вы можете видеть, что одни и те же цвета, формы и размеры повторяются на каждом изображении. Стена повторяет те же яркие, смелые цвета; все цветные карандаши имеют одинаковую форму шестиугольника; пончики все одинакового размера. Куда бы вы ни посмотрели, вы всегда видите один и тот же визуальный вес.
Свежие пончики с разными начинками из местной пекарни от Арины П ХабичБаланс — важный принцип во многих сферах нашей жизни, и он применим и к дизайну. Если вашему дизайну не хватает баланса, он может казаться «неуместным» и неэффективным. Когда вы проектируете, не придерживайтесь чистой статической симметрии; попробуйте поэкспериментировать с различными видами баланса и поиграть с визуальным весом. Посмотрите, что лучше всего подходит для вашего бренда, проекта и тона. Вы можете обнаружить, что можете использовать баланс и симметрию новыми захватывающими способами, которые никогда раньше не использовали.
Изображение сверху: Вид сверху перепелиных яиц в деревянной ложке на зеленом фоне, автор — anastasiafotoss
Уравнение прямой
Линия — это бесконечная линия, которая образует кратчайший путь между любой из двух ее точек.
Уравнение прямой на плоскости
Общий вид линейного уравнения
Любое уравнение прямой на плоскости может быть записано в общем виде
А х + В у + С = 0
, где A и B не равны нулю.
Форма пересечения наклона линейного уравнения
Общее уравнение прямой при B ≠ 0 можно привести к следующему виду
у = к х + Ь
, где k — наклон линии , а b — точка пересечения y . Наклон прямой равен тангенсу угла между этой прямой и положительным направлением оси x. Координата y — это место, где линия пересекает ось y.
k = tg φ
Уравнение прямой, проходящей через две разные точки на плоскости
Если линия проходит через две точки A (x 1 , y 1 ) и B (x 2 , y 2 ), то x 1 ≠ x 2 и y 1 ≠ y 2 , тогда уравнение линии можно найти по следующей формуле
| х — х 1 | = | г — г 1 |
| x 2 — x 1 | л 2 — л 1 |
Параметрические уравнения прямой на плоскости
Параметрическое уравнение линии можно записать как
| х = l т + х 0 | |
| y = m t + y 0 |
где N (x 0 , y 0 ) — координаты точки, лежащей на прямой, a = {l, m} — координаты вектора направления линии.
Каноническое уравнение прямой на плоскости
Если вы знаете координаты точки A (x 0 , y 0 ) Если вы знаете координаты точки n = {l; m}, то уравнение прямой можно записать в канонической форме с помощью следующей формулы
Пример 1. Найдите уравнение прямой, проходящей через две точки A (1, 7) и B (2, 3).
Решение. Воспользуемся формулой уравнения прямой, проходящей через две точки
х — 12 — 1 = у — 73 — 7
Из этого уравнения выразим y через x
х — 11 = у — 7-4
Найдите форму пересечения наклона линейного уравнения.
Умножьте уравнения на -4.
у — 7 = -4 (х — 1)
г = -4x + 11
Найдите параметрические уравнения этой строки
Мы используем MN как вектор направления линии.
МН = {2 — 1; 3–7} = {1; -4}
Используем координаты точки М в параметрических уравнениях линии
х = т + 1у = -4т + 7
Пример 2. Найдите уравнение прямой, проходящей через две точки M (1, 3) и N (2, 3).Решение. Невозможно использовать Уравнение прямой, проходящей через две разные точки, так как M y — N y = 0.
Найдите параметрические уравнения этой прямой. Мы используем MN как вектор направления линии.
МН = {2 — 1; 3–3} = {1; 0}
Используем координаты точки М в параметрических уравнениях линии
х = т + 1у = 3
Уравнение прямой в пространстве
Уравнение прямой, проходящей через две разные точки в пространстве
Если линия проходит через две точки A (x 1 , y 1 , z 1 ) и B (x 2 , y 2 , z 2 ), так что x 1 ≠ x 2 , y 1 ≠ y 2 и z 1 ≠ z 2 , тогда уравнение строки можно найти по следующей формуле
| х — х 1 | = | г — г 1 | = | г — я 1 |
| x 2 — x 1 | л 2 — л 1 | z 2 — z 1 |
Параметрические уравнения прямой в пространстве
Параметрическое уравнение линии можно записать как
| х = l т + х 0 | |
| y = m t + y 0 | |
| z = n t + z 0 |
где (x 0 , y 0 , z 0 ) — координаты точки, лежащей на линии, {l; м; n} — координаты вектора направления линии.
Каноническое уравнение прямой в пространстве
Если вам известны координаты точки A (x 0 , y 0 , z 0 ), которая лежит на прямой, и вектор направления этой прямой n = {l; м; n}, то уравнение прямой можно записать в канонической форме с помощью следующей формулы.
| х — х 0 | = | г — г 0 | = | г — я 0 |
| л | м | n |
Прямая как пересечение двух плоскостей
Если линия является пересечением двух плоскостей, то уравнение прямой может быть найдено как решение следующей системы уравнений
| A 1 x + B 1 y + C 1 z + D 1 = 0 | |
| A 2 x + B 2 y + C 2 z + D 2 = 0 |
при условии отсутствия равенства
| А 1 | = | Б 1 | = | С 1 | . |
 осевая и центральная симметрия — Геометрия — 8 класс
осевая и центральная симметрия — Геометрия — 8 класс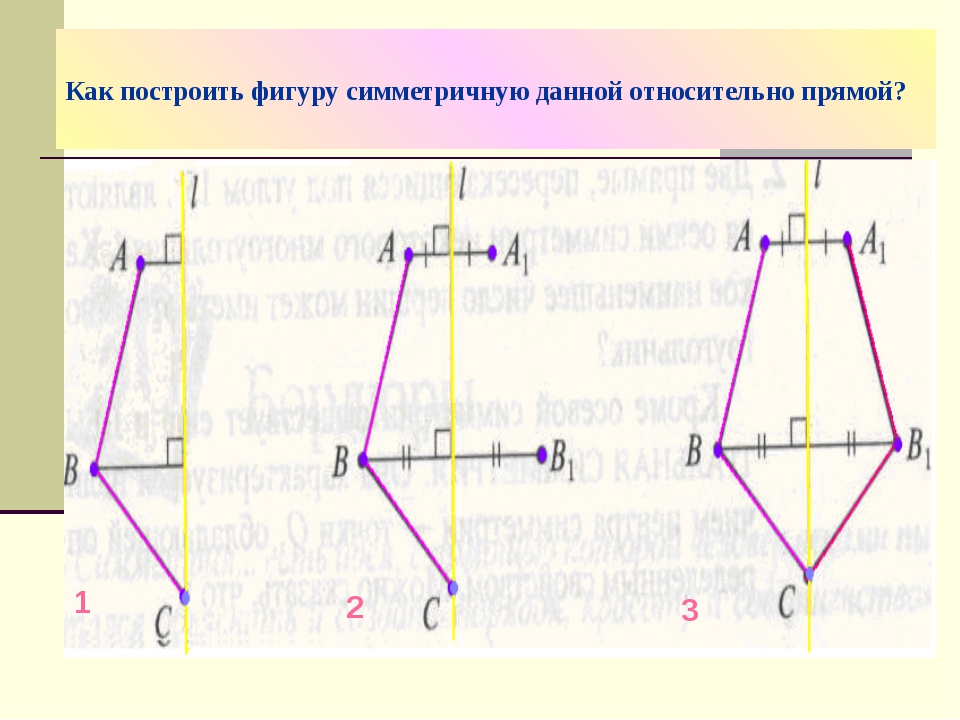 7.3. Осевая симметрия.
7.3. Осевая симметрия.

 Возьмите первую точку ( x 1 , y 1 ) и
подставляем его в уравнение прямой, y = м x + b .Это дает:
Возьмите первую точку ( x 1 , y 1 ) и
подставляем его в уравнение прямой, y = м x + b .Это дает: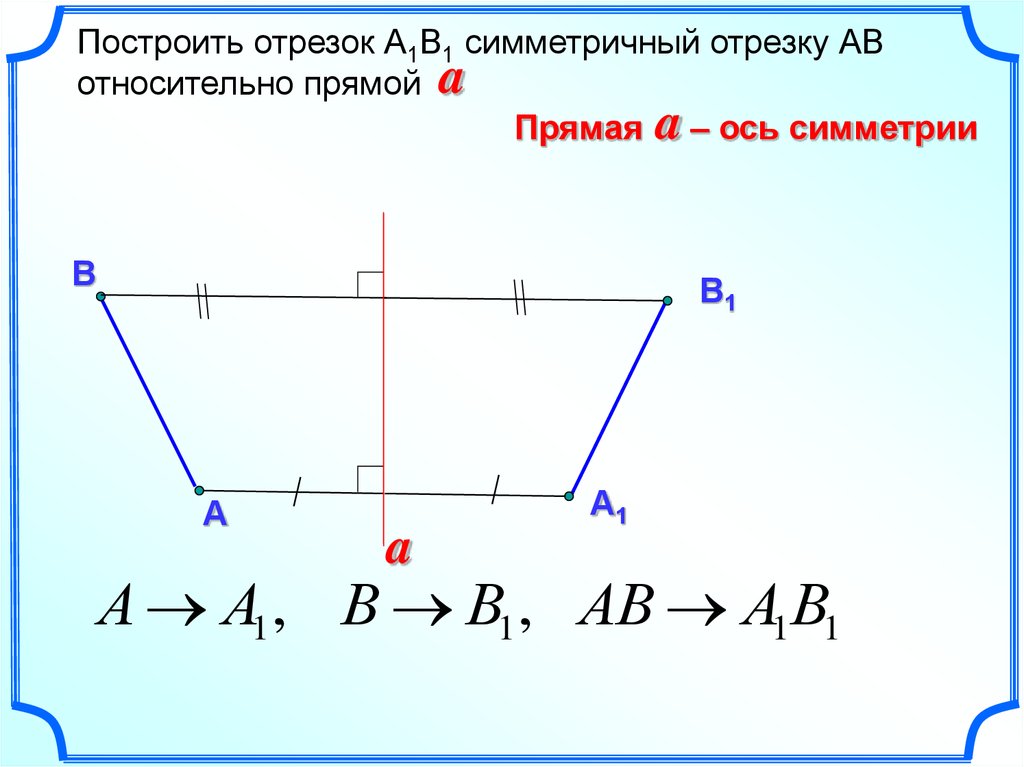 Чтобы быть конкретным, замените номер, который вы
полученное для м в одно уравнение системы уравнений, скажем в y 1 = m x 1 + b .
Это может не выглядеть так, но это уравнение имеет только одну переменную, b ,
и вы легко можете решить эту проблему.
Чтобы быть конкретным, замените номер, который вы
полученное для м в одно уравнение системы уравнений, скажем в y 1 = m x 1 + b .
Это может не выглядеть так, но это уравнение имеет только одну переменную, b ,
и вы легко можете решить эту проблему.