МБОУ ДОД Дворец творчества детей и молодежи города Ростова-на-Дону
Донская академия наук юных исследователей им. Ю.А. Жданова
Математика/Дебют
Исследовательская работа
Тема: «Математические ребусы».
Автор работы:
Бенько Елизавета, 5А класс,
МБОУ СОШ № 7 г. Сальск.
Руководитель: Бабина Наталья Алексеевна,
учитель математики
МБОУ СОШ № 7г. Сальск.
г. Сальск
2015 г.
Оглавление
I Введение……………………………………………………………………..3
II Основная часть………………………………………………………………4-16
2.1.История возникновения и развития ребусов…………………………….4-5
2.2. Математические ребусы на замену букв и «звёздочек» цифрами……5-9
2.3. Математические ребусы с различными предметами …..…………….10-14
2.4.Составление ребусов…………………………………………………………..14-16
III Заключение…………………………………………………………………17
Источники……………………………………………………………………… 18
I
Введение
Математические знания мы применяем не только на уроках математики, но и в повседневной жизни. Мне повезло, что математика мне нравится. Однако, трудность для меня составляют задачи, для решения которых надо применить логические рассуждения. Я читала, что любые свои способности человек может развить, в той или иной мере. Как же развить математические способности? В интернете я нашла массу высказываний такого характера:
-«Чтобы развить математические способности, необходимо решать задачи на сообразительность, задачи-шутки, математические ребусы и головоломки». [10]
-«Разгадывание ребусов является отличной гимнастикой для развития интеллекта школьника».[10]
-«Разгадывание ребусов прекрасно стимулирует развитие интеллекта , развивает умение делать логические выводы, учит мыслить». [11]
Я поверила, что решение различных головоломок поможет мне развить математические способности.
Тема работы: «Математические ребусы».
Цель: научиться решать математические ребусы.
Актуальность темы: на уроках математики необходимо решать задачи не только по определённым правилам, но и нестандартные задачи.
Гипотеза: решение ребусов поможет мне развить логическое мышление.
Степень изученности: в курсе математики школы не рассматриваются ребусы.
Задачи:
- Найти различные источники с информацией о ребусах;
- Изучить математические ребусы различных видов;
- Исследовать возможные пути решения ребусов.
Объект изучения: математические ребусы
Предмет изучения: методы и способы решения математических ребусов
Методы исследования: изучение различных источников информации, анализ, обобщение и систематизация материала.
II
Основная часть
2.1 В начале своей работы я решила выяснить: историю возникновения ребусов и что такое математический ребус.
Зародился ребус во Франции в XV веке. Первоначально ребусом называли особого рода ежегодные выступления во время карнавалов, содержащие остроумные обозрения местной жизни, называвшиеся «новостями дня». В дальнейшем слово «ребус» получило то значение, в котором оно употребляется настоящее время.
Первый печатный сборник ребусов, составленный Этьеном Табуро, был издан во Франции в 1582 году. Затем ребусы распространились в Англии, Германии, Италии.
Английский писатель и математик Чарльз Лютвидж Доджсон, более известный под псевдонимом Льюис Кэрролл, один из самых популярних детских писателей XIX века, автор сказок «Алиса в Стране чудес» и «Алиса в Зазеркалье», часто использовал ребусы в многочисленной переписке с юными почитателями своего творчества. В своих письмах он часто заменял часть слов картинками либо изображал буквы в зеркальном отображении. Для прочтения таких загадочных писем нужна была смекалка, что очень нравилось детям.
В России первые ребусы появились на страницах журнала «Иллюстрация» в 1845 году. Большой популярностью пользовались ребусы, нарисованные художником И. Волковым в журнале «Нива».
Первое упоминание о печатных ребусах во времена Советской власти появились в 1937 году: появились буклеты которые носили название «Как читать ребусы» . Во время Великой Отечественной войны, в 1942 году московская полиграфическая фабрика выпускает сборник ребусов А.А. Рязанова «В часы досуга: ребусы» В 1945 году, после окончания войны выходит небольшая брошюра художника-иллюстратора и иллюзиониста Георгия Кельсиевича Бедарева «Ребусы». [9]
В настоящее время ребус — одна из самых популярных и распространённых игр. В ребусе можно зашифровать пословицы, поговорки, отрывки из стихотворений, отдельные фразы и слова. В математической энциклопедии говорится: « Математическими ребусами называют задания на восстановление записей вычислений».
2.2. Первый тип ─ это те ребусы, в записи которых встречаются звёздочки. Требуется найти набор цифр, при подстановке которых вместо звездочек выполнится условие, сформулированное в задаче.
Решить такой ребус означает найти все возможные наборы цифр, удовлетворяющие условию задачи.
Примеры:
1. Восстановите поврежденную запись
Решение:
Ответ. 99 + 9 = 108
- Восстановите поврежденную запись
Решение:
Ответ. 99 + 99 = 198.
- Решить ребус
Ответ.354 + 384 = 738.
- Решить ребус на умножение.
- Восстановить цифры в записи следующего деления.
Ответ.1431 : 27 = 53.
Второй тип ─ это те ребусы, в записи которых встречаются буквы. Требуется определить цифры, при подстановке которых в эту запись вместо букв выполняется условие, сформулированное в тексте задачи.
При решении ребусов этого типа следует помнить, что разные буквы заменяются разными цифрами, а одинаковые буквы – одинаковыми цифрами.
Примеры.
- Решить ребус.
Решение
Очевидно, Д≤4. В разряде сотен имеем А + А = А, значит, А = 0 (без перехода) или А = 9 (с переходом). Значение А = 0 не подходит, так как в разряде единиц А + А = Р (получаем А = Р = 0). Значит, А = 9, Р = 8, Е = 7. Тогда 2М + 1 = 10 + Т, Т
Ответ. 18969 + 18969 = 37938.
- Решить ребус
Решение
Так как КА + КА + КА оканчивается на КА, то КА = 50, а значит, К = 5, А = 0. Так как Ш + Ш + Ш + 1 оканчивается на 0, то Ш = 3. Так как сумма трех чисел, начинающихся на 5 может начинаться лишь с 1, то С = 1. Рассматривая варианты для О, получаем, что О = 6 или О = 7, а значит, Б = 9 или Б = 2. Итак, получаем два варианта решения:
- Решить ребус
Ответ.
С = 4; П = 3; Т = 2; Р = 7; К = 8; О = 9.
- Решить ребус, если известно, что наибольшая цифра в числе СИЛЕН равна 5:
Решение
Так как наибольшая цифра в числе «СИЛЕН» равна 5, а С = 1, то остальные 4 цифры в данном числе будут 2, 3, 4, 5. Так как Н Е (в самом деле так как Е + 1 = Л, то Л > Е, ведь Л и Е меньше 5 по условию), то Л = 5, Е = 3. А тогда уже легко находим остальные цифры: Ш = 8, Р = 9. В итоге получается: 9382 + 3152 = 12534
В процессе решения я узнала, что при разгадке математических ребусов надо не только уметь хорошо вычислять, используя знания об арифметических действиях их свойствах, но и проявить смекалку, терпение, выдержку и настойчивость. Есть математические ребусы, имеющие несколько решений. Поэтому нельзя ограничиваться отысканием только одного решения.
Мы с моим преподавателем провели исследование по следующим вопросам:
-сколько времени, в среднем, занимает решение несложного ребуса;
-всегда ли школьники находят все решения.
В исследовании приняли участие 23 ученика 5 «A» класса.
Результаты исследований помещены в таблицу 1.
Таблица 1.
№ | Вид ребуса | Затрачено времени (в среднем) | Рассмотрены все случаи решения. (в %) | |
1 | Ребусы со звёздочками | 20 мин | 20 % | |
2 | Ребусы с буквами | 15 мин | 40% |
Анализ данных таблицы позволяет сделать выводы:
1. Решение даже самого простого ребуса методом перебора занимает много времени, так как каждая неизвестная может принимать до десяти значений.
2. Каждое решение нужно доводить до конца, чтобы убедиться, что нет других решений, или найти все решения.
Я заметила, что ограничить варианты перебора по количеству переменных позволят следующие утверждения:
- Если в записи используется 10 различных букв, значит, при решении надо использовать все 10 цифр.
- Если используется более 10 букв, то ребус не имеет решения.
- Если в записи числа буква расположена в старшем разряде, то ее значение не может равняться нулю.
- Если в одном из слагаемых, получаемых при умножении, все буквы совпадают с буквами в множимом, то соответствующий разряд множителя содержит 1 единицу.
- Если отсутствует одно из слагаемых, получаемых при умножении, то соответствующий разряд множителя содержит 0 единиц.
2.3. Кроме рассмотренных мною ребусов существуют и другие. В толковом словаре С. И. Ожегова даётся такое толкование слова «ребус» ─ «загадка», в которой искомое слово или фраза изображены комбинацией фигур, букв или знаков».
Такие ребусы я ещё не решала. Оказалось, что для их отгадывания надо знать 12 правил:
- 1-ое правило. Если перед нарисованным предметом или знаком слева стоит одна или две запятые, то в соответствующем слове надо отбросить одну или две первые буквы.
Пример. ,100 , здесь в слове «сто» надо отбросить первую букву «с» и читать как «то».
- 2-ое правило. Если запятые стоят справа после нарисованного предмета или знака, то в соответствующем слове надо отбросить одну или две последние буквы.
Пример. Здесь в слове «дом» надо отбросить последнюю букву «м» и читать «до».
- 3-е правило. Если над нарисованным предметом или рядом с ним написана и зачёркнута буква, то её надо отбросит. Если же после буквы стоит знак равенства и другая буква, тогда первую букву заменяют второй.
Пример. Л в слове «глаз» надо убрать букву «л» и получим «газ».
- 4-е правило. Если два каких-нибудь предмета или буквы нарисованы одна в другой, то их названия читаются с прибавлением предлога «в».
Пример. В-О-ДА ДА .
5-е правило. Если изображение какой — нибудь буквы состоит из другой буквы или буквосочетаний, то этот рисунок читают с прибавлением предлога «из».
- 6-е правило. Если одна фигура или буква нарисована под другой, то читать надо с прибавлением предлога «на», «над» или «под».
Пример. Читать надо так: З-НА-К.
- 7-е правило. Если за какой-нибудь буквой или предметом стоит другая буква или предмет, то читать надо с прибавлением предлога «за».
Пример. Читается так: КА-ЗА-НЬ.
- 8-е правило. Если по какой-нибудь букве написана другая буква или буквосочетание, то читается с прибавлением предлога «по».
Пример. Читаем: ПО-Р-Т.
- 9-е правило. Если одна из букв прислонена к другой или лежит у другой буквы, то читать надо с прибавлением предлога «у».
Пример. Получаем: Л-У-К.
- 10-е правило. Если в ребусе встречаются изображения предметов в перевёрнутом виде или нарисована стрелка, то их наименования надо читать с конца.
Пример . Вместо «ДОМ» читаем «МОД».
- 11-е правило. Цифры рядом с изображениями задают новый порядок букв.
- Пример. Вместо слова «куб» читаем: «бук»
12-е правило. Часто в ребусах слоги «до», «ре», «ми», «соль», «ля», «си»,изображают соответствующими нотами.
2.3. Изучив, правила, я приступила к решению . Из всех ребусов, которые я искала в различных источниках, я выбирала математические . Сначала я училась решать те, в которых применяется только одно из двенадцати правил. Примеры таких задач:
1. Решение: ЧИ-СЛОН. Получим: «Число».
2. . Решение: ЛУНА-Ч. Уберём две буквы в слове «ЛУНА»: ЛУНА-Ч. Ответ: «Луч».
3. . Решение: Буква «З» находится на букве «К», поэтому читаем с предлогом «на»: З-НА-К. Получим: «Знак».
4. О . Решение: О-ДЖИН. Уберём букву «Ж». Читаем: «Один».
5. . Решение: Цифра «7» находится в букве «О». Читаем: В-О-СЕМЬ. Ответ: «Восемь».
6. Решение: КВА-Д-РОТ. Заменим букву «о» на «а». Ответ: «Квадрат».
2.4. Далее, я приступила к решению более сложных математических ребусов, где надо применить несколько правил.
Решить ребусы:
Решение.
Имеем: СТО-ПЕНЬ.В слове «сто» третью букву «о» заменим на «е». Получим: СТЕ-ПЕНЬ. Ответ: «Степень».
Решение.
Применим четвёртое правило: КОТ-В-Е-КОТ. Применим второе правило: КОТВЕКОТ. Получим: «Ответ».
Решение.
Имеем: ОДИН-А-МЕТР.В слове «один» уберём первую и последнюю буквы и получим ДИ-А-МЕТР. Ответ: «Диаметр».
Решение.
ТРИ-РЕМЕНЬ . Заменим в первом слове первую букву «Т» на «П», получим ПРИ-РЕМЕНЬ. Уберём три последние буквы во втором слове, получим: ПРИ-РЕМ. Стрелка вверху второй картинки показывает, что оставшиеся буквы надо читать в обратном порядке. Ответ: «Пример».
Решение. Имеем: ЛИСТ-Е-ПЕНЬ .Уберём в первом слове две первых буквы, получим СТ-Е-ПЕНЬ. Ответ: «Степень».
Решение.
Так как: по букве «к» написана буква «а»,то имеем: ПО-К-А;
— за слогом «те» находится слог «ль», тогда получим: ЗА-ТЕ-ЛЬ.
Получим: ПО-К-А-ЗА-ТЕ-ЛЬ. Ответ: «Показатель»
Решение.
Имеем: МАК-СЕМЬ-А-КИТ-А. В слове мак букву «к» заменим на «т»,
В слове «семь» уберём первую и последнюю буквы, слово «кит» читаем с конца, так как изображение кита в перевёрнутом виде. Получим: МАТ-ЕМ-А-ТИК-А. Ответ: «Математика».
Решение. Имеем: ПАР-О-ИЗ –В-*ЕДЕ**-КНИГА-Е . В слове «пар» уберём букву «а», в слове «книга» уберём первую букву и две последних. Получим: ПР-О-ИЗ-В-ЕДЕ-НИ-Е. Ответ: «Произведение»
Решение. Имеем: НОС-НО-В-А-КНИГА-Е.В слове «нос» уберём первую букву,В слове «книга» уберём первую букву и две последних. Получим : ОС-НО-В-А-НИ-Е. Ответ: «Основание».
Решение. УС-ЛОБ-ВИЛЫ-Е. В слове «лоб» убираем последнюю букву, а в слове «вилы» — две последние. Получим: УС-ЛО-ВИ-Е. Ответ: «Условие».
Решение. Имеем: П-РАМА-Я. Заменим «а» на «я». Ответ: «Прямая».
Решение. На рисунке: ПЕРО-РЕ-НОС. В слове «перо» убираем две последние буквы. Получим: ПЕ-РЕ-НОС. Ответ: «Перенос».
Решение. Имеем: ДОМ-КА-ЗА- ТЕ-ЕЛЬ . Применим правила. Ответ: «Показатель».
Решение. На рисунке: КОСА-Т-ЕЛЬ-НА-Я. Применим правила. Ответ: «Касательная».
При решении ребусов с предметами я заметила, что:
- Правила лучше запоминаются в процессе решения ребусов.
- Название всего, что изображено на картинках в ребусе, надо читать только в именительном падеже.
- Необходимо учитывать наличие синонимов.
Трудности, которые возникали при решении ребусов:
- Надо правильно назвать изображённый на рисунке предмет.
- Картинка в ребусе может иметь не одно название. Примеры:
-нога, лапа;
-глаз, око;
-флаг, знамя;
— рыба-общее название; сазан, карась, щука — конкретное названия;
-птица ─ общее название: петух, чайка, голубь –конкретные названия.
- Надо понять , как соотносятся между собой фрагменты рисунка.
Пример: рисунок ДА можно прочитать В-О-ДА ( в «о» находится «да») или ДА-В-О («да» находится в «о»). Выбираем подходящее.
Чтобы преодолеть эти трудности, нужны смекалка и логика.
Я составила алгоритм для решения ребусов:
1.Надо назвать по частям изображённые предметы ( возможно это будет несколько синонимов), буквы, цифры.
2.Применить правила к каждому слову.
3. Оставить подходящие слова.
4. Составить по смыслу зашифрованный текст.
2.4. После того, как я решила десятка три ребусов, я попробовала сама составить несколько ребусов.
Решение. Имеем: РАДУГА-УСЫ.В слове радуга заменим букву «у» на «и», уберем две последние буквы, в слове усы уберем последнюю букву. Получим: ради- ус. Ответ: «Радиус».
Решение. Имеем: дом- лук- ь. Слово «дом» читаем с конца, так как изображение дома в перевёрнутом виде. В слове «лук» поменяем порядок букв. Получим: мод- ул- ь. Ответ: «Модуль».
Решение. Имеем: три- уголь- клубника. В слове «три» меняем третью букву на «е» ,в слове клубника уберем четыре первые буквы и одну последнюю. Получим: тре- уголь- ник. Ответ: «Треугольник».
Решение. Имеем: чи- слон- ит- ель. В слове слон уберем две последние буквы. Получим: чи- сл- ит- ель. Ответ: «Числитель» .
Я составила алгоритм составления ребусов:
- Надо задумать слово.
- Подобрать картинки, которые подходят к части слова.
- Лишние буквы удалить с помощью запятых или заменить некоторые буквы.
Составить ребус, оказалось, нетрудно. Главная трудность ─ сгруппировать картинки, чтобы они держались вместе и передвигались вместе с текстом. А, чтобы нарисовать картинки от руки, необходимо затратить много времени.
III
Заключение
Изучив различные источники, я узнала, что такое ребусы, изучила правила их решения, исследовала способы решения.
Ребусы это задачи, представленные в занимательной форме, очень интересны. Их хочется решать, они увлекают своей необычностью, неочевидностью ответа. Появляется желание совершить пусть даже нелёгкий путь поиска решения. Каждое самостоятельно решенное задание – это возможно, небольшая, но всё же победа.
Решая ребусы, я заметила, что это занятие развивает сообразительность, смекалку, а также усидчивость. Формирует внимательность, упорство в достижении цели, способствует творческому поиску чего – то нового, учит терпению, что мне просто необходимо для успешной учёбы.
Опрос показал, что ребусы не так популярны, как, например кроссворды. А ведь даже для взрослых – это хорошая разрядка от трудных ежедневных проблем и замечательный способ проведения семейного досуга.
Полезность этой игры просто трудно переоценить. Я узнала, что условия ребусов могут быть заданы в стихотворной форме. Это очень интересно. Я продолжу изучение ребусов.
Результаты моей работы:
1.Я расширила свой кругозор.
2.Я научилась решать ребусы различных видов.
3.Я научилась составлять ребусы.
5.У меня и у моей семьи появилось новое творческое увлечение, которое поможет мне развить сообразительность, усидчивость, упорство, что так необходимо мне для успешной учёбы.
Источники:
1. Березнев А.В. «Кроссворды, игры, загадки»: Сборник – Ростов-на-Дону, 1998
2. Трошин В.В. « Магия чисел и фигур». Занимательные материалы по математике . М.: Глобус, 2007.
3.Ожёгов С. И. и Шведова Н.Ю. « Толковый словарь Русского языка». М.:ООО «ИТИ Технологии»,2003.
4.Удальцова Н.В. Математика: «Математические шарады и ребусы».Москва.2010.
5. Фарков А. В. «Математические кружки в школе. 5 – 8 классы».
М.: Айрис-пресс, 2008.
6. Шарыгин И. Ф., Шевкин А. В. Математика: Задачи на смекалку: Учеб. пособие для 5 – 6 кл. общеобразоват. учреждений. М.: Просвещение, 2000.
7.http://yandex.ru/images/search?text=%D0%BA%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8%20%D0%9B%D1%8F%D0%B3%D1%83%D1%88%D0%BA%D0%B8%20%D0%BD%D0%B0%D1%80%D0%B8%D1%81%D0%BE%D0%B2%D0%B0%D0%BD%D0%BD%D1%8B%D0%B5&uinfo=sw-1366-sh-768-ww-1350-wh-596-pd-1-wp-16x9_1366x768 – картинки.
8.http://www.igraza.ru/page-1-1-20.html — картинки.
9.http://rebus1.com/index.php?item=rebus&mode=2- история ребусов.
10.http://allriddles.ru/ru/rebuses/ — чем полезны ребусы.
11. http://elancev.narod.ru/kids/ref_reb/ref_reb.htm — чем полезны ребусы.
Ребусы «Математика 5 класс»
Отгадывать загадки, расшифровывать ребусы и шарады любят дети всех возрастов, ведь это не только интересно, но и очень полезно!
Ребусы — головоломка, в которой при помощи картинок, буквенных сочетаний и знаков зашифровано слово. Они популярны не одно столетие, поскольку являются необычайно увлекательной игрой. Решать ребусы можно как одному, так и в весёлой компании, устраивая соревнования. Такие задания помогают расширить кругозор, развивают мышление и воображение, тренируют сообразительность, логику и интуицию, так как для решения даже самого простого ребуса надо многое знать об окружающем мире, уметь рассуждать и делать необходимые выводы.
Ребусы являются неотъемлемой частью и образовательного процесса, ведь они тренируют память, логическое мышление, внимание. Для школьника разгадывание ребусов превращается в захватывающую игру, которая к тому же способствует интеллектуальному развитию, делает ребёнка более внимательным и усидчивым.
Каждый учитель стремится заинтересовать своих учеников и удержать их интерес к изучению своего предмета, повысить мотивацию каждого ученика. Для этого в процесс обучения полезно включать, например, ребусы.
Ребусы будут интересны каждому ученику. Ведь разгадать ребус — это маленький успех. Процесс разгадывания ребусов обязательно принесёт положительные эмоции ученикам.
Ребусы «Математика 5 класс» позволят проверить и систематизировать знания учащихся 5 класса. Их можно использовать в качестве раздаточного материала на уроках математики, а также на внеклассных мероприятиях. Это позволит разнообразить учебный процесс и сделать его интересным и увлекательным.
Здесь вы найдёте ребусы:

А также ответы к ним:




Мастер класс для учащихся
5 классов по теме:
«Решение математических ребусов»
Подготовила:
Черемисина Любовь Владимировна,
учитель математики МБОУ «Троицкая СОШ №1»
с.Троицкое,
2013 год
Пояснительная записка
Пятиклассники активно откликаются на любые предложения учителя поучаствовать во внеклассном мероприятии, олимпиаде или конкурсе. Однако, как показывают результаты, навыков решения нестандартных задач у учащихся 5 классов нет.
Ко всему прочему, в настоящее время учителя испытывают нехватку современной методической литературы, предназначенной для работы со способными учащимися по организации и проведению кружковых занятий, олимпиад по математике.
Учителя осуществляют подготовку учащихся к олимпиадам, опираясь на свой собственный опыт, взгляды, работа ведется на эмпирическом уровне без должной теоретической основы.
Между тем обучение решению нестандартных задач на раннем этапе могло бы развивать математические способности, интерес к предмету у учащихся, гибкое, вариативное мышление ребенка. Меня заинтересовали наработки методического объединения преподавателей математики, физики и информатики ГОУ лицей №1524 г. Москва по подготовке одаренных учащихся 5 класса к олимпиадам по математике. Данный мастер класс можно использовать при проведении элективных курсов, кружковых занятий и на уроках математики.
Цель мастер класса- рассмотреть технологию организации работы учащихся с арифметическими ребусами.
При работе с такими типами заданий следует учитывать несколько технологичных приемов:
1. Следует предлагать детям обратные преобразования: сначала обычный пример сделать арифметическим ребусом, заменив цифры буквами; затем ребус превратить в обычный пример, разгадав числа. Тогда дети будут понимать, откуда берутся одинаковые цифры на месте одинаковых букв, лишний старший разряд, разная цифра в суммах одинаковых слагаемых и т.д.
2. Различные “секреты” ребусов не задавать одновременно, это следует делать поочередно, причем после введения каждого “секрета” и его подробного обсуждения предлагать детям самим придумать ребус с таким “секретом”.
3. Следует учитывать возрастные особенности детей: ребусы с буквами требуют умения учащихся абстрагироваться, выполнять в уме большую часть вычислительных операций.
4. Примеры со * решаются проще, чем ребусы с буквами. Они построены по принципу “распутай клубок”. Поэтому начинать работу следует именно с таких примеров.
Оборудование к мастер классу: компьютер, мультимедийный проектор.
Содержание
Историческая справка.
2.Арифметические ребусы со *.
3.Арифметические ребусы с буквами.
4. Литература.
Ход мастер класса
Краткая историческая справка.
Слово «ребус» происходит от латинского res (вещь) и обозначает представление имен, слов и фраз изображениями, фигурами, композициями из букв и т.п. Само слово появилось из латинской фразы «Non verbis sed rebus», что значит «Не словами, а при помощи вещей». Иногда термин rebus ассоциируют с латинским словом rebis: res (вещь, предмет), rebis (обращение).
Математические ребусы представляют собой примеры обычных арифметических действий (сложения, вычитания, деления и умножения), в которых часть или даже все цифры заменены на точки, звездочки, буквы или другие символы. Решить ребус — означает восстановить первоначальный вид математического равенства.
Существует несколько разновидностей математических ребусов. Например, в буквенных ребусах каждой буквой зашифрована одна определенная цифра. При этом одинаковые цифры шифруются одной и той же буквой, а разным цифрам соответствуют различные буквы. Математический буквенный ребус именуют криптарифмом, если в результате шифрования получилась какая-то осмысленная фраза. Например, УДАР+УДАР=ДРАКА
В математических ребусах зашифрованных иными значками, например звездочками, каждый символ может обозначать любую цифру от 0 до 9. Причём, некоторые цифры могут повторяться несколько раз, а другие не использоваться вовсе. Такие ребусы, зачастую, называют числовыми или цифровыми.
Математический ребус — довольно старая головоломка, изобретатель её не известен.
Первое упоминание об отечественных математических ребусах, автору проекта «Ребус № 1» удалось отыскать в книге выдающегося российского, советского учёного, популяризатора физики, математики и астрономии, одного из основоположников жанра научно-популярной литературы Якова Перельмана «Занимательная арифметика. Загадки и диковинки в мире чисел», выпущенной Ленинградским издательством «Время» в 1926 году (слайды 2-6)
2. Работа с арифметическими ребусами, где нужно заменить * недостающими цифрами и выполнить действие.
— Учитель предлагает внимательно рассмотреть примеры, записанные на доске, и найти «секрет» этих примеров.
3+ 5 = 8 8 – 2 = 6 6 + 4 = 10 10 – 7 = 3
-После того, как учащиеся выясняют, что результат каждого примера является началом следующего («цепочка» примеров), тогда учитель предлагает решить головоломку, которая называется «распутай клубок».
56 – Δ =
– 15 =
18 + 6 = Δ
+ 1 = ►
В ходе рассуждений, возникают вопросы: как решить примеры, в которых нет двух чисел? Почему задание называется «распутай клубок»?
В работе учащиеся выясняют, что один пример решить все таки можно. Таким образом, будет найдено значение Δ. Подставив его в первый пример, находим следующее число и т.д. Теперь детям понятно, почему назвали задание «распутай клубок».
Учитель предлагает детям последовательно решить следующие задания:
Распутать еще один «запутанный клубок
82 + = ►
+ 8 = Δ
Δ – 39 =
94 – 45 =
Превратить цепочку примеров в «запутанный клубок» (для этого некоторые цифры заменить геометрическими фигурами).
4 + 2 = 6 6 – 5 = 1 1 + 7 = 8 8 – 3 = 5
4 + 2 = Δ Δ – 5 = + 7 = – 3 = ►
Дети фиксируют основное правило: одинаковые цифры должны быть заменены одинаковыми значками (и наоборот).
3. Придумать самостоятельно «запутанный клубок». Для этого дети сначала должны составить цепочку примеров.
4. Вставить вместо Δ одну и ту же цифру, чтобы равенство было верным.
1Δ + 3Δ + 5Δ = 111
Дети выполняют это задание путем перебора вариантов:
1 + 1 + 1 = 3 не подходит; 2 + 2 + 2 = 6 не подходит
3 + 3 + 3 = 9 не подходит; 4 + 4 + 4 = 12 не подходит
5 + 5 + 5 = 15 не подходит; 6 + 6 + 6 = 18 не подходит
7 + 7 + 7 = 21 подходит — 21 + (10 + 30 + 50) = 111
Выполняя это задание, учащиеся, знакомятся с алгоритмом выполнения такого задания и формой записи: последовательный перебор возможных вариантов с фиксацией, подходит или нет такой вариант.
— Учитель предлагает детям следующее задание: Восстановить пример:
7 3 Δ 739
+2 6 +236
Δ 7 5 975
После выполнения задания обсудить, с чего начинали, чтобы распутать весь клубок. Выяснить, что, чтобы сложить многозначные числа, нужно сосчитать несколько примеров с однозначными числами, своеобразную цепочку. А такие задания мы выполнять умеем. Главное – найти подсказку, где «начинается клубок».
Совместно с учащимися, формулируем «секреты», которые помогают решать арифметические ребусы:
№1. Одинаковые знаки (буквы) обозначают одинаковые цифры.
№2. Чтобы решить такой пример, нужно найти начало «клубочка» (откуда будет раскручиваться логическое рассуждение).
№3. Нужно учитывать «переполнение» из соседнего разряда.
1
7 3 Δ
+ 2 6
Δ 7 5
Задания на закрепление:
1. Детям предлагается ряд примеров со *.
3 7 0 * * * 5 9 * _* 2 * 4 8 .
+ * 9 * 8 8 0 0 3 * * * *
9 * 4 0 5 0 8 * 2 * * * _ 2 *
* *
0
2. Запиши суммы обычными цифрами:
А А 0 А А В В В В К К 0 К К
+ А 0 А А А + В В В В + К К К К К
. . . 6 6 . . . 9 8 . . . . 5 4
Решая такие задания, дети выясняют еще два «секрета» арифметических ребусов, связанные с «переполнениями» из соседнего разряда:
откуда берется еще один разряд в сумме, и какая цифра там может быть? (только 1).
почему при сложении одинаковых знаков (букв) написаны (а значит, получаются) разные цифры? (виновато «переполнение» из соседнего разряда).
Открытия дополняют составленный ранее перечень «секретов»:
№4. На месте «свободного» старшего разряда в сумме может быть только цифра 1, которая получается из переполнения соседнего разряда.
№5. При сложении двух одинаковых букв могут получиться разные результаты. Виновато в этом «переполнение» из соседнего разряда.
нет переполнения 1 есть переполнение
Т Т Т Т
+ Т Т + Т Т
8 8 . 9 8
цифры одинаковые цифры разные
Значит, Т может быть равно 4, а может быть равно 9. Об этом обязательно следует помнить.
— Учитель предлагает детям решить следующие арифметические ребусы:
* * * + * = * * * * Ответ: 999+1=1000
* * * * * = * 100-99=1
* * * * * = * * * 1000-1=999
Дети сначала теряются, но потом быстро находят решение. Учитель спрашивает, почему была заминка? В чем (предположительно) ожидалась трудность? Учащиеся сообщают, что в этих ребусах нет ни одной известной цифры, только звездочки. Но смогли найти решение, потому что «секреты» арифметических ребусов, выведенные на предыдущем занятии, все равно работают.
Далее учитель предлагает детям несколько арифметических ребусов с буквами. Ребусы нужно решить и перечислить, какие «секреты» из уже известных использовались. Отдельно учитель предлагает фиксировать трудные моменты для поиска новых «секретов».
о х о х о
+ а х а х а
о х о х о х
Ответ: 1 0 1 0 1
+ 9 0 9 0 9
1 0 1 0 1 0 «Секреты» № 1,2, 3,4.
2) т р и
+ т р и
т р и
д ы р а
Ответ: 403
+ 403
403
1209 «Секреты» № 4, 2, 1.
Новый «секрет» №6 – если при сложении трех одинаковых цифр получается такая же, то это могут быть только цифры 0 или 5. Все зависит от того, нужно ли отсюда переполнение в более старший разряд.
г а
+ г о
у г у
Ответ: 9 5
+ 9 6
1 9 1 «Секреты» № 4, 2, 1.
Новые «секреты» :
№7: если при сложении двух одинаковых цифр получается такая же, то это могут быть только цифры 0.
№8: если же есть переполнение в этот разряд, то это может быть и цифра 9. Все зависит от того, нужно ли переполнение в более старший разряд. В данном ребусе не может ноль стоять в начале числа, значит, только 9.
Учитель предлагает детям буквенные ребусы на отработку всех известных «секретов». Обязательно обсуждать результат после нахождения решения: ввести форму записи «последовательности распутывания клубка».
к о ш к а 5 6 3 5 0
+ к о ш к а + 5 6 3 5 0
к о ш к а 5 6 3 5 0
с о б а к а 1 6 9 0 5 0
с – только1.
а + а + а = а только 0, так как из этого разряда не нужно переполнение.
к + к + к = к только 5.
к + к + к = о 5 + 5 + 5 (+ 1 из переполнения)= 6 – это о.
о + о + о = б 6 + 6 + 6 = либо 8 , либо 9.
Остаются цифры 2, 3, 4.
ш + ш + ш = 0 2 + 2 + 2 (+ 1 из переполнения) = 7 не подходит.
3 + 3 + 3 (+ 1 из переполнения) = 10 подходит, ш – 3.
Значит, если есть переполнение, то б – 9.
Домашнее задание: Решите ребусы:
ОДИН+ОДИН=МНОГО
РЕШИ+ЕСЛИ=СИЛЕН
ПОДАЙ-ВОДЫ=ПАША
СОТНЯ х 3 = ТРИСТА
Литература:
1.Система подготовки одаренных учащихся 5 класса к олимпиадам по математике. МО преподавателей математики, физики и информатики. ГОУ лицей №1524 г. Москва. http://do.gendocs.ru/docs/index-39863.html
2. http://rebus1.com/
Ребусы по математике ( 5 класс)
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:
Описание слайда:Ребусы «Математика 5 класс»
2 слайд Описание слайда: 3 слайд
Описание слайда: 3 слайд  Описание слайда: 4 слайд
Описание слайда: 4 слайд  Описание слайда: 5 слайд
Описание слайда: 5 слайд  Описание слайда: 6 слайд
Описание слайда: 6 слайд  Описание слайда: 7 слайд
Описание слайда: 7 слайд  Описание слайда: 8 слайд
Описание слайда: 8 слайд  Описание слайда: 9 слайд
Описание слайда: 9 слайд  Описание слайда: 10 слайд
Описание слайда: 10 слайд  Описание слайда:
Описание слайда:Ответы цирк + фра = цифра р + газ + р + яд = разряд
11 слайд Описание слайда:
Описание слайда:Ответы телотрев + азок = отрезок круг + болт = угол
12 слайд Описание слайда:
Описание слайда:Ответы мыло + мана + я = ломаная плос + кост + ь = плоскость
13 слайд Описание слайда:
Описание слайда:Ответы флешка + флаг = шкала д + щроб + ь = дробь
14 слайд Описание слайда:
Описание слайда:Ответы ф + гора + муха + л + ы = формулы муравей + небо + ние = уравнение
15 слайд Описание слайда:
Описание слайда:Ответы м + ногбо + о + у + г + о + л + ьнок + и + к + и = многоугольники трот + е + у + г + болт + ьник = треугольник
16 слайд Описание слайда:
Описание слайда:Ответы п + гиря + море + у + голь + чайник = прямоугольник п + мыло + щ + лошадь = площадь
17 слайд Описание слайда:
Описание слайда:Ответы парал + л + телефон + п + ипед = параллелепипед

Курс повышения квалификации
Курс повышения квалификации

Курс профессиональной переподготовки
Учитель математики и информатики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Общая информация
Номер материала: ДБ-018971
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Занимательная математика «Реши ребус» (5-8 классы)
Инфоурок › Алгебра ›Презентации›Занимательная математика «Реши ребус» (5-8 классы)Описание презентации по отдельным слайдам:
1 слайд Описание слайда:
Описание слайда:В МИРЕ МАТЕМАТИКЕ РЕШИ РЕБУС Учитель: Даутова Р.Ф.
2 слайд Описание слайда:
Описание слайда:Математика – наука великая, замечательный продукт одной из благороднейших способностей человеческого разума. Д. И. Писарев (1840-1868) Математика, есть царица наук, а арифметика есть царица математики. К. Гаусс (1777-1855) Математику уже затем учить надо, что она ум в порядок приводит. М. В. Ломоносов (1711-1763) Вдохновение нужно в геометрии не меньше, чем в поэзии А. С. Пушкин (1799-1837) Полет – это математика В. П. Чкалов (1904-1938)
3 слайд Описание слайда:
Описание слайда:1.Проверьте свою геометрическую наблюдательность Сосчитайте, сколько всего треугольников в фигуре, изображенной на рисунке.
4 слайд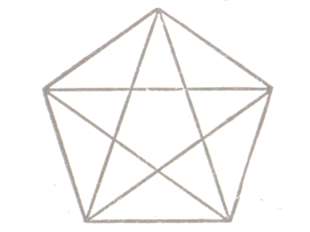 Описание слайда: 5 слайд
Описание слайда: 5 слайд  Описание слайда:
Описание слайда:35
6 слайд Описание слайда:
Описание слайда:1. Архимед 2. Гаусс Карл 3. Евклид 4. Лейбниц Готфрид 5. Ньютон Исаак 6. Пифагор 7. Ферма Пьер 8. Чебышев Пафнутий 9. Эйлер Леонард
7 слайд Описание слайда:
Описание слайда:1. Квадрат 2. Круг 3. Ломаная 4. Параллелограмм 5. Прямоугольник 6. Ромб 7. Трапеция 8. Треугольник 9. Эллипс
8 слайд Описание слайда:
Описание слайда:Дельтоид – это четырехугольник, состоящий из двух равных треугольников, причем две равные стороны должны быть соседними.
9 слайд Описание слайда:
Описание слайда:Через мост проехало 40 автомобилей и велосипедов – всего 100 колес. Сколько проехало велосипедов?
10 слайд Описание слайда:
Описание слайда:30
11 слайд Описание слайда: 12 слайд
Описание слайда: 12 слайд  Описание слайда: 13 слайд
Описание слайда: 13 слайд  Описание слайда:
Описание слайда:Треугольник
14 слайд Описание слайда: 15 слайд
Описание слайда: 15 слайд  Описание слайда:
Описание слайда:Точка
16 слайд Описание слайда: 17 слайд
Описание слайда: 17 слайд  Описание слайда:
Описание слайда:Задача
18 слайд Описание слайда: 19 слайд
Описание слайда: 19 слайд  Описание слайда:
Описание слайда:Число
20 слайд Описание слайда: 21 слайд
Описание слайда: 21 слайд  Описание слайда:
Описание слайда:Ромб
22 слайд Описание слайда: 23 слайд
Описание слайда: 23 слайд  Описание слайда:
Описание слайда:Косинус
24 слайд Описание слайда: 25 слайд
Описание слайда: 25 слайд  Описание слайда:
Описание слайда:Степень
26 слайд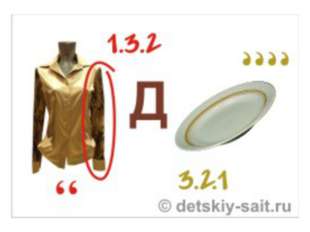 Описание слайда: 27 слайд
Описание слайда: 27 слайд  Описание слайда:
Описание слайда:Квадрат
28 слайд Описание слайда: 29 слайд
Описание слайда: 29 слайд  Описание слайда:
Описание слайда:Плюс
30 слайд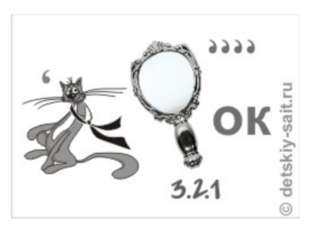 Описание слайда: 31 слайд
Описание слайда: 31 слайд  Описание слайда:
Описание слайда:Отрезок
32 слайд Описание слайда: 33 слайд
Описание слайда: 33 слайд  Описание слайда:
Описание слайда:Вектор
34 слайд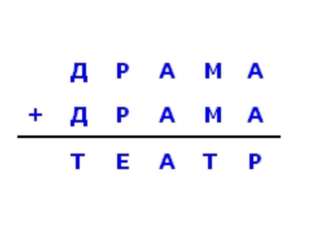 Описание слайда: 35 слайд
Описание слайда: 35 слайд 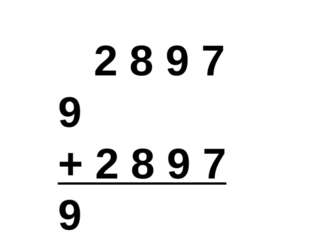 Описание слайда:
Описание слайда:2 8 9 7 9 + 2 8 9 7 9 5 7 9 5 8
36 слайд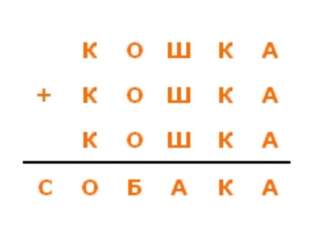 Описание слайда: 37 слайд
Описание слайда: 37 слайд  Описание слайда:
Описание слайда:5 6 3 5 0 + 5 6 3 5 0 5 6 3 5 0 1 6 9 0 5 0
38 слайд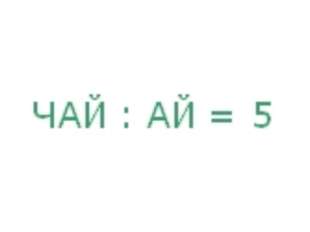 Описание слайда: 39 слайд
Описание слайда: 39 слайд 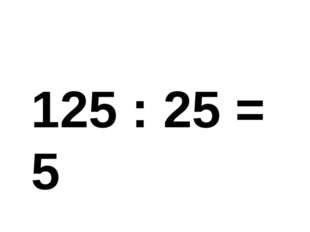 Описание слайда:
Описание слайда:125 : 25 = 5
40 слайд Описание слайда:
Описание слайда:МАТЕМАТИКА

Курс повышения квалификации
Курс повышения квалификации

Курс профессиональной переподготовки
Учитель математики и информатики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Краткое описание документа:
Урок математики довольно сложный предмет, он требует к себе серьезного отношения, и поддается, конечно же, ни всем учащимся, но ведь и слабому ученику тоже надо дать понять, что и он может успешно заниматься по математике. Порой на уроке это не всегда удается, зависит и от темы, и от интеллектуальных способностей ребенка, а вот на внеклассных мероприятиях во время игры, на часах занимательной математики это удается лучше всего, ребенок становится более спокойный, быстро включается в работу с классом и переключается с одного вида деятельности на другой. Все учащиеся активны и им очень нравятся такие мероприятия. Именно поэтому я часто провожу разные часы занимательной математики. Вот один из самых простых мероприятий «Час занимательной математики «Реши ребус»».
Общая информация
Номер материала: 311382
Похожие материалы
Оставьте свой комментарий
Математические ребусы в картинках
1)  показатель
показатель
Пояснение: ПО букве К расположена буква А, ЗА буквой Т стоит ЕЛЬ
2)  наклонная
наклонная
Пояснение: НА К стоит Л, ОН находится НА Я
3)  подобие
подобие
Пояснение: ПОД О находится БИЕ
4)  стереометрия
стереометрия
Пояснение: С, в слове ТЕРмОМЕТР заменяем первую М на Е, в слове ПЯть, убираем последние две цифры и П заменяем на И. Получается, стереометрия.
5)  теорема Пифагора
теорема Пифагора
Пояснение: Т, ОРЕЛ, МАК, ПИ, ФЛАГ, ОР, А.
В слове ОРЕЛ берем буквы по следующему порядку: 3, 1, 2, 3, получается ЕОРЕ. В слове МАК убираем последнюю букву К, получается МА. В слове ФЛАГ вычеркиваем букву Л, получается ФАГ. Соединяем Т, ЕОРЕ, МА, ФАГ, ОР, А, получается ТЕОРЕМА ПИФАГОРА.
6)  теорема
теорема
Пояснение: ТЕО, РАМА. В слове РАМА, заменяем первую букву А на Е. получается РЕМА. Соединяем ТЕО и РЕМА, получается ТЕОРЕМА.
7)  отрезок
отрезок
Пояснение: КОТ, РЕ, ЗОНТ. У слова КОТ, убираем первую букву, получается ОТ. РЕ оставляем без изменений. В слове ЗОНТ, заменяем НТ на К, получается ЗОК. Соединяем ОТ, РЕ, ЗОК, получается ОТРЕЗОК.
8)  задача
задача
Пояснение: ЗА и ДАЧА, получается ЗАДАЧА.
9)  минус
минус
Пояснение: нота МИ, НОС, у которого вторую букву заменяем на У, получается МИНУС
10)  число
число
Пояснение: ОЧКИ и СЛОН, в слове ОЧКИ зачеркиваем 1 и 3 буквы, в слове СЛОН убираем последнюю букву: ЧИ СЛО. Получается, ЧИСЛО.
11) 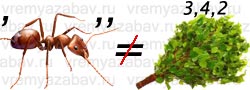 уравнение
уравнение
Пояснение: МУРАВЕЙ, НЕ и ВЕНИК. В МУРАВЕЙ убираем первую букву и две последних – УРАВ, в ВЕНИК берём 3, 4, 2 буквы – НИЕ. Значит: УРАВ НЕ НИЕ, получилось УРАВНЕНИЕ.
12)  ответ
ответ
Пояснение: КОТ в Е, КОТ. Убираем в слове КОТ первую букву – ОТ, находитя В Е, во втором слове КОТ убираем первые две буквы – Т. Значит, ОТ В Е Т. Получается, ОТВЕТ.
13)  пример
пример
Пояснение: ТРИ и РЕМЕНЬ. В ТРИ заменяем первую букву на П, получается ПРИ, в слове РЕМЕНЬ убираем последние 3 буквы и читаем полученное наоборот, получается МЕР. В ответе, получается ПРИМЕР.
14)  задача
задача
Пояснение: ЗА ДА находятся ЧАСЫ, у которых убираем последние две буквы. Получается, ЗАДАЧА.
15)  периметр
периметр
Пояснение: ПЕРО, МИ, РАКЕТА. У слова ПЕРо убираем последнюю букву, ноту МИ читаем наоборот, у слова ракета, берем буквы ЕТР, соединяем: ПЕР ИМ ЕТР. Получается, ПЕРИМЕТР.
16)  степень
степень
Пояснение: СТО, ПЕНЬ. В слове СТо заменяем О на Е, получилось СТЕ. Соединяем СТЕ и ПЕНЬ, получается СТЕПЕНЬ.
17)  знаменатель
знаменатель
Пояснение: З находится НА букве М; в слове ЕНОТ, заменяем О на А, получается ЕНАТ; ЕЛЬ. Соединяем З, НА, М, ЕНАТ, ЕЛЬ, получается ЗНАМЕНАТЕЛЬ.
18)  квадрат
квадрат
Пояснение: К букве В прибавляем справа А. У слова ДАРТС берем буквы под номерами 1, 3, 2, получается ДРА. У слова КИТ, убираем первые две буквы, получается Т. Соединяем К, В, А, ДРА, Т, получается КВАДРАТ.
Ищешь математические ребусы – Клуб Головоломка
В этой головоломке каждая из букв заменяет какую-то цифру. Ваша задача найти эти цифры. Математическая находчивость поможет вам уменьшить количество вариантов.

Решите числовой ребус указанный на рисунке. Вместо одной звездочки должна быть одна цифры. Этот ребус имеет единственное правильное решение.

Решите эту гениальную загадку. Есть сок, кофе и коктейль.Головоломка только для любителей вечеринок 🙂
Напиши свой вариант ответа в комментариях.

Решите фруктовый математический ребус, показанный на рисунке. Чему равно нижнее математическое выражение?

Для решения ребуса необходимо найти цифровое значение, которое соответствует фруктам: яблоко и апельсин.

Реши математический ребус с морскими обитателями

Реши на картинке математический ребус с динозаврами. Определи, какая цифра должна быть вместо знака вопроса.

Попробуй решить математический ребус показанный на рисунке. Найди значения которые соответствую подарочным коробкам. Свой ответ напиши в комментариях.

Для решения этого ребуса, нужно быть особенно внимательным. Обрати внимание на роботов, не все они одинаковые.

Взгляните на математический ребус. Есть убеждение, что его не могут решить правильно около 79% людей. А ты справишься?

математических задач с ответами для 5 класса
- Home
- Математика и Precalculus
- Математические задачи
- Вопросы и проблемы алгебры
- Графики функций, уравнений и алгебры Бесплатные математические листы
- для загрузки
- Аналитические уроки
- и
- Решения Калькуляторы и решатели
- графика
- Бесплатная Диаграммная бумага
- Math Software
- Прикладная математика
- Приложения математики в области физики и техники
- Антенны
- Упражнения по математике Utilisant les Applets
- Исчисление
- Учебные пособия и задачи по исчислению Вопросы
- по исчислению с ответами
- Бесплатные рабочие листы исчисления для загрузки
- Бесплатные рабочие листы исчисления для загрузки
- Бесплатные рабочие листы исчисления для загрузки
- Geometry
- Учебники и проблемы по геометрии
- Онлайн-калькуляторы и решатели геометрии
- Бесплатные рабочие таблицы по геометрии для загрузки
- Тригонометрия
- Учебные пособия по тригонометрии и задачи для самостоятельных тестов ometry
- FreeBSD Скачать
- Подробнее
- Статистика
- Элементарная статистика и вероятностные учебные пособия и задачи
- Математические страницы на французском языке
- Сайт
- Abo но автор
- Скачать
- Электронная почта
- Первичная математика
- Средняя школа по математике
- Средняя школа по математике
- Бесплатная практика для тестов SAT, ACT и Compass Math
- Статистика
- Home
- Математика и Precalculus
- Математические задачи
- Вопросы и проблемы алгебры
- Графики функций, уравнений и алгебры Бесплатные математические листы
- для загрузки
- Аналитические уроки
- и
- Решения Калькуляторы и решатели
- графика
- Бесплатная Диаграммная бумага
- Math Software
- Прикладная математика
- Приложения математики в области физики и техники
- Антенны
На школьной площадке есть несколько детей, нарисован квадрат, и все дети стоят на квадратах в четыре линии, они стоят на одинаковом расстоянии, четверо детей стоят на четырех углах. № 16 Точно противоположно № 6. Сколько там детей?
Проверьте свой ответ: —
Если предположить, что в каждой стороне квадрата есть x детей, то есть в общей сложности 4x-4 детей (не считая угловых детей дважды).
Теперь мы знаем, что по крайней мере 16 детей, таким образом, 4x-4> = 16. x> = 5
Предположим, что первый ребенок сидит в левом нижнем углу, а не три случая
Дело 1: х = 5
, тогда шестой ребенок будет стоять на второй позиции во второй линии квадрата, таким образом, совершенно противоположный ребенок будет сидеть на х + х-2 + х + х-1 = 4х-3-й позиции, то есть 17-й позиции.
Что касается вопроса, то это не так, поэтому x не может быть 5
Дело 2: х = 6
, затем шестой ребенок сидит на углу (точка B), таким образом, совершенно противоположный ребенок находится в положении x + x-2 + x = 3x-2th, т.е.е. Шестнадцатый.
Таким образом, он удовлетворяет всем условиям вопроса.
Таким образом, в данном случае всего 4х-4, то есть 20 детей.
Дело 3: х> 6
, тогда шестой ребенок стоит где-то в нижней строке (точка A), согласно этому совершенно противоположному ребенку будет стоять в положении x + x-2 + x -6 = 3x — 8
для 3x-8 = 16 => x = 24/3 = 8
Таким образом, в данном случае в общей сложности 4x-4 = 28 детей.
,Mental Math 5-го класса
Добро пожаловать на листы 5-го класса Math Salamanders Mental Math.
Здесь вы найдете широкий ассортимент бесплатных 5-х классов Mental Math Worksheets, которые помогут вашему ребенку выучить числовые факты и отработать их числовые навыки.
Наша подборка листов по умственной математике — это отличный способ оттачивать свои навыки и навыки математики.
Листы могут быть использованы различными способами, в качестве теста или пересмотра практики, или как часть еженедельной викторины, чтобы помочь укрепить навыки.
Один из лучших способов использовать эти листы — заставить детей работать в парах, обсуждая вопросы по мере их проработки.
Вопросы были разработаны, чтобы практиковать ряд математических навыков от числа до геометрии и фактов измерения, включая использование времени и денег.
Тесты расположены в порядке сложности, а вопросы в каждом тесте становятся немного сложнее.
Наши 5-й класс Mental Math Worksheets содержат широкий спектр различных вопросов и математических навыков.
Каждый лист содержит 18 вопросов и снабжен листом ответов.
Уровень сложности становится сложнее по мере прохождения листов.
Темы включают в себя:
- ментальная арифметика — сложение, вычитание, умножение и деление;
- вопросов уравнения баланса; Вопросы о геометрии
- , обычно основанные на двухмерных и трехмерных свойствах формы;
- денежных вопросов;
- мер вопросов: длина, вес, объем жидкости;
- дробных вопросов, включая дробные числа и эквивалентные дроби;
- процентов и соотношение вопросов;
- средний, средний, диапазон и мод вопросов;
- вопросов времени
Рабочие листы в этом разделе были разработаны для детей в 4 классе.
Листы имеют тот же формат, что и на этой странице, но на более базовом уровне.
Если вы ищете какую-то онлайн-практику по ментальной математике для 5-го класса, то у нас есть несколько зон практики где вы можете проверить свои знания ряда математических фактов и распечатать результаты онлайн.
Есть сертификаты на победу и мгновенная обратная связь о вашем прогрессе.
Здесь вы найдете ряд бесплатных печатных математических игр 5-го класса.
Все дети любят играть в математические игры, и вы найдете хороший Ряд математических игр 5 класса здесь для вашего ребенка, чтобы играть и наслаждаться.
Следующие игры включают в себя 5-й класс математики занятия, которыми вы и ваш ребенок можете наслаждаться вместе.
Все бесплатные листы 5-го класса по математике в этом разделе следуйте Элементарным Математическим Тестам для 5 класса.
На начальных играх.com, вы найдете банк онлайн математических игр для игры на уровне 5-го класса.
Использование игр поможет вашему ребенку развить свои навыки в веселой и мотивирующей манере.
Используя ссылку ниже, вы откроете веб-сайт основных игр в новом окне браузера.
Математические саламандры надеются, что вам понравится использовать эти бесплатные печатные листы по математике и все наши другие математические игры и ресурсы.
Мы приветствуем любые комментарии о нашем сайте или рабочих листах в поле для комментариев Facebook внизу каждой страницы.
,
бесплатных математических листов 6-го класса
Вы здесь: Главная → Рабочие листы → 6 классЭто обширная коллекция бесплатных печатных математических таблиц для шестого класса, организованных по таким темам, как умножение, деление, показатели степени, разрядность, алгебраическое мышление, десятичные дроби, единицы измерения, отношение, процент, простое факторизация, GCF, LCM, дроби, целые числа и геометрия. Они генерируются случайным образом, распечатываются из вашего браузера и содержат ключ ответа.Рабочие листы поддерживают любую математическую программу 6-го класса, но были специально разработаны для соответствия учебному плану 6-го класса Math Mammoth.
Рабочие листы генерируются случайным образом каждый раз, когда вы нажимаете на ссылки ниже. Вы также можете получить новый, другой, просто обновив страницу в браузере (нажмите F5).
Вы можете распечатать их прямо из окна браузера, но сначала проверьте, как это выглядит в «Предварительном просмотре». Если рабочий лист не умещается на странице, настройте поля, верхний и нижний колонтитулы в настройках страницы вашего браузера.Другой вариант — настроить «масштаб» на 95% или 90% в предварительном просмотре. В некоторых браузерах и принтерах есть опция «Печать по размеру», которая автоматически масштабирует рабочий лист до области печати.
Все рабочие листы поставляются с ключом ответа, размещенным на 2-й странице файла.
В шестом классе учащиеся начнут изучать начальную алгебру (порядок операций, выражения и уравнения). Они узнают о коэффициентах и процентах и начинают использовать целые числа.Студенты также рассматривают длинное деление, факторинг, дробную арифметику и десятичную арифметику. В геометрии основное внимание уделяется области треугольников и многоугольников и объему прямоугольных призм. Другие темы включают в себя округление, показатели, GCF, LCM и единицы измерения. Обратите внимание, что эти бесплатные рабочие листы не охватывают все темы 6-го класса; в частности, они не включают решение проблем.
Умножение и деление и некоторый обзор
Длинное умножение
Длинное деление
- 1-значный делитель, 5-значный дивиденд, без остатка
- 1-значный делитель, 5-значный дивиденд, с остатком
- 1-значный делитель, 6-значный дивиденд, без остатка
- 1-значный делитель, 6-значный дивиденд, с остатком
- 1-значный делитель, 7-значный дивиденд, без остатка
- 1-значный делитель, 7-значный дивиденд, с остатком
 показатель
показатель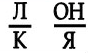 наклонная
наклонная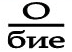 подобие
подобие стереометрия
стереометрия теорема Пифагора
теорема Пифагора теорема
теорема отрезок
отрезок задача
задача