Ответы. Учебник. Часть 1 (с. 33)
Длина ломаной
Ответы к стр. 334. Дополни условие задачи и поставь вопрос так, чтобы она решалась вычитанием. Реши её устно
1) Высота берёзы 15 м, а клёна на 5 меньше. Какая высота клёна?
2) Масса арбуза 8 кг, а тыквы 10 кг. На сколько тыква тяжелее арбуза?
3) На двух веточках смородины 15 ягод. На одной из них 10 ягод. Сколько ягод на другой веточке?
1) 15 — 5 = 10 (м)
2) 10 — 8 = 2 (кг)
3) 15 — 10 = 5 (яг.)
5. За день мимо станции прошло 2 скорых поезда и 6 товарных. Только 3 поезда на этой станции остановились. Сколько поездов прошло мимо станции без остановки?
1) 2 + 6 = 8 (п.)
2) 8 — 3 = 5 (п.)
О т в е т: прошло 5 поездов.
6. До остановки автобуса папа идёт 10 мин, а на автобусе едет на работу на 20 мин больше, чем идёт до остановки. Сколько всего времени он тратит на дорогу?
1) 10 + 20 = 30 (мин)
О т в е т: всего тратит 40 минут.

7. Реши примеры. Покажи, что они круговые.
6 + 6 = 12 → 12 — 5 = 7 → 7 + 4 = 11 → 11 — 3 = 8 → 8 + 6 = 14 → 14 — 5 = 9 → 9 + 4 = 13 → 13 — 7 = 6
Ответ каждого примера является первым числом другого примера.
8. Используя два или три числа на стене домика, набери число, записанное в окошке под крышей (12). Например, 8 и 4 или 4, 6, 2.
9 и 3 или 1, 2 и 9 или 5, 3 и 4 или 7 и 5
Рассмотри рисунок. От дома проложены дорожки к колодцу и к беседке. Какая дорожка длиннее?
Длина дорожки к колодцу 2 + 3 = 5, а длина дорожки к беседке: 3 + 3 = 6. Таким образом, длиннее дорожка к беседке: 6 — 5 = 1.
Ответы по математике. 2 класс. Учебник.
Ответы. Учебник. Часть 1 (с. 33)
3 (60%) от 2 голосующихГДЗ по Математике 2 класс учебник Моро 1 часть ответы стр 33
👉 Ответы к странице 33. Математика 2 класс учебник 1 часть. Авторы: М. И. Моро, С. И. Волкова.
Математика 2 класс учебник 1 часть. Авторы: М. И. Моро, С. И. Волкова.
Дополни условие задачи и поставь вопрос так, чтобы она решалась вычитанием. Реши ее устно.
1) Высота березы 15 м, а клена на 5 м … .
2) Масса арбуза ? кг, а тыквы 10 кг.
3) На двух веточках смородины 15 ягод. На одной из них ? ягод.
Решение:
1) Высота березы 1,5 м, а клёна на 5 м меньше.
Найди высоту клёна.
Ответ: высота клёна 10 метров.
2) Масса арбуза 8 кг, а тыквы 10 кг. На сколько масса тыквы больше массы арбуза?
10-8=2 (кг)
Ответ: тыква тяжелее арбуза на 2 кг.
3) На двух веточках смородины 15 ягод. На одной из них 7 ягод. Сколько ягод на второй веточке?
15-7=8 (яг.)
Ответ: на второй веточке 8 ягод.
Номер 5За день мимо станции прошло 2 скорых поезда и 6 товарных. Только 3 поезда на этой станции остановилось. Сколько поездов прошло мимо станции без остановки?
Решение:
1) 2+6=8 (п. )
)
2) 8-3-5 (п.)
Ответ: 5 поездов прошли без остановки.
Номер 6До остановки автобуса папа идет 10 мин, а на автобусе едет на работу на 20 мин больше, чем идет до остановки. Сколько всего времени он тратит на дорогу?
Решение:
1) 10+20=3 (мин.)
2) 10+30=40 (мин)
Ответ: папа тратит на дорогу 40 минут.
Номер 7Решение:
6+6=12
7+4=11
14-5=9
13-7=6
8+6=14
9+4=13
11-3=8
12-5=7
Номер 8Используя два или три числа на стене домика, набери число, записанное в окошке под крышей (12). Например, 8 и 4 или 4, 6, 2.
Решение:
7 и 5 — это 12
8,3 и 1 — это 12
9 и 3 — это 12
6,5 и 1 — это 12
3,7 и 2 — это 12
4,5 и 3 — это 12
Задание внизу страницыРассмотри рисунок. От дома проложены дорожки к колодцу и к беседке.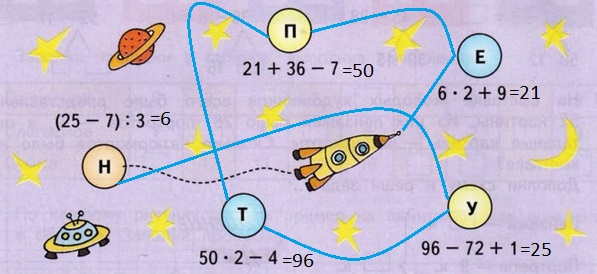
Решение:
Красная дорожка длиннее, чем синяя.
Кругові вирази математика 2 клас
Скачать кругові вирази математика 2 клас djvu
Часть 1. Страница 32 Номер 7 Реши примеры. Покажи, что они круговые. 6 + 6 7 + 4 14 − 5 13 − 7 8 + 6 9 + 4 11 − 3 12 − 5. ГДЗ Математика 2 класс Моро, Бантова, Бельтюкова, Волкова, Степанова. авторы: Моро, Бантова, Бельтюкова, Волкова, Степанова.
издательство: «Просвещение» Ответы и решения. Математика. Как понять круговые примеры второго класса. Ответы и решения. Математика. Как понять круговые примеры второго класса. 0 голосов. 2 просмотров. Как понять круговые примеры второго класса. понять. примеры. Ответ одного примера служит началом для последующего.Не получив правильного результата, невозможно решить следующий пример и правильно составить цепочку.
Ответ последнего примера является началом первого, что и дает название КРУГОВЫЕ ПРИМЕРЫ. Оцените статью. Добавить комментарий Отменить ответ. Имя *. Email *. Сайт. Комментарий. Математика 2 класс. Взаимно обратные задачи. Примеры и решение. Объяснения. Что такое взаимно обратные задачи, Математика 2 класс (Урок№27 — Проверка сложения. Проверка вычитания.) LiameloN Animation.
Добавить комментарий Отменить ответ. Имя *. Email *. Сайт. Комментарий. Математика 2 класс. Взаимно обратные задачи. Примеры и решение. Объяснения. Что такое взаимно обратные задачи, Математика 2 класс (Урок№27 — Проверка сложения. Проверка вычитания.) LiameloN Animation.
Baxış 4,3K9 ay əvvəl. Математика 2 класс Урок№27 — Проверка сложения. Проверка вычитания. мы узнаем: о взаимообратных математических Цепочки примеров 2 класс 1 четверть. Под диктовку. Baxış 83Ay əvvəl. В этом видео задания включают по два арифметических действия.
на уроках математике. 2 класс. Подготовила: учитель начальных классов. школы № Кузнецова О. А. Томск. II классе: (2класс). Игра «Прочитай число». Цель игры — научить детей правильно читать числа, оканчивающиеся двумя. ученики той же команды.
Ученики всего класса подтверждают ответ, показывая. зеленый круг или красный, если с ответом не соглашаются. Затем учитель.
Как решать круговые примеры. Современная математика для школьников младших классов включает в себя основы алгебры и геометрии.
Однако у самих учеников и задачи не вызывают затруднений, поскольку наряду с обычными математическими действиями на уроках математики обучают и началам математической логики. Математика 2 класс. Взаимно обратные задачи. Примеры и решение. Объяснения. Что такое взаимно обратные задачи, Математика 2 класс (Урок№27 — Проверка сложения. Проверка вычитания.) LiameloN Animation.
Baxış 4,3K9 ay əvvəl. Математика 2 класс Урок№27 — Проверка сложения. Проверка вычитания. мы узнаем: о взаимообратных математических Цепочки примеров 2 класс 1 четверть.
Под диктовку. Baxış 83Ay əvvəl. В этом видео задания включают по два арифметических действия. А какой смысл в круговых примерах? Какие цели ставит перед собой процесс, в ходе которого дети изучают круговые примеры? Сильно смахивает на профанацию. Похожие вопросы. Также спрашивают. Мобильная версия · Помощь · Отправить отзыв. urbanisto.ru О компании Реклама Вакансии.
Похожие вопросы. Также спрашивают. Мобильная версия · Помощь · Отправить отзыв. urbanisto.ru О компании Реклама Вакансии.
Похожее:
Кругові приклади 2 клас — flash52.ru
Скачать кругові приклади 2 клас fb2
Как решать круговые примеры. Современная математика для школьников младших классов включает в себя основы алгебры и геометрии. Не зря от родителей первоклашек требуют, чтобы они обучили своих детей навыкам устного счета до 10, а также научили их классифицировать предметы по признакам.
«Круговые примеры. Задачи»» категории «Кружки и факультативы кл.» бесплатно. Будем благодарны, если вы оставите отзыв или посмотрите еще другие материалы на нашем сайте. Спасибо Вам за Ваш труд. В этом году я использую в своей работе Вашу «Математическую шкатулку» 2 класса.
Дети с удовольствием решают Ваши задания. Ярко, наглядно, доступно и очень интересно!. Все, кто учился в школе, помнят, что к задачам составлялась краткая запись. Сейчас вместо краткой записи учителя могут использовать схемы и схематический чертёж к задачам. Это зависит от программы. О том, какие схематические чертежи к задачам бывают и как научить ребенка их составлять, эта статья. Сегодня поговорим о простых задачах, которые решаются сложением и вычитанием. Пример 1. У Кати 7 шариков, а у Зины 2 шарика.
Пример 1. У Кати 7 шариков, а у Зины 2 шарика.
Сколько всего шариков у девочек? При составлении чертежа вводятся понятия «целое» и «части». При сложении целое — это результат (сумма), а при вычитании — у. Реши круговые примеры и прочитай слово. Что ты о нем знаешь? Решение. Представлено ниже со всеми возможными комбинациями.
Для ребенка же во втором классе можно предложить следующий ход рассуждений. Первая цифра не может быть 0, так как тогда мы получим двузначное число. Значит первой цифрой может быть либо тройка либо девятка. 7. Реши примеры. Покажи, что они круговые.
6 + 6 14 — 5 8 + 6 11 — 3 7 + 4 13 — 7 9 + 4 12 — 5 8. Используя два или три числа на стене домика, набери число, записанное в окошке под крышей (12). Например, 8 и 4 или 4, 6, 2. Рассмотри рисунок. От дома проложены дорожки к колодцу и к беседке. Какая дорожка длиннее? ГДЗ решебник и ответы Математика 2 класс. Моро М.И., Бантова М.А., Бельтюкова Г.В., Волкова С.И., Степанова С.В. Учебник часть 1.
Во втором классе наши детки только только познают азы математики. Они еще повторяют и изучают простейшие математические операции, формируют основы логики для решения типовых задач, осваивают новое Что же, этого нового в математике им предстоит узнать еще много, а наша статья будет конкретно посвящена учебнику за 2 класс, по программе Перспектива с года авторы Г.В.
Они еще повторяют и изучают простейшие математические операции, формируют основы логики для решения типовых задач, осваивают новое Что же, этого нового в математике им предстоит узнать еще много, а наша статья будет конкретно посвящена учебнику за 2 класс, по программе Перспектива с года авторы Г.В.
Дорофеев, Т.Н. Миракова, Т.Б. Бука. Обложка учебника с года изменилась, теперь она стала белой, с лабиринтом и ежиками и яблоками. Ответы на задания к учебнику математики 1 часть за 2 класс Дорофеев: Чтобы посмотреть ответы для нужного задания нужно выбрать нужную страницу.
Это же само собой разумеющееся. 👍 Правильный ответ на вопрос «Как понять круговые примеры второго класса » по предмету Математика.
Развернутая система поиска нашего сайта обязательно приведёт вас к нужной информации. Как вариант — оцените ответы на похожие вопросы. Но если вдруг и это не помогло — задавайте свой вопрос знающим оппонентам, которые быстро дадут на него ответ! Искать готовые ответы.
Похожие вопросы. Запиши число единиц у которого ед. второго класса и 79 ед. первого класса ед. второго класса и. Что значит круговые примеры в математике для 2 класса и обязательно ли они должны быть последовательны. Рубрики: Детское развитие/Учебники класс. Метки: математика 2класс. Процитировано 23 раз Понравилось: 6 пользователям.
Запиши число единиц у которого ед. второго класса и 79 ед. первого класса ед. второго класса и. Что значит круговые примеры в математике для 2 класса и обязательно ли они должны быть последовательны. Рубрики: Детское развитие/Учебники класс. Метки: математика 2класс. Процитировано 23 раз Понравилось: 6 пользователям.
Похожее:
Кругові приклади 2 клас — boreyhostel.ru
Скачать кругові приклади 2 клас rtf
Что такое груговые примеры? Кто-нибудь сталкивался? Нам во 2 классе задали, а я не могу найти информацию. 0. Пример Здравствуй, школа! В течение выходных, игнорирую Юбилей ректора и день выпускников одной ооочень знаковой английской школы два профессора МГУ решали пример для 3 класса, заданный их любимой внучке!
0. Пример Здравствуй, школа! В течение выходных, игнорирую Юбилей ректора и день выпускников одной ооочень знаковой английской школы два профессора МГУ решали пример для 3 класса, заданный их любимой внучке!
Кажется, так и не решили. А вы хотите попробовать решить?. Реши круговые примеры и прочитай слово. Что ты о нем знаешь? Решение. Представлено ниже со всеми возможными комбинациями.
Для ребенка же во втором классе можно предложить следующий ход рассуждений. Первая цифра не может быть 0, так как тогда мы получим двузначное число. Значит первой цифрой может быть либо тройка либо девятка. Первый пример: 6+6= Значит второй начинается с числа 12, и т. д. Остальные ответы. Александер Знаток () 10 лет назад. А какой смысл в круговых примерах? Какие цели ставит перед собой процесс, в ходе которого дети изучают круговые примеры?
Сильно смахивает на профанацию. Похожие вопросы. Составь и реши круговые примеры. Решение. 14 − 9 + 3 = 5 + 3 = 8 8 + 7 + 4 = 15 + 4 = 19 19 − 16 + 7 = 3 + 7 = 10 10 + 2 − 6 = 12 − 6 = 6 6 + 8 − 7 = 14 − 7 = 7 7 + 4 + 5 = 11 + 5 = 16 16 − 8 − 5 = 8 − 5 = 3 3 + 15 − 4 = 18 − 4 = ← Предыдущее. Следующее →. Кругові приклади — це приклади в яких кожен наступний приклад починається з відповіді попереднього. Діткам дуже подобаються кругові приклади.
Следующее →. Кругові приклади — це приклади в яких кожен наступний приклад починається з відповіді попереднього. Діткам дуже подобаються кругові приклади.
Спробуйте з дитиною вирішити декілька кругів.
Составь и реши круговые примеры. Решение: Шаг 1: Вычислим первый пример: +8 = 15, полученное число поставим в пустой квадратик следующего примера: Шаг 2: Вычислим следующий пример: 15+ = 8, полученную 8 подставим в следующий пример: Шаг 3: Вычислим 8+=14, и подставим 14 в следующий пустой квадратик. Шаг 4: по аналогии вычислим остальные примеры и подставим в пустые квадратики.
ГДЗ Математика 2 класс Моро М.И. Пожаловаться. Зинаида Никифоровна. ГДЗ по математике, 2 класс, Моро М.И. Реши примеры. Реши примеры. Покажи, что они круговые. Просмотр содержимого документа «Круговые примеры. Устный счет». — х 3. х 2. Круговые примеры и задачки 1 класс. Открытый урок 2 класс. Технологическая карта урока 9 ПРЫЖОК В ДЛИНУ С МЕСТА (ТЕСТИРОВАНИЕ). Технологическая карта урока 4 ТЕСТИРОВАНИЕ ЧЕЛНОЧНОГО БЕГА 3 10 МЕТРОВ (НА ВРЕМЯ).
Похожее:
Страница 33 (учебник Моро 1 часть 2 класс) ответы по математике
4. Дополни условие задачи и поставь вопрос так, чтобы она решалась вычитанием. Реши её устно.1) Высота берёзы 15 м, а клёна на 5 меньше. Какая высота клёна?
15 — 5 = 10 (м) — высота клёнаОтвет: 10 м.
2) Масса арбуза 5 кг, а тыквы 10 кг. На сколько тыква тяжелее арбуза?
10 — 5 = 5 (кг)Ответ: на 5 кг.
3) На двух веточках смородины 15 ягод. На одной из них
На одной из них 10 ягод. Сколько ягод на другой веточке?
15 — 10 = 5 (яг.) — на другой веточке.Ответ: 5 ягод.
1) 2 + 6 = 8 (п.) — всего прошло
2) 8 — 3 = 5 (п.) — прошло без остановкиОтвет: 5 поездов.
1) 10 + 20 = 30 (мин) — на автобусе
2) 10 + 30 = 40 (мин) — на всю дорогуОтвет: 40 минут.
6 + 6 = 12 →
12 — 5 = 7 →
7 + 4 = 11 →
11 — 3 = 8 →
8 + 6 = 14 →
14 — 5 = 9 →
9 + 4 = 13 →
13 — 7 = 6
 Например, 8 и 4 или 4, 6, 2.
Например, 8 и 4 или 4, 6, 2.3 + 9 = 12
4 + 8 = 12
5 + 7 = 12
1 + 2 + 9 = 12
1 + 3 + 8 = 12
1 + 4 + 7 = 12
1 + 5 + 6 = 12
2 + 3 + 7 = 12
2 + 4 + 6 = 12
3 + 4 + 5 = 12
Рассмотри рисунок. От дома проложены дорожки к колодцу и к беседке. Какая дорожка длиннее?
Длина дорожки к колодцу 2 + 3 = 5
Длина дорожки к беседке: 3 + 3 = 6
Длиннее дорожка к беседке: 6 > 5
Реши примеры покажи что. Как решать круговые примеры
Современная математика для школьников младших классов включает в себя основы алгебры и геометрии. Не зря от родителей первоклашек требуют, чтобы они обучили своих детей навыкам устного счета до 10, а также научили их классифицировать предметы по признакам.
Инструкция
Сегодняшние учебники для 1 и 2 классов заполнены такими заданиями, над которыми ломают головы папы и мамы учеников младших классов. Однако у самих учеников примеры и задачи не вызывают затруднений, поскольку наряду с обычными математическими действиями на уроках математики обучают и началам математической логики.
Так называемые «круговые примеры » относятся именно к таким заданиям, в которых надо не просто складывать, вычитать и умножать, но и выстроить логический ряд. Детям задается некоторое количество примеров, которые они должны выполнить в правильной последовательности.Правила круговых примеров таковы.
Все примеры даются вперемешку. Ответ одного примера служит началом для последующего. Из общего количества примеров задания выбираются именно таким образом и выстраиваются в цепочку (столбик).
Не получив правильного результата, невозможно решить следующий пример и правильно составить цепочку. Ответ последнего примера является началом первого, что и дает название «круговые примеры ».
Например: 7+4 5+8 11-6 13-5Решать следует: 7+4=11 11-6=5 5+8=13 13-5=7, ответ каждого примера является началом для последующего, что и составляет цепочку или круг.
Круговые примеры решаются как устно, так и письменно. Детям нравятся задания такого рода, особенно если их приходится решать на время. Поэтому очень часто при решении круговых примеров учителя прибегают к игровой форме обучения. Особенно в младших классах.
Поэтому очень часто при решении круговых примеров учителя прибегают к игровой форме обучения. Особенно в младших классах.
Сказочные герои народных сказок или мультфильмов задают примеры и решают их вместе со школьниками. Как правило, круговые примеры в младших классах содержат простейшие действия на сложение и вычитание однозначных чисел. Однако впоследствии круговые примеры могут содержать несколько действий на сложение, вычитание, деление и умножение двух- и трехзначных чисел.
Внимание, только СЕГОДНЯ!
Все интересное
Умножение — одна из четырех основных арифметических операций, которая часто встречается как в учебе, так и в повседневной жизни. Как можно быстро перемножить два числа? Основу самых сложных математических вычислений составляют четыре основных…
Умножение — одна из четырех основных математических операций, которая лежит в основе многих более сложных функций. При этом фактически умножение основывается на операции сложения: знание об этом позволяет правильно решить любой пример. Для…
Для…
Математика – это ведущая наука, которая требует точности и внимательности. Чтобы научить малыша ее не бояться, правильно подбирайте задания. Первые занятия должны носить развлекательный характер, чтобы полностью заинтересовать ребенка. Вам…
Чтобы упростить дробное рациональное выражение, необходимо произвести арифметические действия в определенном порядке. Сначала выполняются действия в скобках, потом умножение и деление и в последнюю очередь – сложение и вычитание. Числитель и…
Корнем n степени из числа называют такое число, которое при возведении в эту степень даст то число, из которого извлекается корень. Чаще всего, действия производятся с корнями квадратными, которые соответствуют 2 степени. При извлечении корня часто…
К сожалению, универсального метода для решения всевозможных математических задач не существует. Однако имеются некоторые общие приемы и правила, которые нередко помогают догадаться о способе решения разнообразных задач. Инструкция1Найти решение…
Инструкция
Сегодняшние учебники для 1 и 2 классов заполнены такими заданиями, над которыми ломают головы папы и мамы учеников младших классов. Однако у самих учеников и задачи не вызывают затруднений, поскольку наряду с обычными математическими на уроках математики обучают и началам математической логики.
Однако у самих учеников и задачи не вызывают затруднений, поскольку наряду с обычными математическими на уроках математики обучают и началам математической логики.
Так называемые «круговые примеры » именно к таким заданиям, в которых надо не просто складывать, вычитать и умножать, но и выстроить логический ряд. Детям задается некоторое количество примеров, которые они должны выполнить в правильной последовательности.Правила круговых примеров таковы.
Все примеры даются вперемешку. Ответ одного примера служит началом для последующего. Из общего количества примеров задания выбираются именно таким образом и выстраиваются в цепочку (столбик).
Например: 7+4 5+8 11-6 13-5Решать следует: 7+4=11 11-6=5 5+8=13 13-5=7, ответ каждого примера является началом для последующего, что и составляет цепочку или круг.
Источники:
- Задача с использованием круговой диаграммы
Примеры с многозначными числами лучше всего решать столбиком : так и удобнее, и быстрее, и результат будет верным. Чтобы произвести правильные вычисления, необходимо придерживаться определенного алгоритма.
Чтобы произвести правильные вычисления, необходимо придерживаться определенного алгоритма.
Инструкция
При вычитании также начните действия с единиц. Если число того или иного разряда уменьшаемого меньше числа вычитаемого, то займите у следующего разряда 1 десяток или сотню и т.д. и произведите вычисления. Поставьте точку над числом, у которого занимали, чтобы не забыть. При выполнении действий с этим разрядом вычитайте уже из уменьшенного числа. Результат запишите под горизонтальной чертой.
Проверите правильность вычислений. Если вы складывали, тогда из полученной суммы вычтите одно из слагаемых, у вас должно получиться . Если же вы вычитали, тогда сложите полученную разность с вычитаемым, должно получиться уменьшаемое.
Обратите внимание
Обязательно разряды чисел должны находиться друг под другом.
Очень часто при решении задач по алгебре для 7 класса сложность представляют примеры с многочленами. При упрощении примеров или приведении их к заданному виду следует знать основные правила преобразования многочленов. Также ученику потребуются основы работы со скобками. Любой пример можно упростить, сократив выражение на общий делитель, выведя общую часть за скобки или выполнив приведение к общему знаменателю. При любом преобразовании многочлена очень важно учитывать знак каждого его слагаемого.
Также ученику потребуются основы работы со скобками. Любой пример можно упростить, сократив выражение на общий делитель, выведя общую часть за скобки или выполнив приведение к общему знаменателю. При любом преобразовании многочлена очень важно учитывать знак каждого его слагаемого.
Инструкция
Сложите подобные члены. При этом учитывайте , стоящие перед ними. Если перед одним из них стоит знак «-», вместо сложения выполните вычитание членов и с учетом знака же запишите результат. Если знак «-» имеют оба члена, следовательно выполняется их и результат записывается также со знаком «-».
При наличии дробных значений в коэффициентах многочлена, приведите для упрощения примера дроби к общему знаменателю. Для этого умножьте все коэффициенты выражения на одно и то же число так, чтобы при сокращении осталась лишь целая часть. В самом простом случае общий знаменатель является произведением всех знаменателей в дробных коэффициентах. После умножения всех членов, проведите упрощение подобных слагаемых.
После приведения к общему знаменателю и сложению подобных членов вынесите общие части выражения за скобки. Для этого определите группу членов, где имеется одинаковая часть выражения. Поделите коэффициенты группы на общую часть и запишите ее впереди скобок. В оставьте не весь многочлен, а именно данную группу членов с оставшимися от деления коэффициентами.
Не потеряйте знак при выносе за скобки. Если вы хотите общую часть вынести со знаком «-», то для каждого члена в скобках замените знак на противоположный. Остальные члены, не участвующие в выносе за скобки, запишите до или после скобок с сохранением их знака.
Если за скобки выносится общая часть , для группы в скобках производится вычитание показателя выносимой степени. При раскрытии скобок степени подобных членов складываются, а коэффициенты умножаются.
Выражение можно сократить на , если на него делятся все коэффициенты многочлена. Проверьте, нет или в заданном примере общего делителя. Для этого найдите для всех число, на которое нацело поделится каждый из них. Выполните деление всех коэффициентов многочлена.
Выполните деление всех коэффициентов многочлена.
Если для решения примера задано значение буквенной переменной, подставьте ее в преобразованное выражение. Посчитайте результат и запишите. Пример решен.
В наше время всеобщей компьютеризации и высоких технологий невозможно обойтись без хорошего знания математики. Представителям многих профессий необходимо умение считать, думать, находить логические и рациональные решения задач. Основы понимания математики закладываются ещё во время обучения в школе. Современному школьнику в решении множества математических задач, уравнений или примеров помогает разработанный порядок или алгоритм выполнения действий.
Инструкция
Определите порядок выполнения действий, опираясь на следующее — если выражение содержит первой ступени (сложение и / или вычитание) и второй (умножение и / или деление) и в нем есть скобки, как в вашем случае, то сначала выполните действия , а затем действия второй ступени, то есть найдите значение выражения:
Следуйте порядку выполнения действий, вычислите значение выражения:
Для этого найдите произведение десятичной дроби 8,9 на натуральное число 6. Не обращайте внимания на запятую, а затем в полученном произведении отделите справа столько цифр, их отделено запятой дроби. Таким образом, получите 53,4.
Не обращайте внимания на запятую, а затем в полученном произведении отделите справа столько цифр, их отделено запятой дроби. Таким образом, получите 53,4.
Для этого разделите 19,2 на натуральное число 8. Не обращайте внимания на запятую, поставьте в частном запятую тогда, когда кончится деление целой части. Помните, если целая будет меньше делителя, то частное должно начинаться с нуля. Таким образом, получите 2,4
Cумму 90, полученную при выполнении действий в скобках, умножьте на 2, получите 180.
Выполните действия первой ступени по порядку слева направо, вычислите 53,4+180-2,4. Итак, значение выражения равно 231.
Умение решать примеры немаловажно в нашей жизни. Без знания алгебры трудно представить существование бизнеса, работу бартерных систем. Поэтому школьная программа и содержит большой объем алгебраических задач и уравнений, в том числе их систем.
Инструкция
Вспомните, что равенство, содержащее одну или ряд переменных. Если представлено два и больше уравнений, в которых нужно вычислить общие решения, то это система уравнений. Объединение этой системы с помощью фигурной скобки и , что должно производиться одновременно. Решением системы уравнений являются множество пар чисел. Способов решения системы линейных уравнений (то есть системы, объединяющей несколько линейных уравнений) существует несколько.
Если представлено два и больше уравнений, в которых нужно вычислить общие решения, то это система уравнений. Объединение этой системы с помощью фигурной скобки и , что должно производиться одновременно. Решением системы уравнений являются множество пар чисел. Способов решения системы линейных уравнений (то есть системы, объединяющей несколько линейных уравнений) существует несколько.
Рассмотрите представленный вариант решения системы линейных уравнений :
х – 2у=4
7у — х =1Для начала выразите переменную х через переменную у:
х=2у+4Подставьте в уравнение 7у — х=1 вместо х полученную сумму (2у+4) и получите следующее уравнение, которое с легкостью решите:
7у — (2у+4)=1
7у – 2у — 4 = 1
5у = 5
у=1Выполните подстановку вычисленного значения переменной у и вычислите значение переменной х:
х=2у+4, при у=1
х=6Запишите ответ: х=6, у=1.
Для сравнения решите эту же систему линейных уравнений способом сравнения. Выразите одну переменную через другую в каждом из уравнений:Приравняйте выражения, полученные для одноимённых переменных:
х = 2у+4
х = 7у — 1Найти значение одной из переменных, решив представленное уравнение:
2у+4 = 7у — 1
7у-2у=5
5у=5
у=1Подставив результат найденной переменной в исходное выражений для другой переменной, найдите её значение:
х=2у+4
х=6
Наконец, запомните, что систему уравнений можно и методом сложения. Рассмотрите решение следующей системы линейных уравнений
Рассмотрите решение следующей системы линейных уравнений
7х+2у=1
17х+6у=-9Уравняйте модули коэффициентов при -нибудь переменной (в данном случае по модулю 3):
-21х-6у=-3
17х+6у=-9Выполните почленное сложение уравнения системы, получите и вычислите значение переменной:
— 4х = — 12
х=3Составьте вновь систему: уравнение новое, второе — одно из старых
7х+2у=1
— 4х = — 12Подставив значение х в оставшееся уравнение, найдите значение переменной у:
7х+2у=1
7 3+2у=1
21+2у=1
2у=-20
у=-10Запишите ответ: х=3, у=-10.
Видео по теме
Умножение — одна из четырех основных математических операций, которая лежит в основе многих более сложных функций. При этом фактически умножение основывается на операции сложения: знание об этом позволяет правильно решить любой пример.
Для понимания сущности операции умножения необходимо принять во внимание, что в ней участвуют три основных компонента. Один из них носит название первого множителя и представляет собой число, которое подвергается операции умножения. По этой причине у него имеется второе, несколько менее распространенное название — «множимое». Второй компонент операции умножения принято называть вторым множителем: он представляет собой число, на которое умножается множимое. Таким образом, оба эти компонента носят название множителей, что подчеркивает их равноправный статус, а также то, что их можно поменять местами: результат умножения от этого не изменится. Наконец, третий компонент операции умножения, получающийся в ее результате, носит название произведения.
По этой причине у него имеется второе, несколько менее распространенное название — «множимое». Второй компонент операции умножения принято называть вторым множителем: он представляет собой число, на которое умножается множимое. Таким образом, оба эти компонента носят название множителей, что подчеркивает их равноправный статус, а также то, что их можно поменять местами: результат умножения от этого не изменится. Наконец, третий компонент операции умножения, получающийся в ее результате, носит название произведения.
Порядок операции умножения
Сущность операции умножения основывается на более простом арифметическом действии — . Фактически умножение представляет собой суммирование первого множителя, или множимого, такое количество раз, которое соответствует второму множителю. Например, для того, чтобы умножить 8 на 4 необходимо 4 раза сложить число 8, получив в результате 32. Этот способ, помимо обеспечения понимания сущности операции умножения, можно использовать для проверки результата, получившегося при вычислении искомого произведения. При этом следует иметь в виду, осуществление проверки обязательно предполагает, что слагаемые, участвующие в суммировании, одинаковы и соответствуют первому множителю.
При этом следует иметь в виду, осуществление проверки обязательно предполагает, что слагаемые, участвующие в суммировании, одинаковы и соответствуют первому множителю.Решение примеров на умножение
Таким образом, для того, чтобы решить , связанный с необходимостью осуществления умножения, может быть достаточно заданное количество раз сложить необходимое число первых множителей. Такой способ может быть удобен для осуществления практически любых расчетов, связанных с этой операцией. Вместе с тем, в математике достаточно часто встречаются типовые примерыОперация умножения чисел
В операции умножения участвуют три основных элемента. Первый из них, который обычно называют первым множителем или множимым, представляет собой число, которое будет подвергнуто операции умножения. Второй, который именуют вторым множителем, является числом, на которое будет умножен первый множитель. Наконец, результат осуществленной операции умножения чаще всего носит название произведения.При этом следует помнить, что сущность операции умножения фактически основывается на сложении: для ее осуществления необходимо сложить между собой определенное количество первых множителей, причем количество слагаемых этой суммы должно быть равно второму множителю. Помимо вычисления самого произведения двух рассматриваемых множителей, этот алгоритм можно использовать также для проверки получившегося результата.
Помимо вычисления самого произведения двух рассматриваемых множителей, этот алгоритм можно использовать также для проверки получившегося результата.
Пример решения задания на умножение
Рассмотрим пример решения задачи на умножение. Предположим, по условиям задания необходимо вычислить произведение двух чисел, среди которых первый множитель равен 8, а второй 4. В соответствии с определением операции умножения, это фактически означает, что нужно 4 раза сложить цифру 8. В результате получается 32 — это и есть произведение рассматриваемых чисел, то есть результат их умножения.Кроме того, необходимо помнить, что в отношении операции умножения действует так называемый переместительный закон, который устанавливает, что от изменения мест множителей в первоначальном примере его результат не изменится. Таким образом, можно 8 раз сложить цифру 4, получив в результате то же произведение — 32.
Таблица умножения
Понятно, что решать таким способом большое количество однотипных примеров — довольно утомительное занятие. Для того чтобы облегчить эту задачу, была придумана так называемая умножения. Фактически она представляет собой перечень произведений целых положительных однозначных чисел. Проще говоря, таблица умножения — это совокупность результатов перемножения между собой от 1 до 9. Один раз выучив эту таблицу, можно уже не прибегать к осуществлению умножения всякий раз, когда потребуется решить пример на такие простые числа, а просто вспомнить его результат.
Для того чтобы облегчить эту задачу, была придумана так называемая умножения. Фактически она представляет собой перечень произведений целых положительных однозначных чисел. Проще говоря, таблица умножения — это совокупность результатов перемножения между собой от 1 до 9. Один раз выучив эту таблицу, можно уже не прибегать к осуществлению умножения всякий раз, когда потребуется решить пример на такие простые числа, а просто вспомнить его результат.Видео по теме
Инструкция
Так называемые «круговые примеры» относятся именно к таким заданиям, в которых надо не просто складывать, вычитать и умножать, но и выстроить логический ряд. Детям задается некоторое количество примеров, которые они должны выполнить в правильной последовательности.Правила круговых примеров таковы.
Все примеры даются вперемешку. Ответ одного примера служит началом для последующего. Из общего количества примеров задания выбираются именно таким образом и выстраиваются в цепочку (столбик).
Не получив правильного результата, невозможно решить следующий пример и правильно составить цепочку. Ответ последнего примера является началом первого,…
Ответ последнего примера является началом первого,…
0 0
Современная математика для школьников младших классов включает в себя основы алгебры и геометрии. Не зря от родителей первоклашек требуют, чтобы они обучили своих детей навыкам устного счета до 10, а также научили их классифицировать предметы по признакам.
Спонсор размещения P&G Статьи по теме «Как решать круговые примеры» Как решить егэ по математике Как найти коэффициент подобия Как сдать высшую математику
Инструкция
Сегодняшние учебники для 1 и 2 классов заполнены такими заданиями, над которыми ломают головы папы и мамы учеников младших классов. Однако у самих учеников примеры и задачи не вызывают затруднений, поскольку наряду с обычными математическими действиями на уроках математики обучают и началам математической логики.
Так называемые «круговые примеры» относятся именно к таким заданиям, в которых надо не просто складывать, вычитать и умножать, но и выстроить логический ряд. Детям задается некоторое количество примеров, которые они…
Детям задается некоторое количество примеров, которые они…
0 0
Сучасна математика для школярів молодших класів включає в себе основи алгебри і геометрії. Не дарма від батьків першокласників вимагають, щоб вони навчили своїх дітей навичкам усного рахунку до 10, а також навчили їх класифікувати предмети за ознаками.
Інструкція
Сьогоднішні підручники для 1 і 2 класів заповнені такими завданнями, над якими ламають голови тата й мами учнів молодших класів. Однак у самих учнів приклади і завдання не викликають утруднень, оскільки поряд зі звичайними математичними діями на уроках математики навчають та початків математичної логіки.
Так звані «кругові приклади » відносяться саме до таких завданням, в яких треба не просто складати, віднімати і множити, а й вибудувати логічний ряд. Дітям задається деяка кількість прикладів, які вони повинні виконати в правильній последовательности.Правила кругових прикладів такі.
Все приклади даються упереміш. Відповідь одного прикладу служить початком. ..
..
0 0
Как вам такие, кстати из реального учебника, издательства Эксмо. Задачкиуже с правильными ответами))))
1. У стола отпилили один угол. Сколько углов у него теперь?
— Вероятно, на один больше. Хотя, не исключаю, что автор задачки имел в виду обратное. Стол мог быть круглый)))
2. В тарелке лежали три морковки и четыре яблока. Сколько фруктов было в тарелке?
— Вопрос, как я понимаю из ботаники?
3. В люстре горело пять лампочек. Две из них погасли. Сколько лампочек осталось в люстре?
— Ответ очевиден – столько же, сколько и было, т.е. пять.
4. У мамы дочка Даша, сын Саша, собака Дружок и кот Пушок. Сколько детей у мамы?
— Вообще-то, я встречал людей, которые своих кошек и собак именуют не иначе, как своими детками, покупают им особняки, завещают им свои состояния. А потому, для решения этой задачи необходима дополнительная информация о маме, её психологический портрет.
5. В коридоре стоят 8 башмаков. Сколько детей играет в комнате?
-. ..
..
0 0
Круговые примеры. 500. +70. +200. 570. +30. 300. 600. -200. +100. 200. 400. +100. +500. 900. 100. -300. +30. 70. 600. 770. 620. -700. 710. 720. +20. +60. +100. -10.
Слайд 7 из презентации «Путешествие по космосу». Размер архива с презентацией 496 КБ.
Скачать презентацию
Математика 3 класс
краткое содержание других презентаций«Деление круглых чисел» — Сведений науки не следует сообщать учащемуся. Включение в систему знаний и повторение. Мотивация. Проверим себя. Самостоятельная работа с самопроверкой по эталону. Планируемый результат. Собираем рюкзачок. Построение проекта выхода из затруднения. Актуализация и фиксирование индивидуального затруднения в пробном действии. Поставь вопрос к задаче. Первичное закрепление с проговариванием во внешней речи.
«Единицы времени 3 класс» — Перекидной календарь. Отрывной календарь. С чем пришел он к нам ребята. Год. Третий гость на солнце весел, а в тени всегда сердит. С какими гостями пришёл знайка. Настольный…
Настольный…
0 0
c # — что такое циклическая зависимость и как ее решить?
Что такое зависимость?
Чтобы понять, что такое циклическая зависимость, лучше понять, что такое зависимость и что она означает для компилятора.
Допустим, у вас есть проект, и в классе у вас определено следующее:
Открытый класс MyClass
'Здесь код
Частная MyString как строка
'Какой-то код там
Конец класса
При компиляции вашего проекта компилятор запускает класс String, который определен в файле DLL с именем System.Затем он свяжет эту DLL с вашим проектом, поэтому во время выполнения, при определении или выполнении операции со строкой, будет загружена System.dll для их выполнения.
Теперь предположим, что в вашем классе есть следующее определение
'Здесь какой-то код
Частный MyObjet как CustomClass1
'Какой-то код там
Допустим, CustomClass1 определен в другом вашем проекте под названием Project2. DLL:
DLL:
Открытый класс CustomClass1
'Код вашего пользовательского класса
Конец класса
Итак, при компиляции вашего первого проекта компилятор столкнется с определением CustomClass1 , он знает, что оно лежит в Project2.dll и, следовательно, скомпилирует Project2 раньше, чтобы иметь возможность добавить эту ссылку в свой первый проект.
Вот что такое зависимость, она иерархическая, должна быть отправная точка. Даже класс String зависит от других классов, и, в конце концов, все они полагаются на байты или биты для выполнения своей работы, потому что это единственное, что может сделать компьютер — играть с 1 и 0 .
Так круглая часть
Итак, если у вас есть в Project2 ссылка (определение поля или что-то в этом роде), которая ссылается на ваш первый проект, что произойдет?
- Компилятор читает ваш первый проект, затем запускает
CustomClass1 - Затем он пытается скомпилировать Project2, поскольку CustomClass1 определен там
- Затем он запускается в класс, определенный в вашем первом проекте
- Он пытается скомпилировать ваш первый проект, чтобы связать его со вторым
- Затем он переходит к
CustomClass1 - Потом попытался скомпилировать Project2
- Думаю, вы поняли.
 ..
..
Итак, в какой-то момент компилятор выдает ошибку, говоря, что он не может скомпилировать, так как не понимает, что вы пытаетесь сделать …
Да, компьютеры такие тупые.
Как решить?
Иногда бывает сложно решить такие проблемы, но основная идея состоит в том, чтобы построить иерархическую структуру, собрать вместе базовые классы (те, которые не нуждаются в зависимостях), а затем построить их.
Возьмите все классы, которые зависят друг от друга, и соедините их вместе, они образуют слой для того, что вы пытаетесь сделать в своем приложении.
Еще одно решение, позволяющее выбраться из круговой дыры при импорте в Python
Проблема циклического импорта в Python.
Некоторый модуль foo импортирует модуль bar , но bar также импортирует foo .
Само по себе это не обязательно проблема. Python позволяет это.
В зависимости от того, как взаимодействуют оба модуля,
вы можете даже не заметить, что в цепочке зависимостей есть цикл.
Однако, если у вас возникнет проблема, это может привести к серьезному выдергиванию волос.
В сети достаточно мест, где подробно рассказывается об этой проблеме, играть в виноватую («плохой дизайн!») и предлагать возможные решения. Эти решения имеют разную степень уродства или архитектурного зуда: переосмыслить вашу связь / зависимости, ввести абстрактные интерфейсы, объединять модули, разделять модули, использовать локальный импорт, отложить импорт и т. д. Иногда более чистый дизайн или лучшая развязка действительно могут вас выручить круглого импортного отверстия. Но иногда присуща круговая зависимость и единственный выход — уродливые хаки.Но мы отвлеклись.
Циркулярный импорт и хинтинг
Поскольку я начал использовать тип , намекая еще , я заметил, что он
легче попасть в неприятности с круговым импортом.
Это не так уж и неожиданно, поскольку подсказки типа класса обычно требуют от вас большего импорта.
Кроме того, они должны быть импортированы на верхнем уровне. поэтому вы не можете использовать уловки с локальным или отложенным импортом.
поэтому вы не можете использовать уловки с локальным или отложенным импортом.
Пример
Когда у вас есть проблема с циклическим импортом только из-за подсказки типа, есть менее известное решение, которое я хочу показать здесь.
Давайте возьмем этот простой искусственный пример с двумя модулями, которые
нужны друг другу: connection.py определяет интерфейс к чему-то
как REST API, и он может создавать какой-то объект в этом API, называемый Thing :
# connection.py
из вещи импортная вещь
класс ApiConnection:
def get_thing (self) -> Вещь:
вернуть вещь (соединение = сам)
Это Thing (определено в thing.py ) сохраняет ссылку на соединение
чтобы операции с Thing можно было отправлять в API.
# thing.py
из импорта соединения ApiConnection
класс Вещь:
def __init __ (сам, соединение: ApiConnection):
self._conn = соединение
Неудивительно, что круговая зависимость здесь приведет к сбою, в результате получается классическая циклическая трассировка стека импорта, например:
Файл "main.py" из импорта соединения ApiConnection Файл "connection.py" из вещи импортная вещь Файл "thing.py" из импорта соединения ApiConnection ImportError: невозможно импортировать имя 'ApiConnection' из 'соединения'
В шт.py , импорт модуля подключения существует только для подсказки типа ApiConnection .
Это означает, что если вас не слишком заботит этот тип подсказки,
вы могли бы бросить его, чтобы разорвать цикл гибели.
Условный импорт для подсказок типов
Менее известным решением для этого случая является использование условного импорта который активен только в «режиме подсказки типов», но не мешает во время выполнения.
Тип .TYPE_CHECKING постоянная делает это легко возможным.В нашем примере мы меняем thing.py на:
# thing.py
от ввода импорта TYPE_CHECKING
если TYPE_CHECKING:
из импорта соединения ApiConnection
класс Вещь:
def __init __ (сам, соединение: 'ApiConnection'):
self. _conn = соединение
_conn = соединение
Код теперь будет выполняться правильно, так как больше нет проблемы циклического импорта.
Инструменты подсказки, с другой стороны, должны быть
может разрешить подсказку типа ApiConnection в Thing .__ init__ .Моя текущая IDE (PyCharm), например, отлично подходит для функций анализа кода.
К сожалению, подсказка типа должна быть указана как строка «прямой ссылки»
что немного уродливее, чем подсказка обычного типа.
Однако, начиная с Python 3.7, благодаря отложенной оценке аннотаций
PEP563
можно указать подсказку типа без кавычек, но для этого сначала потребуется дополнительный импорт:
из аннотаций импорта __future__
4.5: Равномерное круговое движение — Physics LibreTexts
Цели обучения
- Найдите центростремительное ускорение объекта, движущегося по круговой траектории.
- Используйте уравнения кругового движения, чтобы найти положение, скорость и ускорение частицы, совершающей круговое движение.

- Объясните разницу между центростремительным ускорением и тангенциальным ускорением, возникающим в результате неравномерного кругового движения.
- Оцените центростремительное и тангенциальное ускорение при неравномерном круговом движении и найдите вектор полного ускорения.
Равномерное круговое движение — это особый тип движения, при котором объект движется по кругу с постоянной скоростью.Например, любая точка пропеллера, вращающегося с постоянной скоростью, совершает равномерное круговое движение. Другие примеры — секундная, минутная и часовая стрелки часов. Примечательно, что точки на этих вращающихся объектах действительно ускоряются, хотя скорость вращения постоянна. Чтобы увидеть это, мы должны проанализировать движение в терминах векторов.
Центростремительное ускорение
В одномерной кинематике объекты с постоянной скоростью имеют нулевое ускорение. Однако в двух- и трехмерной кинематике, даже если скорость постоянна, частица может иметь ускорение, если она движется по криволинейной траектории, такой как окружность. В этом случае вектор скорости меняется, или \ (\ frac {d \ vec {v}} {dt} \) ≠ 0. Это показано на рисунке \ (\ PageIndex {1} \). Поскольку частица движется против часовой стрелки во времени \ (\ Delta \) t по круговой траектории, ее вектор положения перемещается из \ (\ vec {r} (t) \) в \ (\ vec {r} (t + \ Delta t ) \). Вектор скорости имеет постоянную величину и касается пути, когда он изменяется с \ (\ vec {v} \) (t) на \ (\ vec {v} \ left (t + \ Delta t \ right) \), только меняя свое направление. Поскольку вектор скорости \ (\ vec {v} (t) \) перпендикулярен вектору положения \ (\ vec {r} \) (t), треугольники, образованные векторами положения и \ (\ Delta \ vec { r} \), а векторы скорости и \ (\ Delta \ vec {v} \) аналогичны.Кроме того, с
В этом случае вектор скорости меняется, или \ (\ frac {d \ vec {v}} {dt} \) ≠ 0. Это показано на рисунке \ (\ PageIndex {1} \). Поскольку частица движется против часовой стрелки во времени \ (\ Delta \) t по круговой траектории, ее вектор положения перемещается из \ (\ vec {r} (t) \) в \ (\ vec {r} (t + \ Delta t ) \). Вектор скорости имеет постоянную величину и касается пути, когда он изменяется с \ (\ vec {v} \) (t) на \ (\ vec {v} \ left (t + \ Delta t \ right) \), только меняя свое направление. Поскольку вектор скорости \ (\ vec {v} (t) \) перпендикулярен вектору положения \ (\ vec {r} \) (t), треугольники, образованные векторами положения и \ (\ Delta \ vec { r} \), а векторы скорости и \ (\ Delta \ vec {v} \) аналогичны.Кроме того, с
\ [| \ vec {r} (t) | = | \ vec {r} (t + \ Delta t) | \ nonumber \]
и
\ [| \ vec {v} (t) | = | \ vec {v} (t + \ Delta t) |, \ nonumber \]
два треугольника равнобедренные. Из этих фактов мы можем сделать утверждение
\ [\ dfrac {\ Delta v} {v} = \ dfrac {\ Delta r} {r} \]
или
\ [\ Delta v = \ dfrac {v} {r} \ Delta r. {2}} {r} \ ldotp \ label {4.27} \]
{2}} {r} \ ldotp \ label {4.27} \]
Направление вектора ускорения — к центру круга (рис. \ (\ PageIndex {2} \)). Это радиальное ускорение, которое называется центростремительным ускорением , поэтому мы даем ему индекс \ (c \). Слово центростремительный происходит от латинских слов centrum (что означает «центр») и petere (что означает искать ») и, таким образом, принимает значение« поиск центра ».
Рисунок \ (\ PageIndex {2} \): Вектор центростремительного ускорения указывает на центр круговой траектории движения и представляет собой ускорение в радиальном направлении.Также показан вектор скорости, касающийся окружности.Давайте рассмотрим несколько примеров, которые иллюстрируют относительные величины скорости, радиуса и центростремительного ускорения.
Пример \ (\ PageIndex {1} \): создание ускорения на 1 g
Самолет летит со скоростью 134,1 м / с по прямой и делает разворот по круговой траектории на уровне земли. Каким должен быть радиус окружности, чтобы вызвать центростремительное ускорение в 1 g для пилота и струи по направлению к центру круговой траектории?
Каким должен быть радиус окружности, чтобы вызвать центростремительное ускорение в 1 g для пилота и струи по направлению к центру круговой траектории?
Стратегия
Учитывая скорость струи, мы можем найти радиус круга в выражении для центростремительного ускорения.{2}} = 1835 \; m = 1,835 \; км \ ldotp \]
Значение
Чтобы создать у пилота большее ускорение, чем g, струе придется либо уменьшить радиус своей круговой траектории, либо увеличить скорость по существующей траектории, либо и то, и другое.
Упражнение 4.5
Радиус маховика 20,0 см. Какова скорость точки на краю маховика, если она испытывает центростремительное ускорение 900,0 см / с 2 ?
Центростремительное ускорение может иметь широкий диапазон значений в зависимости от скорости и радиуса кривизны круговой траектории.Типичные центростремительные ускорения приведены в таблице \ (\ PageIndex {1} \).
| Объект | Центростремительное ускорение (м / с 2 или g) |
|---|---|
| Земля вокруг Солнца | 5,93 x 10 -3 |
| Луна вокруг Земли | 2,73 x 10 -3 |
| Спутник на геостационарной орбите | 0.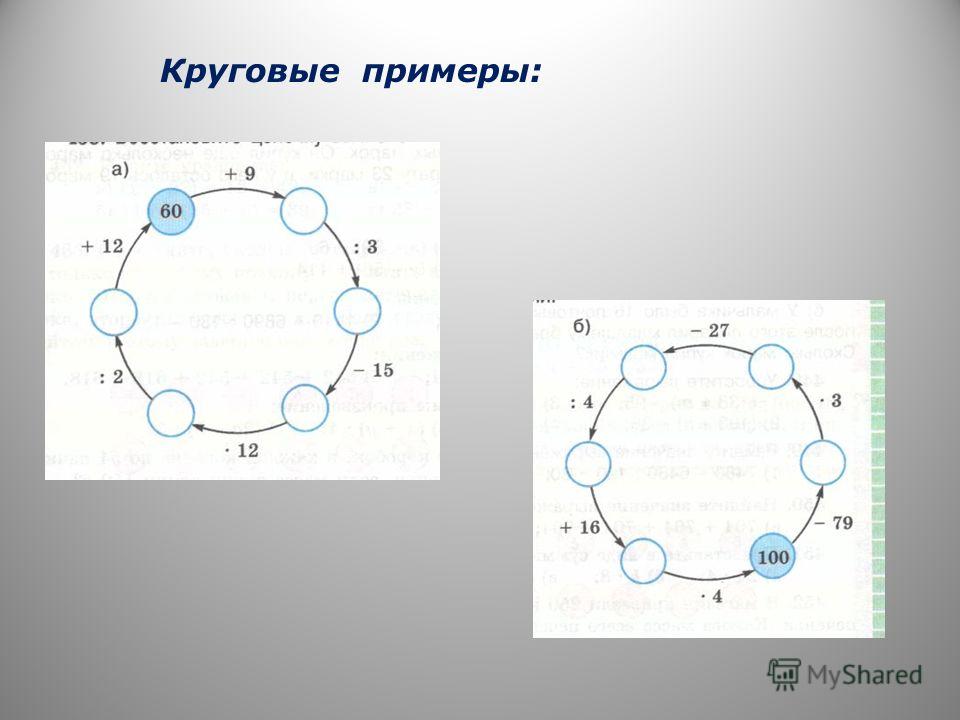 233 233 |
| Внешний край компакт-диска при воспроизведении | 5,75 |
| Струя в бочке рулона | (2-3 г) |
| Американские горки | (5 г) |
| Электрон, вращающийся вокруг протона в простой модели атома Бора | 9,0 x 10 22 |
Уравнения движения для равномерного кругового движения
Частица, совершающая круговое движение, может быть описана ее вектором положения \ (\ vec {r} (t) \).На рисунке \ (\ PageIndex {3} \) показана частица, совершающая круговое движение против часовой стрелки.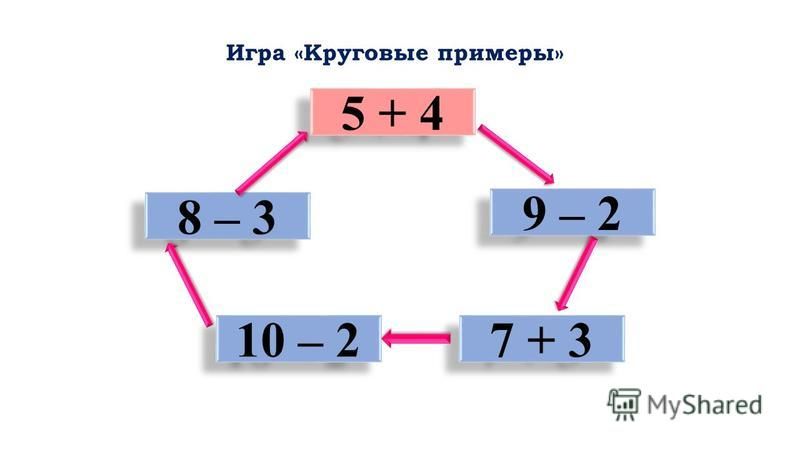 Когда частица движется по окружности, ее вектор положения сметает угол \ (\ theta \) с осью x. Вектор \ (\ vec {r} (t) \), образующий угол \ (\ theta \) с осью x, показан вместе со своими компонентами вдоль осей x и y. Величина вектора положения равна \ (A = | \ vec {r} (t) | \), а также является радиусом круга, так что с точки зрения его компонентов,
Когда частица движется по окружности, ее вектор положения сметает угол \ (\ theta \) с осью x. Вектор \ (\ vec {r} (t) \), образующий угол \ (\ theta \) с осью x, показан вместе со своими компонентами вдоль осей x и y. Величина вектора положения равна \ (A = | \ vec {r} (t) | \), а также является радиусом круга, так что с точки зрения его компонентов,
\ [\ vec {r} (t) = A \ cos \ omega \ hat {i} + A \ sin \ omega t \ hat {j} \ ldotp \ label {4.28} \]
Здесь \ (\ omega \) — постоянная, называемая угловой частотой частицы. Угловая частота измеряется в радианах (рад) в секунду и представляет собой просто количество радианов угловой меры, через которую проходит частица за секунду. Угол \ (θ \), который вектор положения имеет в любой конкретный момент времени, равен \ (\ omega \) t.
Если \ (T \) — период движения или время, чтобы совершить один оборот (\ (2 \ pi \, rad \)), то
Рисунок \ (\ PageIndex {3} \): вектор положения частицы, движущейся по кругу, с ее компонентами по осям x и y. Частица движется против часовой стрелки. Угол \ (\ theta \) — угловая частота \ (\ omega \) в радианах в секунду, умноженная на \ (t \).
Частица движется против часовой стрелки. Угол \ (\ theta \) — угловая частота \ (\ omega \) в радианах в секунду, умноженная на \ (t \).Скорость и ускорение можно получить из функции положения путем дифференцирования:
\ [\ vec {v} (t) = \ frac {d \ vec {r} (t)} {dt} = -A \ omega \ sin \ omega t \ hat {i} + A \ omega \ cos \ омега т \ шляпа {j} \ ldotp \ label {4.29} \]
Из рисунка \ (\ PageIndex {3} \) видно, что вектор скорости касается окружности в месте нахождения частицы и имеет величину A \ (\ omega \).{2} \ vec {r} \) (t).
Пример \ (\ PageIndex {2} \): круговое движение протона
Протон имеет скорость 5 x 10 6 м / с и движется по окружности в плоскости xy радиуса r = 0,175 м. Каково его положение в плоскости xy в момент времени t = 2,0 x 10 −7 с = 200 нс? При t = 0 положение протона составляет 0,175 м \ (\ hat {i} \), и он вращается против часовой стрелки. Набросайте траекторию.
Решение
По приведенным данным протон имеет период и угловую частоту:
\ [T = \ frac {2 \ pi r} {v} = \ frac {2 \ pi (0. {−7} \, мс = 200 \, нс \). Показана траектория протона. Угол, под которым протон движется по окружности, составляет 5,712 рад, что немного меньше одного полного оборота.
{−7} \, мс = 200 \, нс \). Показана траектория протона. Угол, под которым протон движется по окружности, составляет 5,712 рад, что немного меньше одного полного оборота.
Значение
Мы выбрали начальное положение частицы по оси абсцисс. Это было совершенно произвольно. Если бы была задана другая начальная позиция, у нас было бы другое конечное положение при t = 200 нс.
Неравномерное круговое движение
Круговое движение не обязательно должно иметь постоянную скорость.Частица может двигаться по кругу и ускоряться или замедляться, показывая ускорение в направлении движения.
При равномерном круговом движении частица, совершающая круговое движение, имеет постоянную скорость, а круг имеет фиксированный радиус. Если скорость частицы тоже меняется, то мы вводим дополнительное ускорение в направлении, касательном к окружности. Такое ускорение происходит в точке на вершине, которая изменяет скорость вращения, или в любом ускоряющем роторе. В работе «Векторы смещения и скорости» мы показали, что центростремительное ускорение — это скорость изменения направления вектора скорости во времени.Если скорость частицы изменяется, то она имеет тангенциальное ускорение , то есть скорость изменения величины скорости во времени:
В работе «Векторы смещения и скорости» мы показали, что центростремительное ускорение — это скорость изменения направления вектора скорости во времени.Если скорость частицы изменяется, то она имеет тангенциальное ускорение , то есть скорость изменения величины скорости во времени:
\ [a_ {T} = \ frac {d | \ vec {v} |} {dt} \ ldotp \ label {4.31} \]
Направление тангенциального ускорения касается окружности, а направление центростремительного ускорения — радиально внутрь к центру окружности. Таким образом, частица, движущаяся по кругу с тангенциальным ускорением, имеет полное ускорение , которое является векторной суммой центростремительного и тангенциального ускорений:
\ [\ vec {a} = \ vec {a} _ {c} + \ vec {a} _ {T} \ ldotp \ label {4.32} \]
Векторы ускорения показаны на рисунке \ (\ PageIndex {5} \). Обратите внимание, что два вектора ускорения \ (\ vec {a} _ {c} \) и \ (\ vec {a} _ {T} \) перпендикулярны друг другу, причем \ (\ vec {a} _ {c } \) в радиальном направлении и \ (\ vec {a} _ {T} \) в тангенциальном направлении. Общее ускорение \ (\ vec {a} \) указывает под углом между \ (\ vec {a} _ {c} \) и \ (\ vec {a} _ {T} \).
Общее ускорение \ (\ vec {a} \) указывает под углом между \ (\ vec {a} _ {c} \) и \ (\ vec {a} _ {T} \).
Каково полное ускорение частицы при t = 2,0 с?
Стратегия
Нам даны скорость частицы и радиус круга, поэтому мы можем легко вычислить центростремительное ускорение. Направление центростремительного ускорения — к центру круга. Мы находим величину тангенциального ускорения, взяв производную по времени от | v (t) | используя уравнение \ ref {4.{2} \]
и \ (\ theta \) = tan −1 \ (\ left (\ dfrac {3.1} {1.5} \ right) \) = 64 ° от касательной к окружности. См. Рисунок \ (\ PageIndex {6} \).
Рисунок \ (\ PageIndex {6} \): векторы тангенциального и центростремительного ускорения. Чистое ускорение \ (\ vec {a} \) — это векторная сумма двух ускорений.
Чистое ускорение \ (\ vec {a} \) — это векторная сумма двух ускорений.Значение
Направления центростремительного и тангенциального ускорений можно описать более удобно в терминах полярной системы координат с единичными векторами в радиальном и тангенциальном направлениях.Эта система координат, которая используется для движения по криволинейным траекториям, подробно обсуждается далее в книге.
Авторы и ссылки
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими участвующими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Как исправить ошибку «Обнаружена циклическая зависимость» в Google Таблицах
Ошибка «Обнаружена циклическая зависимость» в Google Таблицах — очень распространенная ошибка, которая может возникать при использовании практически любой формулы.Когда вы видите ошибку, обнаруженную циклической зависимостью, отображаемую в вашей электронной таблице Google, это означает, что ваша формула относится к диапазону, содержащему саму формулу, или, другими словами, когда ввод формулы зависит от вывода.
Чтобы исправить обнаруженную ошибку циклической зависимости в Google Таблицах, внесите в таблицу одно из следующих изменений:
- Переместите формулу в другую ячейку, которая не входит в диапазон (диапазоны), к которому формула относится
- Или измените ссылку в своей формуле так, чтобы она не ссылалась на диапазон, содержащий саму формулу
Ошибки круговой зависимости также могут возникать, когда две формулы относятся к диапазону, в котором находится другая формула, в , даже если формула не относится к самой себе (т.е. собственное местонахождение). Точно так же, как ввод одной формулы не может зависеть от данных, которые определяются ее собственным выводом, две формулы не могут одновременно зависеть от вывода друг друга. Это может вызвать запутанную ситуацию, когда одна неправильная формула вызывает две ошибки формулы.
В этой статье я рассмотрю несколько различных примеров того, как вы можете столкнуться с этой ошибкой, обнаруженной циклической зависимостью, в Google Таблицах, а также покажу вам, как исправить ошибку в каждой ситуации.
Когда в вашей электронной таблице возникает ошибка циклической зависимости, в ячейке, содержащей ошибку формулы, в верхнем правом углу отображается небольшой красный треугольник, а в тексте ячейки будет сказано: « #REF! ».
При наведении курсора на ячейку с этой ошибкой появится всплывающее окно, в котором отображается следующее сообщение, как показано на рисунке ниже:
«Обнаружена круговая зависимость. Чтобы разрешить с помощью итеративного вычисления, см. Файл> Настройки электронной таблицы.»
Обычно вам НЕ нужно на самом деле настраивать параметры электронной таблицы, чтобы исправить эту ошибку, поскольку в большинстве случаев ошибка устраняется путем корректировки ссылок на формулы и местоположения, в котором находится формула.
Если формула находится внутри диапазона, на который она ссылается, это означает, что ввод формулы «зависит» от вывода, который невозможно вычислить, и вызывает ошибку.
Вот аналогия, помогающая объяснить ошибку.Это как если бы вам дали следующую математическую задачу:
Вопрос 1: Разделите 10 на ответ на вопрос 1.
Это невозможно решить, потому что результат / ответ не могут быть известны до того, как проблема будет фактически решена.
Или в случае двух формул, которые относятся к выходу / местоположению друг друга, вот еще одна аналогия. Это как если бы вам дали две следующие математические задачи:
Вопрос 1: Каков ответ на вопрос 2?
Вопрос 2: Каков ответ на вопрос 1?
Опять же, это не решаемо.Ответ на каждый вопрос зависит от другого, что заставляет ваш ум кружиться… отсюда и фраза «круговая зависимость».
Не позволяйте этому запутаться, потому что дело в том, что эта логика вызывает ошибку. Все, что вам нужно знать, — это почему это происходит и как это исправить.
Итак, давайте рассмотрим несколько реальных примеров устранения этой ошибки «Обнаружена циклическая зависимость» в вашей электронной таблице Google.
Как исправить обнаруженную ошибку циклической зависимости
Давайте посмотрим на простейший пример обнаруженной ошибки циклической зависимости.
Ниже на изображении показана формула, которая просто относится к одной ячейке. Однако проблема в том, что ячейка, на которую ссылается формула, является ячейкой, в которую вводится формула (формула в ячейке A1 относится к ячейке A1).
Как видите, это вызвало ошибку циклической зависимости.
Следующая формула вызывает ошибку при вводе в ячейку A1:
= A1
Чтобы исправить ошибку, мы можем либо переместить формулу в другую ячейку, либо изменить ссылку в формуле, чтобы она ссылалась на другую ячейку.
В этом случае мы изменим ссылку на ячейку B1.
Как вы можете видеть на изображении ниже, эта настройка устранила ошибку круговой зависимости.
Следующая формула была скорректирована и устраняет ошибку:
= B1
Теперь в ячейке A1 отображается текст, который находится в ячейке B1.
Исправление круговой зависимости при суммировании
Типичная ситуация, когда вы можете столкнуться с ошибкой «Обнаружена циклическая зависимость», — это когда вы суммируете в Google Таблицах.Чаще всего это происходит, когда ваша формула СУММ находится в том же столбце, к которому она относится, и когда ссылка на формулу охватывает весь столбец.
На изображении ниже показана простая формула СУММ, которая пытается суммировать числа в ячейках с A1 по A5.
Но, как видите, формула СУММ относится ко всему столбцу (A). Поскольку формула СУММ вводится в ячейку в столбце A (A6), это вызывает ошибку, обнаруженную циклической зависимостью.
Следующая формула вызывает ошибку при вводе в любом месте столбца A:
= СУММ (A1: A)
Чтобы исправить эту ошибку, мы скорректируем ссылку в формуле так, чтобы она суммировала только значения в ячейках над ней.
Поэтому вместо того, чтобы пытаться суммировать весь столбец, мы обозначим конечную строку в ссылке (строку, которая находится над формулой суммы).
Для этого просто измените диапазон суммы на A1: A5 .
Это исправляет ошибку циклической зависимости, как показано на изображении ниже.
Следующая формула была скорректирована и устраняет ошибку:
= СУММ (A1: A5)
Теперь формула СУММ на изображении выше успешно суммирует ячейки с A1 по A5.(1 + 2 + 3 + 4 + 5 = 15)
Исправление круговой зависимости при фильтрации
В последнем примере нам пришлось скорректировать строки в ссылке на формулу, чтобы исправить ошибку циклической зависимости, но давайте посмотрим на пример, в котором мы скорректируем столбцы в ссылке, чтобы устранить ошибку.
В этом примере предположим, что у нас есть список школьных принадлежностей и их цены, введенные в электронную таблицу, и мы хотим отфильтровать данные с помощью формулы, чтобы отображался список предметов стоимостью более 1 доллара.
Как вы можете видеть на изображении ниже, формула ФИЛЬТР содержит ошибку «Обнаружена циклическая зависимость». Это вызвано ссылкой на исходный диапазон, который на один столбец превышает ширину (с учетом того, где была размещена формула фильтра).
Если формула относится к диапазону A2: D, который содержит столбец D, формулу нельзя поместить в столбец D.
Следующая формула вызывает ошибку при вводе в ячейку D2:
= ФИЛЬТР (A2: D, C2: C> 1)
Чтобы исправить ошибку, показанную на изображении выше, измените диапазон, который относится к исходным данным, с A2: D на A2: C .
После выполнения этой настройки ошибка исправляется, и формула ФИЛЬТРА работает правильно.
Следующая формула была скорректирована и устраняет ошибку:
= ФИЛЬТР (A2: C, C2: C> 1)
Теперь школьные принадлежности фильтруются, чтобы отобразить список предметов стоимостью более 1 доллара.
Этот контент был первоначально создан и написан SpreadsheetClass.com
Исправление циклической зависимости с помощью оператора if / then
Теперь давайте рассмотрим более сложный пример, который может случиться с любым, кто использует формулы в своих электронных таблицах.В этом примере есть две разные формулы, которые взаимодействуют друг с другом, и поскольку одна из них была настроена неправильно, обе отображают ошибку из-за того, что каждая ссылается (зависит) друг от друга.
(Подробнее о том, почему это происходит, см. В начале статьи)
Когда возникает ошибка, подобная той, которая показана на изображении ниже, иногда бывает трудно определить, в какой формуле есть ошибка, из-за двойной ошибки, которую она вызывает.Как и в любом сценарии устранения неполадок… лучше всего начать с самого начала и проследить свой путь через данные / систему, пока не найдете ошибку.
Итак, вот сценарий в этом примере: Столбец A показывает завершение задачи с помощью единиц и нулей. Формулы в столбце B предназначены для ссылки на данные в столбце A и для отображения текста «Да» или «Нет», в зависимости от того, имеет ли каждая ячейка в столбце A номер 1 или номер 0. Затем столбец C относится к ячейкам в столбце B и отображает слова «Завершено» или «Не завершено» в зависимости от того, в каждой ячейке столбца B указано «да» или «нет».
Короче говоря, если ячейка A3 содержит число 1, тогда ячейка B3 должна сказать «Да», а ячейка C3 должна сказать «Завершено».
Но проблема в том, что формула в ячейке B3… вместо того, чтобы ссылаться на 1 и 0 в столбце A, создатель листа допустил ошибку и сослался на столбец C (который, в свою очередь, ссылается на него). Это создает ошибку циклической зависимости в ОБЕИХ формулах, хотя технически только одна из формул была настроена неправильно.
Этот тип смешения часто встречается при использовании большого количества формул в ваших таблицах, особенно когда вы работали весь день и устали.
Чтобы исправить эту формулу, которая исправит обе ошибки циклической зависимости, следуйте инструкциям, приведенным под изображением.
Следующая формула вызывает ошибку при вводе в ячейку B3 из-за другой формулы в ячейке C3, которая относится к ячейке B3:
= ЕСЛИ (C3 = «Завершено», «Да», «Нет»)
В этом случае, чтобы исправить ошибку, нужно не просто изменить ссылку в формуле, потому что вся формула была записана неправильно по ошибке.Поэтому помните, что формулы в столбце B должны отображать слово «Да» в каждой строке / ячейке, если в соседних ячейках столбца A стоит число 1 (и слово «Нет», если в соседней ячейке стоит 0 ).
Исправленная логика для формулы в ячейке B3 выглядит следующим образом: Если ячейка A3 равна 1, отобразить слово «Да», а если нет, отобразить слово «Нет».
Следующая формула была скорректирована и устраняет ошибку:
= ЕСЛИ (A3 = 1, «Да», «Нет»)
Теперь обе формулы работают правильно, и обе ошибки круговой зависимости были исправлены одновременно путем исправления одной формулы.
Теперь столбец B относится к столбцу A, а затем столбец B относится к столбцу C, как и должно быть. Формулы больше не зависят одновременно от результатов друг друга.
Исправить ошибку циклической зависимости при обращении к другой вкладке
Еще один очень распространенный способ столкнуться с ошибкой «Обнаружена циклическая зависимость» — это когда вы ссылаетесь на другую вкладку в своей формуле и забываете включить имя вкладки в свою ссылку.
Приведенные ниже данные показывают список предметов одежды и их размеры, указанные в таблице.Мы хотим отфильтровать данные, используя формулу на другой вкладке, чтобы отображать только те элементы, которые имеют размер «Средний».
На рисунке ниже показана формула ФИЛЬТРА, введенная в ячейку A2, на другой вкладке, чем та, которая содержит исходные данные, показанные выше.
Проблема в том, что при вводе формулы имя вкладки было пропущено.
Так как исходный диапазон — A2: B, а формула находится в ячейке A2, это означает, что формула ссылается на себя. Или, другими словами, ячейка, в которую вводится формула, находится в пределах диапазона, к которому относится формула.Это вызывает ошибку циклической зависимости.
Следующая формула вызывает ошибку при вводе в ячейку A2:
= фильтр (A2: B, B2: B = «Средний»)
Чтобы исправить эту ошибку, просто добавьте имя вкладки к ссылкам в формуле фильтра.
Ссылкой на исходный диапазон будет «Другая вкладка»! A2: B (апострофы должны быть добавлены до и после ссылки на имя вкладки, если в имени вкладки есть пробел).
Следующая формула была скорректирована и устраняет ошибку:
= фильтр («Другая вкладка»! A2: B, «Другая вкладка»! B2: B = «Средний»)
После добавления имени вкладки к ссылкам в формуле ФИЛЬТР ошибка циклической зависимости исчезает, и формула фильтрует правильно, отображая список предметов одежды, которые являются «средними».
Теперь вы знаете, как легко исправить эту ошибку всякий раз, когда она появляется в вашей электронной таблице!
Циклических зависимостей в C ++ | блог pvigier’s
Циклические зависимости в C ++
09 фев 2018 по Пьер
Привет, ребята, прошло много времени с момента последнего поста.
Я пишу этот небольшой пост, чтобы рассказать вам о небольшом скрипте, который я недавно написал. Вы можете найти его здесь, в моей учетной записи github.
Его цель — нарисовать «включаемые» зависимости между классами в проекте C ++. В частности, он позволяет очень легко обнаруживать циклические зависимости или проверять архитектуру проекта.
Вы можете увидеть результат выполнения скрипта в моем проекте:
Мне очень нравится это визуальное представление, которое позволяет увидеть, как взаимодействуют классы.
Однако настоящая причина, по которой я создал этот инструмент, заключается не в том, что мне нравится видеть красивые графики, а в том, что я ненавижу круговые зависимости (обратите внимание, что на графике выше их нет).Я считаю круговые зависимости недостатками дизайна. Но иногда в большом проекте может случиться так, что я случайно создаю круговые зависимости…
Вначале давайте проясним, что такое круговая зависимость.
Предположим, что у вас есть два класса A и B. Если A использует B и наоборот, то существует циклическая зависимость. Однако круговая зависимость может быть более тонкой. Например, это может быть A, который использует B, который использует C, который использует A.
В C ++, если файл «A.h »включает« B.h », тогда« B.h »не может включать« A.h ». Единственный способ для B использовать A — это переадресовать объявление A, использовать указатели или ссылки на A в заголовке и, наконец, включить «A.h» в «B.cpp».
Например, эти три файла должны успешно компилироваться.
А.ч .:
#pragma once
#include "B.h"
класс А
{
частный:
B mB;
};
B.h:
#pragma once
класс А; // предварительное объявление
класс B
{
частный:
А * мА;
};
Б.cpp:
#include "B.h"
#include "A.h" // Мы включаем "A.h" в файл cpp
Это хорошо работает и часто является более простым решением для небольших проектов.
Почему, в конце концов, так много ненависти к циклическим зависимостям?
Я перечислю несколько причин против циклических зависимостей:
- Время компиляции может резко увеличиться: при изменении файла в цикле все остальные файлы придется перекомпилировать.
- Склонен к ошибкам: поскольку несколько фрагментов кода тесно связаны, изменение одного, вероятно, сломает другой.
- Сложнее повторно использовать код: поскольку многие файлы зависят друг от друга, если вы хотите повторно использовать файл в другом проекте, вы должны также использовать другие.
- Сложнее отлаживать: поскольку многие части кода связаны, вам придется просматривать множество файлов, если вы хотите отследить ошибку.
Есть много способов избежать циклических зависимостей. Самый очевидный из них — это хорошо спроектировать проект с независимыми модулями или даже разбить большой проект на меньшие библиотеки.Более того, может быть нормально иметь небольшую циклическую зависимость внутри небольшого модуля / библиотеки, но не во всем проекте.
Паттерны проектирования, такие как внедрение зависимостей, наблюдатель или очередь событий, также могут оказать большую помощь. Кстати, я рекомендую вам взглянуть на «Шаблоны программирования игр» Роберта Нистрома, если вы еще не знакомы с этой книгой.
Наконец, вы можете использовать мой небольшой скрипт для мониторинга архитектуры вашего проекта.
Скрипт довольно простой.Я использую модуль re Python, чтобы найти #include в исходных файлах.
Затем скрипты создают граф и используют порт для Python для графического представления графа. Graphviz создает очень красиво, этот замечательный инструмент также используется, например, Doxygen для создания своей диаграммы.
Вот и все для этого короткого сообщения. Увидимся!
Если вас интересуют мои приключения во время разработки Vagabond, вы можете подписаться на меня в Twitter.
Теги: cpp python
Графические круговые неравенства — Алгебра II
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее то информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Выполните следующие действия, чтобы отправить уведомление:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного расположения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить преподавателям Varsity Tutors найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Ваше заявление: (а) вы добросовестно уверены, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Циркулярные ссылкиExcel — что это такое, как их использовать, примеры и работа со ссылками
Вот небольшой эксперимент, чтобы поразить превосходство.Перейдите в ячейку C3 и напишите = C3 и нажмите Enter. Excel выдавал неприятное сообщение: « Microsoft не знала, что делать. Мы послали инженера службы поддержки к вам домой, но он застрял на объездной дороге возле вашего дома. ”
Ну не совсем. Но когда вы записали формулу = C3 в ячейку C3, вы создали круговую ссылку.
Что такое циркулярный справочник и зачем его использовать?
Циклическая ссылка создается, когда вы прямо или косвенно ссылаетесь на одну и ту же ячейку.
Мы используем циклические ссылки, когда нам нужны циклические ссылки.
Excel Циркулярная ссылка Пример:
Например, (заимствовано из Библии Джона Уокенбаха в Excel 2010), допустим, вы управляете фиктивной компанией Sky is the Ltd.
А у вас странная политика — жертвовать 10% прибыли после уплаты налогов на благотворительность .
Но в вашей стране благотворительные пожертвования не облагаются налогом (это расходы).
Итак, благотворительность = 10% * после налогообложения прибыли
после налогообложения прибыли = (доходы - расходы - благотворительность) * (1-ставка налога)
По определению, благотворительность относится к прибыли после налогообложения, которая относится к благотворительности, таким образом создавая циркулярную ссылку.
Итак, как бы вы узнали, сколько пожертвовать на благотворительность?
Просто, мы пишем формулы с круговыми ссылками, например:
Но подождите, как только вы нажмете клавишу ввода после написания формул, Excel будет кричать кровью и проклинать всю вашу семью за то, что у вас есть круговая ссылка на вашем листе.
Включение режима итеративного расчета
Вы должны включить то, что они называют итеративный режим вычислений , прежде чем формулы заработают.Для этого мы должны перейти в Параметры Excel.
В последних версиях Excel
- Нажмите кнопку «Офис»
- Зайдите в Параметры Excel, это аналогично открытию капота вашего автомобиля, но немного запутывает.
- Найдите «Формулы» слева и щелкните по нему.
- Теперь отметьте «Включить итеративный расчет». Таким образом, вы сообщаете Excel, что нужно итеративно оценивать ссылки до 100 раз (по умолчанию).
- Нажмите ОК, закройте капот.Это все.
В исторических версиях Excel,
- Перейдите в Меню> Инструменты> Параметры> Вкладка «Расчет»
- Установите флажок Итеративный расчет. (см. изображение)
Как только вы это сделаете, ваши формулы будут работать нормально, и вы обнаружите, что необходимо сделать необходимое благотворительное пожертвование.
Как избежать круговых ссылок?
Как вы понимаете, циклические ссылки — это заноза в ячейке. Возможно, вы захотите полностью избавиться от них.К счастью, если вы внимательно осмотритесь и выпите чашку кофе, вы сможете свести большинство циклических ссылок к простым формулам. Например, в приведенном выше случае мы можем рассчитать сумму благотворительной помощи напрямую, используя следующие уравнения.
Но имейте в виду, что в некоторых случаях могут потребоваться циклические ссылки. Например, если вы хотите добавить в книгу отметки времени.
Как найти циркулярные ссылки?
Знаете ли вы, что в книге можно найти все циклические ссылки?
Всякий раз, когда вы видите предупреждение о циклической ссылке, просто перейдите на ленту формул и щелкните параметры проверки ошибок.Здесь вы можете увидеть все круговые ссылки.
Примечание. В Excel 2003 вы можете увидеть то же самое на панели инструментов круговой ссылки (Меню> Вид> Панели инструментов> Круговая ссылка)
Примеры и другие ресурсы по циркулярным ссылкам:
Вы делаете круговые ссылки?
По возможности я стараюсь избегать циклических ссылок.
 ..
.. py"
из импорта соединения ApiConnection
Файл "connection.py"
из вещи импортная вещь
Файл "thing.py"
из импорта соединения ApiConnection
ImportError: невозможно импортировать имя 'ApiConnection' из 'соединения'
py"
из импорта соединения ApiConnection
Файл "connection.py"
из вещи импортная вещь
Файл "thing.py"
из импорта соединения ApiConnection
ImportError: невозможно импортировать имя 'ApiConnection' из 'соединения'
 _conn = соединение
_conn = соединение
