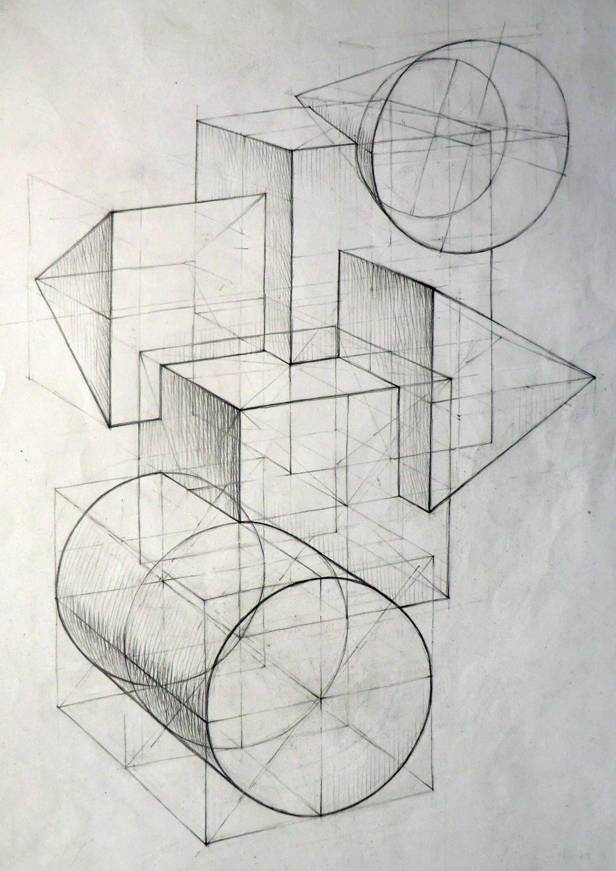
Рисунки геометрических фигур карандашом с тенью (51 фото)
Изображение геометрических фигур можно сравнить с изучением алфавита для того, чтобы начать осваивать язык. Геометрические формы – начальная стадия построения объекта любой сложности. Это можно сравнить с компьютерным моделированием, где построение трехмерного космического корабля начинается с простого кубика. В любой рисунке все изображаемые детали всегда состоят из простых геометрических форм. Следовательно, научившись правильно изображать геометрические фигуры, можно научиться рисовать все остальное. Далее предлагаем посмотреть рисунки геометрических фигур с тенью.
Рисунок карандашом шар.
Рисунок карандашом конус.
Рисунок для срисовки конус.
Рисунок геометрические фигуры.
Геометрические фигуры с тенью.
Цилиндр с тенью.
Геометрические фигуры.
Рисунок карандашом геометрические фигуры.
Рисунок геометрические фигуры.
Геометрические фигуры с тенью.
Геометрические фигуры.
Геометрические фигуры с тенью.
Рисунок карандашом геометрические фигуры.
Геометрические фигуры с тенью.
Шар, куб.
Рисунок геометрические фигуры.
Рисунок для срисовки геометрические фигуры.
Рисунок цилиндр.
Рисунок геометрические фигуры.
Рисунок цилиндр.
Рисунок шар.
Геометрические фигуры
Объемный рисунок
Рисунок карандашом
Фигуры с тенью
Рисунок в блокноте
Геометрические фигуры для срисовки
Крупные фигуры
Правильные пропорции
Рисунок простым карандашом
Треуголники
Яркие фигуры
Геометрические фигуры
Простой рисунок
Разные фигуры
Шар
Конус
Разные фигуры
Рисунок простым карандашом
Рисунок для срисовки
Схема изображения
Фигуры
Правильные фигуры
Конус
Рисунок карандашом
Геометрические фигуры
Объемный рисунок
Поэтапный рисунок
Фигуры с тенями
Правильное изображение
Рисунок карандашом
Мне нравитсяНе нравитсяБудь человеком, проголосуй за пост!
Загрузка. ..
..
Как рисовать геометрические фигуры карандашом? — Ghenadie Sontu Fine Art
Еще один способ – вписывание окружности в квадрат. Точки соприкосновения линий должны находиться в середине каждой стороны четырехугольника. Центральная ось цилиндра должна оставаться перпендикулярной плоскостям окружностей. Следите за искажением пропорций вследствие изменения перспективы.
В разных частях рисунка эллипсы будут иметь разную форму. Это зависит от того, под каким углом вы смотрите на фигуру. Со временем вам понадобиться все меньше вспомогательных линий для создания правильного цилиндра.
Грани
Теперь нам нужно немного ослабить нарисованные линии. На этом этапе делим наш цилиндр, отделяя передний план от заднего. Для этого мы прорисовываем более толстые линии видимых частей фигуры. Причем более толстые линии мы проводим по нижним и верхним дугам. Заднюю видимую часть эллипса вверху фигуры выделяем не так жирно, но она должна оставаться четкой. То есть у нас появляются три типа линий по толщине: толстые линии переднего плана, тонкая линяя заднего плана и едва заметные вспомогательные линии.
Окружности основания цилиндра прорисовывайте насквозь, на этапе штрихования внутренние (невидимые линии) удаляются. Таким образом, вы сможете проследить различия размеров верхнего и нижнего оснований.
Следующий этап: штриховка
При помощи мягкого карандаша мы будем накладывать тон на получившееся изображение, постепенно создавая объем. На начальном этапе лучше всего воспользоваться так называемой диагональной штриховкой. Начинать штриховать цилиндр следует с самых темных участков. Элементы светотени, которые встретятся в процессе выполнения работы, включают в себя блики, полутени, тени, рефлексы и свет. Самым светлым участком будет блик. Здесь наложения тона не требуется.
Следующий участок – это свет, здесь штрих должен быть еле заметным. Зона полутени – это основной тон цилиндра. В области тени мы накладываем самую темную и плотную штриховку. В районе кромки предмета находится рефлекс, тон практически равен полутени. Работать стоит аккуратно, нанося равномерную штриховку.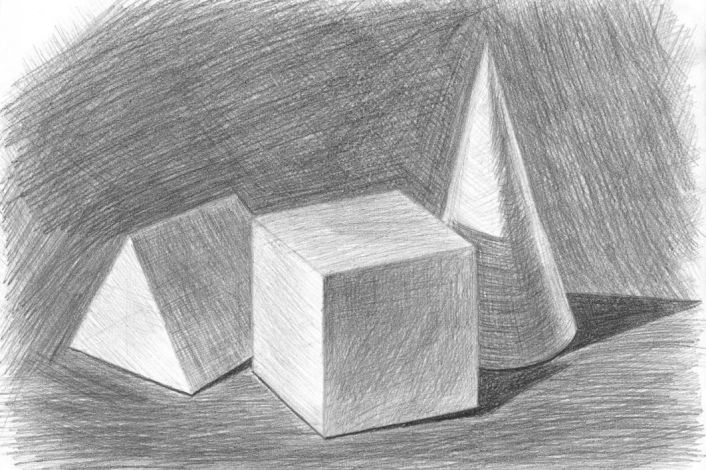 Свет строит форму геометрического тела. От правильности выполнения зависит его итоговый объем. От самого яркого участка (блика) свет расходится по округлой поверхности, переходя в полутень.
Свет строит форму геометрического тела. От правильности выполнения зависит его итоговый объем. От самого яркого участка (блика) свет расходится по округлой поверхности, переходя в полутень.
Цилиндрическая форма помогает рисовальщику понять последовательность распределения светотени. Сложность задачи состоит в том, чтобы сделать переходы между участками плавными и незаметными. На каждом этапе следите за правильной передачей пропорций и градациями тона.
Фон мы не оставляем нетронутым. Он также играет важную роль в восприятии объема и построении пространства. При помощи штриховки тона мы можем передать освещенность.
После того, как вы закончили создавать цилиндр, следует проверить наличие ошибок. Отойдите на расстояние в несколько метров от мольберта, так чтобы изображение было отчетливо видно. То есть, чем больше рисунок, тем дальше нужно от него отдалиться. С такого ракурса видны ошибки в построении. После исправления проверьте правильность выполнения еще раз.
Развитие навыков
Это был самый простой вариант расположения геометрического тела. Когда вы его освоите, то можете переходить к более сложным вариациям: цилиндр в пространстве, в горизонтальном или наклонном положении. В нашей художественной студии вы сможете обучиться азам рисования. Вы научитесь строить не только цилиндр, но и любые геометрические тела в разных положениях. С развитием навыков вы будете переходить к новым этапам, и сможете развить свои художественные способности. Со временем вам не понадобится такое множество вспомогательных линий, и вы с легкостью сможете начать изображать на бумаге сложные элементы.
Когда вы его освоите, то можете переходить к более сложным вариациям: цилиндр в пространстве, в горизонтальном или наклонном положении. В нашей художественной студии вы сможете обучиться азам рисования. Вы научитесь строить не только цилиндр, но и любые геометрические тела в разных положениях. С развитием навыков вы будете переходить к новым этапам, и сможете развить свои художественные способности. Со временем вам не понадобится такое множество вспомогательных линий, и вы с легкостью сможете начать изображать на бумаге сложные элементы.
3д рисунки — инструкции по 3д рисованию для начинающих. Мастер-класс с описанием техники + фото лучших идей рисунка
Сделать красивый, реалистичный рисунок может далеко не каждый человек. Необязательно обладать природным даром, чтобы реально отображать действительность, достаточно запастись большим желанием и трудолюбием, и приступить к учебе.
Объемные рисунки, сделанные своими руками, это прекрасное украшение интерьера, и возможность увлечься творческим процессом.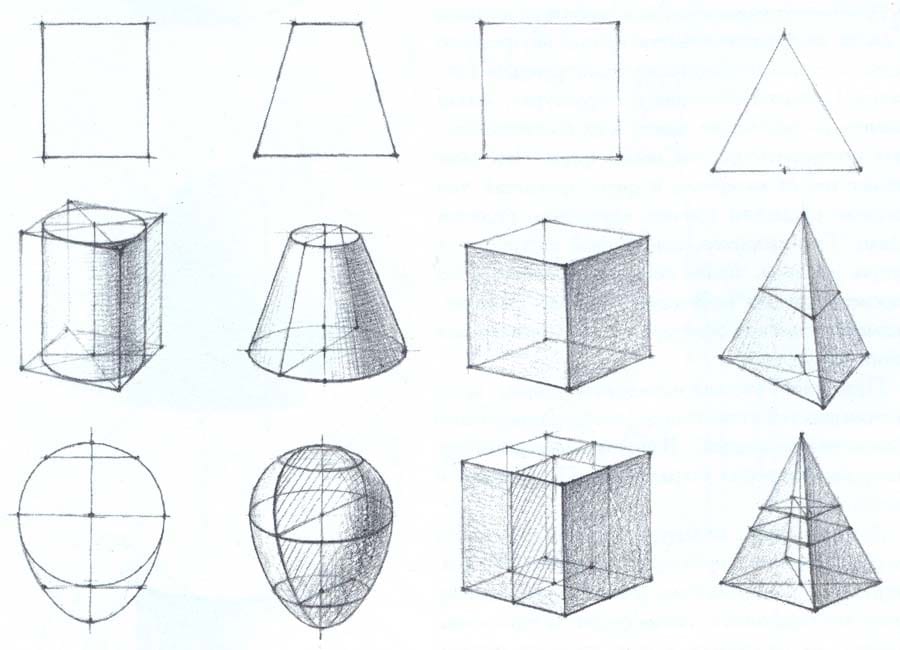
Содержимое обзора:
История возникновения рисунков
Изображения в 3д формате, появились еще в 16 веке. Бродячие художники изображали мелом, на мостовых средневековых улиц, картины, изображающие святой лик Мадонны.
В дальнейшем, власти многих городов стали поощрять такое творчество. Цель, привлечь как можно больше туристов, и пополнить городской бюджет. Но, в народе так и осталась любовь к уличному творчеству.
Трехмерное искусство
С появлением компьютеров, уличное трехмерное рисование стало уступать место трехмерной компьютерной графике. Задача 3д моделирования – создать визуальный, объемный образ изображаемого объекта.
Разновидностью 3д рисунков является граффити, реалистичные картины, которые создают видимость трехмерной сцены.
В современной жизни трехмерное искусство знакомо всему миру. Это, ни с чем несравнимое, захватывающее зрелище. Картины, словно рожденные землей, завораживают буйством красок и ощущением реальности.
Пошаговая инструкция
Изображение объемных рисунков, даже самых простых, создается на бумаге поэтапно. Главное в этом процессе, последовательность. Поэтапная инструкция предусматривает все этапы творческой работы. Прежде всего, необходимо иметь фото или готовый рисунок, который вы хотите воспроизвести на бумаге.
Когда профессионалы художники уверяют, что стоит только захотеть, и каждый человек может нарисовать такие рисунки, откровенно, не верится. Настолько сложным кажется процесс творчества, что многие, даже желая научиться, откладывают свою мечту до лучших времен. А, между тем, напрасно.
Изучив технические нюансы создания объемных картин, пройдя несколько мастер-классов по данной теме, каждый может научиться создавать реалистические изображения. Упорство, терпение и последовательность учения, вот то, чем необходимо запастись человеку, стремящемуся освоить 3д искусство.
Обратите внимание!
Первые шаги в 3д искусстве
Мастер-класс для начинающих, как правило, советует начать процесс рисования с повтора чужих работ.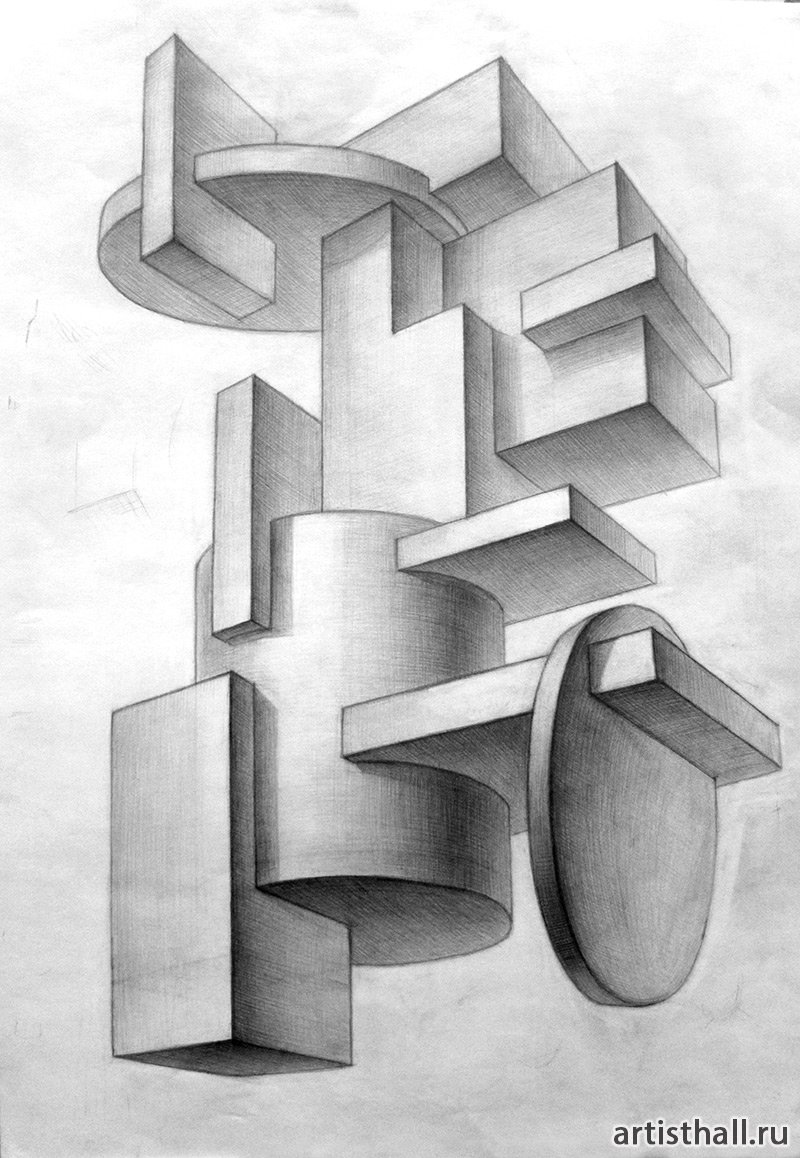 Если вы человек с буйной фантазией, вы можете представить себе невероятный сюжет, но изобразить его реалистично на бумаге, будет вам не под силу. Для этого необходимо постичь логический цикл построения 3д рисунка.
Если вы человек с буйной фантазией, вы можете представить себе невероятный сюжет, но изобразить его реалистично на бумаге, будет вам не под силу. Для этого необходимо постичь логический цикл построения 3д рисунка.
Обычно, учение начинается с самого простого: изображения собственной руки. Для этого обводят карандашом на бумаге руку и часть запястья.
Фломастером рисуют прямые линии до и после контура руки, а на самой руке рисуют дугу. Такие линии проводят по всему листу, на расстоянии 1-2 см друг от друга. Маркерами 3-х цветов закрашивают полоски. Добавляют тень вокруг руки, чтобы она выглядела более объемно.
Смотря на картину, кажется, что рука обтянута цветной эластичной бумагой.
Этот способ рисования называется «разлиновкой». Он идеально подходит для начинающих художников: простой и эффектный способ.
Рисунки карандашом
Визуальные, объемные рисунки позволяют ощутить мир по-иному.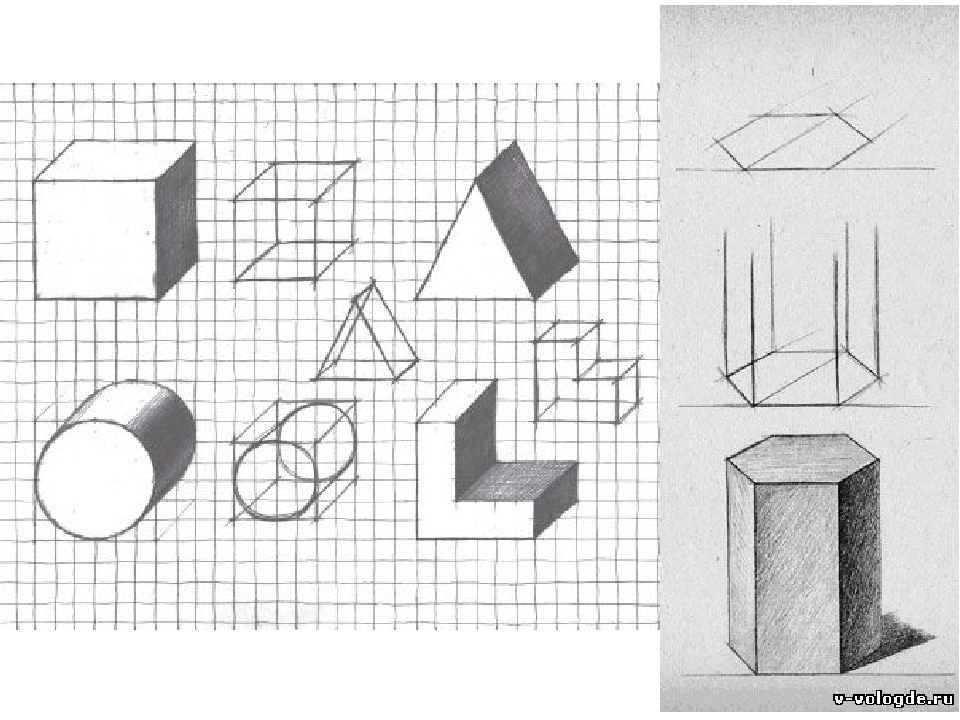
Обратите внимание!
Чтобы изобразить 3д рисунки карандашом, нужно набраться терпения. В начале освоения творчества, не стоит торопиться, карандаш должен описывать плавные линии. Выполняя эти условия, сами поразитесь своим новыми возможностями.
Для этой работы нужно запастись всего лишь карандашом, ластиком, линейкой и ножницами. Рабочим местом для творчества может стать любой стол, где вам удобно работать.
Объемные рисунки по клеточкам
Простая схема рисования бабочки в объемном формате, позволит создать чудо-рисунок, который будет настолько реалистичным, что кажется: бабочка вспорхнет и улетит. 3д рисунки по клеточкам просты в исполнении.
Техника рисования по клеточкам, наиболее приемлема для начинающих:
- Лист бумаги нужно разметить направляющими линиями.- Нанести очертания бабочки.
- Прорисовать детали крыльев и брюшка.
- Стерев ластиком направляющие линии, нужно начать процесс разукрашивания насекомого.

- Изобразить тень, отбрасываемую бабочкой.
- Вырезать часть листа, чтобы верхняя часть туловища и крыльев бабочки были вне листа.
Рисунок завершен.
Обратите внимание!
Первые рисунки
3д рисунки для начинающих, это работа, выполненная в трехмерном формате. При этом, необходимо правильно учесть высоту, ширину и глубину.
Основа техники объемного рисунка, это игра света и тени.
Прежде, чем приступить к рисованию, необходимо проанализировать особенности и нюансы выбранного объекта: форму, угол отбрасываемой тени.
Первый этап рисования, это набросать эскиз рисуемого предмета, определить правильное расположение на бумаге.
Нахождение источника света влияет на отбрасываемую тень, это нужно учесть.
Тени обозначают, переходя от более светлого тона к темному тону.
При помощи ластика тени растушевываются. Это помогает реалистичнее передать изображаемый предмет.
Рисунки на бумаге
Рисуя на бумаге, мы прекрасно сознаем, что он представляет собой плоскость: длину и ширину. Чтобы на этой плоскости придать рисунку глубину и достаточный объем, нужно помнить о линейной перспективе, правильном выборе ракурса, расположения источника света.
Дети любят рисовать героев любимых мультфильмов. Им можно помочь так изобразить, например миньона, что он, словно живой предстанет перед ними на листе бумаги.
Просто нарисовать незатейливую фигурку миньона могут даже первоклассники, а вот придать ему объем нужно научиться.
Разлиновать лист с изображением миньона на полоски шириной 1,5 см, не разлиновывая саму фигуру.
Соединить каждую линию дугой (она будет на фигуре игрушки). Этим можно придать объем изображению. Теперь нанесите тени, учитывая расположение источника света. Тени наносите от светлого тона к темному тону.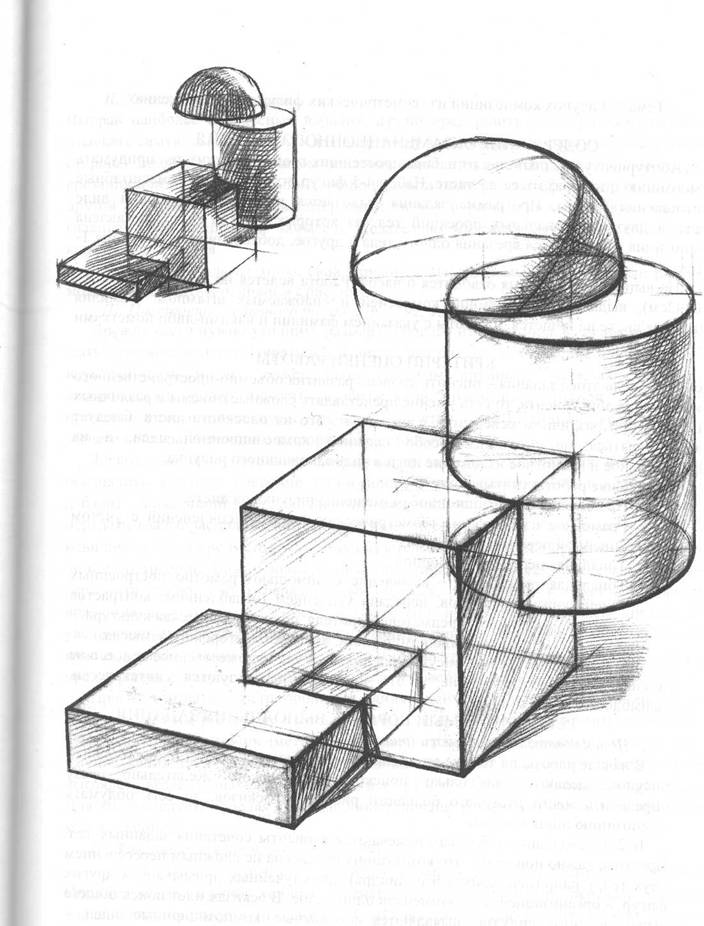 Растушуйте тени, и объемный рисунок на бумаге готов.
Растушуйте тени, и объемный рисунок на бумаге готов.
Ребенок будет просто в восторге от такого миньона.
Доступное творчество
Уверенные в своих способностях люди, без тени колебания приступают к освоению процесса неизвестного им творчества. А вот люди, колеблющиеся, сомневающиеся во всем, мучаются вопросом: «Как нарисовать 3д рисунок?»
На самом деле, на этот вопрос найдете ответ в интернете на сайте «Кругозор» и многих других. На сайтах, приводится инструкции построения объемных изображений для начинающих. Буквально по шагам, объясняется весь процесс творчества от простого рисунка, к более сложному изображению.
Простые рисунки
Любой процесс обучения двигается от простых познаний к фундаментальным знаниям. То же самое и в искусстве объемного изображения предметов.
Легкие 3д рисунки, это те, с чего начинают процесс обучения все новички.
Классика обучения начинается с реалистичного отображения геометрических фигур.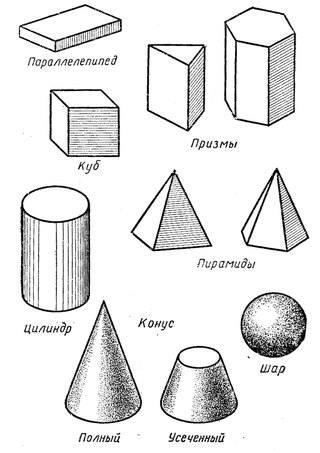
Чтобы куб предстал объемной фигурой, нужно определить источник света и визуально наметить себе тень, отбрасываемую им на лист бумаги. Определившись с этим, начинают создавать игру теней. Растушевав ластиком тени, получим объемное изображение куба.
Рисунки в тетради
Рисование, это захватывающий творческий процесс, которым можно заниматься не один час. Если, считаете, что рисование, это удел избранных людей, то сильно ошибаетесь. Это творчество может освоить каждый человек.
3д рисунки в тетради можно создавать, как в легких вариантах, так и в сложных композициях.
По клеточкам, на начальном этапе, лучше всего срисовывать рисунки. Такой процесс покажет, как лучше соблюдать пропорции, как правильно определить изображение теней.
Тетради в клеточку, идеальным образом подходят для изображения многоуровневых предметов: лестницы, дома. Хотя, в принципе, любой предмет можно изобразить правильным подбором клеточек, для изображения объема.
Хотя, в принципе, любой предмет можно изобразить правильным подбором клеточек, для изображения объема.
Польза от объемного рисования
Всякий вид творчества плодотворно влияет на развитие личности, а рисование в особенности.
У детей развивается чувство вкуса, улучшается моторика рук. Они, благодаря осваиванию трехмерного рисования, совершенствуют навыки работы с карандашом. Получают знания, по определению расположения источника света.
Игра света и тени пригодится им на уроках черчения, а в дальнейшем и начертательной геометрии. Мыслить объемно, это значит видеть мир совершенно с другой позиции. У них развивается координация движений. Рисование делает детей усидчивыми, неспешными и аккуратными в выполнении заданий.
Для взрослых людей, уже состоявшихся в жизни, рисование, это возможность отдохнуть за любимым занятием, снять стресс, после тяжелого трудового дня. Эстетическое удовольствие, которое испытывают взрослые люди, создав трехмерный рисунок, безмерно.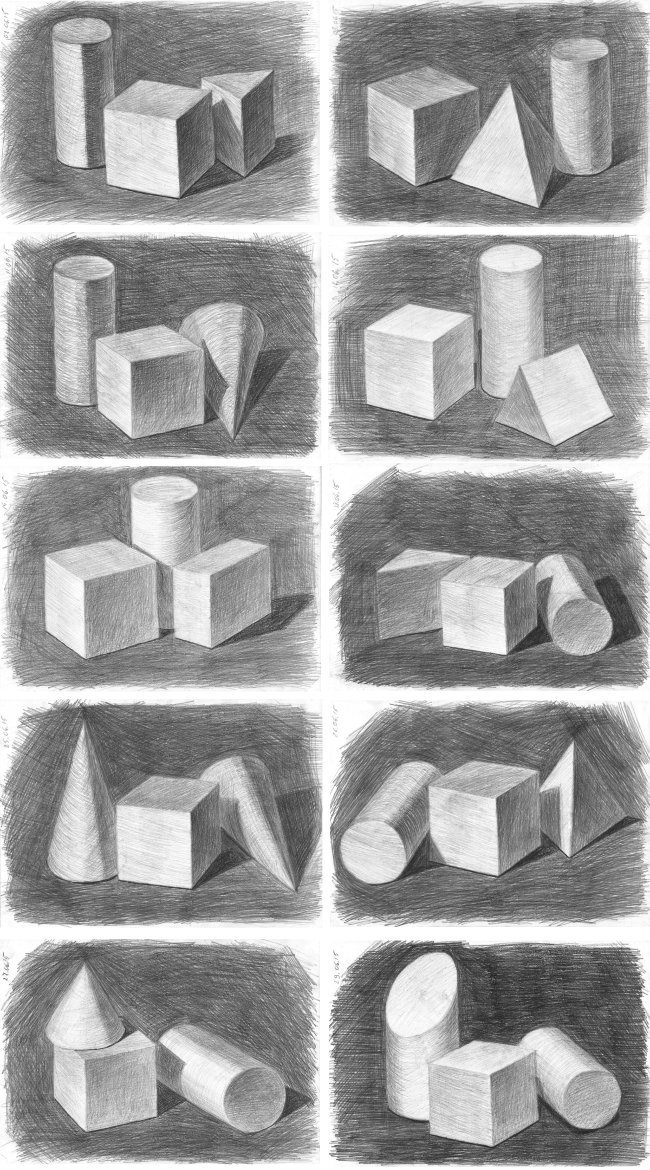 Это повышает самооценку, помогает поверить в свои способности.
Это повышает самооценку, помогает поверить в свои способности.
Умение рисовать, это возможность человека выразить свои мысли, мечты, радость или боль на бумаге, асфальте. Возможности научиться трехмерному изображению предметов в пространстве, есть у каждого человека. Желание, усидчивость, любовь к творчеству, вот то, что поможет людям создавать поистине шедевры изобразительного искусства.
Фото 3д рисунков
Как сделать объемные геометрические фигуры из бумаги, развертки для склеивания: куба, конуса, схемы и шаблоны для вырезания цилиндра, пирамиды, треугольника
Любому ребенку нравится делать яркие и объемные поделки. Творчество можно объединить с изучением математики и склеить вместе с детьми геометрические фигуры.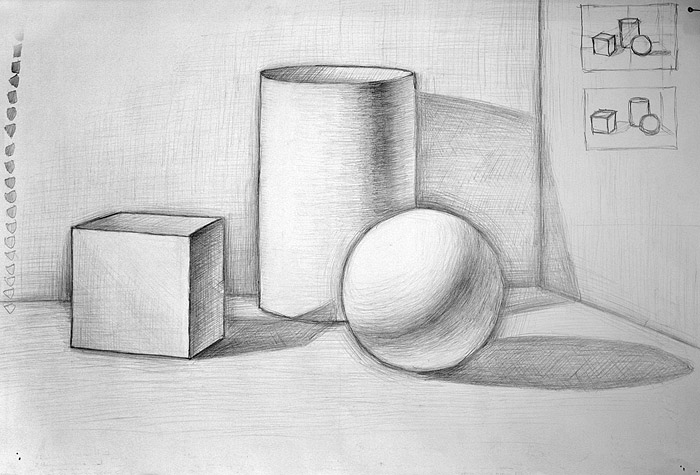
Как вырезать и склеить модели из бумаги
Начинающие конструкторы задаются вопросами, как рисовать и чертить геометрические фигуры, как правильно склеить выкройки и как делают врезки. Проще всего распечатать готовый шаблон. Затем необходимо согнуть фигуру по пунктирным линиям.
Чтобы сгибы получились ровными, к пунктиру прикладывают линейку, по ее форме делают точные загибы. Такой способ особенно помогает, когда речь идет о фигурках из картона или ребенок делает самые сложные макеты. Например, икосаэдр, додекаэдр, тетраэдр.
На последнем этапе необходимо скрепить элементы объекта, места для склейки обозначены на развернутом виде фигуры. Детали из картона приклеивают при помощи ПВА, а бумажные — карандашным клеем.
Основные ошибки при работе с моделями:
- Ребенок делает неправильные сгибы — например, изгиб отклоняется в сторону от пунктира на несколько градусов. В результате модель получится неточной.
Неточности во время вырезания шаблонов. Если малыш отрезал одну из границ для склеивания, то фигурка будет разворачиваться. Здесь на помощь придет взрослый.
Если малыш отрезал одну из границ для склеивания, то фигурка будет разворачиваться. Здесь на помощь придет взрослый.
Развёртки геометрических фигур
Большой выбор развёрток простых геометрических фигур.
Первое знакомство детей с бумажным моделированием всегда начинается с простых геометрических фигур, таких как кубик и пирамида. Не у многих получается склеить кубик с первого раза, иногда требуется несколько дней, чтобы сделать поистине ровный и безупречный куб. Более сложные фигуры цилиндр и конус требуют в несколько раз больше усилий нежели простой кубик. Если вы не умеете аккуратно клеить геометрические фигуры, значит и за сложные модели вам ещё рано браться. Займитесь сами и научите своих детей клеть эти «азы» моделирования по готовым развёрткам.
Для начала я, конечно же, предлагаю научиться клеить обычный кубик. Развёртки сделаны для двух кубиков, большого и маленького. Более сложной фигурой является маленький кубик потому, как клеить его сложнее, чем большой.
Итак, начнём! Скачайте развёртки всех фигур на пяти листах и распечатайте на плотной бумаге. Перед тем, как печатать и клеить геометрические фигуры обязательно ознакомьтесь со статьёй о том, как выбрать бумагу и как вообще правильно вырезать, сгибать и клеить бумагу.
Для более качественной печати советую использовать программу AutoCAD, и даю вам развёртки для этой программы, а также читайте, как распечатывать из автокада. Вырежьте развёртки кубиков с первого листа, по линиям сгиба обязательно проведите иголкой циркуля под железную линейку, чтобы бумага хорошо сгибалась. Теперь можно начинать клеить кубики.
Для экономии бумаги и на всякий пожарный я сделал несколько развёрток маленького кубика, мало ли вам захочется склеить не один кубик или что-то не получится с первого раза. Ещё одна несложная фигура это пирамида, её развёртки найдёте на втором листе. Подобные пирамиды стоили древние египтяне, правда не из бумаги и не таких маленьких размеров 🙂
А это тоже пирамида, только в отличие от предыдущей у неё не четыре, а три грани.
Развёртки трёхгранной пирамиды на первом листе для печати.
И ещё одна забавная пирамидка из пяти граней, её развёртки на 4-ом листе в виде звёздочки в двух экземплярах.
Далее шестигранник, склеить его будет ещё проще, чем пирамиды. Развёртки шестигранника на первом листе.
Более сложная фигура это пятигранник, хотя пятигранник сложнее начертить, нежели склеить.
Развёртки пятигранника на втором листе.
Вот мы и добрались до сложных фигур. Теперь придётся поднапрячься, склеить такие фигуры нелегко! Для начала обычный цилиндр, его развёртки на втором листе.
А это более сложная фигура по сравнению с цилиндром, т.к. в её основании не круг, а овал.
Развёртки этой фигуры на втором листе, для овального основания сделано две запасных детали.
Чтобы аккуратно собрать цилиндр его детали нужно клеить встык. С одной стороны дно можно приклеить без проблем, просто поставьте на стол заранее склеенную трубку, положите на дно кружок и залейте клеем изнутри. Следите, чтобы диаметр трубы и круглого дна плотно подходили друг к другу, без щелей, иначе клей протечёт и всё приклеится к столу. Второй кружок приклеить будет сложнее, поэтому приклейте внутри вспомогательные прямоугольники на расстоянии толщины бумаги от края трубы. Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.
Следите, чтобы диаметр трубы и круглого дна плотно подходили друг к другу, без щелей, иначе клей протечёт и всё приклеится к столу. Второй кружок приклеить будет сложнее, поэтому приклейте внутри вспомогательные прямоугольники на расстоянии толщины бумаги от края трубы. Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.
Цилиндр с овальным основанием можно клеить также как и обычный цилиндр, но он имеет меньшую высоту, поэтому тут проще вставить внутрь гармошку из бумаги, а наверх положить второе основание и по краю приклеить клеем.
Теперь очень сложная фигура – конус. Его детали на третьем листе, запасной кружок для днища на 4-ом листе. Вся сложность склеивания конуса в его острой вершине, а потом ещё будет очень сложно приклеить дно.
Сложная и одновременно простая фигура это шар. Шар состоит из 12-ти пятигранников, развёртки шара на 4-ом листе. Сначала клеится две половинки шара, а потом обе склеиваются вместе.
Довольно интересная фигура – ромб, её детали на третьем листе.
А теперь две очень похожие, но совершенно разные фигуры, их отличие только в основании.
Когда склеите эти обе фигуры, то не сразу поймёте, что это вообще такое, они получились какие-то совсем невосприимчивые.
Ещё одна интересная фигурка это тор, только он у нас очень упрощён, его детали на 5-ом листе.
И наконец, последняя фигура из равносторонних треугольников, даже не знаю, как это назвать, но фигура похожа на звезду. Развёртки этой фигуры на пятом листе.
На сегодня это всё! Я желаю вам успехов в этой нелёгкой работе!
Объемные картины из бумаги своими руками: схемы, шаблоны, оригинальные идеи для украшения интерьера (78 фото)
Нестандартные решения в интерьере всегда вызывают восторг гостей и радуют взор хозяев квартиры. Оригинальной идеей считается выполнение объемных картин из бумаги, сделать их можно своими руками. Такие аксессуары дополнят дизайн любого помещения, добавят уют в обстановку.
Такие аксессуары дополнят дизайн любого помещения, добавят уют в обстановку.
Выполняются работы по схемам и шаблонам в различных техниках. Поделки заключаются в деревянные рамы и украшают комнаты дома.
Объемные картины из бумаги в разных техниках
Настенные композиции придают интерьеру новый характер – они смотрятся оригинально и стильно. Сделать панно своими руками можно при помощи разных техник. Чтобы начать работу, достаточно запастись большим количеством бумаги, красками, кистями и проявить фантазию.
Оригами: как сложить фигурку
Техника, при которой листы бумаги складывают для получения фигурок, называется оригами. С технологией создания простейших форм каждый человек познакомился еще в детстве: на уроках труда такие изделия были востребованы. Методика заключается в поэтапном сложении бумажного листа в определенном порядке. Направление зародилось в Китае, владеть техникой могли только представители высшего сословия.
Картины из бумаги, выполненные с помощью оригами, имеют необычный внешний вид. Изготовление несложное: зачастую ничего вырезать не нужно, стоит только соблюдать правила и этапы сложения листов. Современно смотрятся объемные картины с фигурами животных, их сделать достаточно просто. Принцип создания:
- Распечатка шаблона на цветном принтере.
- Подготовка фона из картона.
- Вырезание и складывание шаблона, его склеивание.
- Фиксация фигурки на картонном фоне.
- Заключение работы в раму.
Смастерить картину в технике оригами сможет ребенок от 6 лет: пусть малыш сам выберет фигурку животного, а родители помогут со складыванием и приклеиванием.
Квиллинг: крутим спиральки
Еще одна модная техника в мире творчества с бумагой – квиллинг. Она подразумевает изображение на плоскости определенной композиции с помощью длинных бумажных полосок. Каждая скручивается в спираль вручную, затем фиксируется клеем на поверхности фона. В результате получается объемная поделка, для которой также можно использовать цветные полоски.
В результате получается объемная поделка, для которой также можно использовать цветные полоски.
Бумагокручение зародилось в XIV веке и ранее считалось настоящим искусством, а позже – хобби для настоящих рукодельниц. Для работы потребуется усидчивость и внимательность, ведь все спирали должны иметь определенный размер, быть ровными. В технике квиллинг красиво получаются птицы, растения, зимние пейзажи – все это можно включить в картину. Для методики кручения бумаги используют инструменты:
- пластиковые доски на пробковом основании с вырезками фигур;
- пинцеты с прямыми, изогнутыми носиками;
- шаблоны для квиллинга;
- квиллинг-коуч для создания ровных завитков;
- стики для кручения.
Все эти приспособления помогут создать красивые картины, но работа будет кропотливой, поэтому придется постараться.
Вытынанки: вырезаем по шаблону
В переводе с украинского языка «вытынать» означает вырезать. Методика заключается в создании ажурных узоров и маленьких картинок на бумаге. Простейшим примером вытынанки считается обычная снежинка, вырезанная из картона. Для работы нет необходимости покупать дорогие материалы и инструменты. Понадобятся канцелярский нож, трафарет, белая бумага, картон подходящего цвета, а также клей ПВА и самовосстанавливающийся коврик. Если последнего нет, можно смело использовать фанеру.
Методика заключается в создании ажурных узоров и маленьких картинок на бумаге. Простейшим примером вытынанки считается обычная снежинка, вырезанная из картона. Для работы нет необходимости покупать дорогие материалы и инструменты. Понадобятся канцелярский нож, трафарет, белая бумага, картон подходящего цвета, а также клей ПВА и самовосстанавливающийся коврик. Если последнего нет, можно смело использовать фанеру.
Поэтапно работа выглядит так:
- На лист фанеры кладут бумагу, сверху накладывают шаблон.
- С помощью острого канцелярского ножа вырезают отверстия по трафарету.
- Сначала вырезают крупные, затем мелкие детали.
- Готовую работу приклеивают к цветному картону и заключают в рамку.
Обрамление можно также сделать своими руками. Хорошо смотрится рамка из ярких разноцветных пуговиц, гофрированного картона и других подручных средств. Картину лучше повесить в детскую комнату, особенно если ребенок помогал ее выполнять.
Декупаж: как сделать объем из бумаги
Техника творчества декупаж подразумевает вырезание и приклеивание фрагментов иллюстрации на поверхность.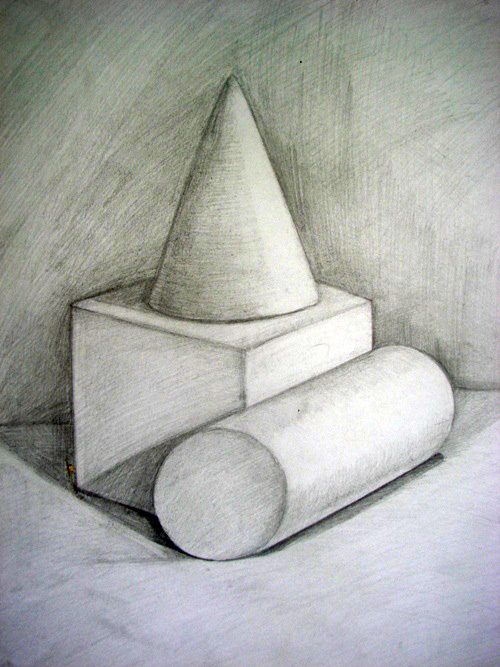 Сделать объемную картину в данной методике несложно, главное – подобрать красивый рисунок и распечатать его в 5-7 экземплярах. Можно использовать многослойные салфетки, тогда также придется приобрести несколько одинаковых элементов.
Сделать объемную картину в данной методике несложно, главное – подобрать красивый рисунок и распечатать его в 5-7 экземплярах. Можно использовать многослойные салфетки, тогда также придется приобрести несколько одинаковых элементов.
Объемная поделка выполняется так:
- Одна из распечатанных картинок (или салфетка) будет основанием. Она приклеивается к твердому картону.
- Каждая последующая картинка будет придавать объем: на первой нужно обрезать часть фона, на второй – некоторые элементы рисунка, на третьей – ближние детали.
- Элементы на первом плане будут выделяющимися, объемными.
- Гофрокартон нарезают кусочками и начинают приклеивать пазлы картины.
- Когда трехмерная работа готова, ее можно покрыть лаком.
В такой технике оригинально смотрятся новогодние пейзажи, животные, изображение леса и природы.
Аппликация – вариант для детей и взрослых
Объемная картина из аппликации подойдет не только в качестве украшения интерьера, но и для поздравления близких друзей, родственников, любимого человека. Такую композицию можно сделать просто и быстро. Необходимо вырезать плоские фигурки, сложить их для объема и приклеить на фон. Несколько идей для аппликации по типу картины:
Такую композицию можно сделать просто и быстро. Необходимо вырезать плоские фигурки, сложить их для объема и приклеить на фон. Несколько идей для аппликации по типу картины:
- монохромные сердца – хороший вариант для поздравления с Днем всех влюбленных;
- изображение дерева (например, каштан с оригинальной формой листа) хорошо подойдет для аппликации;
- весенние цветочки – такую поделку обычно дарят на 8 Марта;
- объемная аппликация с природными мотивами – рисунок лисы на фоне растений, цветов.
Кроме бумаги и картона можно создавать текстильные аппликации на пенопласте. Это еще один вид творческой работы, который поможет смастерить объемную картину. В качестве вспомогательного материала подойдет фетр (его используют для создания мягких элементов).
Плетение: бумажное панно
Картины, выполненные в технике плетения из бумаги, отличаются хрупкостью. Кропотливость работы делает эти изделия дорогостоящими, ведь сначала нужно создать эскиз, после чего изобразить его на основе рисунок с помощью сплетения бумажных трубочек (чтобы они были гибкими, их увлажняют). Для выполнения нередко используют газетные турундочки, предварительно их надо окрасить в белый, а затем в нужный цвет.
Для выполнения нередко используют газетные турундочки, предварительно их надо окрасить в белый, а затем в нужный цвет.
В технике объемного плетения получаются стильные работы. Прекрасно выглядит подборка животных, птиц, окрашенных в яркие цвета. Такое панно отлично дополнят интерьер яркой гостиной или детской комнаты. Объемную картину можно также разместить на стене в прихожей или коридоре.
Папье-маше: разнообразие идей
Работы в этой технике выполняют не на картоне, как остальные картины, а на дереве. Для основания лучше использовать именно этот материал, так как послойное создание объемных деталей требует прочной базы. Массу для работы делают из кусочков бумаги, смешанных с клеем. Для лучшего разбивания комков используют ручной блендер.
Полученную смесь раскладывают на основе, с помощью стеков формируют различные фигуры, в результате получается 3д-картина. На конечном этапе изделие можно покрыть акрилом, а когда высохнет – лаком. Такие художественные работы станут достоинством интерьера.
Декоративные объемные панно из бумаги поэтапно
Чтобы создать объемную картину самостоятельно, необходимо выбрать технику, в которой будет выполнена работа. Затем подобрать нужные материалы, инструменты, придумать идею. Подборки мастер-классов, схем и шаблонов объемных картин из бумаги помогут пошагово создать неповторимые изделия.
Цветы из бумаги: несколько идей
Существует несколько вариантов создания бутонов из бумаги для декоративного панно. Искусственный цветок должен максимально точно передать всю красоту настоящего бутона. Сделать растения можно из обычной цветной, а также гофрированной бумаги. Несколько простых идей для творчества:
- послойные цветы. Выполняются из цветной бумаги по шаблону. Вырезают несколько лепестков, накладывают друг на друга. С помощью зубочистки подкручивают окончания листочков. В серединку приклеивают тычинки яркого цвета;
- кручение в трубочку. Здесь лепестки накручиваются сразу на стебель, сделанный из проволоки, после чего его приклеивают на панно.
 Потребуется гофрированная бумага, из которой вырезают длинную полосу и постепенно фиксируют на стебель. В конце крепят на клей ПВА;
Потребуется гофрированная бумага, из которой вырезают длинную полосу и постепенно фиксируют на стебель. В конце крепят на клей ПВА; - техника косая бахрома. Таким способом можно сделать маки, хризантемы, розы. Цветочный бутон рисуют на бумаге, разрезают лепестки и сгибают их. Затем из тонких цветных листов вырезают бахрому и закручивают ее на основе цветочка.
Тема растений всегда актуальна – такая картина станет прекрасным подарком, а также разбавит интерьер кухни в стиле кантри.
Бабочки: как создать трехмерное насекомое
Простую и объемную бабочку по пошаговому мастер-классу сможет сделать даже ребенок. Хорошо, если ваш малыш будет рисовать основу, а родители помогут ее правильно сложить. Поэтапное выполнение:
- Подготавливают цветную бумагу, картон, клей, ножницы и карандаш.
- Вырезают 2 прямоугольника, один из которых больше другого по размеру.
- Каждый прямоугольник складывают гармошкой.

- Крылья обрезают полукругом, придавая настоящую форму.
- Каждый элемент складывают пополам и склеивают.
- Из картона делают усы и тельце, на окончание усиков можно приклеить бисер.
Объемные картины из бумаги своими руками могут быть выполнены в тематике сада, где на каждом дереве сидит такая трехмерная бабочка. Насекомых можно приклеить к растениям в панно.
Абстракция: используем дополнительные материалы
Стильно и современно выглядят картины с абстракцией. Для выполнения такой работы может пригодиться не только цветная бумага, но и ткань, зерна кофе, кожа. Суть работы заключается в хаотичном расположении элементов для формирования фантазийной поделки. Поэтапно работа выглядит так:
- Подготавливают основание – дерево или плотный картон.
- Делают эскиз – отдельно прорисовывают на бумаге будущее панно.
- Согласно схеме вырезают из бумажных цветных листов, из ткани или кожи отдельные элементы.

- Детали прикладывают к основанию, при этом нужно примерять будущую композицию (желательно пронумеровать каждую деталь).
- Работу начинают из центра. Чтобы панно получилось ярким, лучше использовать разные расцветки.
- Поделку заключают в раму. Если она выполнена из бумаги, ее можно покрыть акриловым лаком для дополнительной защиты.
Оригинально будет смотреться на стене такая картина, если сделать ей подсветку по периметру. Композиция украсит спальню, гостиную и любой современный интерьер, например, в стиле лофт.
Птицы и животные – основа творчества
Конструирование зверей из бумаги – увлекательное и кропотливое занятие. Чтобы реалистично передать все детали, придется использовать большое количество элементов. Например, для воссоздания перьев птицы понадобится нарезать множество полукруглых элементов и наклеить их в определенном порядке. Дополнительно можно использовать пластилин, он выступает клейкой основой на фоне.
Пошаговые действия:
- На фоне рисуют эскиз, куда будут приклеиваться поочередно все элементы.
- Из цветной бумаги вырезают полоски с имитацией крыльев или шерсти.
- На основу послойно приклеивают все полоски (выйдет красиво, если каждый слой будет отличаться на один тон от предыдущего).
В конце создают морду птицы или животного, приклеивают глаза. В такой же технике можно выполнить аппликацию объемной елки, сделать панно в честь Дня космонавтики, изобразив ракету. По аналогии делают буквы, которые нужно приклеить на основу и выложить слово. Таким же способом легко украсить обложку книги.
Фото объемных картин не могут передать всей креативности и красоты их настоящего внешнего вида. Чтобы понять, насколько приятно и оригинально выглядят такие панно, стоит попробовать изготовить их своими руками из бумаги.
Трехмерные фигуры
Трехмерные фигуры Вернуться к содержаниюОбзор базовой геометрии — Урок 9
Обзор урока
Плоскости: параллельные, перпендикулярные и прочие
Точка, линия и плоскость — неопределенные термины. Несколько предположений
были сделаны вокруг них с помощью постулата точка-линия-плоскость в уроке 1.
Для самолетов мы должны добавить еще три предположения ниже.
Несколько предположений
были сделаны вокруг них с помощью постулата точка-линия-плоскость в уроке 1.
Для самолетов мы должны добавить еще три предположения ниже.
|
Самолеты не имеют неровностей и, как линии, продолжаются вечно.Три (неколлинеарные) точки определяют плоскость.
Также определяют три точки: треугольник; линия и точка не на линии;
и две пересекающиеся линии. Ровно один самолет содержит их.
Таким образом, стул на трех ножках стабилен, но большее количество ножек может вызвать
стул качаться.
Поскольку линии не имеют толщины, плоскости также не имеют толщины. Линия, не лежащая на плоскости, может пересекать плоскость не более чем в одной точке.
Линия, не лежащая на плоскости, может пересекать плоскость не более чем в одной точке.
| Мера наименьшего из всех возможных углов определяет угловая мера между линией и плоскостью. |
| Если линия l пересекает плоскость X в точке P , то линия l перпендикулярна плоскости X ( л X ) тогда и только тогда, когда l перпендикулярно каждой линии в X , которая содержит П . |
| Теорема о прямом и плоскости перпендикуляра: Если линия перпендикулярна двум разным линиям в их точке пересечения, то он перпендикулярен плоскости, которая содержит эти прямые. |
Две плоскости равны параллельным плоскостям тогда и только тогда, когда у них нет точек.
общие или они идентичны.
Опять же, это всеобъемлющее определение не используется повсеместно. Расстояние между параллельными плоскостями — это длина сегмента
перпендикулярно плоскостям с конечной точкой в каждой плоскости.
Измеряется расстояние между плоскостью и точкой не на ней.
по перпендикулярному отрезку от точки к плоскости.
Расстояние между параллельными плоскостями — это длина сегмента
перпендикулярно плоскостям с конечной точкой в каждой плоскости.
Измеряется расстояние между плоскостью и точкой не на ней.
по перпендикулярному отрезку от точки к плоскости.
При пересечении двух плоскостей образуются четыре двугранных угла . Меру этих углов можно указать, построив лучей, перпендикулярных линии пересечения, и измеряя те углы образовались. Косые линии — это некомпланарные линии, которые не пересекаются.
Так же, как есть разница между многоугольником и многоугольной областью,
мы различаем поверхность трехмерной фигуры и пространство
он включает.С этого мы начинаем твердую геометрию .
Коробка , поверхность прямоугольного твердого тела , или параллелепипед — одна из важнейших трехмерных фигур.
Коробка имеет шесть граней , каждая из которых представляет собой прямоугольную область. Противоположные грани лежат в параллельных плоскостях. Куб — это прямоугольник с квадратными областями всех граней. ребер — это линейные сегменты, где грани пересекаются.
Конечными точками ребер являются вершин .Коробка имеет 12 ребер и 8 вершин.
На рисунке справа показано типичное двумерное представление.
а также tesserack или гиперкуб — это четырехмерный аналог куба.
На рисунке слева показано двухмерное представление этого четырехмерного объекта.
Подробнее об этом можно
видел и
найденный.
Многие люди с трудом верят, что такое может существовать, поэтому такие книги, как
Плоская земля
(Эбботт, 1884 г.),
Sphereland
(Бюргерс, 1983), и
Флаттерленд
(Стюарт, 2001) были
написано.
Куб — это прямоугольник с квадратными областями всех граней. ребер — это линейные сегменты, где грани пересекаются.
Конечными точками ребер являются вершин .Коробка имеет 12 ребер и 8 вершин.
На рисунке справа показано типичное двумерное представление.
а также tesserack или гиперкуб — это четырехмерный аналог куба.
На рисунке слева показано двухмерное представление этого четырехмерного объекта.
Подробнее об этом можно
видел и
найденный.
Многие люди с трудом верят, что такое может существовать, поэтому такие книги, как
Плоская земля
(Эбботт, 1884 г.),
Sphereland
(Бюргерс, 1983), и
Флаттерленд
(Стюарт, 2001) были
написано.
Цилиндрические твердые тела / поверхности: призмы и цилиндры
| Цилиндрическое тело — это набор точек между областью и
его переводное изображение в пространстве, включая регион и его изображение. Цилиндрическая поверхность является границей цилиндрического твердого тела.  Цилиндр представляет собой поверхность цилиндрического твердого тела с круглым основанием. Призма — это поверхность цилиндрического твердого тела с многоугольным основанием. |
Цилиндрические твердые тела имеют два основания , которые конгруэнтны и параллельны плоскостям. Поверхность, исключая основания, известна как боковая поверхность . Высота или высота — это расстояние между самолетами. баз. Если вектор трансляции перпендикулярен плоскостям основания, цилиндрическое тело — это правый цилиндр или правая призма , в противном случае — косой .Призмы названы по форме их основание. Неосновные грани призмы известны как боковые грани , которые встречаются на боковых гранях . Правая призма, основание которой — правильный многоугольник это обычная призма .
Конические тела / поверхности: пирамиды и конусы
Коническое тело — это набор точек на любом сегменте между областью
(основание ) и точка (вершина ) не в плоскости
основание. Коническая поверхность — это граница конического тела. Пирамида — это поверхность конического твердого тела с многоугольным основанием. Конус — это поверхность конического твердого тела с круглым основанием. |
Конические тела имеют только одно основание .
Пирамиды имеют боковых граней, соединяющих вершины основания.
многоугольник с вершиной . В конусе боковой кромкой является любой отрезок
конечными точками которого являются вершина и точка на основной окружности.Треугольные, неосновные грани пирамиды — это боковых граней .
Пирамиды и конусы также могут быть правыми или наклонными .
Правая пирамида с правильным многоугольным основанием тоже правильная .
Конус также имеет ось , которая является
линия (не сегмент) через вершину и центр основания.
Высота коники — это расстояние между вершиной и вершиной.
самолет, содержащий базу.
В правильной пирамиде наклонная высота — высота любой боковой грани (треугольника).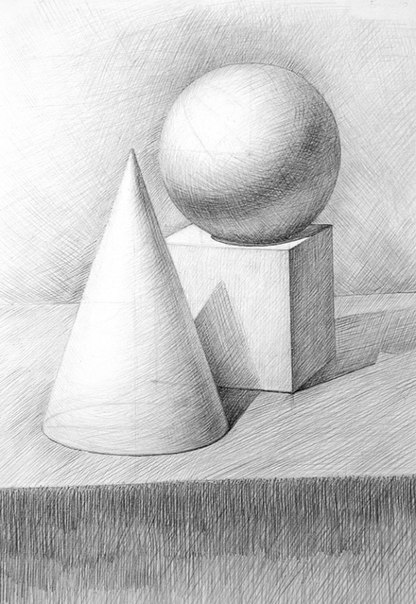 Только в правом конусе она равна длине бокового края.
Конус или пирамида могут быть усеченными — многие стаканы
усеченные конусы. Усеченный конус тоже
известный
как усеченная .
Только в правом конусе она равна длине бокового края.
Конус или пирамида могут быть усеченными — многие стаканы
усеченные конусы. Усеченный конус тоже
известный
как усеченная .
Сферы и прочие предметы круглые
| Сфера — это множество точек в пространстве на определенное расстояние ( радиус ) от точки ( центр ). |
Сферы имеют нулевых оснований .Сферу можно рассматривать как трехмерный аналог круга. Дважды радиус — , диаметр . Hypersphere или 4-ball — это четырехмерный аналог сферы. (Аналог намеренно пишется по-другому, но здесь тоже правильно.) Шар (круг, сфера, гиперсфера) размером n называется шаром n .
| Плоское сечение трехмерной фигуры — это пересечение этой фигуры с плоскостью. |
Сфера и плоскость могут пересекаться очень немногими способами. Во-первых, самолет мог
касайтесь сферы только в точке. Эта плоскость должна быть касательной в этой точке.
таким образом, линия, содержащая центр сферы и точку
пересечение будет нормальным (перпендикулярным) к плоскости. Во-вторых,
плоскость пересекается более чем в одной точке, и в этом случае пересечение
это круг. Это пересечение называется малым кругом .
если плоскость не содержит центр круга, в этом случае
он известен как большой круг .Большие круги делят сферы на полушарий , буквально полусферы. Маршруты большого круга очень
важны в навигации, потому что они содержат кратчайшее расстояние
между двумя точками на поверхности.
Геодезическая — это общий термин для кратчайшего расстояния между двумя точками. Метрика — это термин из общей теории относительности. Так мы измеряем пространство-время.
В терминах дифференциального исчисления это: dx 2 + dy 2 + dz 2 — c 2 dt 2 .
Во-первых, самолет мог
касайтесь сферы только в точке. Эта плоскость должна быть касательной в этой точке.
таким образом, линия, содержащая центр сферы и точку
пересечение будет нормальным (перпендикулярным) к плоскости. Во-вторых,
плоскость пересекается более чем в одной точке, и в этом случае пересечение
это круг. Это пересечение называется малым кругом .
если плоскость не содержит центр круга, в этом случае
он известен как большой круг .Большие круги делят сферы на полушарий , буквально полусферы. Маршруты большого круга очень
важны в навигации, потому что они содержат кратчайшее расстояние
между двумя точками на поверхности.
Геодезическая — это общий термин для кратчайшего расстояния между двумя точками. Метрика — это термин из общей теории относительности. Так мы измеряем пространство-время.
В терминах дифференциального исчисления это: dx 2 + dy 2 + dz 2 — c 2 dt 2 . Antipode прямо противоположное или противоположное; также точки сферы, такие
как земля, которые диаметрально противоположны (противоположные концы диаметра).
Antipode прямо противоположное или противоположное; также точки сферы, такие
как земля, которые диаметрально противоположны (противоположные концы диаметра).
Земля представляет собой сплюснутый сфероид (в форме буквы M & M, то есть сплющенный на полюсах). и из трех взаимно перпендикулярных радиусов повторяется тем длиннее). Вытянутый сфероид больше похож на футбольный мяч или сигару (из трех взаимно перпендикулярных радиусов повторяется тем короче).В эллипсоиде три взаимно перпендикулярных радиуса имеют разную длину. Посмотреть этот сайт для некоторых диаграмм и определений, включая тор или пончик.
Гипотеза Кеплера
К 1606 году Кеплер начал работу над тем, что стало известно как Гипотеза Кеплера после получения письма от Харриота которые работали над проблемой не менее 15 лет. Сэр Уолтер Рэли фактически предложил это своему помощнику Харриоту.Проблема заключается в наиболее эффективной упаковке для пушечных ядер или, в конечном счете, атомов в кристалле, хотя в то время об атомной структуре было известно немного. В конце концов Кеплер предположил, что гранецентрированная кубическая (FCC) [и эквивалентно гексагональная плотная упаковка (HCP)] оба дали оптимальную плотность упаковки сфер. В конечном итоге эта проблема стала частью C проблемы 18 Гильберта. Знаменитый список из 23, созданный в 1900 году. До 1990-х годов это оставалось одним из последних нерешенные проблемы дискретной геометрии.В 1990 г. У-И Сян разослал препринты, а в 1992 г. представил для публикации 100-страничное доказательство, которое осталось не принято в математическом сообществе из-за его нечеткость и отсутствие логической прогрессии. Хотя он был опубликован в International Journal of Mathematics , у некоторых есть «сомнения в серьезности процесса судейства» поскольку «журнал Journal редактируется коллегами Сяна из Беркли». Это «нельзя считать доказательством».» ( Гипотеза Кеплера , Джордж Спиро, 2003, стр. 150.) Примерно в 1996 году Хейлз начал противоречивое доказательство, которое следует вычислительный подход. 9 августа 1998 г. Сэм Хейлз объявил доступность статей и препринтов, доказывающих гипотезу Кеплера. В январе 1999 г. недельный семинар, посвященный исключительно гипотезе Кеплера. прошел в Институте перспективных исследований в Принстоне, где эксперты чистил его со всех сторон. Они требовали публикации в Анналы математики .В конечном итоге он был (будет?) Опубликован, но с беспрецедентным отказом от ответственности, что судьи не могут проверить доказательство.Конические секции
Nappes является множественным числом от Nappe . Конус называется двойным, если мы говорим о полном конусе. который больше похож на песочные часы или две «пирамиды с круговой основой» соединились в их вершинах. Одиночная «пирамида с круговым основанием» — это то, что большинство студентов подумают как конус.Выше показано пересечение плоскости с конусом — двойным ворсанный конус. Эти loci (наборы точек) представляют собой конические секции. Loci имеет множественное число для , локус (набор точек). Эти конические сечения ( круг , эллипс , парабола , и гипербола ) будут изучены более широко в алгебре II. Смотрите эту веб-страницу для получения дополнительной информации.
Платоновы тела
| Платоново тело представляет собой выпуклые многогранники с
все грани одинаковые многоугольники. Как показано ниже, их ровно пять. |
Платоновы тела также известны как правильные многогранники. Тетраэдр также известен как треугольная пирамида . Шестигранник также известен как куб . Двойники особенно важны в кристаллографии, где рассеянное излучение (электроны, нейтроны, рентгеновские лучи) лучше всего изучать в обратном пространстве. Глядя на таблицу выше, обратите внимание на формулу Эйлера который связывает количество граней, вершин и ребер любых многогранников: F + V = E + 2.
Нетрудно показать, что правильных многогранников всего пять. (выпуклый и грани все же правильный многоугольник). Подумайте, сколько одинаковых правильных многоугольников может сойтись в одной вершине. Нам всегда нужно больше двух, если мы собираемся сложить его и оградить любое пространство. Для треугольников (с углом 60 °) шесть составят мозаику плоскости. Следовательно, необходимо учитывать три, четыре и пять, и результаты могут быть рассматриваемый выше как тетраэдр, октаэдр и икосаэдр.Для квадратов (с углом 90 °) четыре будут мозаикой плоскости. Следовательно, нужно рассматривать только три, и куб является результатом. Для пятиугольника (с углом 108 °) четыре превышает 360 °. Следовательно, нужно рассматривать только три, и додекаэдр является результатом. Три шестиугольника (с углом 120 °) образуют мозаику на плоскости. Таким образом, мы исчерпали все возможности, в результате чего получилось пять правильные многогранники или платоновы тела.
Эта ссылка ведет на страницу с описанием пяти платоновых тел с цветные фигурки.Этот сайт есть твердые тела, которые можно вращать. Этот сайт ссылки на многие другие хорошие сайты. Древние связывали пять платоновых тел с огнем (4), землей (6), воздух (8), вода (20) и космос (12).
Твердые тела Архимеда
| В Archimedian Solid твердое тело выпуклое, все вершины идентичны, все грани — правильные многоугольники, но не все одинаковые. |
Твердые тела Архимеда можно классифицировать по набору чисел, который указывает количество сторон многоугольников в каждой вершине.Таким образом, {3,6,6} будет обозначать один треугольник и два шестиугольника в каждой вершине. Остальные двенадцать: {3,8,8}; {4,6,6}; {3,10,10}; {5,6,6}; {3,3,4,4}; {3,3,5,5}; {3,4,4,4}; {4,6,8}; {3,4,4,5}; {4,6,10}; {3,3,3,3,4}; и {3,3,3,3,5}. Эта (неработающая) ссылка ведет на страницу, описывающую тринадцать архимедовых или полурегулярных тел, в комплекте с цветными фигурами.
C 60 — высокосимметричная молекула чистого углерода. Форма такая же, как у футбольного мяча или Archimedian Solid усеченный икосаэдр: {5,6,6}.C 60 часто обозначается как Buckyballs. Технически это твердое тело Архимеда представляет собой усеченный изокаэдр . Это имя происходит от имени Ричарда Бакминстера Фуллера, известен своими геодезических куполов. Степан центр Нотр-Дам является местным примером. C 60 является одним из класса известных соединений как фуллерены также называют в честь американского архитектора выше. Молекула C 60 была открыта в 1985 году, когда группа пытался понять спектры поглощения межзвездной пыли.Их работа принесла им Нобелевскую премию по химии 1996 года. Первоначально производимый в очень малых количествах или извлекаемый из сажи, он теперь доступен и является центром множества разнообразных исследований. Длинные углеродные трубки называются нанотрубки также были произведены. C 60 представляет собой новую, неожиданную кристаллическую форму твердого углерод. Другие формы: тетраэдрическая углеродная связь в алмазе. и соединение листового типа в графите имеет гораздо более долгую историю.Увидеть На этой странице представлена краткая, хорошо задокументированная история C 60 .
Пентамино
Пентамино.Мои исследовательские интересы связаны с утроением пентамино из подмножество 9 из 12. Сможете ли вы утроить все 9 в наборе или даже все 12? Можете ли вы втрое повторить данное пентамино со всеми 220 подмножествами?
Симметрия, виды и сети
Отражения меняют ориентацию, таким образом, как двумерные фигуры, трехмерные фигуры могут также быть прямо конгруэнтным или противоположно конгруэнтным .Это особенно важно в органической химии, где ориентация из четырех связей вокруг углерода (тетраэдр) имеет решающее значение для жизни. Видеть это ссылка для получения дополнительной информации (загрузить плагин звонка). Я думал, что в последние годы была распространена диетическая добавка с обоими изомерами, и много людей погибло, но триптофан похоже, в конечном итоге возникла другая (димерная) проблема.Архитекторы часто рисуют в масштабе видов или планы зданий.Некоторые могут назвать эти отметок . Этот сайт есть сети для многих твердых тел и другие лакомые кусочки.
| Сетка — это двумерная фигура, которую можно складывать на сегменты или изогнутые на своих границах в трехмерную поверхность. |
Раскраска карты
http://www.ams.org/notices/199807/thomas.pdf Сколько цветов необходимо и сколько цветов достаточно, чтобы раскрасить любую карту на плоскости? На сфере (4)? На ленте Мёбиуса (6)? На торе (7)? Карты с границами, состоящими только из прямых или окружностей может понадобиться еще меньше цветов! (Смотрите рисунок справа.) За исключением плоскости / сферы, эти вопросы были легко ответить.Подобно сети, карта представляет собой двумерное приближение для трехмерной фигуры. Когда это карта Земли, часто встречаются различные искажения. Если вы взяли глобус и разрезали его примерно через каждые 15 ° долготы, в результате пробок (см. рисунок слева) можно было уложить ровно. Это было бы довольно точно, но довольно неудобно — разные части одна и та же страна будет на разных глубинах и фактической форме этих стран трудно увидеть.Исторически сложилось так, что проекция Меркатора , созданная обычно используется фламандский картограф 1569 года. Особенно искажены земельные участки вблизи полюсов, что приводит к Африка (11 миллионов миль 2 ) размером с Гренландию (менее 1 миллиона миль 2 ). Это происходит потому, что проекция Меркатора на самом деле является чистой для цилиндра, а не для сферы. Преобразование можно создать, расширив лучи из центра земли на боковую грань цилиндра.Как указано выше, это преобразование не является изометрией. Однако он сохраняет промежуточность и коллинеарность, по линиям долготы и широты. Таким образом, четыре направления (север, юг, восток и запад) находятся на перпендикулярных линиях.
Изучив карты, Фрэнсис Гатри в 1852 году предположил, что любой карту на сфере или плоскости можно выделить / раскрасить всего четыре цвета. Легко видеть, что необходимы четыре цвета (см. Справа).Однако доказательство достаточности части было завершено только в 1976 году. Даже тогда доказательство, предоставленное Хакеном и Аппелем , было спорным. уже много лет. Споры возникли из-за того, что они использовали компьютер чтобы доказать, что нужны были только четыре цвета для каждого из 1952 типов возможных карт. Проблема была встроена в теория графов перед этим анализом.
| Теорема о четырех цветах . Предположим, что области, имеющие общую границу некоторой длины, должны иметь различные цвета.Тогда любая карта регионов на плоскости или сфере может быть раскрашенным таким образом, чтобы нужно было всего четыре цвета. Предположено Гутри в 1852 году; доказано Хакеном и Аппелем в 1976 г. |
Ниже представлен раздаточный материал для домашнего задания 9.8 №26. (Где-то добавить угол наклона / склонения и график двугранных углов.)
Части трехмерных фигур
В геометрии трехмерная фигура — это твердое тело, объект или фигура с тремя измерениями — длиной, шириной и высотой.В отличие от двухмерных форм, трехмерные формы имеют толщину или глубину.
Атрибуты трехмерной фигуры — это грани, ребра и вершины. Три измерения составляют края трехмерной геометрической формы.
Ниже приведены части трехмерной фигуры.
Грани:
Плоские поверхности трехмерных фигур называются гранями.
Кромка:
Сегмент линии, на котором встречаются две грани, называется ребром.
Вершина:
Вершина — это точка, где встречаются 3 ребра.
Пример 1:
Назовите следующую трехмерную фигуру. Также найдите количество граней, ребер и вершин.
Решение:
Название формы = Треугольная пирамида
Граней:
Наблюдая за фигурой выше, мы узнаем, что есть четыре грани.
Имя каждой грани: Грань 1 = ABD Грань 2 = ABC Грань 3 = BCD Грань 4 = ACD |
Края:
Края — это прямые линии, используемые для рисования изображения.
Чтобы нарисовать треугольную пирамиду выше, мы использовали 6 граней. Это
AC, AB, BC, BD, CD и AD.
Вершины:
Вершины — это углы, где встречаются 3 ребра.
Здесь стороны AC, AB и AD пересекаются в точке A. Итак, «A» — одна из вершин данной треугольной пирамиды. Точно так же ребра — это B, C и D.
Итак, данная треугольная пирамида имеет 4 грани, 6 ребер и 4 вершины.
Пример 2:
Назовите следующую трехмерную фигуру.Также найдите количество граней, ребер и вершин.
Решение:
Имя формы = Куб
Грани:
Наблюдая за приведенным выше рисунком, мы узнаем, что существует шесть граней.
Имя каждой грани: Лицевая сторона 1 = ABCD Лицевая сторона 2 = ACEF Лицевая сторона 3 = CDEF Лицевая сторона 4 = BDHG Лицевая сторона 5 = ABEH (Задняя сторона) Лицевая сторона 6 = CDFG (Передняя сторона) |
Края: Края — это прямые линии, используемые для рисования изображения.Здесь мы использовали 12 прямых линий, чтобы нарисовать куб. AB, AC, CD, BD, AE, CF, EF, FG, EH, GH, DG, BH |
Вершины: Вершины — это углы, где встречаются 3 ребра. Вершины: A, B, C, D, E, F, G, H. |
Итак, данный куб имеет 6 граней, 12 ребер и 8 вершин.
Пример 3:
Назовите следующую трехмерную фигуру.Также найдите количество граней, ребер и вершин.
Решение:
Название формы = Пятиугольная пирамида
Граней:
Наблюдая за приведенным выше рисунком, мы узнаем, что существует шесть граней.
Имя каждой грани: Сторона 1 = ABF Сторона 2 = AFE Сторона 3 = AED Сторона 4 = ACD Сторона 5 = ABC Сторона 6 = BCDEF (основа) | ||
Края: Края — это прямые линии, используемые для рисования изображения.Здесь мы использовали 10 прямых линий, чтобы нарисовать пятиугольную призму. AB, AF, AC, AD, AE, BF, BC, CD, DE, EF | ||
Вершины: Вершины — это углы, где встречаются 3 ребра. Вершины: A, B, C, D, E, F. |
Итак, данная пятиугольная пирамида имеет 6 граней, 10 ребер и 6 вершин.
Помимо вышеперечисленного, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.
Если у вас есть отзывы о наших математических материалах, напишите нам:
Мы всегда ценим ваши отзывы.
Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.
ЗАДАЧИ СО СЛОВАМИ
Задачи со словами HCF и LCM
Задачи со словами на простых уравнениях
Задачи со словами на линейных уравнениях
Задачи со словами на квадратных уравнениях
Алгебра 32 Проблемы со словами
Проблемы со словами в поездах
Проблемы со словами по площади и периметру
Проблемы со словами по прямому и обратному изменению
Проблемы со словами по цене за единицу
Проблемы со словами по цене за единицу
Word задачи по сравнению ставок
Преобразование обычных единиц в текстовые задачи
Преобразование метрических единиц в текстовые задачи
Word задачи по простому проценту
Word задачи по сложным процентам
Word по типам ngles
Проблемы со словами с дополнительными и дополнительными углами
Проблемы со словами с двойными фактами
Проблемы со словами тригонометрии
Проблемы со словами в процентах
Проблемы со словами о прибылях и убытках Word
Разметка и разметка Задачи
Задачи с десятичными словами
Задачи со словами о дробях
Задачи со словами о смешанных дробях
Одношаговые задачи с уравнениями со словами
Проблемы с линейными неравенствами
Слово пропорции Задачи
Проблемы со временем и рабочими словами
Задачи со словами на множествах и диаграммах Венна
Проблемы со словами на возрастах
Проблемы со словами в теореме Пифагора
Процент числового слова pr проблемы
Проблемы со словами при постоянной скорости
Проблемы со словами при средней скорости
Проблемы со словами при сумме углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Сокращения прибылей и убытков
Сокращение в процентах
Сокращение в таблице времен
Сокращение времени, скорости и расстояния
Сокращение соотношения и пропорции
Домен и диапазон рациональных функций
Домен и диапазон рациональных функций функции с отверстиями
Графики рациональных функций
Графики рациональных функций с отверстиями
Преобразование повторяющихся десятичных дробей в дроби
Десятичное представление рациональных чисел
Поиск квадратного корня с помощью long di видение
Л.Метод CM для решения задач времени и работы
Преобразование задач со словами в алгебраические выражения
Остаток при делении 2 в степени 256 на 17
Остаток при делении 17 в степени 23 на 16
Сумма всех трехзначных чисел, делимых на 6
Сумма всех трехзначных чисел, делимых на 7
Сумма всех трехзначных чисел, делимых на 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
Калькулятор треугольной призмыФорма треугольной призмы
a = длина стороны a
b = длина стороны b = основание нижнего треугольника b
c = длина стороны c
h = высота призмы
H = высота нижнего треугольника
В = объем
A tot = общая площадь = со всех сторон
A lat = площадь боковой поверхности = все прямоугольные стороны
A верх = площадь верхней поверхности = верхний треугольник
A bot = площадь нижней поверхности = нижний треугольник
Треугольная призма — это твердое геометрическое тело с треугольником в основе.Это трехсторонняя призма, в которой основание и верх — равные треугольники, а остальные 3 стороны — прямоугольники.
Использование калькулятора
Калькулятор позволяет найти объем, площадь поверхности и высоту треугольной призмы. Расчет площади поверхности включает верхнюю, нижнюю, боковые стороны и общую площадь поверхности. Высота рассчитывается исходя из известного объема или площади боковой поверхности.
Единицы: Единицы показаны для удобства, но не влияют на вычисления.Ответы будут одинаковыми в футах, футах 2 , футах 3 или метрах, 2 м, м 3 или любой другой единице измерения.
Значащие цифры: Выберите количество значащих цифр или оставьте значение «Авто», чтобы калькулятор определял точность чисел.
Формулы треугольной призмы по высоте и длинам сторон треугольника a, b и c:
Формула объема треугольной призмы
Находит 3-мерное пространство, занятое треугольной призмой.
\ [V = \ dfrac {1} {4} h \ sqrt {(a + b + c) (b + c-a) (c + a-b) (a + b-c)} \]
\ [V = \ dfrac {1} {4} h \ sqrt {(c + ab) (a + bc)} \\\ times \ sqrt {(a + b + c) (b + ca)} \]
Площадь верхней поверхности треугольной призмы по формуле
Находит площадь треугольной поверхности наверху призмы. Это та же область, что и нижняя поверхность.
\ [A_ {top} = \ dfrac {1} {4} \ sqrt {(a + b + c) (b + c-a) (c + a-b) (a + b-c)} \]
\ [A_ {top} = \ dfrac {1} {4} \ sqrt {(c + ab) (a + bc)} \\\ times \ sqrt {(a + b + c) (b + ca)} \]
Площадь нижней поверхности треугольной призмы по формуле
Находит площадь треугольной поверхности в нижней части призмы.Это та же область, что и верхняя поверхность.
\ [A_ {bot} = \ dfrac {1} {4} \ sqrt {(a + b + c) (b + c-a) (c + a-b) (a + b-c)} \]
\ [A_ {бот} = \ dfrac {1} {4} \ sqrt {(c + ab) (a + bc)} \\\ times \ sqrt {(a + b + c) (b + ca)} \]
Площадь боковой поверхности треугольной призмы по формуле
Находит общую площадь трех прямоугольных сторон призмы. Вы можете представить себе площадь боковой поверхности как общую площадь поверхности призмы за вычетом двух треугольных областей вверху и внизу призмы.
\ [A_ {lat} = h (a + b + c) \]Общая площадь поверхности треугольной призмы по формуле
Находит общую площадь всех сторон треугольной призмы. Общая площадь поверхности призмы включает площадь верхней и нижней сторон треугольника призмы, а также площадь всех трех сторон прямоугольника.
\ [A_ {tot} = A_ {верх} + A_ {бот} + A_ {широта} \]Высота треугольной призмы по формуле
Находит высоту треугольной призмы, решая формулу объема для высоты.Высота h рассчитывается из объема V и длин сторон a, b и c.
\ [h = \ dfrac {4V} {\ sqrt {(a + b + c) (b + c-a) (c + a-b) (a + b-c)}} \]
\ [h = 4V \ div \ left [\, \ sqrt {(c + ab) (a + bc)} \\\ times \ sqrt {(a + b + c) (b + ca)} \, \ справа] \]
Формула высоты треугольной призмы через площадь боковой поверхности
Находит высоту треугольной призмы, решая формулу площади боковой поверхности для высоты.Высота h рассчитывается из площади боковой поверхности A lat и длин сторон a, b и c.
\ [h = \ dfrac {A_ {lat}} {(a + b + c)} \]Номер ссылки
Weisstein, Eric W. «Площадь треугольника». Из MathWorld — веб-ресурса Wolfram, Площадь треугольника.
ГЕОМЕТРИЯ — Тематические тексты
Главная → ГЕОМЕТРИЯ — Тематические текстыТекст 1
Геометрия позволяет нам исследовать свойства пространства в терминах плоских (двухмерных) фигур и твердых (трехмерных) фигур.Мы можем использовать геометрические методы, чтобы нарисовать линию точной длины, разрезать линию пополам, разделить пополам угол, построить треугольник и вычислить площадь сферы. Принципы геометрии были заложены греческим математиком Евклидом (ок. 330 г. до н.э. — 275 г. до н.э.) и с тех пор почти не изменились. Картографирование; Геодезия, проектирование, архитектура и компьютерные схемы — все зависит от геометрии в точном использовании углов, фигур и объема.
Текст 2
Треугольники, квадраты и пятиугольники — все это примеры многоугольников.У правильного многоугольника стороны равной длины и внутренние углы равны. Чем больше сторон у правильного многоугольника, тем больше он будет напоминать круг. Есть два вида многоугольников: выпуклые и входящие. У выпуклого многоугольника все углы направлены внутрь. У входящего многоугольника один или несколько углов направлены внутрь.
Текст 3
Углы образуются в месте пересечения двух прямых линий. Их можно измерить с помощью транспортира или указателя угла. Углы измеряются в единицах, называемых градусами.Градус получается делением окружности круга на 360 частей равного размера. Математики используют маленький кружок как символ для обозначения градусов. Угол, который образует углы квадратов и других прямоугольников, составляет 90 градусов и называется прямым углом. Углы меньше 90 называются острыми углами. Углы от 90 до 180 называются тупыми углами. Углы от 180 до 360 называются углами отражения.
Текст 4
Преобразование — это изменение положения, размера или формы геометрической фигуры (например, треугольника).Основные преобразования — это отражение, увеличение, перемещение и вращение. Другие формы трансформации включают растяжение и сдвиг. Отражение, перемещение и вращение изменяют положение фигуры. Они не изменяют длину сторон или площадь фигуры, и поэтому называются изометриями. Растяжка увеличивает размер фигуры по одной оси. Стрижка похожа на растяжку, но площадь фигуры остается прежней. Увеличение увеличивает размер всей фигуры.
Текст 5
Топология — это современная отрасль геометрии, которая решает реальные проблемы, например, как спланировать пересечение автострад, и превращает их в пространственные головоломки. Пространственные головоломки можно использовать для представления трехмерных задач в двухмерном виде. Это часто упрощает решение проблемы. Топология выросла из попыток решить проблему Кенигсбергского моста.
Сплошные фигуры и объем | GMAT бесплатно
Официальный объем GMAT охватывает два типа трехмерных фигур:
- Прямоугольные тела , также известные как прямоугольные призмы; и
- Цилиндры .
Прямоугольный массив
При работе с прямоугольной призмой может потребоваться вычислить площадь или площадь поверхности. Если размеры твердого тела a, b, и c , то площадь равна
и площадь
При вычислении площади поверхности мы просто вычисляем и складываем площадь трех пар прямоугольников. Если вы думаете о размерах как о длине, ширине и высоте, тогда (то же самое) уравнение будет
.Удобный способ представить уравнение объема — это
В случае прямоугольного твердого тела «основанием» может быть любая из сторон, состоящая из двух измерений, а «высота» — это длина продолжения формы по окончательному размеру.
Эта область для объема применяется не только к прямоугольным твердым телам, но и к цилиндрам:
В данном случае основание — круг. Если нам говорят, что цилиндр является «правильным правильным цилиндром», или мы знаем, что высота перпендикулярна основанию, тогда мы получаем объем, просто умножая площадь круга на высоту:
Площадь поверхности этого цилиндра состоит из верхнего круга, нижнего круга и единственной изогнутой стороны.Если вы думаете об одной изогнутой стороне как об этикетке или обертке на цилиндре, вы можете представить, как развернуть ее, и увидеть, что это прямоугольник высотой х и длиной, равной длине окружности. Следовательно, площадь поверхности составляет
Наконец, хотите верьте, хотите нет, но объем сферы не упоминается в официальных математических рамках GMAT, но, чтобы успокоить скептиков среди вас, я напомню вам, что формула объема сферы составляет
Практические вопросы
Объем двух коробок:
http: // www.gmatfree.com/volume-of-two-boxes
Расстояние в коробке:
http://www.gmatfree.com/distance-within-a-box
Объем из области:
http://www.gmatfree.com/volume-from-area
12-1 Представления трехмерных фигур
1 Соедините точки на бумаге с изометрическими точками, чтобы обозначить края твердого тела.Заштрихуйте верхнюю часть 12-1 изображений трехмерных фигур. Используйте бумагу с изометрическими точками, чтобы зарисовать каждую призму. 1. Треугольная призма высотой 2 единицы с двумя сторонами основания, длина которых составляет 5 единиц и 4 единицы длины. Отметьте угол твердого тела. Нарисуйте 2 единицы вниз, 4 единицы влево и 5 единиц вправо. Затем нарисуйте треугольник в качестве вершины тела. Нарисуйте сегменты на 2 единицы вниз от каждой вершины для вертикальных ребер. Соедините соответствующие вершины, используя пунктирную линию для скрытого края. 2.прямоугольная призма высотой 2 единицы, шириной 3 единицы и длиной 5 единиц Отметьте передний угол твердого тела. Нарисуйте 2 единицы вниз, 3 единицы слева и 5 единиц вправо. Нарисуйте 3 единицы слева от этой последней точки. Затем нарисуйте прямоугольник в верхней части тела. Нарисуйте сегменты на 2 единицы вниз от каждой вершины для вертикальных ребер. Соедините соответствующие вершины, используя пунктирные линии для скрытых краев. 2. Прямоугольная призма высотой 2 единицы, шириной 3 единицы и длиной 5 единиц Отметьте передний угол твердого тела. Нарисуйте 2 единицы вниз, 3 единицы слева и 5 единиц вправо.Нарисуйте 3 единицы слева от этой последней точки. Затем нарисуйте прямоугольник в верхней части тела. Нарисуйте сегменты на 2 единицы вниз от каждой вершины для вертикальных ребер. Соедините соответствующие вершины, используя пунктирные линии для скрытых краев. 3. Используйте бумагу с изометрическими точками и каждый орфографический рисунок, чтобы зарисовать твердое тело. вид сверху: две строки и три столбца. вид слева: Высота фигуры 4 единицы сзади и 3 единицы спереди. вид спереди: темный сегмент указывает на другую высоту. вид справа: высота фигуры 4 единицы сзади и 3 единицы спереди.Руководство esolutions — Создано Cognero Страница 1
2 12-1 Представления трехмерных фигур Используйте бумагу с изометрическими точками и каждый орфографический рисунок для рисования твердого тела. 3. вид сверху: две строки и три столбца. вид слева: Высота фигуры 4 единицы сзади и 3 единицы спереди. вид спереди: темный сегмент указывает на другую высоту. вид справа: высота фигуры 4 единицы сзади и 3 единицы спереди.4. вид сверху: три строки и три столбца. Правый средний столбец отсутствует. вид слева: Высота фигуры 3 единицы. вид спереди: ширина фигуры 3 единицы. вид справа: темные сегменты указывают на изменение глубины, в то время как средний столбец справа отсутствует. Соедините точки на бумаге изометрических точек, чтобы обозначить края твердого тела. Заштрихуйте верхушки каждого столбика. Соедините точки на бумаге с изометрическими точками, чтобы обозначить края твердого тела. Заштрихуйте верхушки каждого столбика. 5. ЕДА Опишите, как можно нарезать сыр так, чтобы кусочки формировали каждую форму.а. прямоугольник b. треугольник c. трапеция 4. Руководство esolutions — Powered by Cognero Страница 2 вид сверху: три ряда и три a. Ломтик сыра имеет форму треугольной призмы.
3 12-1 Представление трехмерных фигур a. Ломтик сыра имеет форму треугольной призмы. Вид спереди, справа или слева на ломтик сыра представляет собой прямоугольник.Итак, чтобы кусочек получился прямоугольной формы, нужно разрезать его вертикально. 6. а. нарезать вертикально b. разрезать по горизонтали c. срез под углом Опишите каждое поперечное сечение. б. Вид сверху на ломтик сыра представляет собой треугольник. Итак, чтобы получился ломтик треугольной формы, нужно разрезать его по горизонтали. Вертикальная плоскость разделит призму на две части с поперечным сечением прямоугольника. прямоугольник c. Правый или левый вид ломтика сыра представляет собой прямоугольник. Итак, чтобы срез получился трапециевидной формы, нужно разрезать его под углом.7. Горизонтальная плоскость, проходящая через вершину, разрежет конус на две части с поперечным сечением треугольника. 6. а. нарезать вертикально b. разрезать по горизонтали c. срез под углом Опишите каждое поперечное сечение. Треугольник Используйте бумагу с изометрическими точками, чтобы нарисовать каждую призму. 8. Куб 3 единицы на каждом краю. Отметьте передний угол твердого тела. Нарисуйте 3 единицы вниз, 3 единицы слева и 3 единицы вправо. Затем нарисуйте 3 единицы слева от этой последней точки. Нарисуйте квадрат в верхней части твердого тела. Нарисуйте сегменты на 3 единицы вниз от каждой вершины для вертикальных ребер.Соедините соответствующие вершины, используя пунктирные линии для скрытых краев. Руководство esolutions — При поддержке Cognero Стр. 3
4 конус на две части с поперечным сечением треугольника. Представления трехмерных фигур треугольник Используйте изометрическую точечную бумагу, чтобы нарисовать каждую призму. 8. Куб 3 единицы на каждом краю. Отметьте передний угол твердого тела. Нарисуйте 3 единицы вниз, 3 единицы слева и 3 единицы вправо.Затем нарисуйте 3 единицы слева от этой последней точки. Нарисуйте квадрат в верхней части твердого тела. Нарисуйте сегменты на 3 единицы вниз от каждой вершины для вертикальных ребер. Соедините соответствующие вершины, используя пунктирные линии для скрытых краев. 9. Треугольная призма высотой 4 единицы с двумя сторонами основания, длина которых составляет 1 единицу и 3 единицы длины. Отметьте угол твердого тела. Вытяните 4 юнита вниз, 1 юнит влево и 3 юнита вправо. Затем нарисуйте треугольник в качестве вершины тела. Нарисуйте сегменты на 4 единицы вниз от каждой вершины для вертикальных ребер.Соедините соответствующие вершины, используя пунктирную линию для скрытого края. 9. Треугольная призма высотой 4 единицы с двумя сторонами основания, длина которых составляет 1 единицу и 3 единицы длины. Отметьте угол твердого тела. Вытяните 4 юнита вниз, 1 юнит влево и 3 юнита вправо. Затем нарисуйте треугольник в качестве вершины тела. Нарисуйте сегменты на 4 единицы вниз от каждой вершины для вертикальных ребер. Соедините соответствующие вершины, используя пунктирную линию для скрытого края. 10. Треугольная призма высотой 4 единицы с двумя сторонами основания, длина которых составляет 2 единицы и длину 6 единиц. Отметьте угол твердого тела.Нарисуйте 4 единицы вниз, 6 единиц влево и 2 единицы вправо. Затем нарисуйте треугольник в качестве вершины тела. Нарисуйте сегменты на 4 единицы вниз от каждой вершины для вертикальных ребер. Соедините соответствующие вершины, используя пунктирную линию для скрытого края. Руководство esolutions — При поддержке Cognero Стр. 4
5 12-1 Представление трехмерных фигур 10. Треугольная призма высотой 4 единицы, с двумя сторонами основания, длина которых составляет 2 единицы и длину 6 единиц. Отметьте угол твердого тела.Нарисуйте 4 единицы вниз, 6 единиц влево и 2 единицы вправо. Затем нарисуйте треугольник в качестве вершины тела. Нарисуйте сегменты на 4 единицы вниз от каждой вершины для вертикальных ребер. Соедините соответствующие вершины, используя пунктирную линию для скрытого края. 11. ИНСТРУМЕНТЫ CCSS Используйте бумагу с изометрическими точками и каждый орфографический рисунок, чтобы нарисовать твердое тело. ИНСТРУМЕНТЫ CCSS Используйте бумагу с изометрическими точками и каждый орфографический рисунок для создания твердого эскиза esolutions. Руководство — Powered by Cognero Страница 5
6 12-1 Представление трехмерных фигур. Руководство по esolutions — Powered by Cognero Страница 6
7 12-1 Изображение трехмерных фигур 15.ИСКУССТВО Кусок глины в форме прямоугольной призмы разрезают пополам, как показано справа. а. Опишите форму поперечного сечения. б. Опишите, как можно разрезать глину, чтобы поперечное сечение получилось треугольником. 14. а. Призма вид спереди представляет собой прямоугольник, поэтому при вертикальном разрезе поперечное сечение будет прямоугольным. б. В каждой вершине пересекаются три ребра. Итак, если отрубить кусок пластилина, получится треугольное сечение. 15. ИСКУССТВО Кусок глины в форме прямоугольной призмы разрезают пополам, как показано справа.а. Опишите форму поперечного сечения. б. Опишите, как можно разрезать глину, чтобы поперечное сечение получилось треугольником. а. прямоугольник b. Отрежьте от глины уголок. Опишите каждое поперечное сечение. а. 16. Вертикальная плоскость разрежет призму на две части с поперечным сечением прямоугольника. Призма вид спереди представляет собой прямоугольник, поэтому при вертикальном разрезе поперечное сечение будет прямоугольным. б. Руководство esolutions — При поддержке Cognero Страница 7 прямоугольник
8 секция а.Прямоугольник представлений трехмерных фигур b. Отрежьте от глины уголок. шестиугольник Опишите каждое поперечное сечение. 16. Вертикальная плоскость разрежет призму на две части с поперечным сечением прямоугольника. 18. Основание конуса — круг. Итак, плоскость, параллельная основанию, даст сечение круга. прямоугольник окружности 17. Основания призмы — шестиугольники. Итак, плоскость, параллельная основанию, даст сечение шестиугольника. 19. Две противоположные стороны поперечного сечения, приходящего на соседние стороны призмы, будут параллельны друг другу.Другая пара противоположных сторон, которые пересекают основания призмы, не будут параллельны. Следовательно, сечение будет трапециевидным. Шестигранная трапеция 18. Основание конуса — круг. Итак, плоскость, параллельная основанию, даст сечение круга. 20. АРХИТЕКТУРА Нарисуйте вид сверху, вид спереди и вид сбоку на дом. Хотя глубина различается, вид сверху представляет собой два соседних прямоугольника, напоминающих больший размер. Руководство по esolutions — Powered by Cognero Page 8
9 12-1 Изображение трехмерных фигур трапеция 20.АРХИТЕКТУРА Нарисуйте вид сверху, вид спереди и вид сбоку на дом. Хотя глубина разная, вид сверху представляет собой два соседних прямоугольника, напоминающих прямоугольник большего размера. Вид спереди — треугольник (крыша) поверх прямоугольника. Хотя глубина разная, вид сверху представляет собой большой прямоугольник над меньшим прямоугольником, напоминающий еще больший прямоугольник. ПЕЧЕНЬЕ Опишите, как надрезать рулет из теста для печенья в форме цилиндра, чтобы получилась каждая форма. 21. круг Вертикальное поперечное сечение цилиндра — это круг, поэтому вам нужно сделать вертикальный разрез в цилиндре, чтобы создать круг.ПЕЧЕНЬЕ Опишите, как надрезать рулет из теста для печенья в форме цилиндра, чтобы получилась каждая форма. 21. круг Вертикальное поперечное сечение цилиндра — это круг, поэтому вам нужно сделать вертикальный разрез в цилиндре, чтобы создать круг. сделайте вертикальный разрез 22. самый длинный прямоугольник. Если разрезать по длине цилиндра, получится прямоугольник. Самый большой прямоугольник получится в результате разрезания цилиндра вдоль его длины через центр. Сделайте горизонтальный разрез в центре оснований.23. овал Овал представляет собой удлиненный круг. Вырежьте тесто для печенья так же, как если бы вы нарезали его, чтобы получился круг, но под углом. Сделайте вертикальный разрез esolutions Manual — Powered by Cognero Страница самый длинный прямоугольник
10 12-1 Сделайте изображения горизонтальным разрезом через трехмерный центр оснований фигур. 23. овал Овал представляет собой удлиненный круг. Вырежьте тесто для печенья так же, как если бы вы нарезали его, чтобы получился круг, но под углом.25. Сделайте горизонтальный разрез не через центр оснований. ИНСТРУМЕНТЫ CCSS Нарисуйте поперечный разрез из вертикального среза каждой фигуры. Поперечный разрез из вертикального среза будет выглядеть так же, как вид спереди фигуры, который выглядит как прямоугольник и треугольник. Прямоугольник представляет собой цилиндр спереди. Треугольник представляет собой вид конуса спереди. Сделайте надрез под углом 24. Более короткий прямоугольник Чтобы получить более короткий прямоугольник, вам нужно сделать надрез по длине цилиндра, но не через центр.Сделайте горизонтальный разрез не через центр оснований. 26. Поперечное сечение вертикального среза будет выглядеть так же, как вид спереди фигуры, которая выглядит как квадрат поверх прямоугольника. Прямоугольник представляет собой вид призмы спереди. Квадрат представляет собой вид куба спереди. 25. ИНСТРУМЕНТЫ CCSS Нарисуйте поперечное сечение из вертикального среза каждой фигуры. Поперечный разрез из вертикального среза будет выглядеть так же, как вид спереди фигуры, который выглядит как прямоугольник и треугольник.Прямоугольник представляет собой цилиндр спереди. Треугольник представляет собой вид конуса спереди. Руководство esolutions — При поддержке Cognero Стр. 10
11 12-1 Представление трехмерных фигур 26. Поперечное сечение вертикального среза будет выглядеть так же, как вид спереди фигуры, который выглядит как квадрат поверх прямоугольника. Прямоугольник представляет собой вид призмы спереди.Квадрат представляет собой вид куба спереди. 27. Поперечное сечение из вертикального среза будет выглядеть так же, как на виде спереди фигуры, которая выглядит как прямоугольник с маленькими квадратами, вырезанными из каждого угла. Квадратные отверстия представляют собой углубления на рисунке. 27. Поперечное сечение из вертикального среза будет выглядеть так же, как на виде спереди фигуры, которая выглядит как прямоугольник с маленькими квадратами, вырезанными из каждого угла. Квадратные отверстия представляют собой углубления на рисунке.28. НАУКА О ЗЕМЛЕ Кристаллы — это твердые тела, в которых атомы расположены в правильных геометрических формах. Нарисуйте поперечное сечение из горизонтального среза каждого кристалла. Затем опишите вращательную симметрию относительно вертикальной оси. а. тетрагональный b. шестиугольный c. Руководство по моноклиническим решениям — Powered by Cognero Стр. 11 a. 28. НАУКА О ЗЕМЛЕ Кристаллы — это твердые тела, в которых поперечное сечение от горизонтального среза будет выглядеть как
12 12-1 Представление трехмерных фигур Кристалл остается неизменным через каждые 60 оборотов вокруг оси.c. а. Поперечное сечение горизонтального среза будет выглядеть так же, как на виде сверху фигуры, которая выглядит как квадрат. Как и все квадраты, поворот на 90 приведет к созданию изображения, идентичного прообразу. Кристалл остается неизменным через каждые 90 оборотов вокруг оси. б. Поперечный разрез из горизонтального среза будет выглядеть так же, как на виде сверху фигуры, которая выглядит как правильный шестиугольник. Кристалл остается неизменным на каждые 180 оборотов вокруг оси. 29. ИСКУССТВО В перспективном чертеже точка схода используется для того, чтобы двухмерный рисунок казался трехмерным.С одной точки схода объекты можно рисовать с разных точек зрения, как показано ниже. а. Нарисуйте горизонтальную линию и точку схода на ней. Нарисуйте прямоугольник где-нибудь над линией и используйте точку схода, чтобы нарисовать перспективу. б. На том же рисунке нарисуйте прямоугольник где-нибудь под линией и используйте точку схода, чтобы нарисовать перспективный рисунок. c. Опишите разные виды двух рисунков. Как и все обычные шестиугольники, поворот на 60 дает изображение, идентичное прообразу.Кристалл остается неизменным на каждые 60 оборотов вокруг оси. c. Поперечное сечение горизонтального среза будет выглядеть так же, как вид сверху на фигуре, который выглядит как прямоугольник с двумя треугольными концами. Кристалл остается неизменным на каждые 180 оборотов вокруг оси. а. а. Нарисуйте прямоугольник, горизонтальную линию и точку схода. Соедините вершины прямоугольника с точкой схода. Соединение, которое будет скрыто от просмотра, должно быть заштриховано. Нарисуйте второй прямоугольник ближе к точке схода.Используйте соединения как расположение вершин. Этот прямоугольник следует заштриховать. Кристалл остается неизменным через каждые 90 оборотов вокруг оси. б. Кристалл остается неизменным на каждые 60 оборотов вокруг оси. c. Кристалл остается неизменным на каждые 180 оборотов вокруг оси. 29. ИСКУССТВО На перспективном рисунке точка схода b. Нарисуйте прямоугольник, горизонтальную линию и точку схода. Соедините вершины прямоугольника с точкой схода. Соединение, которое будет скрыто от просмотра, должно быть заштриховано.Нарисуйте второй прямоугольник ближе к точке схода. Используйте соединения как расположение вершин. Это руководство esolutions — Powered by Cognero Страница 12
13 12-1 Изображение трехмерных фигур b. Нарисуйте прямоугольник, горизонтальную линию и точку схода. Соедините вершины прямоугольника с точкой схода. Соединение, которое будет скрыто от просмотра, должно быть заштриховано.Нарисуйте второй прямоугольник ближе к точке схода. Используйте соединения как расположение вершин. Этот прямоугольник следует заштриховать. б. c. На первом рисунке показан вид объекта снизу. На втором рисунке показан вид объекта сверху. Нарисуйте вид сверху, слева, спереди и справа на каждое твердое тело. c. На первом рисунке показан вид объекта снизу. На втором рисунке показан вид объекта сверху. а. 30. Вид сверху. Высота одного столбца блоков отличается от высоты других, поэтому между этими столбцами должна быть показана черная полоса, указывающая на разную высоту.Вид слева: в этом обзоре нет изменений в глубине. Вид справа: этот вид не меняет глубины. б. Вид спереди: один столбец блоков имеет другую высоту, чем другие, поэтому между этими столбцами должна быть показана черная полоса, чтобы указать разную высоту. c. На первом рисунке показан вид объекта снизу. На втором рисунке показан вид объекта сверху. Руководство esolutions — При поддержке Cognero Стр. 13
14 с.На первом рисунке показан вид 12-1 объекта «Представления» снизу. трехмерного изображения На втором рисунке показан вид на объект сверху. Нарисуйте вид сверху, слева, спереди и справа на каждое твердое тело. 30. Вид сверху. Высота одного столбца блоков отличается от высоты других, поэтому между этими столбцами должна быть показана черная полоса, указывающая на разную высоту. Вид слева: в этом обзоре нет изменений в глубине. Вид справа: этот вид не меняет глубины.Вид спереди: один столбец блоков имеет другую высоту, чем другие, поэтому между этими столбцами должна быть показана черная полоса, чтобы указать разную высоту. 31. Вид сверху: каждый столбец блоков имеет разную высоту, чем другие, поэтому между этими столбцами должна быть показана черная полоса, чтобы указать разную высоту. Вид слева: здесь другая глубина, но из этого вида ее не видно, поэтому показаны 6 блоков без черных полос. Вид справа: каждый ряд блоков имеет разную глубину, чем другие, поэтому между этими рядами должна быть показана черная полоса, чтобы указать разную глубину.Вид спереди: при этом виде нет изменения глубины. 31. Вид сверху: каждый столбец блоков имеет разную высоту, чем другие, поэтому между этими столбцами должна быть показана черная полоса, чтобы указать разную высоту. 32. Вид сверху: 2 блока в нижнем левом углу ниже остальных, поэтому необходимо показать черную полосу, чтобы указать разную высоту. Вид слева: 2 блока в правом нижнем углу находятся на другой глубине, чем другие, поэтому необходимо показать черную полосу, чтобы указать разную глубину.Руководство esolutions — При поддержке Cognero Стр. 14
15 12-1 Представление трехмерных фигур 32. Вид сверху: 2 блока в нижнем левом углу ниже остальных, поэтому необходимо показать черную полосу, чтобы указать разную высоту. Вид слева: 2 блока в правом нижнем углу находятся на другой глубине, чем другие, поэтому необходимо показать черную полосу, чтобы указать разную глубину.Вид справа: 2 блока в левом нижнем углу имеют разную глубину, чем другие, поэтому необходимо показать черную полосу, чтобы указать разную глубину. Вид спереди: блоки в нижнем левом углу имеют другую глубину, чем другие, поэтому необходимо показать черную полосу, чтобы указать разную глубину. 33. Показаны трехмерный вид сверху, спереди и справа. а. Сделайте набросок твердого тела. б. Опишите два различных способа изготовления прямоугольного поперечного сечения. c. Установите связь между передним и правым видами твердого тела и поперечными сечениями твердого тела.а. вид сверху: темный сегмент обозначает другую высоту. вид спереди: правая сторона выше левой. вид справа: Верхняя часть с правой стороны имеет изогнутый верх. Соедините точки на бумаге с изометрическими точками, чтобы обозначить края твердого тела. Заштрихуйте верхушки каждого столбика. б. Сделайте горизонтальный разрез в нижней части фигуры или сделайте вертикальный разрез в левой части фигуры. c. Вид спереди твердого тела — это поперечное сечение при продольном вертикальном разрезе.Правый вид твердого тела — это поперечное сечение, когда делается вертикальный разрез в правой части фигуры. 33. Показаны трехмерный вид сверху, спереди и справа. а. Сделайте набросок твердого тела. б. Опишите два различных способа изготовления прямоугольного поперечного сечения. c. Установите связь между передним и правым видами твердого тела и поперечными сечениями твердого тела. а. вид сверху: темный сегмент обозначает другую высоту. а. б. Сделайте горизонтальный разрез в нижней части фигуры или сделайте вертикальный разрез в левой части фигуры.c. Вид спереди твердого тела — это поперечное сечение при продольном вертикальном разрезе. Правый вид твердого тела — это поперечное сечение, когда делается вертикальный разрез в правой части фигуры. 34. НЕСКОЛЬКО ПРЕДСТАВЛЕНИЙ В этой задаче вы будете исследовать изометрические чертежи. а. GEOMETRIC Создание изометрических чертежей esolutions. Руководство — Powered by Cognero Страница 15
16 рисунка.c. Вид спереди твердого тела — это поперечное сечение при продольном вертикальном разрезе. Правый вид 12-1. Представление твердого тела — трехмерное поперечное сечение, когда вертикальные фигуры разрезаются через правую часть фигуры. 34. НЕСКОЛЬКО ПРЕДСТАВЛЕНИЙ В этой задаче вы будете исследовать изометрические чертежи. а. ГЕОМЕТРИЧЕСКИЙ Создание изометрических чертежей трех различных тел. б. ТАБЛИЦА Создайте таблицу, которая включает количество кубов, необходимых для построения твердого тела, и количество квадратов, видимых на изометрическом чертеже.c. ГЛАГОЛЬНАЯ Существует ли корреляция между количеством кубиков, необходимых для построения твердого тела, и количеством квадратов, видимых на изометрическом чертеже? Объясни. б. Подсчитайте количество кубиков для каждого рисунка. Затем подсчитайте количество квадратов, которые вы видите. c. Для верхнего рисунка мы могли бы переместить куб в самый передний край и поместить его справа от куба на 2 места позади него. У нас по-прежнему будет 6 кубиков, но тогда будет 12 квадратов. Нет; количество квадратов на изометрическом чертеже будет зависеть от расположения кубиков, образующих фигуру.а. а. Создайте три рисунка, разных по размеру, форме и количеству используемых кубиков. б. б. Подсчитайте количество кубиков для каждого рисунка. Затем подсчитайте количество квадратов, которые вы видите. c. Нет; количество квадратов на изометрическом чертеже будет зависеть от расположения кубиков, образующих фигуру. 35. ЗАДАЧА Фигура представляет собой поперечное сечение геометрического тела. Опишите твердое тело и его поперечное сечение. Руководство esolutions — При поддержке Cognero Стр. 16 c. Для верхнего рисунка мы могли переместить куб на
17 с.Нет; количество квадратов на чертеже изометрических изображений 12-1 будет трехмерным, в зависимости от расположения фигур кубиков, образующих фигуру. 35. ЗАДАЧА Фигура представляет собой поперечное сечение геометрического тела. Опишите твердое тело и его поперечное сечение. Поперечное сечение можно создать путем разрезания конуса под углом через его боковую сторону и основание, как показано ниже. Конус разрезается под углом через его боковую сторону и основание. 36. АРГУМЕНТЫ CCSS Определите, является ли следующее утверждение истинным или ложным.Объясните свои рассуждения. Если левый, правый, передний и задний ортогональные виды двух объектов одинаковы, то объекты представляют собой одну и ту же фигуру. Ложь; Пример ответа: два тела могут иметь одинаковые виды слева, справа, сзади и спереди, но быть разными. Твердое тело, состоящее из 3-х слоев по 9 блоков (3 x 3) и аналогичного твердого тела, в котором отсутствует стопка из двух (или четырех) центральных блоков на одной из сторон. Все виды имеют размер 3 х 3 квадрата. Вид сверху был бы другим. Конус разрезается под углом через его боковую сторону и основание.36. АРГУМЕНТЫ CCSS Определите, является ли следующее утверждение истинным или ложным. Объясните свои рассуждения. Если левый, правый, передний и задний ортогональные виды двух объектов одинаковы, то объекты представляют собой одну и ту же фигуру. Ложь; Пример ответа: два тела могут иметь одинаковые виды слева, справа, сзади и спереди, но быть разными. Твердое тело, состоящее из 3-х слоев по 9 блоков (3 x 3) и аналогичного твердого тела, в котором отсутствует стопка из двух (или четырех) центральных блоков на одной из сторон. Все виды имеют размер 3 х 3 квадрата.Вид сверху был бы другим. Ложь; Пример ответа: два тела могут иметь одинаковые виды слева, справа, сзади и спереди, но быть разными. Твердое тело, состоящее из 3-х слоев по 9 блоков (3 x 3) и аналогичного твердого тела, в котором отсутствует стопка из двух (или четырех) центральных блоков на одной из сторон. Все виды имеют размер 3 х 3 квадрата. Вид сверху был бы другим. 37. ОТКРЫТЫЙ КОНЕЦ Используйте изометрическую точечную бумагу, чтобы нарисовать твердое тело, состоящее из 12 кубических единиц. Затем нарисуйте ортогональный чертеж твердого тела. Ложь; Пример ответа: два тела могут иметь одинаковые виды слева, справа, сзади и спереди, но быть разными.Твердое тело, состоящее из 3-х слоев по 9 блоков (3 x 3) и аналогичного твердого тела, в котором отсутствует стопка из двух (или четырех) центральных блоков на одной из сторон. Все виды имеют размер 3 х 3 квадрата. Вид сверху был бы другим. 37. ОТКРЫТЫЙ КОНЕЦ Используйте изометрическую точечную бумагу, чтобы нарисовать твердое тело, состоящее из 12 кубических единиц. Затем нарисуйте ортогональный чертеж твердого тела. Используйте 12 блоков. В качестве примера ответа у нас есть два квадрата по 4 блока в каждом, расположенные друг на друге. Затем у нас есть 2 набора по 2 блока поверх квадратов.Обратите внимание, что вид спереди слева на изображении представляет собой вид спереди твердого тела. Для вида сверху: в середине есть темный сегмент, обозначающий разную высоту. Для левого представления: столбец высотой 4 блока находится сзади, поэтому в левом представлении он будет слева, а столбец из 2 блоков — справа. Для вида спереди: темный сегмент посередине представляет разные глубины. Для правого обзора: столбец высотой 4 блока находится сзади, поэтому в правом обзоре он будет справа, а столбец из 2 блоков — слева.Руководство esolutions — При поддержке Cognero Страница 17
18 различных твердых тел. Твердое тело, состоящее из 3 слоев по 9 блоков (3 x 3), и аналогичное твердое тело, в котором отсутствует стопка из двух (или четырех) центральных блоков на одной из сторон 12-1. Представления Все виды представляют собой 3 x 3 трехмерных квадрата. Цифры сверху будут разными. 37. ОТКРЫТЫЙ КОНЕЦ Используйте изометрическую точечную бумагу, чтобы нарисовать твердое тело, состоящее из 12 кубических единиц.Затем нарисуйте ортогональный чертеж твердого тела. Используйте 12 блоков. В качестве примера ответа у нас есть два квадрата по 4 блока в каждом, расположенные друг на друге. Затем у нас есть 2 набора по 2 блока поверх квадратов. Обратите внимание, что вид спереди слева на изображении представляет собой вид спереди твердого тела. Для вида сверху: в середине есть темный сегмент, обозначающий разную высоту. Для левого представления: столбец высотой 4 блока находится сзади, поэтому в левом представлении он будет слева, а столбец из 2 блоков — справа.Для вида спереди: темный сегмент посередине представляет разные глубины. Для правого обзора: столбец высотой 4 блока находится сзади, поэтому в правом обзоре он будет справа, а столбец из 2 блоков — слева. 38. ЗАДАЧА Нарисуйте вид сверху, вид спереди и вид слева твердой фигуры справа. Вид сверху: 2 блока в центре слева имеют отверстия, поэтому необходимо показать черную полосу, чтобы указать разную глубину. Вид слева: средний блок и верхний правый блок находятся на разной глубине, поэтому необходимо разместить черную полосу.. Вид спереди: 2 блока в середине вверху имеют большую глубину, поэтому необходимо показать черную полосу, чтобы указать разную глубину. 38. ЗАДАЧА Нарисуйте вид сверху, вид спереди и вид слева твердой фигуры справа. Вид сверху: 2 блока в центре слева имеют отверстия, поэтому необходимо показать черную полосу, чтобы указать разную глубину. Вид слева: средний блок и верхний правый блоки находятся на разной глубине, поэтому черная полоса должна быть 39. ЗАПИСЬ В МАТЕМАТИКЕ Гексагональная пирамида — это срез вершины и основания, так что призма разделена на конгруэнтные части.Опишите поперечное сечение. Есть ли способ разделить фигуру на две совпадающие по форме поперечного сечения? Объясни. Руководство esolutions — При поддержке Cognero Страница 18
19 12-1 Представления трехмерных фигур 39. ЗАПИСЬ В МАТЕМАТИКЕ Гексагональная пирамида — это срез вершины и основания, так что призма разделена на конгруэнтные части. Опишите поперечное сечение.Есть ли способ разделить фигуру на две совпадающие по форме поперечного сечения? Объясни. Если правильная шестиугольная пирамида выше разрезана по вершине ha и синей пунктирной линией, соединяющей op основания, поперечное сечение представляет собой треугольник, как показано справа. Есть шесть различных способов разрезать пирамиду на две равные части, потому что фигура имеет симметрию si. Каждый срез должен проходить через вершину t и одну из шести линий симметрии шестиугольника, показанного ниже. В каждом случае поперечное сечение представляет собой треугольник.Только длины сторон треугольников среза смены проходят через линию симметрии, проходящую через шестиугольник, тогда две стороны треугольного креста имеют длину, равную длине сторон tr граней. Когда срез проходит через символьную линию через середины двух сторон шестиугольника, th треугольного сечения будет иметь длину, равную длине треугольных граней пирамиды. Поперечное сечение — треугольник. Пирамида состоит из шести различных срезов, так что образуются две равные части, фигура имеет шесть плоскостей симметрии.В каждом случае это равнобедренный треугольник. Меняются только длины сторон tr. 40. Какой многогранник представлен сеткой, показанной ниже? A куб B октаэдр C треугольная призма D треугольная пирамида Сетка состоит из 4 равносторонних треугольников. Соединив вершины большего треугольника, мы получим треугольную пирамиду. Следовательно, правильный выбор — D. D 41. РАСШИРЕННЫЙ ОТВЕТ Домовладелец хочет построить колоду шириной 3 фута вокруг своего круглого бассейна, как показано ниже. а. Найдите внешний периметр палубы до ближайшего фута, если окружность бассейна составляет около футов.б. Какова площадь верхней части колоды? а. Длина каждой стороны внутренней стороны колоды равна диаметру круга. Используйте формулу, чтобы найти диаметр круга. Ширина стола составляет 3 фута, поэтому длина каждой стороны внешней стороны стола = 32 фута. Поперечное сечение представляет собой треугольник. Пирамида состоит из шести различных срезов, так что образуются две равные части, фигура имеет шесть плоскостей симметрии. В каждом случае это равнобедренный треугольник. Меняются только длины сторон tr.Периметр внешней стороны стола составляет 4 (32) = 128 футов b. Площадь колоды — это разница между площадями двух квадратов. 40. Какой многогранник представлен сеткой, показанной ниже? а. внутренняя сторона палубы = окружность бассейна = π 26 футов; внешняя сторона палубы = = 32 фута; Руководство esolutions — При поддержке Cognero Стр. 19
20 вершин большего треугольника мы получим треугольную пирамиду Следовательно, правильный выбор — D Представления трехмерных фигур D 41.РАСШИРЕННЫЙ ОТВЕТ Домовладелец хочет построить колоду шириной 3 фута вокруг своего круглого бассейна, как показано ниже. а. внутренняя сторона палубы = окружность бассейна = π 26 футов; внешняя сторона палубы = = 32 фута; внешний периметр палубы = 4 32 = 128 футов; б. площадь палубы = (2 3 32) + (2 3 26) = 348 квадратных футов 42. АЛГЕБРА Какое неравенство лучше всего описывает график, показанный ниже? а. Найдите внешний периметр палубы до ближайшего фута, если окружность бассейна составляет около футов. б. Какова площадь верхней части колоды? а.Длина каждой стороны внутренней стороны колоды равна диаметру круга. Используйте формулу, чтобы найти диаметр круга. F G H J Ширина стола составляет 3 фута, поэтому длина каждой стороны внешней стороны стола = 32 фута. Периметр внешней стороны стола составляет 4 (32) = 128 футов. B. Площадь колоды — это разница между площадями двух квадратов. а. внутренняя сторона палубы = окружность бассейна = π 26 футов; внешняя сторона палубы = = 32 фута; внешний периметр палубы = 4 32 = 128 футов; б.площадь палубы = (2 3 32) + (2 3 26) = 348 квадратных футов 42. АЛГЕБРА Какое неравенство лучше всего описывает график, показанный ниже? Наклон линии равен, а точка пересечения по оси Y — 1. Итак, уравнение линии: Граница — пунктирная линия, поэтому символ неравенства — <или>. Область под линией заштрихована, значит, знак неравенства <. Следовательно, неравенство лучше всего описывает график.

 Потребуется гофрированная бумага, из которой вырезают длинную полосу и постепенно фиксируют на стебель. В конце крепят на клей ПВА;
Потребуется гофрированная бумага, из которой вырезают длинную полосу и постепенно фиксируют на стебель. В конце крепят на клей ПВА;