Рисунки по координатам
Мы, учителя, постоянно в поиске: как, не меняя содержание материала, найти способы овладения им и его применения, как заинтересовать учащихся в изучении данной темы, как сформировать у них прочные знания. При изучении темы “Координатная плоскость” можно подойти творчески, по данным координатам точек можно нарисовать знакомую картинку. Такие задания увлекают детей, заинтересовывают, и многие сами затем с удовольствием составляют рисунки по координатам. Эта творческая работа носит и воспитательный характер.
Мною и детьми были составлены данные задания, а некоторые из них взяты из еженедельной учебно-методической газеты “Математика”. На координатной плоскости отмечаем точки, заданные своими координатами, в порядке их следования. А затем соединяем каждую точку с предыдущей кривой или отрезком. Что в результате получится, вы увидите в итоге.
Этот сборник заданий поможет любому учителю
организовать творческий подход к изучению
данной темы и получить хорошие результаты в её
усвоении.
Ласточка
(-5; 4), (-7; 4), (-9; 6), (-11; 6), (-12; 5), (-14; 5), (-12; 4), (-14; 3), (-12; 3), (-11; 2), (-10; 2),
(-9; 1), (-9; 0), (-8; -2), (0; -3), (3; -2), (19; -2), (4; 0), (19; 4), (4; 2), (2; 3), (6; 9), (10; 11), (3; 11), (1; 10), (-5; 4), глаз (-10,5; 4,5).
Утка
(3; 0), (1; 2), (-1; 2), (3; 5), (1; 8), (-3; 7), (-5; 8), (-3; 4), (-6; 3), (-3; 3), (-5; 2),(-5; -2), (-2; -3), (-4; -4), (1; -4), (3; -3), (6; 1), (3; 0) и (-1; 5).
Слоник 1
(-1; 4), (-2; 1), (-3; 2), (-4; 2), (-4; 3), (-6; 4), (-6; 6), (-8; 9), (-7; 10), (-6; 10), (-6; 11), (-5; 10), (-4; 10), (-3; 9), (-1; 9,5), (1; 9), (3; 10), (4; 11), (4; 16), (3; 18), (5; 17), (6; 17), (5; 16), (6; 12), (6; 9), (4; 7), (1; 6),
(2; 5), (5; 4), (5; 3), (4; 4), (1; 2), (1; 0), (3; -4), (4; -5), (1;-7), (1; -6), (0; -4), (-2; -7), (-1,5; -8), (-5; -7), (-4; -6), (-5; -4), (-7;-5), (-7; -7), (-6,5; -8), (-10,5; -8), (-10; -7), (-10; -6), (-11; -7),
(-11; -8), (-14; -6), (-13; -5), (-12; -3), (-13; -2), (-14; -3), (-12; 1), (-10; 3),
(-8; 3), (-6; 4), глаз (-1; 7).
Верблюд
(-10; -2), (-11; -3), (-10,5; -5), (-11; -7), (-12; -10), (-11; -13), (-13; -13), (-13,5; -7,5), (-13; -7), (-12,5; -5), (-13; -3), (-14; -1), (-14; 4), (-15; -6), (-15; -3), (-14; 2), (-11; 4), (-10; 8), (-8; 9),
(-6; 8), (-5; 5), (-3;8),(-1;9), (0;8), (0,5;6), (0,5;4), (3;2,5), (4;3), (5;4), (6;6), (8;7), (9,5;7), (10;6), (11,5;5,5), (12;5), (12;4,5), (11;5), (12;4), (11;4), (10;3,5), (10,5;1,5), (10;0), (6;-3),
(2;-5), (1,5;-7), (1,5;-11), (2,5;-13), (1;-13), (0;-5), (-0,5;-11), (0;-13), (-1,5;-13), (-1,5;-7),
(-2;-5), (-3;-4), (-5;-4,5), (-7;4,5), (-9;-5), (-10;-6), (-9;-12), (-8,5;-13), (-10,5;-13), (-10;-9,5), (-11;-7), глаз (8,5;5,5)
Медведь 1
(4;-4), (4;-6), (8,5;-7,5), (9;-7), (9;-6), (9,5;-5), (9,5;-3,5), (10;-3), (9,5;-2,5), (4;5), (3;6), (2;6), (0;5),(-3;5), (-7;3), (-9;-1), (-8;-5), (-8;-7), (-4,5;-8), (-4,5;-7), (-5;-6,5), (-5;-6), (-4,5;-5), (-4;-5), (-4;-7), (-1;-7),(-1;-6), (-2;-6), (-1;-4), (1;-8), (3;-8), (3;-7), (2;-7), (2;-6), (3;-5), (3;-6), (5;-7),
(7;-7), ухо (6;-4), (6;-3), (7;-2,5), (7,5;-3), глаз (8;-6)
Лось
(-2;2), (-2;-4), (-3;-7), (-1;-7), (1;4), (2;3), (5;3), (7;5), (8;3), (8;-3), (6;-7), (8;-7), (10;-2), (10;1), (11;2,5),(11;0), (12;-2), (9;-7), (11;-7), (14;-2), (13;0), (13;5), (14;6), (11;11), (6;12), (3;12), (1;13), (-3;13), (-4;15),(-5;13), (-7;15), (-8;13), (-10;14), (-9;11), (-12;10), (-13;9), (-12;8),
(-11;9), (-12;8), (-11;8), (-10;7), (-9;8),(-8;7), (-7;8), (-7;7), (-6;7), (-4;5), (-4;-4), (-6;-7), (-4;-7), (-2;-4), глаз (-7;11)
Зайчонок
(5;1), (6;2), (6;3), (5;6), (4;7), (5;8), (6;8), (8;9), (9;9), (7;8), (9;8), (6;7),
(7;6), (9;6), (11;5), (12;3), (12;2), (13;3), (12;1), (7;1), (8;2), (9;2), (8;3), (6;1),
(5;1) и (5;7).
Лиса 1
(0,5;0), (1;2), (1;3), (2;4), (3;3,5), (3,5;4), (2,5;5), (2,5;6), (2;6,5), (2;8,5), (1;7), (0,5;6,5),
(-0,5;7), (-0,5;6), (-1;5,5), (-3;3), (-4;1), (-4,5;-1,5), (-4;-2,5), (-4,5;-3,5), (-3,5;-5), (-1;-6), (1;-7), (2;-8), (3,5;-10), (4,5;-9),(4,5;-7), (4;-6), (3;-5), (0;-4,5), (1;-1,5), (0,5;0).
Собака 1.
(1;-3), (2;-3), (3;-2), (3;3), (4;3), (5;4), (5;6), (4;7), (3;7), (2;6), (3;5), (3;5,5), (4;5), (3;4), (2;5), (-3;5),
(-4;6), (-4;9), (-5;10), (-5;11), (-6;10), (-7;10), (-7;10), (-7;8), (-9;8), (-9;7), (-8;6), (-6;6), (-7;3), (-6;2), (-6;-1), ў(-7;-2), (-7;-3), (-6;-3), (-4;-2), (-4;2), (1;2), (2;-1), (1;-2), (1;-3)
Лиса 2
(7,5;5), (-4;7), (-3;7), (-3;9), (1;1), (3;0), (5;-0,5), (7;-4), (7;-8), (10;-5), (13;-3), (17;-2), (19;-2), (17;-3), (14;-7), (7;-9), (6;-10), (2;-10), (2;-9), (5;-9), (3;-8), (1,5;-6), (0,5;-3),(0,5;-10),(-2,5;10), (-2,5;-9), (-1;-9), (-1;-3), (-3;-10), (-6;-10), (-6;-9), (-4,5;-9), (-3;-4), (-3;0,5), (-4;3), (-5;3),
(-7,5;4), (-7,5;5)
Собака 2.
а) (14;-3), (12;-3), (8,5;-2), (4;3), (2;4), (1;5), (1;8), (-2;5), (-3;5), (-6;3), (-7;1), (-11;-1), (-10;-3), (-6;-4), (-2;-4), (-1;-3), (1;-5), (1;-8), (-2;-10), (-11;-10), (-13;-11), (-13;-13), (4;-13), (5;-12),
(9;-12)
б) (14;-10), (10;-10), (9;-11), (9;-13), (14;-13)
Медведь 2
(-18;4), (-18;3), (-17;3), (-18;2), (-17;2), (-11;1), (-9;0), (-8;-1), (-11;-6), (-12;-8), (-14;-10),
(-10;-10), (-8;-6), (-5;-4), (-4;-7), (-4;-8), (-6;-10), (-1;-10), (-1;-2), (1;-4), (5;-4), (5;-8), (3;-10), (8;-10), (10;-4), (12;-6), (10;-8), (15;-8), (14;-2), (15;2), (14;6), (12;8), (8,9), (4;9), (0;8), (-6;9), (-11;7), (-15;6), (-18;4)
Воробей
(-6;1), (-5;-2), (-9;-7), (-9;-8), (-5;-8), (-1;-5), (3;-4), (5;-1), (8;1), (9;3), (2;2), (4;6), (3;11), (2;11), (-2;6), (-2;2), (-4;4), (-5;4), (-6;3), (-6;2), (-7;2), (-6;1)
Ёжик
(2;-1), (3,5;0,5), (4;-1), (5;0), (4;2), (2;1), (2;3), (4;5), (4;6), (2;5), (1;7), (1;8), (0;7), (0;9), (-1;7), (-2;8),(-2;7), (-3;7), (-2;6), (-4;6), (-3;5), (-4;5), (-3;4), (-5;4), (-4;3), (-5;3), (-4;2), (-6;2), (-5;1), (-6;1), (-5;0),(-6;0), (-5;-1), (-6;-2), (-4;-2), (-5;-3), (-3;-4), (-4;-5), (-2;-5), (-1;-6), (3;-6), (3;-5), (1;-5), (1;-4), (2;-3), (2;-1)
Заяц
(-14;2), (-12;4), (-10;5), (-8;10), (-7;11), (-8;5), (-7;4), (-5;1), (-3;1,5), (3;0), (8;1), (10;0), (11;2), (12;1), (12;0), (11,5;-1), (13;-5), (14;-4,5), (15;-9), (15;-11), (13,5;-6,5), (11;-8), (8;-5), (-1;-7),
(-5;-6), (-7;-7), (-9;-7), (-11;-6,5), (-13;-7), (-15;-6), (-12;-5,5), (-9;-6),
(-11;-1), (-13;0), (-14;2).
Голубь
(-4;8), (-5;7), (-5;6), (-6;5), (-5;5), (-5;4), (-7;0), (-5;-5), (-1;-7), (3;-7), (9;-2), (13;-2), (14;-1), (6;1),(8;4), (15;7), (3;8), (2;7), (0;3), (-1;3), (-2;4), (-1;6), (-2;8), (-4;8)
Снегирь
(5;-2), (0;3), (-1;3), (-1,5;2,5), (-1;2), (-1;0), (0;-1), (2;-1,5), (3,5;-1,5), (5;-2)
Ландыш
(6,5;12), (6,75;11,5), (7;10,5), (6,5;10), (6,25;11), (6;10,5), (6,25;11,5), (6,5;12), (6,5;12,5), (5;10,5), (6;9,5)(6,5;8), (5,75;8,5), (5,5;7,5), (5,25;8,5), (4,5;8), (5;9,5), (5,5;10), (5;10,5), (3;8), (3,5;8),(4,5;7), (4,5;6,5),(5;5,5), (4,25;6), (4;5), (3,75;6), (3;5,5), (3,5;6,5), (3,5;7), (4;7,5), (3,5;8), (3;8), (1,5;6), (3;4,5), (3,5;3), (2,75;3,5), (2,5;2,5), (2,25;3,5), (1,5;3), (2;4,5), (2,5;5), (1,5;6), (0,5;0), (0,5;1,5), (1,5;7,5), (0,5;10,5), (-1,5;13), (-3;10,5), (-4;6), (-3,5;4), (0,5;0), (0;-3).
Машина
(-3,5;0,5), (-2,5;0,5), (-1,5;3,5), (0,5;3,5), (0,5;-0,5), (1;-0,5), (1;0), (1,5;0),
(5,5;4), (5,75;4), (6,75;5), (5,5;5), (5,5;8), (8,5;5), (7,25;5), (6,25;4), (6,5;4),
(4,5;2), (6;0) (6,5;0), (6,5;-1.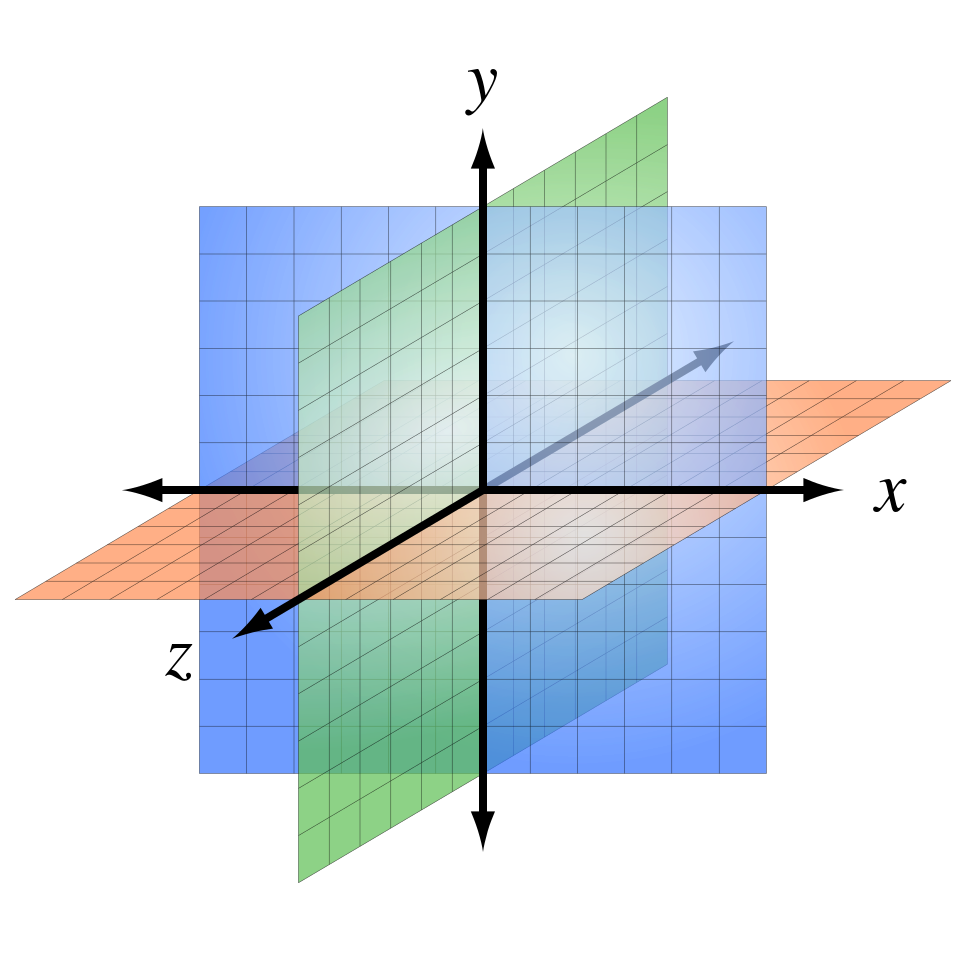
(6;-1,5), (6;-2), (5,5;-2,5), (4,5;-2,5),(4;-2), (4;-1,5), (0;-1,5), (0;-2), (-0,5;-2,5), (-1.5;-2,5),
(-2;-2), (-2;-1.5), (-3,5;-1.5), (-3,5;0,5).
Кошечка
(-2;-7), (-4;-7), (-3;-5), (-6;-2), (-7;-3), (-7;6), (-6;5), (-4;5), (-3;6), (-3;3), (-4;2), (-3;1), (-1;3), (1;3), (4;1), (4;2), (3;6), (4;7), (5;7), (6;6), (5;1), (5;-5), (6;-6), (5;-7), (3;-7), (4;-5), (2;-3), (2;-2), (1;-1), (-1;-1),(-2;-2),(-1;-6), (-2;-7)
усы 1) (-9;5), (-5;3), (-2;2).
2) (-2;3), (-8;3),
3) (-9;2), (-5;3), (-1;5)
глаза (-6;4) и (-4;4)..
<Рисунок 1>
Рыбка
(-4;2), (-3;4), (2;4), (3;3), (5;2), (7;0), (5;-2), (3;-2), (2;-4), (0;-4), (-1;-2), (-5;0), (-7;-2), (-8;-1), (-7;1), (-8;3), (-7;4), (-5;2), (-2;2), (0;3), (3;3) и глаз (5;0).
Мышонок
(-6;-5), (-4,5;-4,5), (-3;-3,5), (-1,5;-2), (-2;1), (-2;0), (-1,5;1), (-1;1,5), (0,2), (0,5;2), (0,5;1,5), (0,5;2,5), (1;2,5), (1;2), (1,5;2), (2,5;1,5), (2,5;1), (1,5;1), (1,5;0,5), (2;0,5), (1,5;0), (1;0),
(0,5;-1), (0;-1,5), (1;-1,5), (0;-2), (-1,5;-2), глаз (1,5;1,5).
Лебедь
(2;12), (2;13), (3;13,5), (4;13,5), (5;13), (3;4), (8;4), (6;1), (3;1), (2;2), (2;4), (4;11), (4;12,5), (3,5;12,5), (2;11), (2;12), (3;12), и (3;3), (4;2), (6;2), и (2,5;12,5).
Петух
( 1,5;5.5), ( 2,5;3,5), (2; 3), (2,5; 3), (3; 3,5), (3;4,5), (2,5;5,5), (3,5;6), (2,5;6,5), (3;7), (2,5;7), (2,5;7), (2;7)(2;8), (1,5;7), (1,5;8,5), (1;7), (1;6,5), (0,5;6), (0,5;5), (-0,5;4), (-2,5;3), (-4,5;4),
(-5;5), (-4,5;6), (-5,5;8), (-6,5;8,5), (-7,5;8), (-8,5;7), (-9;6), (-9;4), (-8,5;2,5), (-8,5;1), (-8;0),
(-8;1), (-7,5;0,5), (-7,5;2), (-7;0,5), (-6,5;1,5),
Векторы в пространстве и метод координат
Существует два способа решения задач по стереометрии
Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.
Способ хорош тем, что развивает мозги и пространственное воображение.
Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.
Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.
Система координат в пространстве
Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.
Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.
Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма
Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .
Сумма векторов:
Разность векторов:
Произведение вектора на число:
Скалярное произведение векторов:
Косинус угла между векторами:
Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.
Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.
Запишем координаты векторов:
и найдем косинус угла между векторами и :
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.
Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.
Координаты точек A, B и C найти легко:
Из прямоугольного треугольника AOS найдем
Координаты вершины пирамиды:
Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Найдем координаты векторов и
и угол между ними:
Покажем теперь, как вписать систему координат в треугольную призму:
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1
Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.
Запишем координаты точек:
Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
Значит, пользуемся формулами для координат середины
отрезка.
Найдем координаты векторов и , а затем угол между ними:
Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
Плоскость в пространстве задается уравнением:
Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Покажем, как это делается.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).
Уравнение плоскости выглядит так:
Подставим в него по очереди координаты точек M, N и K.
Для точки M:
То есть A + C + D = 0.
Для точки N:
Аналогично для точки K:
Получили систему из трех уравнений:
В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.
Пусть, например, D = −2. Тогда:
Выразим C и B через A и подставим в третье уравнение:
Решив систему, получим:
Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:
Вектор — это нормаль к плоскости MNK.
Уравнение плоскости, проходящей через заданную точку имеет вид:
Угол между плоскостями равен углу между нормалями к этим плоскостям:
Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.![]()
Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.
Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.
Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF.
Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.
Упростим систему:
Пусть С = -1. Тогда A = B = 2.
Уравнение плоскости AEF:
Нормаль к плоскости AEF:
Найдем угол между плоскостями:
5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂
Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».
Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?
«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.
Итак, AA1 = √3
Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор .
Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D». Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Координаты вектора — тоже:
Находим угол между плоскостями, равный углу между нормалями к ним:
Зная косинус угла, находим его тангенс по формуле
Получим:
Ответ:
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.
Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.
Находим синус угла между прямой m и плоскостью α по формуле:
6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
Как всегда, рисуем чертеж и выбираем систему координат
Находим координаты вектора .
Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Найдем угол между прямой и плоскостью:
Ответ:
Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA1 = . Найдите расстояние от точки A до плоскости A1DB.
Построим чертеж и выпишем координаты точек:
Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D
Решим эту систему. Выберем
Тогда
Уравнение плоскости A1DB имеет вид:
Дальше все просто. Находим расстояние от точки A до плоскости A1DB:
В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.
Ликбез по картографическим проекциям с картинками / Хабр
Визуализация данных самого разного рода, имеющих некое географическое распределение, в последнее время получает все большее и большее распространение. Тут, на Хабре, статьи с картами встречаются чуть ли не каждую неделю. Карты в статьях очень разные, но роднит их одно: как правило, в них используются всего две картографические проекции, при том — не самые удачные из существующих. Мне бы хотелось дать несколько наглядных примеров проекций, которые выглядят более эстетично и лучше приспособлены для разных видов визуализации. В этой статье будут рассмотрены общемировые проекции и проекции большей части Земли, так как визуализация чего-либо на карте мира, пожалуй, является наиболее распространенной из подобных задач.Легкое введение
Поскольку статья ориентирована на вопросы визуализации данных, я не буду касаться глубоко теории проекций (датумов, конформности, равноугольности и тому подобного), кроме общих принципов их построения. Также, я буду говорить тут о «проекциях», формально подразумевая «систему координат», coordinate reference system, потому что для карт таких масштабов не имеет смысла отдельно рассматривать проекцию и датум. Математики здесь тоже практически не будет, кроме простой геометрии. Желающие ознакомиться с математическими принципами, могут это сделать по статьям на Wolfram MathWorld. Так что изучающим программирование в области геоинформационных систем или их опытным пользователям, эта статья, возможно, будет не очень полезна.
Перед началом, объясню пару вещей. Все примеры будут даваться с использованием набора данных государственных границ с вот этого сайта и набора данных Blue Marble Next Generation с сайта NASA. Последний включает в себя синтезированные безоблачные снимки земной поверхности за каждый из двенадцати месяцев 2004-го года, что позволит внести некоторое разнообразие в иллюстрации.
Я очень люблю открытый софт, но использовать GDAL в данном случае мне показалось неэффективно — некоторых не очень ходовых, но полезных проекций в его реализации на данный момент либо нет, либо я плохо смотрел исходники, а потому иллюстрации я готовил в коммерческой программе GlobalMapper, которой пользуюсь уже много лет, и которая славится поддержкой внушительного списка систем координат.
Названия проекций и некоторые термины я буду давать и англоязычные, потому что если кому-то захочется поискать материалы по этой теме, русскоязычных источников в сети найдется несколько меньше (объем статей в Википедии на русском меньше в несколько раз). Для большинства проекций я постараюсь дать не только названия, но и коды EPSG и/или WKID, а также название проекции в библиотеке PROJ.4, широко используемой в открытом софте (например, в пакете R) для поддержки систем координат.
Некоторые проекции, возможно, окажутся кому-то знакомыми по картинке с xkcd, но все из них тут рассмотрены не будут.
Проблема
Начнем с того, что же это за самые распространенные проекции, и что с ними не так.
Первая проекция — так называемая «Географическая», она же – Geographic projection, Latitude/Longitude, Plate carrée EPSG:4326 WKID:54001 PROJ.4:longlat. Строго говоря, она даже не совсем является проекцией, потому что получается путем интерпретации полярных угловых координат, как линейных прямоугольных, без всяких вычислений. Эту проекцию используют, потому что она способна отобразить всю поверхность Земли целиком и потому, что она самая простая математически, а данные очень часто распространяются не спроецированными, то есть именно в географических координатах (градусах широты и долготы).
Что же получается? Получается прямоугольник, где точки полюсов обращены в линии (верхнюю и нижнюю границы). Чем дальше от экватора, тем сильнее любой объект на карте оказывается сплюснут по вертикали и растянут по горизонтали. Как я уже сказал, это худо-бедно годится для отображения глобальных наборов данных, но полярные территории (Канада, Норвегия, Швеция, север России, Финляндия, Гренландия, Антарктида, Исландия) оказываются искажены. Проекции, которые позволяют избежать этого, существуют, и о них пойдет речь дальше. Единственная причина использовать эту проекцию — ее предельная простота программной реализации — нужно просто отобразить систему координат от -180º до 180º по X и от -90º до 90º по Y на плоскость, считая угловые единицы линейными.
Другая весьма популярная проекция — «проекция Меркатора», Mercator projection PROJ.4:merc. Она также используется для визуализации данных, покрывающих весь мир, но ее популярность продиктована не только простотой — ее варианты являются стандартом де-факто для глобальных картографических сервисов, таких как Google Maps, Bing Maps, Here. С ней глубоко связаны картографические библиотеки OpenLayers, Leaflet, API упомянутых выше сервисов. В варианте Google и OpenStreetMap она носит название Web Mercator и имеет код EPSG/WKID:3857, иногда на нее также ссылаются, как на EPSG:900913. Принцип ее построения не сильно сложнее Географической – это проекция на цилиндр, чья ось совпадает с географической осью Земли, проецирование происходит линиями, выходящими из центра планеты, от чего ошибка растяжения приполярных областей по горизонтали оказывается скомпенсирована пропорциональным растяжением по вертикали. Проблема с этим только в том, что карта получится слишком большой по вертикали, если попытаться отобразить и север Гренландии. Потому обычно отбрасывают 16° полярных областей (в равной пропорции или больше — с юга).
На чей-то взгляд выглядит чуть лучше, чем Географическая, но одну проблему мы уже упомянули, а вторая — чем ближе объект к полюсам, тем он кажется больше, хотя его форма уже не так искажена. Потому, если предмет визуализации — плотность маркеров на единицу территории или расстояния, такой способ отображения будет вводить в заблуждение. При грамотном выборе способа визуализации, конечно, это можно скомпенсировать, а для каких-то случаев это вообще не проблема: например, если величина какого-то показателя в целой стране соотнесена с цветом этой страны на карте, эффект растяжения площадей не сказывается. Эта проекция сохраняет только форму объектов, потому очертания континентов и стран выглядят довольно узнаваемо. И, как я уже сказал, она — ваш первый и самый простой вариант при создании интерактивных веб-карт.
Варианты решения
Что же делать с глобальными данными, если нам по какой-то причине понадобилась проекция, лучше сохраняющая такие свойства объектов, как форма, площадь, расстояния и углы? Законы геометрии не дают нам сохранить все эти свойства сразу, развернув круглую поверхность Земли на плоскость. Однако, для визуализации данных более всего важна эстетика и восприятие, а не сохранение свойств, как для навигационных или измерительных задач. Потому становится возможным подобрать такую проекцию, искажения в которой были бы равномерно распределены по свойствам. И таких проекций существует довольно много. Существуют три самых известных, обладающих сходными свойствами: «Тройная проекция Винкеля» Winkel Tripel WKID:54042 PROJ.4:wintri, «проекция Робинсона» Robinson projection WKID:54030 PROJ.4:robin, «проекция Каврайского» (Kavrayskiy projection). Первая и последняя имеют визуально минимальные искажения, а неспециалисту, не видя градусной сетки, вообще весьма сложно различить их, потому я приведу иллюстрацию для Winkel Tripel, как той, которая лично мне нравится больше всего.
Вот так описание этой проекции выглядит в формате ESRI WKT:PROJCS["Robinson",
GEOGCS["GCS_WGS_1984",
DATUM["D_WGS84",
SPHEROID["WGS84",6378137,298.257223563]
],
PRIMEM["Greenwich",0],
UNIT["Degree",0.017453292519943295]
],
PROJECTION["Robinson"],
PARAMETER["central_meridian",0],
PARAMETER["false_easting",0],
PARAMETER["false_northing",0],
UNIT["Meter",1]
]
Как легко видеть, хотя искажение контуров и некоторое увеличение площади стран к полюсам здесь также наблюдаются, но это нельзя даже сравнивать с растяжением Географической проекции и пропорциональным увеличением проекции Меркатора.
Тут стоит сделать небольшое отступление и обратить внимание на то, что вид этой проекции по умолчанию страдает одним недостатком, который касается и других общемировых проекций. Дело в том, что если за центральный меридиан — линию, соединяющую северный и южный полюс через центр карты (longitude of origin) — принять нулевой меридиан, то карта будет разрезана по 180-му. Но при этом треть Чукотки окажется на левом краю карты, а две трети — на правом. Чтобы сделать карту красивее, разрез должен проходить где-то в районе 169-го западного меридиана восточнее острова Ратманова, для чего за центральный должен быть принят 11-й. Вот иллюстрация того, что получается:
А вот измененное для этого случая описание в ESRI WKT:PROJCS["Robinson",
GEOGCS["GCS_WGS_1984",
DATUM["D_WGS84",
SPHEROID["WGS84",6378137,298.257223563]
],
PRIMEM["Greenwich",0],
UNIT["Degree",0.017453292519943295]
],
PROJECTION["Robinson"],
PARAMETER["central_meridian",11],
PARAMETER["false_easting",0],
PARAMETER["false_northing",0],
UNIT["Meter",1]
]
В формате определения системы координат для PROJ.4 долгота центра проекции задается параметром +lon_0=.
11-й меридиан — «магическое» число: практически все мировые проекции, имеющие равномерный масштаб вдоль экватора, могут быть разрезаны по Берингову проливу, если за центральный принять именно его, а не нулевой.
Замечу, что задумываясь о выборе проекции, стоит принимать во внимание все существующие реальные требования к визуализации. Например, если данные касаются климата, то может иметь смысл либо нанести на карту линии широты, либо использовать проекцию, где они горизонтальны, а не загибаются к краям карты (то есть, отказаться от Тройной Винкеля в пользу, например, Робинсона). В данном случае, это позволит легче и точнее оценить относительную близость разных мест к полюсам и экватору. Еще один весомый плюс проекции Робинсона — то, что она поддерживается множеством софта, в том числе открытого, тогда как про некоторые другие этого сказать нельзя.
Иногда, когда требуется максимально сохранить какое-то свойство, например — соотношение площадей объектов (стран) — эстетическая сторона страдает. Но поскольку это все же может для чего-то понадобиться, я приведу один пример такой проекции — «проекцию Моллвейде», Mollweide projection WKID:54009 PROJ.4:moll.
Как видно, она довольно сильно напоминает проекцию Робинсона, но с той разницей, что полюса все же стянуты в точки, от чего форма приполярных областей выглядит сильно искаженной. Но пропорции площадей стран, как и требовалось, сохраняются куда лучше.
Самым молодым конкурентом этих проекций является проекция Natural Earth PROJ.4:natearth — она представляет из себя гибрид проекций Каврайского и Робинсона, а ее параметры были подобраны группой американских, швейцарских и словенских специалистов в 2007 году, тогда как возраст большинства картографических проекций — не менее полувека.
Для перепроецирования данных в нее существует некоторое количество инструментов, которые были написаны специально для этого, но ее поддержка еще далека от повсеместной.
Немного экзотики и специальных случаев
Конечно, все многообразие проекций на этом не заканчивается. Их изобретено немало. Некоторые просто выглядят странно (скажем, проекция Бонне изображает Землю в виде фигуры, напоминающей разрезанное яблоко или стилизованное сердце), некоторые — предназначены для особых ситуаций. Например, готов поспорить, что очень многие видели на картинках карту мира, которая похожа на корку мандарина, которую сняли и расплющили. Это, наверняка, была «Разрывная гомолосинусоидальная проекция Гуда» Interrupted Goode Homolosine projection WKID:54052.
Вид ее вполне достоин названия. Ее назначение — отображать размер объектов (и в некоторой степени — форму) близко к естественным пропорциям. Ее главная проблема, кроме названия и странного вида, состоит в том, что путем подбора центрального меридиана невозможно добиться того, чтобы ни один крупный кусок суши не был разрезан. Обязательно пострадает что-то из списка: Гренландия, Исландия, Чукотка, Аляска. Лично на мой взгляд, проще привести отдельно изображения стран, чем использовать такую карту, если вы не хотите стилизовать свою работу под середину XX века.
Существуют проекции, которые по своей природе никак не отнести к общемировым, но мне бы хотелось рассмотреть их здесь, потому что они способны показать земной шар, то есть как-бы вид планеты из космоса. Одна из них — «Проекция вертикальной ближней перспективы» Vertical Near-Side Perspective projection WKID:54049. Ее особое свойство — показывать земную поверхность в такой перспективе, как она выглядит с определенной высоты. Высота над эллипсоидом (идеализированной фигурой, моделирующей Землю) задается для этой проекции в явном виде.
На иллюстрации эта проекция имеет широту и долготу центра, равные широте и долготе Москвы, а высоту — 5000000 метров. Чем больше это расстояние, тем сильнее изображение Земли становится похоже на ее изображение в проекции, которую мы рассмотрим последней.
Проекция, которая показывает вид на Землю в параллельной перспективе, то есть как-бы с бесконечного расстояния, называется «Ортографическая проекция» Orthographic projection WKID:43041 PROJ.4:ortho. В каком-то смысле, она знакома всем, кто когда-либо пользовался Google Earth. Я говорю, что в каком-то смысле, потому что «направление взгляда» в этой проекции всегда перпендикулярно поверхности Земли, тогда как в Google Earth его можно наклонять как угодно.
Для нее, как и для предыдущей проекции, можно задать центральные широту и долготу, чтобы ориентировать Землю желаемым образом. Например, можно показать полушарие с центром в какой-то точке, о которой идет речь — скажем, иллюстрируя транспортные потоки континентального масштаба, исходящие от одного предприятия. Сделав две карты с противоположными значениями координат, можно получить карту всего мира (правда, на краях искажения будут очень велики). Генерация последовательности карт с плавным изменением центральной точки даст кадры для анимации вращающейся планеты без всякой трехмерной графики.
Если статья окажется интересной, постараюсь написать продолжение о проекциях, используемых для отображения отдельных стран или регионов, ориентированную, как и эта статья, на базовые свойства этих проекций для задачи визуализации данных, инфографики и тому подобного.
Геометрия формирования изображений — Записки преподавателя
Написано специально для студентов Бизнес‑информатики, которые только начинают осваивать OpenCV и всякий там Computer Vision, которым тяжело с математикой
Здесь с геометрической точки зрения объясняются основы формирование изображения.
В частности, рассматривается математика, стоящая за тем, как точка в 3D‑изображении проецируется на плоскость изображения.
Статья по своей природе не математическая и предназначена исключительно для новичков. Тем не менее, что такое перемножение матриц знать надо.
Проблема
Для понимания задачи, предположим, что у нас есть камера, установленная в комнате.
Зная, что в комнате есть точка \mathbf{P} в трехмерном пространстве (3D‑точка, Декартова система координатએ), мы хотим найти координаты пикселя (u, v) этой 3D‑точки на снимке, сделанном камерой.
В этом контексте есть три системы координат. Давайте с ними разберёмся.
1. Мировая система координат
Рисунок 1 — мировая система координат и система координат камеры связаны поворотом и перемещением. Эти шесть параметров (3 для поворота и 3 для перемещения) называются внешними параметрами камеры.Чтобы определить расположение точек в помещении, нам нужно сначала определить систему координат этого помещения. Это требует знания двух вещей:
- начало координат: можно произвольно назвать любой угол комнаты началом (0, 0, 0).
- направление осей X, Y, Z: оси X и Y можно направить в плоскости пола вдоль двух стенок, а ось Z вдоль вертикального угла стены.
Принимая во внимание всё это, можно найти три координаты любой точки в комнате, измерив расстояние от неё до начала координат по осям X, Y и Z.
Эта система координат, связанная с комнатой, называется мировой системой координат. На рисунке 1 она показан осями оранжевого цвета. Мы будем использовать жирный шрифт (например, X_w), чтобы показать ось, и обычный шрифт, чтобы показать координату точки (например, X_w).
Давайте рассмотрим точку Р в этой комнате. В мировой системе координат координаты Р задаются по осям (X_w, Y_w, Z_w). Вы можете найти X_w, Y_w, и Z_w координаты этой точки, просто измеряя расстояние от этой точки до начала координат по трем осям.
2. Система Координат Камеры
А теперь давайте поставим камеру в комнате.
Снимать будем этой камерой и поэтому нас интересует связанная с ней трехмерная система координат.
Если бы мы поместили камеру в начало координат комнаты и выровняли ее таким образом, чтобы ее оси X, Y и Z совпадали с осями X_w, Y_w и Z_w комнаты, то эти две системы координат были бы одинаковыми.
Однако, это вряд ли возможно на практике. Мы хотели бы поставить камеру в любом месте и она должна видеть любое месте. Поэтому нам нужно найти связь между координатами 3D‑комнаты (т.е. мира) и координатами 3D‑камеры.
Допустим, наша камера стоит где‑то произвольно (t_X, t_Y, t_Z) в комнате. На техническом жаргоне мы можем перевести координаты камеры по (t_X, t_Y, t_Z) по отношению к мировым координатам.
Камера может также смотреть куда угодно. Другими словами, можно сказать, что камера вращается относительно мировой системы координат.
Вращение в 3D определяется тремя параметрами — тангаж, рыскание и крен. Образно это представляется движением руки от локтя: вверх‑вниз — тангаж, слева‑направо — рыскание, вращение кулака — крен.
Однако часто для математической манипуляции удобно задавать вращение в виде матрицы 3 × 3. Теперь вы можете подумать, что матрица 3 × 3 имеет 9 элементов и, следовательно, 9 параметров, но у вращения только 3 параметра. И это правильно, именно поэтому любая произвольная матрица 3 × 3 не является матрицей вращения. Не вдаваясь в детали, давайте пока просто узнаем, что матрица вращения имеет только три степени свободы, хотя она имеет 9 элементов.
Вернемся к нашей первоначальной проблеме. Мировая координата и координаты камеры связаны матрицей вращения \mathbf{R} и вектором перемещения 3 элементов \mathbf{t}
Что это значит?
Это значит, что точка \mathbf{P}, имеющая координаты (X_w, Y_w, Z_w) в мировой системе координат, в системе координат камеры будет иметь другие значения (X_c, Y_c, Z_c). Система координат камеры на рисунке изображена красным цветом.
Эти координаты связаны следующим уравнением.
\begin{bmatrix}X_c\\Y_c\\Z_c\end{bmatrix}= \mathbf{R} \begin{bmatrix}X_w\\Y_w\\Z_w\end{bmatrix} + \mathbf{t}
Обратите внимание, что представление вращения в виде матрицы позволило нам выполнять вращение простым умножением матрицы вместо утомительной манипуляции символами, требуемой в других представлениях, таких как тангаж, рыскание, крен. Я надеюсь, что это поможет вам понять, почему мы описываем вращение, используя матрицы.
Иногда приведенное выше выражение пишется в более компактной форме. Вектор перевода 3 × 1 добавляется в виде столбца в конец матрицы вращения 3 × 3, чтобы получить матрицу 3 × 4, называемую внешней матрицей .
\begin{bmatrix} X_c\\ Y_c\\ Z_c \end{bmatrix}= \begin{bmatrix} \mathbf{R} / \mathbf{t} \end{bmatrix} \begin{bmatrix} X_w\\ Y_w\ \ Z_w \\ 1 \end{bmatrix}
где, внешняя матрица \mathbf{P} задается с помощью
\mathbf{P} = \begin{bmatrix} \mathbf{R} / \mathbf{t} \end{bmatrix}
Однородные координаты: в проективной геометрии мы часто работаем с забавным представлением координат, где к координатам добавляется дополнительное измерение. Трехмерная точка (X, Y, Z) в декартовых координатах может быть записана как (X, Y, Z, 1) в однородных координатах. В более общем случае точка в однородной координате (X, Y, Z, W) совпадает с точкой (X / W, Y/ W, Z / W) в декартовых координатах. Однородные координаты позволяют нам представлять бесконечные величины, используя конечные числа. Например, точку на бесконечности можно представить в виде (1, 1, 1, 0) в однородных координатах. Вы можете заметить, что мы использовали однородные координаты в уравнении 2 для представления мировых координат.
3. Система координат изображения
Рисунок 2 — проекция точки P на плоскость изображенияПосле того, как мы получим точку в трехмерной системе координат камеры, применяя вращение и перевод к точкам мировых координат, мы находимся в положении, когда можем спроецировать точку на плоскости изображения для вычисления местоположение точки на изображении.
На изображении выше мы смотрим на точку \mathbf{P} с координатами (X_c, Y_c, Z_c) в системе координат камеры. Напомним только, что если бы мы не знали координаты этой точки в системе координат камеры, мы могли бы преобразовать ее координаты в мировой системе координат, используя внешнюю матрицу, чтобы получить координаты в системе координат камеры, используя уравнение 2.
Рисунок 2, показывает проекцию камеры в случае простой камеры с контактным отверстием.
Оптический центрએ (ось наблюдения) представлен с помощью O_c. В действительности на плоскости формируется перевернутое изображение. Для математического удобства мы просто делаем все вычисления, как будто плоскость изображения находится перед оптическим центром, потому что изображение, считанное с матрицы, может быть тривиально повернуто на 180 градусов, чтобы компенсировать инверсию. На практике даже этого не требуется. Всё еще проще: реальная светочувствительная матрица камеры просто читается начиная самого нижнего ряда в обратном порядке (справа налево), а затем снизу вверх для каждого ряда. Такой метод автоматически формируется правильное изображение и по вертикали и по горизонтали. Так что на практике нет необходимости переворачивать изображение.
Плоскость изображения размещается на расстоянии \mathbf{\phi} (фокусное расстояниеએ) от оптического центра.
Используя геометрию средней школы (подобные треугольники), мы можем показать проектное изображение (x, y) 3D‑точки (X_c, Y_c, Z_c), заданной.
x = f \frac{X_c}{Z_c} \\ y = f \frac{Y_c}{Z_c}
Приведенные выше два уравнения можно переписать в матричной форме следующим образом:
\begin{bmatrix}x’\\y’\\z’\end{bmatrix} = \begin{bmatrix}f&0&0\\0&f&0\\0&0&1\end{bmatrix} \begin{bmatrix}X_c\\Y_c\\Z_c\end{bmatrix}
Матрица \mathbf{К}, показанная ниже, называется внутренней матрицей и содержит внутренние параметры камеры.
\mathbf{K} = \begin{bmatrix}f&0&0\\0&f&0\\0&0&1\end{bmatrix}
Приведенная выше простая матрица показывает только фокусное расстояние.
Однако, пиксели в светочувствительной матрице камеры могут быть не квадратными, и поэтому мы можем иметь два разных фокусных f_x и f_y расстояния.
Оптический центр (c_x, c_y) камеры может не совпадать с центром системы координат изображения.
Кроме того, может наблюдаться небольшой перекос \mathbf{\gamma} между осями \mathbf{x} и \mathbf{y} датчика камеры.
Учитывая это все, матрицу камеры нужно переписать так:
\mathbf{K} = \begin{bmatrix}f_x&\gamma&c_x\\0&f_y&c_y\\0&0&1\end{bmatrix}
Рисунок 3 — показывает более реалистичный сценарий, когда система координат пикселя изображения имеет начало координат в верхнем левом углу. Внутренняя матрица камеры должна учитывать расположение главной точки, наклон осей и потенциально различные фокусные расстояния вдоль различных осейВ приведенном выше уравнении координаты \mathbf{x} и \mathbf{y} пикселей находятся относительно центра изображения. Однако при работе с изображениями источник находится в верхнем левом углу изображения.
Давайте представим координаты изображения по (u, v).
\begin{bmatrix}u’\\v’\\w’\end{bmatrix} = \begin{bmatrix}f_x&\gamma&c_x\\0&f_y&c_y\\0&0&1\end{bmatrix} \begin{bmatrix}X_c\\Y_c\\Z_c\end{bmatrix}
где,
u = \frac{u’}{w’} \\ v = \frac{v’}{w’}
Итого
Проецирование трехмерной точки в мировой системе координат на пиксельные координаты камеры выполняется в три этапа.
- Трехмерная точка преобразуется из мировых координат в координаты камеры с помощью внешней матрицы, которая состоит из вращения и перемещения между двумя системами координат.
- Новая трехмерная точка в системе координат камеры проецируется на плоскость изображения с помощью встроенной матрицы, которая состоит из внутренних параметров камеры, таких как фокусное расстояние, оптический центр и т. д.
В следующем посте этой серии мы узнаем о калибровке камеры и о том, как выполнять ее с помощью функции OpenCV.
Оригинал (англ.): Geometry of Image Formation
Геометрия формирования изображений, опубликовано К ВВ, лицензия — Creative Commons Attribution-NonCommercial 4.0 International.
Респект и уважуха
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра
Числовая ось
Определение 1. Числовой осью (числовой прямой, координатной прямой) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление
O → x
указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.
Рис.1
Определение 2. Отрезок, длина которого принята за единицу длины, называют масштабом.
Каждая точка числовой оси имеет координату, являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .
Прямоугольная декартова система координат на плоскости
Определение 3. Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).
Рис.2
Замечание. Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат, в отличие от левых систем координат, в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.
Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA1 и AA2 на прямые Ox и Oy соответственно (рис.3).
Рис.3
Определение 4. Абсциссой точки A называют координату точки A1 на числовой оси Ox , ординатой точки A называют координату точки A2 на числовой оси Oy .
Обозначение. Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).
Рис.4
Замечание. Точка O , называемая началом координат, имеет координаты O (0 ; 0) .
Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс, а числовую ось Oy называют осью ординат (рис. 5).
Определение 6. Каждая прямоугольная декартова система координат делит плоскость на 4 четверти (квадранта), нумерация которых показана на рисунке 5.
Рис.5
Определение 7. Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью.
Замечание. Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.
Формула для расстояния между двумя точками координатной плоскости
Утверждение 1. Расстояние между двумя точками координатной плоскости
A1 (x1 ; y1) и A2 (x2 ; y2)
вычисляется по формуле
Доказательство. Рассмотрим рисунок 6.
Рис.6
Поскольку в прямоугольном треугольнике A1A2B длина катета A1B равна | x2 – x1| а длина катета A2B равна | y2 – y1| , то по теореме Пифагора
| | A1A2|2 = = ( x2 – x1)2 + ( y2 – y1)2 . | (1) |
Следовательно,
что и требовалось доказать.
Уравнение окружности на координатной плоскости
Рассмотрим на координатной плоскости Oxy (рис. 7) окружность радиуса R с центром в точке A0 (x0 ; y0) .
Рис.7
Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:
( x – x0)2 + ( y – y0)2 = R2.
Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A0 (x0 ; y0) .
Следствие. Уравнение окружности радиуса R с центром в начале координат имеет вид
x2 + y2 = R2.
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра
Определения координатной (числовой) прямой и координатной плоскости даны в разделе нашего справочника«Декартовы координаты точек плоскости. Уравнение окружности»
Настоящий раздел посвящен введению прямоугольных декартовых координат точек в пространстве.
Определение 1. Прямоугольной декартовой системой координат Oxyz в пространстве называют три числовых прямых Ox , Oy , Oz в пространстве, удовлетворяющих следующим условиям:
- Прямые пересекаются в одной точке (точка O ), которую называют началом координат.
- Точка O является началом координат на каждой из числовых прямых Ox , Oy , Oz .
- Прямые Ox , Oy , Oz попарно перпендикулярны.
- На прямых Ox , Oy , Oz выбран одинаковый масштаб.
Различают правые и левые прямоугольные декартовы системы координат в пространстве.
Определение 2. Прямоугольную декартову систему координат Oxyz в пространстве называют правой системой, если она удовлетворяет следующим двум условиям:
- Прямые (оси) Ox и Oy образуют правую систему координат на плоскости Oxy .
Прямая (ось) Oz направлена так, что, наблюдая со стороны положительного направления оси Oz, мы видим, что поворот от положительного направления оси Ox до положительного направления оси Oy , осуществленный против часовой стрелки, является поворотом на угол 90°.
Определение 3. Левой прямоугольной декартовой системой координат в пространстве называют такую прямоугольную декартову систему координат в пространстве, которая не является правой прямоугольной декартовой системой координат.
Правые прямоугольные декартовы системы координат обычно изображают так, как показано на рисунках 1.
Рис.1
Левые системы координат используются очень редко.
Рассмотрим какую-нибудь правую прямоугольную декартову систему координат Oxyz в пространстве. Тогда положение произвольной точки P в пространстве (рис.2) будет определяться тремя координатами x , y , z , которые вычисляются по следующему правилу.
Рис.2
Проведем через точку P плоскость, параллельную плоскости Oyz , и обозначим символом P1 точку пересечения этой плоскости с прямой Ox (рис.2). Координатой x точки P служит координата точки P1 на числовой прямой Ox .
Проведем через точку P плоскость, параллельную плоскости Oxz , и обозначим символом P2 точку пересечения этой плоскости с прямой Oy (рис.2). Координатой y точки P служит координата точки P2 на числовой прямой Oy .
Проведем через точку P плоскость, параллельную плоскости Oxy , и обозначим символом P3 точку пересечения этой плоскости с прямой Oz (рис.2). Координатой z точки P служит координата точки P3 на числовой прямой Oz .
Координаты точки P принято обозначать так:
P = (x ; y ; z)
Оси правой прямоугольной декартовой системы координат Ox , Oy , Oz называют осью абсцисс, осью ординат и осью аппликат соответственно.
Координаты x , y , z точки P называют абсциссой, ординатой и аппликатой точки P соответственно.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Системы координат, преобразования и единицы — SVG Tiny 1.2
Системы координат, преобразования и единицы — SVG Tiny 1.2Содержание
7.1 Введение
Для всех медиа холст описывает «пространство, в котором отображается содержимое SVG». В холст бесконечен для каждого измерения пространства, но рендеринг происходит относительно конечная прямоугольная область холст. Этот конечная прямоугольная область называется SVG область просмотра. Для визуального media ([CSS2], раздел 7.3.1), SVG область просмотра это область просмотра, в которой пользователь видит содержимое SVG.
Размер SVG область просмотра (т.е. его ширина и высота) определяется в процессе переговоров (см. Установка размера исходного окна просмотра) между фрагментом документа SVG и его родителем (реальным или неявным). Как только окно просмотра установлено, Пользовательский агент SVG должен установить начальный область просмотра система координат и начальная пользователь система координат (см. Исходная система координат).Окно просмотра система координат также называется область просмотра и пользовательская система координат также называется пространство пользователя .
Новое пользовательское пространство (т.е. новая текущая система координат) может быть установлена в любом месте в пределах фрагмент документа SVG, указав трансформации в виде матрицы преобразования или простые операции преобразования, такие как поворот, наклон, масштабирование и перемещение (см. Преобразования системы координат).Создание новых пользовательских пространств через координаты системные преобразования являются фундаментальными операциями для 2D-графики и представляют собой обычный метод управления размером, положением, поворотом и перекос графических объектов.
Также могут быть созданы новые видовые экраны. От установив новое окно просмотра, можно предоставить новый ссылочный прямоугольник для «подгонки» изображения к определенному прямоугольная область. («Подогнать» означает, что данное изображение преобразовано в такой способ, которым его ограничивающая рамка в пространстве пользователя точно совпадает с краями заданного область просмотра.)
7.2 Начальное окно просмотра
Пользовательский агент SVG ведет переговоры со своим родителем пользовательский агент для определения области просмотра в который пользовательский агент SVG может отобразить документ. В некоторых случаях содержимое SVG будет встроено (по ссылке или в строке) внутри содержащий документ. Этот содержащий документ может включать атрибуты, свойства и / или другие параметры (явные или неявные), которые определяют или подсказки о размерах область просмотра для содержимого SVG.Сам контент SVG при желании может предоставлять информацию о соответствующем окне просмотра регион для контента через ‘ширина’ и ‘высота’ Атрибуты XML в ‘svg’ элемент. В процессе переговоров используется любая информация, предоставленная содержащий документ и сам контент SVG, чтобы выбрать область просмотра расположение и размер.
Если формат родительского документа определяет правила для ссылочных или встроенных графическое содержимое, то процесс согласования определяется родительским спецификация формата документа.Если родительский документ оформлен с помощью CSS, тогда процесс переговоров должен следовать правилам CSS для заменяемых элементов. Если есть свойства ширины и высоты CSS (или соответствующие свойства XSL) на ссылочном элементе (или самый корневой элемент ‘svg’ для встроенного содержимого SVG), которых достаточно, чтобы установить ширину и высоту области просмотра, затем эти свойства позиционирования устанавливают ширина, высота и соотношение сторон.
Если родительский документ отсутствует, пользовательский агент SVG должен использовать ‘ширина’ и атрибуты ‘height’ на самом корневом элементе ‘svg’ элемент в качестве ширины и высоты для область просмотра.
Обратите внимание, что время завершения согласования размера области просмотра зависит от реализации. Авторы, которым нужно быть уверенным в размерах области просмотра следует сделать это с помощью событие нагрузки или обработчики событий resize.
7.3 Начальная система координат
Для svg элемент, SVG пользовательский агент должен установить начальный область просмотра система координат и начальная пользователь систему координат так, чтобы две системы координат были идентичный.Начало обеих систем координат должно быть в начале координат область просмотра и одна единица в исходной системе координат должна равняться одному «пикселю» (т. е. а пикселей единиц, как определено в CSS ([CSS2], раздел 4.3.2)) в область просмотра. В большинстве случаев, например, отдельные документы SVG или Фрагменты документа SVG встроенный (по ссылке или встроенный) в родительских документах XML, где макет родительского элемента определяется CSS [CSS2] или XSL [XSL], Пользовательский агент SVG должен установить начальный область просмотра система координат (и, следовательно, начальная система координат пользователя) таким образом, что его начало находится вверху / слева от область просмотра с положительной осью X, направленной вправо, положительной осью Y направлен вниз, а текст отображается в вертикальном положении, что означает глифы ориентированы таким образом, что латинские символы и полноразмерные идеографические символы для азиатских шрифтов имеют верхний край соответствующих глифов ориентированы вверх, а правый край соответствующих глифов ориентирован направо.
Если реализация SVG является частью пользовательский агент который поддерживает стилизацию XML-документов с использованием CSS2-совместимого пикселей единиц, затем Пользовательский агент SVG должен получить свое начальное значение для размера пикселей единиц в реальном мире единицы для соответствия значению, используемому для других операций стилизации XML; в противном случае, если пользовательский агент может определить размер блока пикселей из окружающей среды, он должен используйте это значение; в противном случае следует выбрать подходящий размер для одного пикселей единиц.Во всех случаях размер пикселей и должен быть в соответствие с правила описано в CSS ([CSS2], раздел 4.3.2).
Пример 07_02 ниже показывает, что начальная система координат имеет начало вверху / слева, а ось x указывает на вправо, а ось Y — вниз. В исходной системе координат пользователя одна пользовательская единица, равная родительской (неявной или явной) пользовательский агент «пиксель».
7.4 Преобразования системы координат
Новое пользовательское пространство (т.е. новую текущую систему координат) можно установить, указав трансформации в виде «трансформации» атрибут на контейнер или графический элемент, или viewBox атрибут в ‘svg’ элемент. Преобразование и viewBox Атрибуты преобразуют координаты и длину пользовательского пространства на родственные атрибуты на данном элементе (см. эффект от Атрибут ‘transform’ в siblin
Что такое декартова система координат
- БЕСПЛАТНАЯ ЗАПИСЬ КЛАСС
- КОНКУРСНЫЕ ЭКЗАМЕНА
- BNAT
- Классы
- Класс 1-3
- Класс 4-5
- Класс 6-10
- Класс 11-12
- CBSE
- Книги NCERT
- Книги NCERT для класса 5
- Книги NCERT для класса 6
- Книги NCERT для класса 7
- Книги NCERT для класса 8
- Книги NCERT для класса 9
- Книги NCERT для класса 10
- NCERT Книги для класса 11
- NCERT Книги для класса 12
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- NCERT Exemplar Class 12
- RS Aggarwal
- Решения RS Aggarwal класса 12
- Решения RS Aggarwal класса 11
- RS Aggarwal Решения класса 10
- Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- RD Sharma
- RD Sharma Class 6 Solutions
- RD Sharma Class 7 Решения
- Решения RD Sharma Class 8
- Решения RD Sharma Class 9
- Решения RD Sharma Class 10
- Решения RD Sharma Class 11
- Решения RD Sharma Class 12
- PHYSICS
- Mechanics
- Optics
- Термодинамика
- Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- MATHS
- Теорема Пифагора
- Простые числа
- Наборы вероятностей и статистика
- Тр Игонометрические функции
- Взаимосвязи и функции
- Последовательность и ряды
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Доли деления
- БИОЛОГИЯ
- Микробиология
- ФОРМУЛЫ
- Математические формулы
- Алгебровые формулы
- Формулы тригонометрии
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- Физические калькуляторы
- Химические калькуляторы
- PBS
- Образцы документов для класса 6
- Образцы документов CBSE для класса 7
- Образцы документов CBSE для класса 8
- Образцы документов CBSE для класса 9
- Образцы документов CBSE для класса 10
- Образцы документов CBSE для класса 1 1
- Образцы документов CBSE для класса 12
- Вопросники предыдущего года CBSE
- Вопросники предыдущего года CBSE Класс 10
- Вопросники предыдущего года CBSE Класс 12
- HC Verma Solutions
- HC Verma Solutions Класс 11 по физике
- HC Verma Solutions Class 12 Physics
- Lakhmir Singh Solutions
- Lakhmir Singh Class 9 Solutions
- Lakhmir Singh Class 10 Solutions
- Lakhmir Singh Class 8 Solutions
- CBSE Notes
- Class 6 Примечания CBSE
- Примечания CBSE класса 7
- Примечания CBSE класса 8
- Примечания CBSE класса 9
- Примечания CBSE класса 10
- Примечания CBSE класса 11
- Примечания CBSE класса 12
- Примечания к редакции CBSE
- CBSE Примечания к редакции класса 9
- CBSE Примечания к редакции класса 10
- CBSE Примечания к редакции класса 11
- Примечания к редакции класса 12 CBSE
- Дополнительные вопросы CBSE
- Дополнительные вопросы по математике CBSE класса 8
- Дополнительные вопросы по науке класса 8 CBSE
- Дополнительные вопросы по математике класса 9 CBSE
- CBSE Class 9 Science Extra Вопросы
- CBSE Class 10 Дополнительные вопросы по математике
- CBSE Class 10 Science Extra Questions
- CBSE Class
- Class 3
- Class 4
- Class 5
- Class 6
- Class 7
- Class 8
- Класс 9
- Класс 10
- Класс 11
- Класс 12
- Учебные решения
- Книги NCERT
- Решения NCERT
- Решения NCERT для класса 11
- Решения NCERT для класса 11 по физике
- Решения NCERT для класса 11 Химия
- Решения NCERT для биологии класса 11
- Решение NCERT s Для класса 11 по математике
- NCERT Solutions Class 11 Accountancy
- NCERT Solutions Class 11 Business Studies
- NCERT Solutions Class 11 Economics
- NCERT Solutions Class 11 Statistics
- NCERT Solutions Class 11 Commerce
- NCERT Solutions for Class 12
- Решения NCERT для физики класса 12
- Решения NCERT для химии класса 12
- Решения NCERT для биологии класса 12
- Решения NCERT для математики класса 12
- Решения NCERT, класс 12 Бухгалтерский учет
- Решения NCERT, класс 12, бизнес-исследования
- NCERT Solutions Class 12 Economics
- NCERT Solutions Class 12 Accountancy Part 1
- NCERT Solutions Class 12 Accountancy Part 2
- NCERT Solutions Class 12 Micro-Economics
- NCERT Solutions Class 12 Commerce
- NCERT Solutions Class 12 Macro-Economics
- NCERT Solut Ионы Для класса 4
- Решения NCERT для математики класса 4
- Решения NCERT для класса 4 EVS
- Решения NCERT для класса 5
- Решения NCERT для математики класса 5
- Решения NCERT для класса 5 EVS
- Решения NCERT для класса 6
- Решения NCERT для математики класса 6
- Решения NCERT для науки класса 6
- Решения NCERT для социальных наук класса 6
- Решения NCERT для класса 6 Английский язык
- Решения NCERT для класса 7
- Решения NCERT для математики класса 7
- Решения NCERT для науки класса 7
- Решения NCERT для класса 7 социальные науки
- Решения NCERT для класса 7 Английский язык
- Решения NCERT для класса 8
- Решения NCERT для математики класса 8
- Решения NCERT для науки 8 класса
- Решения NCERT для социальных наук 8 класса ce
- Решения NCERT для класса 8 Английский
- Решения NCERT для класса 9
- Решения NCERT для социальных наук класса 9
- Решения NCERT для математики класса 9
- Решения NCERT для математики класса 9 Глава 1
- Решения NCERT для математики класса 9 Глава 2
- Решения NCERT для математики класса 9 Глава 3
- Решения NCERT для математики класса 9 Глава 4
- Решения NCERT для математики класса 9 Глава 5
- Решения NCERT для математики класса 9 Глава 6
- Решения NCERT для математики класса 9 Глава 7
- Решения NCERT для математики класса 9 Глава 8
- Решения NCERT для математики класса 9 Глава 9
- Решения NCERT для математики класса 9 Глава 10
- Решения NCERT для математики класса 9 Глава 11
- Решения NCERT для математики класса 9 Глава 12
- Решения NCERT для математики класса 9 Глава 13
- NCER Решения T для математики класса 9 Глава 14
- Решения NCERT для математики класса 9 Глава 15
- Решения NCERT для науки класса 9
- Решения NCERT для науки класса 9 Глава 1
- Решения NCERT для науки класса 9 Глава 2
- Решения NCERT для науки класса 9 Глава 3
- Решения NCERT для науки класса 9 Глава 4
- Решения NCERT для науки класса 9 Глава 5
- Решения NCERT для науки класса 9 Глава 6
- Решения NCERT для науки класса 9 Глава 7
- Решения NCERT для науки класса 9 Глава 8
- Решения NCERT для науки класса 9 Глава 9
- Решения NCERT для науки класса 9 Глава 10
- Решения NCERT для науки класса 9 Глава 12
- Решения NCERT для науки класса 9 Глава 11
- Решения NCERT для класса 11
4-х квадрантный график координат Pi cture
Координатный график Mystery Pictures
График Mystery Pictures Graph Бесплатная загрузка электронной книги в формате PDF: Graph Mystery Pictures Загрузить или прочитать электронную книгу Координатный график Mystery Pictures в формате PDF Из лучшего руководства пользователя Условия базы данных из двух
ПодробнееЦветные графические изображения с координатами
Color Graph Pictures Бесплатная загрузка электронной книги в формате PDF: Color Graph Pictures Download or Read Online ebook Color Graph Координаты изображений в формате PDF из базы данных Best User Guide с целыми числами, а также
ПодробнееГрафические квадратичные функции
Проблема 1 Парабола Изучите данные в L 1 и L справа.Пусть L 1 будет значением x, а L будет значениями y для графика. 1. Как связаны значения x и y? Какой узор вы видите? Чтобы войти в
ПодробнееПостроение графиков линейных уравнений
Построение графиков линейных уравнений I. Построение графиков линейных уравнений a. Графики уравнений первой степени (линейных) всегда будут прямыми линиями. б. Графики линий могут иметь положительный наклон отрицательный наклон нулевой наклон
ПодробнееЦелые числа (страницы 294 298)
A Целые числа (стр. 294 298) Целое число — это любое число из этого набора целых чисел и их противоположностей: {3, 2 ,, 0 ,, 2, 3,}.Целые числа больше нуля являются положительными целыми числами. Можно написать
Подробнее7.4A / 7.4B УЧАЩИЕСЯ ЗАДАНИЕ № 1
7.4A / 7.4B ЗАДАНИЕ УЧАЩИХСЯ № 1 Напишите формулу, которая могла бы использоваться для определения радиуса круга, r, с учетом длины окружности, C. Формула в таблице математики для 7 класса, которая связывает
ПодробнееФормулы, функции и диаграммы
Формулы, функции и диаграммы :: 167 8 Формулы, функции и диаграммы 8.1 ВВЕДЕНИЕ В этом уроке вы можете вводить формулы и функции, а также выполнять математические вычисления. Вы также сможете
ПодробнееМатематика принятия решений EdExcel 1
EdExcel Decision Mathematics 1 Линейное программирование Раздел 1: Формулирование и решение в графическом виде Примечания и примеры Эти примечания содержат подразделы о: Формулировке задач LP Решение задач LP Минимизация
ПодробнееШпаргалки по алгебре
Таблицы Шпаргалки по алгебре предоставляют вам инструмент для обучения ваших учеников конспектированию, решению задач и организационным навыкам в контексте уроков алгебры.Эти листы обучают концепции
ПодробнееУРАВНЕНИЯ И НЕРАВЕНСТВА
УРАВНЕНИЯ И НЕРАВЕНСТВА Линейные уравнения и наклон 1. Наклон a. Рассчитайте наклон прямой по двум точкам b. Вычислите наклон прямой, параллельной заданной. c. Рассчитать наклон прямой
ПодробнееАлгебра I Словарные карточки
Алгебра I Словарные карточки Содержание Выражения и операции Натуральные числа Целые числа Целые числа Рациональные числа Иррациональные числа Действительные числа Абсолютное значение Порядок операций Выражение
ПодробнееПовторение по математике 113 к экзамену I
Повторение по математике 113 к экзамену I, раздел 1.1 Декартова система координат, наклон и уравнение линии (1.) Прямоугольная или декартова система координат Вы должны иметь возможность маркировать квадранты в прямоугольнике
ПодробнееСмысл чисел и операции
Смысл чисел и операции, представляющие как они: 6.N.1 6.N.2 6.N.3 6.N.4 6.N.5 6.N.6 6.N.7 6.N.8 6. №.9 6.N.10 6.N.11 6.N.12 6.N.13. 6.N.14 6.N.15 Продемонстрируйте понимание положительных целочисленных показателей
ПодробнееИнтерактивные таблицы Excel:
Интерактивные электронные таблицы Excel: создание инструментов визуализации для улучшения вашего ориентированного на учащихся класса математики и естественных наук Скотт А.Sinex Департамент физических наук и инженерии Prince George
ПодробнееГЛАВА 1 Линейные уравнения
ГЛАВА 1 Линейные уравнения 1.1. Линии Прямоугольную систему координат также называют декартовой плоскостью. Он образован двумя линиями действительных чисел, горизонтальной осью или осью x и вертикальной осью или
. ПодробнееНеделя 1: Функции и уравнения
Неделя 1: Функции и уравнения Цели: Обзор функций Знакомство с моделированием с использованием линейных и квадратичных функций Решение уравнений и систем Рекомендуемая литература для учебников: Глава 2: 2.1-2.2, и Глава
ПодробнееЛаборатория Джефферсона Математика Sol Практика
Лаборатория математики Sol Практика Бесплатная электронная книга в формате PDF Скачать: Lab Math Sol Практика Скачать или прочитать электронную книгу Джефферсон лабораторная математическая практика в формате PDF Из базы данных Best User Guide Выполните следующие действия
ПодробнееНаучное построение графиков в Excel 2010
Научное построение графиков в Excel 2010 При запуске Excel вы увидите экран, показанный ниже.Различные части дисплея помечены красным цветом со стрелками для определения терминов, используемых в оставшейся части этого обзора.
ПодробнееMicroStrategy Desktop
MicroStrategy Desktop Краткое руководство пользователя MicroStrategy Desktop позволяет бизнес-профессионалам, таким как вы, легко и просто изучать данные без прямой поддержки со стороны ИТ-специалистов. 1 Импорт данных из
ПодробнееЧасть 1: Справочная информация — Графики
Кафедра физики и геологии Графическая астрономия 1401 Необходимое оборудование Кол-во Компьютер с программным обеспечением Data Studio 1 1.1 Графики Часть 1: Предпосылки — Графики В науке очень важно найти и
ПодробнееПонимание основного исчисления
Понимание основного исчисления С.К. Чанг Посвящается всем людям, которые помогли мне в моей жизни. i Предисловие Эта книга представляет собой переработанную и расширенную версию конспектов лекций по основам исчисления и другим
ПодробнееГистограммы и точечные диаграммы
КОНДЕНСИРОВАННАЯ ЛЕСА 1.1 Гистограммы и точечные диаграммы В этом уроке вы будете интерпретировать и создавать различные графики, находить некоторые сводные значения для набора данных, делать выводы о наборе данных на основе графиков
ПодробнееСКОЛЬКО Я ПОТОРАЮ НА ГАЗ?
СКОЛЬКО Я ПОТОРАЮ НА ГАЗ? Результат (цель урока) Учащиеся будут использовать текущую и будущую цену на бензин для построения T-диаграмм, написания алгебраических уравнений и построения уравнений на графике.
Подробнее2.5 Преобразования функций
2.5 Преобразования функций Раздел 2.5 Примечания Стр. 1 Сначала мы рассмотрим основные графики, которые вы должны знать, как рисовать: Функция квадратного корня Абсолютное значение Функция Идентичность Функция Домен: [
ПодробнееГрафические квадратные уравнения
.4 Графические квадратные уравнения. 4 ЦЕЛЬ. Построение графика квадратного уравнения b нанесение точек на график В разделе 6.3 мы научились составлять графики уравнений первой степени. Подобные методы позволят нам построить квадратные уравнения
. ПодробнееЛИНЕЙНЫЕ УРАВНЕНИЯ ОТ ДВУХ ПЕРЕМЕННЫХ.
66 МАТЕМАТИКА ГЛАВА 4 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИ Основное применение аналитического искусства состоит в том, чтобы преобразовать математические задачи в уравнения и представить эти уравнения в самых простых терминах, которые Подробнее
Объемы революции
Математика. Тома революции. Об этом уроке. Этот урок знакомит студентов с физическим методом визуализации трехмерных тел и специальной процедурой для построения эскизов твердого тела вращения.Студенты
Подробнееegyptigstudentroom.com
МЕЖДУНАРОДНЫЕ ЭКЗАМЕНЫ КЕМБРИДЖСКОГО УНИВЕРСИТЕТА Международный общий аттестат о среднем образовании * 5128615949 * МАТЕМАТИКА 0580/04, 0581/04 Документ 4 (расширенный) Май / июнь 2007 г. Дополнительные материалы:
ПодробнееJiji St Math Dot Shapes
Jiji St Math Dot Бесплатная электронная книга в формате PDF Скачать: Jiji St Math Dot Загрузить или прочитать электронную книгу Jiji St Math Dot shape в формате PDF Из лучшего руководства пользователя База данных Научно-исследовательский институт MIND — JiJi Store 3 Visualize
ПодробнееПостроение графиков — форма наклона-пересечения
2.3 Построение графика — форма пересечения наклона Цель: составить уравнение линии с известным наклоном и точкой пересечения по оси Y. При построении линии мы нашли один метод, который можно использовать, — это составить таблицу значений. Однако
ПодробнееСредний уровень PowerPoint
Промежуточные диаграммы и шаблоны PowerPoint Автор: Джим Уодделл Последнее изменение: январь 2002 г. Темы для обсуждения: Создание диаграмм 2 Создание диаграммы. 2 Линейные диаграммы и точечные диаграммы. 4 Создание линейной диаграммы.
ПодробнееГрафическая информация
Части типичного графика Графическая информация В типичном графике, используемом для оценки поведения, время и поведение являются двумя рассматриваемыми переменными. Каждая точка данных на графике дает две части информации:
ПодробнееПРОЕКТ СТУДЕНЧЕСКОГО ИЗОБРАЖЕНИЯ MARS
ПРОЕКТ MARS STUDENT IMAGING Практическое руководство по анализу данных Образовательная программа Mars Образовательная программа Университета штата Аризона Практическое руководство по анализу данных Этот набор действий разработан, чтобы помочь вам организовать данные, которые вы собираете
ПодробнееСЕРТИФИКАЦИЯ ДЛЯ НОУТБУКА MATH 60
СЕРТИФИКАЦИЯ ДЛЯ НОУТБУКА MATH 60 Глава # 1: Целые и действительные числа 1.1a 1.1b 1.2 1.3 1.4 1.8 Глава № 2: Алгебраические выражения, линейные уравнения и приложения 2.1a 2.1b 2.1c 2.2 2.3a 2.3b 2.4 2.5
ПодробнееME 111: Инженерный чертеж
ME 111: Лекция по инженерному черчению № 14 (10.10.2011) Разработка поверхностей http://www.iitg.ernet.in/arindam.dey/me111.htm http://www.iitg.ernet.in/rkbc /me111.htm http://shilloi.iitg.ernet.in/~psr/ Индийский
ПодробнееExcel — создание диаграмм
Excel — Создание диаграмм Говорят, что картинка стоит тысячи слов, и это правда.Графики профессионального вида улучшают визуализацию вашей статистики, финансовых отчетов или презентаций. Excel
ПодробнееРешение математики с помощью стрелки
Math The Arrow Way Скачать бесплатную электронную книгу в формате PDF: Math The Arrow Way Скачать или прочитать электронную книгу по решению математических задач в формате PDF из The Best User Guide Database 4 СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ И
ПодробнееОсновы понимания
Упражнение: TEKS: Изучение преобразований Основные понятия.(5) Инструменты геометрического мышления. Методы работы с пространственными фигурами и их свойствами важны для понимания лежащих в основе
ПодробнееЛинейные уравнения. Найдите домен и диапазон следующего набора. {(4,5), (7,8), (-1,3), (3,3), (2, -3)}
Область линейных уравнений и область значений — это набор возможных значений x-компоненты точки в форме (x, y). Диапазон относится к набору возможных значений y-компоненты точки в
. ПодробнееЛестница прогресса геометрии
Лестничная диаграмма прогресса в геометрии Математика имеет смысл Основание Цели на конец года стр. 2 Математика имеет смысл 1 2 Цели на конец блока стр. 3 Математика имеет смысл 3 4 Цели на конец блока стр. 4 Математика дает
Подробнее2.2 Потребность в системах координат
Рисунок 2.2. Декартова система координат.
Места на поверхности Земли измеряются и представляются в координатах ; координата — это набор из двух или более чисел, определяющих положение точки, линии или другой геометрической фигуры по отношению к некоторой системе отсчета. Простейшей системой такого типа является декартова система координат , названная в честь математика и философа 17 века Рене Декарта.Декартова система координат, подобная той, что приведена выше на рисунке 2, представляет собой просто сетку, образованную соединением двух шкал измерения, горизонтальной (x) и одной вертикальной (y). Точка, в которой оба x и y равны нулю, называется началом системы координат. На приведенном выше рисунке начало координат (0,0) расположено в центре сетки (пересечение двух жирных линий). Все остальные позиции указываются относительно начала координат. Координата правого верхнего угла сетки — (6,3).Нижний левый угол (-6, -3).
Рисунок 2.3. Географическая (или «геодезическая») система координат.
Декартова и другие двумерные (плоские) системы координат удобны благодаря своей простоте. Они не совсем подходят для указания географического положения. Однако географическая система координат, как показано на рисунке 3, разработана специально для определения положений на приблизительно сферической поверхности Земли. Вместо двух линейных шкал измерения x и y, географическая система координат объединяет две изогнутые шкалы измерения.
Вы, наверное, уже встречали термины широта и долгота в своих исследованиях. Сравнение этих двух шкал приведено ниже на Рисунке 4. Шкала север-юг, называемая широты (обозначенная греческим символом фи ), находится в диапазоне от + 90 ° (или 90 ° с.ш.) на Северном полюсе до -90 ° (или 90 ° ю.ш.) на южном полюсе, а экватор равен 0 °. Линия широты также известна как параллель .
Шкала восток-запад, называемая долготой (условно обозначается греческим символом лямбда ), находится в диапазоне от + 180 ° до -180 °.Поскольку Земля круглая, + 180 ° (или 180 ° E) и -180 ° (или 180 ° W) — это одна и та же линия сетки. Линия долготы называется меридианом . Эта линия сетки +/- 180 примерно соответствует международной линии дат , у которой есть отклонения, которые проходят вокруг некоторых территорий и групп островов, так что им не нужно справляться с путаницей в соседних местах, находящихся в двух разных днях. Напротив международной линии перемены дат на другой стороне земного шара находится нулевой меридиан , линия долготы, определенная международным договором как 0 °.В более высоких широтах длина параллелей уменьшается до нуля на 90 ° северной и южной широты. Линии долготы не параллельны, а сходятся к полюсам. Таким образом, хотя градус долготы на экваторе равен расстоянию около 111 километров, это расстояние уменьшается до нуля на полюсах.
Рисунок 2.4. Географическая система координат.
Фото: Рэчел Бьянкетти © Университет штата Пенсильвания, имеет лицензию CC BY-NC-SA 4.0Попробуйте это: приложение для практики географической системы координат
Встречали ли вы когда-нибудь термины «широта» или «долгота»? Насколько хорошо вы действительно понимаете географическую систему координат? Наш опыт показывает, что, хотя каждый, кто входит в этот класс, слышал о широте и долготе, только около половины могут указать на местоположение на карте, указанное парой географических координат.Веб-сайты, указанные ниже, позволяют проверить свои знания. Вы будете практиковаться, нажимая на земном шаре места, заданные случайно сгенерированными географическими координатами.
Игра-викторина по карте
Практика долготы и широты
2.2.1 Географические координаты
Мы обсудили тот факт, что и широта, и долгота измеряются в градусах, но что насчет того, когда нам нужно более точное измерение детализации? Чтобы записать географические координаты, мы можем разделить градусы на минуты и секунды.Градус равен шестидесяти минутам, а каждая минута — шестидесяти секундам. Географические координаты часто необходимо преобразовывать, чтобы георегистрировать один слой данных на другом. Географические координаты могут быть выражены в десятичных градусах или в градусах, минутах и секундах . Иногда вам нужно преобразовать одну форму в другую.
Вот как это работает:
Чтобы преобразовать широту -89,40062 из десятичных градусов в градусы, минуты, секунды:
Вычтите число целых градусов (89 °) из общего числа (89.40062 °). (Знак минус используется в десятичном формате градуса только для обозначения того, что значение является западной долготой или южной широтой.) В этом примере знак минус указывает на юг, поэтому следите за этим.
Умножьте остаток на 60 минут (0,40062 x 60 = 24,0372).
Вычтите из произведения количество минут (24 фута).
Умножьте остаток на 60 секунд (0,0372 x 60 = 2,232). Округлите (в данном случае с точностью до секунды).
Соберите части; результат 89 ° 24 ‘2 «ю.ш.Если бы исходной точкой была долгота -89,400062, единственная разница была бы в том, что буква S, указанная выше, была бы заменена на W.
. Чтобы преобразовать 43 ° 4 ’31 «из градусов, минут, секунд в десятичные градусы, используйте простую формулу ниже:
DD = Градусы + (Минуты / 60) + (Секунды / 3600)
Разделите количество секунд на 60 (31 ÷ 60 = 0,5166).
Добавьте частное шага (1) к целому количеству минут (4 + 0,5166).
Разделите результат шага (2) на 60 (4.5166 ÷ 60 = 0,0753).
Добавьте частное из шага (3) к целому числу градусов (43 + 0,0753).
Результат 43.0753 °
Практика викторины
зарегистрированных студентов штата Пенсильвания должны вернуться, чтобы пройти тест по самооценке на предмет географических координат .
Вы можете проходить практические викторины сколько угодно раз. Они не оцениваются и никак не влияют на вашу оценку.
2.2.2 Плоские координаты
До сих пор вы читали о декартовых системах координат, но это не единственный вид двумерной системы координат.Плоская система координат может рассматриваться как сопоставление любых двух шкал измерения. Другими словами, если вы разместите две линейки под прямым углом, так что отметки «0» на линейках выровнены, вы определите систему координат плоскости. Правителей называют «топорами». Как и в случае с декартовыми координатами, абсолютное положение любой точки в пространстве в системе плоских координат определяется в единицах измерения расстояния по осям x (восток-запад) и y (север-юг).Позиция, определяемая координатами (1,1), находится на одну единицу правее и на одну единицу выше начала координат (0,0). Сетка универсальной поперечной проекции Меркатора (UTM) представляет собой широко используемый тип системы координат на географической плоскости, в которой позиции задаются как восточные (расстояния в метрах, к востоку от исходной точки) и северные (расстояния к северу от исходной точки).
Некоторые преобразования координат просты. Преобразование плоских координат без географической привязки в полярные координаты без привязки, более подробно описанное ниже в главе, включает не что иное, как замену одного вида координат другим.
Рисунок 2.5. Одно и то же положение задано в двух системах плоских координат без привязки: декартовой (слева) и полярной (справа).
2.2.3 UTM: Универсальная поперечная проекция Меркатора
Рисунок 2.6. Десять зон UTM, охватывающих территорию США
.Сетка географической системы координат широты и долготы состоит из двух изогнутых шкал измерения , которые соответствуют почти сферической форме Земли. Как обсуждалось выше, географические координаты могут быть указаны в градусах, минутах и угловых секундах.Изогнутые сетки неудобно использовать для нанесения позиций на плоские карты. Кроме того, вычисление расстояний, направлений и площадей со сферическими координатами затруднительно по сравнению с расчетом с плоскими координатами. По этим причинам картографы и военные в Европе и США разработали систему координат UTM. Сетки UTM теперь являются стандартом не только для печатных топографических карт, но и для географической привязки цифровых данных, составляющих новую «Национальную карту США» (NationalMap.gov).
«Поперечная проекция Меркатора» относится к способу преобразования географических координат из сферической модели Земли в плоские координаты. Акт математического преобразования географических сферических координат в плоские координаты обязательно смещает большую часть (но не все) преобразованных координат в некоторой степени. Из-за этого масштаб карты меняется в пределах спроецированных (плоских) сеток системы координат UTM. Таким образом, координаты UTM обеспечивают точные спецификации местоположения, но с известной степенью позиционной ошибки в зависимости от того, где находится место.
Ниже показан юго-западный угол топографической карты государственного колледжа в масштабе 1:24 000 (где 1 дюйм на карте соответствует 2000 футов в мире) в округе Сентер, штат Пенсильвания, опубликованной Геологической службой США (USGS). . Обратите внимание, что указаны географические координаты (40 ° 45 ‘северной широты, 77 ° 52’ 30 дюймов западной долготы) угла. Однако также показаны галочки и метки, представляющие две системы координат плоскости, универсальную поперечную проекцию Меркатора (UTM). система и система координат штата (SPC).Галочка на западном краю карты, обозначенная «4515», представляет линию сетки UTM (называемую «северное положение»), которая проходит параллельно экватору и на 4 515 000 метров к северу от него. Отметки «258» и «259» представляют линии сетки, которые проходят перпендикулярно экватору и 258 000 метров и 259 000 метров к востоку, соответственно, от исходной точки сетки UTM Zone 18 North (см. Ее расположение на рис. 6 выше). В отличие от линий долготы, «восточные направления» UTM прямые и не сходятся на полюсах Земли.
Рисунок 2.7. Юго-западный угол топографической карты USGS с отметками и метками сетки для трех различных систем координат, включая систему координат UTM.
Универсальная поперечная система Меркатора на самом деле не универсальна, но она покрывает почти всю поверхность Земли. Исключаются только полярные области — широты выше 84 ° северной широты и 80 ° южной широты. (Полярные системы координат используются для определения положений за пределами этих широт.) Система UTM делит остальную часть поверхности Земли на 60 зон, каждая из которых охватывает 6 ° долготы.Они пронумерованы с запада на восток от 1 до 60, начиная с 180 ° западной долготы
Сетка широты, долготы и системы координат
Автор: GIS Geography · Последнее обновление: 18 октября 2020 г.
Сетка широты, долготы и системы координат
Вот как можно запомнить широту и долготу:
Широта линии проходят с востока на запад и параллельны друг другу. Если вы идете на север, значения широты увеличиваются. Наконец, значения широты (значения Y) находятся в диапазоне от -90 до +90 градусов.
Но долготы линии идут с севера на юг. Они сходятся на полюсах. А его координаты X находятся в диапазоне от -180 до +180 градусов.
Координаты широты и долготы составляют нашу географическую систему координат.
Системы координат карты
Вы можете указать координаты широты и долготы любого местоположения на Земле.
Геодезия — это область исследований, которая определяет форму и размер Земли. Геодезисты используют системы координат, такие как WGS84, NAD27 и NAD83.В каждой системе координат геодисты используют математику, чтобы дать каждой позиции на Земле уникальные координаты.
Географическая система координат определяет двумерные координаты на основе поверхности Земли. Он имеет угловую единицу измерения, нулевой меридиан и нулевую точку (которая содержит сфероид).
Как показано на изображении ниже, линии долготы имеют координаты X от -180 до +180 градусов. Координаты долготы С другой стороны, линии широты имеют значения Y, которые находятся в диапазоне от -90 до +90 градусов.Координаты широтыэкватор — это место, где мы измеряем север и юг. Например, все к северу от экватора имеет положительные значения широты. В то время как все к югу от экватора имеет отрицательные значения широты.
Гринвичский меридиан (или нулевой меридиан) — это нулевая линия долготы, от которой мы отсчитываем восток и запад. Фактически, нулевая линия проходит через Королевскую обсерваторию в Гринвиче, Англия, поэтому мы называем ее тем, чем она является сегодня. В географической системе координат нулевой меридиан — это линия с долготой 0 °.
Большинство горизонтальных датумов определяют экватор как нулевую линию широты. На экваторе мы измеряем север и юг. Принимая во внимание, что Гринвичский меридиан (или нулевой меридиан) — это нулевая линия долготы, от которой мы измеряем восток и запад.
Вместе эти линии служат ориентиром для широты и долготы, которые всегда зигзагообразно переходят друг в друга . Эта географическая сетка дает уникальную широту и долготу для каждой точки на Земле.
Найдите что-нибудь на Земле с помощью координат
Координаты — это пары (X, Y) в двумерном пространстве, привязанные к горизонтальной системе координат.В то время как тройки (X, Y, Z) точек не только имеют положение, но также имеют высоту, привязанную к вертикальной системе координат. Другими словами, значения X и Y представляют горизонтальное положение. Принимая во внимание, что Z-значение представляет вертикальное положение.
Географические системы координат используют эллипсоид для аппроксимации всех местоположений на поверхности земли. Тогда как датум определяет поверхность.
Горизонтальная точка отсчета имеет большую ось, которая представляет собой самый длинный диаметр эллипса.Кроме того, у него есть малая ось, которая представляет собой самый короткий диаметр эллипса. Наконец, горизонтальная система координат имеет радиус, который представляет положение поверхности относительно центра Земли.
Что такое система координат?
Опорный эллипсоид — это математическая модель формы Земли с большой осью вдоль экваториального радиуса. В географической системе координат используются долгота и широта, выраженные в десятичных градусах. Например, WGS 1984 и NAD 1983 являются сегодня наиболее распространенными датумами.До 1983 года наиболее распространенным источником данных был NAD27.
Картографы записывают сферические координаты (широты и долготы) в градусах-минутах-секундах (DMS) и десятичных градусах. Для градусов-минут-секунд минуты находятся в диапазоне от 0 до 60. Например, географическая координата, выраженная в градусах-минутах-секундах для Нью-Йорка:
.- Широта: 40 градусов, 42 минуты, 51 секунда N
- Долгота: 74 градуса, 0 минут, 21 секунда з.д.
Вы также можете выражать географические координаты в десятичных градусах.Это просто еще один способ представить одно и то же место в другом формате. Например, вот Нью-Йорк в десятичных градусах:
.- Широта: 40.714
- Долгота: -74,006
У Федеральной комиссии по связи есть инструмент преобразования DMS-Decimal, который преобразует широту и долготу между десятичными градусами и градусами, минутами и секундами.
Сетка широты, долготы и сферической системы координат
Когда вы складываете две координаты в пару (X, Y), вы можете найти что угодно на Земле.
Широта и долгота образуют сетку нашей системы координат.
Кроме того, координаты можно выражать по-разному. Например, вы можете использовать десятичные градусы или градусы-минуты-секунды.
Благодаря нашим географическим координатам вы можете точно определить любую точку на Земле, например, с помощью GPS-приемников. И это включает в себя место, где вы читаете эту статью прямо сейчас.
декартовых координат
Декартовы координаты могут использоваться, чтобы определить, где мы находимся на карте или графике.
Декартовы координаты
Используя декартовы координаты, мы отмечаем точку на графике цифрой , насколько далеко вдоль и , насколько далеко она выше :
| Точка (12,5) находится на 12 единиц вперед и на 5 единиц вверх. |
Их также называют прямоугольными координатами , потому что это похоже на то, как мы формируем прямоугольник.
Ось X и Y
| Направление влево-вправо ( по горизонтали ) обычно называется X . | |
| Направление вверх-вниз ( вертикальное ) обычно называется Y . |
| Сложите их вместе на графике… | |
… и мы готовы к работе | |
Где они пересекаются — это точка «0»,
| |
Ось : опорная линия, от которой расстояния измеряются.
Множественное число Axis — Axes , произносится как ax-eez
Пример:
Балл (6,4) это
6 единиц в поперечнике (в направлении x ) и
На 4 единицы вверх (в направлении и )
Так (6,4) означает:
Идите по 6, затем вверх по 4, затем «нанесите точку».
И вы можете запомнить какая ось какая по:
x — это КРЕСТ, поэтому x — ПОПЕРЕЧНО страницы.
Сложить как 2 числовые строки
Это как если бы мы соединили две числовые линии, одна идет влево-вправо, а другая — вниз-вверх.
Направление
При увеличении x точка перемещается дальше на вправо . | |
По мере увеличения y точка перемещается дальше на вверх на . |
Запись координат
Координаты всегда пишутся в определенном порядке:
- сначала горизонтальное расстояние,
- , затем вертикальное расстояние.
Это называется «заказанной парой » ( пара, номеров в специальном заказе )
И обычно числа разделяются запятой, а вокруг всего этого ставятся круглые скобки:
(3,2)
Пример: (3,2) означает 3 единицы вправо и 2 единицы вверх
Пример: (0,5) означает 0 единиц вправо и 5 единиц вверх.
Другими словами, всего на 5 единиц больше.
Происхождение
Точке (0,0) присваивается специальное имя «Начало», а иногда и буква «О».
Абсцисса и Ордината
Вы можете услышать слова «Абсцисса» и «Ордината» … это просто значения x и y:
- Абсцисса: значение по горизонтали («x») в паре координат: как далеко вдоль точка находится на
- Ордината: значение по вертикали («y») в паре координат: как далеко вверх или вниз точка находится на
«Декартово»…?
Их называют декартовыми , потому что идея была развита математиком и философом Рене Декарт , который также был известен как Картезий .
Он также известен тем, что сказал «Я думаю, следовательно, я» .
А как насчет отрицательных значений X и Y?
Как и в случае с числовой линией, у нас могут быть и отрицательные значения.
Отрицательный: начало с нуля и направление в противоположном направлении :
- Отрицательный x идет влево
- Отрицательный y идет вниз
Итак, для отрицательного числа:
|
Четыре квадрантаКогда мы включаем отрицательные значения, оси x и y делят пространство на 4 части: Квадранты I, II, III и IV (пронумерованы против часовой стрелки) |
В квадранте I и x, и y положительны, но…
- в квадранте II x отрицательно (y все еще положительно),
- в квадранте III и x, и y отрицательны, а
- в квадранте IV x снова положителен, а y отрицателен.
Как это:
|
Пример: Точка «А» (3,2) находится на 3 единицы вперед и на 2 единицы вверх.
Оба x и y положительны, так что эта точка находится в «квадранте I»
Пример: точка «C» (-2, -1) проходит на 2 единицы в отрицательном направлении и на 1 единицу вниз (т. Е. В отрицательном направлении).
Оба x и y отрицательны, поэтому эта точка находится в «квадранте III»
Примечание: слово Quadrant происходит от quad , что означает четыре . Например, четырех младенцев, рожденных при одном рождении, называют четвероногих , четвероногих животных — четвероногих .а четырехугольник — четырехсторонний многоугольник.
Размеры: 1, 2, 3 и более …
Подумайте об этом:
| 1 | На номерную линию можно идти только: , поэтому для любой позиции нужно всего одно число |
|---|---|
| 2 | Декартовы координаты могут идти: , поэтому для любой позиции нужно два числа |
| 3 | Как найти точку в реальном мире (например, кончик носа)? Нам нужно знать:
, то есть три числа или 3 измерения! |
3 Размеры
Декартовы координаты могут использоваться для определения местоположения точек в 3 измерениях, как в этом примере:
| Здесь точка (2, 4, 5) показана в трехмерных декартовых координатах. |