Что такое неравенство? Как решать неравенства?

        Для начала неплохо бы разобраться, что же такое неравенство вообще, как оно устроено и что с ним можно (и нужно) делать. Разбираемся?

        Итак…

 

Что такое неравенство?

        Говоря простым языком, берём любое уравнение и значок «=» (равно) заменяем на другой значок (>, <, ≥, ≤, ≠). Вот и получается – неравенство.

        Уравнения бывают всякими – линейными, квадратными, дробными, показательными, логарифмическими, тригонометрическими, иррациональными и т.д.

        Соответственно, и неравенства также бывают линейные, квадратные и… в общем, всякие.)

        Теперь поговорим о значках неравенств. Что о них нужно знать? Неравенства со значками «

>» (больше) или «<» (меньше) называются строгими. Неравенства со значками «≥» (больше или равно) или «≤» (меньше или равно) называются нестрогими. Значок «≠» (не равно) стоит особняком, но неравенства с таким значком приходится решать постоянно. И мы обязательно порешаем.)

        Сам значок обычно не оказывает существенного влияния на ход решения. Зато в самом конце решения, при оформлении окончательного ответа, смысл значка проявляется в полную силу! В чём мы с вами и убедимся на конкретных примерах.

        Что ещё нужно знать о неравенствах? Неравенства, как и равенства, бывают

верные и неверные. Здесь всё предельно ясно. Например, 2>1 – верное неравенство. А вот неравенство 2<1 – неверное.

        Неравенства – ближайшие родственники уравнений. Стало быть, проблемы при решении уравнений будут автоматически приводить к полному провалу и в неравенствах. Срочно повторите решение основных типов уравнений, у кого проблемы! Я серьёзно.) Иначе в неравенствах будете тормозить нещадно… И не надейтесь, что при изложении, скажем, материала по решению квадратных неравенств я буду отдельно разжёвывать, что такое дискриминант или как рисовать график параболы.) Прошу быть к этому готовыми! Так что по ссылочкам-то гуляйте, гуляйте.)

 

Зачем нужны неравенства?

        Вопрос резонный. Затем же, зачем нам нужны и уравнения. Для жизни.)

        В обычной жизни неравенства вы видите повсюду. Причём не только видите, но и… решаете их! Сами того не замечая. Сомневаетесь?) Пожалуйста! Вот вам зашифрованные житейские примеры неравенств. Хранение при такой-то температуре (скажем, от 0°С до +25°С) – неравенство. Штраф за превышение скорости – неравенство. Распределение призовых мест в соревновании – тоже неравенство. Срок действия проездного на метро – неравенство. Опоздание на урок (поезд, самолёт) – и тут неравенство!

        Одним словом, с неравенствами мы с вами сталкиваемся всякий раз, как только нам нужно оценивать или сравнивать какие-то величины. Совершенно любые. Это может быть температура в помещении, скорость автомобиля, время в пути, расходы в магазине, баланс денег на телефоне, рост, вес – да всё что угодно. Всё что мы можем выразить числом, как-то количественно оценить или с чем-то сравнить, приводит нас к понятию неравенства. Верного или неверного.)

 

Как решать неравенства?

        Решение любого неравенства состоит из двух ключевых пунктов.

 

        Это:

        1. Тождественные преобразования неравенств.

        2. Работа с числовой прямой.

 

        Оба эти пункта – основы. Каждый из них одинаково важен. Если есть проблемы хотя бы в одном из них, то попытка решения любого, даже самого простенького неравенства, обречена на провал. Оно нам надо? Согласен, не надо.

       Про первый пункт (тождественные преобразования) подробненько поговорим в этом уроке. Тут всё просто. Второй пункт (работа с числовой осью) поинтереснее будет. Его рассмотрим в следующем уроке.

 

        Итак, вникаем.

        Разные типы неравенств (линейные, квадратные, дробные, показательные, тригонометрические, иррациональные и т.д.) решаются по-разному. На каждый тип — свой собственный способ, свой специальный приём. Но! Все эти специальные приёмы применимы только к некоторому, так называемому

стандартному виду неравенства. Т.е. неравенство любого типа первым делом нужно подготовить к применению своего способа.

        Такая подготовка работает для неравенств любого вида. Работает безотказно. И проста до безобразия.) Нужно, всего-навсего, правильно выполнять два (всего два!) элементарных базовых преобразования. Эти преобразования знакомы каждому. Но, что характерно, ляпы в этих самых преобразованиях — и есть основная проблема в решении неравенств, да… Стало быть, надо освоить эти преобразования. Называются они вот как:

 

Тождественные преобразования неравенств.

        Тождественные преобразования неравенств очень похожи на тождественные преобразования уравнений. Собственно, именно в этом и таится основная засада в решении неравенств! Отличия проскакивают мимо головы и… приплыли.) Поэтому я особо выделю эти отличия.

        Итак:

        1. Первое тождественное преобразование неравенств:

        К обеим частям неравенства можно прибавить (или отнять) любое (но одинаковое!) число или выражение (в том числе и с переменной). Знак неравенства от этого не изменится.

        На практике это преобразование выглядит как знакомый всем старый добрый перенос членов из одной части неравенства в другую со сменой знака. Со сменой знака члена, а не неравенства! Знак самого неравенства сохраняется.

        Например, надо решить такое линейное неравенство:

        5x – 3 < 4х + 2

        Тут и думать нечего, вспоминаем нашу мантру — «с иксами влево, без иксов – вправо…»

И действуем:

        5х – 4х < 2 + 3

        Знак неравенства при переносе не трогаем!

        Осталось слева привести подобные, а справа посчитать. Получим:

        x < 5

        Это правильный ответ.

        Если вы – новичок и пока не знаете, как решать линейные неравенства, не беда. В отдельном уроке порешаем. Я сейчас не об этом. А о том, что первое тождественное преобразование неравенств полностью совпадает с аналогичным преобразованием для уравнений! Один в один. А вот второе тождественное преобразование в неравенствах резко отличается от такового в уравнениях. К нему и переходим.

 

        2. Второе тождественное преобразование неравенств:

        2.1. Обе части неравенства можно умножить (разделить) на одно и то же положительное

число. На любое положительное число. Знак неравенства при этом сохраняется.

        2.2. Обе части неравенства можно умножить (разделить) на одно и то же отрицательное число. На любое отрицательное число. Знак неравенства при этом меняется на противоположный.

        Вы ведь помните, что уравнение мы имеем право умножать или делить на что попало. И на число, и на выражение с иксом. Лишь бы не на ноль. Ему, уравнению, от этого хоть бы хны. Не меняется оно. А вот неравенства более чувствительны к умножению/делению.

        Вот вам наглядный пример на долгую память. Возьмём неравенство, не вызывающее сомнений:

        3>2

        Умножим обе части на положительное число +2, получим:

        6>4

        Возражения есть? Нету. А теперь умножим обе части на отрицательное число -2, получим:

        -6>-4

        А вот это уже откровенная ахинея! Бред! Ибо минус шесть никак не больше минус четырёх. Но… стоит только изменить знак неравенства на противоположный, как всё сразу становится на свои места:

        -6<-4

        Про бред и ахинею я не просто так ругаюсь. «Забыл(а) сменить знак неравенства…» – это самая распространённая ошибка

в решении неравенств. Именно на этом несложном преобразовании столько учеников сыпется! Которые забывают… Вот и ругаюсь. Авось, запомнится…)

        Самые внимательные, возможно, уже заметили, что неравенство нельзя умножать на выражение с иксом. Что ж, респект, как говорится.) А почему нельзя, как вы думаете? Очень просто. Мы же ничего не знаем про знак этого самого выражения с иксом! Оно может быть положительным, может быть отрицательным. Следовательно, мы понятия не имеем, какой знак неравенства ставить после умножения. Менять его или нет? Непонятно… Конечно, это ограничение (запрет на умножение/деление неравенства на выражение с иксом) можно и обойти. Если очень уж припрёт.) Но это – отдельная тема.

        Зачем нужно второе преобразование? Да всё за тем же, зачем оно нужно и в уравнениях! Избавляться от коэффициентов. На которые, напоминаю, перенос влево-вправо не распространяется. Например, что-нибудь крутое типа:

        9-3х > 0

        С девяткой-то всё ясно. Переносим вправо по первому преобразованию, получаем:

        -3х > -9

        Знак неравенства сохраняется!

        А вот теперь соображаем, что в ответе нас всегда интересует чистый икс. А тройка с минусом – мешает. Вот тут-то нам и нужно второе преобразование! Делим, как в уравнениях, обе части на -3. Внимание! Делим на отрицательное число!

        Знак неравенства меняется на противоположный!

        Получаем:

        x < 3

        Это ответ.)

        Ещё раз. В этом уроке мы с вами пока что не решаем неравенства. Мы всего лишь тренируемся правильно применять базовые преобразования! Просто на конкретных примерах гораздо нагляднее демонстрировать сам процесс.) Стало быть, если запись окончательного ответа x<3 пока что кажется вам полной китайщиной, не страшно. Совсем скоро мы с вами начнём тренироваться на кошках конкретных типах неравенств (с иксами, да…) – и все эти буковки и значки обретут смысл.

        Итак, с первым пунктом – тождественными преобразованиями – разобрались (надеюсь…). Но для успешного решения неравенств одних только тождественных преобразований, чаще всего, недостаточно. Именно этим неравенства и отличаются от уравнений. Поэтому пора переходить ко второму пункту. К работе с числовой осью.

        Об этом – в следующей теме.

Неравенства. Верные и неверные неравенства. Математика (2 класс)

Математика, 2 класс

Тема урока: «Неравенства. Верные и неверные неравенства»

-познакомить с понятием «неравенство» и видами неравенств;

-совершенствовать вычислительные умения и навыки;

— совершенствовать умение решать задачи.

1

2

3

4

4.1

4.2

4.3

5

5.1

5.2

6

6.1

6.2

7

7.1

7.2*

8

9

10

Орг. момент

Сегодня наш урок будет необычным, мы отправимся в путешествие.

А на каком виде транспорта, отгадайте:

Чудо-птица, алый хвост,

Полетела в стаю звёзд.

Проверим готовность к уроку:

-Руки?

-Ноги?

-Локти?

-Спина?

Проверка домашнего задания

От жителей далёкой планеты «Решай-считай» пришло к нам послание. Проверив д/з, мы попробуем его расшифровать.

-Сравнивая числовые выражения, мы поставили знак «равно». У нас при записи получились равенства.

— А что значит «неравенство»? И какие бывают неравенста?

Постановка цели и задач урока

Тема нашего урока : «Неравенства. Верные и неверные неравенства»

Какую цель мы поставим перед собой?

Что поможет достигнуть эту цель?

В конце урока сигнальными карточками вы оцените свою работу на уроке:

работал в полную силу,

работал хорошо, но были ошибки

надо подтянуться

Устный счёт

Много заданий у нас впереди.

Ну, а сейчас тренировки нужны.

Для достижения цели нам понадобятся не только математические знания, но и умение работать вместе, прийти на помощь друг другу в трудную минуту.

Решив примеры, вы расшифруете девиз нашего урока:

80-15 22+18 93-6 90-40 19+7 42+50 62-20

65 40 87 50 26 92 42

Каждый парашют должен приземлиться в заданной точке-ответе

Начинаем тренировку,

Чтобы сильным стать и ловким.

Круговые примеры «Центрифуга»

(это устройство, создающее перегрузки под действием центробежной силы)

-10 -42

-4

86

18+

36+ 2+

Сравните числа и числовые выражения:

1гр 2гр 3гр

85…43 28…57 14…54

79-20…50 35+5…60 46+4…30

38…53+7 96…50-30 48…90-30

Неравенства. Верные и неверные неравенства

Подготовка закончилась. Мы готовы к полёту.

Любой космический маршрут

Открыт для тех, кто любит труд.

Откройте наши путеводители (ученик стр. 90), приготовьте бортовые журналы (тетради).

В предыдущем задании мы сравнивали

-числа,

-числа и числовые выражения.

Между числами 85…43 28…57

стоят знаки < или >(нет знака =). Значит это неравенство. А мы уже встречались с неравенствами?

Рассмотрите следующие неравенства

79-20…50 35+5…60

Что можно о них сказать, правильно ли стоит знак? Значит это верное неравенство. В математике слово «правильно» заменили словом «верно». А если знак изменить? Будет ли верным это неравенство?

Значит это неверное неравенство.

стр.90 №2

-выпишите верные неравенства.

Какие неравенства называются верными? (верно поставлен знак)

ФИЗКУЛЬТМИНУТКА

Космонавты всегда занимаются спортом и делают зарядку. Даже в полёте они находят время на спортивные упражнения:

В небе плавает луна.

В облака зашла она.

Раз, два, три, четыре, пять-

Можем мы луну достать.

Шесть, семь, восемь, девять, десять-

И пониже перевесить.

Десять, девять, восемь, семь-

Чтоб луна светила всем.

стр.91 №4

-вставить недостающие числа, чтобы неравенства были верными

(В тетрадь записываем 1 нерав-во, устно проговариваем с другими числами)

Решение задач изученных видов

Любой космонавт должен хорошо уметь решать задачи.

стр.91 №6

Выполняем необходимые расчеты в бортовых журналах

ФИЗКУЛЬТМИНУТКА

Чтоб глаза твои зорче были,

Чтоб очки тебе не носить,

Эти лёгкие движения

Предлагаю повторить!

упр. 1

круговые движения глазами по часовой стрелке- 4 раза,

против часовой стрелки-4 раза

упр. 2

вверх, вниз-4 раза вправо, влево-4 раза

упр. 3

откинуться на спинку стула, сделать глубокий вдох, наклониться вперёд-выдох -4 раза

стр.91 №5

кратк. усл.

Было-92арб. Было-92 арб Было-?

Пр.-46 арб. Пр-? Пр-46 арб

Ост.- ? Ост-46 арб Ост- 46 арб

Закрепление пройденного материала

Составьте верное неравенство:

-с числами15 и 2;

-с числом и числовым выражением

45 и 15+25

Жители планеты «Решай-считай» предлагают вам выполнить самостоятельно задание:

сравните числа и числовые выражения

39-23…20

47…69+2

37+ 13…42+28

Оцените правильность выполнения задания

стр. 90 №3 1 столбик

Рассмотрите внимательно числовые выражения. Кто может не вычисляя сравнить? Какие неравенства получились верные или неверные?

Это интересно. Математика в числах

*12 апреля 1961 г Юрий Алексеевич Гагарин на космической ракете «Восток»

поднялся в космос. Его полёт продолжался 108 минут.

* К полёту космонавтов готовят от 6 до 12 лет

*В космическом пространстве побывало 3 наших земляка (соотечественника):

Пётр Климук, Владимир Ковалёнок, Олег Новицкий.

О. Новицкий пробыл на борту космической станции 4 месяца и приземлился 16 марта 2013г.

*Сколько планет в солнечной системе?

8-Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун.

(До 2006 года считалось 9. Плутон не входит в список планет)

Итог урока. Рефлексия

Кем мы были на уроке?

Что нового узнали?

С какими неравенствами познакомились?

Цель урока достигнута?

Продолжите высказывания.

Оцените свою работу на уроке.

Д/З стр91 №1

Ракета

-На месте!

-На месте!

-У края!

-Прямая!

21-12=30-21

82-34=60-12

Оцените правильность выполнения Д/З на линеечке самооценки

— Познакомить с понятием «неравенство» и видами неравенств;

-совершенствовать вычислительные умения и навыки;

-совершенствовать умение решать задачи

Ученики решают примеры и прикрепляют карточки с ответами.

Переворачивают карточки-ответы, читают девиз:

«Один за всех и все за одного»

К доске выходят ученики и вставляют пропущенные знаки

Да, когда сравнивали числа и числовые выражения. И при сравнении ставили знаки < или >

Нет

1 ученик у доски

34 <49

10 >25-20

72+(6+2)> 72

Остальные ученики выполняют задание в тетради

…+1< 5(Ч:0,1,2,3)

7-… >3 (Ч:0,1,2,3)

10-…> 5 (Ч:0,1,2,3,4)

Задача

1 нед.=7 дн.

2 нед.=14дн.

14+2=16дн.

Ответ: 16 дней.

Задача

92-46=46(арб.)

Составление обратных задач:

1) В магазине было 92 арбуза. Сколько арбузов продали, если в магазине осталось 46 арбузов?

2)Сколько арбузов было в магазине, если за день продали 46 арбузов и столько же арбузов осталось?

15 >2

45 >15+25

39-23 < 20

47 < 69+2

42+28>37+ 13

51-18 >51-19

38+41 >38+40

Космонавтами Исследователями

Числовые равенства и неравенства | интернет проект BeginnerSchool.ru

Чтобы получить запись, называемую числовым равенством, надо два числовых выражения соединить знаком равенства (=).

Пример:

Представленный пример является верным числовым равенством, но числовое равенство может быть неверным:

Давайте разберем свойства числовых равенств.

1. Если числовое равенство верно, то прибавив к обеим частям этого равенства одно и тоже число мы получим верное числовое равенство.

Например:

Проверим равенство

(12 + 3) = (9 + 6)

12 + 3 = 15 и 9 + 6 = 15

Равенство верно, теперь проверим свойство

(12 + 3) + (5 – 2) = (9 + 6) + (5 – 2)

15 + (5 – 2) = 15 + (5 – 2)

18 = 18

В обоих случаях равенства верны

 

То же самое произойдет, если мы вычтем одно и то же числовое выражение из обеих частей верного числового равенства.

Проверим это свойство на предыдущем примере заменив действие сложение на вычитание:

(12 + 3) – (5 – 2) = (9 + 6) – (5 – 2)

15 + (5 – 2) = 15 + (5 – 2)

12 = 12

Как мы видим равенство верно.

 

2. Если числовое равенство верно, то умножив обе части этого равенства на одно и тоже числовое выражение мы получим верное числовое равенство.

Проверим и это свойство:

(75 – 3) = (15 + 57)

75 – 3 = 72 и 15 + 57 = 72 это равенство верно

(75 – 3) · (10 – 2) = (15 + 57) · (10 – 2)

72 · (10 – 2) = 72 · 8 = 576

576 = 576

Свойство доказано.

3. Если числовое равенство верно, то разделив обе части этого равенства на одно и тоже числовое выражение мы получим верное числовое равенство. Правда, это выражение справедливо только если числовое выражение не равно нулю, так как на ноль делить нельзя.

 

 

Проверим это свойство:

(12 + 3) : (5 – 2) = (9 + 6) : (5 – 2)

15 : 3 = 15 : 3

5 = 5

Что и требовалось доказать.

Если одно числовое выражение не равно другому, то сравним оба выражения поставим между ними знак сравнения – больше (>) или меньше (<). Мы получим числовое неравенство.

(3 · 4) < (3 · 6)

(10 + 25)

Числовые неравенства также могут быть верными и неверными:

(25 – 5) : 5 > 10 – это неравенство неверно

(25 – 5) : 5 < 10 – это неравенство верно

Спасибо, что Вы с нами!

Понравилась статья — поделитесь с друзьями:

Оставляйте пожалуйста комментарии в форме ниже

Линейные неравенства, решение и примеры

Основные понятия

Алгебра не всем дается легко с первого раза. Чтобы не запутаться во всех темах и правилах, важно изучать темы последовательно и по чуть-чуть. Сегодня узнаем, как решать линейные неравенства.

Неравенство — это алгебраическое выражение, в котором используются знаки ≠, <, >, ≤, ≥.

Линейные неравенства — это неравенства вида:

• ax + b < 0,
• ax + b > 0,
• ax + b ≥ 0,
• ax + b ≤ 0,

где a и b — любые числа, a ≠ 0, x — неизвестная переменная. Как решаются неравенства рассмотрим далее в статье. 

Решение — значение переменной, при котором неравенство становится верным.

Решить неравенство значит сделать так, чтобы в левой части осталось только неизвестное в первой степени с коэффициентом равном единице.

Типы неравенств

1. Строгие — используют только больше (>) или меньше (<):

• a < b — это значит, что a меньше, чем b.
• a > b — это значит, что a больше, чем b.
• a > b и b < a означают одно и тоже, то есть равносильны.

2. Нестрогие — используют сравнения ≥ (больше или равно) или ≤ (меньше или равно):

• a ≤ b — это значит, что a меньше либо равно b.
• a ≥ b — это значит, что a больше либо равно b.
• знаки ⩽ и ⩾ являются противоположными.

3. Другие типы:

• a ≠ b — означает, что a не равно b.
• a ≫ b — означает, что a намного больше, чем b.
• a ≪ b — означает, что a намного меньше, чем b.
• знаки >> и << противоположны.

Линейные неравенства: свойства и правила

Вспомним свойства числовых неравенств:

1. Если а > b , то b < а. Также наоборот: а < b, то b > а.
2. Если а > b и b > c, то а > c. И также если а < b и b < c, то а < c.
3. Если а > b, то а + c > b+ c (и а – c > b – c).

Если же а < b, то а + c < b + c (и а – c < b – c). К обеим частям можно прибавлять или вычитать одну и ту же величину.

4. Если а > b и c > d, то а + c > b + d.

Если а < b и c < d, то а + c < b + d.

Два неравенства одинакового смысла можно почленно складывать. Но важно перепроверять из-за возможных исключений. Например, если из 12 > 8 почленно вычесть 3 > 2, получим верный ответ 9 > 6. Если из 12 > 8 почленно вычесть 7 > 2, то полученное будет неверным.

5. Если а > b и c < d, то а – c > b – d.

Если а < b и c > d, то а – c < b – d.

Из одного неравенства можно почленно вычесть другое противоположного смысла, оставляя знак того, из которого вычиталось.

6. Если а > b, m — положительное число, то mа > mb и 
   

Обе части можно умножить или разделить на одно положительное число (знак при этом остаётся тем же).

Если же а > b, n — отрицательное число, то nа < nb и 

Обе части можно умножить или разделить на одно отрицательное число, при этом знак поменять на противоположный.

7. Если а > b и c > d, где а, b, c, d > 0, то аc > bd.

Если а < b и c < d, где а, b, c, d > 0, то аc < bd.

Неравенства одного смысла на множестве положительных чисел можно почленно перемножать.

Следствие данного правила или квадратный пример: если а > b, где а, b > 0, то а2 > b2, и если а < b, то а2 < b2. На множестве положительных чисел обе части можно возвести в квадрат.

8. Если а > b, где а, b > 0, то 
   

Если а < b , то 

Решением неравенства с одной переменной называется значение переменной, которое трансформирует его в верное числовое неравенство.

Важно знать

Два неравенства можно назвать равносильными, если у них одинаковые решения.

Чтобы упростить процесс нахождения корней неравенства, нужно провести равносильные преобразования — то заменить данное неравенство более простым. При этом все решения должны быть сохранены без возникновения посторонних корней.

Свойства выше помогут нам использовать следующие правила.

Правила линейных неравенств Любой член можно перенести из одной части в другую с противоположным знаком. Знак неравенства при этом не меняется. 2x − 3 > 6 ⇒ 2x > 6 + 3 ⇒ 2x > 9. Обе части можно умножить или разделить на одно положительное число. Знак неравенства при этом не меняется. Умножим обе части на пять 2x > 9 ⇒ 10x > 45. Обе части можно умножить или разделить на одно отрицательное число. Знак неравенства при этом меняется на противоположный. Разделим обе части на минус два 2x > 9 ⇒ 2x : –2 > 9 : -2 ⇒ x < 4,5.

Решение линейных неравенств

Со школьных уроков мы помним, что у неравенств нет ярко выраженных различий, поэтому рассмотрим несколько определений.

Определение 1. Линейное неравенство с неизвестной переменной x имеет вид ax + b > 0, когда вместо > используется любой знак < , ≤ , ≥ , а и b — действительные числа, a ≠ 0.

Определение 2. Неравенства называют линейными с одной переменной, когда ax < c или ax > c , где x — переменная, a, c — некоторые числа.

Мы не знаем может ли коэффициент равняться нулю, поэтому: 0 * x > c и 0 * x < c можно записать в форме нестрогого неравенства: ax ≤ c, ax ≥ c . Такое уравнение принято называть линейным. Его главные различия:

• форма записи ax + b > 0 — в первом и ax > c — во втором;
• допустимость равенства нулю: a ≠ 0 — в первом, a = 0 — во втором.

Неравенства ax + b > 0 и ax > c равносильные, так как получены переносом слагаемого из одной части в другую.

Определение 3. Линейные неравенства с одной переменной x выглядят так:

• ax + b < 0,
• ax + b > 0,
• ax + b ≤ 0,
• ax + b ≥ 0,

где a и b — действительные числа. А на месте x может быть обычное число.

Равносильные преобразования

Для решения ax + b < 0 (≤, >, ≥) нужно применить равносильные преобразования неравенства. Рассмотрим два случая: когда коэффициент равен и не равен нулю.

Алгоритм решения ax + b < 0 при a ≠ 0

• перенесем число b в правую часть с противоположным знаком,
• получим равносильное: ax < −b;
• произведем деление обеих частей на число не равное нулю.

Когда a положительное, то знак остается, если a — отрицательное, знак меняется на противоположный.

Рассмотрим пример: 4x + 16 ≤ 0.

Как решаем: В данном случае a = 4 и b = 16, то есть коэффициент при x не равен нулю. Применим вышеописанный алгоритм.

• Перенесем слагаемое 16 в другую часть с измененным знаком: 4x ≤ −16.
• Произведем деление обеих частей на 4. Меняем знак, так как 4 — положительное число: 4x : 4 ≤ −16 : 4 ⇒ x ≤ −4. 
• Неравенство x ≤ −4 является равносильным. То есть решением является любое действительное число, которое меньше или равно 4.

Ответ: x ≤ −4 или числовой промежуток (−∞, −4].

При решении ax + b < 0, когда а = 0, получается 0 * x + b < 0. На рассмотрение берется b < 0, после выясняется верное оно или нет.

Вернемся к определению решения неравенства. При любом значении x мы получаем числовое неравенство вида b < 0. При подстановке любого t вместо x, получаем 0 * t + b < 0 , где b < 0. Если оно верно, то для решения подойдет любое значение. Когда b < 0 неверно, тогда данное уравнение не имеет решений, так как нет ни одного значения переменной, которое может привести к верному числовому равенству.

Числовое неравенство вида b < 0 (≤, > , ≥) является верным, когда исходное имеет решение при любом значении. Неверно тогда, когда исходное не имеет решений.

Рассмотрим пример: 0 * x + 5 > 0.

Как решаем:

• Данное неравенство 0 * x + 5 > 0 может принимать любое значение x.
• Получается верное числовое неравенство 5 > 0. Значит его решением может быть любое число.

Ответ: промежуток (− ∞ , + ∞).

Метод интервалов

Метод интервалов можно применять для линейных неравенств, когда значение коэффициента x не равно нулю.

Метод интервалов это:

• введение функции y = ax + b;
• поиск нулей для разбиения области определения на промежутки;
• отметить полученные корни на координатной прямой;
• определение знаков и отмечание их на интервалах.

Алгоритм решения ax + b < 0 (≤, >, ≥) при a ≠ 0 с использованием метода интервалов:

• найдем нули функции y = ax + b для решения уравнения ax + b = 0.

Если a ≠ 0, тогда решением будет единственный корень — х₀;

• начертим координатную прямую с изображением точки с координатой х₀, при строгом неравенстве точку рисуем выколотой, при нестрогом — закрашенной;
• определим знаки функции y = ax + b на промежутках.

Для этого найдем значения функции в точках на промежутке;

• если решение неравенства со знаками > или ≥ — добавляем штриховку над положительным промежутком на координатной прямой, если < или ≤ н — над отрицательным промежутком.

Рассмотрим пример: −3x + 12 > 0.

Как решаем:

1. В соответствии с алгоритмом, сначала найдем корень уравнения − 6x + 12 = 0,

−6x = −12,

x = 2.

Изобразим координатную прямую с отмеченной выколотой точкой, так как неравенство является строгим.

2. Определим знаки на промежутках.

Чтобы определить на промежутке (−∞, 2), необходимо вычислить функцию y = −6x + 12 при х = 1. Получается, что −6 * 1 + 12 = 6, 6 > 0. Знак на промежутке является положительным.

Определяем знак на промежутке (2, + ∞) , тогда подставляем значение х = 3. Получится, что −6 * 3 + 12 = − 6, − 6 < 0 . Знак на промежутке является отрицательным. 

3. Выполним решение со знаком >. Штриховку сделаем над положительным промежутком.
   

По чертежу делаем вывод, что решение имеет вид (−∞, 4) или x < 4.

Ответ: (−∞, 4) или x < 4.

Графический способ

Смысл графического решения неравенств заключается в том, чтобы найти промежутки, которые необходимо изобразить на графике.

Алгоритм решения y = ax + b графическим способом

• во время решения ax + b < 0 определить промежуток, где график изображен ниже оси Ох;
• во время решения ax + b ≤ 0 определить промежуток, где график изображается ниже Ох или совпадает с осью;
• во время решения ax + b > 0 произвести определение промежутка, где график изображается выше Ох;
• во время решения ax + b ≥ 0 определить промежуток, где график находится выше оси Ох или совпадает.

Рассмотрим пример: −5 * x − √3 > 0.

Как решаем

• Так как коэффициент при x отрицательный, данная прямая является убывающей.
• Координаты точки пересечения с Ох равны −√3 : 5.
• Неравенство имеет знак >, значит нужно обратить внимание на промежуток выше оси Ох.
• Поэтому открытый числовой луч (−∞, −√3 : 5) будет решением.

Ответ: (−∞, −√3 : 5) или x < −√3 : 5.

Линейные неравенства в 8 классе — это маленький кирпич, который будет заложен в целый фундамент знаний. Мы верим, что у все получится!

Чтобы ребенок чувствовал себя увереннее на сложных контрольных и улучшил оценки в школе, запишите его на уроки математики в Skysmart. Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.

Числовые неравенства и их свойства 🐲 СПАДИЛО.РУ

Определение

Числовое неравенство – это неравенство, в котором по обе стороны от знака неравенства содержатся числа или числовые выражения. Результат сравнения записывают с помощью знаков =, <, >.

Например, 24=24; 46>13, 67<21, –15>–65.

В зависимости от конкретных чисел используется способ сравнения, но существует способ, который охватывает все числа, он основывается на следующем определении.

Способ сравнения чисел

Число а больше числа b, если разность (а – b) является положительным числом; число а меньше числа b, если разность (а – b) является отрицательным числом; число а равно числу b, если разность (а – b ) является равным нулю числом.

Пример №1.

1. 123>118, так как 123–118=5, a 5>0;
2. –15>–65, так как –15–(–65)= –15+65=50, a 50>0
3. 118<123, так как 118–123=–5, a –5<0;
4. –90<–50, так как –90–(–50)=–90+50=–40, а –40<0
5. 451=451, так как 451–451=0

Основные свойства числового неравенства

1. Если обе части верного неравенства умножить или разделить на одно и то же положительное число, то получится верное неравенство.
2. Если обе части верного неравенства умножить или разделить на одно и то же отрицательное число и изменить знак неравенства на противоположный, то получится верное неравенство.
3. Если a и b положительные числа, причем a<b, то:

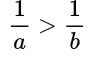
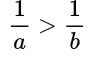Пример №2.

1. Дано неравенство 45>21. Если обе части умножим на одно и то же положительное число, например, 10, то получится верное неравенство 450>210.
2. Дано неравенство 95>35. Обе части разделим на одно и то же отрицательное число (–5), при этом знак неравенства изменим на противоположный: 95:(–5)<35:(–5), получим верное неравенство –19<–7.
3. Даны числа 17 и 52, где 17<52. Если разделить число 1 на каждое из них, то получим: Это неравенство получим в соответствии со следствием из свойства №3.

Числовые равенства и неравенства. Методика изучения числовых равенств и неравенств.

Числовые равенства и неравенства. Методика изучения числовых равенств и неравенств.

Возьмём два числовых выражения 32-20 и 144 : 12.

Соединим их знаком равенства. 32 -20 = 144 : 12 (и), т. к. 12=12

Получим высказывание, которое называется числовым равенством.

Это высказывание истинно.

14 + 4 • 8 = 4 • 9 (л), т. к. 46≠ 36

Определение 1. Два числа или два числовых выражения, соединённые знаком равенства, называются числовым равенством.

Определение 2. Высказывание вида a = b , где а и в числовые выражения, называется числовым равенством.

Символически числовое равенство записывается так: a = b.

Если знаком равенства соединены 2 числовых выражения, значения которых равны, то получится истинное числовое равенство, если не равны, то ложное.

Таким образом, с логической точки зрения числовое равенство — это высказывание, истинное или ложное.

Числовое равенство истинно, если значения числовых выражений, стоящих в левой и правой частях равенства, совпадают.

Свойства истинных числовых равенств

1) Если к обеим частям истинного числового равенства прибавить одно и то же число с, или числовое выражение, имеющее смысл, то получится истинное числовое равенство.

Если a = b (и), то a +c = b + c тоже истинно.

Дано: a = b истинное числовое равенство, c – число или числовое выражение, имеющее смысл

Доказать: a +c = b + c (и).

Доказательство:

По свойству рефлексивности отношения «равно» можно записать a +c = a + c .

По условию a = b , в правой части равенства заменим а на в, получим, а + с = в + с ч.т.д.

Следствие: Любой член истинного числового равенства можно переносить из одной части в другую, поменяв знак на противоположный.

a + m = b + m + n

a = — m + b + m + n

a = b + n

2) Если обе части истинного числового равенства умножить на одно и то же число с, или числовое выражение, имеющее смысл, то получится истинное числовое равенство.

Если a = b (и), то a • c = b • c тоже истинно.

Дано: a = b истинное числовое равенство, c – число или числовое выражение, имеющее смысл

Доказать: a •c = b • c (и).

Доказательство:

По свойству рефлексивности отношения «равно» можно записать a • c = a • c .

По условию a = b , в правой части равенства заменим а на в, получим, а • с = в • с ч.т.д.

Следствие: Обе части истинного числового равенства можно разделить на одно и то же число, не равное нулю.

В начальной школе истинные числовые равенства называют верными, ложные– неверными.

II. Повторение.

-Какие выражения называются числовыми выражениями? (Они образуются из чисел, знаков действий и скобок).

-Что такое значение числового выражения? (Если выполнить все действия, указанные в выражении, получим число, которое называется значением числового выражения).

-Существуют ли числовые выражения, значения которых нельзя найти?

Какие действия выполняются раньше 1 или 2 ступени? (действия второй ступени (умножение и деление), а затем действия первой ступени (сложение и вычитание)).

-Что называется выражением с переменной (Запись, состоящая из чисел, знаков действий, скобок и букв)

-Областью определения выражения с переменной? (множество тех значений переменной, при которых выражение имеет смысл).

-Какие преобразования относятся к тождественным?

-приведение подобных;

-раскрытие скобок;

-приведение дробей к общему знаменателю;

-группировка или заключение в скобки)

-Что такое тождественное преобразование? (Замена выражения с переменной другим выражением тождественно равным ему называется тождественным преобразованием).

-Как называются такие записи: (3 + 2)) — 12 или 3х-у:+)8, (их нельзя назвать ни числовым выражением, ни выражением с переменной).

Задача 1. Найти значение выражения Зх(х-2) + 4(х-2) при х = 6.

Решение.

1 способ. Подставим число 6 вместо переменной в данное выражение: 3-6(6-2) + 4(6-2). Чтобы найти значение полученного числового выражения, выполним все указанные действия:

3-6-(6-2) + 4-(6-2) = 18-4 + 4-4 = 72+ 16 = 88. Следовательно, при х = 6 значение выражения

Зх(х-2)+4(х-2) равно 88.

2 способ. Прежде чем подставлять число 6 в данное выражение, упростим его:

Зх(х-2) + 4(х-2) = (х-2)(Зх+4). И затем, подставив в полученное выражение вместо Х число 6, выполним действия: (6-2)-(3-6 + 4)= 4-(18+4) = 4-22 = 88.

Обратим внимание на следующее: и при первом способе решения задачи, и при втором мы одно выражение заменяли другим. Например, выражение 18-4+4-4 заменяли выражением 72+16, а выражение Зх (х-2) + 4(х-2)-выражением (х — 2)(3х + 4), причем эти замены привели к одному и тому же результату. В математике, описывая решение данной задачи, говорят, что мы выполняли тождественные преобразования выражений.

-Какие два выражения называются тождественно равными? (если при любых значениях переменных из области определения выражений их соответственные значения равны).

— Как получить тождество? (Если два тождественно равных на некотором множестве выражения соединить знаком равенства, то получим предложение, которое называют тождеством на этом множестве).

Например, 5(х + 2) = 5х + 10 — тождество на множестве действительных чисел, потому что для всех действительных чисел значения выражения 5(х + 2) и 5х + 10 совпадают. Используя обозначение квантора общности, это тождество можно записать так: ( х  R) 5(х + 2) = 5х + 10. Тождествами считают и верные числовые равенства.

Замена выражения другим, тождественно равным ему на некотором множестве, называется тождественным преобразованием данного выражения на этом множестве.

Задача 2. Разложить на множители выражение ax—bx+ab—b².

Решение. Сгруппируем члены данного выражения по два (первый со вторым, третий с четвертым): ax—bx+ab—b² = = (ax—bx) + (ab—b²). Это преобразование возможно на основании свойства ассоциативности сложения действительных чисел.

Вынесем в полученном выражении из каждой скобки общий множитель: (ax—bx)+(ab—b²) = x(a—b)+b(a—b) — это преобразование возможно на основании свойства дистрибутивности умножения относительно вычитания действительных чисел.

В полученном выражении слагаемые имеют общий множитель, вынесем его за скобки: x(a—b)+b(a—b) = (a—b)(x—b). Основой выполненного преобразования является свойство дистрибутивности умножения относительно сложения.

Итак, ax—bx+ab—b² — (a—b)(x—b).

Числовые неравенства.

I. Повторение изученного:

— Какое предложение называют числовым равенством?

— Приведите примеры числовых равенств.

Возьмем, например, числовые выражения 3 + 2 и 6 — 1 и соединим их знаком равенства 3 + 2 = 6-1. Оно истинное. Если же соединить знаком равенства 3 + 2 и 7 — 3, то получим ложное числовое равенство 3 + 2 = 7-3.

— Можно ли числовое равенство считать высказыванием? (Да)

— Какое числовое равенство истинно? (Если значения числовых выражений, стоящих в левой и правой частях равенства, совпадают).

— Назовите свойства истинных числовых равенств.

Если к обеим частям истинного числового равенства прибавить одно и то же числовое выражение, имеющее смысл, то получим также истинное числовое равенство.

Если обе части истинного числового равенства умножить на одно и то же числовое выражение, имеющее смысл, то получим также истинное числовое равенство.

Если два числовых выражения соединить знаком «>» или «<», то получим числовое неравенство.

Определение. Два числовых выражения, соединённые знаком «>» или «<», образуют числовое неравенство.

Например, если соединить выражение 6 + 2 и 13-7 знаком «>», то получим истинное числовое неравенство 6 + 2 > 13-7 (И). Если соединить те же выражения знаком «<», получим ложное числовое неравенство 6 +2 < 13-7(Л).

Таким образом, с логической точки зрения числовое неравенство — это высказывание, истинное или ложное. А, следовательно, к числовым неравенствам можно применить логические операции.

Конъюнкцию двух числовых неравенств принято записывать в виде двойного неравенства.

(5 > 4 /\ 5 < 6) <=> (4 < 5 < 6)

Дизъюнкцию числового равенства и неравенства записывают в виде нестрогого неравенства

(5 > 4 V 5 = 4) <=> (5≥ 4 )

Определение. Если два числовых неравенства имеют одинаковые знаки, то их называют неравенствами одинакового смысла, если у неравенств разные знаки, то неравенствами противоположного смысла.

a >b и c > d – одинакового смысла;

a >b и c < d – противоположного смысла.

Рассмотрим свойства истинных числовых неравенств.

Свойство 1.

Для любых чисел a и b верно, что если a >b, то a — b > 0.

(a, b) (a >b =>a — b > 0).

Доказательство:

Нам дано, что a >b.По опр отношения «>», существует такое натуральное число к, что a = b + к. => по 2 опр разности a — b = к. Так как к N , к > 0, то a — b > 0 ч.т.д.

Свойство 2.

Если к обеим частям истинного числового неравенства прибавить одно и то же числовое выражение, имеющее смысл, то получим также истинное числовое неравенство.

(a, b, с) (a >b => a +с > b + с).

Доказательство:

По условию a > b, тогда по 1 свойству a — b > 0 => (a — b) + (с – с) > 0 =>применяем сочет свойство (a + с) — (b + с) > 0 => по свойству 1 a +с > b + с ч.т.д.

Свойство 3.

Обе части истинного числового неравенства можно умножать на одно и то же положительное число, в результате получим истинное числовое неравенство того же смысла.

(a, b, с>0) (a >b => a • с > b • с).

Доказательство:

По условию a > b, => a — b > 0 => (a — b) • с > 0 =>применяем распределит свойство a • с — b • с > 0 => a • с > b • с ч.т.д.

Свойство 4.

Обе части истинного числового неравенства можно умножать на одно и то же отрицательное число, в результате получим истинное числовое неравенство противоположного смысла (с противоположным знаком).

(a, b, с<0) (a >b => a • с < b • с).

Свойство 5

Истинные числовые неравенства одинакового смысла можно почленно складывать, в результате получается неравенство того же смысла.

(a, b, с, d) (a >b и c >d => a + c > b +d).

Свойство 6

Истинные числовые неравенства противоположного смысла можно почленно вычитать, сохраняя знак того неравенства, из которого вычитаем.

(a, b, с, d) (a > b и c => a — c > b — d).

Свойство 7

Истинные числовые неравенства одинакового смысла с положительными частями можно почленно перемножать, в результате получается истинное числовое неравенство того же смысла.

(a, b, с, d) (a >b >0 и c >d >0 => a • c > b • d).

Свойство 8

Истинные числовые неравенства одинакового смысла с отрицательными частями можно почленно перемножать, в результате получается истинное числовое неравенство противоположного смысла.

(a, b, с, d) (a < b < 0 и c < d < 0 => a • c > b • d).

Свойство 9

Обе части истинного числового неравенства можно возводить в одну и ту же степень с натуральным показателем, при этом получается неравенство того же смысла.

(a, b и nN ) (a > b => aⁿ > bⁿ).

Линейные неравенства с одной переменной 🐲 СПАДИЛО.РУ

Определение

Выражение с одной переменной, содержащее знак неравенства, называется неравенством с одной переменной. Например:

23х+11<11x+5; 6x–10; х>9

Неравенства такого вида называют линейными неравенствами с одной переменной, так как х в них в первой степени.

Вспомним, что в зависимости от знака неравенства, их называют строгие знаки (< и >) или нестрогие знаки (≤ и ≥).

Решением неравенства с одной переменной является значение переменной, при котором данное неравенство обращается в верное числовое неравенство.

Решить неравенство – это значит найти все его решения или доказать, что решений нет.

При решении неравенства с одной переменной пользуются следующими свойствами.

Свойства неравенств

1. Если из одной части неравенства перенести слагаемое в другую часть, поменяв при этом знак слагаемого на противоположный, то получится равносильное ему неравенство;
2. Если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство;
3. Если обе части неравенства умножить или разделить на одно и то же отрицательное число и изменить знак неравенства на противоположный, то получится равносильное ему неравенство.

Рассмотрим решение линейных неравенств с одной переменной на примерах.

Пример №1. Решить неравенство:

6х–13<x–3

Перенесем слагаемые из одной части в другую, изменяя знаки у слагаемых, которые будем переносить, на противоположные:

6х–x < –3+13

Теперь приведем подобные слагаемые в каждой части неравенства: 5х<10. Дальше разделим обе части неравенства на число 5 (коэффициент при х), получим: х<2. Множество решений данного неравенства состоит из всех чисел, которые меньше минус двух. Ответ можно записать в виде неравенства х<2, либо в виде числового промежутка (–∞;-2). Вспомним, что около знака «бесконечность» всегда ставится круглая скобка, а так как неравенство строгое (знак «меньше»), то и у числа два также ставится «круглая» скобка). Это множество чисел можно показать на числовом луче (точка, которая показывает число 2, будет «выколотая», так как неравенство строгое):

Пример №2. Решить неравенство:

12–2х≤х–6

Выполним перенос слагаемых:

–х–2х–6–12

Приведем подобные слагаемые: –3х–18. Разделим обе части неравенства на минус три и изменим знак неравенства на противоположный: х≥6. Значит, множество решений данного неравенства – это все числа, которые больше или равны 6. Ответ можно записать, как в виде нестрогого (знак «больше или равно») неравенства х≥6, так и в виде числового промежутка [6;+), (видим около числа 6 «квадратную» скобку), показав его на числовом луче, где точка, обозначающая число 6, закрашена, ее называют «приколотой» точкой, так как неравенство нестрогое.

В рассмотренных примерах мы получали неравенства, у которых коэффициент при переменной не равен нулю. Но есть случаи, когда получается неравенство вида 0•х>a или 0•х<a (возможны и нестрогие знаки). В этом случае неравенство либо не имеет решений, либо решением является любое число.

Пример №3. Решить неравенство:

3х–15<3x–56

Выполняя перенос слагаемых и приведение подобных, получим неравенство:

0х<–41

Данное неравенство при любом значении х будет иметь вид 0<–41, что является неверным. Значит, оно не имеет решений, следовательно, и данное по условию неравенство не имеет решений.

Пример №4. Решить неравенство:

5х+24>5x+14

Выполним все необходимые действия, получим:

0х>–10

Данное неравенство при любом значении х будет иметь вид 0>–10, а это верное неравенство, значит х – любое число. Следовательно, ответ в данном неравенстве – «х – любое число».

Устранение неравенств

Иногда нам нужно решить такие неравенства:

Символ	слов	Пример
>	больше	х + 3 > 2
<	менее	7x < 28
≥	больше или равно	5 ≥ x — 1
≤	меньше или равно	2 года + 1 ≤ 7

Решение

Наша цель — иметь x (или другую переменную) отдельно слева от знака неравенства:

Примерно так:		х <5
или:		г ≥ 11

Мы называем это «решенным».

Пример: x + 2> 12

Вычтем 2 с обеих сторон:

х + 2 — 2> 12 — 2

Упростить:

х> 10

Решено!

Как решить

Решение неравенств очень похоже на решение уравнений … мы делаем почти то же самое …

… но мы также должны обратить внимание на направление неравенства .

Направление: куда «указывает» стрелка

Некоторые вещи могут изменить направление !

<становится>

> становится <

≤ становится ≥

≥ становится ≤

Безопасные дела

Эти вещи не влияют на направление неравенства:

• Сложить (или вычесть) число с обеих сторон
• Умножьте (или разделите) обе стороны на положительное число
• Упростить сторону

Пример: 3x <7 + 3

Мы можем упростить 7 + 3, не затрагивая неравенство:

3x <10

Но эти вещи действительно меняют направление неравенства (например, «<" становится ">«):

Пример: 2y + 7 <12

Когда мы меняем местами левую и правую части, мы также должны изменить направление неравенства :

12 > 2лет + 7

Вот подробности:

Сложение или вычитание значения

Часто мы можем решить неравенства, добавляя (или вычитая) число с обеих сторон (точно так же, как во Введении в алгебру), например:

Пример: x + 3 <7

Если вычесть 3 с обеих сторон, получим:

х + 3 — 3 <7 — 3

х <4

И вот наше решение: x <4

Другими словами, x может быть любым значением меньше 4.

Что мы сделали?

Мы пошли от этого: Кому:				х + 3 <7 х <4

И это хорошо работает для , прибавляя и , вычитая , потому что, если мы прибавляем (или вычитаем) одинаковую сумму с обеих сторон, это не влияет на неравенство

Пример: У Алекса больше монет, чем у Билли.Если и Алекс, и Билли получат по три монеты больше, у Алекс все равно будет больше монет, чем у Билли.

Что, если я решу, но «x» справа?

Неважно, просто поменяйте местами стороны, но переверните знак , чтобы он все еще «указывал» на правильное значение!

Пример: 12

Если отнять 5 с обеих сторон, получим:

12 — 5 — 5

7 <х

Вот и решение!

Но это нормально, если поставить «x» слева…

… так давайте обратим внимание (и знак неравенства!):

x> 7

Вы видите, как знак неравенства все еще «указывает» на меньшее значение (7)?

И вот наше решение: x> 7

Примечание: «x» может быть справа , но людям обычно нравится видеть его слева.

Умножение или деление на значение

Также мы умножаем или делим обе стороны на значение (как в алгебре — умножение).

Но мы должны быть немного осторожнее (как вы увидите).

Положительные значения

Все хорошо, если мы хотим умножить или разделить на положительное число :

Пример: 3y <15

Если разделить обе части на 3, получим:

3 года /3 <15 /3

г <5

И вот наше решение: y <5

Отрицательные значения

Когда мы умножаем или делим на отрицательное число , мы должны обратить неравенство.

Почему?

Ну, посмотрите на числовую строку!

Например, от 3 до 7 это , увеличение ,
, но от −3 до −7 — , уменьшение.

−7 <−3	7> 3

Видите, как меняет знак неравенства (с <на>)?

Давайте попробуем пример:

Пример: −2y <−8

Разделим обе части на −2… и отменяют неравенство !

−2y <−8

−2y / −2 > −8 / −2

г> 4

И это правильное решение: y> 4

(Обратите внимание, что я перевернул неравенство в той же строке , разделенное на отрицательное число.)

Итак, запомните:

При умножении или делении на отрицательное число отменяет неравенство

Умножение или деление на переменные

Вот еще один (хитрый!) Пример:

Пример: bx <3b

Кажется легко просто разделить обе стороны на b , что дает нам:

х <3

… но подождите … если b равно отрицательное значение , нам нужно изменить неравенство следующим образом:

x> 3

Но мы не знаем, положительное или отрицательное значение b, поэтому мы не можем ответить на этот вопрос !

Чтобы помочь вам понять, представьте, что замените b на 1 или −1 в примере bx <3b :

• , если b равно 1 , то ответ будет x <3
• , но если b равно −1 , тогда мы решаем −x <−3 , и ответим x> 3

Ответом может быть x <3 или x> 3 , и мы не можем выбрать, потому что не знаем b .

Так:

Не пытайтесь делить на переменную для решения неравенства (если вы не знаете, что переменная всегда положительна или всегда отрицательна).

Пример побольше

Пример: x − 3 2 <−5

Во-первых, давайте уберем «/ 2», умножив обе части на 2.

Поскольку мы умножаем на положительное число, неравенства не изменятся.

x − 3 2 × 2 <−5 × 2

х-3 <-10

Теперь прибавьте 3 к обеим сторонам:

х − 3 + 3 <−10 + 3

х <−7

И вот наше решение: x <−7

Два неравенства сразу!

Как решить задачу сразу с двумя неравенствами?

Пример:

−2 < 6−2x 3 <4

Во-первых, давайте очистим «/ 3», умножив каждую часть на 3.

Поскольку мы умножаем на положительное число, неравенства не меняются:

−6 <6−2x <12

Теперь вычтите 6 из каждой части:

−12 <−2x <6

Теперь разделите каждую часть на 2 (положительное число, чтобы неравенства снова не изменились):

−6 <−x <3

Теперь умножьте каждую часть на -1. Поскольку мы умножаем на отрицательное число , неравенства изменяют направление .

6> х> −3

И это решение!

Но для наглядности лучше иметь меньшее число слева, большее — справа. Так что давайте поменяем их местами (и убедимся, что неравенства указывают правильно):

−3 <х <6

Сводка

• Многие простые неравенства могут быть решены путем сложения, вычитания, умножения или деления обеих частей, пока не останется переменная сама по себе.
• Но это изменит направление неравенства:
  • Умножение или деление обеих сторон на отрицательное число
  • Замена левой и правой сторон
• Не умножайте и не делите на переменную (если вы не знаете, что она всегда положительна или всегда отрицательна)

.

Решайте неравенства и системы с помощью программы «Пошаговое решение математических задач»

Неравенства

Раздел неравенств QuickMath позволяет решить практически любое неравенство или систему неравенств в одной переменной. В большинстве случаев можно найти точные решения. Даже когда это невозможно, QuickMath может дать вам приблизительные решения практически с любым требуемым уровнем точности. Кроме того, вы можете отобразить регионы, удовлетворяющие одному или нескольким неравенствам по двум переменным, четко видя, где происходят пересечения этих регионов.

Что такое неравенство?

Неравенства состоят из двух или более алгебраических выражений, соединенных символами неравенства. Символы неравенства:

<	менее
>	больше
<=	меньше или равно
> =	больше или равно
! = Или <>	не равно

Вот несколько примеров неравенства:

2 х — 9> 0 x 2 — 3 x + 5 <= 0 | 5x — 1 | <> 5 х 3 + 1 <= 0

Решить

Команду «Решить» можно использовать для решения одного неравенства для одного неизвестно на основной странице решения или для одновременного решения системы многих неравенств в одном неизвестном на странице расширенного решения.2–5 <0

Другими словами, QuickMath попытается найти решения, удовлетворяющие сразу обоим неравенствам.

Перейти на страницу решения

Участок

Команда Plot из раздела Graphs построит график любого неравенства, связанного с две переменные. Чтобы построить область, удовлетворяющую единственному неравенству с участием x и y, перейдите к основному страница построения неравенства, где вы можете ввести неравенство и указать верхний и нижний пределы x и y, по которым вы хотите построить график за.Продвинутый Страница построения неравенства позволяет вам построить объединение или пересечение до 8 регионов на одном графике. Вы можете контролировать такие вещи, как или не показывать оси, где оси должны быть расположены и какой аспект соотношение сюжета должно быть. Кроме того, у вас есть возможность показать каждый отдельный регион самостоятельно.

Уравнение говорит, что два выражения равны, а неравенство говорит что одно выражение больше, больше или равно, меньше или меньше или равно другому.Как и в случае с уравнениями, значение переменной для что неравенство истинно, является решением неравенства, а множество всех таких решений является множество решений неравенства. Два неравенства с одинаковое множество решений являются эквивалентными неравенствами. Неравенства решаются с помощью следующие свойства неравенства.

СВОЙСТВА НЕРАВЕНСТВА

Для действительных чисел a, b и c:

(a)

(Одно и то же число может быть добавлено к обеим сторонам неравенства без изменения набор решений.)

б)

(Обе части неравенства можно умножить на одно и то же положительное число без изменения набора раствора.)

(в)

(Обе части неравенства можно умножить на одно и то же отрицательное число без изменения множества решений, пока направление неравенства символ перевернут.)
Замена <на> приводит к эквивалентным свойствам.

ПРИМЕЧАНИЕ Поскольку деление определяется в терминах умножения, слово «умноженный» может быть заменен на «разделенный» на части (b) и (c) свойств неравенства.

Обратите особое внимание на часть (c): если обе стороны неравенства умноженное на отрицательное число, направление символа неравенства должно быть наоборот. Например, начиная с истинного утверждения — 3 <5 и умножая обе стороны на положительное число 2 дают

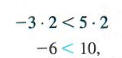
по-прежнему верное заявление. С другой стороны, начиная с — 3 <5 и умножение обеих сторон на отрицательное число -2 дает истинный результат, только если направление символа неравенства обратное.

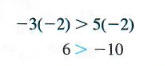
Аналогичная ситуация возникает при делении обеих сторон на отрицательное число. В Резюмируя, можно сделать следующее заявление.

При умножении или делении обеих сторон неравенства на минус числа, мы должны изменить направление символа неравенства, чтобы получить эквивалентное неравенство.

ЛИНЕЙНЫЕ НЕРАВЕНСТВА Линейное неравенство определяется аналогично линейное уравнение.

Линейное неравенство по одной переменной — это неравенство, которое можно записать в виде форма

, где a <> 0.

Пример 1
Решите неравенство -3x + 5> -7.
Воспользуйтесь свойствами неравенства. Сложение — 5 с обеих сторон дает

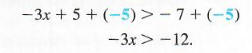
Теперь умножьте обе стороны на -1/3. (Мы также можем разделить на -3.) Поскольку -1/3 < 0, измените направление символа неравенства на противоположное.

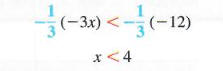
Исходному неравенству удовлетворяет любое действительное число меньше 4. множество решений можно записать {x | x <4}. График множества решений показан на Фигура 2.6, где скобки используются, чтобы показать, что 4 само по себе не принадлежит к набору решений.

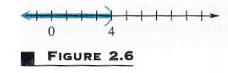
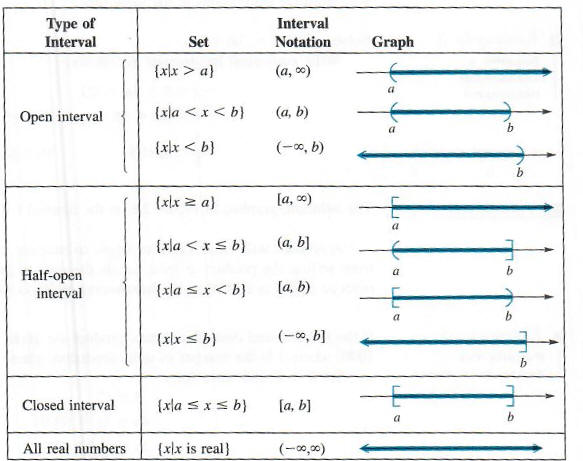
Набор {x | x <4}, набор решений неравенства в Примере 1, является примером интервала. Упрощенное обозначение, называемое обозначением интервалов, используется для интервалы записи. В этих обозначениях интервал в примере 1 можно записать как (-oo, 4). Символ -oo не является действительным числом; он используется, чтобы показать, что интервал включает все действительные числа меньше 4.Интервал (-oo, 4) является примером открытый интервал, поскольку конечная точка, 4, не является частью интервала. Примеры другие наборы, записанные в интервальной записи, показаны ниже. Квадратная скобка - это используется, чтобы показать, что число является частью графика, а круглые скобки используются для указывают, что число не является частью графика. Когда два действительных числа a и b используются для записи интервала в следующей диаграмме, предполагается, что a <б.

Пример 2
Решите 4 — 3y <7 + 2y.Запишите решение в интервальной записи и на графике решение на числовой прямой. Напишите следующую серию эквивалентных неравенства.

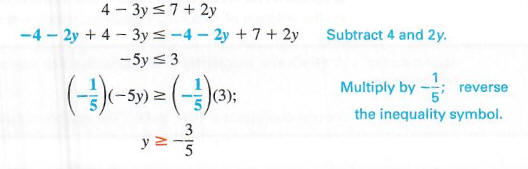
В нотации создателя множеств набор решений равен {y | y> = 3/5}, а в интервале обозначение множество решений (-3/5, oo). См. Рисунок 2.7 с графиком набора решений.

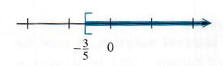
Отныне решения всех неравенств будут записываться с интервалом обозначение.

ТРЕХЧАСТНЫЕ НЕРАВЕНСТВА Неравенство -2 <5 + 3m <20 в следующем пример говорит, что 5 + 3м составляет от -2 до 20.Это неравенство можно решить используя расширение указанных выше свойств неравенства, работая со всеми три выражения одновременно.

Решить -2 <5 + 3m <20.
Запишите эквивалентные неравенства следующим образом.

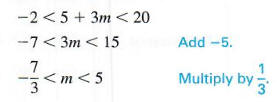
Решение показано на Рисунке 2.8

КВАДРАТИЧЕСКИЕ НЕРАВЕНСТВА Решение квадратичных неравенств зависит от решение квадратных уравнений.

Квадратичное неравенство — это неравенство, которое можно записать в виде

Мы обсудим квадратичные неравенства в следующем разделе.

Перейти на страницу графика неравенств

.

Simple English Wikipedia, бесплатная энциклопедия

Неравенство — это когда один объект равен: ^{[1] [2]}

• Меньше, чем остальные (a a меньше b )
• Больше, чем другой (a> b {\ displaystyle a> b} означает, что a больше, чем b )
• Не меньше другого (a≥b {\ displaystyle a \ geq b} означает, что a не меньше b , то есть либо больше, либо равно b )
• Не больше другого (a≤b {\ displaystyle a \ leq b} означает, что a не больше b , или меньше или равно b )

Неравенство иногда используется для назовите утверждение, что одно выражение меньше, больше, не меньше или не больше другого.

Неравенство 1 Это решение уравнения x + 4> 12

Неравенство в математике — это когда два решения или ответа сравниваются на большее или меньшее чем. Это когда сравниваются два или все же множество решений, не равных по количеству. Разрешить неравенство — значит найти его решения. Когда вы подставляете число в переменную и утверждение истинно, тогда это решение. Когда вы подставляете число в переменную, и тогда утверждение неверно, число не является решением этого утверждения.

Решение неравенства — это поиск решения данной переменной. Это нахождение относительного порядка набора. Неравенство может иметь множество решений, но обычно мы ищем только решения, так как действительные числа. Правильный способ чтения неравенства — слева направо, как и другие уравнения, но с той лишь разницей, что они имеют разные правила для каждого уравнения.

Например, рассмотрим неравенство x + 4> 12, где x — действительное число. Во-первых, нужно найти x и убедиться, что это действительно решение.Ответ будет x> 8, и это верное утверждение. Это выражение касается положения x в наборе действительных чисел. Числовая линия — это один из способов показать местоположение относительно всех других действительных чисел. ^[3] (См. Рисунок Неравенство 1)

Линейное неравенство Пример линейного неравенства

Существует пять различных видов неравенства:

1. Первый вид — это линейные неравенства, которые представляют собой неравенства, различающие выражения на меньшее или равное, меньшее или большее или равное, большее чем.Если мы заменим неравенство отношением равенства, то результатом будет линейное уравнение.
2. Второй вид — это комбинации неравенств, которые должны удовлетворять неравенствам. Здесь нужно сначала иметь число в наборах решений, так что числа, удовлетворяющие неравенствам, будут значениями в пересечении двух наборов решений. ^[4]
3. Третий вид — это неравенства, включающие абсолютные значения, что означает, что значения могут быть перефразированы как комбинации неравенств, включающих абсолютные значения.
4. Четвертый вид неравенств называется полиномиальными неравенствами, что означает, что они непрерывны и их графики не имеют скачков или разрывов.
5. И последнее, но не менее важное, это рациональные неравенства, которые означают, что это форма одного полинома, деленного на другой полином. Другими словами, графики рациональных функций не имеют разрывов и не представлены в нулях знаменателя.

абсолютное значение Пример, показывающий абсолютное значение Пример добавления неравенств.

Есть четыре способа решить квадратные уравнения:

1. Сложите или вычтите одинаковое число с обеих сторон.
2. Сдвиньте стороны и измените расположение знака неравенства.
3. Умножьте одинаковое число с обеих сторон.
4. Разделите одинаковое положительное или отрицательное число на обе стороны. пример умножения неравенства

Кроме того, для решения неравенства потребуется два шага. Первый — это упростить, используя обратное сложение или вычитание.Второй — еще больше упростить, используя обратную величину умножения или деления. Обратите внимание, что при умножении или делении неравенства на отрицательное число символ неравенства необходимо перевернуть. ^{[5] [6]}

Примеры решения неравенств [изменить | изменить источник]

Неравенство 2 Решение уравнения -6y

Неравенство — это математическое утверждение, объясняющее, что два значения не равны и различны. Уравнение a ≠ b означает, что a не равно b .Неравенство одинаково для любого уравнения, с той (единственной) разницей, что неравенство не использует знак равенства, а символы неравенства. Неравенство b> a означает, что b больше a. Ограничения скорости, знаки и другие используют неравенство, чтобы выразить их.

Решая неравенство, человек должен иметь верное утверждение. Когда вы делите или умножаете неравенство с отрицательным числом с обеих сторон, утверждение неверно. Чтобы утверждение было правильным с отрицательным числом, нужно изменить направление символа неравенства.Когда число является положительным числом, переворачивать символ не нужно. Неравенство — это правдивое заявление.

Например, начните с истинного утверждения -6 y <-12. Когда обе стороны разделены на -6, результат станет y <2. В этом утверждении символ необходимо перевернуть, чтобы получить истинное утверждение, которое дает y> 2 как правильный ответ. В числовой строке (см. Рисунок Неравенство 2) замкнутый заштрихованный кружок указывает, что он включен в набор решений.Открытый кружок указывает на то, что он не входит в набор решений. ^[7]

.

Свойства неравенств

Неравенство говорит нам об относительном размере двух значений.

(Вы можете сначала прочитать краткое введение в неравенство)

Четыре неравенства

Символ	слов	Пример
>	больше	х + 3> 2
<	менее	7x <28
≥	больше или равно	5 ≥ х − 1
≤	меньше или равно	2 года + 1 ≤ 7

Символ «указывает» на меньшее значение

Недвижимость

Неравенства имеют свойства… все со специальными именами!

Здесь мы перечисляем каждый из них с примерами.

Примечание: значения a , b и c , которые мы используем ниже, являются действительными числами.

Переходное свойство

Когда мы соединяем неравенства по порядку, мы можем «перепрыгнуть» через среднее неравенство.

Если a и b

Аналогично:

Если a> b и b> c, то a> c

Пример:

• Если Алекс старше Билли и
• Билли старше Кэрол,

тогда Алекс тоже должен быть старше Кэрол!

Свойство разворота

Мы можем поменять местами на и на , если мы убедимся, что символ все еще «указывает» на меньшее значение.

• Если a> b, то b
• Если a a

Пример: Алекс старше Билли, поэтому Билли моложе Алекса

Закон трихотомии

«Закон трихотомии» говорит, что истинно только одно из следующего:

В этом есть смысл, правда? a должно быть либо на меньше, чем b , либо должно быть равно b , либо должно быть больше b .Это должен быть один из них, и только один из них.

Пример: У Алекса денег больше, чем у Билли

Мы могли бы написать это так:

а> б

Итак, мы также знаем, что:

• Алекс имеет , а не , у него на меньше денег, чем у Билли (не a
• У Алекса , а у столько же денег, сколько у Билли (не a = b)

(Конечно!)

Сложение и вычитание

Добавление c к обеим сторонам неравенства всего сдвигает все вдоль , и неравенство остается прежним.

Если a + c + c

Пример: У Алекса меньше денег, чем у Билли.

Если и Алекс, и Билли получат на 3 доллара больше, то у Алекс все равно будет меньше денег, чем у Билли.

Аналогично:

• Если a
• Если a> b, то a + c> b + c, и
• Если a> b, то a — c> b — c

Таким образом, добавление (или вычитание) одного и того же значения к a и b не изменит неравенство

Умножение и деление

Когда мы умножаем и a, и b на положительное число , неравенство остается неизменным .

Но когда мы умножаем и a, и b на отрицательное число , неравенство меняет местами !

Обратите внимание, что a становится b после умножения на (-2)
Но неравенство остается неизменным при умножении на +3

Вот правила:

• Если a c положительно , то ac
• Если a c отрицательно , то ac> bc (неравенство меняет местами!)

«Положительный» пример:

Пример: 3 балла Алекса на ниже, чем баллов Билли 7.

а <б

Если и Алексу, и Билли удастся удвоить своих баллов (× 2), баллы Алекса все равно будут ниже, чем баллы Билли.

2a <2b

Но при умножении на отрицательное происходит обратное:

Но если набрать минус , то Алекс теряет 3 очков, а Билли теряет 7 очков

.

Итак, Алекс теперь сделал лучше , чем Билли!

-a> -b

Почему умножение на отрицательное меняет знак?

Ну, посмотрите на числовую строку!

Например, от −3 до −7 это , уменьшение , а от 3 до 7 — , увеличение .

Обратите внимание, что −7 <−3

но + 7> +3

Значит, знак неравенства меняется на противоположный (с <на>)

Инверсная добавка

Как мы только что видели, добавление минусов перед a и b изменяет направление неравенства. Это называется «аддитивная инверсия»:

• Если a −b
• Если a> b, то −a <−b

Это действительно то же самое, что умножение на (-1), и именно поэтому оно меняет направление.

Пример: У Алекса денег больше, чем у Билли, поэтому Алекс впереди.

Но новый закон гласит: «Теперь все ваши деньги — это долг , который вы должны выплатить упорным трудом»

Итак, теперь Алекс хуже, чем Билли.

Мультипликативная обратная

Взятие обратной величины (1 / значение) для a и b может изменить направление неравенства.

Когда a и b равны , оба положительные или , оба отрицательные :

• Если a 1 / b
• Если a> b, то 1 / a <1 / b

Пример: Алекс и Билли преодолевают путь длиной 12 километров.

Алекс бежит со скоростью 6 км / ч , а Билли идет со скоростью 4 км / ч .

Скорость Алекса больше, чем скорость Билли

6> 4

Но время Алекса меньше времени Билли:

12/6 <12/4

2 часа <3 часа

Но когда либо a, либо b отрицательны (не оба), направление остается прежним:

• Если a
• Если a> b, то 1 / a> 1 / b

Неотрицательная собственность квадратов

Число в квадрате больше или равно нулю:

а ² ≥ 0

Пример:

• (3) ² = 9
• (−3) ² = 9
• (0) ² = 0

Всегда больше (или равно) нулю

Свойство квадратного корня

Извлечение квадратного корня не изменит неравенство (но только если и a, и b больше или равны нулю) .

Если a ≤ b, то √a ≤ √b
(для a, b ≥ 0)

.

No related posts.