Решение неравенств любого вида. Онлайн калькулятор с примерами

Решение неравенств онлайн

Перед тем как решать неравенства, необходимо хорошо усвоить как решаются уравнения.

Не важно каким является неравенство – строгим () или нестрогим (≤, ≥), первым делом приступают к решению уравнения, заменив знак неравенства на равенство (=).

Поясним что означает решить неравенство?

После изучения уравнений в голове у школьника складывается следующая картина: нужно найти такие значения переменной, при которых обе части уравнения принимают одинаковые значения. Другими словами, найти все точки, в которых выполняется равенство. Всё правильно!

Когда говорят о неравенствах, имеют в виду нахождение интервалов (отрезков), на которых выполняется неравенство. Если в неравенстве две переменные, то решением будут уже не интервалы, а какие-то площади на плоскости. Догадайтесь сами, что будет решением неравенства от трех переменных?

Как решать неравенства?

Универсальным способом решения неравенств считают метод интервалов (он же метод промежутков), который заключается в определении всех интервалов, в границах которых будет выполняться заданное неравенство.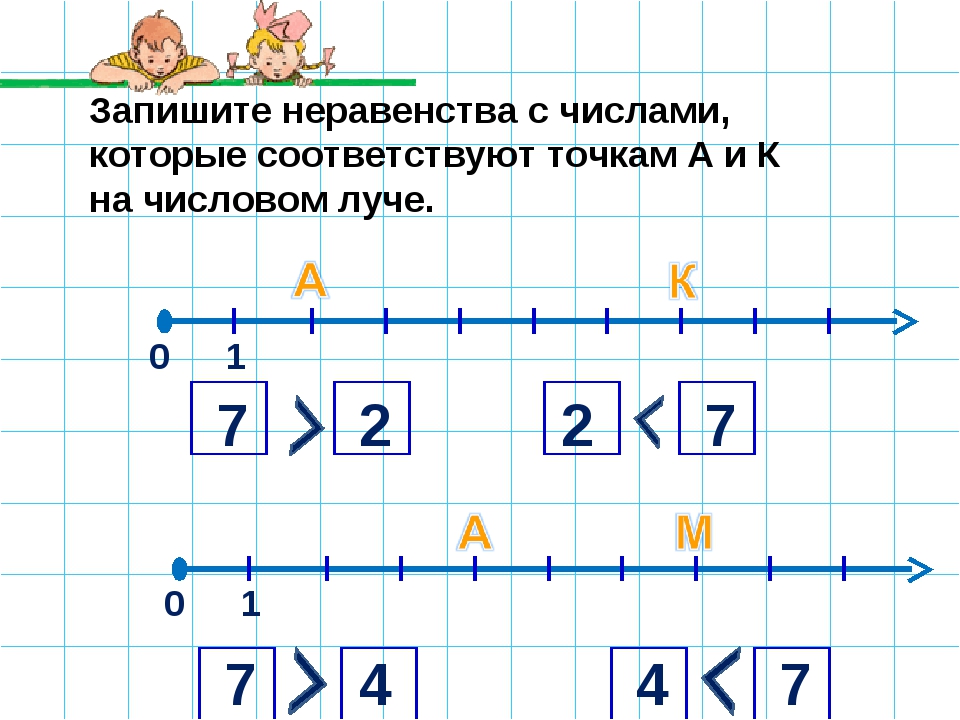

Не вдаваясь в тип неравенства, в данном случае это не суть, требуется решить соответствующее уравнение и определить его корни с последующим обозначением этих решений на числовой оси.

Можно сказать на этом полдела сделано. Далее, взяв любую точку на каждом интервале, осталось определить выполняется ли само неравенство? Если выполняется, то он входит в решение неравенства. Ели нет, то пропускаем его.

Как правильно записывать решение неравенства?

Когда вы определили интервалы решений неравенства, нужно грамотно выписать само решение. Есть важный нюанс – входят ли границы интервалов в решение?

Тут всё просто. Если решение уравнения удовлетворяет ОДЗ и неравенство является нестрогим, то граница интервала входит в решение неравенства. В противном случае – нет.

Рассматривая каждый интервал, решением неравенства может оказаться сам интервал, либо полуинтервал (когда одна из его границ удовлетворяет неравенству), либо отрезок – интервал вместе с его границами.

Важный момент

Не думайте, что решением неравенства могут быть только интервалы, полуинтервалы и отрезки. Нет, в решение могут входить и отдельно взятые точки.

Например, у неравенства |x|≤0 всего одно решение – это точка 0.

А у неравенства |x|

Для чего нужен калькулятор неравенств?

Калькулятор неравенств выдает правильный итоговый ответ. При этом в большинстве случаев приводится иллюстрация числовой оси или плоскости. Видно, входят ли границы интервалов в решение или нет – точки отображаются закрашенными или проколотыми.

Благодаря онлайн калькулятору неравенств можно проверить правильно ли вы нашли корни уравнения, отметили их на числовой оси и проверили на интервалах (и границах) выполнение условия неравенства?

Если ваш ответ расходится с ответом калькулятора, то однозначно нужно перепроверить свое решение и выявить допущенную ошибку.

Решение неравенств: основные ошибки и полезные лайфхаки

Вы умеете решать неравенства? Уверены?

Вспомним для начала, что вообще можно делать с неравенствами и чего с ними делать нельзя.

При решении неравенств мы можем:

1. Умножать обе части неравенства на число или выражение, не равное нулю.
При умножении обеих частей неравенства на положительное число знак неравенства сохраняется.

При умножении обеих частей неравенства на отрицательное число знак неравенства меняется на противоположный.

2. Можем возводить обе части неравенства в квадрат при условии, что они неотрицательны

3. Имея дело с показательным или логарифмическим неравенством, мы можем «отбрасывать» основания или логарифмы. Если основание степени или логарифма больше единицы – знак неравенства будет тот же. Если основание степени или логарифма положительно и меньше единицы – знак неравенства меняется на противоположный.

Конечно, мы не просто «отбрасываем» основания степеней или логарифмы. Мы пользуемся свойствами монотонности соответствующих функций. Если основание степени больше единицы, показательная функция монотонно возрастает. Если основание положительно и меньше единицы – показательная функция монотонно убывает.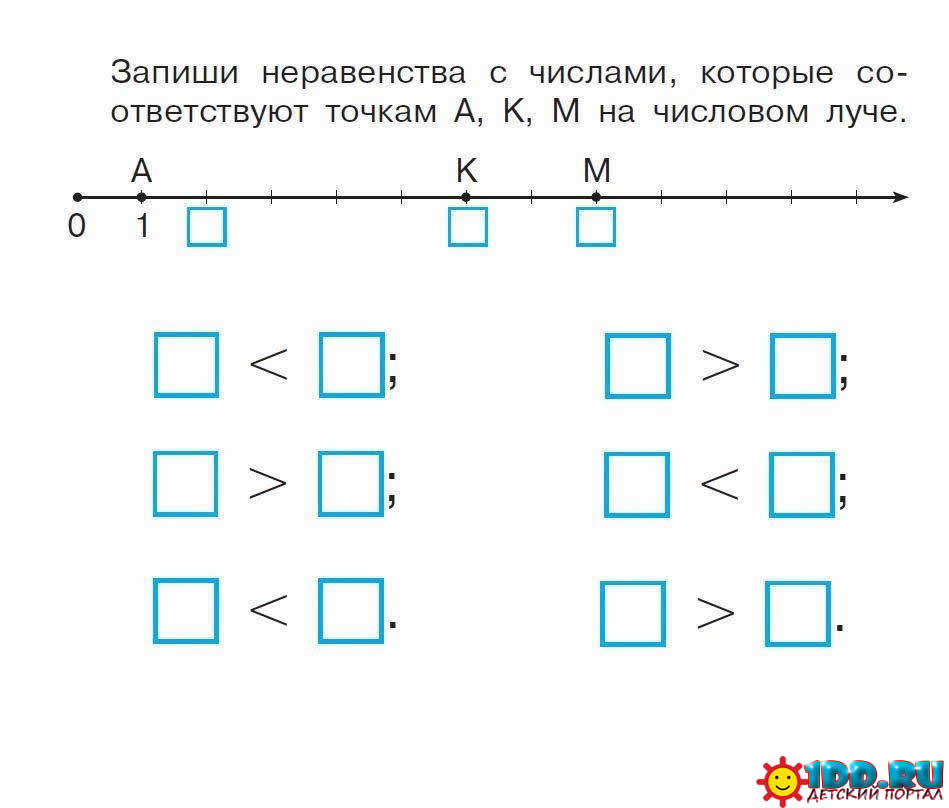

Аналогично ведет себя и логарифмическая функция.

4. При решении показательных или логарифмических неравенств применяется метод рационализации (замены множителя).

5. Общее правило. Если неравенство можно хоть как-то упростить – это необходимо сделать! Иначе его решение может занять восемь страниц и два часа времени.

Чего нельзя делать при решении неравенств? Вот 7 ловушек, в которые часто попадают абитуриенты.

1. Нельзя умножать (или делить) неравенство на выражение, знака которого мы не знаем.

Например, в неравенстве > нельзя поделить левую и правую часть на . Правильный способ: перенести всё в левую часть неравенства, разложить на множители и решить неравенство методом интервалов.

> 0

> 0

Получаем, что < 0 или > . «Сократив» на , который может быть отрицательным, мы не получили бы правильного ответа.

2. Извлекать из неравенства корень тоже нельзя. Такого действия просто нет.

Как, например, решить неравенство

>

Перенесем все в левую часть неравенства, чтобы в правой остался ноль.

> 0

Разложим левую часть на множители.

> 0

Решим неравенство, пользуясь свойствами квадратичной функции , и запишем ответ: < или > .

Запомним: ответы типа « > » абсурдны.

Как решать неравенство > 0? Это типичная «ловушка для абитуриентов». Так и хочется сказать, что > 0 (то есть извлечь корень из неравенства). Но этого делать нельзя. Выражение положительно при всех , кроме нуля. Правильное решение неравенства: .

4. Возводить обе части неравенства в квадрат можно только если они неотрицательны.

5. Помним о том, в каких случаях знак показательного или логарифмического неравенства меняется, а в каких – остается тем же. «Отбрасывая» логарифмы, делаем это грамотно.

6. Если в неравенстве есть дроби, корни четной степени или логарифмы – там обязательно будет область допустимых значений.

7. Сложная тем для старшеклассников – задачи с модулем. Проверьте, умеете ли вы их решать.

При решении неравенств большое значение имеет правильное оформление. Рекомендуется оформлять решение как цепочку равносильных переходов: от исходного неравенства к равносильному ему неравенству или системе.

Обратите внимание на приемы, позволяющие решать неравенства легко, быстро и без лишних вычислений.

А теперь – полезный лайфхак для решения дробно-рациональных неравенств.

Решите неравенство

Запишем ОДЗ:

Что будет, если действовать «по шаблону» — то есть собрать всё в левой части неравенства и привести к одному знаменателю? — Будет много вычислений и выражение четвертой степени.

Может быть, сделаем проще? Представим дробь в виде суммы дробей и .

Продолжаем упрощать левую часть:

Теперь можно и привести дроби к одному знаменателю.

Все, больше ничего не пишем. Решаем неравенство методом интервалов.

Ответ: .

Памятка по теме «неравенство» 4 класс

Неравенством называют математическое высказывание, содержащее знаки «больше» ( > ) или «меньше» ( < ). Например, 4<8; 9>7 и т.д. Неравенство может содержать переменную. Например, x<7. В таком случае на место переменной можно подставить число, которое удовлетворяет или не удовлетворяет неравенству. Например, для неравенства x<7 число 39 не удовлетворяет неравенству, так как неравенство 39<7 — неверное; а число 5 удовлетворяет неравенству, так как неравенство 5<7 – верное. Решить неравенство – значит найти значение (число или числа), которое удовлетворяет этому неравенству. «Ответ» неравенства называется его решением. Например, для неравенства x<7 число 5 является решением.

У неравенства может быть несколько решений (чисел, удовлетворяющих ему). Например, для неравенства x<7 число 5 не является единственным решением, так как числа от 0 до 6 тоже меньше 7. Если мы напишем числа от 0 до 6, то перечислим все решения неравенства x<7. В таком случае решения неравенства записывают как множество. Например, для неравенства x<7 решением является множество {0, 1, 2, 3, 4, 5, 6}. А для неравенства x>7 решением является множество {8, 9, 10, 11, 12, …} (это значит, что множество можно продолжить).

Неравенства бывают строгими и нестрогими. Например, 4<8; 9>7 – строгие неравенства. В нестрогих неравенствах используются знаки «больше или равно» (≥) и «меньше или равно» (≤). Решением нестрогих неравенств являются числа, подставив которые выполняется хотя бы одно из условий «больше» или «равно». Например, неравенство 6≤8 (6 меньше или равно 8). Решением этого неравенства является множество чисел {0, 1, 2, 3, 4, 5, 6, 7, 8}.

Неравенства x>3 и x<7 можно объединить. Так получаем двойное неравенство 3<x<7. Решением такого неравенства являются числа от 3 до 7, то есть множество чисел {4, 5, 6}. Двойные неравенства так же могут быть нестрогими. Например, неравенство 3≤x≤7, решением которого является множество чисел {3, 4, 5, 6, 7}.

Для поиска решения неравенств удобно использовать числовые лучи. Например, найдем решение двойного неравенства 3<x<7. Для этого построим числовой луч удобного промежутка. Отметим на числовом луче точки 3 и 7, так как они даны в условии неравенства. Так на числовом луче хорошо видно, что неравенству удовлетворяют числа от 3 до 7 (сами числа 3 и 7 не входят в решение, так как неравенство строгое, поэтому точно полностью закрашены). Решением неравенства является множество чисел {4, 5, 6}. Так же рассуждаем для решения нестрогих неравенств. Например, построим числовой луч для решения неравенства 3≤x≤7. На числовом луче видно решение неравенства – множество чисел {3, 4, 5, 6, 7} (числа 3 и 7 входят в решение, поэтому не закрашены).

Картинки равенства и неравенства 1 класс примеры (32 фото)

раздражает 30%, 964 голоса

964 голоса 30%

964 голоса — 30% из всех голосов

ОЧЕНЬ БЕСИТ И РАЗДРОЖАЕТ^*18%, 584 голоса

584 голоса 18%

584 голоса — 18% из всех голосов

ЭТО САМОЕ АДСКОЕ ЧТО ЕСТЬ НА СВЕТЕ!!!!^*13%, 429 голосов

429 голосов 13%

429 голосов — 13% из всех голосов

ОЧЕНЬ НАДОЕДАЕТ^*7%, 218 голосов

218 голосов 7%

218 голосов — 7% из всех голосов

не интересует/безразлична 6%, 201 голос

201 голос 6%

201 голос — 6% из всех голосов

бесит, надоедает и я ее ненавижу^*4%, 130 голосов

130 голосов 4%

130 голосов — 4% из всех голосов

капец как раздржает!!!!!!!!!!^*3%, 103 голоса

103 голоса 3%

103 голоса — 3% из всех голосов

Мне пофиг, я анимешник^*3%, 103 голоса

103 голоса 3%

103 голоса — 3% из всех голосов

Нейтрально. Может даже безразлично✨^*3%, 82 голоса

82 голоса 3%

82 голоса — 3% из всех голосов

раздражает эта реклама^*2%, 75 голосов

75 голосов 2%

75 голосов — 2% из всех голосов

достала до нельзя^*2%, 66 голосов

66 голосов 2%

66 голосов — 2% из всех голосов

Без различна^*2%, 56 голосов

56 голосов 2%

56 голосов — 2% из всех голосов

очень классные рекламы^*1%, 44 голоса

44 голоса 1%

44 голоса — 1% из всех голосов

Изучаю рекламу 1%, 43 голоса

43 голоса 1%

43 голоса — 1% из всех голосов

нравится реклама 1%, 36 голосов

36 голосов 1%

36 голосов — 1% из всех голосов

Никогда не задумывался^*1%, 35 голосов

35 голосов 1%

35 голосов — 1% из всех голосов

без разницы тока дома надо учится и сидеть не играть^*1%, 25 голосов

25 голосов 1%

25 голосов — 1% из всех голосов

Урок 11. равенство. неравенство. знаки «>», «

Математика, 1 класс

Урок 11. Равенство. Неравенство. Знаки «>», «<», «=»

Перечень вопросов, рассматриваемых на уроке:

1. Определять место знаков больше, меньше, равно

2. Писать знаки >,<,=

3. Называть равенство, неравенство.

Глоссарий

Равенство – это когда одно количество равно другому.

Неравенство – это когда одна сторона выражения не равна второй.

Если носик галочки смотрит направо — это знак больше (>).

Если носик галочки смотри налево – это знак меньше (<).

Знак равенства (=) в математике, в логике и других точных науках — символ, который пишется между двумя одинаковыми по своему значению выражениями.

Ключевые слова

Знак >; знак <; знак =

Основная литература:

1.Моро М. И., Волкова С. И., Степанова С. В. Математика. Учебник. 1 кл. В 2 ч. М.: Просвещение, 2017.

Дополнительная литература:

1. Моро М. И., Волкова С. И. Математика. Рабочая тетрадь. 1 кл. В 2 ч. пособие для общеобразовательных организаций. — М.: Просвещение, 201 с.

Основное содержание урока

1. Сегодня мы отправляемся в магазин, чтобы купить Оле и Ане к уроку технологии все учебные принадлежности.

Для урока понадобится 1 пачка пластилина и две пачки картона.

По сколько пачек пластилина получили девочки? ( по одной пачке)

Можно сказать, что девочки получили одинаковое количество пластилина.

2. Для технологии необходимо две пачки картона.

По сколько пачек картона получили девочки? (по две пачки)

Можно сказать, что девочки получили одинаковое количество картона.

3. В математике используется специальный значок, чтобы записать, что число предметов одинаковое.

Можно записать цифрами и использовать для слов «одинаково», «равно» специальный значок «=»,1 = 1

=

2 = 2 (аналогично)

Две палочки напишут дети,

И что получится в ответе,

Ведь каждый выучил давно,

Как пишется тот знак: РАВНО!

Такие записи называются равенствами.

Это равенства. Записать равенства можно с помощью знака «=».

Докажем, что одинаковое количество предметов с помощью стрелочек образует пары.

На схеме каждый предмет обозначим кружочком и образуем пары. Покажем стрелочкой.

Оля Аня

Лишних фигур не осталось. Значит, поровну, одинаково.

Можно записать 1 = 1

6. 2 + 1 = 3

Как можно прочитать эту запись?

(Числовое равенство)

Под этим высказыванием понимают два числовых выражения, которые стоят по обе стороны от знака « =».

Обе части записи равны между собой.

1. В каком количестве нужно было для урока картона? А пластилина?

Чтобы узнать, каких предметов потребовалось больше или меньше, используют специальные значки «>», « <».

Если с какой- то стороны больше или меньше, то запись будет называться «неравенство».

Два больше одного.

Картон Пластилин

Если слева больше число, чем справа, то используют знак «>».

2 > 1

1. А если число слева меньше, чем справа, то ставим знак меньше «<».

1 < 2

1. Такие записи называются неравенства:

4 > 3, 4 < 5

Разбор типового тренировочного задания

Выберите нужный знак и распределите на две группы.

Дополните каждую группу своими записями.

6 (=, >, <) 9

1 (=, >, <) 3

2 (=, >, <) 2

3 (=, >, <) 3

Правильный ответ:

Равенства: 2 = 2, 3 = 3

Неравенства: 6 < 9, 1 < 3

Конспект «Числовые неравенства. Сравнение чисел»

Числовые неравенства. Сравнение чисел

Ключевые слова: числовые неравенства, строгие и нестрогие, двoйные неравенства, верные и невeрные, сравнение чисел.

---

Числовые неравенства

При сравнении любых чисел c и d может выполняться только один из трех случаев:

1.   c > d (c больше d)
2.   c < d (c меньше d)
3.   c = d (c равно d)

Выражения c > d и c < d называются неравенствами.

Определение 1. Неравенством называются два числа или алгебраических выражения, соединенных между собой знаком > (больше ) или < (меньше).

Например: 5 < 7; -8 > -10; 2(а — b) > 0

Определение 2. Строгими называются неравенства вида а > b; а < b. Нестрогими называются неравенства вида а ≥ b; а ≤ b.

а ≥ b читают так: а больше или равно b или а не меньше b.
а ≤ b читают так: а меньше или равно b или а не больше b.

Строгие (c > а и с < b) и нестрогие (с ≥ а и с ≤ b) неравенства могут быть записаны двойными неравенствами: а < с < b (строгое) или а ≤ с ≤ b (нестрогое). Их начинают читать со среднего члена слева на право, например: с больше а, но меньше b.

Например:
с ≥ 0 и с ≤ 3, то 0 ≤ с ≤ 3 — нестрогое неравенство
3 > 2 и 3 < 5, то 2 < 3 < 5 — строгое неравенство

Определение 3. Неравенства а > b и с > d или а < b и c < d называют неравенствами одинакового смысла. Неравенства а > b и с < d имеют противоположный смысл.

Например: 12 > 6 и 7 < 8 — неравенства разного (противоположного) смысла, а 15 < 16 и 10 < 11 — одного смысла.

Определение 4. Неравенства бывают верными (5 > 3) и неверными (6 > 10).

Например: а ≥ 6 при а = 6, 7, 8… неравенство верное; при а = 5, 4, 3… нeравенство неверное.

Выражение а ≠ b тоже называют нерaвенствoм.

 

Сравнение чисел

При сравнении чисел составляют их рaзнoсть и выясняют, ка кое число получается в ответе — положительное, отрицательное или нуль.

Определение 5. Число а называется большим числа b, если разнoсть чиceл а – b пoлoжительное число: а > b, если а – b > 0, и наоборот, еcли а – b > 0, тo а > b.

Например:
15 > 10, так как 15 – 10 = 5; 5 > 0
20 – 18 = 2, 2 > 0; следовательно, 20 > 18

Определение 6. Чиcло а мeньше числa b, если разность а – b отpицaтельное число: а < b, если а – b < 0, и наоборот, если а – b < 0, то а < b.

Если разность c – d = 0, то c = d.

Например:
7 < 12, так как 7 – 15 = –5, –5 < 0
9 – 10 = –1, –1 < 0, то 9 < 10
11 – 11 = 0, то 11 = 11

На числовой оси бOльшее число изображается точкoй, стоящей правее тoчки, изображающей меньшее число: а > b, значит, точка с кooрдинатой а лежит правее точки с кooрдинатой b, а если а < b, то левее.

Все отрицательные числа расположены левее нуля, а положительные — правее нуля (все положительные числа больше нуля и отрицательных чисел).

 

---

Вы смотрели конспект по математике «Числовые неравенства. Сравнение чисел». Если у Вас есть диплом ВУЗа или колледжа и Вы хотите преподавать математику в школе, то «Институт современных технологий, управления и бизнеса» приглашает Вас пройти обучение:  Учитель математики дистанционная переподготовка.

Вернуться в раздел «Математика»

Как написать неравенство из слова Задача

Этот урок покажет вам, как написать неравенство, чтобы описать реальную ситуацию или когда дается утверждение.

Несколько ключевых слов, о которых следует помнить.

Максимум означает «не больше», «меньше или равно» или «не больше»

Математический символ, который вы будете использовать не больше, будет ≤

Как минимум означает «нет». меньше «или» больше или равно «

Математический символ, который вы будете использовать по крайней мере, равен ≥

Теперь давайте попрактикуемся в написании неравенств для следующих ситуаций.

Как написать неравенство: простые примеры

Пример № 1

Предположим, пища с низким содержанием натрия содержит не более 140 мг на порцию. Напишите неравенство, моделирующее эту ситуацию.

Раствор

Пусть s = количество миллиграммов натрия в порции пищи с низким содержанием натрия.

Тогда s ≤ 140

Пример № 2

Рост человека не превышает 10 футов. Напишите неравенство, моделирующее эту ситуацию.

Решение

Пусть h будет ростом человека

Тогда h ≤ 10

Пример № 3

Пища с высоким содержанием клетчатки содержит не менее 5 г клетчатки на порцию. Напишите неравенство, моделирующее эту ситуацию.

Раствор

Пусть f будет количеством граммов клетчатки в продуктах с высоким содержанием клетчатки.

Тогда f ≥ 5

Как написать неравенство: наглядные примеры

Example # 4

Еженедельный доход Альфреда составляет не менее 500 долларов с фиксированным доходом в 200 долларов при работе в банке и 12 долларов в час на другой работе.Напишите неравенство, моделирующее эту ситуацию.

Решение

Пусть x будет количеством часов, которые Альфред работал в неделю.

Фиксированный доход + переменный доход ≥ 500

200 + 12x ≥ 500

Example # 5

Согласно законам о пожарной безопасности, ресторан, расположенный на улице Джефферсона, может одновременно посещать не более 75 человек. Сейчас в ресторане 30 человек, включая обедающих. Напишите неравенство, моделирующее эту ситуацию.

Решение

Количество людей, которые все еще могут войти в ресторан, плюс количество людей, которые уже находятся в ресторане, не может превышать 75.

Мы можем позволить x быть количеством людей, которые еще могут прийти внутри ресторана.

х + 30 ≤ 75

1. Введение в физику

   18 ноя, 20 13:20

   Первоклассное введение в физику.Универсальный ресурс для глубокого понимания важных концепций физики

   Подробнее

Новые уроки математики

Ваша электронная почта в безопасности. Мы будем использовать его только для информирования вас о новых уроках математики.

1.5 Устранение неравенств. Запишите каждое неравенство, используя обозначения интервалов, и проиллюстрируйте каждое неравенство, используя числовую линию.

Презентация на тему: «1.5 Устранение неравенств. Запишите каждое неравенство, используя интервальную нотацию, и проиллюстрируйте каждое неравенство, используя строку с действительными числами »- стенограмма презентации:

1 1. 5 Устранение неравенств

2

3

4 Запишите каждое неравенство, используя обозначения интервалов, и проиллюстрируйте каждое неравенство, используя числовую линию.

5 Запишите каждый интервал как неравенство и проиллюстрируйте каждое неравенство с помощью вещественной числовой прямой.

6 Решение неравенств 1. Исключите все дроби, умножив НОК 2. Используйте свойство распределения 3. Объедините все одинаковые члены 4. Выделите переменный член 5. Разделите (отрицательное — изменение знака неравенства) 6.Запишите свое решение в интервальной записи 7. Изобразите неравенство на числовой прямой.

8 Решите каждое неравенство и выразите свой ответ, используя интервальную нотацию. Изобразите каждое неравенство с помощью вещественной числовой прямой.

12 1. Выделите выражение абсолютного значения 2. Перепишите уравнение абсолютного значения как два отдельных уравнения 3.Один положительный, а другой отрицательный 4. Решите каждое уравнение и проверьте уравнения абсолютных значений.

Меню урока Основная идея и новый словарь Пример 1: Запишите неравенства Пример 2: Запишите неравенства Пример 3: Запишите неравенства Пример 4: Запишите неравенства.

Презентация на тему: «Основная идея меню урока и новый словарь. Пример 1: Напишите неравенства, Пример 2: Запишите неравенства, Пример 3: Запишите неравенства, Пример 4: Запишите неравенства» — стенограмма презентации:

1

2 Меню урока Основная идея и новый словарь Пример 1: Запишите неравенства Пример 2: Запишите неравенства Пример 3: Запишите неравенства Пример 4: Запишите неравенства Пример 5: Определите истинность неравенства Пример 6: Определите истинность неравенства Пример 7: Изобразите график Пример неравенства 8: графическое изображение неравенства

3 Основная идея / Словарь Пишите и графически неравенства. неравенство

4 Пример 1 Запишите неравенства Напишите неравенство для предложения. Иоганну нужно меньше 2 часов, чтобы покрасить свою комнату. Пусть r = количество часов. Ответ: r <2

5 Пример 1 CYP A.c <5 B.c> 5 C.c ≤ 5 D.c ≥ 5 Напишите неравенство для предложения. Для приготовления шариков из попкорна необходимо более 5 чашек попкорна.

6 Пример 2 Напишите неравенство для предложения. Лена прошла более 20 миль на благотворительность. Запишите неравенства. Пусть w = количество миль. Ответ: w> 20

7 Пример 2 CYP A.d <3 B.d> 3 C.d ≤ 3 D.d ≥ 3 Напишите неравенство для предложения. У Джоша меньше трех дней на то, чтобы вернуть книги из библиотеки.

8 Пример 3 Запишите неравенства Напишите неравенство для предложения. Чтобы получить скидку на продукты, необходимо потратить не менее 30 долларов. Пусть g = сумма, потраченная на продукты. Ответ: г ≥ 30

9 Пример 3 CYP A.f <7 B.f> 7 C.f ≤ 7 D.f ≥ 7 Запишите неравенство для предложения. В аквариуме может поместиться не более 7 рыб.

10 Пример 4 Напишите неравенство для предложения. В машине может находиться не более 5 человек. Напишите неравенства Пусть p = количество людей. Ответ: p ≤ 5

11 Пример 4 CYP A.x> 6 B.x <6 C.x ≥ 6 D.x ≤ 6 Напишите неравенство для предложения. Растению необходимо как минимум 6 часов солнечного света.

12 Пример 5 Определите истинность неравенства. Укажите, истинно ли неравенство x — 4 <6 для x = 0.x - 4 <6 Запишем неравенство. - 4 <6 Упростить. 0-4 <6 Заменить x на 0.