Отрезок — что это такое в математике и в жизни
Что такое отрезок? Ответ на этот вопрос кажется весьма простым, когда вы учитесь в школе. Но с возрастом школьный курс математики постепенно забывается настолько, что такие простые вещи становятся не столь очевидными.
Отрезок — что это за фигура
Не стоит недооценивать значимость геометрических понятий в человеческой жизни, так как иногда эти знания помогают решать вполне реальные задачи, а не только блистать кругозором в кругу друзей.
Отрезок — это составная часть прямой, расположенная между двумя точками.
Вы можете дать определение также исходя из структурного подхода:
Отрезок — это такая математическая фигура, которая состоит из следующих элементов:
- начало отрезка;
- конец фигуры;
- прямая линия.
С этими составными частями вы можете ознакомиться на слайде:
В связи с тем, что границы отрезка отмечаются точками, которые в рамках математики выделяются латинскими буквами, сама фигура описывается двумя буквами, например, NK.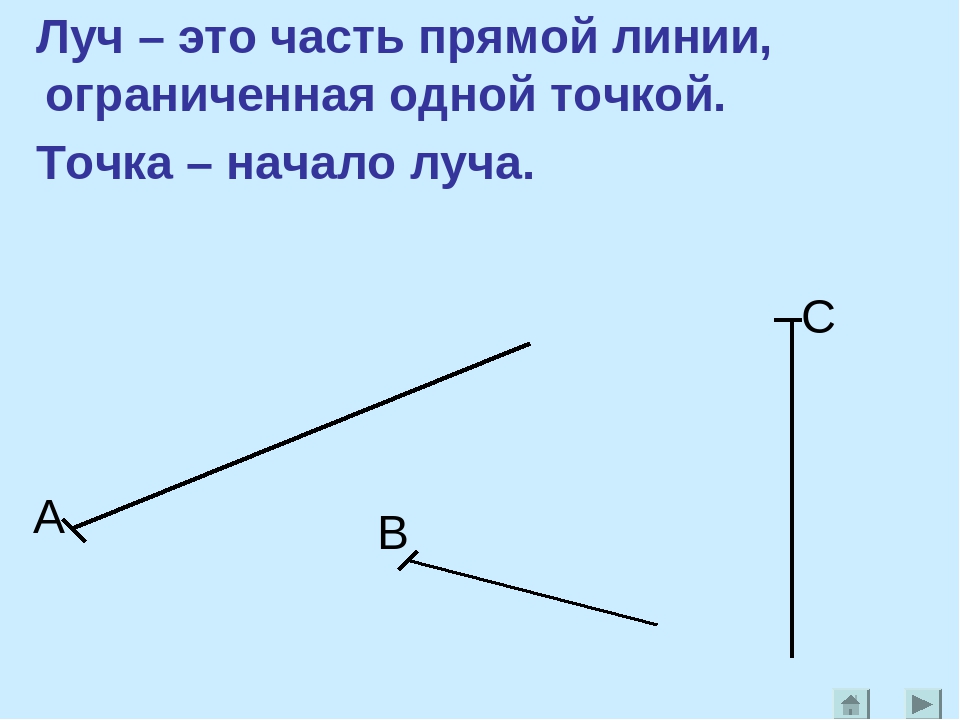
Пример визуального изображения отрезка вы видите на рисунке: точки N и K являются началом и концом.
Важная характеристика, которая присуща любому отрезку – его длина.
Основные меры измерения длины отрезков– это миллиметр, сантиметр, метр, километр.
Из математической трактовки следует, что отрезок – это такая прямая, которая расположена между двумя точками не выходя за их пределы. При этом одна же точка может быть концом множества отрезков.
Такую ситуацию вы видите на рисунке: точка А является общей для всех отрезков. При этом точки B, C, D — индивидуальны для каждого из отрезков.
Сравнение отрезка с геометрическими фигурами
В математике существуют три очень похожих понятия – это отрезок, луч, прямая. Учащиеся нередко задают такой вопрос «Что такое отрезок, чем он отличается от луча и прямой?». Давайте сразу определимся с понятиями, которые позволят вам понять разницу между фигурами.
Отрезок — это часть линии, которая проходит от точки начала до точки, обозначающей конец.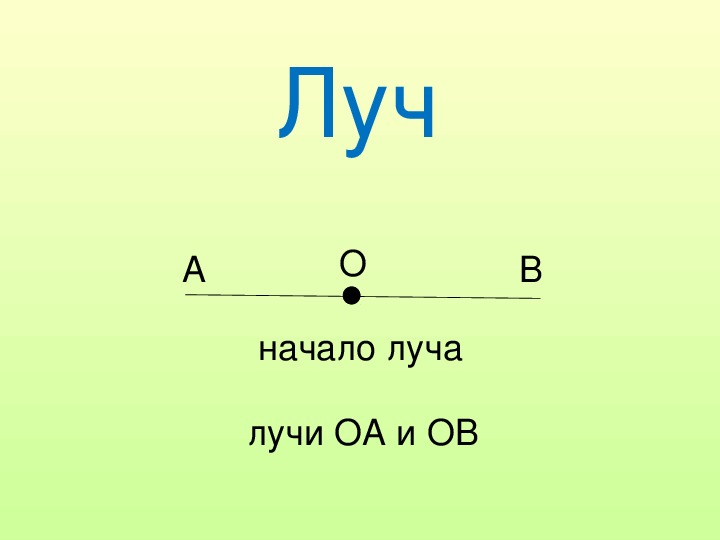
Луч — составная часть прямой, которая ограничена точкой с одной стороны. С другого конца луч продлевается до бесконечности.
Прямая — это линия, не подверженная искривлениям, у которой к тому же, в отличие от отрезков, отсутствуют начало и конец.
Сравнив 3 понятия, вы можете убедиться, что луч совмещает ограниченность отрезка и бесконечность прямой.
Примечательно, что прямая и луч бесконечны, поэтому вы сможете измерить длину только у отрезков.
У вас может возникнуть вопрос: «Как быстро определить, что именно перед вами — отрезок, луч или прямая?». Визуально идентифицировать геометрические фигуры можно по количеству ограничивающих их длину точек:
1 точка — луч;
2 точки — отрезок;
Нет точек — прямая.
Направленный отрезок
В статье вы увидели базовый вид отрезка — ненаправленный. Это отрезок, у которого невозможно определить, что является его началом, а что — концом.
Существует второй вид отрезков – направленные.
Альтернативное название этой математической фигуры — вектор.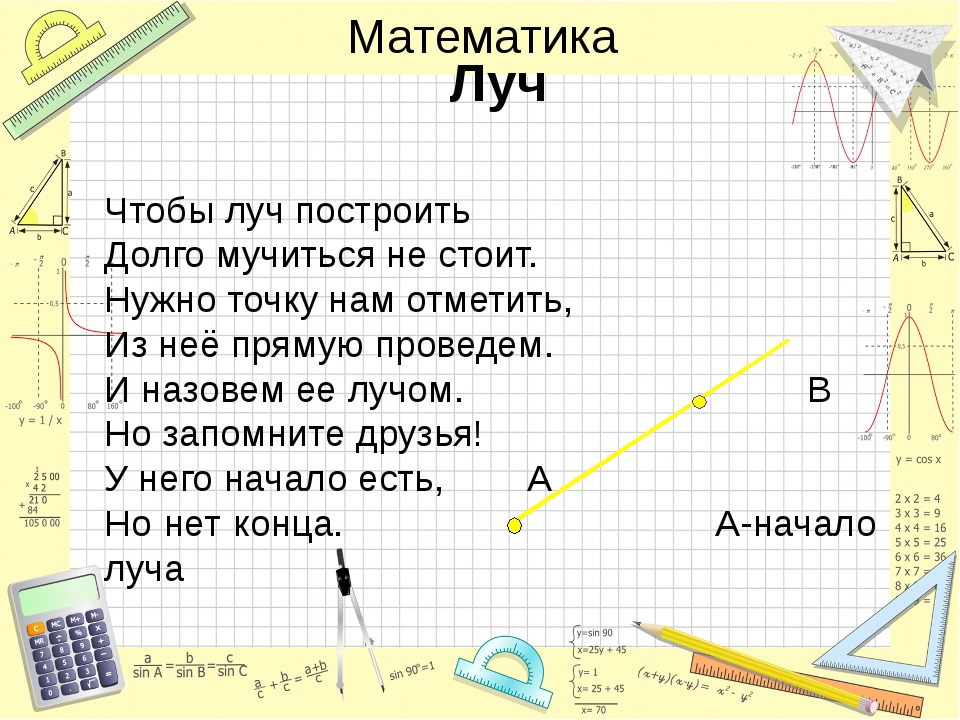
Особенностью направленного отрезка является то, что одна из точек, ограничивающих его длину, обозначается стрелкой. Она указывает, что именно там находится конец. Соответственно часть вектора, обозначенная точкой — это его начало.
Характерной чертой вектора является то, что он может быть описан не только двумя латинскими буквами, но и одной маленькой буквой, над которой располагается стрелка.
Направленный отрезок вместо показателя длины имеет характеристику — модуль, которая измеряется величинами, измеряющими расстояние – миллиметр, сантиметр, метр, километр.
В процессе работы с отрезками возникает вопрос: «Как рассчитать модуль вектора с использованием системы координат?».
Вы определите его следующим образом:
- координаты начала и конца возведите во вторую степень;
- два полученных числа суммируйте между собой;
- вычислите квадратный корень из результата предыдущего действия и получите модуль.
Направленные отрезки, которые лежат на одной прямой или параллельных прямых – это коллинеарные направленные отрезки.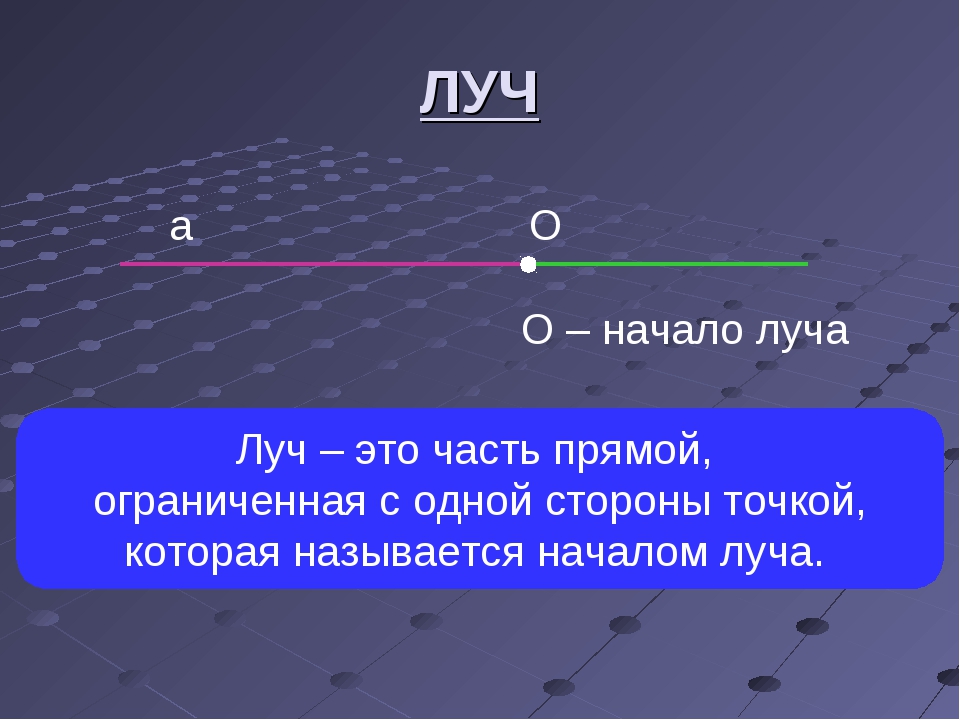
Направленные отрезки, расположенные на параллельных прямых – это коллинеарные направленные отрезки.
Нулевой вектор — это отрезок, у которого одна точка включает начало и его конец.
Отрезки, соединённые в ломаную линию
Ломаная линия — это совокупность соединённых между собой отрезков, в которой окончание одного отрезка совпадает с начальной точкой другого. Каждая из составных частей ломаной линии называется звеном.
Ломаная линия содержит три типа вершин — точек, из которых состоят отрезки:
- начальная точка фигуры;
- конечная точка фигуры;
- промежуточные точки фигуры, которые являются началом или концом одного из звеньев (отрезков).
Первое и последнее звенья фигуры имеют по одной точке, которую они не делят с другими звеньями, а все остальные точки являются одновременно концом одного отрезка и началом другого, поэтому количество точек ломаной линии всегда на одну больше числа составляющих её отрезков.
Сравнение отрезков
Сравнить два отрезка — это значит сделать вывод о том, одинаковы ли они, или один по размеру больше другого.
Если наложить один отрезок на другой и они совпадут — это значит, что фигуры равны.
Наложение не всегда является возможным, поэтому для сравнения размеров отрезков вы можете использовать циркуль или линейку.
Отрезок: разные значения слова
Обратите внимание, что отрезок — это не только математическое понятие, хотя наибольшее распространение получило именно в этой точной науке.
Часто слово употребляется для характеристики временного промежутка — «отрезок времени»
Так же вы можете услышать словосочетание — «отрезок пути». Эта фраза обозначает расстояние — составную часть путешествия. Суть слова «отрезок» — ограничение какого-либо понятия, которое подлежит измерению.
Также рекомендуем прочитать:
Отрезок. Луч / Виды линий / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Виды линий
- Отрезок.
 Луч
Луч
Прежде, чем поговорить о луче и отрезке, повтори тему «Прямая линия» в нашем справочнике.
Отрезок
У отрезка есть начало и конец.
Часто отрезки обозначают буквами.
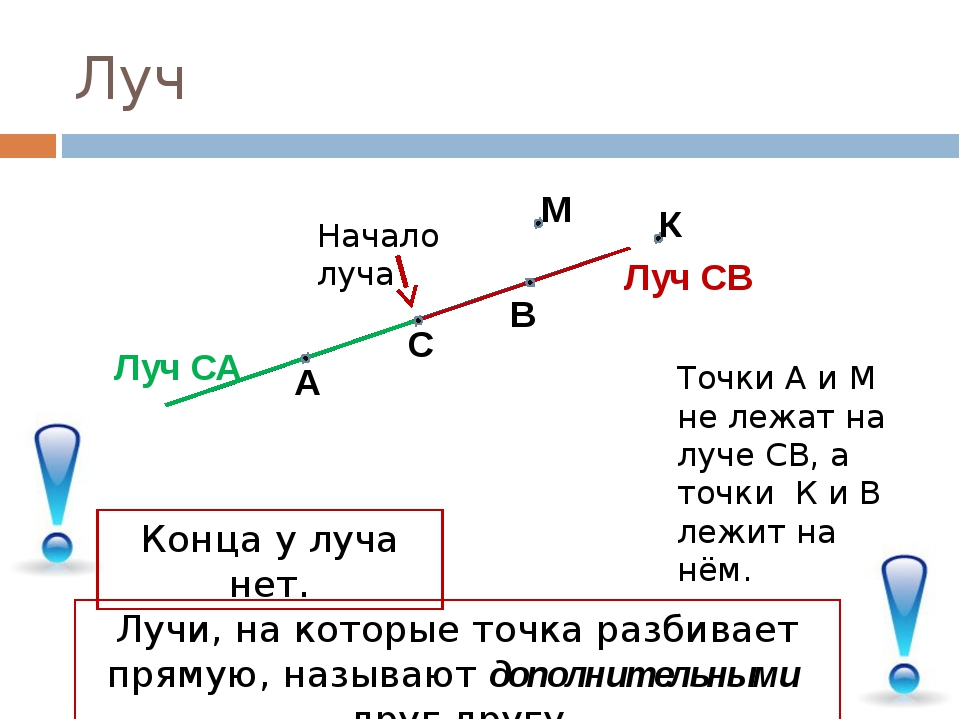
Луч
У луча есть начало, но нет конца.
Луч тоже можно обозначать буквами.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Точка. Кривая. Прямая линия
Ломаная линия
Длиннее. Короче. Уже. Шире. Одинаковые по длине и ширине
Виды линий
Правило встречается в следующих упражнениях:
1 класс
Страница 58, Моро, Волкова, Степанова, Учебник, часть 1
Страница 78, Моро, Волкова, Степанова, Учебник, часть 1
Страница 109, Моро, Волкова, Степанова, Учебник, часть 1
Страница 31, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 32, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 12.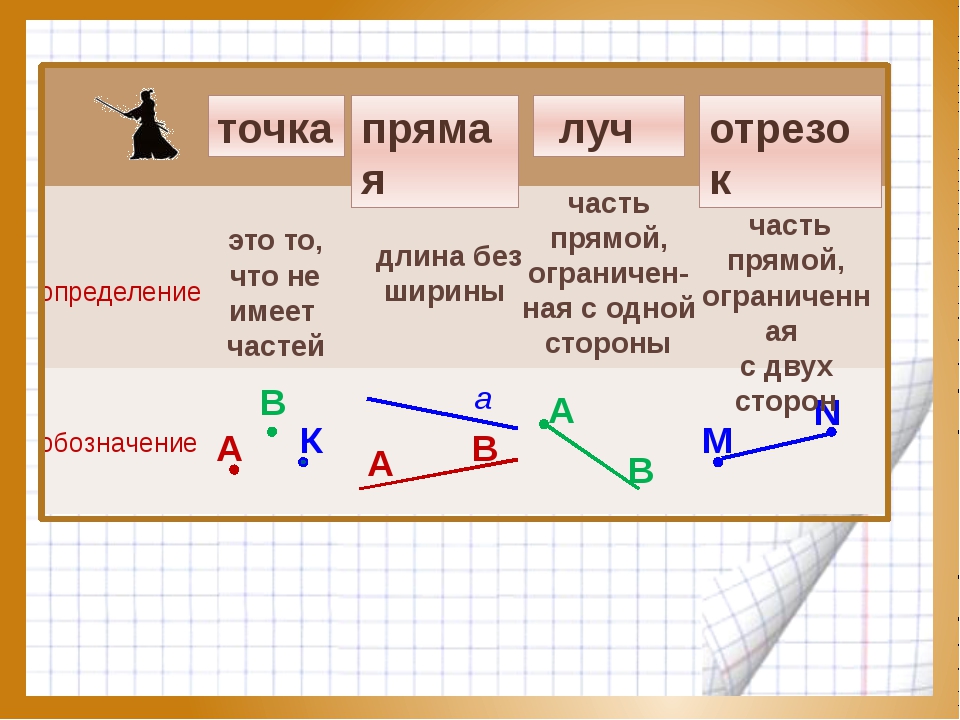 Вариант 1. № 3,
Волкова, Проверочные работы
Вариант 1. № 3,
Волкова, Проверочные работы
Страница 13. Вариант 2. № 3, Волкова, Проверочные работы
Страница 23. Вариант 2. № 2, Волкова, Проверочные работы
Страница 5, Моро, Волкова, Степанова, Учебник, часть 2
Страница 33, Моро, Волкова, Степанова, Учебник, часть 2
2 класс
Страница 31, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 78, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 83, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Задание 4, Моро, Волкова, Рабочая тетрадь, часть 1
Задание 2, Моро, Волкова, Рабочая тетрадь, часть 1
Задание 131, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 70, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 84, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 31, Моро, Волкова, Рабочая тетрадь, часть 2
Страница 59, Моро, Волкова, Рабочая тетрадь, часть 2
3 класс
Страница 8, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 10, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 14, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 15, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 107, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 11. Вариант 2. № 1,
Моро, Волкова, Проверочные работы
Вариант 2. № 1,
Моро, Волкова, Проверочные работы
Страница 9, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 19, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 28, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 57, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
4 класс
Страница 13, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 26, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 69, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 29, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 57, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 75, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 29. Вариант 2. Проверочная работа 3,
Моро, Волкова, Проверочные работы
Вариант 2. Проверочная работа 3,
Моро, Волкова, Проверочные работы
Страница 17, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 69, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 97, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
© budu5.com, 2020
Пользовательское соглашение
Copyright
Онлайн урок: Отрезок. Длина отрезка по предмету Математика 5 класс
Длина в геометрии — это величина, которая характеризует протяженность.
Длина отрезка — это расстояние между концами отрезка.
Так как каждый отрезок имеет длину, отрезки можно измерять и сравнивать.
Существует несколько способов сравнения отрезков.
1. Приблизительный способ сравнения.
Данный способ сравнения применяют только в том случае, когда длины отрезков явно отличаются.
Пример: Даны два отрезка АВ и ЕР
Очевидно, что отрезок АВ длиннее отрезка ЕР, значит, АВ > ЕР
2. Совмещение отрезков — более точный способ сравнения отрезков.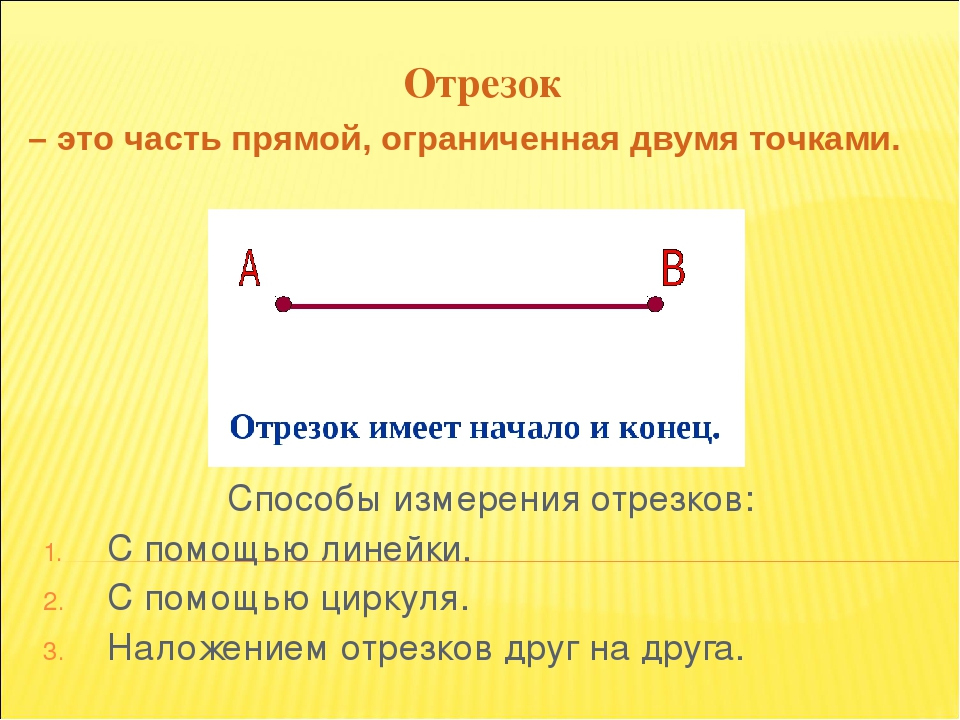
Метод заключается в следующем: совмещаются два отрезка друг с другом так, чтобы совпали их концы с одной стороны.
По расположению других концов относительно друг друга можно оценить какой из отрезков длиннее, а какой короче.
Если при наложении отрезков друг на друга длины отрезков совпадут, то отрезки равны (отрезки в этом случае будут равными фигурами).
Если при наложении отрезков друг на друга один из отрезков будет составлять часть второго, то первый отрезок является короче второго (т.е. длина первого меньше длины второго).
Пример: Даны два отрезка АВ и ОЕ
Совместим левый конец А отрезка АВ и левый конец О отрезка ОЕ.
Можно заметить, что отрезок ОЕ составляет часть отрезка АВ.
Значит, отрезок ОЕ короче отрезка АВ.
Данный метод удобен, если есть возможность перемещать отрезки, совмещать один с другим.
3. Сравнение отрезков с помощью измерителя.
Если нет возможности перемещать сравниваемые отрезки, то можно использовать промежуточный измеритель.
В математике для этих целей используют специальный чертежный инструмент, который называется циркулем.
Чтобы сравнить отрезки с помощью циркуля, необходимо совместить концы отрезка с ножками циркуля.
Не меняя раствор циркуля, приложить его ко второму отрезку и сравнить.
- Если ножки циркуля совпадают с концами сравниваемого отрезка, то отрезки считаются равными.
- Если отрезок выходит за пределы расставленных ножек циркуля, то он больше исходного отрезка.
- Если же отрезок находится между концами измерителя, то сравниваемый отрезок меньше исходного.
Если нет возможности сравнить отрезки наложением и нет циркуля под рукой, то в качестве измерителя можно использовать нитку.
В таком случае нужно нитку приложить к исходному отрезку, на нитке по отрезку сделать замер, затем нитку приложить ко второму отрезку, оценить расположение замера на нитке по отношению к исследуемому отрезку, сделать вывод.
Пример:
Пусть даны три отрезка СD, АЕ, BG
Сравним эти отрезки с помощью циркуля.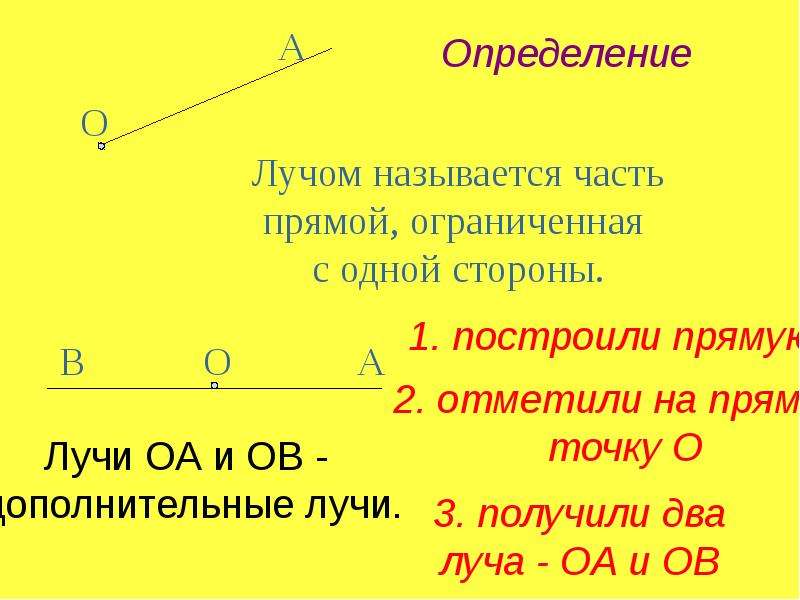
Соединим ножки циркуля с концами С и D отрезка СD.
Приложим циркуль с заданным раствором к отрезку АЕ.
Концы измерителя совпали с точками отрезка АЕ, значит, отрезки CD и AE равны: (CD = AE).
Приложим циркуль с заданным раствором к отрезку BG.
Отрезок выходит за концы измерителя, т.е. является частью отрезка BG, следовательно, отрезок BG длиннее отрезка СD: (BG > СD).
Все рассмотренные способы сравнения длины отрезков проводят без определения значения длины сравниваемых отрезков.
4. Существует еще один способ сравнения длины отрезков путем измерения их длинны.
Для этого необходимо сначала измерить длину каждого отрезка, далее сравнить полученные значения их длины и сделать вывод.
Большим будет являться тот отрезок, длина которого больше.
Соответственно, если длины измеряемых отрезков равны, то и отрезки равны.
У меня есть дополнительная информация к этой части урока!
ЗакрытьЛоманая линия
Если последовательно соединить отрезки так, чтобы конец одного отрезка являлся началом следующего (при этом соседние отрезки не лежат на одной прямой), то образуется геометрическая фигура, которая называется ломаной линией.
Отрезки, из которых состоит ломаная линия, называют звеньями.
Концы отрезков называют вершинами ломаной.
Самые крайние вершины ломаной называют концами ломаной
Обозначение ломаной линии составляют из названий вершин этой ломаной, называя их по порядку.
Длиной ломаной называется сумма длин всех ее звеньев.
Рассмотрим пример:
На рисунке изображена ломаная линия АBCDE.
Вершины ломаной АBCDE: А, B, C, D, Е.
Звенья ломаной АBCDE: AB, BC, CD, DE.
A и E — концы ломаной.
Найдем длину ломаной АВСDE:
АВСDE = AB+ BC+ CD+ DE = 2 см + 3 см + 4 см + 5 см = 14 см
Ломаная, концы которой совмещаются, называется замкнутой.
Многоугольником называется фигура, ограниченная замкнутой ломаной линией, звенья которой не пересекаются.
Отрезки (звенья) ломаной линии называют сторонами многоугольника.
Общие точки двух отрезков (сторон) многоугольника называют его вершинами.
Каждая пара сторон многоугольника, сходящиеся в одной точке, образуют углы многоугольника.
Количество сторон и количество углов в многоугольнике совпадают.
Вершины, стороны и углы многоугольника обозначаются аналогично ломаной линии.
Многоугольник принято обозначать и называть по его вершинам, начиная с любой вершины и называя их последовательно, в любом порядке.
Рассмотрим пример:
На рисунке изображен многоугольник АBCDEF.
Вершины многоугольника АBCDEF: А, B, C, D, Е, F.
Стороны многоугольника АBCDEF: AB, BC, CD, DE, EF, FA.
Любые многоугольники можно сравнить: два многоугольника называются равными, если они совпадают при наложении.
Зная длину каждой стороны многоугольника, можно найти периметр этого многоугольника.
Периметр многоугольника — это сумма длин всех сторон.
Периметр многоугольника принято обозначать заглавной латинской буквой Р
Найдем периметр многоугольника АBCDEF (изображенного на рисунке):
РАВСDEF = AB+ BC+ CD+ DE+ EF+ FA = 2 см + 3 см + 2 см + 2 см + 3 см + 2 см = 14 см.
Существует огромное множество различных видов многоугольников.
Обычно многоугольники различают по числу сторон и углов.
Например: пятиугольник имеет 5 углов и 5 сторон, шестиугольник — 6 углов и 6 сторон.
Многоугольник с наименьшим числом вершин, сторон и углов называют треугольником.
Треугольник — плоская геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, соединяющих эти точки.
Треугольник часто обозначают символом «Δ» и тремя заглавными латинскими буквами, которые обозначают его вершины.
Рассмотрим пример:
На рисунке изображен треугольник АBC (Δ АBC).
А, В, С — вершины треугольника АBC.
Отрезки AB, BC, АC— стороны треугольника АBC.
Периметр треугольника- это сумма длин трех его сторон.
Найдем периметр треугольника АBC (изображенного на рисунке):
РАВС = AB+ BC+ АС = 4 см + 6 см + 3 см = 13 см.
ЛУЧ — это… Что такое ЛУЧ?
луч — луч/ … Морфемно-орфографический словарь
Луч-5Б — Заказчик … Википедия
Луч-10 — Связать? Луч 10 мобильная симплексная ЧМ радиостанция УКВ диапазона радиотелефонного диспетчерского комплекса «Луч» производства ОАО «Завод ЭЛЕКТРОПРИБОР», г. Владимир, Россия. Сертификат: N ОС/1 РС 796. Радиостанция Луч 10М предназначена для… … Википедия
Владимир, Россия. Сертификат: N ОС/1 РС 796. Радиостанция Луч 10М предназначена для… … Википедия
ЛУЧ — муж. прямой путь невесомого вещества, от точки исхода до встречи им предмета; понятие отвлеченное, предполагающее, что вещества эти исходят в виде нитей или тонких струек; употр. б.ч. о свете, иногда о тепле и пр. Солнечный луч, исходящий от… … Толковый словарь Даля
луч — сущ., м., употр. часто Морфология: (нет) чего? луча, чему? лучу, (вижу) что? луч, чем? лучом, о чём? о луче; мн. что? лучи, (нет) чего? лучей, чему? лучам, (вижу) что? лучи, чем? лучами, о чём? о лучах 1. Лучом называют узкую полоску света,… … Толковый словарь Дмитриева
ЛУЧ — ЛУЧ, луча, муж. 1. Воспринимаемая глазом узкая полоса света, исходящая от какого нибудь светящегося предмета. Косые лучи заходящего солнца. Лучи восходящего солнца. Звездный луч. Сноп лучей. «Ночью в колыбель младенца месяц луч свой заронил.»… … Толковый словарь Ушакова
ЛУЧ — ЛУЧ, а, муж. 1. Узкая полоса света, исходящая от яркого светящегося предмета. Солнечный л. Л. прожектора. Л. надежды (перен.: проблеск надежды). Л. света в тёмном царстве (перен.: о чём н. радостном, светлом в тёмной, отсталой среде). 2.… … Толковый словарь Ожегова
1. Узкая полоса света, исходящая от яркого светящегося предмета. Солнечный л. Л. прожектора. Л. надежды (перен.: проблеск надежды). Л. света в тёмном царстве (перен.: о чём н. радостном, светлом в тёмной, отсталой среде). 2.… … Толковый словарь Ожегова
луч — См. малость, немного бросать лучи, обдавать лучами, обливать лучами… Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские словари, 1999. луч малость, немного; полупрямая; свч лучи, поток, лучик, гнюс,… … Словарь синонимов
Луч — (в многомерном пространстве) [ray] множество точек, удовлетворяющих условию x = λa при том, что произвольный множитель λ ≥ 0 и вектор a ≠ 0. При λ = 0 луч является полупрямой, исходящей из начала координат. Пример и рис. см. в статье… … Экономико-математический словарь
луч — падает • действие, субъект луч проникает • действие, субъект направить луч • перемещение / передача … Глагольной сочетаемости непредметных имён
ЛУЧ — (1) линия, вдоль которой распространяется энергия (см. ), испущенного в определённом направлении источником света или звука. Различают Л.: падающий, отражённый и преломлённый; (2) Л. необыкновенный один из двух поляризованных Л. (др. луч (см.)),… … Большая политехническая энциклопедия
), испущенного в определённом направлении источником света или звука. Различают Л.: падающий, отражённый и преломлённый; (2) Л. необыкновенный один из двух поляризованных Л. (др. луч (см.)),… … Большая политехническая энциклопедия
понятие, как начертить и обозначить, отличие от светового
Все мы когда-то изучали в школе геометрию, но далеко не каждый из нас вспомнит, что представляет собой отрезок. А уж тем более мало кто сможет объяснить понятие лучей, и как они обозначаются. Давайте постараемся в этой статье напомнить себе данные определения и рассмотрим их в математике. Также определим, что такое луч, и чем он отличается от светового. Если вникнуть, то понять будет несложно.…
Вконтакте
Google+
Мой мир
Определение понятий
Для начала давайте вспомним, что называется геометрией. Геометрия — это раздел математики, изучающий геометрические фигуры и их свойства. К ним относятся треугольник, квадрат, прямоугольник, параллелепипед, круг, овал, ромб, цилиндр и т. п. Простейшая фигура — это прямая. Она является бесконечной и не имеет начала. Две прямые пересекутся только в одной единственной точке. Через одну точку можно проводить бессчетное количество прямых линий. Каждая точка на линии делит ее на два.
п. Простейшая фигура — это прямая. Она является бесконечной и не имеет начала. Две прямые пересекутся только в одной единственной точке. Через одну точку можно проводить бессчетное количество прямых линий. Каждая точка на линии делит ее на два.
Это интересно: как обозначается площадь, примеры для вычисления.
Открытый луч
Он состоит из точек, расположенных по одну сторону. Все понятия данных подмножеств можно именовать таким образом. Луч обозначают одной строчной латинской буквой или двумя заглавными, когда одна точка — начало (например, О), а вторая лежит на нем (например, F, К и Е) .
В основе геометрической фигуры, имеющей углы, лежат полупрямые. Они начинаются в точке, где пересекаются, но второй стороной направлены в бесконечность. Начало делит прямую на 2 части. На письме его обычно именуют двумя заглавными (OF) или одной буквой латиницы (а, в, с). Если дана прямая, то записывается ОВ в закругленных скобках: (ОВ). Если же это отрезок — в квадратных скобках.
Если же это отрезок — в квадратных скобках.Таким образом, луч — это часть прямой. Через любую точку можно провести множество прямых, но через 2 несовпадающие — только одну. Последние могут быть взаимодействовать только в трех вариантах: пересекаться, скрещиваться, быть параллельными друг другу. Существуют линейные уравнения, которые задают прямую на плоскости.
Обозначения в геометрии
Вариантов для обозначения несколько:
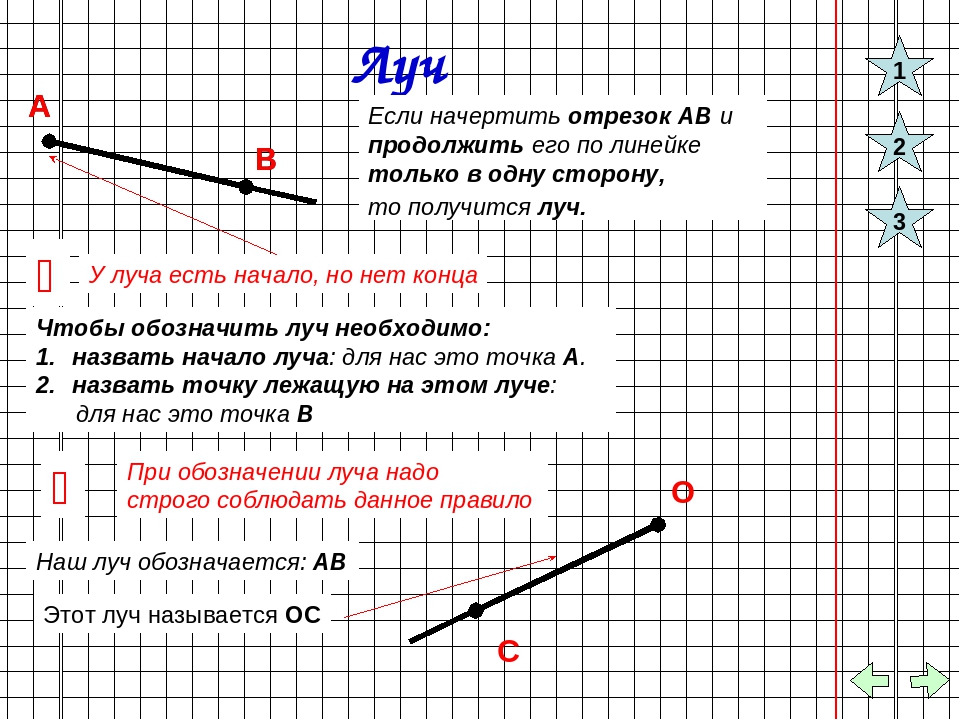
- Попробуйте провести на тетрадном листе линию. Представим, что у вас имеется полупрямая «О». Точка О — исходная, другой быть не может. Это самый распространенный способ.
- Данный метод более интересен: нашу полупрямую возможно назвать не одной буквой. К примеру, на одной линии может быть их две, где первая — начало (буква О), а вторая расположена на каком-то расстоянии. Представим, что на отрезке длиной 10 сантиметров начало названо буквой О, а на расстоянии четырех сантиметров от (О) находится вторая точка (В). Тогда его обозначают «ОВ».

- Третий способ — это когда О у нас располагается не в начале, а с каким-то отступом. Итак, снова начертите прямую с длиной десять сантиметров, отступите слева один сантиметр и отметьте начало. Снова назовите буквой О. В центре точку не ставьте, но обозначьте данную область буквой К. В этот раз буква О — это его начало. Название читается как «ОК»:
- Для начала начертим дополняющие лучи. Как мы уже разобрались, на прямой нужно поставить точку (называем ее О), она производная и разделяет ее на 2 линии, которые пересечься не могут.
- Перейдем к следующему этапу. Теперь нам нужно начертить продолжение — линию, имеющую общее начало с основополагающей, но не совпадающей с нею. А именно: дополняющая линия не является продолжением.
- Чтоб начертить продолжение, проведем из О прямую, которая не располагается на дополняющих, но имеет с ними одно начало. После того как начертили, отметим на новом луче точку В. ОВ теперь лежит на его продолжении из О.
Нужно знать: Что такое горизонталь и горизонтальное положение?
Отличие световых лучей от геометрических
В геометрии таковые понятия очень схожи.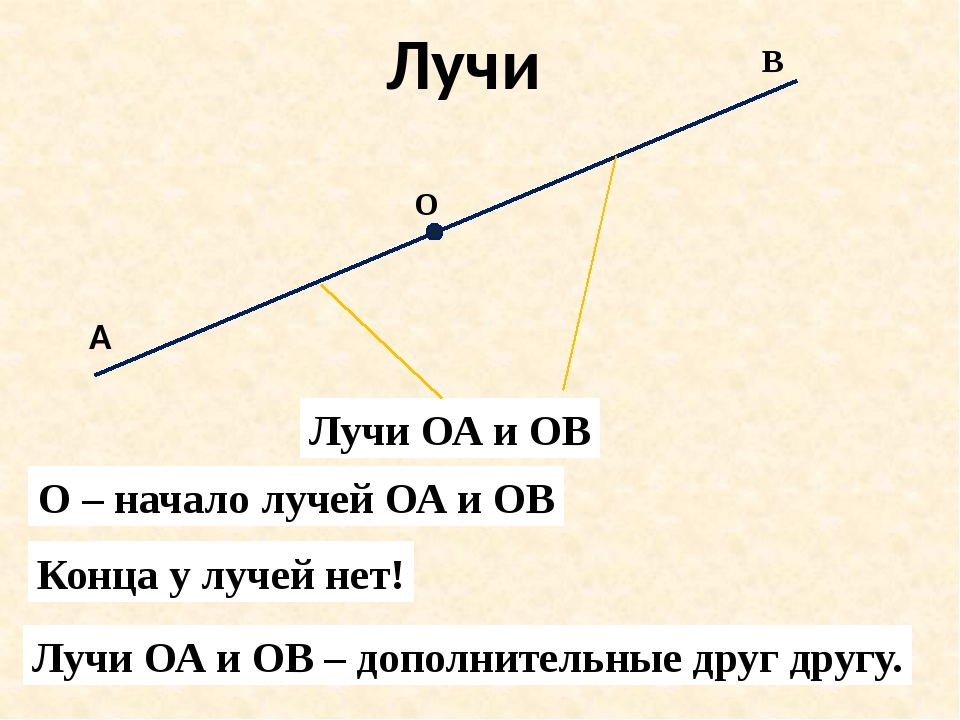 Луч — это линия, но она является энергией света. Другими словами — это небольшой пучок света. В оптике данное понятие, как и понятие прямой, в геометрии — базовое. У световых нет сконцентрированного направления, происходит дифракция. Но когда поток света очень сильный, расходимостью пренебрегают, и можно выделять четкое направление.
Луч — это линия, но она является энергией света. Другими словами — это небольшой пучок света. В оптике данное понятие, как и понятие прямой, в геометрии — базовое. У световых нет сконцентрированного направления, происходит дифракция. Но когда поток света очень сильный, расходимостью пренебрегают, и можно выделять четкое направление.
Что такое модуль числа в математике
Термин (module) в буквальном переводе с латинского означает «мера». Это понятие было введено в математику английским учёным Р. Котесом. А немецкий математик К. Вейерштрасс ввёл в обращение знак модуля — символ, которым это понятие обозначается при написании.…
Вконтакте
Google+
Мой мир
Впервые данное понятие изучается в математике по программе 6 класса средней школы. Согласно одному из определений, модуль — это абсолютное значение действительного числа. Другими словами, чтобы узнать модуль действительного числа, необходимо отбросить его знак.
Согласно одному из определений, модуль — это абсолютное значение действительного числа. Другими словами, чтобы узнать модуль действительного числа, необходимо отбросить его знак.
Графически абсолютное значение а обозначается как |a|.
Основная отличительная черта этого понятия заключается в том, что он всегда является неотрицательной величиной.
Числа, которые отличаются друг от друга только знаком, называются противоположными. Если значение положительное, то противоположное ему будет отрицательным, а ноль является противоположным самому себе.
Это интересно: умножение на 0 — правило для любого числа.
Геометрическое значение
Если рассматривать понятие модуля с позиций геометрии, то он будет обозначать расстояние, которое измеряется в единичных отрезках от начала координат до заданной точки. Это определение полностью раскрывает геометрический смысл изучаемого термина.
- Для примера можно взять координатную прямую и на ней нанести 2 произвольные точки.
 Допустим, одна из точек (А) будет иметь числовое значение 5, а вторая (В) — 6.
Допустим, одна из точек (А) будет иметь числовое значение 5, а вторая (В) — 6. - Если рассмотреть полученный чертёж, можно увидеть, что точка, А находится на расстоянии 5 единиц от нуля (начала координат). Точка В находится от нуля на 6 единиц. Таким образом, модулем точки, А будет число 5, а модулем точки В — число 6.
- В этом случае графическое обозначение выражения будет следующим: | 5 | = 5.
- Иными словами, если взять любое произвольное число и обозначить его на координатной прямой в виде точки А, то расстояние от нуля до этой точки и будет модулем числа А.
Графически это можно выразить следующим образом: |a| = OA.
Это интересно: признак перпендикулярности прямой и плоскости, теория и практика.
Свойства абсолютной величины
Ниже будут рассмотрены все математические свойства этого понятия и способы записи в виде буквенных выражений:
- Модулем любой цифры является величина неотрицательная. Таким образом, абсолютным значением положительной величины будет выступать она сама.
 Графически эта закономерность выражается следующим образом: |a| = a, если a> 0.
Графически эта закономерность выражается следующим образом: |a| = a, если a> 0. - Модули противоположных величин равны друг другу Это объясняется тем фактом, что на координатной прямой противоположные числа хотя и располагаются в разных точках, но находятся на одинаковом расстоянии от начальной точки отсчёта. Графически это выражается как: |а| = |-а|.
- Третьим свойством является то, что абсолютным значением нуля равняется сам нуль. Это условие считается верным в том случае, когда действительное число является нулем. Поскольку нулю соответствует начало отсчета в системе координат, то модулем числа ноль является сам ноль по определению. Графически: |0| = 0|.
- Еще одним важным свойством является то, что абсолютное значение произведений двух любых действительных чисел равняется произведению двух этих величин. Это условие необходимо рассмотреть более подробно. Иначе говоря, абсолютным значением произведения величин, А и В будет АВ в случае если оба этих значения положительные или же оба отрицательные, или -АВ при условии, что одно из этих чисел будет отрицательным.
 В записи эта закономерность будет выглядеть следующим образом: |А*В| = |А| * |В|.
В записи эта закономерность будет выглядеть следующим образом: |А*В| = |А| * |В|. - Абсолютная величина суммы любых двух действительных чисел меньше или равна сумме их модулей.
- Абсолютная величина разности двух произвольных величин меньше или равна разности двух абсолютных величин.
- Если в математическом выражении имеется постоянный положительный множитель, его можно выносить за знак | |.
- Такое же правило распространяется и на показатель степени выражения.
Это интересно: что такое разность в математике?
Особенности решения уравнений с модулем
Если говорить о решении математических уравнений и неравенств, в которых содержится module, то необходимо помнить, что для их решения потребуется открыть этот знак.К примеру, если знак абсолютной величины содержит в себе некоторое математическое выражение, то перед тем как раскрыть модуль, необходимо учитывать действующие математические определения.
|А + 5| = А + 5, если, А больше или равняется нулю.
5-А, если, А значение меньше нуля.
В некоторых случаях знак может раскрываться однозначно при любых значениях переменной.
Рассмотрим ещё одни пример. Построим координатную прямую, на которой отметим все числовые значения абсолютной величиной которых будет 5.
Для начала необходимо начертить координатную прямую, обозначить на ней начало координат и задать размер единичного отрезка. Кроме того, прямая должна иметь направление. Теперь на этой прямой необходимо нанести разметки, которые будут равны величине единичного отрезка.
Таким образом, мы можем увидеть, что на этой координатной прямой будут две интересующие нас точки со значениями 5 и -5.
Видео: Модуль числа. Математика 6 класс.
Основные математические определения
| На этой странице мы собрали несколько основных определений. Для получения дополнительных определений, объяснений и т. Д. Воспользуйтесь поиском выше. |
| Или найдите свое слово в: |
| Иллюстрированный математический словарь |
Основные операции
В базовой математике есть много способов сказать то же самое:
Символ | Используемых слов |
|---|---|
+ | Сложение, Сложение, Сумма, Плюс, Увеличение, Итого |
— | Вычитание, Вычитание, Минус, Меньше, Разница, Уменьшение, Убрать, Вычесть |
× | Умножение, умножение, произведение, на, раз, партии по |
÷ | Division, Divide, Quotient, Goes Into, сколько раз |
Дополнение есть…
… объединение двух или более чисел (или вещей) для получения нового результата.
Суммируемые числа называются « добавления »:
Вычитание …
… отбирая один номер у другого.
Minuend — Subtrahend = Разница
Minuend : число, из которого нужно вычесть.
Subtrahend : число, которое нужно вычесть.
Разница : результат вычитания одного числа из другого.
Умножение …
… (в простейшем виде) повторное сложение .
Здесь мы видим, что 6 + 6 + 6 (три шестерки) составляют 18:
Можно также сказать, что 3 + 3 + 3 + 3 + 3 + 3 (шесть троек) составляют 18
Но мы также можем умножать на дроби или десятичные дроби, что выходит за рамки простой идеи повторного сложения:
Пример: 3.5 × 5 = 17,5
, что составляет 3,5 лота из 5 или 5 лотов из 3,5
Подразделение…
… разделение на равные части или группы. Это результат «честного обмена».
УDivision есть свои особые слова, которые нужно запомнить.
Давайте возьмем простой вопрос: 22 разделить на 5 . Ответ: 4 , осталось 2 .
Здесь мы видим важные слова:
Что также может быть в такой форме:
Дробь есть…
… часть целого.
Верхняя часть (числитель) говорит , сколько деталей у нас .
В нижней части (знаменатель) указано , на сколько частей целое делится на .
Подробнее см. Дроби.
Десятичное число …
… число который содержит десятичную точку.
Подробнее см. Десятичные дроби.
Процент есть…
… частей на 100. Символ%
Пример: 25% означает 25 на 100 (25% этого поля — зеленое)
Подробнее см. В разделе «Проценты».
Среднее (Среднее) составляет …
… сумма , деленная на количество .
Мы вычисляем среднее значение на , складывая все значения , затем делим на , сколько значений .
Пример: какое среднее значение для 9, 2, 12 и 5?
Сложите все значения: 9 + 2 + 12 + 5 = 28
Разделите на сколько значений (их четыре): 28 ÷ 4 = 7
Таким образом, среднее значение составляет 7
Подробнее см. Среднее значение.
Исчерпывающий список математических символов и их значений
Вам трудно вспомнить точное значение обозначения при решении математических уравнений? Не волнуйтесь, ScienceStruck здесь, чтобы помочь вам. Вот список математических символов и их значения для справки.
Знаете ли вы?
Первыми математическими символами, которые были использованы, были шифры. Они были введены еще до того, как была введена письменность.
Хотите написать для нас? Что ж, мы ищем хороших писателей, которые хотят распространять информацию. Свяжитесь с нами, и мы поговорим …
Давайте работать вместе!
Математика или математика считаются языком науки, жизненно важным для понимания и объяснения естественных явлений и явлений. Это также один из самых страшных предметов для большинства студентов во всем мире. Произнесите слово математика, и даже взрослые, как известно, вздрагивают при одном упоминании этого слова! Мы не будем углубляться в причины этого, но разнообразие символов, используемых в уравнениях, также добавляет страха.В каждом разделе математики есть свои особые символы, которые представляют определенное понятие. Таким образом, вам необходимо иметь хотя бы готовый список ссылок на эти соглашения, чтобы вы не перепутали одно с другим.
Мы составили сводный список всех символов, используемых в различных областях математики. Итак, в следующий раз, когда вы попытаетесь решить какую-либо математическую задачу, вы по крайней мере будете знать, что означают обозначения!
Основные символы
плюс
Означает сложение значений.
минус
Он символизирует вычитание значений.
Умножение
Означает умножение значений.
Дивизион
Обозначает разделение ценностей.
равно
Означает, что две стороны равны.
Не равно
Обозначает, что две стороны неравны.
Больше
Хотите написать для нас? Что ж, мы ищем хороших писателей, которые хотят распространять информацию. Свяжитесь с нами, и мы поговорим …
Давайте работать вместе!
Показывает, что одно значение больше другого.
Менее
Это означает, что одно значение меньше другого.
Больше или равно
Обозначает, что одно значение больше или равно другому.
Меньше или равно
Указывает, что одно значение меньше или равно другому.
по модулю
Означает нахождение остатка от деления двух чисел.
Плюс — минус / Минус — плюс
Обозначает, что значение может быть как плюсовым, так и минусовым.
Круглые скобки
Подразумевает, что вычисление уравнения внутри него должно быть выполнено в первую очередь.
Кронштейны
[]
Указывает, что вычисление уравнения внутри него должно быть выполнено в первую очередь.
Показатель
Обозначает, сколько раз число использовалось при умножении.
квадратный корень
Он символизирует значение, которое можно умножить само на себя, чтобы получить исходное число.
Кубический корень
Дает значение, которое можно умножить само на себя три раза, чтобы получить исходное число.
Корень четвертой степени
Это значение, которое можно умножить само на себя четыре раза, чтобы получить исходное число.
Корень N (корень)
Показывает значение, которое можно умножить само на себя n раз, чтобы получить исходное число.
процентов
Означает соотношение, выраженное в долях от 100.
промилле
Он символизирует количество частей на тысячу.
На миллион
Указывает количество частей на миллион.
На миллиард
Означает количество частей на миллиард.
Пер-триллион
Он символизирует количество частей на триллион.
Геометрические символы
Угол
Обозначает фигуру, образованную двумя лучами.
Измеренный угол
Обозначает угол, значение которого известно.
Угол прямой
Указывает угол, который делит пополам угол, образованный двумя прямыми линиями.
Сферический угол
Он символизирует угол между двумя пересекающимися дугами сферы.
угловых минут
Дает угловое измерение, равное 1/60 одного градуса.
градусов
Указывает на измерение плоского угла, представляющего один полный оборот.
секунд дуги
Обозначает угловое измерение, равное 1/60 одной угловой минуты.
Строка
Показывает прямую линию с незначительной шириной и толщиной.
Линейный сегмент
Обозначает часть строки с определенными начальной и конечной точками.
Луч
Указывает линию с начальной точкой, но без конечной точки.
Арка
Обозначает часть окружности круга или кривой.
Перпендикуляр
Обозначает линии, расположенные под прямым углом друг к другу.
Конгруэнт
Символизирует предметы схожей геометрической формы и размера.
Параллельный
Обозначает линии, которые находятся на одинаковом расстоянии друг от друга.
Сходство
Обозначает объекты схожей формы, но не одинакового размера.
Треугольник
Обозначает полигон с тремя вершинами и тремя отрезками в качестве ребер.
Расстояние
Он символизирует расстояние между точками x и y.
Грады
Он обозначает единицу измерения плоского угла и равен 1/400 1 оборота (360 градусов).
Пи
Дает отношение длины окружности к диаметру круга.
Рад
Обозначает единицу измерения угла.
Алгебраные символы
Эквивалентность
Указывает переменные, имеющие одинаковое или идентичное значение.
X переменная
Обозначает неизвестное значение.
Он по определению символизирует равенство.
Указывает переменные, которые равны по определению.
Пропорциональный
Обозначает изменения в переменных, которые всегда связаны друг с другом, с использованием константы.
Приближение
Он символизирует переменные, которые приблизительно равны друг другу.
Слабое приближение
Обозначает переменные, которые слабо похожи друг на друга.
Факториал
Означает произведение всех целых чисел, меньших или равных n.
Лемниската / символ бесконечности
Указывает на переменную без ограничений.
Намного больше, чем
Указывает, что одна переменная намного больше другой.
Намного меньше, чем
Он обозначает, что одна переменная намного меньше другой.
Кронштейн потолочный
Указывает на округление значения переменной до большего целого числа.
Напольные кронштейны
Относится к округлению значения переменной до меньшего целого числа.
Функция
Он определяет одну переменную по отношению к другой.
Абсолютное значение
Выдает неотрицательное значение x, игнорируя его знак.
Заглавная пи
Дает произведение всех значений в указанном диапазоне.
Закрытый интервал
Дает интервал с указанными конечными точками.
Функциональный состав
Он объединяет функции таким образом, что выход из функции становится входом для другой функции.
Открытый интервал
Означает, что интервал не имеет границ, то есть без каких-либо конечных точек.
Дельта
Это относится к изменению или разнице в ценностях.
Дискриминант
Дает природу корней квадратного уравнения.
Сигма (суммирование)
Это относится к суммированию всех значений в указанном диапазоне.
Двойное суммирование
Означает суммирование значений в двух диапазонах.
Константа Эйлера-Маскерони
Константа равна 0.527721566…
Константа Е / число Эйлера
Его значение равно 2,718281828…
Константа золотого сечения
Указывает, что отношение двух переменных должно быть равно отношению их суммы к большей из двух переменных.
Символы линейной алгебры
Перекрестное произведение (вектор)
Это относится к умножению величин векторов и угла между ними.
Точечное произведение (скалярное)
Означает умножение абсолютных величин векторов на косинус угла между ними.
Кронштейны
Указывает прямоугольный массив чисел, упорядоченный по строкам и столбцам.
Определитель
Дает значение, связанное с квадратной матрицей.
Норма
Он присваивает положительную длину (размер) каждому ненулевому вектору в пространстве.
Обратная матрица
Он символизирует матрицу, умножение которой на исходную матрицу является идентичной матрицей.
транспонировать
Это относится к матрице, образованной заменой строк данной матрицы столбцами и наоборот.
Эрмитова матрица
Это означает матрицу с комплексными элементами, в которой i-я строка и j-й столбец равны комплексному сопряжению j-й строки и i-го столбца.
Размер
Дает количество строк и столбцов матрицы, записанное как строки x столбцы.
Матрица, ранг
Указывает количество ненулевых строк (или столбцов) в сокращенной матрице.
Символы вероятности и статистики
Вероятностная функция
Означает вероятность наступления события A.
Плотность вероятности
f (x)
Интеграл функции непрерывной случайной величины дает вероятность того, что значение переменной находится в заданном интервале.
Перекресток
Обозначает вероятность наступления событий A и B.
Союз
Обозначает вероятность наступления событий A или B.
Функция условной вероятности
Обозначает вероятность возникновения события A, когда событие B произошло.
Кумулятивная функция распределения
Обозначает вероятность того, что случайная величина X примет значения, меньшие или равные x.
Ожидаемое значение
Обозначает ожидаемое значение случайной величины X.
Среднее по совокупности
Обозначает среднее арифметическое значение совокупности с учетом каждого члена совокупности.
Разница
Он выражает разброс чисел данного набора.
Условное ожидание
Обозначает ожидаемое значение случайной величины X, когда задана переменная Y.
Стандартное отклонение
Обозначает отклонение от существующего среднего значения.
Стандартный балл
Указывает количество стандартных отклонений переменной от среднего.
Ковариация
Он измеряет, насколько две случайные величины, X и Y, изменяются вместе.
Медиана
Обозначает среднее значение случайной величины X.
Корреляция
Обозначает статистическую взаимосвязь между двумя случайными величинами X и Y.
Режим
Обозначает наиболее часто встречающееся значение в данном наборе.
Средний
Означает среднее арифметическое между максимальным и минимальным значением набора.
Медиана выборки
Обозначает среднее значение всех значений данного набора.
Нижний / первый квартиль
Обозначает 25-й процентиль данного набора данных.
Медиана / второй квартиль
Обозначает медиану данного набора.
Верхний / третий квартиль
Обозначает 75-й процентиль данного набора данных.
Среднее значение
Обозначает среднее значение данных набора, то есть сумму данных набора, деленную на количество записей в наборе.
Стандартное отклонение выборки
Указывает стандартное отклонение набора данных в выбранном размере выборки.
Вариация выборки
Указывает на дисперсию набора данных в выбранном размере выборки.
Распределение Бернулли
Он обозначает теоретическое распределение количества успехов в конечном наборе данных с постоянной вероятностью успеха.
Распределение x
Указывает на распределение случайной величины X.
Равномерное распределение
Указывает вероятность того, что каждое значение в данном наборе данных имеет одинаковую длину интервала в заданном диапазоне от a до b.
Нормальное (гауссово) распределение
Указывает вероятность того, что наблюдение окажется между двумя действительными числами.
Экспоненциальное распределение
Обозначает распределение вероятностей, которое описывает время между непрерывно происходящими событиями с постоянной средней скоростью.
Гамма-распределение
Обозначает непрерывное двухпараметрическое распределение, из которого выводятся распределения хи-квадрат и экспоненциальные распределения.
Распределение хи-квадрат
Обозначает распределение суммы квадратов k независимой стандартной нормальной случайной величины.
F распределение
Обозначает функцию распределения вероятностей, которая представляет собой отношение двух независимых случайных величин, каждая из которых имеет распределение хи-квадрат и делится на количество степеней свободы (k).
Биномиальное распределение
Он обозначает дискретное распределение вероятностей количества успехов в n экспериментах, где каждый успех определяется вероятностью p.
Геометрическое распределение
Означает отрицательное биномиальное распределение, которое используется для определения количества неудач до единичного успеха.
Гипергеометрическое распределение
Используется для расчета случайного выбора переменной без повторения.
Комбинаторика
Комбинация
Указывает на возможное расположение вещей без определенного порядка.
Перестановка
Обозначает возможное расположение вещей в определенном порядке.
Теория множеств
Что такое финансовая математика | Финансовая математика
Финансовая математика — это применение математических методов к финансовым проблемам. (Иногда используются эквивалентные названия: количественные финансы, финансовый инжиниринг, математические финансы и вычислительные финансы.) Он основан на инструментах вероятности, статистики, стохастических процессов и экономической теории. Традиционно инвестиционные банки, коммерческие банки, хедж-фонды, страховые компании, корпоративные казначейства и регулирующие органы применяют методы финансовой математики для решения таких задач, как оценка производных ценных бумаг, структурирование портфеля, управление рисками и моделирование сценариев.Отрасли, которые зависят от сырьевых товаров (например, энергетика, производство), также используют финансовую математику. Количественный анализ повысил эффективность и строгость финансовых рынков и инвестиционного процесса и приобретает все большее значение при решении нормативных вопросов.
Количественное финансирование как подраздел экономики занимается оценкой активов и финансовых инструментов, а также распределением ресурсов. Многовековой опыт позволил сформировать фундаментальные теории о том, как функционирует экономика и как мы оцениваем активы.Модели описывают отношения между фундаментальными переменными, такими как цены на активы, движения рынка и процентные ставки. Эти математические инструменты позволяют нам делать выводы, которые иначе трудно найти или которые не сразу очевидны из интуиции. Примером применения моделей является стресс-тестирование банков. В частности, с помощью современных вычислительных методов мы можем хранить огромные объемы данных и моделировать множество переменных одновременно, что дает возможность моделировать довольно большие и сложные системы.Таким образом, методы научных вычислений, такие как численный анализ, моделирование Монте-Карло и оптимизация, являются важной частью финансовой математики.
Большая часть любой науки — это способность создавать проверяемые гипотезы, основанные на фундаментальном понимании объектов исследования, и доказывать или опровергать гипотезы посредством повторяемых исследований. В этом свете математика является языком представления теорий и предоставляет инструменты для проверки их достоверности. Например, в теории ценообразования опционов Блэка, Шоулза и Мертона представлена модель движения цен акций, и в сочетании с теорией, которая утверждает, что безрисковые инвестиции получат безрисковую норму прибыли, т.
 Луч
Луч
 Допустим, одна из точек (А) будет иметь числовое значение 5, а вторая (В) — 6.
Допустим, одна из точек (А) будет иметь числовое значение 5, а вторая (В) — 6. Графически эта закономерность выражается следующим образом: |a| = a, если a> 0.
Графически эта закономерность выражается следующим образом: |a| = a, если a> 0.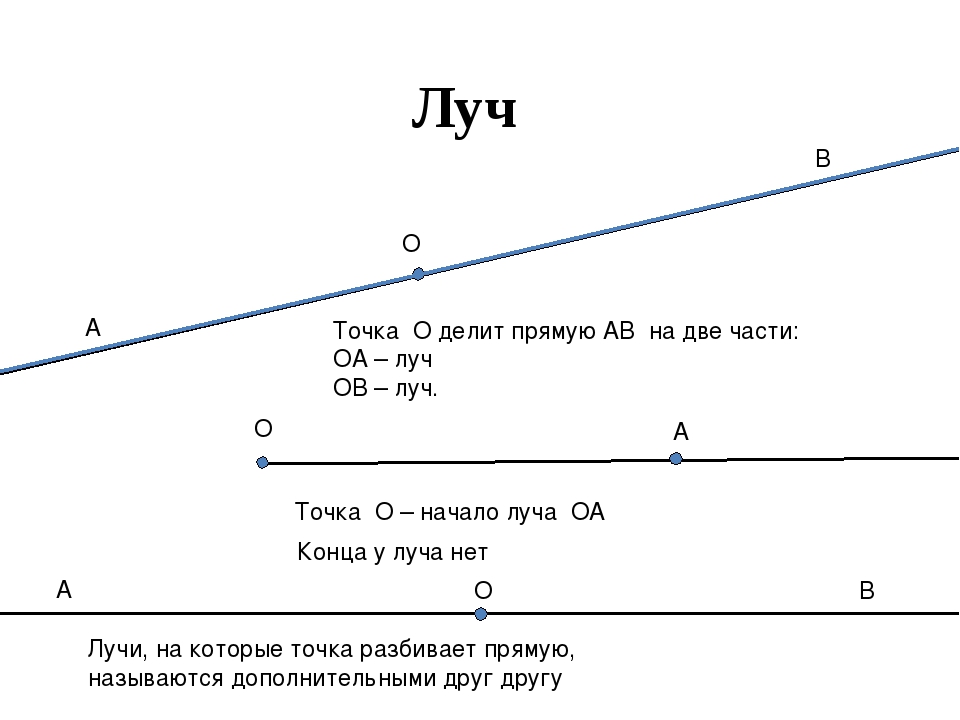 В записи эта закономерность будет выглядеть следующим образом: |А*В| = |А| * |В|.
В записи эта закономерность будет выглядеть следующим образом: |А*В| = |А| * |В|.