Урок математики. Тема: «Ось симметрии»

Цели:

• образовательные:
  • дать представление о симметрии;
  • познакомить с основными видами симметрии на плоскости и в пространстве;
  • выработать прочные навыки построения симметричных фигур;
  • расширить представления об известных фигурах, познакомив со свойствами, связанных с симметрией;
  • показать возможности использования симметрии при решении различных задач;
  • закрепить полученные знания;
• общеучебные:
  • научить настраивать себя на работу;
  • научить вести контроль за собой и соседом по парте;
  • научить оценивать себя и соседа по парте;
• развивающие:
  • активизировать самостоятельную деятельность;
  • развивать познавательную деятельность;
  • учить обобщать и систематизировать полученную информацию;
• воспитательные:
  • воспитываать у учащихся “чувство плеча”;
  • воспитывать коммуникативность;
  • прививать культуру общения.

ХОД УРОКА

Перед каждым лежат ножницы и лист бумаги.

Задание 1 (3 мин).

 

– Возьмем лист бумаги, сложим его попалам и вырежем какую-нибудь фигурку. Теперь развернем лист и посмотрим на линию сгиба.

Вопрос: Какую функцию выполняет эта линия?

Предполагаемый ответ: Эта линия делит фигуру пополам.

Вопрос: Как расположены все точки фигуры на двух получившихся половинках?

Предполагаемый ответ: Все точки половинок находятся на равном расстоянии от линии сгиба и на одном уровне.

– Значит, линия сгиба делит фигурку пополам так, что 1 половинка является копией 2 половинки, т.е. эта линия непростая, она обладает замечательным свойством (все точки относительно ее находятся на одинаковом расстоянии), эта линия – ось симметрии.

Задание 2 (2 мин).

– Вырезать снежинку, найти ось симметрии, охарактеризовать ее.

Задание 3 (5 мин).

– Начертить в тетради окружность.

Что такое ось симметрии 🚩 как нарисовать осевую симметрию 🚩 Математика

В широком смысле симметрией именуется сохранение чего-либо неизменным при каких-то преобразованиях. Обладают таким свойством и некоторые геометрические фигуры.

Применительно к геометрической фигуре симметрия означает, что если данную фигуру преобразовать – например, повернуть – некоторые ее свойства останутся прежними.

Возможность таких преобразований различается от фигуры к фигуре. Например, круг можно сколько угодно вращать вокруг точки, расположенной в его центре, он так и останется кругом, ничто для него не изменится.

Понятие симметрии можно объяснить, не прибегая к вращению. Достаточно провести через центр круга прямую и построить в любом месте фигуры перпендикулярный ей отрезок, соединяющий две точки на окружности. Точка пересечения с прямой будет делить данный отрезок на две части, которые будут равны друг другу.

Иными словами, прямая разделила фигуру на две равные части. Точки частей фигуры, расположенные на прямых, перпендикулярных данной, находятся на равном расстоянии от нее. Вот эта пряма и будет называться осью симметрии. Симметрия такого рода – относительно прямой – называется осевой симметрией.

У разных фигур количество осей симметрии будет различным. Например, у круга и шара таких осей множество. У равностороннего треугольника осью симметрии будет перпендикуляр, опущенный на каждую из сторон, следовательно, у него три оси. У квадрата и прямоугольника можно провести четыре оси симметрии. Две из них перпендикулярны сторонам четырехугольников, а две другие являются диагоналями. А вот у равнобедренного треугольника ось симметрии только одна, располагающаяся меду равными его сторонами.

Осевая симметрия встречается и в природе. Ее можно наблюдать в двух вариантах.

Первый вид – радиальная симметрия, предполагающая наличие нескольких осей. Она характерна, например, для морских звезд. Более высокоразвитым организмам присуща билатеральная, или двусторонняя симметрия с единственной осью, делящей тело на две части.

Человеческому телу тоже присуща билатеральная симметрия, но идеальной ее назвать нельзя. Симметрично расположены ноги, руки, глаза, легкие, но не сердце, печень или селезенка. Отклонения от билатеральной симметрии заметны даже внешне. Например, крайне редко бывает так, чтобы у человека на обеих щеках были одинаковые родинки.

Сколько осей симметрии имеет квадрат?

Считать квадрат частным случаем трапеции нельзя по определению:

Поскольку у квадрата противоположные стороны попарно-параллельны, то эта фигура не подходит под определение трапеции, у которой только две стороны параллельны, а две другие — нет. Эта не параллельность боковых сторон для трапеции является обязательной!

Также трапецию нельзя считать ни частным случаем ромба, ни параллелограмма, ни прямоугольника.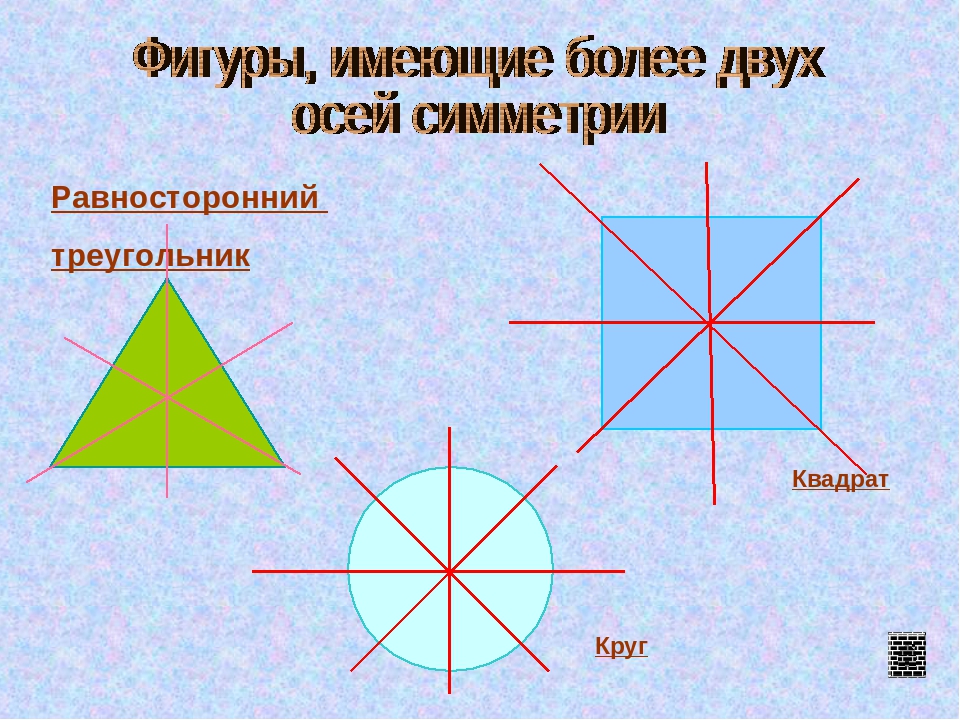

7 месяцев назад

Если окружность вписана в квадрат, то диаметр этой окружности будет равен стороне квадрата, следовательно, длина окружности равна:

L=Пи*D

, где L — длина окружности, а D — размер стороны описанного квадрата (равный диаметру окружности)

7 месяцев назад

Нет ромб не является квадратом,так как квадрат — это квадрат.Он имеет 4 равных угла,чего совсем не скажешь о ромбе.Да,у него есть тоже четыре угла,но какие? Две пары углов с разными градусами.Он играет свою роль в геометрии и не только,а квадрат — свою.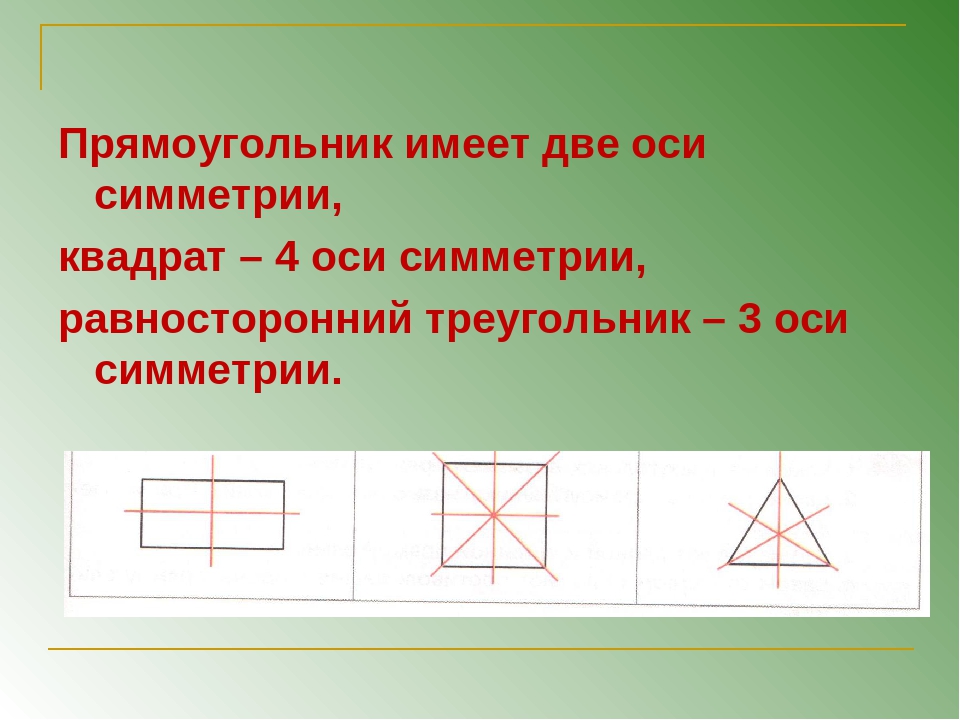 Даже если говорить к примеру о другой сфере его применения,как,если именно эти фигуры соотнести с человеческой натурой.к этому относятся — квадрат,круг,треугол­ьник.Как видите ромба здесь даже нет.Ромб играет свою роль,но в других человеческих технологиях.

7 месяцев назад

Магию геометрии вы можете познать если занимаетесь проектированием или ходя бы моделированием конструкций, элементов, деталей или проектированием. Вот там это четко видно: их свойства, качества, результативные навыки. Я работаю преподавателем строительных дисциплин сравнительно не давно, но узнавая данные характеристики и привнося их в примеры быта и окружающих конструкции студентам становится очень интересно.

8 месяцев назад

1. 2.

7 месяцев назад

Порядок симметрии вращения окружности

Порядок вращательной симметрии круга: сколько раз круг подходит к самому себе за полный оборот на 360 градусов.

Окружность имеет бесконечный «порядок вращательной симметрии».

Говоря упрощенно, круг всегда вписывается в исходный контур, независимо от того, сколько раз он поворачивается.

Следовательно,

Окружность имеет бесконечный порядок симметрии вращения

Порядок вращательной симметрии — еще несколько примеров

Пример 1:

Каков порядок симметрии вращения равностороннего треугольника?

Решение:

Как объясняется в определении, мы должны проверить, сколько раз равносторонний треугольник подходит к самому себе за полный оборот на 360 градусов.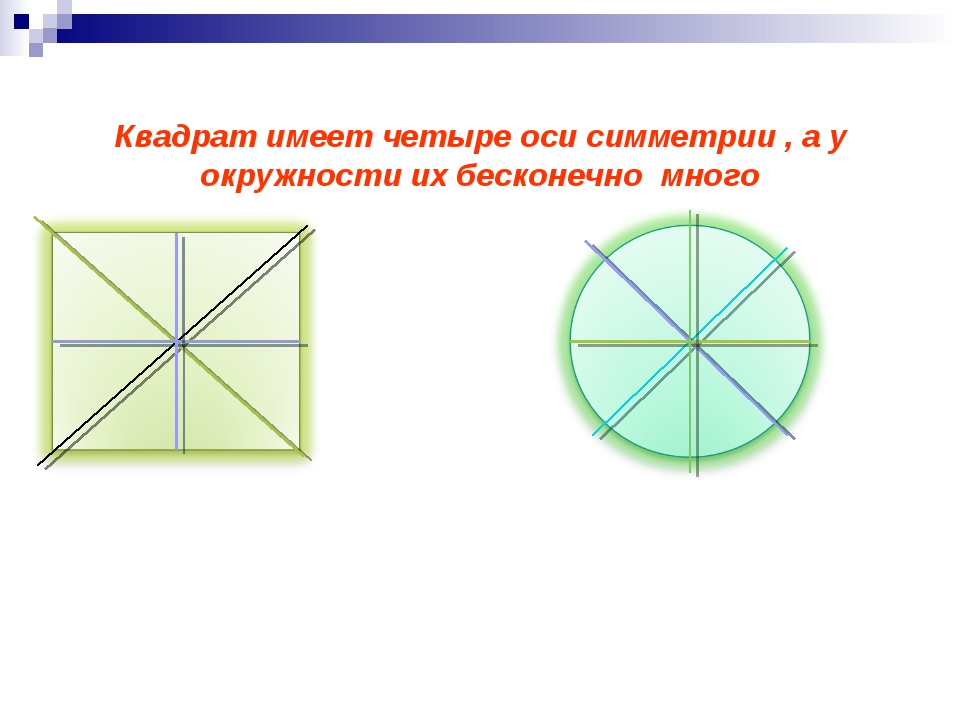

Посмотрите на изображения равностороннего треугольника в порядке A, B и C. A — исходное изображение. Изображения B и C создаются путем поворота исходного изображения A.

Когда мы смотрим на вышеприведенные изображения равностороннего треугольника, он подходит к самому себе 3 раза за полный оборот на 360 градусов.

Итак, равносторонний треугольник имеет вращательную симметрию порядка 3.

Пример 2:

Каков порядок вращательной симметрии квадрата?

Решение:

Посмотрите на изображения квадрата в порядке A, B, C, D и E.А — исходное изображение. Изображения B, C, D и E генерируются путем поворота исходного изображения A.

Когда мы смотрим на изображения квадрата выше, он умещается на себе 4 раза за полный оборот на 360 градусов.

Итак, квадрат имеет вращательную симметрию порядка 4.

Пример 3:

Каков порядок вращательной симметрии правильного пятиугольника?

Решение:

Пожалуйста, посмотрите на изображения правильного пятиугольника в порядке A, B, C, D, E и F. А — исходное изображение. Изображения B, C, D, E и F создаются путем поворота исходного изображения A.

Когда мы смотрим на приведенные выше изображения правильного пятиугольника, он подходит к самому себе 5 раз за полный оборот на 360 градусов.

Итак, правильный пятиугольник имеет вращательную симметрию пятого порядка.

Пример 4:

Каков порядок вращательной симметрии параллелограмма?

Решение:

Посмотрите изображения параллелограмма в порядке A, B и C.А — исходное изображение. Изображения B и C создаются путем поворота исходного изображения A.

Когда мы смотрим на приведенные выше изображения параллелограмма, он подходит к себе 2 раза за полный оборот на 360 градусов.

Итак, параллелограмм имеет вращательную симметрию порядка 2.

Пример 5:

Каков порядок вращательной симметрии равнобедренного треугольника?

Решение:

Посмотрите изображения равнобедренного треугольника в порядке A и B.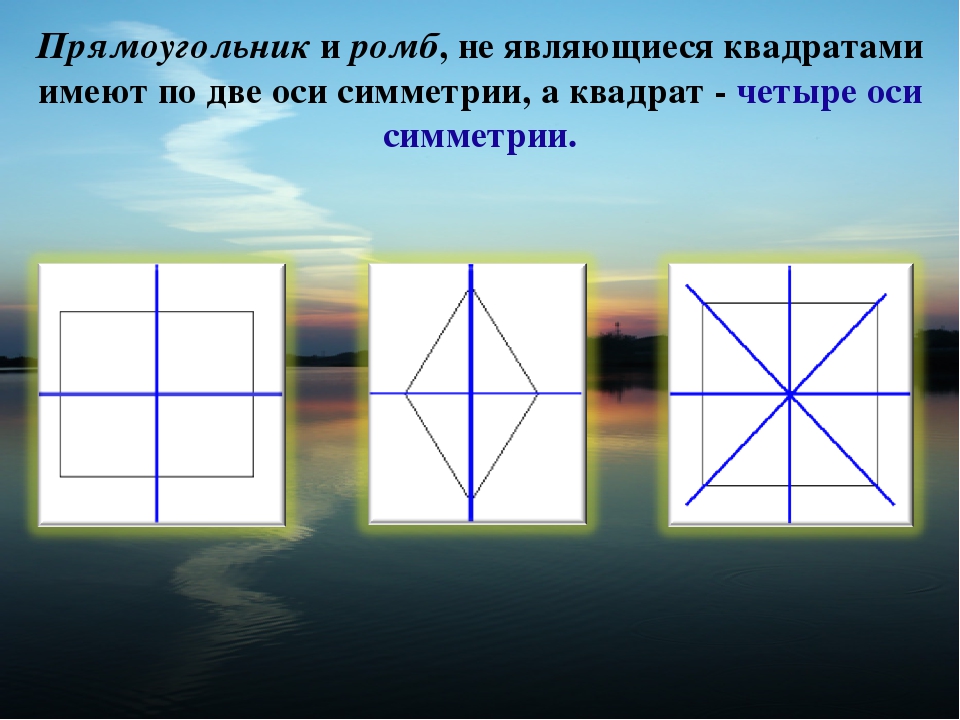 А — исходное изображение. Изображение B создается путем поворота исходного изображения A.

Когда мы смотрим на приведенные выше изображения равнобедренного треугольника, он ложится на себя 1 раз за полный оборот на 360 градусов.

Итак, равнобедренный треугольник имеет вращательную симметрию порядка 1.

Пример 6:

Каков порядок вращательной симметрии разностороннего треугольника?

Решение:

Посмотрите изображения разностороннего треугольника в порядке A и B.А — исходное изображение. Изображение B создается путем поворота исходного изображения A.

Когда мы смотрим на приведенные выше изображения равнобедренного треугольника, он ложится на себя 1 раз за полный оборот на 360 градусов.

Итак, разносторонний треугольник имеет вращательную симметрию порядка 1.

Пример 7:

Каков порядок вращательной симметрии трапеции?

Решение:

Посмотрите изображения трапеции в порядке A и B.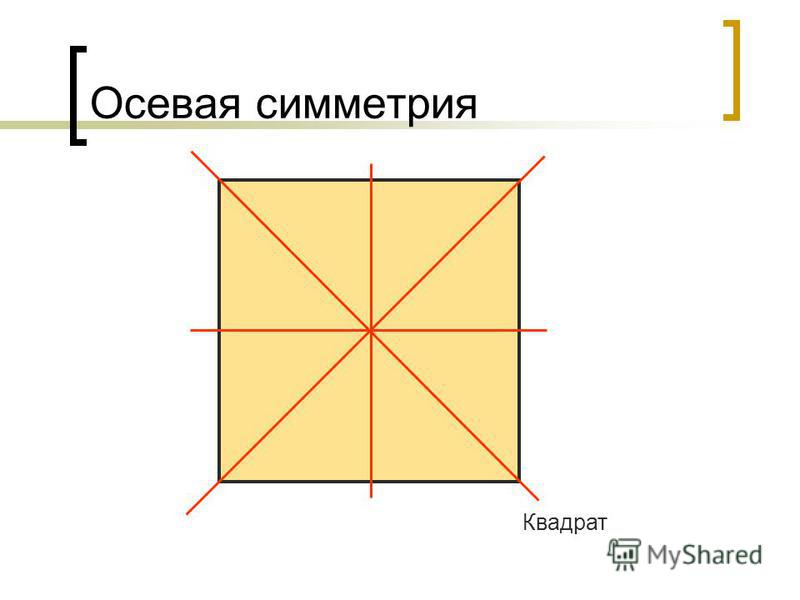 А — исходное изображение. Изображение B создается путем поворота исходного изображения A.

Когда мы смотрим на вышеприведенные изображения трапеции, она ложится на себя 1 раз за полный оборот на 360 градусов.

Итак, трапеция имеет вращательную симметрию порядка 1.

Пример 8:

Каков порядок вращательной симметрии равнобедренной трапеции?

Решение:

Посмотрите изображения равнобедренной трапеции в порядке A и B.А — исходное изображение. Изображение B создается путем поворота исходного изображения A.

Когда мы смотрим на вышеприведенные изображения равнобедренной трапеции, она ложится на себя 1 раз за полный оборот на 360 градусов.

Итак, равнобедренная трапеция имеет вращательную симметрию порядка 1.

Пример 9:

Каков порядок вращательной симметрии воздушного змея?

Решение:

Пожалуйста, посмотрите изображения кайта в порядке A и B.А — исходное изображение.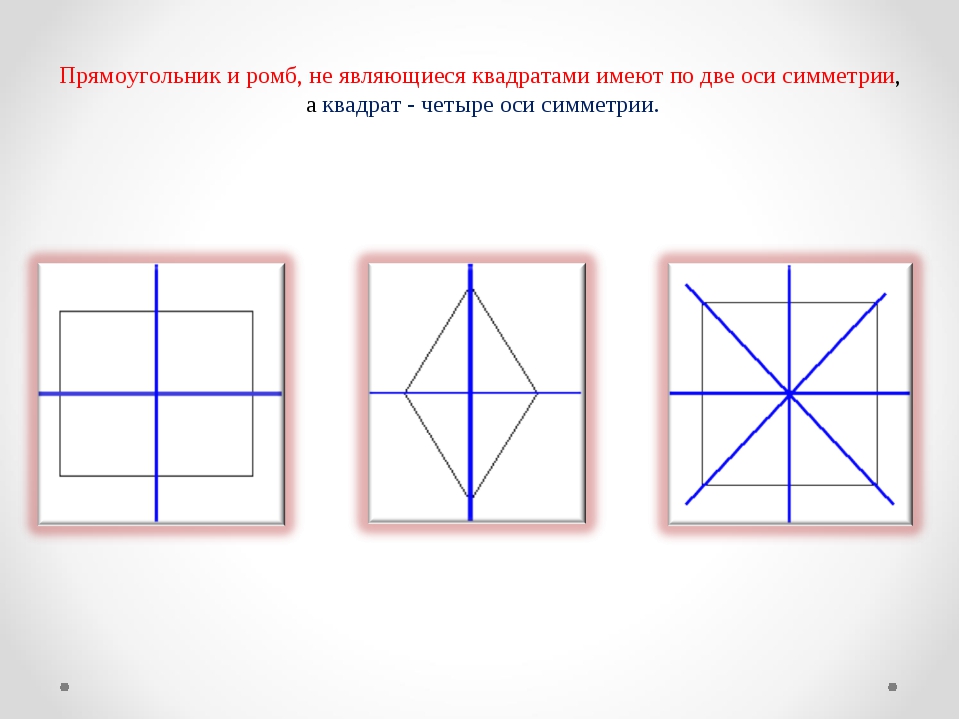 Изображение B создается путем поворота исходного изображения A.

Когда мы смотрим на изображения воздушного змея выше, он надевается на себя 1 раз за полный оборот на 360 градусов.

Итак, кайт имеет вращательную симметрию порядка 1.

Пример 10:

Каков порядок вращательной симметрии ромба?

Решение:

Посмотрите изображения ромба в порядке A, B и C. A — исходное изображение.Изображения B и C создаются путем поворота исходного изображения A.

Когда мы смотрим на вышеприведенные изображения ромба, он ложится на себя 2 раза за полный оборот на 360 градусов.

Итак, ромб имеет вращательную симметрию порядка 2.

Пример 11:

Каков порядок вращательной симметрии эллипса?

Решение:

Посмотрите изображения эллипса в порядке A, B и C. A — исходное изображение.Изображения B и C создаются путем поворота исходного изображения A.

Когда мы смотрим на вышеприведенные изображения эллипса, он ложится на себя 2 раза за полный оборот на 360 градусов.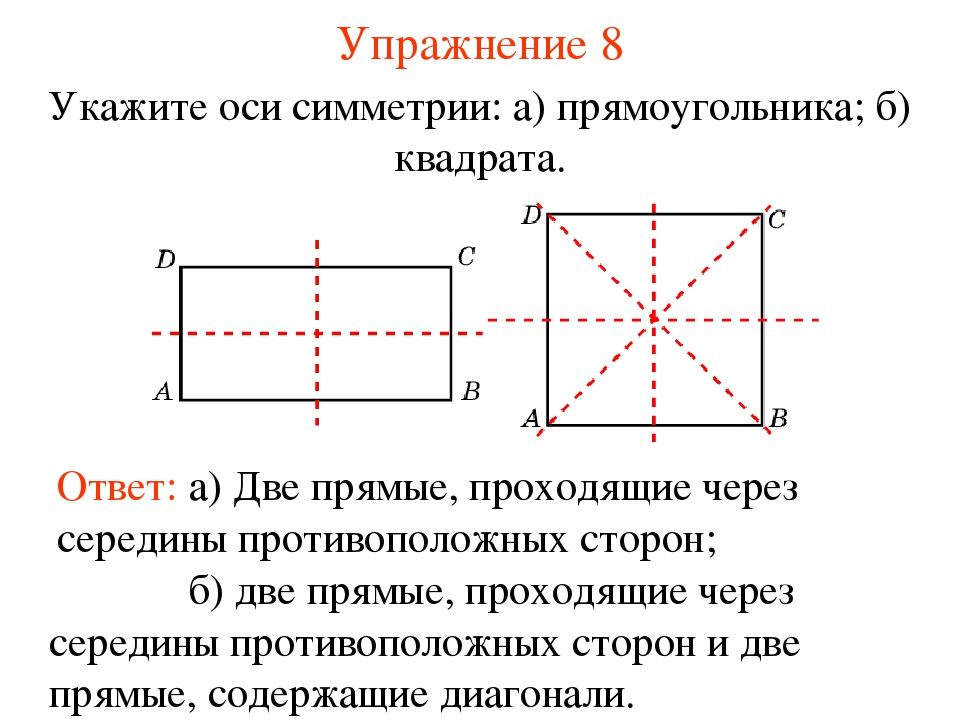

Итак, эллипс имеет вращательную симметрию порядка 2.

Помимо вышеперечисленного, если вам нужно что-то еще, воспользуйтесь нашим пользовательским поиском Google здесь.

Если у вас есть отзывы о наших математических материалах, напишите нам:

v4formath @ gmail.com

Мы всегда ценим ваши отзывы.

Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.

ЗАДАЧИ СО СЛОВАМИ

Задачи со словами HCF и LCM

Задачи со словами на простых уравнениях

Задачи со словами на линейных уравнениях

Задачи со словами на квадратных уравнениях

Алгебраные задачи со словами

Проблемы со словами в поездах

Проблемы со словами по площади и периметру

Проблемы со словами по прямой и обратной вариации

Проблемы со словами по цене за единицу

Проблемы со словами по цене за единицу

Word задачи по сравнению ставок

Преобразование общепринятых единиц в текстовые задачи

Преобразование в метрические единицы в словесных задачах

Словарные задачи по простому проценту

Словарные задачи по сложным процентам

ngles

Проблемы с дополнительными и дополнительными углами в словах

Проблемы со словами с двойными фактами

Проблемы со словами в тригонометрии

Проблемы со словами в процентах

Проблемы со словами о прибылях и убытках

Разметка и разметка Задачи

Задачи с десятичными словами

Задачи со словами о дробях

Задачи со словами о смешанных фракциях

Одношаговые задачи с уравнениями со словами

Проблемы со словами о линейных неравенствах

Соотношение и пропорции Задачи со словами

Проблемы со временем и рабочими словами

Задачи со словами на множествах и диаграммах Венна

Проблемы со словами на возрастах

Проблемы со словами по теореме Пифагора

Процент числового слова pr проблемы

Проблемы со словами на постоянной скорости

Проблемы со словами на средней скорости

Проблемы со словами на сумме углов треугольника 180 градусов

ДРУГИЕ ТЕМЫ

Сокращения прибылей и убытков

Сокращение в процентах

Сокращение в таблице времен

Сокращение времени, скорости и расстояния

Сокращение соотношения и пропорции

Область и диапазон рациональных функций

Область и диапазон рациональных функций функции с отверстиями

График рациональных функций

График рациональных функций с отверстиями

Преобразование повторяющихся десятичных дробей в дроби

Десятичное представление рациональных чисел

Поиск квадратного корня с помощью long di видение

L. Метод CM для решения временных и рабочих задач

Преобразование словесных задач в алгебраические выражения

Остаток при делении 2 в степени 256 на 17

Остаток при делении 17 в степени 23 на 16

Сумма всех трехзначных чисел, делимых на 6

Сумма всех трехзначных чисел, делимых на 7

Сумма всех трехзначных чисел, делимых на 8

Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4

Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами

Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3

Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6

Группа симметрий квадрата

Вспомните со страницы Группа симметрий равностороннего треугольника, что если у нас есть равносторонний треугольник, вершины которого помечены как $ 1 $, $ 2 $ и $ 3 $, и если $ G = \ {\ rho_0, \ rho_1, \ rho_2, \ mu_1 , \ mu_2, \ mu_3 \} $ — это группа симметрий, где $ \ rho_0, \ rho_1, \ rho_2: \ {1, 2, 3 \} \ to \ {1, 2, 3 \} $ — функции, соответственно определяющие поворот против часовой стрелки вокруг центра равностороннего треугольника на $ 0 ^ {\ circ} $, $ 120 ^ {\ circ} $, и $ 240 ^ {\ circ} $ и $ \ mu_1 \ \ mu_2, \ mu_3: \ {1, 2, 3 \} \ to \ {1, 2, 3 \} $ — это функции, определяющие осевые перевороты вдоль линий, которые пересекают вершины треугольника и перпендикулярно делят пополам соседнее ребро, и если $ \ circ: G \ to G $ определяет для каждого $ f_1, f_2 \ in G $ композиция $ f_1 $ и $ f_2 $, i.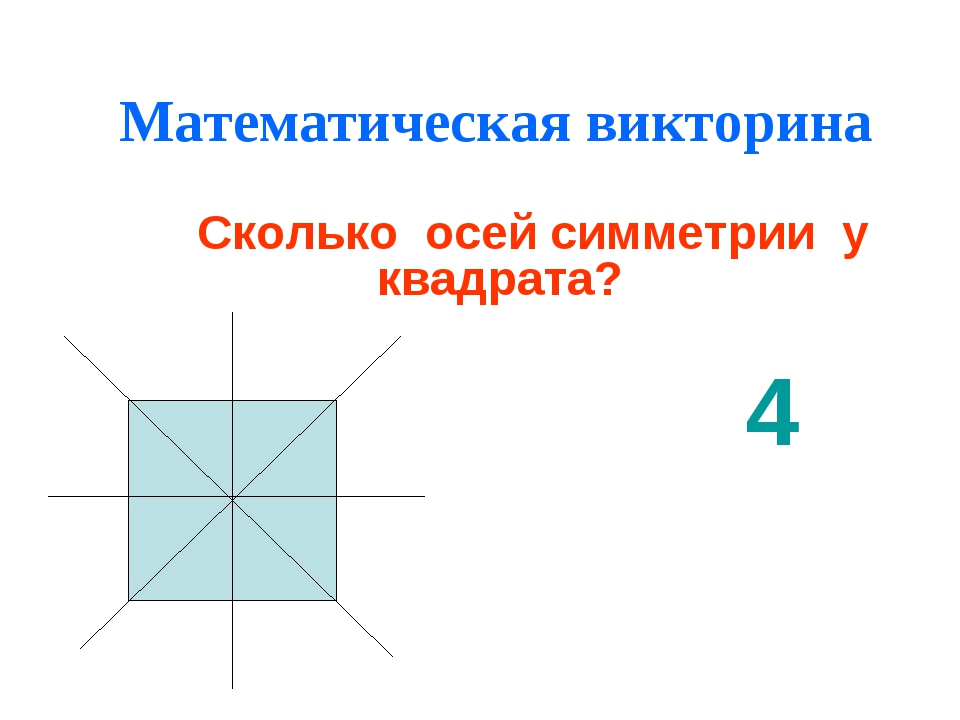 {\ circ} $ производят:

Другой тип симметрии, который мы можем определить, — это переворот оси вдоль серединного перпендикуляра квадрата, к которому мы можем перевернуть две серединные перпендикулярные стороны:

Применяя эти перпендикулярные осевые перевороты к исходному квадрату, мы получаем:

Последний тип симметрии, который мы можем определить, — это осевые перевороты по биссектрисам квадрата, к которому снова есть две биссектрисы по диагонали, которые мы можем перевернуть:

Применяя эти диагональные осевые перевороты к исходному квадрату, мы получаем:

Пусть $ \ rho_0, \ rho_1, \ rho_2, \ rho_3: \ {1, 2, 3, 4 \} \ to \ {1, 2, 3, 4 \} $ — функции, которые представляют симметрии вращения, пусть $ \ mu_1, \ mu_2: \ {1, 2, 3, 4 \} \ to \ {1, 2, 3, 4 \} $ — функции, представляющие срединно-перпендикулярные осевые симметрии, и пусть $ \ delta_1, \ delta_2: \ {1, 2, 3, 4 \} \ to \ {1, 2, 3, 4 \} $ — функции, представляющие диагональные биссектрисы осевые симметрии.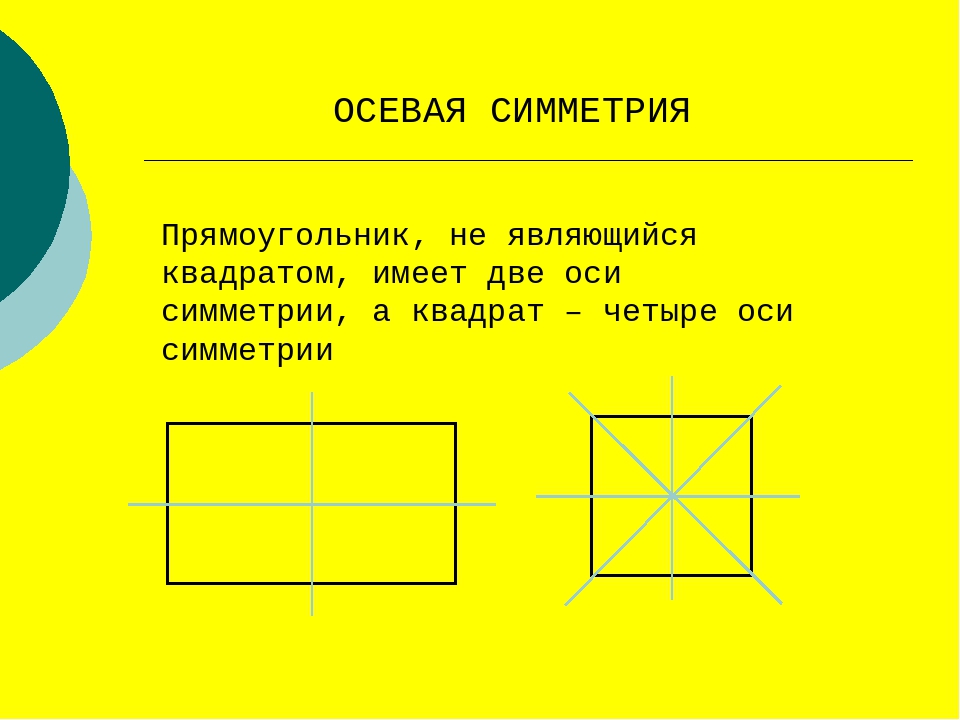 Каждую из этих функций можно описать как матрицу размером $ 2 \ times 4 $, в которой первая строка перечисляет исходное расположение вершин на квадрате, а вторая строка перечисляет изменение положения вершин после применения определенных симметрий. У нас это:

(1)

\ begin {align} \ quad \ rho_0 = \ begin {pmatrix} 1 & 2 & 3 & 4 \\ 1 & 2 & 3 & 4 \ end {pmatrix} \ quad, \ quad \ rho_1 = \ begin {pmatrix} 1 & 2 & 3 & 4 \\ 4 & 1 & 2 & 3 \ end {pmatrix} \ quad, \ quad \ rho_2 = \ begin {pmatrix} 1 & 2 & 3 & 4 \\ 3 & 4 & 1 & 2 \ end {pmatrix} \ quad, \ quad \ rho_3 = \ begin {pmatrix} 1 & 2 & 3 & 4 \\ 2 & 3 & 4 & 1 \ end {pmatrix} \ end {align}

(2)

\ begin {align} \ quad \ mu_1 = \ begin {pmatrix} 1 & 2 & 3 & 4 \\ 4 & 3 & 2 & 1 \ end {pmatrix} \ quad, \ quad \ mu_2 = \ begin {pmatrix} 1 и 2 и 3 и 4 \\ 2 и 1 и 4 и 3 \ end {pmatrix} \ end {align}

(3)

\ begin {align} \ quad \ delta_1 = \ begin {pmatrix} 1 & 2 & 3 & 4 \\ 1 & 4 & 3 & 2 \ end {pmatrix} \ quad, \ quad \ delta_2 = \ begin {pmatrix} 1 и 2 и 3 и 4 \\ 3 и 2 и 1 и 4 \ end {pmatrix} \ end {align}

Пусть $ G = \ {\ rho_0, \ rho_1, \ rho_2, \ rho_3, \ mu_1, \ mu_2, \ delta_1, \ delta_2 \} $ и пусть $ \ circ: G \ to G $ определено для всех $ f_1 , f_2 \ in G $ как композиция функций, то есть $ (f_1 \ circ f_2) (x) = f_1 (f_2 (x)) $. Тогда $ (G, \ circ) $ снова является группой. В следующей таблице показаны все возможные композиции элементов в $ G $:

Таблица выше показывает нам, что $ G $ замкнут относительно $ \ circ $, что $ \ rho_0 $ является единичным элементом по отношению к $ \ circ $, и что каждый элемент в $ G $ имеет обратный (поскольку каждая строка и каждый столбец имеет композицию, равную $ \ rho_0 $. Мы уже доказали, что $ \ circ $ ассоциативно, поэтому действительно $ (G, \ circ) $ — группа. Кроме того, из таблицы выше мы видим, что $ (G, \ circ) $ не абелева, поскольку:

(4)

\ begin {align} \ quad \ mu_1 \ circ \ rho_3 = \ delta_2 \ neq \ delta_1 \ rho_3 \ circ \ mu_1 \ end {align}

Симметрия графиков — Темы в предварительном исчислении

16

Тест на симметрию: четные и нечетные функции

ПОСМОТРЕТЬ ПРАВУЮ СТОРОНУ графика функции:

Теперь нарисуем левую часть — так, чтобы график был симметричным относительно оси y :

В данном случае

f (- x ) = f ( x ).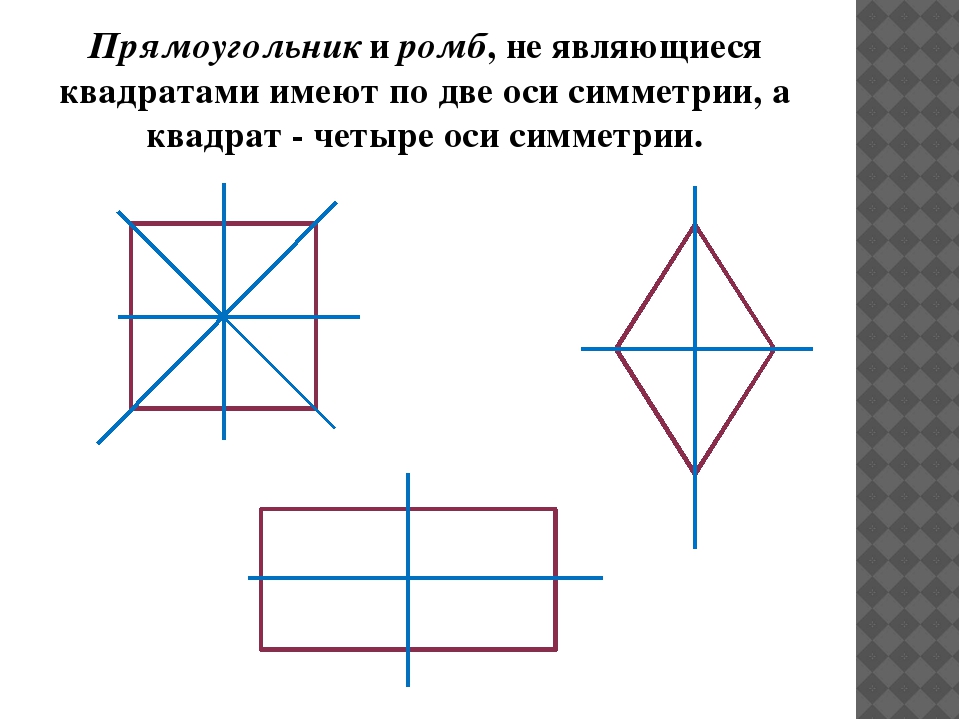

Высота кривой в точке — x составляет , что равно высоте кривой в точке x — на каждые x в области f .

Опять же, пусть это будет правая часть:

Теперь нарисуем левую часть — так, чтобы график был симметричным относительно начала координат:

Каждая точка с правой стороны отражается через начало координат.В данном случае

f (- x ) = — f ( x ).

Значение f при — x — это отрицательное значение значения при x .

(Отражение через начало координат эквивалентно отражению относительно оси y , за которым следует отражение относительно оси x .)

Тест на симметрию: четные и нечетные функции

Симметрия, таким образом, зависит от поведения f ( x ) на другой стороне оси y — при минус-x : f (- x ).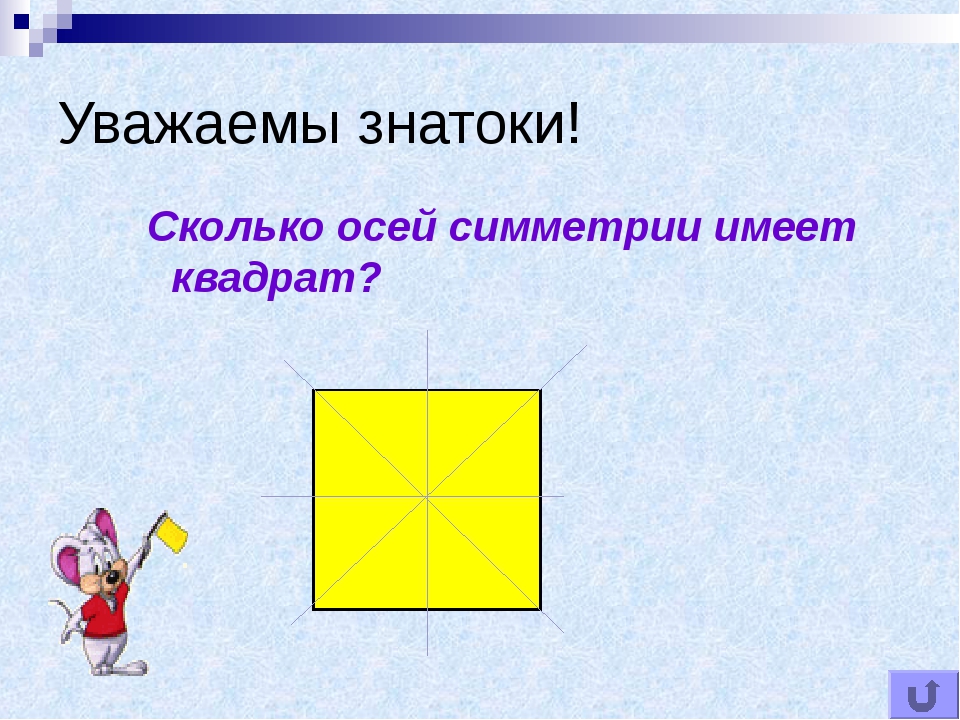

Вот тест:

Если f (- x ) = f ( x ),

, то график f ( x ) симметричен относительно оси y .

Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).

Если f (- x ) = — f ( x ),

, то график f ( x ) симметричен относительно начала координат.

Функция, симметричная относительно оси y , называется четной функцией.

Функция, симметричная относительно начала координат, называется нечетной функцией.

Пример 1. Проверьте эту функцию на симметрию:

f ( x ) = x ⁴ + x ² + 3

Решение . Мы должны посмотреть на f (- x ):

f (- x )	=	(- x ) 4 + (- x ) 2 + 3
	=	x 4 + x 2 + 3
	=	f ( x ).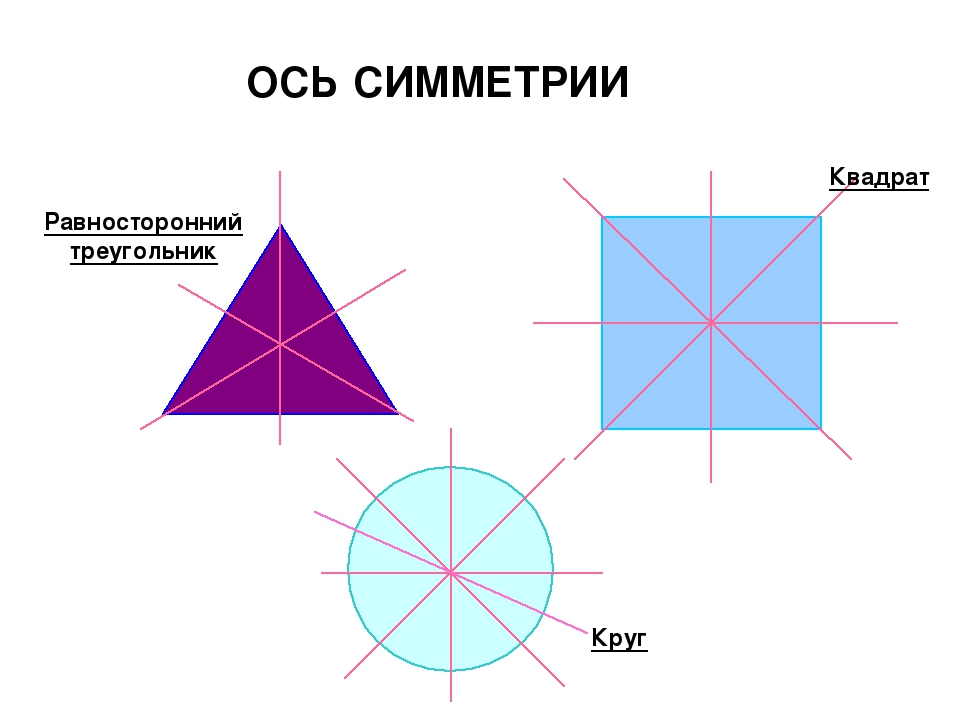

Поскольку f (- x ) = f ( x ), эта функция симметрична относительно оси y . Это четная функция.

Пример 2. Проверить эту функцию на симметрию:

f ( x ) = x ⁵ + x ³ + x

Решение . Опять же, мы должны посмотреть на f (- x ):

f (- x )	=	(- x ) 5 + (- x ) 3 + (- x )
	=	— x 5 — x 3 — x
	=	— ( x 5 + x 3 + x )
	=	— f ( x ).

Поскольку f (- x ) = — f ( x ), эта функция симметрична относительно начала координат. Это странная функция.

Проблема. Проверьте симметрию каждого из следующих пунктов. f ( x ) четное, нечетное или ни одно?

a) f ( x ) = x ³ + x ² + x + 1

Ответ. Ни то, ни другое, потому что f (- x ) ≠ f ( x ) и f (- x ) ≠ — f ( x ).

b) f ( x ) = 2 x ³ — 4 x

Ответ. f ( x ) является нечетным — он симметричен относительно начала координат, потому что f (- x ) = — f ( x ).

c) f ( x ) = 7 x ² — 11

Ответ. f ( x ) является четным — он симметричен относительно оси y — потому что f (- x ) = f ( x ).

Примечание: Многочлен будет четной функцией, если все экспоненты равны четный.

Многочлен будет нечетной функцией, если все показатели равны странный.

Но есть четные и нечетные функции, которые не являются полиномами. В тригонометрии y = cos x — четная функция, а y = sin x — нечетная.

Следовательно, речь идет о тесте f (- x ).

Следующая тема: Переводы

Содержание | Дом

---

Сделайте пожертвование, чтобы TheMathPage оставался в сети.
Даже 1 доллар поможет.

---

Авторские права © 2020 Лоуренс Спектор

Вопросы или комментарии?

Эл. Почта: [email protected]

Квадратичные функции | Функции | Сиявула

Используйте свои наброски функций, приведенных выше, чтобы заполнить следующую таблицу (первый столбец заполнен в качестве примера):

	\ (y_1 \)	\ (y_2 \)	\ (y_3 \)	\ (y_4 \)
(q981) значение из	\ (q = 0 \)
эффект \ (q \)	\ (y _ {\ text {int}} = 0 \)
значение \ (a \)	\ (a = 1 \)
эффект \ (a \)	стандартная парабола
точка поворота \ ((0; 0) \)
ось симметрии	\ (x = 0 \) (\ (y \) — ось)
домен	\ (\ {x: x \ in \ mathbb {R} \} \)
диапазон	\ (\ {y: y \ geq 0 \} \)	9097 9

	\ (y_1 \)	\ (y_2 \)	\ (y_3 \)	\ (y_4 \)
(q981) значение из	\ (q = \ text {0} \)	\ (q = \ text {0} \)	\ (q = — \ text {1} \)	\ (q = \ text { 4} \)
эффект \ (q \)	\ (y _ {\ text {int}} = 0 \)	\ (y _ {\ text {int}} = 0 \)	\ (y _ {\ text {int}} = -1 \), сдвигает \ (\ text {1} \) блок вниз	\ (y _ {\ text {int}} = 4 \), сдвигает \ (\ текст {4} \) блок вверх
значение \ (a \)	\ (a = 1 \)	\ (a = \ frac {1} {2} \)	\ ( a = -1 \)	\ (a = -2 \)
эффект \ (a \)	стандартная парабола	улыбка, мин.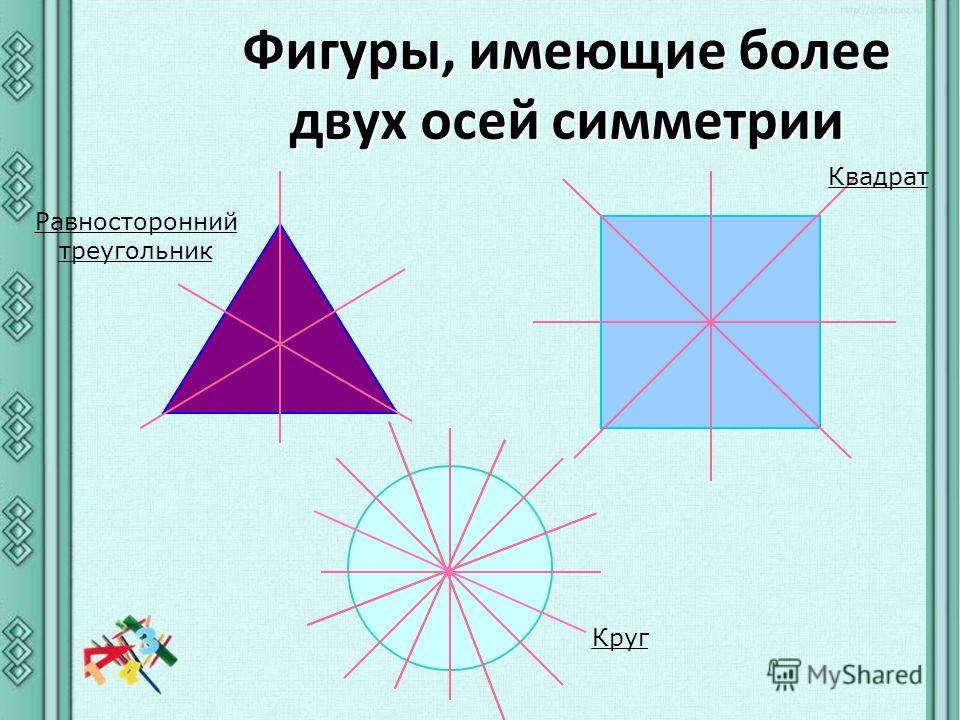 No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Copyright © 2024 Решения идз рябушко Карта сайта