Категория: Разное

Как построить центральную симметрию: Осевая и центральная симметрия. Математика, 6 класс: уроки, тесты, задания.

Содержание

Осевая и центральная симметрия. Математика, 6 класс: уроки, тесты, задания.

1. Симметричные точки

Сложность: лёгкое

2
2. Симметричные точки относительно оси

Сложность: лёгкое

1
3. Ось симметрии фигуры

Сложность: среднее

2
4. Оси симметрии фигуры

Сложность: среднее

2
5. Симметричная окраска

Сложность: среднее

1
6. Симметричные фигуры

Сложность: сложное

3
7. Симметрия на числовой оси

Сложность: сложное

3

Понятие движения. Симметрия. Геометрия, 9 класс: уроки, тесты, задания.

1. Центральная и осевая симметрия

Сложность: лёгкое

2. Центральная симметрия на отрезке

Сложность: лёгкое

3. Ось симметрии графика квадратичной функции

Сложность: лёгкое

4. Центральная симметрия, координатная плоскость

Сложность: лёгкое

5. Осевая симметрия, координатная плоскость

Сложность: лёгкое

6.
 Центральная симметрия, координаты симметричной точки

Сложность: среднее

7. Определение центра симметрии фигур

Сложность: среднее

8. Центральная симметрия, симметричные четырёхугольники

Сложность: среднее

9. Осевая симметрия, координаты симметричной точки

Сложность: среднее

10. Ось симметрии данного четырёхугольника, симметричные точки

Сложность: среднее

11. Буквы и цифры, имеющие центр или ось симметрии

Сложность: среднее

12. Определение осей симметрии фигур

Сложность: среднее

13. Центральная и осевая симметрия, координаты симметричной точки

Сложность: среднее

14. Осевая симметрия, симметричные треугольники относительно прямой x = t

Сложность: среднее

15. Осевая симметрия, симметричные треугольники относительно прямой y = t

Сложность: среднее

16. Осевая симметрия относительно прямой на координатной плоскости

Сложность: сложное

17. Симметричные графики функций, осевая симметрия

Сложность: сложное

Симметрия в архитектуре — виды, применение и примеры объектов

Определение понятия и виды

В Википедии о ней говорится как о фундаментальном природном принципе.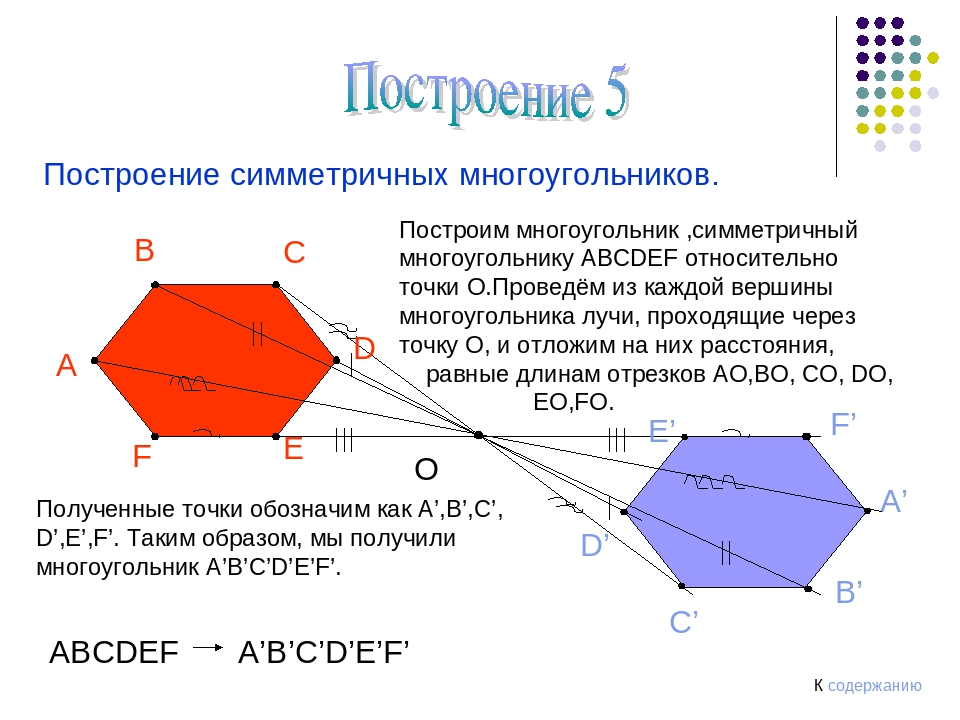 В природе это явление может проявляться как в живых, так и в неживых формах. В неживой природе оно наиболее выражено в кристаллах. В растительном и животном мире — свойственно значительному числу организмов и проявляется в виде взаимного расположения одинаковых частей тела относительно его центральной оси.

Она не только обуславливает строение биологического тела, но и влияет на формирование определенных систем жизнедеятельности организма. Для многих живых форм наличие центральной оси тела отвечает за устойчивость в однородной среде и на поверхности, что объясняется, по-видимому, воздействием силы планетарного притяжения.

Эволюционное развитие жизни на планете Земля привело к возникновению такого вида существ, как Homo Sapiens — «Человек разумный», что предопределило появление социальной эволюции и таких закономерных понятий, как «культура», «цивилизация» и «социосистема».

На протяжении многих тысяч лет, в процессе наблюдения за природными объектами человеческими существами был сделан вывод о том, что наиболее жизнеспособными формами являются отвечающие основополагающему соответствию схожих частей друг другу относительно общего центра.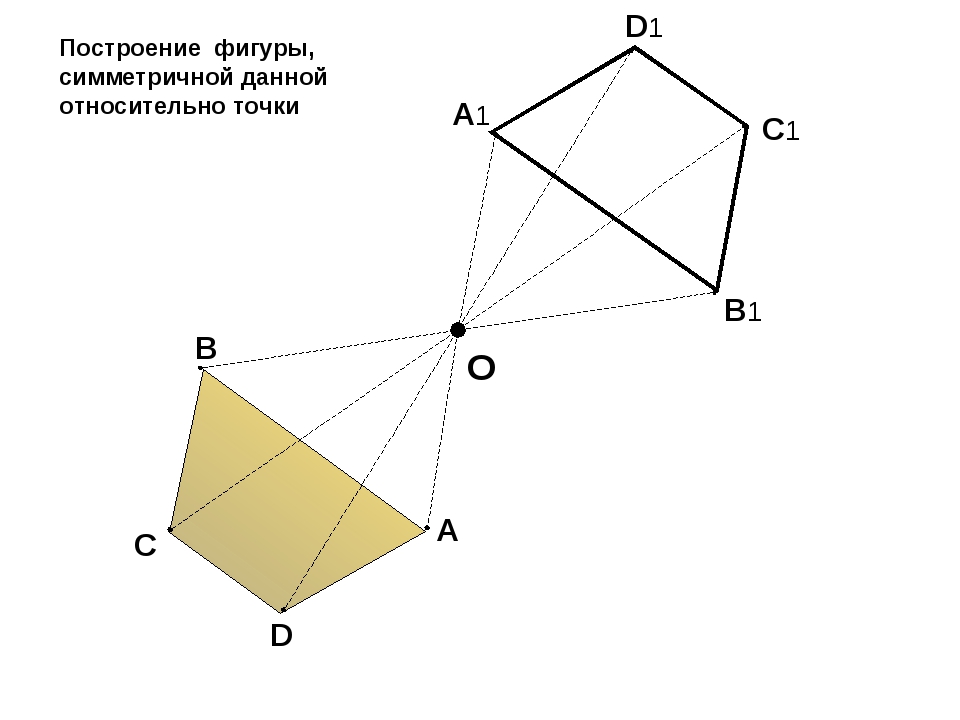 Так родилось понимание принципа, который можно считать базовым для человеческой культуры как степени единства в организации жизнедеятельности людей.

Если рассматривать культуру как развернутую форму религиозного культа, представленную в виде философии, науки, архитектуры, искусства, то во всех этих проявлениях присутствует этот признак. Он наблюдается в символах мировых религий, поскольку в нем заключена духовная основа, являющаяся продуктом творческого преобразования духом первозданных сил природы.

В древнегреческом языке слово «симметрия» соответствовало понятию «соразмерность», образованному сочетанием слов «совместно» и «мерю». Если рассматривать явление в архитектуре, то внимание следует уделить пропорциональному соотношению архитектурных деталей, их упорядоченности и красоте при взаимном расположении. Это формирует силуэт здания, воспринимаемый слева, справа, сверху и снизу, о чем в своем докладе, сделанном в Триеннале в 1951 г. , упомянул выдающийся французский архитектор Ле Корбюзье.

Анализ выдающихся произведений зодчества позволяет выделить основные виды симметрии в архитектуре, используемые при создании строительных объектов:

  • зеркальная;
  • осевая;
  • центральная;
  • переносная;
  • винтовая.

Прием отражения в архитектуре

Зеркальная симметрия — это наиболее распространенный прием, используемый в традиционной архитектуре. Суть его заключается в зеркальном копировании одной части здания относительно другой посредством центральной плоскости симметрии, вырождающейся в вертикальную прямую, проходящую обычно через центральный вход. Этот вид симметрии главным образом использовался при решении фасадов сооружений, подчеркивая их значимость.

Гармония в природе и человеческом обществе была основной темой, которую олицетворяла собой зеркальная симметрия. Большая часть храмов и дворцов древних цивилизаций Египта, Месопотамии, античных Греции и Рима построена по этому принципу, что можно увидеть в архитектурной композиции сохранившихся зданий, а также на картинках, воссоздающих внешний облик безвозвратно утраченных. Среди них можно выделить:

  • Храм богини Изиды на острове Филе.
  • Ворота Иштар.
  • Древнегреческий храм Парфенон на афинском Акрополе.
  • Древнеримский храм Портуна на Бычьем форуме в Риме.

В I тысячелетии нашей эры были возведены величественные культовые сооружения в Южной Европе, Индии, Китае, Мезоамерике, где в композиции фасадов использовалась зеркальная симметрия:

  • Собор Святой Софии в Константинополе.
  • Индуистский храм Ранганатхи в Шрирангаме.
  • Дачаньдянь — Дворец Великих Свершений в Китае.
  • Храм Воинов в Чичен-Ице.

В средневековой архитектуре Европы, Ближнего Востока, Средней Азии, Японии также применялся принцип зеркальной симметрии:

  • Пизанский собор.
  • Миланский собор.
  • Собор Парижской Богоматери.
  • Мечеть Масджид аль-Харам — Заповедная мечеть в Мекке.
  • Мечеть Калян в Бухаре.
  • Храм Феникса монастыря Бёдо-ин в Японии.

Эпоха Ренессанса, возродившая античные культурные традиции, оказала значимое влияние на развитие архитектуры эпох Просвещения и Нового времени. Здания этих исторических периодов построены с неизменным соблюдением общего правила зеркальной симметрии:

  • Собор Святого Петра (Рим).
  • Церковь Санта-Сусанна (Рим).
  • Собор Святого Павла (Лондон).
  • Исаакиевский кафедральный собор (Санкт-Петербург).

Осевая соразмерность

Осевая симметрия в архитектуре применялась в проектах культовых и дворцовых ансамблей, организации квартальной застройки городов, планировании парковых комплексов. При этом взаимное симметричное размещение архитектурных объемов соподчинялось срединной оси композиции, проходящей в виде прямой линии по центральной части главных улиц, транспортных магистралей и парадных аллей, которые могли служить путями продвижения торжественных процессий.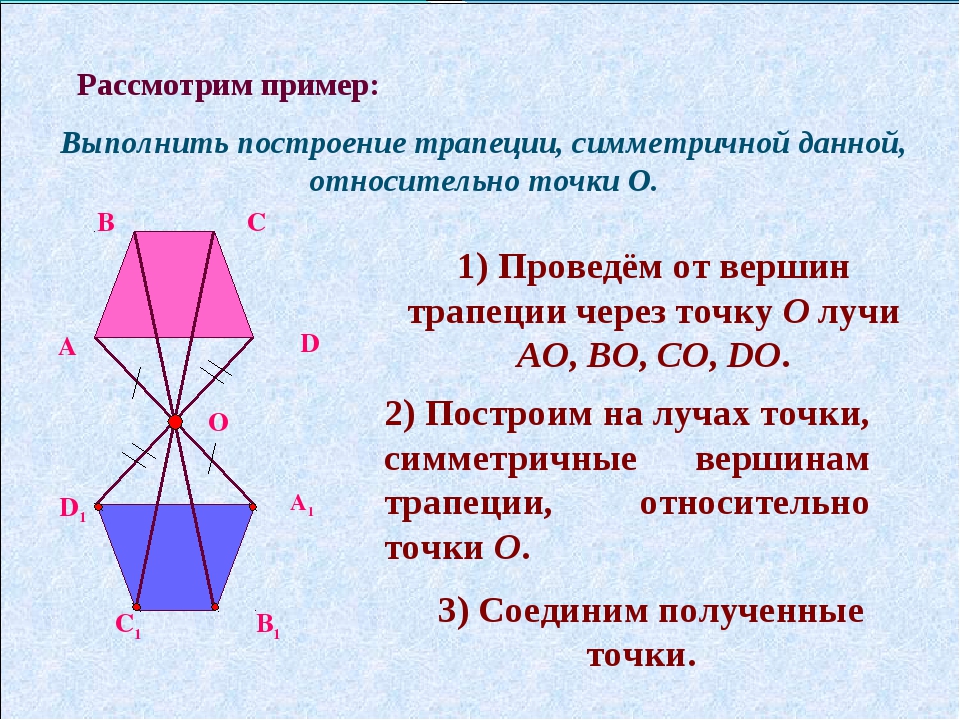

Можно сказать, что этот прием является характерным для объектов, расположенных на горизонтальной плоскости и занимающих значительные площади.

В качестве примеров следует отметить:

  • Запретный город в центре Пекина.
  • Центральная часть Санкт-Петербурга.
  • Парковый комплекс в Версале.

Центрально-симметричные объекты

Центральная симметрия в архитектуре (второе название — поворотная) характерна для круглых сооружений: храмов, башен, парковых павильонов. Базовые архитектурные элементы, такие как колонны, также создавались по принципам центральной симметрии.

Для выполнения условий центральной симметрии объекту необходимо иметь центральную точку, через которую проходит вертикальная ось, вокруг которой равномерно размещаются архитектурные детали. В качестве примеров применения в архитектуре можно назвать:

  • Храм Весты (Рим).
  • Колонна Траяна (Рим).
  • Вандомская колонна (Париж).
  • Александровская колонна (Санкт-Петербург).
  • Останкинская телебашня (Москва).

Перенос элементов вдоль прямой

Переносная или трансляционная разновидность предусматривает использование однородных элементов, расположенных на одинаковом расстоянии друг от друга, образующих общую форму. При этом осуществляется ритмическое сообщение между всеми деталями композиции. Расстояние между элементами определяется как шаг.

Чаще всего такой вариант используется в рисунке декоративных орнаментов при оформлении фасадов и интерьеров зданий. Одним из примеров использования трансляционной разновидности можно считать меандр. Подобный геометрический орнамент можно часто встретить на фасадах и во внутреннем оформлении дворцов в городе Санкт-Петербурге.

Преобразование объектов по винтовой оси

Винтовая или спиральная симметрия обычно встречается в виде винтовых лестниц или пандусов, а также в виде витых колонн. Геометрия таких объектов подчиняется правилу, при котором форма преобразуется путем переноса и поворота объекта вокруг неподвижной оси. Яркими образчиками использования винтовой вариации в архитектуре представляются:

  • Минарет Большой мечети в Самарре.
  • Музей Соломона Гуггенхайма в Нью-Йорке.
  • Небоскреб Мери-Экс в Лондоне.

Диссимметрия и асимметрия

Если смотреть на природу строгим взглядом математика, то можно отметить отсутствие идеальной симметрии. Это обусловлено процессом постоянного роста и деления клеток, а также влиянием факторов внешнего окружения. К примеру, основу живых организмов составляют киральные биомолекулы, чьи компоненты не обладают симметрией между своими правыми и левыми сторонами.

Диссимметрия является частичной несоразмерностью отдельных элементов композиции. Для диссимметрии характерно произвольное расположение частей в рамках симметричной системы.

Полное нарушение принципов симметрии обуславливается понятием «асимметрия», что в переводе с древнегреческого языка означает — «несоразмерность». С древнейших времен асимметричные элементы использовались в искусстве, а также в зодчестве. Особенность приема заключается в создании единого гармоничного образа, состоящего из разнородных частей, пребывающих в визуальном равновесии.

В традиционной архитектуре по принципам асимметрии были возведены средневековые замки Европы:

  • Замок Гродно в Нижней Силезии.
  • Вентспилский замок в Латвии.
  • Замок герцогов Бретонских во Франции.

Ярким образцом архитектурной асимметрии можно назвать Храм Василия Блаженого в Москве.

Краткий период постмодерна обогатил архитектуру многообразием асимметричных форм. Вот примеры некоторых из них:

  • Музей Гуггенхайма в Бильбао.
  • Бизнес-центр «Доминион Тауэр» в Москве.
  • Центральная библиотека в Сиэтле.

С внедрением массового строительства симметрия в градостроительстве и архитектуре практически перестала применяться, уступив диссимметрии и асимметрии. Это объясняется усложнением производственных процессов и технологических схем в современном строительном деле. Примером подчинения этим условиям может служить планировка Челябинска и современной части Санкт-Петербурга.


что называется, какие фигуры обладают, свойства

Понятие

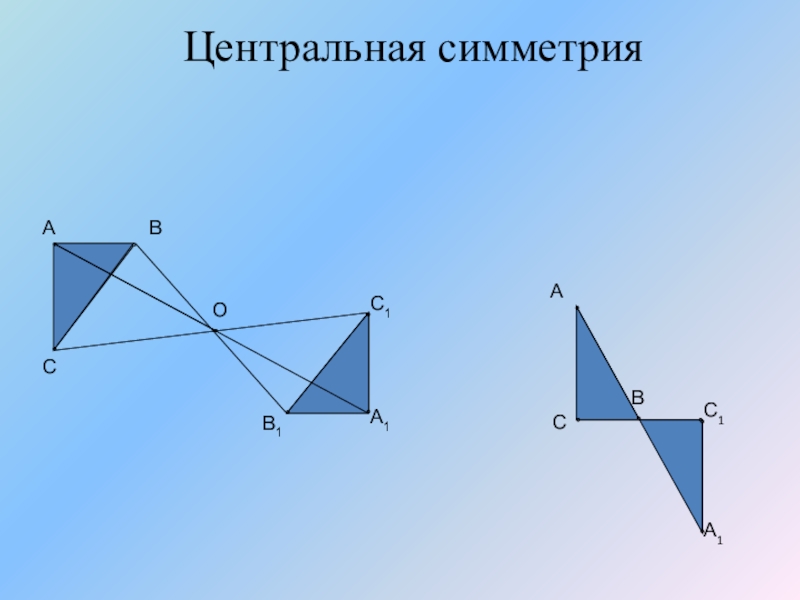
Определение

Центральная симметрия — это свойство фигуры, у которой есть некоторые точки В и В1, соединяющие отрезок и совпадающие в пространстве относительно фиксированного элемента — центральной точки С.

Симметричными могут быть и части фигуры. Для этого они должны быть соразмерными относительно центра. То есть при предполагаемом сгибе фигуры по центру все точки двух половин должны совпасть в пространстве.

Свойства

Одно из свойств симметрии — движение. Это значит, что при изменении положения все точки окажутся на том же расстоянии друг от друга, что и были, то есть симметрия сохранится.

Примечание

Изменение в пространстве предполагает поворот фигуры на 180°.

Центральная точка симметрии всегда неподвижна.

Прямая, проходящая через центр, симметрична сама себе.

Если прямая не проходит через центр, то она является параллельной. Это можно доказать путем построения двух прямых параллельных друг другу с центральной точкой, не лежащей ни на одной из линий. Соединяя симметричные точки, получим два равнобедренных треугольника, которые лежат накрест, а основания их останутся параллельными.

 

Формула

Так как точка симметрии является центральной, то отрезки прямой, симметричные относительно этой точки, должны быть равны. Представим линию, соединенную точками А и В. Центром пусть будет Х. Верным можно считать равенство АХ=АВ. Если происходит движение, то А переходит в точку А1, а В в В1. Центральная точка Х остается неподвижной. В этом случае АВ = А1В1.

Фигуры с центральной симметрией

К таким фигурам относится параллелограм, так как в центральной точке пересекаются его диагонали. Каждая из фигур, получившаяся в результате пересечения, является симметричной.

У окружности центр находится посередине, а точки, лежащие на ней, являются симметричными.

Аналогичными свойствами обладают ромб и квадрат.

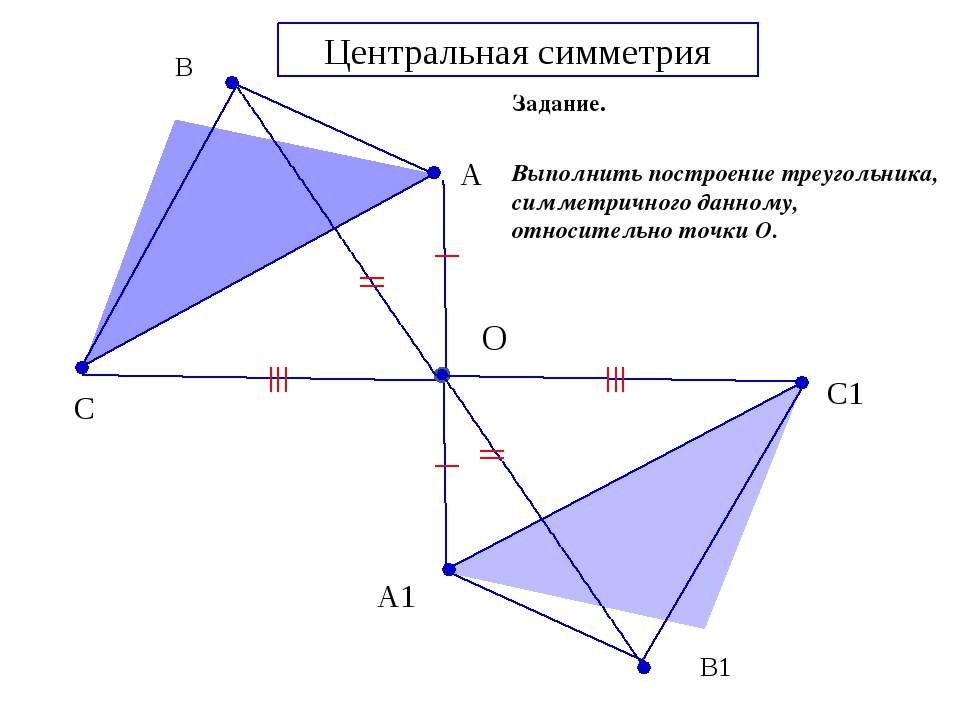
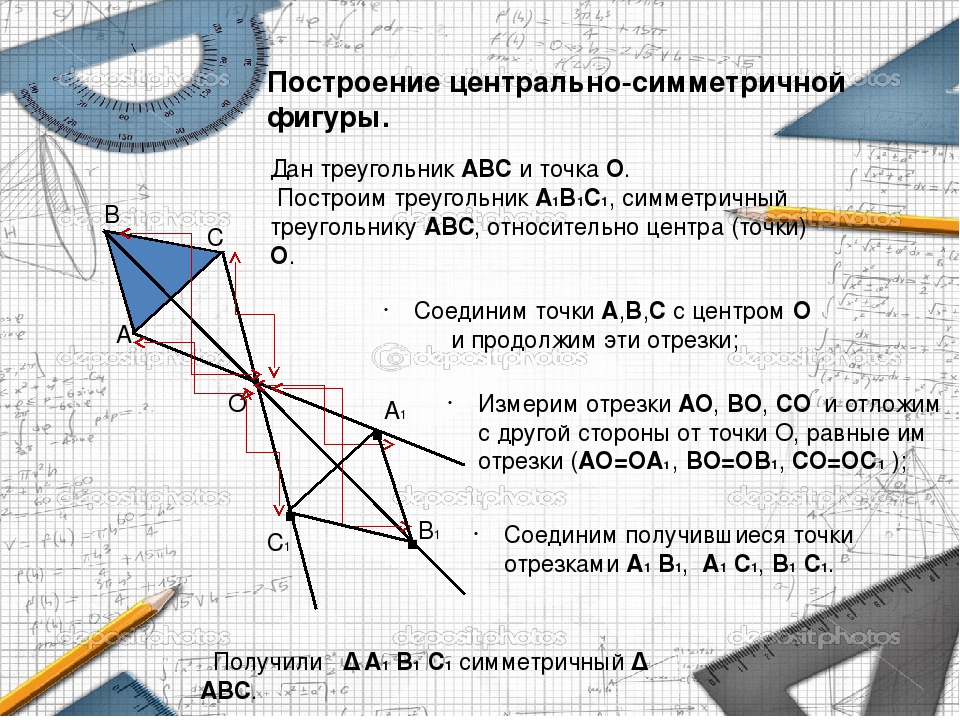
Как построить

Для построения симметрии относительно центральной точки, нужно начертить линию. Затем от одной из точек отложить отрезок, равный расстоянию между двумя первыми точками, и отметить третью. В результате вторая точка станет центром симметрии.

Примеры

Центральная симметрия часто встречается в окружающих нас предметах. В природе это любые круглые предметы: плоды кокоса, арбуза, томата, шапка одуванчика. Цветы симметричны относительно своей центральной части. Пчелиные соты представляют собой идеальные ромбы. Микроскопические капли воды, замерзая, образуют симметричные снежинки.

Симметрия свойственна многим предметам, созданным человеком: колесо, дорожные знаки, начертание букв.

Все виды симметрии, и центральная в частности, находят применение в строительстве и архитектуре. Принципа соразмерности придерживались все сторонники классицизма в искусстве.

определение, свойства, обозначение, фигуры обладающие симметрией

Что такое осевая симметрия в геометрии 

Симметрия – это свойство геометрических фигур отражаться. Симметрия относительно точки называется центральной. Осевая симметрия – это симметрия относительно прямой.

Если точка A и точка B симметричны относительно прямой n, то прямая называется осью симметрии n и проходит через середину отрезка AB. Обозначение осевой симметрии – Sn, таким образом симметрия точек A и B обозначается так:

Sn (А) = В.

Другое название осевой симметрии – вращательная – применяется в естественных науках. Данное понятие означает отражение предметов касательно поворотов вокруг прямой.

Свойства осевой симметрии

  1. Осевая симметрия переводит прямую в прямую, луч – в луч, отрезок – в отрезок, плоскость в плоскость.
  2. Неподвижными являются: ось симметрии и все точки на ней, все прямые и плоскости, перпендикулярные оси симметрии.
  3. Обратное преобразование осевой симметрии есть та же осевая симметрия.
  4. Осевая симметрия – это поворот относительно оси симметрии на 180°.

Теорема и доказательство

Теорема

Осевая симметрия – это движение, то есть при преобразовании осевой симметрии расстояние между точками сохраняется. 

Если отрезок MN симметричен отрезку M1N1  относительно прямой a, то MN = M1N1. 

Чтобы доказать, что MN = M1N1, сделаем дополнительные построения:

  • P – это точка пересечения MM1 и прямой a;
  • Q – это точка пересечения NN1 и прямой a; 
  • построим отрезок MK, перпендикулярный NN1;
  • тогда точка K отразится в точку K1.

Докажем, что прямоугольные треугольники MNK и M1N1K1 равны. Стороны MN и M1N1 являются гипотенузами данных треугольников, поэтому, нужно доказать равенство катетов.

МК = М1К1 , так как перпендикулярны к параллельным прямым.

По построению:

NK = NQ – KQ,

N1K1 = N1Q – K1Q. 

Точка N отобразилась в точку N1,  значит:

NK = N1K1.

Итак, треугольники равны по двум катетам, следовательно, их гипотенузы равны, то есть  MN = M1N1, что и требовалось доказать.

Фигуры, обладающие симметрией

Осевой симметрией обладает угол, а биссектриса является осью симметрии.

Пример №1

Из произвольной точки одной стороны угла опустим перпендикуляр к биссектрисе и продлим его до другой стороны угла:

Рассмотрим Δ KAO и Δ MAO:

  • AO – общая сторона
  • Из свойства биссектрисы: ∠ MAO = ∠KAO
  • Треугольники KAO и MAO прямоугольные,

Отсюда следует, что KO = OM, поэтому точки K и M симметричны касательно биссектрисы угла.

Следовательно, равнобедренный треугольник тоже симметричен относительно биссектрисы, проведенной к основанию.

Пример №2

Равносторонний треугольник имеет три оси симметрии – биссектрисы, медианы, высоты каждого угла:

Пример №3

У прямоугольника две оси симметрии. Каждая из них проходит через середины противоположных сторон.

Пример №4

Ромб обладает двумя осями симметрии – это прямые, содержащие его диагонали.

Пример №5

Квадрат имеет 4 оси симметрии, так как он одновременно и ромб, и прямоугольник.

Пример №6

У окружности бесконечное множество осей симметрии – это все прямые, проведенные через центр круга.

Симметрия в повседневной жизни

Симметрия стала частью жизни человека уже в древние времена. Орнаменты с признаками зеркального отражения встречаются на античных зданиях, древнегреческих вазах. Свойство пропорционального расположения заимствовано в науку из природы. 

Зеркальное отражение часто встречается в живой и неживой природе. Этой характеристикой обладают снежинки. В растительном мире одинаково расположены противоположные элементы растений: большинство листьев зеркально отражаются сравнительно среднего стебля. В животном мире законы симметрии проявляются в наличии у животных правой и левой сторон. Большинство представителей фауны обладает парными частями тела: уши, лапы, глаза, крылья, рога. Ярким образцом зеркальной симметрии считается бабочка. Прямая, условно проведенная вдоль туловища насекомого по центру, является осью симметрии.

Поскольку человек – это часть природы, в своем творчестве он использует принцип симметрии. В искусстве свойство отражения применяется для создания красоты и гармонии. В архитектуре пропорциональность выполняет практическую функцию – придает зданиям устойчивость и надежность. В предметах быта можно встретить одинаковость в расположении частей узоров на коврах, принтов на ткани, рисунков обоев.

Стремление к созданию симметричного, предположительно, связано с притяжением Земли – гравитацией. Человек интуитивно считает симметрию формулой устойчивости. Принцип зеркального отражения играет важную роль в человеческой жизни. Тяга к гармонии и красоте побуждает человечество придерживаться правил пропорциональности.

Осевая симметрия | Треугольники

Осевая симметрия — это симметрия относительно прямой.

Пусть дана некоторая прямая g.

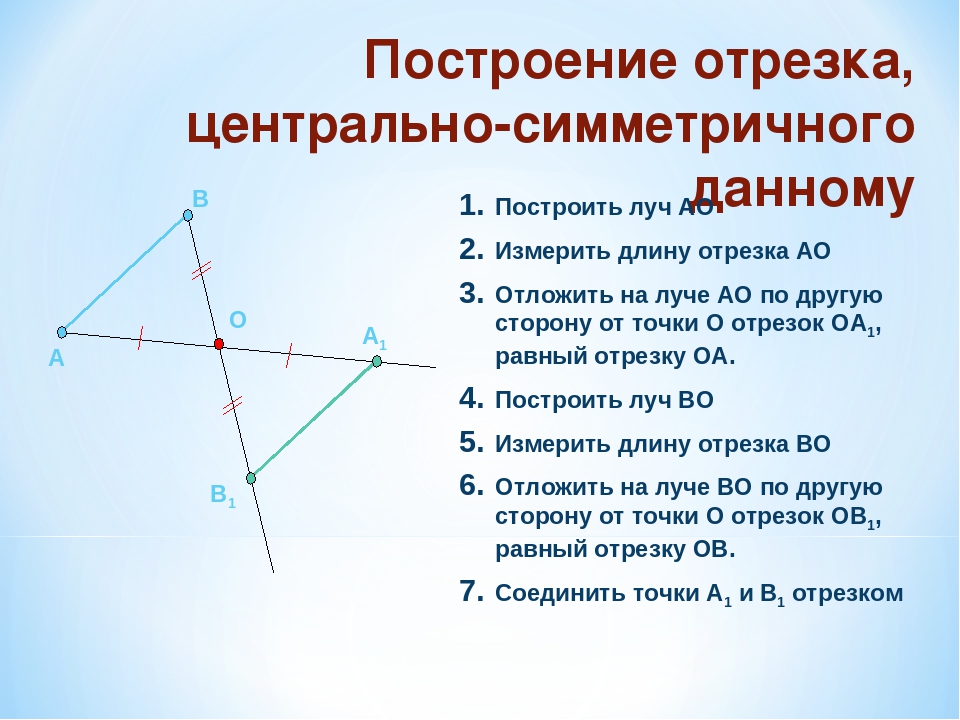
Чтобы построить точку, симметричную некоторой точке A относительно прямой g, надо:

1) Провести из точки A к прямой g перпендикуляр AO.

 

2) На продолжении перпендикуляра с другой стороны от прямой g отложить отрезок OA1, равный отрезку AO: OA1=AO.

Полученная точка A1 симметрична точке A относительно прямой g.

Прямая g называется осью симметрии.

Таким образом, точки A и A1 симметричны относительно прямой g, если эта прямая проходит через середину отрезка AA1 и перпендикулярна к нему.

Если точка A лежит на прямой g, то симметричная ей точка есть сама точка A.

Преобразование фигуры F  в фигуру F1, при котором каждая её точка A переходит в точку A1, симметричную относительно данной прямой g, называется преобразованием симметрии относительно прямой g.

Фигуры F и F1 называются фигурами, симметричными относительно прямой g.

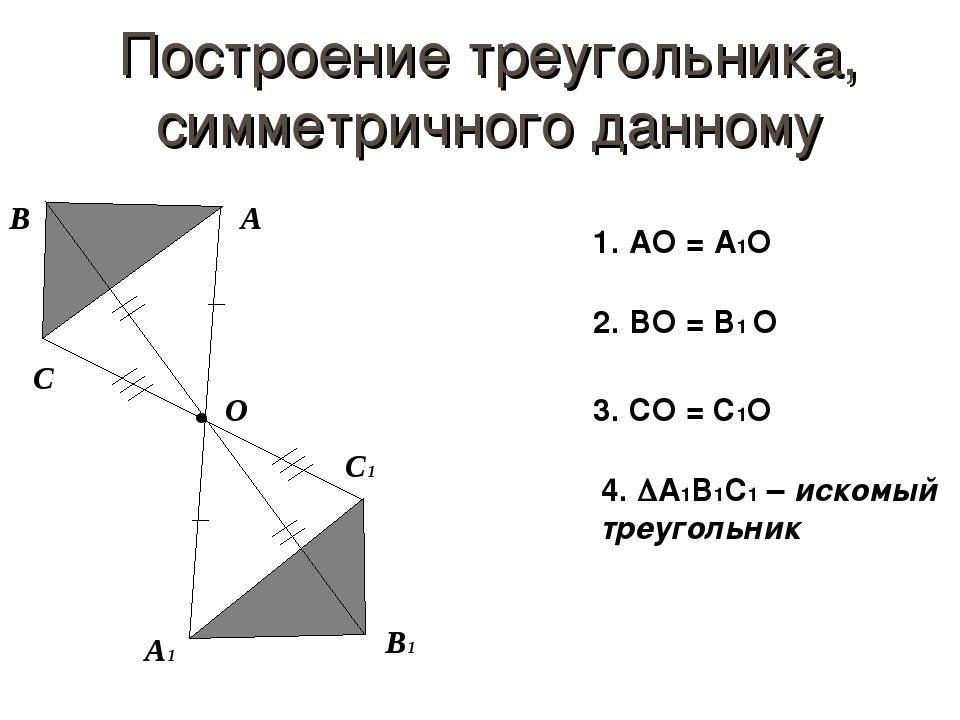
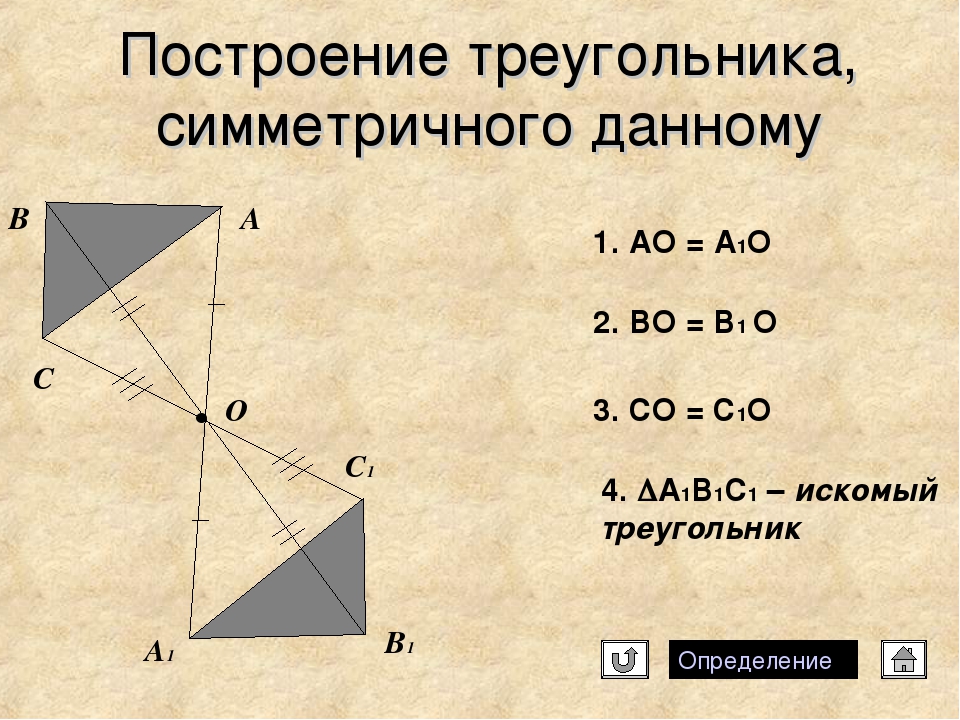
Чтобы построить треугольник, симметричный данному относительно прямой g, достаточно построить точки, симметричные вершинам треугольника, и соединить их отрезками.

Например, треугольники ABC и A1B1C1 симметричны относительно прямой g.

Если преобразование симметрии относительно прямой g переводит фигуру в себя, то такая фигура называется симметричной относительно прямой g, а прямая g называется её осью симметрии.

Симметричная фигура своей осью симметрии делится на две равные половины. Если симметричную фигуру нарисовать на бумаге, вырезать и согнуть по оси симметрии, то эти половинки совпадут.

Примеры фигур, симметричных относительно прямой.

1) Прямоугольник.

Прямоугольник имеет 2 оси симметрии: прямые, проходящие через точку пересечения диагоналей параллельно сторонам.

2) Ромб.

Ромб имеет две оси симметрии:

прямые, на которых лежат его диагонали.

3) Квадрат, как ромб и прямоугольник, имеет четыре оси симметрии: прямые, содержащие его диагонали, и прямые, проходящие через точку пересечения диагоналей параллельно сторонам.

4) Окружность.

Окружность имеет бесконечное множество осей симметрии:

любая прямая, содержащая диаметр, является осью симметрии окружности.

5) Прямая.

Прямая также имеет бесконечное множество осей симметрии: любая перпендикулярная ей прямая является для данной прямой осью симметрии.

6) Равнобедренная трапеция.

Равнобедренная трапеция — фигура, симметричная относительно прямой,перпендикулярной основаниям и проходящей через их середины.

7) Равнобедренный треугольник.

Равнобедренный треугольник имеет одну ось симметрии:

прямую, проходящую через высоту (медиану, биссектрису), проведённую к основанию.

 

8) Равносторонний треугольник.

Равносторонний треугольник имеет три оси симметрии:

прямые, содержащие его высоты (медианы, биссектрисы).

 

9) Угол.

Угол — фигура, симметричная относительно прямой, содержащей его биссектрису.

 

Теорема.

Осевая симметрия является движением.

Balance 101: как использовать симметрию и асимметрию в дизайне

Успешные графические дизайнеры знают, что владение визуальной концепцией баланса — ключ к эффективному общению. Когда ваши проекты достигают баланса — что может происходить как с симметричным, так и с асимметричным дизайном, — они достигают большей гармонии, и ваша аудитория будет тратить меньше энергии, воспринимая информацию.

Разобраться в симметрии и асимметрии несложно, но поначалу понять это может быть непросто.Вот почему мы рассмотрим несколько примеров, чтобы убедиться, что все предельно ясно.

Что такое визуальный баланс? А что такое симметрия?
–

Симметрия и баланс взаимосвязаны. Но это не совсем одно и то же. Взгляните на их определения:

Симметрия — это визуальное качество повторяющихся частей изображения вдоль оси, вдоль пути или вокруг центра.

Асимметрия , с другой стороны, относится ко всему, что не является симметричным.

Balance — это визуальный принцип, при котором дизайн выглядит одинаково взвешенным по всей композиции.

Balance измеряет визуальный вес вашей композиции, который влияет на то, насколько каждый элемент привлекает внимание вашей аудитории.

Есть четыре основных способа достижения баланса:

Весы симметричные

Симметричный баланс возникает, когда ваша композиция имеет одинаковый визуальный вес с каждой стороны оси. Представьте себе идеальные зеркальные изображения, смотрящие друг на друга вокруг центральной оси.

Этот тип весов отличается изяществом и простотой. На это приятно смотреть, но при этом очень предсказуемо.

Весы асимметричные

Композиция с неравным весом с обеих сторон имеет асимметричный баланс.

Более интересный визуально, чем его симметричный аналог, этот визуальный прием имеет большую точку фокусировки с одной стороны и несколько менее значимых точек фокусировки с другой.

Весы радиальные

Когда визуальные элементы исходят из общей центральной точки, это называется радиальным балансом.Представьте себе лучи солнечного света, исходящие от солнца.

Весы из мозаики

Думайте о мозаичном балансе как о организованном хаосе, который может выглядеть как шум, но на самом деле создает баланс благодаря отсутствию четкой точки фокусировки.

Каждый элемент имеет общий акцент, и ни один элемент не доминирует в композиции.

Различные типы симметрии и асимметрии
—

Баланс — это ключ к великолепному дизайну, но симметрия — один из инструментов, которые вы можете использовать для его достижения.Вот краткий обзор четырех типов симметрии.

Отражательная симметрия

Представьте, что вы берете яблоко и разрезаете его пополам. Обе стороны являются зеркальными отражениями по центральной линии, и это зеркальная симметрия.

Этот метод, также известный как двусторонняя симметрия, используется по вертикали, горизонтали или диагонали.

Отражательная симметрия может быть идеальной симметрией, то есть обе стороны изображения идентичны. Однако во многих случаях — например, на лице — будут тонкие различия с каждой стороны.

Трансляционная симметрия

Представьте себе одну и ту же форму, повторяющуюся снова и снова.

Это трансляционная симметрия — когда визуальные элементы повторяются в одном месте в пространстве. Это повторение может происходить на любой длине и в любом направлении.

Вращательная симметрия

Представьте движущиеся колеса автомобиля и крутящиеся ветряные мельницы, и вы получите симметрию вращения.

Этот метод, также известный как радиальная симметрия, включает в себя вращение всех визуальных элементов вокруг центра под любым углом.Этот тип симметрии идеально подходит для передачи ощущения движения, динамического действия или скорости.

Симметрия скольжения, отражающая

Мы все видели шаги на песке или снегу. Подумайте о том, как каждый шаг отражает противоположную ногу, но из-за движения каждый след не совпадает с другим.

Глайд-отражательная симметрия — это игра на отражательной симметрии, но она включает в себя сдвиг положения каждого зеркального изображения. Подобно вращательной симметрии, он также передает ощущение движения вперед.

Асимметрия

Если композиция не попадает в вышеперечисленные категории, вероятно, она асимметрична.

Асимметрия как дизайнера бросает вызов и помогает вам. Сбалансированный, симметричный дизайн обычно более привлекателен, потому что наш глаз находит его более интересным и привлекательным.

Вам придется немного усерднее работать, чтобы достичь баланса с асимметричными визуальными элементами, но вы также сможете экспериментировать с неожиданными узорами и формами, чего вы просто не можете сделать с симметрией.

Примеры баланса в графическом дизайне
—

Лучший способ узнать о балансе — это посмотреть на несколько реальных примеров симметрии и асимметрии в действии.

Логотипы

Airbnb

Логотип Airbnb — пример чистой симметрии отражения.

via Airbnb

Если провести вертикальную линию прямо посередине, обе половинки будут совершенно одинаковыми. Чтобы создать подобную отражательную симметрию, используйте простые формы и минималистичный логотип, в котором не будет много сложных частей.

Google

Словесный знак Google является примером асимметричного баланса.

через Google

Первые три буквы заметно шире, чем последние три, что создает ощущение большей визуальной значимости в первой половине словесного знака.

Веб-дизайн

Яблоко

Веб-страница Apple Mac является прекрасным примером отличной симметрии отражения.

через Apple

Не только экраны MacBook имеют одинаковую длину по обе стороны от вертикальной центральной оси, но и линии шрифта в заголовке и подзаголовке выше также находятся на одинаковом расстоянии по обе стороны от оси.

Атлантика

На этом веб-сайте новостного журнала представлены столбцы разной длины и увеличенный визуальный вес изображений с левой стороны для общего вида, который изо всех сил пытается достичь баланса.

via The Atlantic

Большого визуального баланса можно достичь, сделав столбцы одинаковой длины и равномерно распределив изображения по обе стороны от вертикальной центральной оси.

Визитки

InClean

Визитная карточка InClean с простым дизайном обеспечивает идеальную симметрию и баланс.

Идеально центрированная копия с большим количеством белого пространства придает этой минималистичной композиции сбалансированность и модность.

Привет

Ультра-минималистичная визитка с напечатанным на одной стороне только словом «Hallo» — композиция с явной асимметрией и преднамеренным дисбалансом.

Некоторым может показаться, что крупный шрифт слишком подавляющий. Другие могли бы увидеть в этом суть дизайна. Подобная композиция находится на грани между сбалансированным и несбалансированным.

Понимание баланса для разработки лучших продуктов
—

Знание того, как правильно использовать симметрию и асимметрию, является ключом к передаче вашей истории посредством графического дизайна. Используя принцип хорошего баланса, вы можете превратить обычный дизайн в нечто эффектное и запоминающееся.

Нужен идеально сбалансированный дизайн?
Наши дизайнеры могут помочь вам создать что угодно.

Эта статья написана Марком Шенкером при участии Сэма Лундквиста.

Руководство пользователя по симметрии

.

Последний раз этот документ редактировался 08.09.2019. Первоначальными авторами были Ингемар Андре и Фрэнк ДиМайо.

Многие белки собираются в структуры с внутренней симметрией. Код симметрии в Rosetta3 был разработан, чтобы обеспечить основу для обеспечения симметрии конформации среди эквивалентных субъединиц в сборке. Чтобы сохранить симметрию в моделировании Rosetta, необходимо симметрично связать три различных типа степеней свободы: основа, боковая цепь и твердое тело.Как только Поза становится симметричной, Розетта содержит все механизмы для поддержания симметрии для всех типов операций, которые изменяют конформацию. В этом документе описываются основные механизмы, отвечающие за симметрию. Типичный пользователь не будет напрямую взаимодействовать с этим базовым кодом, вместо этого контроль и описание симметрии в системе поддерживается с помощью определений входной симметрии.

Белки могут иметь различную симметрию. Наиболее распространенная из них — циклическая симметрия, которая включает n-кратное вращение вокруг оси симметрии (симметрия Cn).Большинство симметричных белков являются гомодимерами, имеющими симметрию C2. Другой распространенной группой являются диэдральные симметрии, которые объединяют одну ось симметрии n-го порядка с перпендикулярной осью симметрии второго порядка. Например, симметрия D2 включает димер димеров. Еще более сложные симметрии можно найти в кубической группе. Особый интерес представляет симметрия икосаэдра, обнаруженная в вирусных капсидах. Икосаэдры обладают 2-кратной, 3-кратной и 5-кратной симметрией. Выходя за рамки симметрии точечной группы, белки могут образовывать филаменты, используя спиральную симметрию, которая включает в себя как вращательную, так и трансляционную симметрию.Наконец, белки кристаллизуются с симметрией пространственных групп, типом симметрии, не обнаруженным в биогенных белках.

Rosetta способна описать все эти типы симметрий. Единственное ограничение — все повторяющиеся единицы в системе должны иметь химически идентичную среду. Самая маленькая повторяющаяся единица с этим свойством является асимметричной единицей системы. Асимметричный блок обычно идентичен субъединице.

Предполагая, что используемый вами протокол адаптирован к симметрии (если вы не видите, как адаптировать ваш протокол для использования симметрии, в этом разделе описаны шаги по использованию симметрии в Rosetta.

  1. Создайте файл определения симметрии.
  2. При необходимости измените файл определения симметрии. Обычно это связано с изменением строк set_dof.
  3. Добавьте флаги, связанные с симметрией.
  4. Убедитесь, что вы используете двоичный формат файлов без вывода сообщений при выводе файлов без вывода сообщений.

Как создавать определения симметрии

Чтобы помочь в создании файла определения симметрии из симметричной (или почти симметричной) PDB, приложение — make_symmdef_file.pl — включен в src / apps / public / symry. Запуск этого приложения без аргументов дает обзор использования; см. make_symmdef_file для более подробной информации. Также здесь присутствует учебник.

Чтобы помочь в создании файлов определения симметрии с нуля, как правило, для предсказания denovo, в src / apps / public / symry добавлен make_symmdef_file_denovo.py . Запуск этого приложения без аргументов дает обзор использования; см. make_symmdef_file_denovo для получения более подробной информации.

Как сгенерировать симметрию кристалла без создания файла symmdef

Если вы хотите смоделировать структуру в ее кристаллической решетке, файл определения симметрии не нужен. Вместо этого можно использовать флаг -symmetry_definition CRYST1 . Если используется эта опция, есть два других соответствующих флага:

-interaction_shell ## определяет расстояние (в Ангстремах) от входной структуры для создания симметричных партнеров.

-refinable_lattice позволяет уточнять параметры решетки

В качестве альтернативы тот же контроль предоставляется через RosettaScripts.Для создания систем с симметрией трехмерной решетки:
Сделайте решетку из входной PDB и строки CRYST1. Включите все субъединицы в «contact_dist».

Существует также движок, предназначенный для обработки симметрий двумерной решетки:
Сделайте 2D-решетку из входной PDB и строки CRYST1. Линия CRYST1 должна соответствовать одной из 17 групп слоев.

Есть два движка, предназначенные для манипулирования симметрией решетки (оба работают с 2D и 3D):

  <имя DockLatticeMover = Crystdock fullatom = 1 trans_step = 1 rot_step = 2 ncycles = 100 scorefxn = talaris2013 />
Стыковка внутри кристаллической решетки. Если fullatom = 1, выполняется стыковка полного атома с репаками и минимальными шагами; если fullatom = 0, вам необходимо предоставить функцию энергии центроида (например, score4_smooth), и она также добавит перемещения решетки. trans_step и rot_step дают величину возмущения; ncycles — количество шагов для выполнения.
Преобразование обратно в асимметричную позу с действительной линией CRYST1

Общие параметры использования симметрии в протоколах

-симметрия: определение_симметрии my_symdef_file

Прочитать файл определения симметрии my_symdef_file. Если my_symdef_file — это специальный тег CRYST1 , используйте вместо этого строку CRYST1 входного файла PDB для генерации симметрии решетки.

-симметрия: initialize_rigid_body_dofs

Если вы хотите инициализировать размещение твердого тела в соответствии с файлом определения симметрии.

-симметрия: perturb_rigid_body_dofs АНГСТРОМЫ ГРАДУСЫ

Если вы хотите применить возмущение твердого тела к исходной конформации твердого тела. Значения перекрывают данные SymDof?

В этом разделе представлен список протоколов, которые были перенесены для использования симметрии. Если здесь найден интересующий вас протокол, вы можете просто следовать инструкциям в разделе Как работать с симметрией. Этот список наверняка не будет время от времени обновляться должным образом, поэтому вам, возможно, придется заглядывать в код.Пожалуйста, добавляйте сюда новые протоколы по мере их переноса.

Общие

  • MinMover
  • PackRotamersMover
  • FastRelax
  • Оценка : IE — ScoreFunction теперь поддерживает симметрию

Приложения

  • Оценка приложения: src / apps / pilot / score.cc
  • Симметричная стыковка: см. Src / apps / pilot / andre / SymDock.cc
  • Складывание и закрепление: см. Src / protocol / topology_broker / FoldandDockClaimer.куб.см
  • Протоколы Relax: см. Src /tocols / relax.cc

В следующем разделе описывается, как поддерживается симметрия при изменении степеней свободы в системе, а также при подсчете и минимизации конформации. Симметрия реализована как НАСТОЯЩИЕ остатки с дополнительными ВИРТУАЛЬНЫМИ остатками, чтобы помочь. Это означает, что если вы включите симметрию, они будут выведены, включены в измерения расстояний и т. Д.

Симметрия жесткого тела

Отношения твердого тела между асимметричными узлами в симметричной сборке определяются операциями симметрии группы симметрии.Например, в гомодимере субъединицы связаны двухкратным вращением вокруг оси симметрии. Знания оси вращения и центра вращения достаточно, чтобы создать симметричную систему из единого блока. В этом описании два субблока описаны в одной системе координат, и симметрия кодируется в операциях симметрии, которые применяются к одному субблоку для генерации других копий. Эта структура приводит к трудностям в описании сложных симметрий и выполнении минимизации на основе энергии.Вместо этого в rosetta каждая субъединица имеет свою собственную систему координат, причем каждая субъединица принимает одни и те же координаты в своей соответствующей системе координат. Вместо того, чтобы иметь координаты субъединиц, связанных операциями симметрии, системы координат субъединиц связаны симметрией. В случае гомодимера есть две системы координат, которые связаны двойным вращением, и каждая субъединица имеет одинаковые координаты в своей соответствующей системе координат. Теперь, если мы настроим системы координат симметрично, то любое изменение конформации, которое применяется в одной системе координат, будет поддерживать общую симметрию, если та же операция применяется в других системах координат.Таким образом, если мы применим скачок твердого тела к первой субъединице димера, а затем применим тот же переход ко второй субъединице, то димер останется симметричным после этой операции.

Rosetta использует виртуальные остатки (VRT) для кодирования кадров координат субъединиц. Остатки VRT имеют начало координат X и Y. Каждая субъединица через переход твердого тела связана с такими виртуалами. Для димера самая простая установка включает наличие двух остатков VRT, где координаты одного остатка VRT связаны двойным вращением с другим.Для более сложных симметрий обычно используются дополнительные слои виртуальных остатков, которые иногда соединяются переходами с другими виртуальными остатками, где каждый виртуальный остаток кодирует систему координат. Настройка обычно представляет собой древовидную структуру виртуальных остатков, а в верхней части корневого остатка указывается координата всей симметричной сборки в декартовой системе координат. Эта корневая система координат позволяет, например, подогнать сборку к электронной плотности или мембране.

Некоторые из остатков ВРТ имеют особый статус: они хозяева. Мастера управляют своими подчиненными виртуальными машинами. Если применяется переход от мастера, тот же переход применяется к его подчиненным. Могут применяться только прыжки мастеров. Эта работа выполняется функциями set_jump в классе SymmetricConformation, которые реплицируют переходы от мастера к подчиненному.

Координаты виртуальных остатков указываются в файле определения симметрии. Анализ определений симметрии выполняется классом SymmData.Информация в классе SymmData затем используется для вставки остатков VRT в симметричную конформацию при построении симметричной позы. Объект SymmData также используется для инициализации класса SymmetryInfo, который хранится в классе SymmetricConformation. SymmetryInfo хранит всю информацию о симметрии, которую несет поза.

Симметрия магистрали

Поддержание симметрии магистрали тривиально после того, как были установлены кадры координат субъединиц.Когда угол кручения изменяется в главном подблоке, такое же кручение устанавливается для подчиненных подблоков. Это делается функцией set_torsion в классе SymmetricConformation.

Симметрия боковой цепи

Симметрия Siechain поддерживается таким же образом, как и симметрия магистрали. Конформации боковой цепи обычно меняются через pack_rotamers или rotamer_trials. Существуют симметричные версии этих функций: symric_pack_rotamers и symric_rotamer_trials.

Симметричная разметка

В симметричной системе все асимметричные единицы химически идентичны и, следовательно, имеют одинаковую энергию.Нам нужно только оценить энергию одной асимметричной единицы и умножить ее на количество асимметричных единиц, чтобы найти энергию всей системы. Этот тип более умной оценки дает очень большой прирост производительности, но делает ее немного более сложной, чем в асимметричной системе. Для правильного подсчета очков нам нужно указать rosetta, как их подсчитывать. Во-первых, розетта должна знать, за какую асимметричную единицу нужно забивать. Обычно это не имеет значения, и для удобства мы обычно оцениваем первую асимметричную единицу в системе.Но иногда это имеет значение: если мы представляем симметричную систему только с подмножеством единиц в полной системе, нам нужно подумать о краевых эффектах. Например, в волокне субъединицы на концах не находятся в той же среде, что и субъединицы в центре волокна. Здесь мы должны выбрать оценку для расположенной в центре субъединицы для представления общей энергии. Во-вторых, нам нужно сказать, как оценивающая субъединица взаимодействует с другими субъединицами. В тримере с субъединицами A, B и C, если A является оценивающей субъединицей, значит, оценивающая субъединица A взаимодействует как с B, так и с C.Однако A взаимодействует с B и C идентичным образом, поэтому нам нужно только рассчитать взаимодействие A: B и умножить его на 3, чтобы получить общее взаимодействие субъединица-субъединица. Полная энергия в этой системе равна E = 3 * A + 3 * A: B (3 * A + 3 * A: C будет таким же). Это информация, которую вы вводите в rosetta через файл определения симметрии.

Даже если вам нужно только меньшее количество субъединиц для оценки комплекса, вам, возможно, придется явно представить большее количество асимметричных единиц для минимизации и упаковки.Правило таково: подсчитывающая субъединица должна иметь всех своих взаимодействующих соседей. Это самая маленькая система, которую можно явно смоделировать.

Симметричная минимизация

Все асимметричные блоки при сборке имеют одинаковую среду. Также сопряжены движения твердого тела. В димере производное энергии от расстояния вдоль линии между центрами масс может быть вычислено как производное от единственной субъединицы с r, равным двум, потому что они движутся одинаково навстречу друг другу.Обычно это верно для любой симметричной системы, которая имеет одинаковые координаты в одинаковых системах отсчета. Когда мы минимизируем энергию, мы позволяем оптимизировать только основные прыжки и кручения главных субъединиц, и производная всей системы может быть вычислена как производная, умноженная на количество асимметричных единиц в системе. Это огромное ускорение. Еще одно ускорение связано с тем, что в симметричной системе только некоторые степени свободы имеют смысл изменять.Для асимметричного димера вам нужно шесть степеней свободы, чтобы описать относительную ориентацию двух субъединиц. В симметричном димере только 4 степени свободы необходимы для описания относительного отношения твердого тела: 3 степени свободы вращения для одиночной субъединицы и одно расстояние вдоль вектора между центрами масс субъединиц. При минимизации нам нужно только оптимизировать симметричные степени свободы в системе. Каковы эти степени свободы, зависит от симметрии системы, и эта информация должна быть передана rosetta через файл определения симметрии.

  • В дополнение к подробному объяснению, приведенному ниже, существует также практическое руководство, которое может помочь понять определения симметрии. Его можно найти в demos / tutorials / Symmetry / Symmetry.md — или щелкните здесь.

Все, что Rosetta должна знать о симметрии системы, закодировано в файле определения симметрии. Он сообщает rosetta, как оценивать конструкцию, как поддерживать симметрию при возмущениях твердого тела, какие степени свободы допускаются для перемещения, как изначально настроить систему и как возмущать систему.Правильно указанный файл определения симметрии позволит вам сохранить симметрию и абсолютную систему координат вашей входной белковой сборки. Вы также можете настроить симметрию для предсказания denovo, когда известна только группа симметрии. Файлы определения симметрии обычно генерируются сценариями, и в типичном случае требуется очень небольшое изменение этих файлов. Создавать эти файлы вручную очень сложно для сложных симметрий. Ниже приводится описание полей в файлах определения симметрии:

  имя_симметрии my_pdb_P_1_21_1

строка, описывающая симметрию системы.Это может быть что угодно.

  E = 2 * VRT_0_0_0_0_base + 1 * (VRT_0_0_0_0_base: VRT_0_0_0_1_base) + 3 * (VRT_0_0_0_0_base: VRT_0_n1_0_0_base) + 4 * (VRT_204_base) + 4 * (VRT_204_base)

 
 Линия E: это то, как сказать Розетте, как оценивать структуру. В этом примере субъединица, которая связана с виртуальным остатком VRT_0_0_0_0_base, является оценивающей субъединицей, а внутренняя энергия в этой субъединице умножается на 2, чтобы получить полную энергию. Добавляют межмолекулярные энергии из подключенной субъединицы VRT_0_0_0_0_base к субъединицам, подключенным к VRT_0_0_0_1_base, VRT_0_n1_0_0_base и VRT_1_0_0_0_base с коэффициентами 1,3 и 4, соответственно.Множители должны быть  целыми числами . 


 
  anchor_residue 29  
 Переход субъединицы закреплен на остатке 29.
  virtual_coordinates_start
 xyz VRT_0_0_0_0 1.000,0.000,0.000 0.000,1.000,0.000 -1.363,24.921,7.618
 xyz VRT_0_0_0_0_base 1.000,0.000,0.000 0.000,1.000,0.000 -2.363,23.921,6.618
 xyz VRT_0_0_0_1 1.000,0.000,0.000 0.000,1.000,0.000 -12.385,24.921,43.670
 xyz VRT_0_0_0_1_base 1.000,0.000,0.000 0.000,1.000,0.000 -13.385,23.921,42.670
 xyz VRT_0_0_0_n1 1.000,0.000,0.000 0.000,1.000,0.000 9.660,24.921, -28.435
 xyz VRT_0_0_0_n1_base 1.000,0.000,0.000 0.000,1.000,0.000 8.660,23.921, -29.435
 xyz VRT_0_n1_0_0 1.000,0.000,0.000 0.000,1.000,0.000 -32.063,24.921,7.618
 xyz VRT_0_n1_0_0_base 1.000,0.000,0.000 0.000,1.000,0.000 -33.063,23.921,6.618
 xyz VRT_0_1_0_0 1.000,0.000,0.000 0.000,1.000,0.000 29.337,24.921,7.618
 xyz VRT_0_1_0_0_base 1.000,0.000,0.000 0.000,1.000,0.000 28.337,23.921,6.618
 xyz VRT_1_0_0_0 -1,000,0,000,0,000 0.000,1,000,0,000 1,363,42,471, -7,618
 xyz VRT_1_0_0_0_base -1.000,0.000,0.000 0.000,1.000,0.000 2.363,41.471, -6.618
 xyz VRT_1_0_n1_0 -1.000,0.000,0.000 0.000,1.000,0.000 1.363,7.371, -7.618
 xyz VRT_1_0_n1_0_base -1.000,0.000,0.000 0.000,1.000,0.000 2.363,6.371, -6.618
 xyz VRT_1_0_0_1 -1.000,0.000,0.000 0.000,1.000,0.000 -9.660,42.471,28.435
 xyz VRT_1_0_0_1_base -1.000,0.000,0.000 0.000,1.000,0.000 -8.660,41.471,29.435
 xyz VRT_1_0_n1_1 -1.000,0.000,0.000 0.000,1.000,0.000 -9.660,7.371,28.435
 xyz VRT_1_0_n1_1_base -1.000,0.000,0.000 0.000,1.000,0.000 -8.660,6.371,29.435
 virtual_coordinates_stop  
 Определите координаты виртуальных остатков. Есть три тройки (X, Y и ORIGIN), каждая из которых имеет три координаты, описывающие единичные векторы (для X и Y) и центр (ORIGIN). Вы можете использовать уникальное имя для этих виртуальных книг.
  connect_virtual JUMP_0_0_0_0_to_subunit VRT_0_0_0_0_base SUBUNIT
 connect_virtual JUMP_0_0_0_1_to_subunit VRT_0_0_0_1_base SUBUNIT
 connect_virtual JUMP_0_0_0_n1_to_subunit VRT_0_0_0_n1_base SUBUNIT
 connect_virtual JUMP_0_n1_0_0_to_subunit VRT_0_n1_0_0_base SUBUNIT
 connect_virtual JUMP_0_1_0_0_to_subunit VRT_0_1_0_0_base SUBUNIT
 connect_virtual JUMP_1_0_0_0_to_subunit VRT_1_0_0_0_base SUBUNIT
 connect_virtual JUMP_1_0_n1_0_to_subunit VRT_1_0_n1_0_base SUBUNIT
 connect_virtual JUMP_1_0_0_1_to_subunit VRT_1_0_0_1_base SUBUNIT
 connect_virtual JUMP_1_0_n1_1_to_subunit VRT_1_0_n1_1_base SUBUNIT
 connect_virtual JUMP_0_0_0_0_to_com VRT_0_0_0_0 VRT_0_0_0_0_base
 connect_virtual JUMP_0_0_0_1_to_com VRT_0_0_0_1 VRT_0_0_0_1_base
 connect_virtual JUMP_0_0_0_n1_to_com VRT_0_0_0_n1 VRT_0_0_0_n1_base
 connect_virtual JUMP_0_n1_0_0_to_com VRT_0_n1_0_0 VRT_0_n1_0_0_base  
 операторов connect_virtual кодируют скачки в системе.Например,
  connect_virtual JUMP_0_0_0_0_to_com VRT_0_0_0_0 VRT_0_0_0_0_base  
 означает, что виртуалы JUMP_0_0_0_0_to_com и VRT_0_0_0_0_base должны быть соединены скачком. Назовем этот прыжок JUMP_0_0_0_0_to_com. Для этого имени можно выбрать любую строку. Если второй переход - SUBUNIT, то это означает, что указан переход от виртуального к субблоку.
  set_dof JUMP_0_0_0_0_to_com x z
set_dof JUMP_0_0_0_0_to_subunit angle_x angle_y angle_z  
 операторов set_dof определяют, какие степени свободы разрешены для конкретного прыжка.Это x, y, z для переводов и angle_x, angle_y, angle_z для вращений. Set_dof следует устанавливать только для основного прыжка. Если с переходом не связан оператор set_dof, то по умолчанию переход не может быть перемещен. Обратите внимание, что движители, которые нарушают переходы, должны быть чувствительны к данным SymDof, хранящимся в SymmetryInfo, чтобы можно было использовать эти ограничения dof. Вы по-прежнему можете вручную установить степенями свободы прыжков, которые не должны двигаться, чтобы сохранить симметрию, если вы устанавливаете прыжки вручную!
 Вы также можете закодировать начальное размещение подразделений, изменив эту строку.Например:
  set_dof JUMP_0_0_0_0_to_com x (20) z (10:20)  
 означает, что x следует установить равным 20 ангстрем, а z следует выбрать случайным образом в диапазоне 10-20. Для углов:
  set_dof JUMP_0_0_0_0_to_subunit angle_x (360) angle_y (360) angle_z (360)  
 означает, что ротация должна быть полностью случайной. Вы также можете кодировать размеры возмущений твердого тела:
  set_dof JUMP_0_0_0_0_to_com x (20: 5) z (10:20)  
 Здесь, что возмущения вдоль x-направления должны быть гауссовскими с размером 5.Чтобы это можно было использовать в rosetta, протокол, который вы используете, должен использовать объекты SymDof в своих средствах перемещения. Ниже в разделе о том, как работать с симметрией, объясняется, как этого добиться.
  set_jump_group JUMPGROUP1 JUMP_0_0_0_0_to_subunit JUMP_0_0_0_1_to_subunit JUMP_0_0_0_n1_to_subunit JUMP_0_n1_0_0_to_subunit JUMP_0_1_0_0_to_subunit JUMP_1_0_0_0_to_subunit JUMP_1_0_n1_0_to_subunit JUMP_1_0_0_1_to_subunit JUMP_1_0_n1_1_to_subunit  
 Эти операторы сообщают rosetta, какие переходы участвуют в отношениях ведущий / ведомый.Первый прыжок в группе - мастер. Название группы прыжков можно выбрать произвольно.
 Если вы запускаете кейс denovo, где у вас нет входной симметричной структуры, вы можете захотеть сгенерировать определение симметрии вручную. Существует дополнительный формат, который можно использовать для создания виртуальных остатков с помощью спецификации операций поворота и перевода. Например:
  имя_симметрии c3
 субъединицы 3
 перецентровать
 number_of_interfaces 1
 E = 3 * VRT1 + 3 * (VRT1: VRT2)
 anchor_residue 17
 virtual_transforms_start
 начало -1,0,0 0,1,0 0,0,0
 гниль Rz 3
 virtual_transforms_stop
 connect_virtual JUMP1 VRT1 VRT2
 connect_virtual JUMP2 VRT2 VRT3
 set_dof BASEJUMP x (50) angle_x angle_y angle_z  
 Обратите внимание, что мы не даем названия остаткам VRT, которые они автоматически присваивают VRT1, VRT2 ,...так далее. Группы переходов также рассчитываются автоматически. Между виртуалами автоматически добавляются переходы.
  перецентр  
 Указывает rosetta повторно центрировать входную субъединицу так, чтобы CA якорного остатка находился в начале координат (0,0,0).
  virtual_transforms_start  
 Виртуальные остатки будут указываться посредством операций вращения и перевода вместо жестко заданных координат.
  virtual_transforms_start последовательный  
 последовательные ключевые слова сигнализируют о том, что для каждого виртуального объекта, который размещен, будут применены все преобразования между  virtual_transforms_start  и  virtual_transforms_stop .По умолчанию
  начало -1,0,0 0,1,0 0,0,0  
 - это позиция первого виртуального остатка в системе (единичные векторы X, Y и координаты ORGIN). Первое преобразование (я) будет применено к этому виртуальному объекту для генерации второго.
  гниль Rz 3  
 применяет 3-кратное вращение вокруг абсолютной оси z. (вы можете использовать Rx, Ry и Rz). Вы также можете сказать:
  rot Rz_angle 120  
, что означает необходимость вращения на 120 градусов.
  транс 4,5,2  
 кодирует операцию перевода, три числа задают вектор перевода.
  Симметрии с зеркальными операциями 
 Rosetta также предлагает поддержку симметрии с помощью зеркальных операций. Зеркальная симметрия задается с помощью «обратного виртуального» остатка, который определяет левую локальную систему координат. Эти обратные виртуалы могут использоваться для определения зеркальной симметрии следующим образом:
  имя_симметрии Cs
E = 2 * VRT0 + 1 * (VRT0: VRT1)
anchor_residue 1
virtual_coordinates_start
xyz VRT0 1.0,0,0,0,0 0,0,1,0,0,0 0,0,0,0,0,0
xyzM VRT1 1,0,0,0,0,0 0,0,1,0,0,0 0,0,0,0,0,0
virtual_coordinates_stop
connect_virtual JUMP0 VRT0 ПОДБЛОК
connect_virtual JUMP1 VRT1 ПОДБЛОК
connect_virtual JUMP01 VRT0 VRT1
set_dof JUMP0 x y z angle_x angle_y angle_z
set_jump_group JUMPGROUP2 JUMP0 JUMP1  
 Выше xyzM объявляет обратный виртуальный остаток. Подключение этого инверсного виртуального устройства к субблоку делает подключенный субблок инвертированным. Приведенный выше фрагмент декларирует симметричную систему  Cs  с зеркальной плоскостью по XY.
 Кристаллическая симметрия с зеркальными операциями автоматически обрабатывается с помощью  -symmetry_definition CRYST1  (см. Выше).
  Опции для прямого контакта 
  тип слайда (СЛУЧАЙНЫЙ | ПОСЛЕДОВАТЕЛЬНЫЙ | ПОСЛЕДОВАТЕЛЬНЫЙ)  
 Управляет выполнением многомерных движений скольжения в контакт. Например, для симметрии dn существует два направления скольжения. Слайд может быть выполнен путем случайного выбора направления слайда для каждого шага слайда (RANDOM), случайного выбора направления, которое следует сдвинуть первым, но всегда последовательно пройти через оба (SEQUENTIAL) или определить порядок самостоятельно (ORDERED_SEQUENTIAL).СЛУЧАЙНОЕ по умолчанию.
  тип_ критерия слайда (CEN_DOCK_SCORE | FA_REP_SCORE | КОНТАКТЫ)  
 Определяет критерии отказа от слайда. Либо CEN_DOCK_SCORE, FA_REP_SCORE, либо количество контактов. CEN_DOCK_SCORE по умолчанию.
  slide_criteria_val (значение | АВТОМАТИЧЕСКИЙ)  
 Устанавливает фактическое значение, когда перемещение слайда прекращается с учетом типа критерия. По умолчанию установлено значение АВТОМАТИЧЕСКИЙ, что означает, что ROSETTA решит это сама.Действительно полезно только для типа КОНТАКТЫ.
  slide_order название перехода  
 Если вы используете тип слайдов ORDERED_SEQUENTIAL, вы можете указать порядок, в котором будут посещаться переходы, соответствующие разрешенным переводам. Используются имена переходов, определенные в файле определения симметрии.
 Есть несколько необходимых шагов, чтобы ваш протокол бесперебойно работал с симметричными структурами. Главный руководящий принцип заключается в том, что любую операцию, изменяющую форму позы, возможно, придется изменить.
  Настройка симметричной позы  Вызовите SetupForSymmetryMover (src / protocol / move / symry / SetupForSymmetryMover.cc) в начале протокола до того, как произойдут какие-либо конформационные изменения в позе. Это принимает входную позу мономера и создает симметричную основу олигомера на основе файла symry_definition.
  Подсчет баллов  Используйте ScoreFunctionOP или ScoreFunctionCOP вместо ScoreFunction, поскольку симметричная функция оценки (SymmetricScoreFunction) является производной от ScoreFunction.Это будет автоматически при использовании ScoreFunctionFactory. ScoreFunctionFactory проверяет, был ли файл определения симметрии определен как опция, и в этом случае создает функцию SymmetricScoreFunction.
  Packing and RotamerTrials  Если поза симметрична, используйте симметричные версии PackRotamersMover и RotamerTrialsMover (src / protocol / move / SymPackRotamerMover.cc и src / protocol / move / SymRotamerTrialsMover)
  Свертывание  Если поза симметрична, используйте симметричные версии MinimizeMover (src /tocols / move / SymMinimizeMover.куб.см)
  Манипуляции с деревом свертки  Если вы изменяете дерево свертки в протоколе, убедитесь, что симметричная структура правильно обновлена. Простая
 Симметрия
 - Основы GD&T 
  Символ GD&T:  
  Относительно Datum : Да 
  Применимо MMC или LMC:  Нет 
  Выноска на чертеже:  
6
0 Описание: Симметрия GD&T - это трехмерный допуск, который используется для обеспечения того, чтобы два элемента детали были однородными на базовой плоскости.Установленная «истинная» центральная плоскость устанавливается по исходной точке, и для того, чтобы симметрия была в пределах допуска, среднее расстояние между каждой точкой на двух поверхностных элементах должно находиться рядом с этой центральной плоскостью. У каждого набора точек на опорных объектах будет средняя точка, которая находится прямо между ними. Если вы возьмете все средние точки всей поверхности, они должны находиться в пределах зоны допуска, чтобы быть в спецификации. Симметрия - не очень распространенная выноска GD&T, поскольку она имеет очень ограниченное функциональное использование (положение центрирования выполняется с помощью Position), а проверка и измерение симметрии могут быть трудными (см. Заключительные примечания).
  GD & T Толерантность зона: 
 параллельных плоскостей на равных сторонах центральной базовой плоскости. Все средние точки симметричных поверхностей должны находиться в пределах этой зоны.
  Калибровка / Измерение: 
 Как указывалось ранее, симметрию очень трудно измерить. Из-за того, что его зона допуска ограничена виртуальной плоскостью, у вас не может быть датчика, чтобы правильно измерить этот элемент быстро. Обычно для измерения симметрии настраивается КИМ для расчета теоретической базовой плоскости средней точки, измерения поверхностей обеих требуемых поверхностей, а затем определения местоположения средних точек по отношению к базовой плоскости.Это сложный и иногда неточный метод определения симметричности детали.
  Связь с другими символами GD&T: 
 Симметрия - это некруглая версия концентричности. В то время как концентричность действительно является фокусом симметрии относительно базовой оси, символ симметрии фокусируется на симметрии относительно базовой плоскости. Оба символа указывают на то, что теоретическая центральная точка привязки ограничена определенным пределом, чтобы гарантировать однородность всей конструкции.
  Когда используется: 
 Если вы хотите убедиться, что центральная плоскость двух симметричных элементов всегда удерживается точно по центру И имеет ровную форму вдоль поверхности детали. Этот символ может использоваться только для баланса массы и распределения формы. Однако в большинстве случаев лучше избегать использования, так как это очень сложная выноска для измерения и ее легко заменить допуском положения.
  Пример: 
 Если у вас есть вращающийся карданный шарнир, канавка, которая должна всегда иметь равномерный баланс, вам нужно будет убедиться, что сопрягаемая часть всегда расположена так, чтобы попадать в центр канавки и что форма поверхности должным образом сбалансирована… Вместо того, чтобы расширять канавку, вызывающую ослабление соединения, вы можете ограничить его симметрией.
 Пример симметрии 1: обозначьте симметрию, чтобы обеспечить центрирование канавки на средней плоскости блока защелки.
 Затем необходимо измерить деталь, чтобы убедиться, что все средние точки сторон блока защелки симметричны относительно центральной оси. Часть должна быть измерена следующим образом:
  1.  Меры шириной и расположение обоего сторон опорного блока с помощью базовой точки A (40 мм), а также определить, где точная среднюю плоскость расположена, чтобы установить нашу зону допуска.
  2.  Сторона 1 и Сторона 2 детали сканируются на предмет их фактических профилей
  3.  С помощью программы средние точки сканирования Стороны 1 и Стороны 2 накладываются на плоскости виртуальных зон допуска и определяются, находятся ли они в пределах допуска.
  
  Заключительные примечания: 
  В большинстве случаев следует избегать симметрии из-за ее особых функциональных требований и сложности измерения.  С помощью плоскостности, параллельности и истинного положения вы можете определить точно такие же ограничения на детали, хотя и требуются дополнительные выноски и измерения.Однако, поскольку истинное положение может быть измерено с помощью датчика (если используется MMC), а плоскостность автоматически контролируется размером и измеряется непосредственно с поверхностей, ими можно управлять в процессе и не требовать своевременных измерений КИМ.
, Томми, 4 ноября 2014 г.
 Станьте инженером в своей компании
 Изучите GD&T в удобном для вас темпе и с уверенностью примените его в реальном мире.
 Пройдите обучение GD&T
 Симметрия [Центр документации] 
 Эта страница существует в разделе Old ArtZone Wiki этого сайта.Прочтите информацию, представленную на связанной странице, чтобы лучше понять значение этого факта.
 Меню Options вкладки Parameter включает команду  Symmetry , которая открывает диалоговое окно  Symmetry , показанное на следующем рисунке. Симметрия может быть полезной экономией времени при создании сцен, потому что вы можете позировать часть фигуры, а затем применить симметрию, чтобы применить ту же позу к частям другой стороны фигуры. Таким образом, диалоговое окно «Симметрия» может значительно ускорить и упростить работу по позированию.
 В диалоговом окне «Симметрия» есть две вкладки:  Параметры  и  Параметры . Сделав выбор на одной или обеих вкладках, выберите  Принять  в нижней части экрана, чтобы выполнить выбранное действие (я), или  Отменить , чтобы закрыть диалоговое окно Симметрия и отменить изменения.
 Параметры симметрии 
 Вкладка  «Параметры» , показанная ниже, управляет тем, как симметрия применяется к выбранной фигуре. В настоящее время доступны следующие варианты:
  •   Узлы : вы можете выбрать применение симметрии либо к уже выбранным  элементам , либо к фигуре  Корневой узел , то есть ко всей фигуре (чтобы все части были идеально симметричными)
  •   Распространение : Вы можете использовать это, чтобы выбрать  Нет  (где изменения не перемещаются вниз по иерархии от выбранного элемента (ов)) или внести изменения  Рекурсивно , где применяется симметрия ко всем дочерним костям выбранных узлов (то есть изменения коснутся не только выбранных узлов, но и их дочерних костей.)
  •   Направление : В каком направлении вы вносите эти изменения? Слева направо, где изменения на левой стороне фигуры перемещаются вправо, справа налево, где изменения перемещаются в противоположном направлении. Вы также можете поменять местами влево и вправо, что удобно, если вы хотите полностью отразить позу.
  •   Узлы туловища : определяет, что вы хотите сделать с частями, которые проходят вдоль средней линии фигуры (например, бедро, живот, грудь, шея и голова человека.) Вы можете выбрать  Leave Alone , при котором эти элементы останутся на месте,  Mirror Y | Z Rotations , который установит параметры Side-Side и Twist для элементов центральной линии в противоположность текущим настройкам, или вы можете выбрать  Zero Parameters , который установит эти два параметра на ноль.
  •   Префикс левого узла : Позволяет вам установить первые буквы всех «левых» дочерних костей (то есть костей, которые находятся на «левой» стороне фигуры), которые  DAZ  Studio должен искать при настройке симметрии.
  •   Префикс правого узла : Выполняет те же функции, что и префикс левого узла, но устанавливает их для всех затронутых костей «правой» стороны.
  •   Transforms : эти флажки позволяют вам выбрать, что именно вы хотите изменить - вращение дочерней кости (по каждой оси), перемещение дочерней кости (по каждой оси) или масштабирование (общее масштабирование или выборочно по каждой оси по желанию) .)
 Параметры симметрии 
 Вкладка  «Настройки»  контролирует, какие параметры будут включены при применении симметрии сейчас и при использовании этой функции в будущем (пока не будут изменены).Доступные варианты:
  •   Set Preferred Options : Это позволяет вам установить эти параметры сейчас (или, альтернативно, когда выбран «Set Preferred Options on Accept», устанавливать предпочтения всякий раз, когда вы используете эту функцию.)
  •   Прочитать предпочтительные параметры : Эта кнопка позволяет увидеть, какие настройки симметрии сохранены в данный момент.
  •   Восстановить параметры по умолчанию : Эта кнопка сбрасывает все настройки симметрии до заводских значений по умолчанию (которые показаны на этих рисунках.)
 Документация MEEP 
 Документация MEEP
  •  Руководство
  •  Введение
  •  Загрузить
  •  Часто задаваемые вопросы
  •  Установка
  •  Собрать из исходного кода
  •  Благодарности
  •  Лицензия и авторские права
 Характеристики
  •  Материалы
  •  Субпиксельное сглаживание
  •  Использование симметрии
  •  Идеально согласованные слои
  •  Parallel Meep (Параллельный звук)
  •  Синхронизация магнитного и электрического полей
  •  Разложение мод
  •  Полевые функции
  •  Функция Run - это не цикл
  •  Решетка Йи
  •  Единицы и нелинейность
  •  2d ячейка с волновым вектором вне плоскости
  •  Собственный преобразователь частоты
 Интерфейс Python
  •  Пользовательский интерфейс
  •  Информация для разработчиков
  •  Учебное пособие / Основы
  •  Учебное пособие / Цилиндрические координаты
  •  Учебное пособие / Резонансные режимы и передача в волноводной полости
  •  Учебное пособие / Дисперсия материалов
  •  Учебное пособие / Генерация третьей гармоники
  •  Учебное пособие / Спектры ближнего и дальнего поля
  •  Учебное пособие / Локальная плотность состояний
  •  Учебное пособие / Оптические силы
  •  Учебное пособие / Гиротропные среды
  •  Учебное пособие / Многоуровневая атомная восприимчивость
  •  Учебное пособие / Решатель частотной области
  •  Учебное пособие / Источник собственных мод
  •  Учебное пособие / Пользовательский источник
  •  Учебное пособие / Разложение режимов
  •  Учебное пособие / Импорт GDSII
  •  Учебное пособие / Дополнительный решатель
 Схема интерфейса
  •  Пользовательский интерфейс
  •  Учебное пособие / Основы
  •  Учебное пособие / Цилиндрические координаты
  •  Учебное пособие / Резонансные режимы и передача в волноводной полости
  •  Учебное пособие / Дисперсия материалов
  •  Учебное пособие / Генерация третьей гармоники
  •  Учебное пособие / Спектры ближнего и дальнего поля
  •  Учебное пособие / Локальная плотность состояний
  •  Учебное пособие / Оптические силы
  •  Учебное пособие / Гиротропные среды
  •  Учебное пособие / Многоуровневая атомная восприимчивость
  •  Учебное пособие / Решатель частотной области
  •  Учебное пособие / Источник собственных мод
  •  Учебное пособие / Пользовательский источник
  •  Учебное пособие / Разложение режимов
  •  Учебник / Силы Казимира
  •  Информация о хитрости и схеме
 Интерфейс C ++
  •  Информация для разработчиков
  •  Чанки и симметрия
 Инструмент симметрии 
 С помощью инструмента  Symmetry  вы можете интерактивно исправить незначительные ошибки симметрии.Modo использует допуск на расстояние, чтобы решить, есть ли у вершин соответствующая вершина на противоположной стороне оси симметрии. Если Modo находит вершину в пределах допуска, он перемещает эту вершину, чтобы она соответствовала своему партнеру на другой стороне сетки.
  Примечание:  Симметрия должна быть активна для использования этого инструмента. Вы активируете функцию  Symmetry , выбрав ось из списка  Symmetry  на панели инструментов Modo  Modes  или выбрав  Edit >  Symmetry >  axis для зеркального отражения по .См. Раздел «Применение точности» для получения подробной информации.
 Использование инструмента симметрии 
 1. Нажмите кнопку  Symmetry  в верхней части окна просмотра.
 2. Добавьте геометрию к вашей сцене.
 3. В строке меню щелкните  Геометрия >  Инструмент симметрии .
 4. Щелкните в области просмотра и перетащите, чтобы увеличить пороговое расстояние.
 Свойства  инструмента симметрии  отображаются на левой панели. Modo указывает несимметричные вершины желтыми квадратами, которые исчезают при увеличении порога. Если все указанные вершины (желтые квадраты) не исчезают, повторно примените инструмент с текущим порогом, щелкнув средней кнопкой мыши. Это может очистить оставшиеся вершины.
  Примечание:  При включении  Использовать топологию  работает только в том случае, если некоторая часть модели изначально симметрична.Если это не так, снимите флажок  Использовать топологию .
  Порог 
 Указывает пороговое значение.Вы можете интерактивно настроить значение  Threshold , перетащив его в окно 3D-просмотра. Или введите конкретное значение.
  Использовать топологию 
 Когда этот параметр включен, работает рекурсивно из точки, которую Modo знает как симметричную, и предполагает, что аналогично связанные соседи также должны быть симметричными, вместо того, чтобы находить соответствующую вершину непосредственно поперек оси.Это позволяет получить гораздо более надежное решение, потому что меньше шансов рассмотреть одну вершину, а затем найти неправильную соответствующую вершину.
 
Добавить комментарий 
Ваш адрес email не будет опубликован. Обязательные поля помечены *