Как провести оси симметрии фигур. Ось симметрии — что это такое? Фигуры, имеющие ось симметрии
I . Симметрия в математике :
Основные понятия и определения.
Осевая симметрия (определения, план построения, примеры)
Центральная симметрия (определения, план построения, при меры)
Обобщающая таблица (все свойства, особенности)
II . Применения симметрии:
1) в математике
2) в химии
3) в биологии, ботанике и зоологии
4) в искусстве, литературе и архитектуре
1. Основные понятия симметрии и ее виды.Понятие симметрии пр оходит
через всю историю человечества. Оно
встречается уже у истоков человеческого
знания. Возникло оно в связи с изучением
живого организма, а именно человека.
И употреблялось скульпторами ещё в 5
веке до н. э. Слово “симметрия” греческое,
оно означает “соразмерность,
пропорциональность, одинаковость в
расположении частей”. Его широко
используют все без исключения направления
современной науки. Об этой закономерности
задумывались многие великие люди.
Например, Л. Н. Толстой говорил: “Стоя
перед черной доской и рисуя на ней мелом
разные фигуры, я вдруг был поражен
мыслью: почему симметрия понятна
глазу? Что такое симметрия? Это врожденное
чувство, отвечал я сам себе. На чем же
оно основано?”. Действительно
симметричность приятна глазу. Кто не
любовался симметричностью творений
природы: листьями, цветами, птицами,
животными; или творениями человека:
зданиями, техникой, – всем тем, что нас
с детства окружает, тем, что стремится
к красоте и гармонии. Герман Вейль
сказал: “Симметрия является той
идеей, посредством которой человек на
протяжении веков пытался постичь и
создать порядок, красоту и совершенство”.
Герман Вейль – это немецкий математик.
Его деятельность приходится на первую
половину ХХ века. Именно он сформулировал
определение симметрии, установил по
каким признакам усмотреть наличие или,
наоборот, отсутствие симметрии в том
или ином случае.
2. Осевая симметрия.
2.1 Основные определения
Определение. Две точки А и А 1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА 1 и перпендикулярна к нему. Каждая точка прямой а считается симметричной самой себе.
Определение. Фигура называется симметричной относительно прямой а , если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая а называется осью симметрии фигуры. Говорят также, что фигура обладает осевой симметрией.
2.2 План построения
И так, для построения симметричной фигуры относительно прямой от каждой точки проводим перпендикуляр к данной прямой и продлеваем его на такое же расстояние, отмечаем полученную точку. Так поступаем с каждой точкой, получаем симметричные вершины новой фигуры. Затем последовательно их соединяем и получаем симметричную фигуру данной относительной оси.
2.3 Примеры фигур, обладающих осевой симметрией.
3. Центральная симметрия
3.1 Основные определения
Определение . Две точки А и А 1 называются симметричными относительно точки О, если О — середина отрезка АА 1 . Точка О считается симметричной самой себе.
Определение. Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.
3.2 План построения
Построение треугольника симметричного данному относительно центра О.
Чтобы построить
точку, симметричную точке А относительно
точки О ,
достаточно провести прямую ОА (рис. 46) и по другую
сторону от точки О отложить
отрезок, равный отрезку ОА .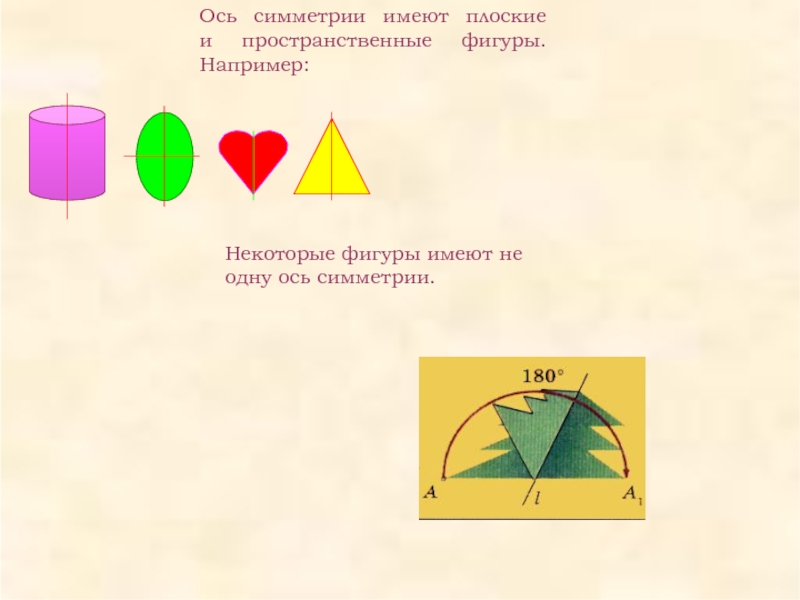 Иными
словами, точки А
и
;
В и
;
С и симметричны
относительно некоторой точки
О. На рис. 46
построен треугольник, симметричный
треугольнику ABC относительно
точки О. Эти
треугольники равны.
Иными
словами, точки А
и
;
В и
;
С и симметричны
относительно некоторой точки
О. На рис. 46
построен треугольник, симметричный
треугольнику ABC относительно
точки О. Эти
треугольники равны.
Построение симметричных точек относительно центра.
На рисунке точки М и М 1 , N и N 1 симметричны относительно точки О, а точки Р и Q не симметричны относительно этой точки.
Вообще фигуры, симметричные относительно некоторой точки, равны.
3.3 Примеры
Приведём примеры фигур, обладающие центральной симметрией. Простейшими фигурами, обладающими центральной симметрией, является окружность и параллелограмм.
Точка О называется центром симметрии фигуры. В подобных случаях фигура обладает центральной симметрией. Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма- точка пересечения его диагоналей.
Прямая также обладает центральной симметрией, однако в отличие от окружности и параллелограмма, которые имеют только один центр симметрии (точка О на рисунке) у прямой их бесконечно много — любая точка прямой является её центром симметрии.
На рисунках показан угол симметричный относительно вершины, отрезок симметричный другому отрезку относительно центра А и четырехугольник симметричный относительно своей вершины М.
Примером фигуры, не имеющей центра симметрии, является треугольник.
4. Итог урока
Обобщим полученные знания. Сегодня на уроке мы познакомились с двумя основными видами симметрии: центральная и осевая. Посмотрим на экран и систематизируем полученные знания.
Обобщающая таблица
Осевая симметрия | Центральная симметрия | |
Особенность | Все точки фигуры должны быть симметричны относительно какой-нибудь прямой. | Все
точки фигуры должны, симметричны
относительно точки, выбранной в
качестве центра симметрии. |
Свойства | 1. Симметричные точки лежат на перпендикулярах к прямой. 3. Прямые переходят в прямые, углы в равные углы. 4. Сохраняются размеры и формы фигур. | 1. Симметричные точки лежат на прямой, проходящей через центр и данную точку фигуры. 2. Расстояние от точки до прямой равно расстоянию от прямой до симметричной точки. 3. Сохраняются размеры и формы фигур. |
II. Применение симметрии
Математика | На уроках алгебры мы изучили графики функций y=x и y=x На рисунках представлены различные картинки, изображенные с помощью ветвей парабол. (а) Октаэдр, (б) ромбический додекаэдр, (в) гексагональной октаэдр. | |
Русский язык | Печатные буквы русского алфавита тоже обладают различными видами симметрий. В русском языке есть «симметричные» слова — палиндромы , которые можно читать одинаково в двух направлениях. | А Д Л М П Т Ф Ш – вертикальная ось В Е З К С Э Ю — горизонтальная ось Ж Н О Х — и вертикальная и горизонтальная Б Г И Й Р У Ц Ч Щ Я – ни какой оси Радар шалаш Алла Анна |
Литература | Могут быть палиндромичес- кими и предложения. Брюсов написал стихотворение «Голос луны», в котором каждая строка — палиндром. Посмотрите на четверости -шие А.С.Пушкина «Медный всадник». Если провести линию после второй строчки мы можем заметить элементы осевой симметрии | А роза упала на лапу Азора. Я иду с мечем судия. (Державин) «Искать такси» «Аргентина манит негра», «Ценит негра аргентинец», «Леша
на полке клопа нашел». В гранит оделася Нева; Мосты повисли над водами; Темно-зелеными садами Ее покрылись острова… |
Биология | Тело человека построено по принципу двусторонней симметрии. Большинство из нас рассматривает мозг как единую структуру, в действительности он разделён на две половины. Эти две части — два полушария — плотно прилегают друг к другу. В полном соответствии с общей симметрией тела человека каждое полушарие представляет собой почти точное зеркальное отображение другого Управление основными движениями тела человека и его сенсорными функциями равномерно распределено между двумя полушариями мозга. Левое полушарие контролирует правую сторону мозга, а правое — левую сторону. |
Ботаника | Цветок считается симметричным, когда каждый околоцветник состоит из равного числа частей. Цветки, имея парные части, считаются цветками с двойной симметрией и т.д. Тройная симметрия обычна для однодольных растений, пятерная — для двудольных Характерной чертой строения растений и их развития является спиральность. Обратите внимание на побеги листорасположения – это тоже своеобразный вид спирали – винтовая. Еще Гёте, который был не только великим поэтом, но и естествоиспытателем, считал спиральность одним из характерных признаков всех организмов, проявлением самой сокровенной сущности жизни. Спирально закручиваются усики растений, по спирали происходит рост тканей в стволах деревьев, по спирали расположены семечки в подсолнечнике, спиральные движения наблюдаются при росте корней и побегов. | Характерной чертой строения растений и их развития является спиральность. Посмотрите на сосновую шишку.
Чешуйки на ее поверхности расположены
строго закономерно — по двум спиралям,
которые пересекаются приблизительно
под прямым углом. |
Зоология | Под симметрией у животных понимают соответствие в размерах, форме и очертаниях, а также относительное расположение частей тела, находящихся на противоположных сторонах разделяющей линии. При радиальной или лучистой симметрии тело имеет форму короткого или длинного цилиндра либо сосуда с центральной осью, от которого отходят в радиальном порядке части тела. Это кишечнополостные, иглокожие, морские звёзды. При билатеральной симметрии осей симметрии три, но симметричных сторон только одна пара. Потому что две другие стороны — брюшная и спинная — друг на друга не похожи. Этот вид симметрии характерен для большинства животных, в том числе насекомых, рыб, земноводных, рептилий, птиц, млекопитающих. | Осевая симметрия |
Различные виды симметрии физических явлений: симметрия электрического и магнитного полей (рис. 1) Во взаимно перпендикулярных плоскостях симметрично распространение электромагнитных волн (рис. 2) | рис.1 рис.2 | |
Искусство | В произведениях искусства часто можно наблюдать зеркальную симметрию. Зеркальная» симметрия широко встречается в произведениях искусства примитивных цивилизаций и в древней живописи. Средневековые религиозные картины также характеризуются этим видом симметрии. Одно
из лучших ранних произведений Рафаэля
– «Обручение Марии» — создано в
1504 году. Под солнечным голубым
небом раскинулась долина, увенчанная
белокаменным храмом. На первом
плане – обряд обручения.
Первосвященник сближает руки
Марии и Иосифа. За Марией – группа
девушек, за Иосифом – юношей. Обе
части симметричной композиции
скреплены встречным движением
персонажей. |
Химия | Молекула воды имеет плоскость симметрии (прямая вертикальная линия).Исключительно важную роль в мире живой природы играют молекулы ДНК (дезоксирибонуклеиновая кислота). Это двуцепочечный высокомолекулярный полимер, мономером которого являются нуклеотиды. Молекулы ДНК имеют структуру двойной спирали, построенной по принципу комплементарности. | |
Архите ктура | Издавна человек использовал симметрию в архитектуре. Особенно блистательно использовали симметрию в архитектурных сооружениях древние зодчие. Причем древнегреческие архитекторы были убеждены, что в своих произведениях они руководствуются законами, которые управляют природой. Выбирая симметричные формы, художник тем самым выражал свое понимание природной гармонии как устойчивости и равновесия. В городе Осло, столице Норвегии, есть выразительный ансамбль природы и художественных произведений. Это Фрогнер – парк – комплекс садово-парковой скульптуры, который создавался в течение 40 лет. | Дом Пашкова Лувр (Париж) |
© Сухачева Елена Владимировна, 2008-2009гг.
Жизнь людей наполнена симметрией. Это удобно, красиво, не нужно выдумывать новых стандартов. Но что она есть на самом деле и так ли красива в природе, как принято считать?
Симметрия
С древних времен люди стремятся упорядочить мир вокруг себя. Поэтому что-то считается красивым, а что-то не очень. С эстетической точки зрения как привлекательные рассматриваются золотое и серебряное сечения, а также, разумеется, симметрия. Этот термин имеет греческое происхождение и дословно означает «соразмерность». Разумеется, речь идет не только о совпадении по этому признаку, но также и по некоторым другим.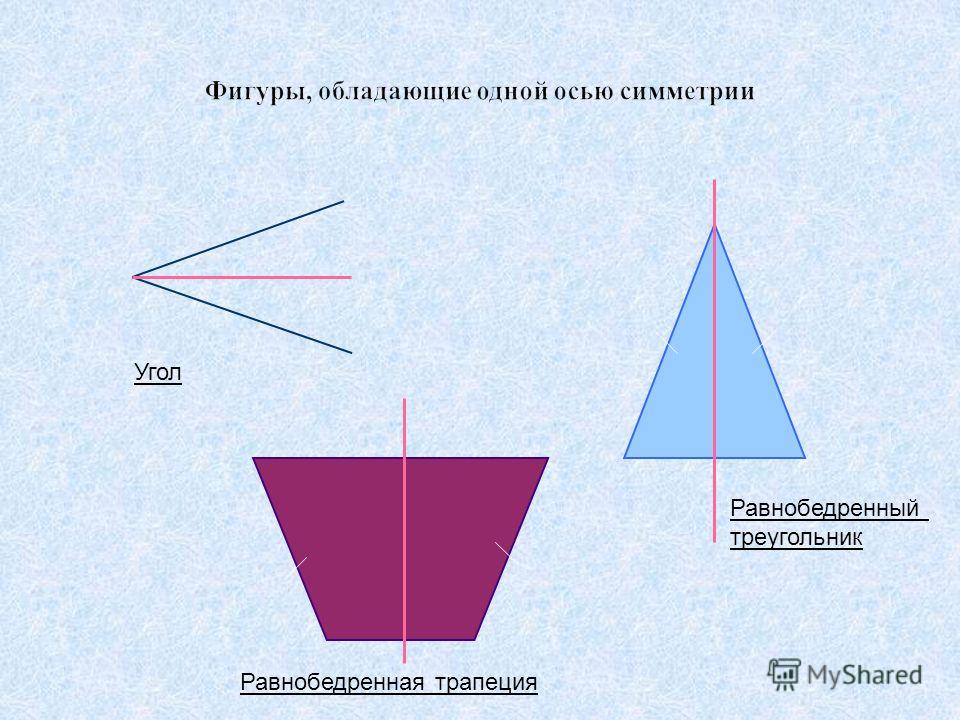 В общем смысле симметрия — это такое свойство объекта, когда в результате тех или иных образований результат равен исходным данным. Это встречается как в живой, так и в неживой природе, а также в предметах, сделанных человеком.
В общем смысле симметрия — это такое свойство объекта, когда в результате тех или иных образований результат равен исходным данным. Это встречается как в живой, так и в неживой природе, а также в предметах, сделанных человеком.
Прежде всего термин «симметрия» употребляется в геометрии, но находит применение во многих научных областях, причем его значение остается в общем и целом неизменным. Это явление достаточно часто встречается и считается интересным, поскольку различается несколько его видов, а также элементов. Использование симметрии также интересно, ведь она встречается не только в природе, но и в орнаментах на ткани, бордюрах зданий и многих других рукотворных предметах. Стоит рассмотреть это явление поподробнее, поскольку это крайне увлекательно.
Употребление термина в других научных областях
В дальнейшем симметрия будет рассматриваться с точки зрения геометрии, однако стоит упомянуть, что данное слово используется не только здесь. Биология, вирусология, химия, физика, кристаллография — все это неполный список областей, в которых данное явление изучается с различных сторон и в разных условиях. От того, к какой науке относится этот термин, зависит, например, классификация. Так, разделение на типы серьезно варьируется, хотя некоторые основные, пожалуй, остаются неизменными везде.
Классификация
Различают несколько основных типов симметрии, из которых наиболее часто встречаются три:
Кроме того, в геометрии различают также следующие типы, они встречаются значительно реже, но не менее любопытны:
- скользящая;
- вращательная;
- точечная;
- поступательная;
- винтовая;
- фрактальная;
- и т. д.
В биологии все виды называются несколько иначе, хотя по сути могут быть такими же. Подразделение на те или иные группы происходит на основании наличия или отсутствия, а также количества некоторых элементов, таких как центры, плоскости и оси симметрии. Их следует рассмотреть отдельно и более подробно.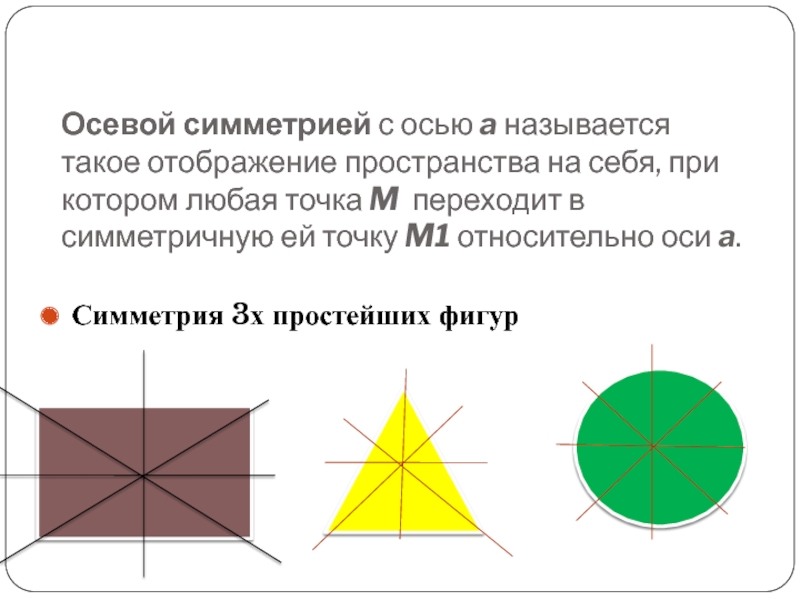
Базовые элементы
В явлении выделяют некоторые черты, одна из которых обязательно присутствует. Так называемые базовые элементы включают в себя плоскости, центры и оси симметрии. Именно в соответствии с их наличием, отсутствием и количеством определяется тип.
Центром симметрии называют точку внутри фигуры или кристалла, в которой сходятся линии, соединяющие попарно все параллельные друг другу стороны. Разумеется, он существует не всегда. Если есть стороны, к которым нет параллельной пары, то такую точку найти невозможно, поскольку ее нет. В соответствии с определением, очевидно, что центр симметрии — это то, через что фигура может быть отражена сама на себя. Примером может служить, например, окружность и точка в ее середине. Этот элемент обычно обозначается как C.
Плоскость симметрии, разумеется, воображаема, но именно она делит фигуру на две равные друг другу части. Она может проходить через одну или несколько сторон, быть параллельной ей, а может делить их. Для одной и той же фигуры может существовать сразу несколько плоскостей. Эти элементы обычно обозначаются как P.
Но, пожалуй, наиболее часто встречается то, что называют «оси симметрии». Это нередкое явление можно увидеть как в геометрии, так и в природе. И оно достойно отдельного рассмотрения.
Оси
Часто элементом, относительно которого фигуру можно назвать симметричной,
выступает прямая или отрезок. В любом случае речь идет не о точке и не о плоскости. Тогда рассматриваются фигур. Их может быть очень много, и расположены они могут быть как угодно: делить стороны или быть параллельными им, а также пересекать углы или не делать этого. Оси симметрии обычно обозначаются как L.
Примерами могут служить равнобедренные и В первом случае будет вертикальная ось симметрии, по обе стороны от которой равные грани, а во втором линии будут пересекать каждый угол и совпадать со всеми биссектрисами, медианами и высотами. Обычные же треугольники ею не обладают.
Кстати, совокупность всех вышеназванных элементов в кристаллографии и стереометрии называется степенью симметрии. Этот показатель зависит от количества осей, плоскостей и центров.
Примеры в геометрии
Условно можно разделить все множество объектов изучения математиков на фигуры, имеющие ось симметрии, и такие, у которых ее нет. В первую категорию автоматически попадают все окружности, овалы, а также некоторые частные случаи, остальные же попадают во вторую группу.
Как и в случае, когда говорилось про ось симметрии треугольника, данный элемент для четырехугольника существует не всегда. Для квадрата, прямоугольника, ромба или параллелограмма он есть, а для неправильной фигуры, соответственно, нет. Для окружности оси симметрии — это множество прямых, которые проходят через ее центр.
Кроме того, интересно рассмотреть и объемные фигуры с этой точки зрения. Хотя бы одной осью симметрии помимо всех правильных многоугольников и шара будут обладать некоторые конусы, а также пирамиды, параллелограммы и некоторые другие. Каждый случай необходимо рассматривать отдельно.
Примеры в природе
В жизни называется билатеральной, она встречается наиболее
часто. Любой человек и очень многие животные тому пример. Осевая же называется радиальной и встречается гораздо реже, как правило, в растительном мире. И все-таки они есть. Например, стоит подумать, сколько осей симметрии имеет звезда, и имеет ли она их вообще? Разумеется, речь идет о морских обитателях, а не о предмете изучения астрономов. И правильным ответом будет такой: это зависит от количества лучей звезды, например пять, если она пятиконечная.
Кроме того, радиальная симметрия наблюдается у многих цветков: ромашки, васильки, подсолнухи и т. д. Примеров огромное количество, они буквально везде вокруг.
Аритмия
Этот термин, прежде всего, напоминает большинству о медицине и кардиологии, однако он изначально имеет несколько другое значение. В данном случае синонимом будет «асимметрия», то есть отсутствие или нарушение регулярности в том или ином виде. Ее можно встретить как случайность, а иногда она может стать прекрасным приемом, например, в одежде или архитектуре. Ведь симметричных зданий очень много, но знаменитая чуть наклонена, и хоть она не одна такая, но это самый известный пример. Известно, что так получилось случайно, но в этом есть своя прелесть.
В данном случае синонимом будет «асимметрия», то есть отсутствие или нарушение регулярности в том или ином виде. Ее можно встретить как случайность, а иногда она может стать прекрасным приемом, например, в одежде или архитектуре. Ведь симметричных зданий очень много, но знаменитая чуть наклонена, и хоть она не одна такая, но это самый известный пример. Известно, что так получилось случайно, но в этом есть своя прелесть.
Кроме того, очевидно, что лица и тела людей и животных тоже не полностью симметричны. Проводились даже исследования, согласно результатам которых «правильные» лица расценивались как неживые или просто непривлекательные. Все-таки восприятие симметрии и это явление само по себе удивительны и пока не до конца изучены, а потому крайне интересны.
«Симметрия вокруг нас» — Все виды осевой симметрии. Вращения. Греческое слово симметрия означает «пропорциональность», «гармония». Произвольная. Центральная относительно точки. Симметрия в пространстве. Вращения (поворотная). В геометрии есть фигуры, которые имеют. Симметрия. Осевая. Один вид симметрии. Вокруг нас. Центральная.
«В мире симметрии» — Орнаменты, фризы имеют в своей основе периодически повторяющийся узор. Симметричны формы жука, червяка, гриба, листа, цветка и др. Большинство зданий зеркально симметричны. Во всем ли в жизни должна быть симметрия? Зачем надо знать о симметрии, изучая технические науки? Что такое симметрия? Симметрия в природе и технике.
«Симметрия в искусстве» — Центрально- осевая симметрия в архитектуре. II.1. Пропорция в архитектуре. Палаццо Спада (Рим). По характеру своих творческих возможностей периодичность — универсальное явление. III. Ле-Корбюэье. Ритм является одним из основных элементов выразительности мелодии. Р. Декарт. Ж. А. Фабр. Геометрические методы изображения пространственных фигур:
«Точка симметрии» — Фигуры, не имеющие осей симметрии. Точка О называется центром симметрии. Две точки А и А1 называются симметричными относительно О, если О середина отрезка АА1.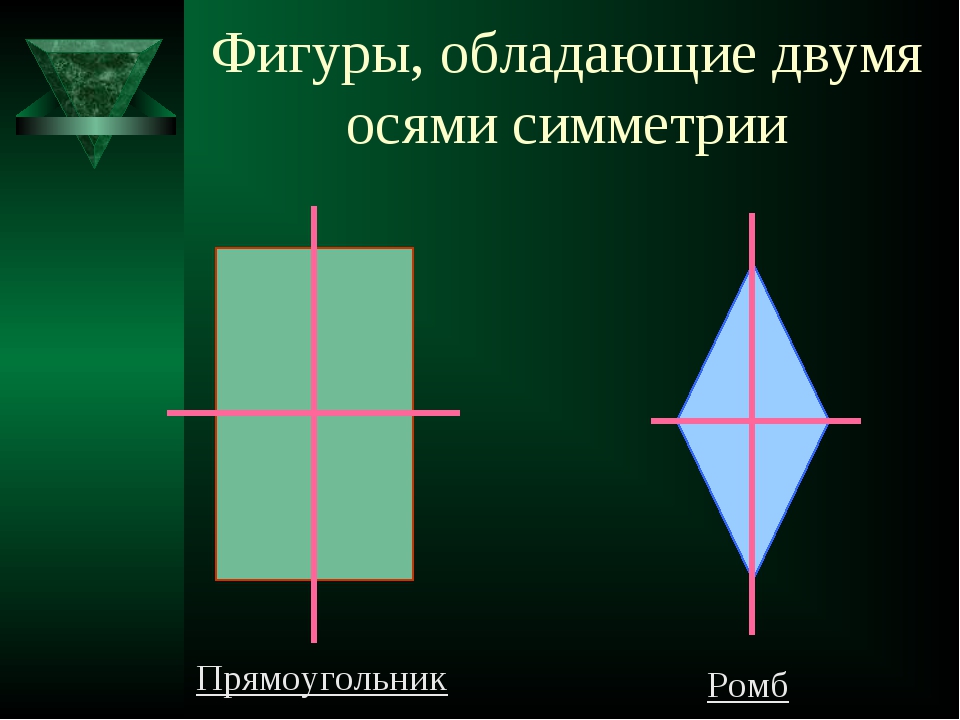 Равнобочная трапеция имеет только осевую симметрию. Симметрия в природе. Прямоугольник и ромб, не являющиеся квадратами, имеют две оси симметрии.
Равнобочная трапеция имеет только осевую симметрию. Симметрия в природе. Прямоугольник и ромб, не являющиеся квадратами, имеют две оси симметрии.
«Математическая симметрия» — Однако у сложных молекул, как правило, отсутствует симметрия. Палиндромы. Осевая. Центральная симметрия. Осевая симметрия. Типы симметрии. Симметрия в биологии. Вращательная симметрия. Симметрия в искусствах. ИМЕЕТ МНОГО ОБЩЕГО С ПОСТУПАТЕЛЬНОЙ СИММЕТРИЕЙ В МАТЕМАТИКЕ. Спиральная симметрия. Поступательная.
«Виды симметрии» — Центральная симметрия является движением. Зеркальный двойник оказывается «вывернутым» вдоль направления перпендикулярного к плоскости зеркала. Осевая симметрия также является движением. Теорема. Параллельный перенос. Центральная симметрия. Виды движения. Понятие движения. Параллельный перенос – один из видов движения.
Всего в теме 11 презентаций
20 мая 2014Жизнь людей наполнена симметрией. Это удобно, красиво, не нужно выдумывать новых стандартов. Но что она есть на самом деле и так ли красива в природе, как принято считать?
Симметрия
С древних времен люди стремятся упорядочить мир вокруг себя. Поэтому что-то считается красивым, а что-то не очень. С эстетической точки зрения как привлекательные рассматриваются золотое и серебряное сечения, а также, разумеется, симметрия. Этот термин имеет греческое происхождение и дословно означает «соразмерность». Разумеется, речь идет не только о совпадении по этому признаку, но также и по некоторым другим. В общем смысле симметрия — это такое свойство объекта, когда в результате тех или иных образований результат равен исходным данным. Это встречается как в живой, так и в неживой природе, а также в предметах, сделанных человеком.
Прежде всего термин «симметрия» употребляется в геометрии, но находит применение во многих научных областях, причем его значение остается в общем и целом неизменным. Это явление достаточно часто встречается и считается интересным, поскольку различается несколько его видов, а также элементов. Использование симметрии также интересно, ведь она встречается не только в природе, но и в орнаментах на ткани, бордюрах зданий и многих других рукотворных предметах. Стоит рассмотреть это явление поподробнее, поскольку это крайне увлекательно.
Использование симметрии также интересно, ведь она встречается не только в природе, но и в орнаментах на ткани, бордюрах зданий и многих других рукотворных предметах. Стоит рассмотреть это явление поподробнее, поскольку это крайне увлекательно.
Употребление термина в других научных областях
В дальнейшем симметрия будет рассматриваться с точки зрения геометрии, однако стоит упомянуть, что данное слово используется не только здесь. Биология, вирусология, химия, физика, кристаллография — все это неполный список областей, в которых данное явление изучается с различных сторон и в разных условиях. От того, к какой науке относится этот термин, зависит, например, классификация. Так, разделение на типы серьезно варьируется, хотя некоторые основные, пожалуй, остаются неизменными везде.
Видео по теме
Классификация
Различают несколько основных типов симметрии, из которых наиболее часто встречаются три:
Кроме того, в геометрии различают также следующие типы, они встречаются значительно реже, но не менее любопытны:
- скользящая;
- вращательная;
- точечная;
- поступательная;
- винтовая;
- фрактальная;
- и т. д.
В биологии все виды называются несколько иначе, хотя по сути могут быть такими же. Подразделение на те или иные группы происходит на основании наличия или отсутствия, а также количества некоторых элементов, таких как центры, плоскости и оси симметрии. Их следует рассмотреть отдельно и более подробно.
Базовые элементы
В явлении выделяют некоторые черты, одна из которых обязательно присутствует. Так называемые базовые элементы включают в себя плоскости, центры и оси симметрии. Именно в соответствии с их наличием, отсутствием и количеством определяется тип.
Центром симметрии называют точку внутри фигуры или кристалла, в которой сходятся линии, соединяющие попарно все параллельные друг другу стороны. Разумеется, он существует не всегда. Если есть стороны, к которым нет параллельной пары, то такую точку найти невозможно, поскольку ее нет. В соответствии с определением, очевидно, что центр симметрии — это то, через что фигура может быть отражена сама на себя. Примером может служить, например, окружность и точка в ее середине. Этот элемент обычно обозначается как C.
В соответствии с определением, очевидно, что центр симметрии — это то, через что фигура может быть отражена сама на себя. Примером может служить, например, окружность и точка в ее середине. Этот элемент обычно обозначается как C.
Плоскость симметрии, разумеется, воображаема, но именно она делит фигуру на две равные друг другу части. Она может проходить через одну или несколько сторон, быть параллельной ей, а может делить их. Для одной и той же фигуры может существовать сразу несколько плоскостей. Эти элементы обычно обозначаются как P.
Но, пожалуй, наиболее часто встречается то, что называют «оси симметрии». Это нередкое явление можно увидеть как в геометрии, так и в природе. И оно достойно отдельного рассмотрения.
Оси
Часто элементом, относительно которого фигуру можно назвать симметричной,
выступает прямая или отрезок. В любом случае речь идет не о точке и не о плоскости. Тогда рассматриваются оси симметрии фигур. Их может быть очень много, и расположены они могут быть как угодно: делить стороны или быть параллельными им, а также пересекать углы или не делать этого. Оси симметрии обычно обозначаются как L.
Примерами могут служить равнобедренные и равносторонние треугольники. В первом случае будет вертикальная ось симметрии, по обе стороны от которой равные грани, а во втором линии будут пересекать каждый угол и совпадать со всеми биссектрисами, медианами и высотами. Обычные же треугольники ею не обладают.
Кстати, совокупность всех вышеназванных элементов в кристаллографии и стереометрии называется степенью симметрии. Этот показатель зависит от количества осей, плоскостей и центров.
Примеры в геометрии
Условно можно разделить все множество объектов изучения математиков на фигуры, имеющие ось симметрии, и такие, у которых ее нет. В первую категорию автоматически попадают все правильные многоугольники, окружности, овалы, а также некоторые частные случаи, остальные же попадают во вторую группу.
Как и в случае, когда говорилось про ось симметрии треугольника, данный элемент для четырехугольника существует не всегда.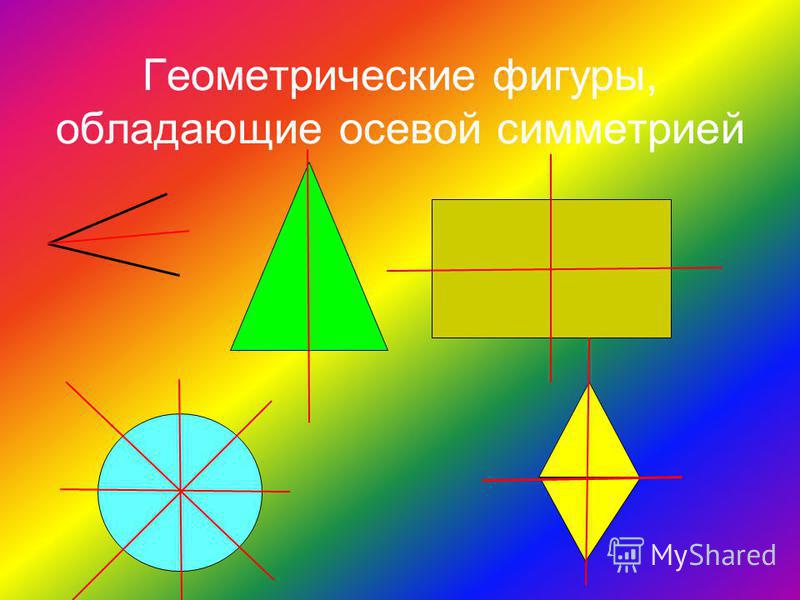 Для квадрата, прямоугольника, ромба или параллелограмма он есть, а для неправильной фигуры, соответственно, нет. Для окружности оси симметрии — это множество прямых, которые проходят через ее центр.
Для квадрата, прямоугольника, ромба или параллелограмма он есть, а для неправильной фигуры, соответственно, нет. Для окружности оси симметрии — это множество прямых, которые проходят через ее центр.
Кроме того, интересно рассмотреть и объемные фигуры с этой точки зрения. Хотя бы одной осью симметрии помимо всех правильных многоугольников и шара будут обладать некоторые конусы, а также пирамиды, параллелограммы и некоторые другие. Каждый случай необходимо рассматривать отдельно.
Примеры в природе
Зеркальная симметрия в жизни называется билатеральной, она встречается наиболее
часто. Любой человек и очень многие животные тому пример. Осевая же называется радиальной и встречается гораздо реже, как правило, в растительном мире. И все-таки они есть. Например, стоит подумать, сколько осей симметрии имеет звезда, и имеет ли она их вообще? Разумеется, речь идет о морских обитателях, а не о предмете изучения астрономов. И правильным ответом будет такой: это зависит от количества лучей звезды, например пять, если она пятиконечная.
Кроме того, радиальная симметрия наблюдается у многих цветков: ромашки, васильки, подсолнухи и т. д. Примеров огромное количество, они буквально везде вокруг.
Аритмия
Этот термин, прежде всего, напоминает большинству о медицине и кардиологии, однако он изначально имеет несколько другое значение. В данном случае синонимом будет «асимметрия», то есть отсутствие или нарушение регулярности в том или ином виде. Ее можно встретить как случайность, а иногда она может стать прекрасным приемом, например, в одежде или архитектуре. Ведь симметричных зданий очень много, но знаменитая Пизанская башня чуть наклонена, и хоть она не одна такая, но это самый известный пример. Известно, что так получилось случайно, но в этом есть своя прелесть.
Кроме того, очевидно, что лица и тела людей и животных тоже не полностью симметричны. Проводились даже исследования, согласно результатам которых «правильные» лица расценивались как неживые или просто непривлекательные. Все-таки восприятие симметрии и это явление само по себе удивительны и пока не до конца изучены, а потому крайне интересны.
Все-таки восприятие симметрии и это явление само по себе удивительны и пока не до конца изучены, а потому крайне интересны.
Вам понадобится
- — свойства симметричных точек;
- — свойства симметричных фигур;
- — линейка;
- — угольник;
- — циркуль;
- — карандаш;
- — лист бумаги;
- — компьютер с графическим редактором.
Инструкция
Проведите прямую a, которая будет являться осью симметрии. Если ее координаты не заданы, начертите ее произвольно. С одной стороны от этой прямой поставьте произвольную точку A. необходимо найти симметричную точку.
Полезный совет
Свойства симметрии постоянно используются в программе AutoCAD. Для этого используется опция Mirror. Для построения равнобедренного треугольника или равнобедренной трапеции достаточно начертить нижнее основание и угол между ним и боковой стороной. Отразите их с помощью указанной команды и продлите боковые стороны до необходимой величины. В случае с треугольником это будет точка их пересечения, а для трапеции — заданная величина.
С симметрией вы постоянно сталкиваетесь в графических редакторах, когда пользуетесь опцией «отразить по вертикали/горизонтали». В этом случае за ось симметрии берется прямая, соответствующая одной из вертикальных или горизонтальных сторон рамки рисунка.
Источники:
- как начертить центральную симметрию
Построение сечения конуса не такая уж сложная задача. Главное — соблюдать строгую последовательность действий. Тогда данная задача будет легко выполнима и не потребует от Вас больших трудозатрат.
Вам понадобится
- — бумага;
- — ручка;
- — циркль;
- — линейка.
Инструкция
При ответе на этот вопрос, сначала следует определиться – какими параметрами задано сечение.
Пусть это будет прямая пересечения плоскости l с плоскостью и точка О, которая местом пересечения с его сечением.
Построение иллюстрирует рис.1. Первый шаг построения сечения – это через центр сечения его диаметра, продленного до l перпендикулярно этой линии.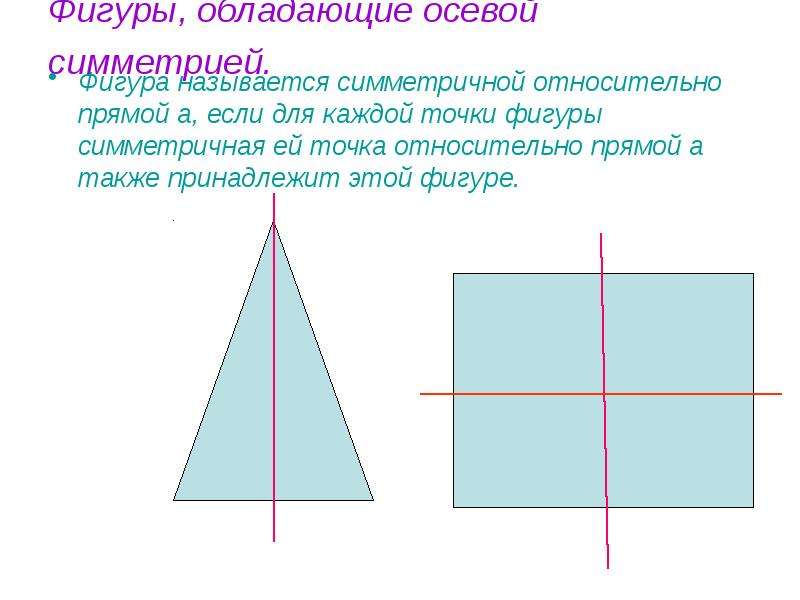 В итоге получается точка L. Далее через т.О проведите прямую LW, и постройте две направляющие конуса, лежащие в главном сечении О2М и О2С. В пересечении этих направляющих лежат точка Q, а также уже показанная точка W. Это первые две точки искомого сечения.
В итоге получается точка L. Далее через т.О проведите прямую LW, и постройте две направляющие конуса, лежащие в главном сечении О2М и О2С. В пересечении этих направляющих лежат точка Q, а также уже показанная точка W. Это первые две точки искомого сечения.
Теперь проведите в основании конуса ВВ1 перпендикулярный МС и постройте образующие перпендикулярного сечения О2В и О2В1. В этом сечении через т.О проведите прямую RG, параллельную ВВ1. Т.R и т.G — еще две точки искомого сечения. Если бы сечения бал известен, то его можно было бы построить уже на этой стадии. Однако это вовсе не эллипс, а нечто эллипсообразное, имеющее симметрию относительно отрезка QW. Поэтому следует строить как можно больше точек сечения, чтобы соединяя их в дальнейшем плавной кривой получить наиболее достоверный эскиз.
Постройте произвольную точку сечения. Для этого проведите в основании конуса произвольный диаметр AN и постройте соответствующие направляющие О2A и O2N. Через т.О проведите прямую, проходящую через PQ и WG, до ее пересечения с только что построенными направляющими в точках P и E. Это еще две точки искомого сечения. Продолжая так же и дальше, можно сколь угодно искомых точек.
Правда, процедуру их получения можно немного упростить пользуясь симметрией относительно QW. Для этого можно в плоскости искомого сечения провести прямые SS’, параллельные RG до пересечения их с поверхность конуса. Построение завершается скруглением построенной ломаной из хорд. Достаточно построить половину искомого сечения в силу уже упомянутой симметрии относительно QW.
Видео по теме
Вам требуется начертить график тригонометрической функции ? Освойте алгоритм действий на примере построения синусоиды. Для решения поставленной задачи используйте метод исследования.
Вам понадобится
- — линейка;
- — карандаш;
- — знание основ тригонометрии.
Инструкция
Видео по теме
Обратите внимание
Если две полуоси однополосного гиперболоида равны, то фигуру можно получить путем вращения гиперболы с полуосями, одна из которых вышеуказанная, а другая, отличающаяся от двух равных, вокруг мнимой оси.
Полезный совет
При рассмотрении этой фигуры относительно осей Oxz и Oyz видно, что ее главными сечениями являются гиперболы. А при разрезе данной пространственной фигуры вращения плоскостью Oxy ее сечение представляет собой эллипс. Горловой эллипс однополосного гиперболоида проходит через начало координат, ведь z=0.
Горловой эллипс описывается уравнением x²/a² +y²/b²=1, а другие эллипсы составляются по уравнению x²/a² +y²/b²=1+h²/c².
Источники:
- Эллипсоиды, параболоиды, гиперболоиды. Прямолинейные образующие
Форма пятиконечной звезды повсеместно используется человеком с древних времен. Мы считаем ее форму прекрасной, так как бессознательно различаем в ней соотношения золотого сечения, т.е. красота пятиконечной звезды обоснована математически. Первым описал построение пятиконечной звезды Евклид в своих «Началах». Давайте же приобщимся к его опыту.
Вам понадобится
- линейка;
- карандаш;
- циркуль;
- транспортир.
Инструкция
Построение звезды сводится к построению с последующим соединением его вершин друг с другом последовательно через одну. Для того чтобы построить правильный необходимо разбить окружность на пять .
Постройте произвольную окружность при помощи циркуля. Обозначьте ее центр точкой O.
Отметьте точку A и при помощи линейки начертите отрезок ОА. Теперь необходимо разделить отрезок OA пополам, для этого из точки А проведите дугу радиусом ОА до пересечения ее с окружностью в двух точках M и N. Постройте отрезок MN. Точка Е, в которой MN пересекает OA, будет делить отрезок OA пополам.
Восстановите перпендикуляр OD к радиусу ОА и соедините точку D и E. Сделайте засечку B на OA из точки E радиусом ED.
Теперь при помощи отрезка DB разметьте окружность на пять равных частей. Обозначьте вершины правильного пятиугольника последовательно цифрами от 1 до 5. Соедините точки в следующей последовательности: 1 с 3, 2 с 4, 3 с 5, 4 с 1, 5 с 2.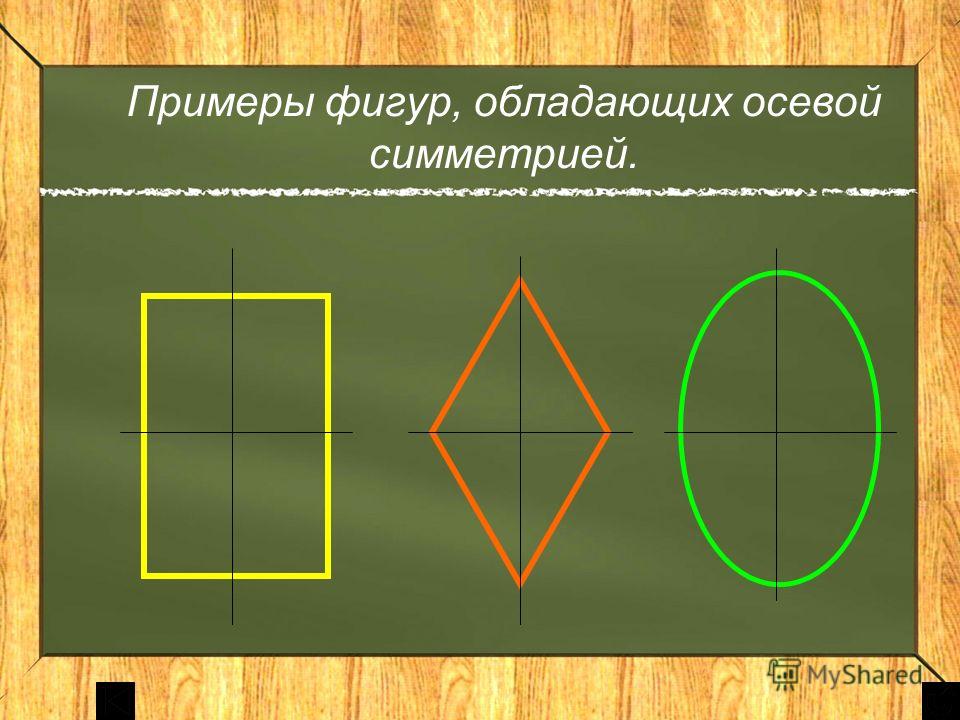 Вот и правильная пятиконечная звезда, в правильный пятиугольник. Именно таким способом строил
Вот и правильная пятиконечная звезда, в правильный пятиугольник. Именно таким способом строил
Урок математики. Тема: «Ось симметрии»
Цели:
- образовательные:
- дать представление о симметрии;
- познакомить с основными видами симметрии на плоскости и в пространстве;
- выработать прочные навыки построения симметричных фигур;
- расширить представления об известных фигурах, познакомив со свойствами, связанных с симметрией;
- показать возможности использования симметрии при решении различных задач;
- закрепить полученные знания;
- общеучебные:
- научить настраивать себя на работу;
- научить вести контроль за собой и соседом по парте;
- научить оценивать себя и соседа по парте;
- развивающие:
- активизировать самостоятельную деятельность;
- развивать познавательную деятельность;
- учить обобщать и систематизировать полученную информацию;
- воспитательные:
- воспитываать у учащихся “чувство плеча”;
- воспитывать коммуникативность;
- прививать культуру общения.
ХОД УРОКА
Перед каждым лежат ножницы и лист бумаги.
Задание 1 (3 мин).
– Возьмем лист бумаги, сложим его попалам и вырежем какую-нибудь фигурку. Теперь развернем лист и посмотрим на линию сгиба.
Вопрос: Какую функцию выполняет эта линия?
Предполагаемый ответ: Эта линия делит фигуру пополам.
Вопрос: Как расположены все точки фигуры на двух получившихся половинках?
Предполагаемый ответ: Все точки половинок
находятся на равном расстоянии от линии сгиба и
на одном уровне.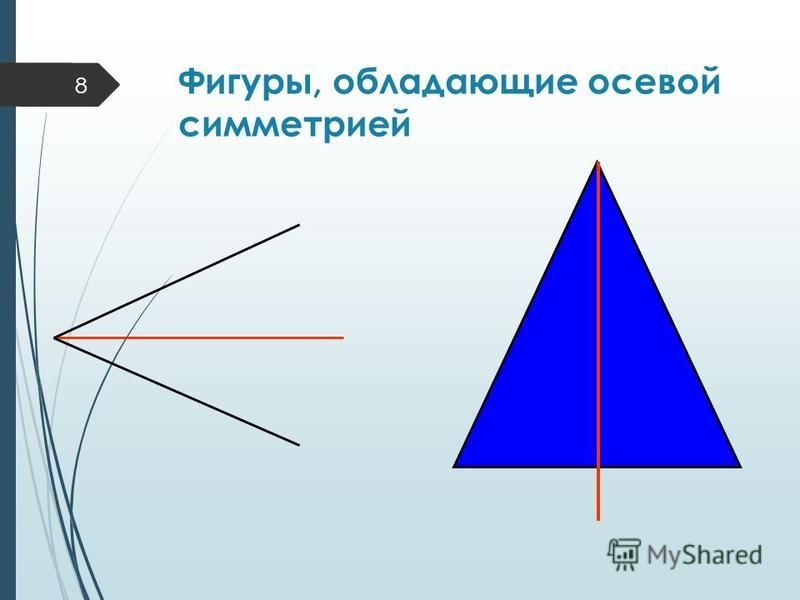
– Значит, линия сгиба делит фигурку пополам так, что 1 половинка является копией 2 половинки, т.е. эта линия непростая, она обладает замечательным свойством (все точки относительно ее находятся на одинаковом расстоянии), эта линия – ось симметрии.
Задание 2 (2 мин).
– Вырезать снежинку, найти ось симметрии, охарактеризовать ее.
Задание 3 (5 мин).
– Начертить в тетради окружность.
Вопрос: Определить, как проходит ось симметрии?
Предполагаемый ответ: По-разному.
Вопрос: Так сколько осей симметрии имеет окружность?
Предполагаемый ответ: Много.
– Правильно, окружность имеет множество осей симметрии. Такой же замечательной фигурой является шар (пространственная фигура)
Вопрос: Какие еще фигуры имеют не одну ось симметрии?
Предполагаемый ответ: Квадрат, прямоугольник, равнобедренный и равносторонний треугольники.
– Рассмотрим объемные фигуры: куб, пирамиду, конус, цилиндр и т.д. Эти фигуры тоже имеют ось симметрии. Определите, сколько осей симметрии у квадрата, прямоугольника, равностороннего треугольника и у предложенных объемных фигур?
Раздаю учащимся половинки фигурок из пластилина.
Задание 4 (3 мин).
– Используя полученную информацию, долепить недостающую часть фигурки.
Примечание: фигурка может быть и плоскостной, и объемной. Важно, чтобы учащиеся определили, как проходит ось симметрии, и долепили недостающий элемент. Правильность выполнения определяет сосед по парте, оценивает, насколько правильно проделана работа.
Из шнурка одного цвета на рабочем столе
выложена линия (замкнутая, незамкнутая, с
самопересечением, без самопересечения).
Задание 5 (групповая работа 5 мин).
– Определить визуально ось симметрии и относительно нее достроить из шнурка другого цвета вторую часть.
Правильность выполненной работы определяется самими учениками.
Перед учащимися представлены элементы рисунков
Задание 6 (2 мин).
– Найдите симметричные части этих рисунков.
Для закрепления пройденного материала предлагаю следующие задания, предусмотренные на 15 мин.:
1. Прямая ОР – ось симметрии треугольника КОМ.
Назовите все равные элементы треугольника КОР и КОМ. Каков вид этих треугольников?
2. Начертите в тетради несколько равнобедренных треугольников с общим основанием равным 6 см.
3. Начертите отрезок АВ. Постройте прямую перпендикулярную отрезку АВ и проходящую через его середину. Отметьте на ней точки С и D так, чтобы четырехугольник АСВD был симметричен относительно прямой АВ.
– Наши первоначальные представления о форме
относятся к очень отдаленной эпохе древнего
каменного века – палеолита. В течение сотен
тысячелетий этого периода люди жили в пещерах, в
условиях мало отличавшихся от жизни животных.
Люди изготовляли орудия для охоты и рыболовства,
вырабатывали язык для общения друг с другом, а в
эпоху позднего палеолита украшали свое
существование, создавая произведения искусства,
статуэтки и рисунки, в которых обнаруживается
замечательное чувство формы.
Когда произошел переход от простого собирания
пищи к активному ее производству, от охоты и
рыболовства к земледелию, человечество вступает
в новый каменный век, в неолит.
Человек неолита обладал острым чувством
геометрической формы. Обжиг и раскраска глиняных
сосудов, изготовление камышовых циновок, корзин,
тканей, позже – обработка металлов вырабатывали
представления о плоскостных и пространственных
фигурах. Неолитические орнаменты радовали глаз,
выявляя равенство и симметрию.
Неолитические орнаменты радовали глаз,
выявляя равенство и симметрию.
– А где в природе встречается симметрия?
Предполагаемый ответ: крылья бабочек, жуков, листья деревьев…
– Симметрию можно наблюдать и в архитектуре. Строя здания, строители четко придерживаются симметрии.
Поэтому здания получаются такие красивые. Также примером симметрии служит человек, животные.
Задание на дом:
1. Придумать свой орнамент, изобразить его на
листе формат А4 (можно нарисовать в виде ковра).
2. Нарисовать бабочек, отметить, где присутствуют
элементы симметрии.
Фигуры, имеющие две оси симметрии. Старт в науке
Цели:
- образовательные:
- дать представление о симметрии;
- познакомить с основными видами симметрии на плоскости и в пространстве;
- выработать прочные навыки построения симметричных фигур;
- расширить представления об известных фигурах, познакомив со свойствами, связанных с симметрией;
- показать возможности использования симметрии при решении различных задач;
- закрепить полученные знания;
- общеучебные:
- научить настраивать себя на работу;
- научить вести контроль за собой и соседом по парте;
- научить оценивать себя и соседа по парте;
- развивающие:
- активизировать самостоятельную деятельность;
- развивать познавательную деятельность;
- учить обобщать и систематизировать полученную информацию;
- воспитательные:
- воспитываать у учащихся “чувство плеча”;
- воспитывать коммуникативность;
- прививать культуру общения.
ХОД УРОКА
Перед каждым лежат ножницы и лист бумаги.
Задание 1 (3 мин).
– Возьмем лист бумаги, сложим его попалам и
вырежем какую-нибудь фигурку. Теперь развернем
лист и посмотрим на линию сгиба.
Теперь развернем
лист и посмотрим на линию сгиба.
Вопрос: Какую функцию выполняет эта линия?
Предполагаемый ответ: Эта линия делит фигуру пополам.
Вопрос: Как расположены все точки фигуры на двух получившихся половинках?
Предполагаемый ответ: Все точки половинок находятся на равном расстоянии от линии сгиба и на одном уровне.
– Значит, линия сгиба делит фигурку пополам так, что 1 половинка является копией 2 половинки, т.е. эта линия непростая, она обладает замечательным свойством (все точки относительно ее находятся на одинаковом расстоянии), эта линия – ось симметрии.
Задание 2 (2 мин).
– Вырезать снежинку, найти ось симметрии, охарактеризовать ее.
Задание 3 (5 мин).
– Начертить в тетради окружность.
Вопрос: Определить, как проходит ось симметрии?
Предполагаемый ответ: По-разному.
Вопрос: Так сколько осей симметрии имеет окружность?
Предполагаемый ответ: Много.
– Правильно, окружность имеет множество осей симметрии. Такой же замечательной фигурой является шар (пространственная фигура)
Вопрос: Какие еще фигуры имеют не одну ось симметрии?
Предполагаемый ответ: Квадрат, прямоугольник, равнобедренный и равносторонний треугольники.
– Рассмотрим объемные фигуры: куб, пирамиду, конус, цилиндр и т.д. Эти фигуры тоже имеют ось симметрии.Определите, сколько осей симметрии у квадрата, прямоугольника, равностороннего треугольника и у предложенных объемных фигур?
Раздаю учащимся половинки фигурок из пластилина.
Задание 4 (3 мин).
– Используя полученную информацию, долепить недостающую часть фигурки.
Примечание: фигурка может быть и
плоскостной, и объемной. Важно, чтобы учащиеся
определили, как проходит ось симметрии, и
долепили недостающий элемент. Правильность
выполнения определяет сосед по парте, оценивает,
насколько правильно проделана работа.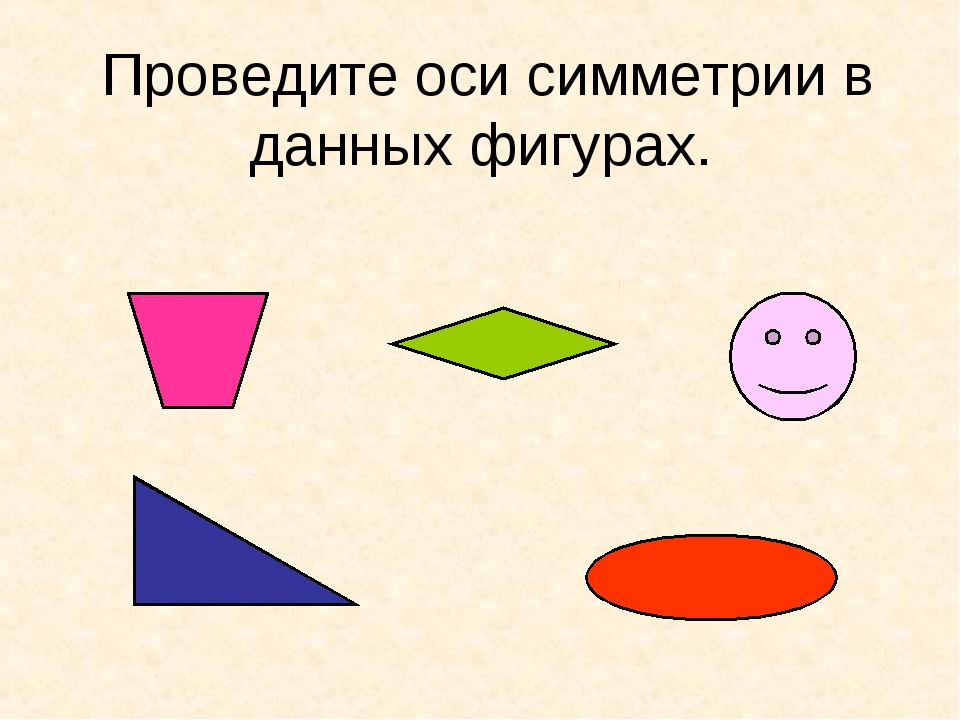
Из шнурка одного цвета на рабочем столе выложена линия (замкнутая, незамкнутая, с самопересечением, без самопересечения).
Задание 5 (групповая работа 5 мин).
– Определить визуально ось симметрии и относительно нее достроить из шнурка другого цвета вторую часть.
Правильность выполненной работы определяется самими учениками.
Перед учащимися представлены элементы рисунков
Задание 6 (2 мин).
– Найдите симметричные части этих рисунков.
Для закрепления пройденного материала предлагаю следующие задания, предусмотренные на 15 мин.:
Назовите все равные элементы треугольника КОР и КОМ. Каков вид этих треугольников?
2. Начертите в тетради несколько равнобедренных треугольников с общим основанием равным 6 см.
3. Начертите отрезок АВ. Постройте прямую перпендикулярную отрезку АВ и проходящую через его середину. Отметьте на ней точки С и D так, чтобы четырехугольник АСВD был симметричен относительно прямой АВ.
– Наши первоначальные представления о форме
относятся к очень отдаленной эпохе древнего
каменного века – палеолита. В течение сотен
тысячелетий этого периода люди жили в пещерах, в
условиях мало отличавшихся от жизни животных.
Люди изготовляли орудия для охоты и рыболовства,
вырабатывали язык для общения друг с другом, а в
эпоху позднего палеолита украшали свое
существование, создавая произведения искусства,
статуэтки и рисунки, в которых обнаруживается
замечательное чувство формы.
Когда произошел переход от простого собирания
пищи к активному ее производству, от охоты и
рыболовства к земледелию, человечество вступает
в новый каменный век, в неолит.
Человек неолита обладал острым чувством
геометрической формы. Обжиг и раскраска глиняных
сосудов, изготовление камышовых циновок, корзин,
тканей, позже – обработка металлов вырабатывали
представления о плоскостных и пространственных
фигурах. Неолитические орнаменты радовали глаз,
выявляя равенство и симметрию.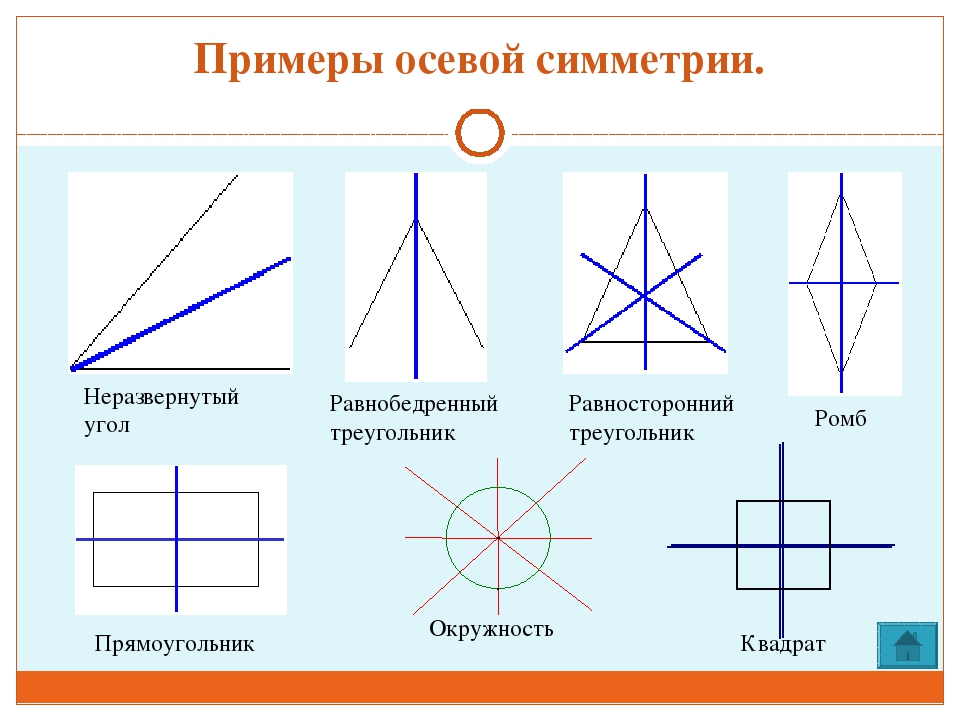
– А где в природе встречается симметрия?
Предполагаемый ответ: крылья бабочек, жуков, листья деревьев…
– Симметрию можно наблюдать и в архитектуре. Строя здания, строители четко придерживаются симметрии.
Поэтому здания получаются такие красивые. Также примером симметрии служит человек, животные.
Задание на дом:
1. Придумать свой орнамент, изобразить его на
листе формат А4 (можно нарисовать в виде ковра).
2. Нарисовать бабочек, отметить, где присутствуют
элементы симметрии.
Жизнь людей наполнена симметрией. Это удобно, красиво, не нужно выдумывать новых стандартов. Но что она есть на самом деле и так ли красива в природе, как принято считать?
Симметрия
С древних времен люди стремятся упорядочить мир вокруг себя. Поэтому что-то считается красивым, а что-то не очень. С эстетической точки зрения как привлекательные рассматриваются золотое и серебряное сечения, а также, разумеется, симметрия. Этот термин имеет греческое происхождение и дословно означает «соразмерность». Разумеется, речь идет не только о совпадении по этому признаку, но также и по некоторым другим. В общем смысле симметрия — это такое свойство объекта, когда в результате тех или иных образований результат равен исходным данным. Это встречается как в живой, так и в неживой природе, а также в предметах, сделанных человеком.
Прежде всего термин «симметрия» употребляется в геометрии, но находит применение во многих научных областях, причем его значение остается в общем и целом неизменным. Это явление достаточно часто встречается и считается интересным, поскольку различается несколько его видов, а также элементов. Использование симметрии также интересно, ведь она встречается не только в природе, но и в орнаментах на ткани, бордюрах зданий и многих других рукотворных предметах. Стоит рассмотреть это явление поподробнее, поскольку это крайне увлекательно.
Употребление термина в других научных областях
В дальнейшем симметрия будет рассматриваться с точки зрения геометрии, однако стоит упомянуть, что данное слово используется не только здесь. Биология, вирусология, химия, физика, кристаллография — все это неполный список областей, в которых данное явление изучается с различных сторон и в разных условиях. От того, к какой науке относится этот термин, зависит, например, классификация. Так, разделение на типы серьезно варьируется, хотя некоторые основные, пожалуй, остаются неизменными везде.
Биология, вирусология, химия, физика, кристаллография — все это неполный список областей, в которых данное явление изучается с различных сторон и в разных условиях. От того, к какой науке относится этот термин, зависит, например, классификация. Так, разделение на типы серьезно варьируется, хотя некоторые основные, пожалуй, остаются неизменными везде.
Видео по теме
Классификация
Различают несколько основных типов симметрии, из которых наиболее часто встречаются три:
Кроме того, в геометрии различают также следующие типы, они встречаются значительно реже, но не менее любопытны:
- скользящая;
- вращательная;
- точечная;
- поступательная;
- винтовая;
- фрактальная;
- и т. д.
В биологии все виды называются несколько иначе, хотя по сути могут быть такими же. Подразделение на те или иные группы происходит на основании наличия или отсутствия, а также количества некоторых элементов, таких как центры, плоскости и оси симметрии. Их следует рассмотреть отдельно и более подробно.
Базовые элементы
В явлении выделяют некоторые черты, одна из которых обязательно присутствует. Так называемые базовые элементы включают в себя плоскости, центры и оси симметрии. Именно в соответствии с их наличием, отсутствием и количеством определяется тип.
Центром симметрии называют точку внутри фигуры или кристалла, в которой сходятся линии, соединяющие попарно все параллельные друг другу стороны. Разумеется, он существует не всегда. Если есть стороны, к которым нет параллельной пары, то такую точку найти невозможно, поскольку ее нет. В соответствии с определением, очевидно, что центр симметрии — это то, через что фигура может быть отражена сама на себя. Примером может служить, например, окружность и точка в ее середине. Этот элемент обычно обозначается как C.
Плоскость симметрии, разумеется, воображаема, но именно она делит фигуру на две равные друг другу части. Она может проходить через одну или несколько сторон, быть параллельной ей, а может делить их. Для одной и той же фигуры может существовать сразу несколько плоскостей. Эти элементы обычно обозначаются как P.
Для одной и той же фигуры может существовать сразу несколько плоскостей. Эти элементы обычно обозначаются как P.
Но, пожалуй, наиболее часто встречается то, что называют «оси симметрии». Это нередкое явление можно увидеть как в геометрии, так и в природе. И оно достойно отдельного рассмотрения.
Оси
Часто элементом, относительно которого фигуру можно назвать симметричной,
выступает прямая или отрезок. В любом случае речь идет не о точке и не о плоскости. Тогда рассматриваются оси симметрии фигур. Их может быть очень много, и расположены они могут быть как угодно: делить стороны или быть параллельными им, а также пересекать углы или не делать этого. Оси симметрии обычно обозначаются как L.
Примерами могут служить равнобедренные и равносторонние треугольники. В первом случае будет вертикальная ось симметрии, по обе стороны от которой равные грани, а во втором линии будут пересекать каждый угол и совпадать со всеми биссектрисами, медианами и высотами. Обычные же треугольники ею не обладают.
Кстати, совокупность всех вышеназванных элементов в кристаллографии и стереометрии называется степенью симметрии. Этот показатель зависит от количества осей, плоскостей и центров.
Примеры в геометрии
Условно можно разделить все множество объектов изучения математиков на фигуры, имеющие ось симметрии, и такие, у которых ее нет. В первую категорию автоматически попадают все правильные многоугольники, окружности, овалы, а также некоторые частные случаи, остальные же попадают во вторую группу.
Как и в случае, когда говорилось про ось симметрии треугольника, данный элемент для четырехугольника существует не всегда. Для квадрата, прямоугольника, ромба или параллелограмма он есть, а для неправильной фигуры, соответственно, нет. Для окружности оси симметрии — это множество прямых, которые проходят через ее центр.
Кроме того, интересно рассмотреть и объемные фигуры с этой точки зрения. Хотя бы одной осью симметрии помимо всех правильных многоугольников и шара будут обладать некоторые конусы, а также пирамиды, параллелограммы и некоторые другие.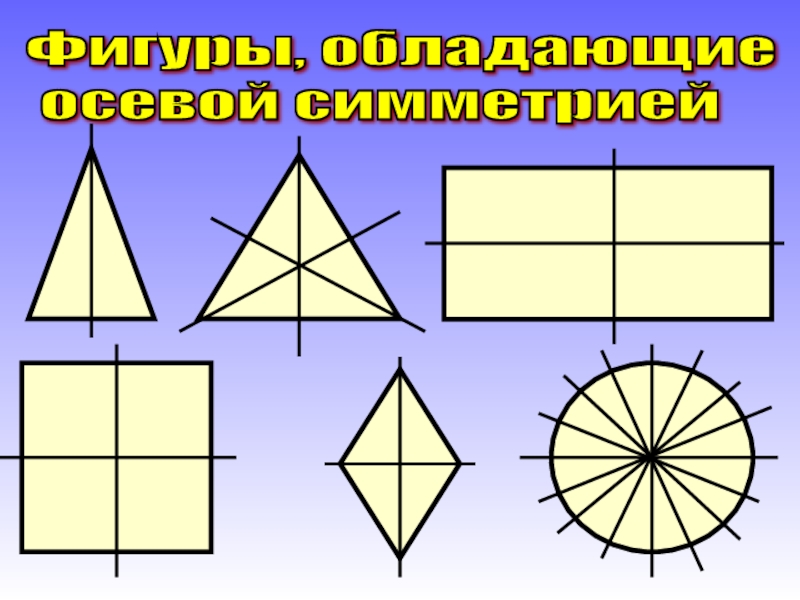 Каждый случай необходимо рассматривать отдельно.
Каждый случай необходимо рассматривать отдельно.
Примеры в природе
Зеркальная симметрия в жизни называется билатеральной, она встречается наиболее
часто. Любой человек и очень многие животные тому пример. Осевая же называется радиальной и встречается гораздо реже, как правило, в растительном мире. И все-таки они есть. Например, стоит подумать, сколько осей симметрии имеет звезда, и имеет ли она их вообще? Разумеется, речь идет о морских обитателях, а не о предмете изучения астрономов. И правильным ответом будет такой: это зависит от количества лучей звезды, например пять, если она пятиконечная.
Кроме того, радиальная симметрия наблюдается у многих цветков: ромашки, васильки, подсолнухи и т. д. Примеров огромное количество, они буквально везде вокруг.
Аритмия
Этот термин, прежде всего, напоминает большинству о медицине и кардиологии, однако он изначально имеет несколько другое значение. В данном случае синонимом будет «асимметрия», то есть отсутствие или нарушение регулярности в том или ином виде. Ее можно встретить как случайность, а иногда она может стать прекрасным приемом, например, в одежде или архитектуре. Ведь симметричных зданий очень много, но знаменитая Пизанская башня чуть наклонена, и хоть она не одна такая, но это самый известный пример. Известно, что так получилось случайно, но в этом есть своя прелесть.
Кроме того, очевидно, что лица и тела людей и животных тоже не полностью симметричны. Проводились даже исследования, согласно результатам которых «правильные» лица расценивались как неживые или просто непривлекательные. Все-таки восприятие симметрии и это явление само по себе удивительны и пока не до конца изучены, а потому крайне интересны.
Сколько разных осей симметрии сможет иметь какой — нибудь треугольник, зависит от его геометрической формы. Если это равносторонний треугольник, тогда у него будут сразу целых три оси симметрии.
А в случае если это равнобедренний треугольник, у него будет только одна ось симметрии.
Сын сестры как раз проходит эту тему в школе на уроках геометрии. Ось симметрии — это прямая линия, при повороте вокруг которой на конкретный угол симметричная фигура займет такое же положение в пространстве, которое она занимала до поворота, а на место одних ее частей станут такие же другие. В равнобедренном треугольнике — три, в прямоугольном — одна, в остальных — нет, так как у них стороны не равны между собой.
Это, смотря какой треугольник. У равностороннего треугольника имеются три оси симметрии, которые проходят через три его вершины. Равнобедренный треугольник, соответственно имеет одну ось симметрии. Остальные треугольники, оси симметрии не имеют.
Самое простое, что можно запомнить — это у равностороннего треугольника три стороны равны и он имеет три оси симметрии
От этого легче запомнить следующее
Нет равных сторон, то есть все стороны разные,значит нет осей симметрии
А в равнобедренном треугольнике всего одна ось
Нельзя просто ответить, сколько осей симметрии у треугольника, не разобравшись с тем, о каком именно треугольнике идет речь.
У треугольника равностороннего имеется три оси симметрии, соответственно.
У треугольника равнобедренного имеется всего лишь одна ось симметрии.
У любых других треугольников с разными по длине сторонами вообще нет ни одной оси симметрии.
Треугольник, у которого все стороны разные по величине, не имеет осей симметрии.
Прямоугольный треугольник может иметь одну ось симметрии в случае, если его катеты равны.
В треугольнике, у которого две стороны равны (равнобедренном) можно провести одну ось, а у которого все три стороны равны (равностороннем) — три.
Прежде, чем ответить на вопрос о том, сколько осей симметрии имеет треугольник, сначала нужно вообще вспомнить, что такое ось симметрии.
Так вот, говоря просто, в геометрии ось симметрии — это линия, если по которой согнуть фигуру, то получим одинаковые половинки.
но стоит помнить, что треугольники тоже бывают разными.
Так вот, равнобедренный треугольник (треугольник с двумя равными сторонами) имеет одну ось симметрии.
Равносторонний треугольник соответственно имеет 3 оси симметрии, так как все стороны у этого треугольника равны.
А вот разносторонний треугольник вообще осей симметрии не имеет. Хоть как его складывай и хоть где прямые линии проводи, но раз стороны разные, то и двух одинаковых половиной не получится.
Насколько помню геометрию, у равностороннего треугольника три оси симметрии, проходящие через его вершины, это его биссектрисы. У прямоугольного треугольника, как и разностороннего, тупоугольного и остроугольного треугольников осей симметрии вообще нет, а у равнобедренного она одна.
А проверить это легко — просто представить линию, по которой его можно разрезать надвое так, чтобы получить два одинаковых треугольника.
Так как треугольники бывают разные, то и оси симметрии у них соответственно в разных количествах. Например, треугольник с разными сторонами вообще без осей симметрии. А у равностороннего их аж три. Есть еще один вид треугольника, который имеет одну ось симметрии. У него две стороны равны, и один прямой угол.
Произвольный треугольник не имеет осей симметрии. Равнобедренный треугольник имеет одну ось симметрии — это медиана к одиночной стороне. Равносторонний треугольник имеет три оси симметрии — это три его медианы.
«Симметрия » в переводе с греческого означает «соразмерность» (повторяемость). Симметричные тела и предметы состоят из равнозначных, правильно повторяющихся в пространстве частей. Особенно разнообразна симметрия кристаллов. Различные кристаллы отличаются большей или меньшей симметричностью. Она является их важнейшим и специфическим свойством, отражающим закономерность внутреннего строения.
По более точному определению симметрия – это закономерная повторяемость элементов (или частей) фигуры или какого-либо тела, при которой фигура совмещается сама с собой при некоторых преобразованиях (вращение вокруг оси, отражение в плоскости). Подавляющее большинство кристаллов обладает симметрией.
Понятие симметрии включает в себя составные части – элементы симметрии. Сюда относятся плоскость симметрии , ось симметрии , центр симметрии , или центр инверсии .
Плоскость симметрии делит кристалл на две зеркально равные части. Обозначается она буквой Р. Части, на которые плоскость симметрии рассекает многогранник, относятся одна к другой, как предмет к своему изображению в зеркале разные кристаллы имеют различное количество плоскостей симметрии, которое ставится перед буквой Р. Наибольшее количество таких плоскостей у природных кристаллов – девять 9Р. В кристалле серы насчитывается 3Р, а у гипса только одна. Значит, в одном кристалле может быть несколько плоскостей симметрии. В некоторых кристаллах плоскость симметрии отсутствует.
Относительно элементов ограничения плоскость симметрии может занимать следующее положение:
- проходит через ребра;
- лежать перпендикулярно к ребрам в их серединах;
- проходить через грань перпендикулярно к ней;
- пересекать гранные углы в их вершинах.
В кристаллах возможны следующие количества плоскостей симметрии: 9Р, 7Р, 6Р, 5Р, 4Р, 3Р, 2Р, Р, отсутствие плоскости симметрии.
Ось симметрии
Ось симметрии – воображаемая ось, при повороте вокруг которой на некоторый угол фигура совмещается сама с собой в пространстве. Она обозначается буквой L. У кристаллов при вращении вокруг оси симметрии на полный оборот одинаковые элементы ограничения (грани, ребра, углы) могут повторяться только 2, 3, 4, 6 раз. Соответственно этому оси будут называться осями симметрии второго, третьего, четвертого и шестого порядка и обозначаться: L2, L3, L4 и L6.Порядок оси определяется числом совмещений при повороте на 360⁰С.
Ось симметрии первого порядка не принимается во внимание, так как ею обладают вообще не фигуры, в том числе и несимметричные. Количество осей одного и того же порядка пишут перед буквой L: 6L6, 3L4 и т.п.
Центр симметрии
Центр симметрии – это точка внутри кристалла, в которой пересекаются и делятся пополам линии, соединяющие одинаковые элементы ограничения кристалла (грани, ребра, углы). Обозначается она буквой С. Практически присутствие центра симметрии будет сказываться в том, что каждое ребро многогранника имеет параллельное себе ребро, каждая грань – такую же параллельную себе зеркально-обратную грань. Если же в многограннике присутствуют грани, не имеющие себе параллельных, то такой многогранник не обладает центром симметрии.
Достаточно поставить многогранник гранью на стол, чтобы заметить, имеется ли сверху такая же параллельная ей зеркально-обратная грань. Конечно, на параллельность нужно проверить все типы граней.
Существует ряд простых закономерностей, по которым сочетаются друг с другом элементы симметрии. Значение этих правил облегчает их нахождение.
- Линия пересечения двух или нескольких плоскостей является осью симметрии. Порядок такой оси равен числу пересекающихся в ней плоскостей.
- L6 может присутствовать в кристалле только в единственном числе.
- С L6 не могут комбинироваться ни L4, ни L3, но может сочетаться L2 причем L6 и L2 должны быть перпендикулярны; в таком случае присутствует 6L2.
- L4 может встречаться в единственном числе или трех взаимно перпендикулярных осей.
- L3 может встречаться в единственном числе или с 4L3.
Степенью симметрии называется совокупность всех элементов симметрии, которыми обладает данный кристалл.
Кристалл, имеющий форму куба, обладает высокой степенью симметрии. В нем присутствуют три оси симметрии четвертого порядка (3L4), проходящие через середины граней куба, четыре оси симметрии третьего порядка (4L3), проходящие через вершины трехгранных углов, и шесть осей второго порядка (6L2), проходящих через середины ребер. В точке пересечения осей симметрии располагается центр симметрии куба (С). Кроме того, в кубе можно провести девять плоскостей симметрии (9Р). Элементы симметрии кристалла можно изобразить кристаллографической формулой.
Для куба формула имеет вид: 9P, 3L4, 4L3, 6L2, C.
Русский ученый А.В. Гадолин в 1869 г. показал, что у кристаллов возможны 32 различных сочетания элементов симметрии, составляющих классы (виды) симметрии. Таким образом, класс объединяет группу кристаллов с одинаковой степенью симметрии.
Что же такое ось симметрии? Это множество точек, которые образуют прямую, являющуюся основой симметрии, то есть, если от прямой отложили определенное расстояние с одной стороны, то оно отразится и в другую сторону в таком же размере. Осью может выступать все, что угодно, — точка, прямая, плоскость и так далее. Но об этом лучше говорить на наглядных примерах.
Симметрия
Для того чтобы понять, что такое ось симметрии, нужно вникнуть в само определение симметрии. Это соответствие определенного фрагмента тела относительно какой-либо оси, когда его структура неизменна, а свойства и форма такого объекта остаются прежними относительно его преобразований. Можно сказать, что симметрия — свойство тел к отображению. Когда фрагмент не может иметь подобного соответствия, это называется асимметрией или же аритмией.
Некоторые фигуры не имеют симметрии, поэтому они и называются неправильными или же асимметричными. К таким относятся различные трапеции (кроме равнобедренной), треугольники (кроме равнобедренного и равностороннего) и другие.
Виды симметрии
Также обсудим некоторые виды симметрии, чтобы до конца изучить это понятие. Их разделяют так:
История симметрии
Само понятие симметрии часто бывает отправной точкой в теориях и гипотезах ученых древних времен, которые были уверены в математической гармонии мироздания, а также в проявлении божественного начала. Древние греки свято верили в то, что Вселенная симметрична, потому что симметрия великолепна. Человек очень давно использовал идею симметрии в своих познаниях картины мироздания.
В V веке до нашей эры Пифагор считал сферу самой совершенной формой и думал, что Земля имеет форму сферы и таким же образом движется. Также он полагал, что Земля движется по форме какого-то «центрального огня», вокруг которого должны были вращаться 6 планет (известные на то время), Луна, Солнце и все другие звезды.
А философ Платон считал многогранники олицетворением четырех природных стихий:
- тетраэдр — огонь, так как его вершина направлена вверх;
- куб — земля, так как это самое устойчивое тело;
- октаэдр — воздух, нет каких-либо объяснений;
- икосаэдр — вода, так как тело не имеет грубых геометрических форм, углов и так далее;
- образом всей Вселенной являлся додекаэдр.
Из-за всех этих теорий правильные многогранники называют телами Платона.
Симметрией пользовались еще зодчие Древней Греции. Все их постройки были симметричны, об этом свидетельствуют изображения древнего храма Зевса в Олимпии.
Голландский художник М. К. Эшер также прибегал к симметрии в своих картинах. В частности, мозаика из двух птиц, летящих навстречу, стала основой картины «День и ночь».
Также и наши искусствоведы не пренебрегали правилами симметрии, что видно на примере картины Васнецова В. М. «Богатыри».
Что уж там говорить, симметрия — ключевое понятие для всех деятелей искусства на протяжении многих веков, но в XX веке ее смысл оценили также все деятели точных наук. Точным свидетельством являются физические и космологические теории, например, теория относительности, теория струн, абсолютно вся квантовая механика. Со времен Древнего Вавилона и, заканчивая передовыми открытиями современной науки, прослеживаются пути изучения симметрии и открытия ее основных законов.
Симметрия геометрических фигур и тел
Рассмотрим внимательнее геометрические тела. Например, осью симметрии параболы является прямая, проходящая через ее вершину и рассекающая данное тело пополам. У этой фигуры имеется одна единственная ось.
А с геометрическими фигурами дело обстоит иначе. Ось симметрии прямоугольника — также прямая, но их несколько. Можно провести ось параллельно отрезкам ширины, а можно — длины. Но не все так просто. Вот прямая не имеет осей симметрии, так как ее конец не определен. Могла существовать только центральная симметрия, но, соответственно, и таковой не будет.
Следует также знать то, что некоторые тела имеют множество осей симметрии. Об этом догадаться несложно. Даже не нужно говорить о том, сколько осей симметрии имеет окружность. Любая прямая, проходящая через центр окружности, является таковой и этих прямых — бесконечное множество.
У некоторые четырехугольников может быть две оси симметрии. Но вторые должны быть перпендикулярны. Это происходит в случае с ромбом и прямоугольником. В первом оси симметрии — диагонали, а во втором — средние линии. Множество таковых осей только у квадрата.
Симметрия в природе
Природа поражает множеством примеров симметрии. Даже наше человеческое тело устроено симметрично. Два глаза, два уха, нос и рот расположены симметрично относительно центральной оси лица. Руки, ноги и все тело в общем устроено симметрично оси, проходящей через середину нашего тела.
А сколько примеров окружает нас постоянно! Это цветы, листья, лепестки, овощи и фрукты, животные и даже соты пчел имеют ярко выраженную геометрическую форму и симметрию. Вся природа устроена упорядоченно, всему есть свое место, что еще раз подтверждает совершенство законов природы, в которых симметрия — основное условие.
Вывод
Нас постоянно окружают какие-либо явления и предметы, например, радуга, капля, цветы, лепестки и так далее. Их симметрия — очевидна, в какой-то степени она обусловлена гравитацией. Часто в природе под понятием «симметрия» понимают регулярную смену дня и ночи, времен года и так далее.
Подобные свойства наблюдаются везде, где есть порядок и равенство. Также и сами законы природы — астрономические, химические, биологические и даже генетические подчинены определенным принципам симметрии, так как имеют совершенную системность, а значит, сбалансированность имеет всеохватывающий масштаб. Следовательно, осевая симметрия — один из основополагающих законов мироздания в целом.
Понятие о симметрии. Элементы симметрии
«Симметрия» в переводе с греческого означает «соразмерность» (повторяемость). Симметричные тела и предметы состоят из равнозначных, правильно повторяющихся в пространстве частей. Особенно разнообразна симметрия кристаллов. Различные кристаллы отличаются большей или меньшей симметричностью. Она является их важнейшим и специфическим свойством, отражающим закономерность внутреннего строения.
По более точному определению симметрия – это закономерная повторяемость элементов (или частей) фигуры или какого-либо тела, при которой фигура совмещается сама с собой при некоторых преобразованиях (вращение вокруг оси, отражение в плоскости). Подавляющее большинство кристаллов обладает симметрией.
Понятие симметрии включает в себя составные части – элементы симметрии. Сюда относятся плоскость симметрии, ось симметрии, центр симметрии, или центр инверсии.
Плоскость симметрииПлоскость симметрии делит кристалл на две зеркально равные части. Обозначается она буквой Р. Части, на которые плоскость симметрии рассекает многогранник, относятся одна к другой, как предмет к своему изображению в зеркале разные кристаллы имеют различное количество плоскостей симметрии, которое ставится перед буквой Р. Наибольшее количество таких плоскостей у природных кристаллов – девять 9Р. В кристалле серы насчитывается 3Р, а у гипса только одна. Значит, в одном кристалле может быть несколько плоскостей симметрии. В некоторых кристаллах плоскость симметрии отсутствует.
Относительно элементов ограничения плоскость симметрии может занимать следующее положение:
- проходит через ребра;
- лежать перпендикулярно к ребрам в их серединах;
- проходить через грань перпендикулярно к ней;
- пересекать гранные углы в их вершинах.
В кристаллах возможны следующие количества плоскостей симметрии: 9Р, 7Р, 6Р, 5Р, 4Р, 3Р, 2Р, Р, отсутствие плоскости симметрии.
Ось симметрии
Ось симметрии – воображаемая ось, при повороте вокруг которой на некоторый угол фигура совмещается сама с собой в пространстве. Она обозначается буквой L. У кристаллов при вращении вокруг оси симметрии на полный оборот одинаковые элементы ограничения (грани, ребра, углы) могут повторяться только 2, 3, 4, 6 раз. Соответственно этому оси будут называться осями симметрии второго, третьего, четвертого и шестого порядка и обозначаться: L2, L3, L4 и L6.Порядок оси определяется числом совмещений при повороте на 360⁰С.
Ось симметрии первого порядка не принимается во внимание, так как ею обладают вообще не фигуры, в том числе и несимметричные. Количество осей одного и того же порядка пишут перед буквой L: 6L6, 3L4 и т.п.
Центр симметрии
Центр симметрии – это точка внутри кристалла, в которой пересекаются и делятся пополам линии, соединяющие одинаковые элементы ограничения кристалла (грани, ребра, углы). Обозначается она буквой С. Практически присутствие центра симметрии будет сказываться в том, что каждое ребро многогранника имеет параллельное себе ребро, каждая грань – такую же параллельную себе зеркально-обратную грань. Если же в многограннике присутствуют грани, не имеющие себе параллельных, то такой многогранник не обладает центром симметрии.
Достаточно поставить многогранник гранью на стол, чтобы заметить, имеется ли сверху такая же параллельная ей зеркально-обратная грань. Конечно, на параллельность нужно проверить все типы граней.
Существует ряд простых закономерностей, по которым сочетаются друг с другом элементы симметрии. Значение этих правил облегчает их нахождение.
- Линия пересечения двух или нескольких плоскостей является осью симметрии. Порядок такой оси равен числу пересекающихся в ней плоскостей.
- L6 может присутствовать в кристалле только в единственном числе.
- С L6 не могут комбинироваться ни L4, ни L3, но может сочетаться L2 причем L6 и L2 должны быть перпендикулярны; в таком случае присутствует 6L2.
- L4 может встречаться в единственном числе или трех взаимно перпендикулярных осей.
- L3 может встречаться в единственном числе или с 4L3.
Степенью симметрии называется совокупность всех элементов симметрии, которыми обладает данный кристалл.
Кристалл, имеющий форму куба, обладает высокой степенью симметрии. В нем присутствуют три оси симметрии четвертого порядка (3L4), проходящие через середины граней куба, четыре оси симметрии третьего порядка (4L3), проходящие через вершины трехгранных углов, и шесть осей второго порядка (6L2), проходящих через середины ребер. В точке пересечения осей симметрии располагается центр симметрии куба (С). Кроме того, в кубе можно провести девять плоскостей симметрии (9Р). Элементы симметрии кристалла можно изобразить кристаллографической формулой.
Для куба формула имеет вид: 9P, 3L4, 4L3, 6L2, C.
Русский ученый А.В. Гадолин в 1869 г. показал, что у кристаллов возможны 32 различных сочетания элементов симметрии, составляющих классы (виды) симметрии. Таким образом, класс объединяет группу кристаллов с одинаковой степенью симметрии.
Домашнее задание по математике по теме «Симметрия»
Каждый учитель знает, что домашнее задание должно быть одновременно и дидактически строго целесообразным, и привлекательным для учеников.
Авторское домашнее задание по математике
Тема : Симметрия фигур
Цель: отработка понятия симметрии, ось симметрии
Класс – 5 класс;
Сложность – задания не сложные
Время выполнения – 15-20 минут.
Тип задания – индивидуальное;
Способ проверки – оценивание работ в классе учащимися и учителем.
Учащимся предлагается выполнить дома практические работы:
РАБОТА № 1
Цель: определить количество осей симметрии у геометрических фигур
Задание:
Вырезать из бумаги прямоугольный треугольник, равнобедренный треугольник, прямоугольник, квадрат, круг
Найдите их ось симметрии перегибанием
Нарисуйте ось симметрии цветным карандашом
Сделайте вывод о количестве осей симметрии: Геометрические фигуры могут иметь________________________________________________________
РАБОТА №2
Цель: определить какие из букв русского языка имеют оси симметрии
Задание:
Написать или скопировать алфавит.
Определить, какие из букв имеют горизонтальную ось симметрии и провести её.
Определить, какие из букв имеют вертикальную ось симметрии и провести её.
Сделайте вывод:
Горизонтальную ось симметрии имеют буквы_________________
Вертикальную ось симметрии имеют буквы_______________
Горизонтальную и вертикальную ось симметрии имеют буквы____________
РАБОТА №3
Цель: определить какие из цифр языка имеют оси симметрии
Задание:
Записать цифру, имеющую ось симметрии и провести её.
РАБОТА 4
Задание:
1.Нарисовать любую фигуру, имеющую ось симметрии.
2. Придумать слово, все буквы которого имеют ось симметрии /например, ПОТОП/.
Проверка домашнего задания на уроке:
РАБОТА №1.
Один из учащихся демонстрирует оси симметрии фигур, остальные- оценивают правильность выполнения дома задания и количество правильных ответов отражают в листе самооценки./за каждое правильно выполненное задание 1балл/
Работа №2.
Учащиеся называют
Буквы, имеющие горизонтальную ось симметрии | В Е Ж З К Н О С Ф Х Э Ю |
Буквы, имеющие вертикальную ось симметрии | А Д Ж Л М Н О П Т Ф Х Ш |
Буквы, имеющие горизонтальную и вертикальную ось симметрии | Ж Н О Х Ф |
Определяют самостоятельно количество правильно найденных букв и отражают результат выполнения в листе самооценки./каждая правильно записанная буква – 1балл/
Работа №3
Ответ: 3;8;0
Учащиеся оценивают себя сами/ количество правильно записанных цифр-количество баллов/. Результат отражают в листе самооценки
Работа №4.Оценивает сосед по парте(за правильно выполненное задание по 2 балла) и количество набранных баллов заносит в лист самооценки.
Учащийся находит сумму набранных баллов и переводит в отметку.
Лист самооценки______________________________
Баллы | Шкала перевода баллов в отметку | |
Работа №1 | более 38 – «5» от 34до 37 – «4» от 25 до 33 – «3» | |
Работа №2 | ||
Работа №3 | ||
Работа №4 | ||
Итого: | Отметка: |
Симметрия плоскости симметрии — Справочник химика 21
Классификация основана на трех элементах симметрии плоскости симметрии, л-кратной оси симметрии и и-кратной зеркально-поворотной оси симметрии. Центр симметрии самостоятельно не рассматривается, так как он геометрически идентичен зеркально-поворотной оси симметрии второго порядка. На основании перечисленных трех элементов симметрии можно разделить молекулярные модели на две основные группы и пять категорий. Для каждой категории с помощью символов Шен-флиса введем типы симметрии, относящиеся к ней. [c.25]Важнейшая особенность кристаллов состоит в том, что они являются симметричными фигурами, отдельные части которых можно полностью совместить друг с другом либо поворотом, либо зеркальным отражением. Симметрия кристаллов является характерным признаком, посредством которого можно провести классификацию кристаллических форм. В кристаллах различают следующие элементы симметрии. Плоскость симметрии—воображаемая плоскость, разделяющая кристалл иа две части так, что одна из частей является зеркальным отражением другой. Ось симметрии — линия, при вращении вокруг которой кристалл несколько раз может совместиться с самим собой. Центр симметрии — точка внутри кристалла, в которой пересекаются и разделяются пополам линии, соединяющие соответственные точки на поверхности кристалла. [c.69]
Основным условием хиральности молекул является отсутствие центра симметрии, плоскости симметрии, зеркально-поворотной оси симметрии 5п в молекуле. [c.168]
Только эти четыре элемента симметрии — плоскость симметрии, простая ось симметрии, центр инверсии и инверсионная ось—встречаются в кристаллах как в отдельности, так и в виде их комбинаций друг с другом. Комбинаций этих элементов симметрии может в кристалле существовать только 32. Называются они точечными группами симметрии, так как при выводе их все элементы предполагаются проходящими через одну точку внутри кристалла. В соответствии с возможными группами симметрии все кристаллы также делятся на 32 класса. Для обозначения отдельных классов применяются чаще всего следующие символы. Цифрами 1, 2, 3, 4, 6 обозначают пять классов только с одной простой осью симметрии, причем класс 1 означает отсутствие элементов симметрии. Символы 22,32,42,62 означают четыре класса, где-к осям 2, 3, 4 и 6 порядков добавлена перпендикулярная ось второго порядка. В классах т, 2/т, 3/т, 4/т и б/т к осям 1, 2, 3, 4 и 6-го порядков добавлена горизонтальная (перпендикулярная) плоскость симметрии, а в классах тт, 2>т, Ат и 6т к указанным осям добавлена вертикальная (т. е. проходящая через ось) плоскость симметрии. Остальные 14 классов выводятся через добавление двух плоскостей симметрии и инверсионной оси. [c.15]
Наиболее привычный из всех элементов симметрии — плоскость симметрии, делящая фигуру на две части, каждая из которых является зеркальным изображением другой (рис. П1.48, б). Осью симметрии С называется такая ось, вращением вокруг которой можно привести геометрическую фигуру в положение, неотличимое от первоначального. Число п называется порядком оси оно показывает, сколько раз при повороте на 360° геометрическая фигура занимает идентичные [c.234]
Представления об элементах симметрии и классификации кристаллических форм. Отображением пространственной структуры монокристалла служит его кристаллическая решетка. Таким образом, различие геометрических форм кристаллов тех или иных веществ связано с особенностями симметрии их кристаллических решеток. Обычно оценивают следующие элементы симметрии в монокристалле оси симметрии, плоскости симметрии и центры симметрии. Если при повороте на определенный угол вокруг воображаемой оси кристаллическая решетка совмещается сама с собой, то это свидетельствует о наличии в кристалле оси симметрии. Если в кристалле можно провести одну или несколько плоскостей таким образом, что одна часть кристаллической решетки будет зеркальным отображением другой, значит в кристалле наличие плоскостей симметрии. Наконец, когда отражение всех узлов решетки в какой-либо точке кристалла приводит к их совмещению, говорят о существовании центра симметрии. В 1890 г. Е. С. Федоров провел расчет всех возможных сочетаний элементов симметрии и установил, что число устойчивых сочетаний равно 230. По-видимому, этой цифрой исчерпывается все многообразие возможных кристаллических структур в природе. [c.74]
Основанием для деления кристаллов на системы сначала служило положение осей кристаллов, а затем число плоскостей симметрии. Плоскостью симметрии называют плоскость, которая делит кристалл на две одинаковые части. [c.133]
Прибавление к осям симметрии плоскости симметрии может быть осуществлено параллельно оси, перпендикулярно к оси и наклонно. [c.27]
Одной из важнейших характеристик равновесной геометрической конфигурации молекулы является симметрия этой конфигурации. Для того чтобы определить точнее, что мы подразумеваем под симметрией молекулы (или симметрией ядерной конфигурации), необходимо ввести представление об операциях симметрии. Под операциями симметрии для молекулы подразумеваются операции отражения молекулы в плоскости, поворота молекулы как целого вокруг некоторой оси, отражения в центре или, наконец, вращения вокруг некоторой оси с последующим отражением в плоскости. Этим операциям симметрии соответствуют элементы симметрии— плоскости симметрии, оси симметрии, центр симметрии и зеркально-поворотные оси симметрии. Поясним характер этих элементов симметрии и сосй-ветствующих им операций на примерах простейших молекул, причем будем рассматривать только равновесную геометрическую конфигурацию ядер молекулы. [c.202]
Примеры Символ симметрии Плоскости симметрии Ось симметрии Зеркально- поворотная ось [c.474]
Элементы симметрии включают ось симметрии, плоскость симметрии, центр симметрии, альтернантную ось симметрии. [c.124]
Элементы симметрии можно применить для классификации кристаллов. Для удобства иллюстрации вновь используем модель параллелепипеда. Представим себе крайний случай, когда система характеризуется наинизшей симметрией, т. е. нет центра симметрии, плоскостей симметрии и осей симметрии, за исключением оси первого порядка, которая [c.230]
Если заместители неодинаковы, то это скажется только на, 2-изомере, теряющем единственный имевшийся у него элемент симметрии—плоскость симметрии—и приобретающем в результате этого возможность существовать в оптически деятельных формах. Что касается 1,3-изомеров, то они теряют лишь часть элементов симметрии ( с-форма лишается одной из двух плоскостей симметрии (проходящей через атомы 2 и 4), а транс-форма теряет только ось симметрии. Поэтому, несмотря на разные заместители, эти изомеры нельзя разделить на оптически деятельные стереоизомерные формы. [c.29]
Молекулы, имеющие только оси (кроме осей n/z, коллинеарных осям Sn), относят к точечным группам S . Обе точечные группы, содержащие молекулы с единственными элементами симметрии — плоскостью симметрии а (5j) или центром симметрии ( 2 = i), обозначают С или (=83) соответственно. Молекулы, обладающие осью наряду с коллинеарной осью Si (т. е. перпендикулярной ст-плоскостью), относят к точечным группам Спь-Молекулы, которые, кроме оси С , имеют также п перпендикулярных осей Si (т. е. п 0-плоскостей, содержащих оси С ), принадлежат к точечным группам ). Молекулы с диэдрической симметрией и осью S , коллинеарной главной оси, относят к точечным группам Ъпн- Молекулы диэдрической симметрии с п осями S , перпендикулярными главной оси, принадлежат к точечным группам [c.10]
В приведенных примерах, чтобы совместить фигуру до оказания на нее определенного действия и после него, ма поворачиваем фигуру вокруг осей. Эти оси называются ося. ми симметрии. Существуют и другие элементы симметрии плоскость симметрии и центр симметрии. Элементы симмет- [c.65]
Каждая молекула с плоскостью симметрии имеет ось 51 (или 7)—это ось, перпендикулярная плоскости симметрии. У химиков обычно принято использовать в качестве элемента симметрии плоскость симметрии, а не ось особенно если это единственный элемент симметрии в молекуле. Так, например, в хлорэтилене (рис. 17, а) плоскость симметрии является плоскостью молекулы (плоскость ху), а ось г — осью 5х. Поворот на 360° вокруг оси 2 и отражение в перпендикулярной к ней плоскости ху приводит к исходной ориентации молекулы. Конечно, поворот на 360° вокруг любой оси возвращает молекулу в исходное положение, но [c.27]
Во многих молекулах атомы в равновесном состоянии расположены симметрично относительно некоторых плоскостей, осей или относительно некоторой точки (центра). Принято говорить в этом случае, что молекула в равновесной конфигурации обладает симметрией по отношению к элементам симметрии плоскостям симметрии, осям симметрии, зеркально-поворотным осям и центрам симметрии. [c.180]
Другой критерий для установления симметричности или асимметричности предмета основывается на исследовании элементов симметрии. Плоскостью симметрии называется плоскость, разделяющая предмет на две тождественные половины, относящиеся друг к другу как предмет к своему зеркальному изображению. Предмет обладает центром симметрии тогда, когда внутри его существует точка, расположенная так, что любая проходящая через нее прямая встречает в обоих направлениях одни и те же структурные формы. Асимметричным является любой предмет, не обладающий плоскостью и центром симметрии. [c.30]
На рис. 11.17, б изображены элементы симметрии пространственной группы О A2d. Цифры около горизонтальных чередующихся осей симметрии 2 и 2 , различающихся оперением стрелок, указывают высоту положения осей над плоскостью чертежа. Цифры около вертикальных осей показывают высоту положения виртуальных центров симметрии. Плоскости симметрии являются диагональными плоскостями скользящего отражения со сдвигом, равным /4-, стрелки показывают направления сдвигов. Размножая точку, взятую в частных или в общем положениях, можно найти координаты эквивалентных точек, которые приводятся в таблицах пространственных групп. Для рассматриваемой группы Did — J42d находим положения точек [c.62]
Если рассмотреть симметрию молекул оптически активных соединений, то окажется, что эти молекулы не обладают ни плоскостями, ни центрами симметрии. Плоскостью симметрии называется плоскость, разделяющая тело на две зеркально симметричные половины (т. е. таким образом, что одна половина является зеркальным изображением другой). Центр симметрии — это точка, обладающая тем свойством, что если на любой прямой, проходящей через нее, отложить равные отрезки по обе стороны от центра, то получим эквивалентные точки тела. Это означает, что молекула, которая хотя бы в одной из своих конформаций обладает плоскостью или центром симметрии, является ахиральной (т. е. нехиральной) дру- [c.88]
Подобно любой системе материальных точек молекула может иметь один или несколько элементов симметрии плоскость симметрии, центр симметрии, ось симметрии порядка р. Каждому элементу симметрии соответствует операция симметрии отражение в плоскости симметрии или в центре симметрии либо вращение на угол Зб07р вокруг оси симметрии. Линейная молекула имеет бесконечное число элементов симметрии (любая плоскость, проходящая через межъядерную ось, является плоскостью симметрии) [c.119]
Первый тип включает молекулы, имеющие асимметрический атом углерода С. В этих молекулах имеется один, два или несколько атомов углерода, связанного с различными остатками молекул. Простейшим примером такой молекулы может быть фторхлорбромметан СНР(С1)Вг. Она не имеет никаких элементов симметрии (осей симметрии, плоскостей симметрии, зеркально-поворотных осей, центра симметрии). [c.37]
Для 1,2- и 1,3-структур этих кислот возможны пространственные (геометрические) цис- и тршс-изомеры. Из них гра с-1,2-изомер существует также в виде двух оптических антиподов (энантиомеров). Изомер кислоты цис-1,2 и геометрические изомеры циклобутан-1,3-дикарбоновой кислоты не имеют оптических изомеров, так как их молекулы обладают элементом симметрии (плоскостью симметрии). [c.55]
Относится к кристаллам, напр, к кварцу (лево- и правовращающему плоскость поляризации). Э. возможен у низкосимметрич. кристаллов (не имеющих ценфа симметрии, плоскости симметрии и зеркальных осей симметрии). [c.255]
Монозамещенные алканы, кроме изобутана и других углеводородов типа (К)зСН, лишены осей симметрии. Плоскость симметрии имеется лишь в алканах, где третичный углеродный атом замещен двумя одинаковыми радикалами (например, 3-метилпен-тан и т. д.). В то же время в диметилалканах некоторые конформации в симметрично-замещенных структурах, например в 2,7-ди-метилоктане, имеют оси симметрии 2-го порядка. Плоскости симметрии в таких структурах легко заметить в каждом конкретном случае. [c.18]
Как упоминалось выше, этот тип изомерии присущ соединениям, которые не обладают ни одним из следующих элементов симметрии центр симметрии, плоскость симметрии и зеркально-поворотная ось. По аналогии с геометрическими изомерами оптическая изомерия может наблюдаться лишь для тех элементов, которые образуют кинетически инертные комплексы, причем лиганды сами по себе должны быть оптически неактивными. В литературе приводятся также сведения об оптической изомерии некоторых ионов, например А1(1П), d(H), Zn(II), образующих кинетически лабильные комплексы однако попытки повторного синтеза этих комплексов оказались неудачными. Примерами оптических изомеров могут служить комплексы [iFe(dipy)з] +, [Ре(рЬеп)з]2+, [Со(еп)з] + и т. д., структуры которых изображены ниже [c.60]
Dnd — группа диэдральной симметрии, дополненная па плоскостями симметрии плоскости симметрии делят пополам ди-эдральные углы Сг осей и пересекаются на основной С оси (пример циклогексан в креслообразной конформации Dzd) [c.26]
Элементами симметрии молекул являются центр симметрии, плоскость симметрии, ось симметрии и зеркаль-но-поворотная ось они обозначаются соответственно [c.139]
Кристаллическому строению вещества присущи следующие элементы симметрии плоскость симметрии, ось симметрии и центр симмётрии. Пользуясь элементами симметрии, все разнообразие кристаллических разновидностей классифицируют на 7 систем, состоящих из 32 классов, или видов симметрии, к которым относят тот или иной кристалл. [c.130]
Основы спектроскопического определения наличия быстрого взаимопревращения эквивалентных таутомеров состоят в следующем. В любом спектре (например, инфракрасном), если вследствие принципа неопределенности А -Двремя наблюдения становится гораздо более коротким, чем время жизни таутомера, будут наблюдаться спектральные частоты одного таутомера и вид спектра не будет зависеть от температ фы. Однако в случае протонного магнитного резонанса энергии настолько малы, что время наблюдения становится относительно большим — от миллисекунд до секунд. Если при некоторой температуре время жизни таутомера сравнимо со временем наблюдения сигнала, то ниже этой температуры будет наблюдаться дискретный спектр, не меняющийся при изменении температуры. В спектре будут наблюдаться сигналы протонов, входящих в состав индивидуальных таутомеров. Выше определенной температуры будет наблюдаться другой спектр, также дискретный и не зависящий от температуры, однако сигналы протонов будут такими, которые наблюдались бы, если бы имелась дополнительная симметрия (плоскость симметрии), обусловленная усредненной структурой, т. е. размазыванием подвижных связей. В интервале между этими пороговыми температурами будет наблюдаться диффузный спектр, меняющийся с температурой. В описываемом случае разные дискретные спектры, соответствующие теории, были получены при —50 °С и при 180 °С, а в интервале между этими температурами спектр был диффузным и зависел от температуры. Хотя эти спектры количественно не анализировались, качественно из них следует, что время жизни таутомера при О °С должно быть порядка сантисекунды. [c.728]
Важной особенностью большинства К. является их симметрия, к-рая описывается при помощи алементов симметрии (оси симметрии, плоскости симметрии, центра инверсии), каждый из к-рых производт одну или несколько операций, совмещающих равные части фигуры друг с другом так, что и вся фигура сов.мещается сама с собой. [c.424]
В кристаллографической литературе существует больщой разнобой в обозначении элементов симметрии. Плоскость симметрии в большинстве случаев обозначается Р или Е (Ebene), особые плоскости, как, например, перпендикулярные главной поворотной оси (например, оси 6-го порядка в шестигранной призме) иногда обозначаются тт. Поворотные оси п-то порядка обозначаются L , (гира), и т. п. Центр инверсии —z, Сит. п. В наиболее принятых обозначениях элементы симметрии шестигранной [c.37]
Ось симметрии — определение. Фигуры, имеющие ось симметрии
Что же такое ось симметрии? Это множество точек, которые образуют прямую, являющуюся основой симметрии, то есть, если от прямой отложили определенное расстояние с одной стороны, то оно отразится и в другую сторону в таком же размере. Осью может выступать все, что угодно, — точка, прямая, плоскость и так далее. Но об этом лучше говорить на наглядных примерах.
Симметрия
Для того чтобы понять, что такое ось симметрии, нужно вникнуть в само определение симметрии. Это соответствие определенного фрагмента тела относительно какой-либо оси, когда его структура неизменна, а свойства и форма такого объекта остаются прежними относительно его преобразований. Можно сказать, что симметрия — свойство тел к отображению. Когда фрагмент не может иметь подобного соответствия, это называется асимметрией или же аритмией.
Некоторые фигуры не имеют симметрии, поэтому они и называются неправильными или же асимметричными. К таким относятся различные трапеции (кроме равнобедренной), треугольники (кроме равнобедренного и равностороннего) и другие.
Виды симметрии
Также обсудим некоторые виды симметрии, чтобы до конца изучить это понятие. Их разделяют так:
- Осевая. Осью симметрии является прямая, проходящая через центр тела. Как это? Если наложить части вокруг оси симметрии, то они будут равными. Это можно увидеть на примере сферы.
- Зеркальная. Осью симметрии здесь является прямая, относительно которой тело можно отразить и получить обратное отображение. Например, крылья бабочки зеркально симметричны.
- Центральная. Осью симметрии является точка в центре тела, относительно которой при всех преобразованиях части тела равны при наложении.
История симметрии
Само понятие симметрии часто бывает отправной точкой в теориях и гипотезах ученых древних времен, которые были уверены в математической гармонии мироздания, а также в проявлении божественного начала. Древние греки свято верили в то, что Вселенная симметрична, потому что симметрия великолепна. Человек очень давно использовал идею симметрии в своих познаниях картины мироздания.
В V веке до нашей эры Пифагор считал сферу самой совершенной формой и думал, что Земля имеет форму сферы и таким же образом движется. Также он полагал, что Земля движется по форме какого-то «центрального огня», вокруг которого должны были вращаться 6 планет (известные на то время), Луна, Солнце и все другие звезды.
А философ Платон считал многогранники олицетворением четырех природных стихий:
- тетраэдр — огонь, так как его вершина направлена вверх;
- куб — земля, так как это самое устойчивое тело;
- октаэдр — воздух, нет каких-либо объяснений;
- икосаэдр — вода, так как тело не имеет грубых геометрических форм, углов и так далее;
- образом всей Вселенной являлся додекаэдр.
Из-за всех этих теорий правильные многогранники называют телами Платона.
Симметрией пользовались еще зодчие Древней Греции. Все их постройки были симметричны, об этом свидетельствуют изображения древнего храма Зевса в Олимпии.
Голландский художник М. К. Эшер также прибегал к симметрии в своих картинах. В частности, мозаика из двух птиц, летящих навстречу, стала основой картины «День и ночь».
Также и наши искусствоведы не пренебрегали правилами симметрии, что видно на примере картины Васнецова В. М. «Богатыри».
Что уж там говорить, симметрия — ключевое понятие для всех деятелей искусства на протяжении многих веков, но в XX веке ее смысл оценили также все деятели точных наук. Точным свидетельством являются физические и космологические теории, например, теория относительности, теория струн, абсолютно вся квантовая механика. Со времен Древнего Вавилона и, заканчивая передовыми открытиями современной науки, прослеживаются пути изучения симметрии и открытия ее основных законов.
Симметрия геометрических фигур и тел
Рассмотрим внимательнее геометрические тела. Например, осью симметрии параболы является прямая, проходящая через ее вершину и рассекающая данное тело пополам. У этой фигуры имеется одна единственная ось.
А с геометрическими фигурами дело обстоит иначе. Ось симметрии прямоугольника — также прямая, но их несколько. Можно провести ось параллельно отрезкам ширины, а можно — длины. Но не все так просто. Вот прямая не имеет осей симметрии, так как ее конец не определен. Могла существовать только центральная симметрия, но, соответственно, и таковой не будет.
Следует также знать то, что некоторые тела имеют множество осей симметрии. Об этом догадаться несложно. Даже не нужно говорить о том, сколько осей симметрии имеет окружность. Любая прямая, проходящая через центр окружности, является таковой и этих прямых — бесконечное множество.
У некоторые четырехугольников может быть две оси симметрии. Но вторые должны быть перпендикулярны. Это происходит в случае с ромбом и прямоугольником. В первом оси симметрии — диагонали, а во втором — средние линии. Множество таковых осей только у квадрата.
Симметрия в природе
Природа поражает множеством примеров симметрии. Даже наше человеческое тело устроено симметрично. Два глаза, два уха, нос и рот расположены симметрично относительно центральной оси лица. Руки, ноги и все тело в общем устроено симметрично оси, проходящей через середину нашего тела.
А сколько примеров окружает нас постоянно! Это цветы, листья, лепестки, овощи и фрукты, животные и даже соты пчел имеют ярко выраженную геометрическую форму и симметрию. Вся природа устроена упорядоченно, всему есть свое место, что еще раз подтверждает совершенство законов природы, в которых симметрия — основное условие.
Вывод
Нас постоянно окружают какие-либо явления и предметы, например, радуга, капля, цветы, лепестки и так далее. Их симметрия — очевидна, в какой-то степени она обусловлена гравитацией. Часто в природе под понятием «симметрия» понимают регулярную смену дня и ночи, времен года и так далее.
Подобные свойства наблюдаются везде, где есть порядок и равенство. Также и сами законы природы — астрономические, химические, биологические и даже генетические подчинены определенным принципам симметрии, так как имеют совершенную системность, а значит, сбалансированность имеет всеохватывающий масштаб. Следовательно, осевая симметрия — один из основополагающих законов мироздания в целом.
| Телефон : | 780-427-5318 | ||||||||||||||
| (Composer d’abord le 310-0000 pour obtenir une ligne sans frais) | |||||||||||||||
| Телекопье: | 780-427-1179 | ||||||||||||||
| Adresse de Courriel: | cshelpdesk @ gov. {2} + b x + c \ end {уравнение} \) где a, b — коэффициенты при «x» c — постоянная форма.{2} + k \ end {Equation} \) где (h, k) — вершина параболы. В форме вершины можно сказать, что x = h, поскольку ось симметрии и вершина лежат на одной прямой.
Вывод параболического уравнения обсуждается на следующем занятии ниже. Калькулятор осей симметрии Ось симметрии и вычислитель вершин показаны ниже. ИспользованиеЭто поможет вам рассчитать положение оси симметрии с помощью уравнения стандартной формы. Калькулятор области симметрии помогает определить фактическое положение параболы. Примеры осей симметрии Мы можем видеть эту ось симметрии даже в природе, такой как цветы, берег реки, здания и т. Д. Мы можем наблюдать ось симметрии в Тадж-Махале, культовом мраморном сооружении Индии. Некоторые из примеров оси симметрии в природе перечислены ниже. Вывести ось симметрии параболы Формула оси симметрии для параболы: \ [\ begin {equal} x = \ frac {-b} {2a} \ end {equal} \] Почему ось симметрии находится в \ (\ begin {Equation} x = \ frac {-b} {2a} \ end {Equation} \)? Вот как это. По определению оси симметрии параболы, это вертикальная линия, разделяющая параболу на две идентичные половины.{2} + b x = 0 \ end {equal} \] \ [\ begin {уравнение} x (ax + b) = 0 \ end {уравнение} \] \ [\ begin {уравнение} (ax + b) = 0 \ end {уравнение} \] (поскольку взятие \ (\ begin {уравнение} x \ end {уравнение} \) с другой стороны) \ [\ begin {уравнение} x = \ frac {-b} {a} \ end {уравнение} \] Следовательно, два значения x равны \ (\ begin {формула} 0, \ frac {-b} {a} \ end {уравнение} \) Формула средней точки: \ begin {уравнение} x = \ frac {x_ {1} + x_ {2}} {2} \ end {уравнение} \ [\ begin {уравнение} x = \ frac {0+ \ left (\ frac {-b} {a} \ right)} {2} \ end {уравнение} \]
Парабола может быть двух видов. Может быть горизонтальным или вертикальным, но это основано на оси симметрии. Если ось симметрии вертикальна, то парабола вертикальна. Если ось симметрии горизонтальна, то парабола горизонтальна. Поскольку ось симметрии лежит на оси x, мы берем точку пересечения с y.
Определить ось симметрии по графику Пример 1 .{2} + b y + c \ end {формула} \] Следовательно, a = 4, b = 5 и c = 3 Мы знаем, что \ [\ begin {equal} y = \ frac {-b} {2a} \ end {Equal} \] \ [\ begin {уравнение} y = \ frac {-5} {2 (4)} \ end {уравнение} \] \ [\ begin {уравнение} \, следовательно, y = -0,625 \ end {уравнение} \] Решенные примеры 1. Помогите Анне определить форму, которая удовлетворяет определению оси симметрии. Решение Определение оси симметрии утверждает, что это прямая линия, разделяющая объект на две идентичные половины. Ось симметрии должна создавать зеркальное отображение. Это форма, симметричная как по горизонтали, так и по вертикали. Ось симметрии образует две идентичные половинки.
Мистер Джейд вызывает своего ученика Джорджа, чтобы он нарисовал ось симметрии на графике вдоль оси x. Помогите Джорджу нарисовать ось симметрии. Подсказка: a = 3, b = -12 & c = 5 Решение Мы знаем, что \ [\ begin {equal} x = \ frac {-b} {2a} \ end {equal} \] Применение значений a и b. \ [\ begin {уравнение} x = \ frac {- (- 12)} {2 (3)} \ end {уравнение} \] \ [\ begin {уравнение} \ поэтому x = 2 \ end {уравнение} \]
1. Симметрична ли парабола относительно оси x или оси y? 2. Каково уравнение оси симметрии этой параболы? Интерактивные вопросыВот несколько занятий для вас. Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат. Какая форма имеет бесконечные линии (или) ось симметрии? Подведем итогиМини-урок был посвящен увлекательной концепции оси симметрии. Математическое путешествие вокруг оси симметрии начинается с того, что ученик уже знает, и переходит к творческому созданию новой концепции в молодых умах.Сделано таким образом, чтобы оно не только было понятным и понятным, но и навсегда осталось с ними. В этом заключается магия Куэмат. О компании CuemathВ Cuemath наша команда математиков стремится сделать обучение интересным для наших любимых читателей, студентов! Благодаря интерактивному и увлекательному подходу «обучение-обучение-обучение» учителя исследуют тему со всех сторон. Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, это логическое мышление и интеллектуальный подход к обучению, в которые мы, в Cuemath, верим.{2} + b x + c \ end {формула} \) Формула оси симметрии: \ [\ begin {уравнение} x = \ frac {-b} {2a} \ end {уравнение} \] Ось симметрии — CuemathПосмотрите на изображение шестиугольника ниже. {2} + b x + c \ end {уравнение} \) где a, b — коэффициенты при «x» c — постоянная форма.{2} + k \ end {Equation} \) где (h, k) — вершина параболы. В форме вершины можно сказать, что x = h, поскольку ось симметрии и вершина лежат на одной прямой.
Вывод параболического уравнения обсуждается на следующем занятии ниже. Калькулятор осей симметрии Ось симметрии и вычислитель вершин показаны ниже. ИспользованиеЭто поможет вам рассчитать положение оси симметрии с помощью уравнения стандартной формы. Калькулятор области симметрии помогает определить фактическое положение параболы. Примеры осей симметрии Мы можем видеть эту ось симметрии даже в природе, такой как цветы, берег реки, здания и т. Д. Мы можем наблюдать ось симметрии в Тадж-Махале, культовом мраморном сооружении Индии. Некоторые из примеров оси симметрии в природе перечислены ниже. Вывести ось симметрии параболы Формула оси симметрии для параболы: \ [\ begin {equal} x = \ frac {-b} {2a} \ end {equal} \] Почему ось симметрии находится в \ (\ begin {Equation} x = \ frac {-b} {2a} \ end {Equation} \)? Вот как это. По определению оси симметрии параболы, это вертикальная линия, разделяющая параболу на две идентичные половины.{2} + b x = 0 \ end {equal} \] \ [\ begin {уравнение} x (ax + b) = 0 \ end {уравнение} \] \ [\ begin {уравнение} (ax + b) = 0 \ end {уравнение} \] (поскольку взятие \ (\ begin {уравнение} x \ end {уравнение} \) с другой стороны) \ [\ begin {уравнение} x = \ frac {-b} {a} \ end {уравнение} \] Следовательно, два значения x равны \ (\ begin {формула} 0, \ frac {-b} {a} \ end {уравнение} \) Формула средней точки: \ begin {уравнение} x = \ frac {x_ {1} + x_ {2}} {2} \ end {уравнение} \ [\ begin {уравнение} x = \ frac {0+ \ left (\ frac {-b} {a} \ right)} {2} \ end {уравнение} \]
Парабола может быть двух видов. Может быть горизонтальным или вертикальным, но это основано на оси симметрии. Если ось симметрии вертикальна, то парабола вертикальна. Если ось симметрии горизонтальна, то парабола горизонтальна. Поскольку ось симметрии лежит на оси x, мы берем точку пересечения с y.
Определить ось симметрии по графику Пример 1 .{2} + b y + c \ end {формула} \] Следовательно, a = 4, b = 5 и c = 3 Мы знаем, что \ [\ begin {equal} y = \ frac {-b} {2a} \ end {Equal} \] \ [\ begin {уравнение} y = \ frac {-5} {2 (4)} \ end {уравнение} \] \ [\ begin {уравнение} \, следовательно, y = -0,625 \ end {уравнение} \] Решенные примеры 1. Помогите Анне определить форму, которая удовлетворяет определению оси симметрии. Решение Определение оси симметрии утверждает, что это прямая линия, разделяющая объект на две идентичные половины. Ось симметрии должна создавать зеркальное отображение. Это форма, симметричная как по горизонтали, так и по вертикали. Ось симметрии образует две идентичные половинки.
Мистер Джейд вызывает своего ученика Джорджа, чтобы он нарисовал ось симметрии на графике вдоль оси x. Помогите Джорджу нарисовать ось симметрии. Подсказка: a = 3, b = -12 & c = 5 Решение Мы знаем, что \ [\ begin {equal} x = \ frac {-b} {2a} \ end {equal} \] Применение значений a и b. \ [\ begin {уравнение} x = \ frac {- (- 12)} {2 (3)} \ end {уравнение} \] \ [\ begin {уравнение} \ поэтому x = 2 \ end {уравнение} \]
1. Симметрична ли парабола относительно оси x или оси y? 2. Каково уравнение оси симметрии этой параболы? Интерактивные вопросыВот несколько занятий для вас. Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат. Какая форма имеет бесконечные линии (или) ось симметрии? Подведем итогиМини-урок был посвящен увлекательной концепции оси симметрии. Математическое путешествие вокруг оси симметрии начинается с того, что ученик уже знает, и переходит к творческому созданию новой концепции в молодых умах.Сделано таким образом, чтобы оно не только было понятным и понятным, но и навсегда осталось с ними. В этом заключается магия Куэмат. О компании CuemathВ Cuemath наша команда математиков стремится сделать обучение интересным для наших любимых читателей, студентов! Благодаря интерактивному и увлекательному подходу «обучение-обучение-обучение» учителя исследуют тему со всех сторон. Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, это логическое мышление и интеллектуальный подход к обучению, в которые мы, в Cuemath, верим.{2} + b x + c \ end {формула} \) Формула оси симметрии: \ [\ begin {уравнение} x = \ frac {-b} {2a} \ end {уравнение} \] Вершина и ось симметрии — КонцепцияВ параболе вершина является самой высокой или самой низкой точкой параболы. Чтобы вычислить вершину параболы, мы можем сначала вычислить значение x, разделив значение, противоположное значению «b», на 2, умноженное на значение «a». Вершина — это самая высокая точка, если парабола открывается вниз, и самая низкая точка, если парабола открывается вверх.Ось симметрии — это линия, которая разрезает параболу на 2 совпадающие половины, а вершина лежит на оси симметрии. Одна из вещей, о которой вы действительно захотите узнать, если мы графически изображаем параболы, — это как найти вершину, а также как найти ось симметрии. Они довольно просты, если вы освоите их. | [латекс] \ left (h, \ text {} k + p \ right) [/ latex] | [латекс] y = k-p [/ латекс] | [латекс] \ влево (h \ pm 2p, \ text {} k + p \ right) [/ latex] | |||||||||||
(a) Когда [латекс] p> 0 [/ латекс], парабола открывается вправо.{2} = 4p \ left (x-h \ right) [/ latex], тогда:
- используйте данное уравнение для определения [латекс] h [/ латекс] и [латекс] k [/ латекс] для вершины, [латекс] \ left (h, k \ right) [/ latex]
- используйте значение [latex] k [/ latex] для определения оси симметрии, [latex] y = k [/ latex]
- установите [latex] 4p [/ latex] равным коэффициенту [latex] \ left (x-h \ right) [/ latex] в данном уравнении, чтобы решить для [latex] p [/ latex]. Если [latex] p> 0 [/ latex], парабола открывается вправо. Если [latex] p <0 [/ latex], парабола открывается влево.{2} = 4p \ left (y-k \ right) [/ latex], тогда:
- используйте данное уравнение для определения [латекс] h [/ латекс] и [латекс] k [/ латекс] для вершины, [латекс] \ left (h, k \ right) [/ latex]
- используйте значение [latex] h [/ latex] для определения оси симметрии, [latex] x = h [/ latex]
- установите [latex] 4p [/ latex] равным коэффициенту [latex] \ left (y-k \ right) [/ latex] в данном уравнении, чтобы решить для [latex] p [/ latex]. Если [latex] p> 0 [/ latex], парабола раскрывается. Если [latex] p <0 [/ latex], парабола открывается вниз.
- используйте [latex] h, k [/ latex] и [latex] p [/ latex], чтобы найти координаты фокуса, [latex] \ left (h, \ text {} k + p \ right) [/ латекс]
- используйте [latex] k [/ latex] и [latex] p [/ latex], чтобы найти уравнение директрисы, [latex] y = k-p [/ latex]
- используйте [latex] h, k [/ latex] и [latex] p [/ latex], чтобы найти конечные точки фокусного диаметра, [latex] \ left (h \ pm 2p, \ text {} k + p \ справа) [/ латекс]
- Постройте вершину, ось симметрии, фокус, направляющую и диаметр фокуса и нарисуйте плавную кривую, чтобы сформировать параболу. {2} -8x — 28y — 208 = 0 [/ latex].{2} = 4 \ cdot 7 \ cdot \ left (y + 8 \ right) \ end {gather} [/ latex]
Отсюда следует, что:
- вершина [латекс] \ left (h, k \ right) = \ left (4, -8 \ right) [/ latex]
- ось симметрии [латекс] x = h = 4 [/ латекс]
- , так как [latex] p = 7, p> 0 [/ latex] и парабола открывается
- координаты фокуса [латекс] \ left (h, k + p \ right) = \ left (4, -8 + 7 \ right) = \ left (4, -1 \ right) [/ latex]
- уравнение директрисы [латекс] y = k-p = -8 — 7 = -15 [/ latex]
- конечные точки фокусного диаметра: [латекс] \ left (h \ pm 2p, k + p \ right) = \ left (4 \ pm 2 \ left (7 \ right), — 8 + 7 \ right) [/ латекс] или [латекс] \ left (-10, -1 \ right) [/ latex] и [latex] \ left (18, -1 \ right) [/ latex]
Затем мы рисуем вершину, ось симметрии, фокус, директрису и диаметр фокуса и рисуем плавную кривую, чтобы сформировать параболу.{2} = — 20 \ влево (у — 3 \ вправо) [/ латекс]. Определите и обозначьте вершину, ось симметрии, фокус, направляющую и конечные точки фокусного диаметра.
Показать решениеВершина: [латекс] \ влево (-2,3 \ вправо) [/ латекс]; Ось симметрии: [латекс] x = -2 [/ латекс]; Фокус: [латекс] \ влево (-2, -2 \ вправо) [/ латекс]; Направляющая: [латекс] y = 8 [/ латекс]; Конечные точки прямой кишки: [латекс] \ влево (-12, -2 \ вправо) [/ латекс] и [латекс] \ влево (8, -2 \ вправо) [/ латекс].
Решение прикладных задач с использованием парабол
Как мы упоминали в начале раздела, параболы используются для проектирования многих объектов, которые мы используем каждый день, таких как телескопы, подвесные мосты, микрофоны и радарное оборудование.Параболические зеркала, такие как то, которое используется для освещения олимпийского факела, обладают уникальным отражающим свойством. Когда лучи света, параллельные оси симметрии параболы , направляются к любой поверхности зеркала, свет отражается прямо в фокус. Вот почему олимпийский факел зажигается, когда он находится в фокусе параболического зеркала.
Отражающее свойство парабол
Параболические зеркала способны фокусировать энергию солнца в одну точку, повышая температуру на сотни градусов за считанные секунды.Таким образом, параболические зеркала используются во многих недорогих, энергоэффективных солнечных устройствах, таких как солнечные плиты, солнечные обогреватели и даже разжигатели огня для путешествий.
Пример: решение прикладных задач с использованием парабол
Поперечный разрез конструкции путевого солнечного пожарного стартера. Солнечные лучи отражаются от параболического зеркала в направлении объекта, прикрепленного к воспламенителю. Поскольку воспламенитель расположен в фокусе параболы, отраженные лучи заставляют объект гореть всего за секунды.{2} = 6,8 года && \ text {Заменить 2} \ text {0,25 вместо} x. \\ & y \ приблизительно 0,74 && \ text {Решить для} y. \ end {align} [/ latex]
Блюдо имеет глубину около 0,74 дюйма.
Попробуй
Солнечные плиты размером с балкон были разработаны для семей, живущих в Индии. Верх тарелки имеет диаметр 1600 мм. Солнечные лучи отражаются от параболического зеркала в сторону «плиты», расположенной на расстоянии 320 мм от основания.
- Найдите уравнение, моделирующее поперечное сечение солнечной плиты.{2} = 1280x [/ латекс]
- Глубина плиты 500 мм
Внесите свой вклад!
У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.
Улучшить эту страницуПодробнее
Как отразить график по оси X
Отражение по оси X
Прежде чем мы перейдем к отражениям по оси Y, убедитесь, что вы освежили свою память о том, как выполнять простые вертикальные и горизонтальные переводы.
Как отражать по оси X:
Одно из самых простых преобразований, которое вы можете выполнить с помощью простых функций, — это отразить его поперек оси x или другой горизонтальной оси. В потенциальном тестовом вопросе это можно сформулировать по-разному, поэтому убедитесь, что вы понимаете следующие термины как еще один способ сказать «выполнить отражение по оси x»:
1) График y = −f (x) y = -f (x) y = −f (x)
2) График −f (x) -f (x) −f (x)
3) Отражение по оси xxx
Чтобы сделать это, процесс чрезвычайно прост: для любой функции, какой бы сложной она ни была, просто выберите легко определяемые координаты, разделите координату y на (-1), а затем заново постройте график. эти координаты.Вот и все!
Лучший способ попрактиковаться в рисовании отражений по оси Y — это выполнить пример задачи:
Пример:
Учитывая график y = f (x) y = f (x) y = f (x), как показано, набросок y = −f (x) y = -f (x) y = −f (x).
Помните, единственный шаг, который мы должны сделать перед построением отражения −f (x) -f (x) −f (x), — это просто разделить y-координаты легко определяемых точек на нашем графике выше на (- 1). Когда мы говорим «легко определяемые точки», мы имеем в виду только точки, для которых вы знаете значения x и y , точно .Не выбирайте точки, в которых вам нужно оценить значения, так как это излишне усложняет задачу. Ниже приведены несколько изображений, которые помогут вам наглядно представить, как решить эту проблему.
Шаг 1. Знайте, что мы отражаемся поперек оси x
Поскольку нас попросили построить отражение –f (x) f (x) f (x), очень важно, чтобы вы поняли, что это означает, что нас просят построить отражение по оси x. При рисовании отражений по осям xxx и yyy очень легко запутаться в некоторых обозначениях.Поэтому перед решением любой проблемы с отражением убедитесь, что вы знаете, что вас просят сделать.
Шаг 2: Определите точки, которые легко определить
Помните, выберите несколько точек (обычно достаточно 3), которые легко выделить, что означает, что вы точно знаете, каковы значения x и y. В этом случае давайте выберем (-2, -3), (-1, 0) и (0,3).
Выберите три точки и графикШаг 3. Разделите эти точки на (-1)
Хотя значения xxx остаются прежними, все, что нам нужно сделать, это разделить значения yyy на (-1)!
Разделите значения y на -1Шаг 4: Нанесите новые точки
Постройте новые точки после деления значений y на -1И все! Все просто, правда?
Что такое ось симметрии:
В некоторых случаях вам будет предложено выполнить горизонтальные отражения поперек оси симметрии, которая не является осью x.Но прежде чем мы перейдем к решению этой проблемы, важно знать, что мы подразумеваем под «осью симметрии». Ось симметрии — это просто горизонтальная линия, по которой мы выполняем отражение. Это может быть ось x или любая горизонтальная линия с уравнением yyy = constant, например yyy = 2, yyy = -16 и т. Д.
Как найти ось симметрии:
Нахождение оси симметрии, как и построение самих отражений, также является простым процессом. В этом случае все, что нам нужно сделать, это выбрать ту же точку как на функции, так и на ее отражении, посчитать расстояние между ними, разделить его на 2 и посчитать это расстояние от одного из графиков.Это потому, что, по его определению, ось симметрии находится на , точно в середине функции и ее отражения.
Лучший способ попрактиковаться в поиске оси симметрии — это решить задачу-пример.
Пример:
Найдите ось симметрии для двух функций, показанных на изображениях ниже.
График A для отражения через ось x График B для отражения через ось xОпять же, все, что нам нужно сделать для решения этой проблемы, — это выбрать одну и ту же точку в обеих функциях, посчитать расстояние между ними, разделить на 2 и затем добавить это расстояние к одной из наших функций.Давайте выберем исходную точку для этих функций, так как с ней легче всего работать.
Расстояние до одной и той же точки в двух функцияхТеперь, посчитав расстояние между этими двумя точками, вы должны получить ответ 2 единицы. Последний шаг — разделить это значение на 2, что даст нам 1. Теперь мы знаем, что наша ось симметрии находится точно на на одну единицу ниже начала координат верхней функции или выше начала координат нижней функции. Глядя на график, мы получаем yyy = 5 как нашу ось симметрии! Давайте посмотрим, как бы это выглядело, если бы там была настоящая строка:
Воображаемая линия для отражения через ось xВот и все! Вы можете узнать дальше, как построить графики преобразований тригонометрических функций и как определять тригонометрические функции по их графикам, в других разделах.
Как сделать рисунок в реальном зеркале в Adobe Illustrator CC
В некоторых графических и 3D редакторах есть функция Live Mirror Drawing, которая позволяет рисовать одновременно с обеих сторон одной или нескольких осей симметрии. К сожалению, Adobe Illustrator не имеет этой функции, хотя это очень мощное и многофункциональное приложение. Однако мы можем реализовать рисование Live Mirror в Illustrator, используя только его основные функции. Вы узнаете, как это сделать, прочитав сегодняшнюю статью.
Подробности руководства
Окончательное изображение
Как всегда, это последнее изображение, которое мы будем создавать:
Создание шаблона для чертежа Live Mirror
Шаг 1
Откройте Adobe Illustrator и создайте новый документ (Файл> Новый) . Размеры артборда и цветовой режим нового документа зависят только от ваших предпочтений. Возьмите инструмент Rectangle Tool (M) и создайте прямоугольник размером больше, чем размер монтажной области.Цвета обводки прямоугольника не имеют никакого значения, но вам нужно установить заливку на 0, чтобы увидеть предварительный просмотр зеркального изображения.
Шаг 2
Включите линейки (Command / Ctrl + R) и создайте горизонтальные и вертикальные направляющие, перетаскивая их с соответствующих линеек. Направляющие должны проходить через центр созданного прямоугольника.
Создавать направляющие нет необходимости, поскольку они просто показывают положение осей симметрии.Мы в основном настраиваем их для нашего собственного удобства.Шаг 3
Создайте случайный объект на монтажной области. Я создал стрелку, указывающую направление пути.
Шаг 4
Выберите весь слой на панели «Слои » .
Теперь перейдите в Effect> Distort & Transform> Transform … и в диалоговом окне укажите ось симметрии и количество копий, равное 1. Для визуального контроля над ситуацией отметьте опцию Preview и нажмите OK.
Ваш шаблон готов, вы можете приступить к рисованию.Рисунок Live Mirror
Шаг 5
Отключите видимость созданного объекта (в моем случае это стрелка) на панели слоев .
Шаг 6
Теперь выберите любой из инструментов рисования, например Paint Brush Tool (B) , и создайте путь.
Как видите, мы имеем непосредственную симметрию относительно горизонтальной оси.При этом вы можете рисовать по обе стороны от оси симметрии.К сожалению, у этого метода есть два недостатка, о которых я, конечно же, должен вас предупредить. При пересечении оси симметрии связь созданного пути с его зеркальной копией отсутствует.
Путь существует по обе стороны от оси симметрии. Это нужно учитывать и стараться не пересекать ось симметрии, если, конечно, вы этого не планируете.Также вы не можете рисовать за пределами прямоугольника, созданного на первом шаге, так как это нарушит симметрию всей системы.Вот почему мы создали прямоугольник, который больше монтажной области.
Редактирование шаблона чертежа Live Mirror
Шаг 7
Вы всегда можете сбросить настройки шаблона.


 Число таких спиралей
у сосновых шишек равно 8 и 13 или 13 и
21.
Число таких спиралей
у сосновых шишек равно 8 и 13 или 13 и
21.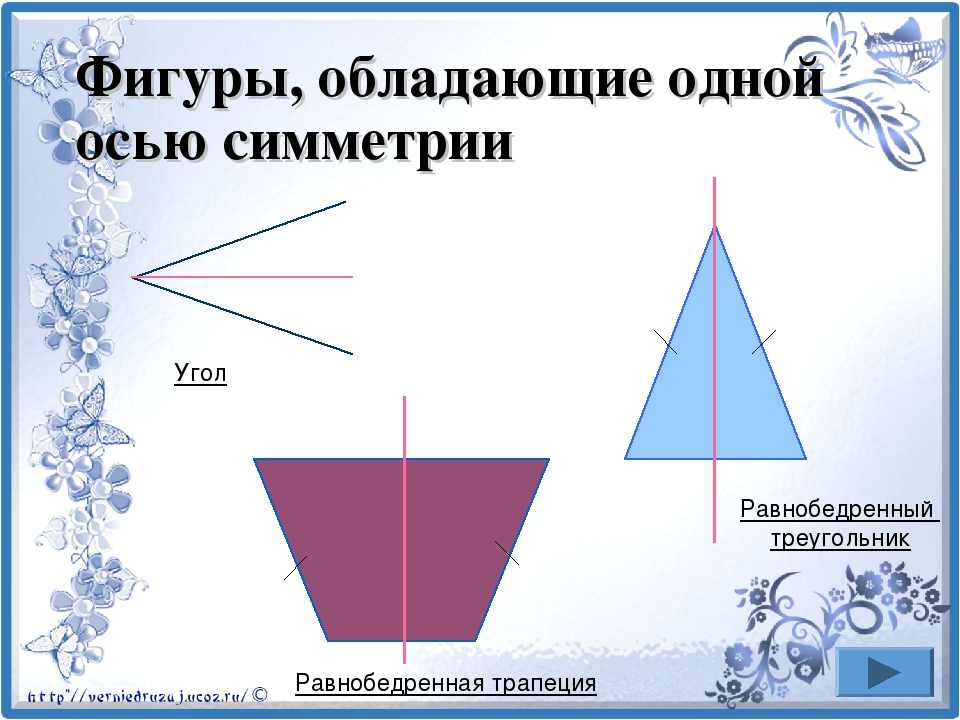 На современный вкус
композиция такой картины скучна,
поскольку симметрия слишком очевидна.
На современный вкус
композиция такой картины скучна,
поскольку симметрия слишком очевидна.