На в математике это какой знак: Таблица математических символов — это… Что такое Таблица математических символов?

Таблица математических символов — это… Что такое Таблица математических символов?

В математике повсеместно используются символы для упрощения и сокращения текста. Ниже приведён список наиболее часто встречающихся математических обозначений, соответствующие команды в TeXе, объяснения и примеры использования.

Кроме указанных символов, иногда используются их зеркальные отражения, например, обозначает то же, что и

Знаки операций или математические символы — знаки, которые символизируют определённые математические действия со своими аргументами.

Символ (Unicode)	Название	Значение	Пример
	Произношение
	Раздел математики
⇒ → ⊃	Импликация, следование	означает «если верно, то также верно». (→ может использоваться вместо ⇒ или для обозначения функции, см. ниже.) (⊃ может использоваться вместо ⇒, или для обозначения надмножества, см. ниже.).	верно, но неверно (так как также является решением).
	«влечёт» или «если…, то»
	везде
⇔	Равносильность	означает « верно тогда и только тогда, когда верно».
	«если и только если» или «равносильно»
	везде
∧	Конъюнкция	истинно тогда и только тогда, когда и оба истинны.	, если — натуральное число.
	«и»
	Математическая логика
∨	Дизъюнкция	истинно, когда хотя бы одно из условий и истинно.	, если — натуральное число.
	«или»
	Математическая логика
¬	Отрицание	истинно тогда и только тогда, когда ложно .
	«не»
	Математическая логика
∀	Квантор всеобщности	обозначает « верно для всех ».
	«Для любых», «Для всех»
	Математическая логика
∃	Квантор существования	означает «существует хотя бы один такой, что верно »	(подходит число 5)
	«существует»
	Математическая логика
=	Равенство	обозначает « и обозначают одно и то же значение».	1 + 2 = 6 − 3
	«равно»
	везде
:= :⇔	Определение	означает « по определению равен ». означает « по определению равносильно »	(Гиперболический косинус) (Исключающее или)
	«равно/равносильно по определению»
	везде
{ , }	Множество элементов	означает множество, элементами которого являются , и .	(множество натуральных чисел)
	«Множество…»
	Теория множеств
{ \| } { : }	Множество элементов, удовлетворяющих условию	означает множество всех таких, что верно .
	«Множество всех… таких, что верно…»
	Теория множеств
∅ {}	Пустое множество	и означают множество, не содержащее ни одного элемента.
	«Пустое множество»
	Теория множеств
∈ ∉	Принадлежность/непринадлежность к множеству	означает « является элементом множества » означает « не является элементом множества »
	«принадлежит», «из» «не принадлежит»
	Теория множеств
⊆ ⊂	Подмножество	означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ).
	«является подмножеством», «включено в»
	Теория множеств
⊇ ⊃	Надмножество	означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ).
	«является надмножеством», «включает в себя»
	Теория множеств
⊊	Собственное подмножество	означает и .
	«является собственным подмножеством», «строго включается в»
	Теория множеств
⊋	Собственное надмножество	означает и .
	«является собственным надмножеством», «строго включает в себя»
	Теория множеств
∪	Объединение	означает множество элементов, принадлежащих или (или обоим сразу).
	«Объединение … и …», «…, объединённое с …»
	Теория множеств
⋂	Пересечение	означает множество элементов, принадлежащих и , и .
	«Пересечение … и … », «…, пересечённое с …»
	Теория множеств
\	Разность множеств	означает множество элементов, принадлежащих , но не принадлежащих .
	«разность … и … », «минус», «… без …»
	Теория множеств
→	Функция	означает функцию с областью определения и областью прибытия (областью значений) .	Функция , определённая как
	«из … в»,
	везде
↦	Отображение	означает, что образом после применения функции будет .	Функцию, определённую как , можно записать так:
	«отображается в»
	везде
N или ℕ	Натуральные числа	означает множество или реже (в зависимости от ситуации).
	«Эн»
	Числа
Z или ℤ	Целые числа	означает множество
	«Зед»
	Числа
Q или ℚ	Рациональные числа	означает
	«Ку»
	Числа
R или ℝ	Вещественные числа, или действительные числа	означает множество всех пределов последовательностей из	( — комплексное число: )
	«Эр»
	Числа
C или ℂ	Комплексные числа	означает множество
	«Це»
	Числа
< >	Сравнение	обозначает, что строго меньше . означает, что строго больше .
	«меньше чем», «больше чем»
	Отношение порядка
≤ или ⩽ ≥ или ⩾	Сравнение	означает, что меньше или равен . означает, что больше или равен .
	«меньше или равно»; «больше или равно»
	Отношение порядка
≈	Приблизительное равенство	с точностью до означает, что 2,718 отличается от не больше чем на .	с точностью до .
	«приблизительно равно»
	Числа
√	Арифметический квадратный корень	означает неотрицательное действительное число, которое в квадрате даёт .
	«Корень квадратный из …»
	Числа
∞	Бесконечность	и суть элементы расширенного множества действительных чисел. Эти символы обозначают числа, меньшее/большее всех действительных чисел.
	«Плюс/минус бесконечность»
	Числа
\| \|	Модуль числа (абсолютное значение), модуль комплексного числа или мощность множества	обозначает абсолютную величину . обозначает мощность множества и равняется, если конечно, числу элементов .
	«Модуль»; «Мощность»
	Числа и Теория множеств
∑	Сумма, сумма ряда	означает «сумма , где принимает значения от 1 до », то есть . означает сумму ряда, состоящего из .
	«Сумма … по … от … до …»
	Арифметика, Математический анализ
∏	Произведение	означает «произведение для всех от 1 до », то есть
	«Произведение … по … от … до …»
	Арифметика
!	Факториал	означает «произведение всех натуральных чисел от 1 до включительно, то есть
	« факториал»
	Комбинаторика
∫	Интеграл	означает «интеграл от до функции от по переменной ».
	«Интеграл (от … до …) функции … по (или d)…»
	Математический анализ
df/dx f'(x)	Производная	или означает «(первая) производная функции от по переменной ».
	«Производная … по …»
	Математический анализ
	Производная -го порядка	или (во втором случае если — фиксированное число, то оно пишется римскими цифрами) означает «-я производная функции от по переменной ».
	«-я производная … по …»
	Математический анализ

Некоторые символы математического языка — урок. Алгебра, 8 класс.

Натуральные числа — это числа, используемые для счёта предметов или для указания порядкового номера того или иного предмета среди однородных предметов.

Множество всех натуральных чисел обычно обозначают буквой &naturals;.

Если к натуральным числам присоединить число \(0\) и все целые отрицательные числа: \(-1, -2, -3, -4…\) — то получится множество целых чисел. Это множество обычно обозначают буквой &integers;.

Если к множеству целых чисел присоединить все обыкновенные дроби: 13,5152,−85… и т. д. — то получится множество рациональных чисел. Это множество обычно обозначают буквой &Qopf;.

Множество &Qopf; рациональных чисел — это множество, состоящее из чисел вида mn;−mn (где \(m\), \(n\) — натуральные числа) и числа \(0\).

Понятно, что &naturals; — часть множества &integers;, а &integers; — часть множества &Qopf;. Для описания этой ситуации в математике также имеется специальное обозначение: &naturals;⊂&integers;;&integers;⊂&Qopf;.

Математический символ ⊂ называют знаком включения (одного множества в другое).

Запись x∈X означает, что \(x\) — один из элементов множества \(X\).

А запись A⊂B означает, что множество \(A\) представляет собой часть множества \(B\). Математики чаще говорят так: \(A\) — подмножество множества \(B\).

Для записи, что элемент \(x\) не принадлежит множеству \(X\) или что множество \(A\) не является частью (подмножеством) множества \(B\), используют те же символы, но перечёркнутые косой чертой: x∉X,A⊄B.

Приведём несколько примеров использования введённых математических символов для сокращения записи верных математических утверждений — их называют также истинными высказываниями.

Пример:

7∈&naturals;;7∈&integers;;7∈&Qopf;;−5∉&naturals;;&naturals;⊂&Qopf;;&integers;⊄&naturals;;2∈1;6;1;3⊂−2;8.

Любое рациональное число можно записать в виде конечной десятичной дроби или в виде бесконечной десятичной периодической дроби:

722=0,3181818…=0,3(18);4=4,000…=4,(0);7,3777=7,37770000…=7,3777(0).

Верно и обратное: любую бесконечную десятичную периодическую дробь можно представить в виде обыкновенной дроби. Это значит, что любая бесконечная десятичная периодическая дробь есть рациональное число.

Покажем на примере, как бесконечную десятичную периодическую дробь превращают в обыкновенную дробь.

Пример:

1,(23)=12299=12399;1,5(23)=1523−5990=1518990=1259495.

Математические знаки и символы: список, таблица, история возникновения

Когда люди долгое время взаимодействуют в рамках определенной сферы деятельности, они начинают искать способ оптимизировать процесс коммуникации. Система математических знаков и символов представляет собой искусственный язык, который был разработан, чтобы уменьшить объем графически передаваемой информации и при этом полностью сохранить заложенный в сообщение смысл.

Любой язык требует изучения, и язык математики в этом плане – не исключение. Чтобы понимать значение формул, уравнений и графиков, требуется заранее владеть определенной информацией, разбираться в терминах, системе обозначений и т. д. При отсутствии такого знания текст будет восприниматься как написанный на незнакомом иностранном языке.

В соответствии с запросами общества графические символы для более простых математических операций (например, обозначение сложения и вычитания) были выработаны раньше, чем для сложных понятий наподобие интеграла или дифференциала. Чем сложнее понятие, тем более сложным знаком оно обычно обозначается.

Содержание

Модели образования графических обозначений

На ранних этапах развития цивилизации люди связывали простейшие математические операции с привычными для них понятиями на основе ассоциаций. Например, в Древнем Египте сложение и вычитание обозначались рисунком идущих ног: направленные по направлению чтения строки они обозначали «плюс», а в обратную сторону – «минус».

Цифры, пожалуй, во всех культурах изначально обозначались соответствующим количеством черточек. Позже для записи стали использоваться условные обозначения — это экономило время, а также место на материальных носителях. Часто в качестве символов использовались буквы: такая стратегия получила распространение в греческом, латинском и многих других языках мира.

таблица математические символы и греческие буквы

История возникновения математических символов и знаков знает два наиболее продуктивных способа образования графических элементов.

Преобразование словесного представления

Изначально любое математическое понятие выражается некоторым словом или словосочетанием и не имеет собственного графического представления (помимо лексического). Однако выполнение расчетов и написание формул словами – процедура длительная и занимающая неоправданно много места на материальном носителе.

Распространенный способ создания математических символов – трансформация лексического представления понятия в графический элемент. Иначе говоря, слово, обозначающее понятие, с течением времени сокращается или преобразуется каким-либо другим способом.

Например, основной гипотезой происхождения знака «плюс» является его сокращение от латинского et, аналогом которого в русском языке является союз «и». Постепенно в скорописи первая буква перестала писаться, а t сократилась до креста.

Другой пример – знак «икс», обозначающий неизвестное, который изначально представлял собой сокращение от арабского слова «нечто». Сходным образом произошли знаки для обозначения квадратного корня, процента, интеграла, логарифма и др. В таблице математических символов и знаков можно встретить более десятка графических элементов, появившихся таким образом.

Назначение произвольного символа

Второй распространенный вариант образования математических знаков и символов – назначение символа произвольным образом. В этом случае слово и графическое обозначение между собой не связаны — знак обычно утверждается в результате рекомендации одного из членов научного сообщества.

Например, знаки умножения, деления, равенства были предложены математиками Уильямом Отредом, Иоганном Раном и Робертом Рекордом. В некоторых случаях несколько математических знаков могли быть введены в науку одним ученым. В частности, Готфрид Вильгельм Лейбниц предложил целый ряд символов, в том числе интеграла, дифференциала, производной.

Простейшие операции

Такие знаки, как «плюс» и «минус», а также символы, обозначающие умножение и деление, знает каждый школьник, несмотря на то, что для последних двух упомянутых операций существует несколько возможных графических знаков.

Можно с уверенностью говорить, что складывать и вычитать люди умели ещё за много тысячелетий до нашей эры, а вот стандартизованные математические знаки и символы, обозначающие данные действия и известные нам сегодня, появились лишь к XIV-XV столетию.

математические обозначения знаки буквы и сокращения

Впрочем, несмотря на установление определенной договоренности в научном сообществе, умножение и в наше время может изображаться тремя различными знаками (диагональный крестик, точка, звёздочка), а деление – двумя (горизонтальная черта с точками сверху и снизу или наклонная черта).

Латинские буквы

На протяжении многих столетий научное сообщество использовало для обмена информацией исключительно латынь, и многие математические термины и знаки обнаруживают свои истоки именно в этом языке. В некоторых случаях графические элементы стали результатом сокращения слов, реже – их намеренного или случайного преобразования (например, вследствие описки).

Обозначение процента («%»), вероятнее всего, происходит от ошибочного написания сокращения cto (cento, т. е. «сотая доля»). Сходным образом произошёл знак «плюс», история которого описана выше.

Гораздо большее количество символов было образовано путём намеренного сокращения слова, хотя это не всегда очевидно. Далеко не каждый человек узнает в знаке квадратного корня букву R, т. е. первый знак в слове Radix («корень»). Символ интеграла также представляет собой первую букву слова Summa, однако интуитивно она похожа на прописную f без горизонтальной черты. К слову, в первой публикации издатели совершили именно такую ошибку, напечатав f вместо данного символа.

Греческие буквы

В качестве графических обозначений для различных понятий используются не только латинские, но и греческие буквы. В таблице математических символов можно найти целый ряд примеров такого наименования.

Число Пи, представляющее собой отношение длины окружности к её диаметру, произошло от первой буквы греческого слова, обозначающего окружность. Существует ещё несколько менее известных иррациональных чисел, обозначаемых буквами греческого алфавита.

таблица математических символов и знаков

Крайне распространенным знаком в математике является «дельта», отражающая величину изменения значения переменных. Ещё одним употребительным знаком является «сигма», выполняющая функцию знака суммы.

Более того, практически все греческие буквы так или иначе используются в математике. Однако данные математические знаки и символы и их значение знают только люди, занимающиеся наукой профессионально. В быту и повседневной жизни эти знания человеку не требуются.

Знаки логики

Как ни странно, многие интуитивно понятные символы были придуманы совсем недавно.

В частности, горизонтальная стрелка, заменяющая слово «следовательно», была предложена лишь в 1922 года Давидом Гильбертом. Кванторы существования и всеобщности, т. е. знаки, читающиеся как: «существует…» и «для любого…», были введены в 1897 и 1935 году соответственно.

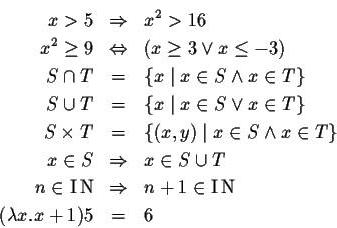математические знаки и символы и их значение

Символы из области теории множеств были придуманы в 1888-1889 гг. А перечеркнутый круг, который сегодня известен любому учащемуся средней школы как знак пустого множества, появился в 1939 году.

Таким образом, знаки для столь непростых понятий, как интеграл или логарифм, были придуманы на столетия раньше, чем некоторые интуитивно понятные символы, легко воспринимаемые и усваиваемые даже без предварительной подготовки.

Математические символы на английском

Ввиду того, что значительная часть понятий была описана в научных трудах на латыни, ряд названий математических знаков и символов на английском и русском языке одинаковы. Например: Plus («плюс»), Integral («интеграл»), Delta function («дельта-функция»), Perpendicular («перпендикулярный»), Parallel («параллельный»), Null («нуль»).

Часть понятий в двух языках называются различным образом: так, деление – это Division, умножение – Multiplication. В редких случаях английское название для математического знака получает некоторое распространение в русском языке: например, косая черта в последние годы нередко именуется «слешем» (англ. Slash).

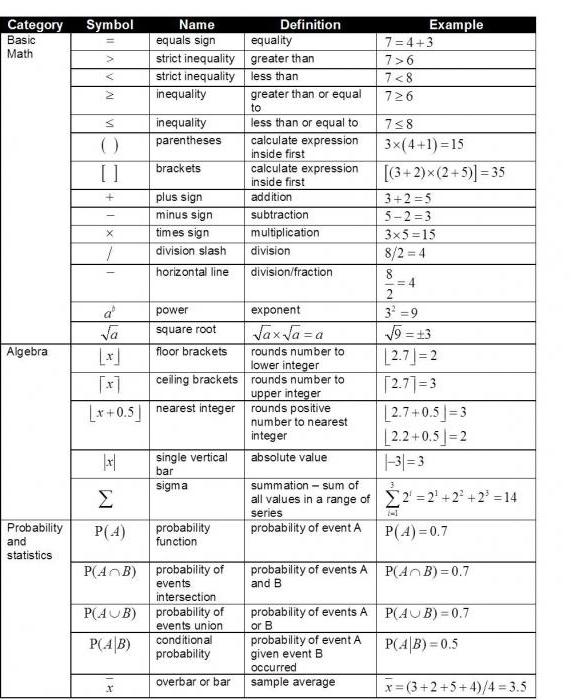
Таблица символов

Самый простой и удобный способ ознакомиться с перечнем математических знаков – посмотреть специальную таблицу, в которой содержатся знаки операций, символы математической логики, теории множеств, геометрии, комбинаторики, математического анализа, линейной алгебры. В данной таблице представлены основные математические знаки на английском языке.

Математические знаки в текстовом редакторе

При выполнении различного рода работ зачастую требуется использовать формулы, где употребляются знаки, отсутствующие на клавиатуре компьютера.

Как и графические элементы из практически любой области знаний, математические знаки и символы в «Ворде» можно найти во вкладке «Вставка». В версиях программы 2003 или 2007 года существует опция «Вставка символа»: при нажатии на кнопку в правой части панели пользователь увидит таблицу, в которой представлены все необходимые математические знаки, греческие строчные и прописные буквы, различные виды скобок и многое другое.

В версиях программы, вышедших после 2010 года, разработана более удобная опция. При нажатии на кнопку «Формула» происходит переход в конструктор формул, где предусмотрено использование дробей, занесения данных под корень, смена регистра (для обозначения степеней или порядковых номеров переменных). Здесь же могут быть найдены все знаки из таблицы, представленной выше.

Стоит ли учить математические символы

Система математических обозначений представляет собой искусственный язык, который лишь упрощает процесс записи, но не может принести понимание предмета стороннему наблюдателю. Таким образом, запоминание знаков без изучения терминов, правил, логических связей между понятиями не приведет к овладению данной областью знаний.

математические знаки и символы на английском

Человеческий мозг легко усваивает знаки, буквы и сокращения – математические обозначения запоминаются сами при изучении предмета. Понимание смысла каждого конкретного действия создает настолько прочные ассоциативные связи, что знаки, обозначающие термины, а зачастую и формулы, связанные с ними, остаются в памяти на многие годы и даже десятилетия.

В заключение

Поскольку любой язык, в том числе искусственный, является открытым к изменениям и дополнениям, число математических знаков и символов непременно будет расти с течением времени. Не исключено, что какие-то элементы будут заменены или скорректированы, а другие – стандартизованы в единственно возможном виде, что актуально, например, для знаков умножения или деления.

Умение пользоваться математическими символами на уровне полного школьного курса является в современном мире практически необходимым. В условиях бурного развития информационных технологий и науки, повсеместной алгоритмизации и автоматизации владение математическим аппаратом следует воспринимать как данность, а освоение математических символов – как неотъемлемую его часть.

Поскольку расчеты используются и в гуманитарной сфере, и в экономике, и в естественных науках, и, разумеется, в области техники и высоких технологий, понимание математических понятий и знание символов станет полезным для любого специалиста.

Таблица знаков в геометрии и их значения: пересечение, подобие

Знак	Название	Значение/описание	Пример
∠	угол	фигура, состоящая из двух лучей и вершины	∠ABC = 30°
	острый угол	угол от 0 до 90 градусов	∠AOB = 60°
	прямой угол	угол, равный 90 граусам	∠AOB = 90°
	тупой угол	угол от 90 до 180 градусов	∠AOB = 120°
	развернутый угол	угол, равный 180 градусам	∠AOB = 180°
° (или deg)	градус	единица измерения угла, равна 1/360 окружности	45°
′	минута	единици измерения угла, 1° = 60′	α = 70°59′
″	секунда	единици измерения угла, 1′ = 60″	α = 70°59′59″
	линия	бесконечная прямая без начала и конца
	отрезок	участок на прямой между точками A и B
	луч	бесконечная прямая, имеющая начало в точке A, но не имеющая конца
	дуга	дуга, образованная между точками A и B
⊥	перпендикулярность	линии (прямые), расположенные под углом 90° по отношению друг к другу	AC ⊥ BC
∥	параллельность	непересекающиеся прямые (линии)	AB ∥ CD
∩	пересечение	множество одинаковых элементов, принадлежащих как множеству A, так и B	A ∩ B
∈ / ∉	принадлежность/ непринадлежность	элемент является/не является элементом заданного множества	a ∈ S
≅	конгуэнтность	эквивалентность геометрических форм и размеров	∆ABC ≅ ∆XYZ
~	подобие	та же форма, но разные размеры	∆ABC ~ ∆XYZ
Δ	треугольник	фигура треугольника	ΔABC ≅ ΔBCD
\|x-y\|	дистанция	дистанция между точками X и Y	\| x-y \| = 5
π	константа «Пи»	отношение длины окружности к диаметру круга, c = π⋅d = 2⋅π⋅r	π = 3.141592654…
рад (rad) или ^c	радиан	единица измерения угла	360° = 2π ^c

Знаки математические — Большая советская энциклопедия

Зна́ки математические

Условные обозначения, предназначенные для записи математических понятий, предложений и выкладок. Например, √2

(квадратный корень из двух), 3 > 2 (три больше двух) и т.п.

Развитие математической символики было тесно связано с общим развитием понятий и методов математики. Первыми З. м. были знаки для изображения чисел — Цифры, возникновение которых, по-видимому, предшествовало письменности. Наиболее древние системы нумерации — вавилонская и египетская — появились ещё за 3¹/₂ тысячелетия до н. э.

Первые З. м. для произвольных величин появились много позднее (начиная с 5—4 вв. до н. э.) в Греции. Величины (площади, объёмы, углы) изображались в виде отрезков, а произведение двух произвольных однородных величин — в виде прямоугольника, построенного на соответствующих отрезках. В «Началах» Евклида (3 в. до н. э.) величины обозначаются двумя буквами — начальной и конечной буквами соответствующего отрезка, а иногда и одной. У Архимеда (3 в. до нашей эры) последний способ становится обычным. Подобное обозначение содержало в себе возможности развития буквенного исчисления. Однако в классической античной математике буквенного исчисления создано не было.

Начатки буквенного изображения и исчисления возникают в позднеэллинистическую эпоху в результате освобождения алгебры от геометрической формы. Диофант (вероятно, 3 в.) записывал неизвестную (х) и её степени следующими знаками:

[ — от греческого термина δυναμις (dynamis — сила), обозначавшего квадрат неизвестной, — от греческого χυβος (k_ybos) — куб]. Справа от неизвестной или её степеней Диофант писал коэффициенты, например 3х⁵ изображалось

(где = 3). При сложении Диофант приписывал слагаемые друг к другу, для вычитания употреблял специальный знак ; равенство Диофант обозначал буквой ι [от греческого ισος (isos) — равный]. Например, уравнение

(x³ + 8x) — (5x² + 1) = х

у Диофанта записалось бы так:

(здесь

означает, что единица не имеет множителя в виде степени неизвестного).

Несколько веков спустя индийцы ввели различные З. м. для нескольких неизвестных (сокращения наименований цветов, обозначавших неизвестные), квадрата, квадратного корня, вычитаемого числа. Так, уравнение

3х² + 10x — 8 = x² + 1

в записи Брахмагупты (См. Брахмагупта) (7 в.) имело бы вид:

йа ва 3 йа 10 ру 8

йа ва 1 йа 0 ру 1

(йа — от йават — тават — неизвестное, ва — от варга — квадратное число, ру — от рупа — монета рупия — свободный член, точка над числом означает вычитаемое число).

Создание современной алгебраической символики относится к 14—17 вв.; оно определялось успехами практической арифметики и учения об уравнениях. В различных странах стихийно появляются З. м. для некоторых действий и для степеней неизвестной величины. Проходят многие десятилетия и даже века, прежде чем вырабатывается тот или иной удобный символ. Так, в конце 15 и. Н. Шюке и Л. Пачоли употребляли знаки сложения и вычитания

(от лат. plus и minus), немецкие математики ввели современные + (вероятно, сокращение лат. et) и —. Ещё в 17 в. можно насчитать около десятка З. м. для действия умножения.

Различны были и З. м. неизвестной и её степеней. В 16 — начале 17 вв. конкурировало более десяти обозначений для одного только квадрата неизвестной, например се (от census — латинский термин, служивший переводом греческого δυναμις, Q (от quadratum), , A (2), , Aii, aa, a² и др. Так, уравнение

x³ + 5x = 12

имело бы у итальянского математика Дж. Кардано (1545) вид:

у немецкого математика М. Штифеля (1544):

у итальянского математика Р. Бомбелли (1572):

французского математика Ф. Виета (1591):

у английского математика Т. Гарриота (1631):

В 16 и начале 17 вв. входят в употребление знаки равенства и скобки: квадратные (Р. Бомбелли, 1550), круглые (Н. Тарталья, 1556), фигурные (Ф. Виет, 1593). В 16 в. современный вид принимает запись дробей.

Значительным шагом вперёд в развитии математической символики явилось введение Виетом (1591) З. м. для произвольных постоянных величин в виде прописных согласных букв латинского алфавита В, D, что дало ему возможность впервые записывать алгебраические уравнения с произвольными коэффициентами и оперировать ими. Неизвестные Виет изображал гласными прописными буквами А, Е,… Например, запись Виета

[cubus — куб, planus — плоский, т. е. В — двумерная величина; solidus — телесный (трёхмерный), размерность отмечалась для того, чтобы все члены были однородны] в наших символах выглядит так:

x₃ + 3bx = d.

Виет явился творцом алгебраических формул. Р. Декарт (1637) придал знакам алгебры современный вид, обозначая неизвестные последними буквами лат. алфавита х, у, z, а произвольные данные величины — начальными буквами а, b, с. Ему же принадлежит нынешняя запись степени. Обозначения Декарта обладали большим преимуществом по сравнению со всеми предыдущими. Поэтому они скоро получили всеобщее признание.

Дальнейшее развитие З. м. было тесно связано с созданием анализа бесконечно малых, для разработки символики которого основа была уже в большой мере подготовлена в алгебре.

Даты возникновения некоторых математических знаков

знак	значение	Кто ввёл	Когда введён
Знаки индивидуальных объектов
∞	бесконечность	Дж. Валлис	1655
e	основание натуральных логарифмов	Л. Эйлер	1736
π	отношение длины окружности к диаметру	У. Джонс Л. Эйлер	1706 1736
i	корень квадратный из -1	Л. Эйлер	1777 (в печати 1794)
i j k	единичные векторы, орты	У. Гамильтон	1853
П (а)	угол параллельности	Н.И. Лобачевский	1835
Знаки переменных объектов
x,y, z	неизвестные или переменные величины	Р. Декарт	1637
r	вектор	О. Коши	1853
Знаки индивидуальных операций
+	сложение	немецкие математики	Конец 15 в.
–	вычитание
×	умножение	У. Оутред	1631
․	умножение	Г. Лейбниц	1698
:	деление	Г. Лейбниц	1684
a², a³,…, aⁿ	степени	Р. Декарт	1637

		И. Ньютон	1676
	корни	К. Рудольф	1525
		А. Жирар	1629
Log	логарифм	И. Кеплер	1624

log		Б. Кавальери	1632
sin	синус	Л. Эйлер	1748
cos	косинус
tg	тангенс	Л. Эйлер	1753
arc.sin	арксинус	Ж. Лагранж	1772
Sh	гиперболический синус	В. Риккати	1757
Ch	гиперболический косинус
dx, ddx, …	дифференциал	Г. Лейбниц	1675 (в печати
d²x, d³x,…		1684)
	интеграл	Г. Лейбниц	1675 (в печати 1686)
	производная	Г. Лейбниц	1675
ƒ’x	производная	Ж. Лагранж	1770, 1779
y’
ƒ'(x)
Δx	разность	Л. Эйлер	1755
	частная производная	А. Лежандр	1786
	определённый интеграл	Ж. Фурье	1819-22
Σ	сумма	Л. Эйлер	1755
П	произведение	К. Гаусс	1812
!	факториал	К. Крамп	1808
	x		модуль	К. Вейерштрасс	1841
lim	предел	У. Гамильтон,	1853,
lim	многие математики	начало 20 в.
n = ∞
lim
n → ∞
ξ	дзета-функция	Б. Риман	1857
Г	гамма-функция	А. Лежандр	1808
В	бета-функция	Ж. Бине	1839
Δ	дельта (оператор Лапласа)	Р. Мёрфи	1833
∇	набла (оператор Гамильтона)	У. Гамильтон	1853
Знаки переменных операций
φx	функция	И. Бернули	1718

f (x)		Л. Эйлер	1734
Знаки индивидуальных отношений
=	равенство	Р. Рекорд	1557
>	больше	Т. Гарриот	1631
<	меньше
≡	сравнимость	К. Гаусс	1801
			параллельность	У. Оутред	1677
⊥	перпендикулярность	П. Эригон	1634

И. Ньютон в своём методе флюксий и флюент (1666 и следующие гг.) ввёл знаки для последовательных флюксий (производных) величины (в виде

и для бесконечно малого приращения o. Несколько ранее Дж. Валлис (1655) предложил знак бесконечности ∞.

Создателем современной символики дифференциального и интегрального исчислений является Г. Лейбниц. Ему, в частности, принадлежат употребляемые ныне З. м. дифференциалов

dx, d ²x, d ³x

и интеграла

Огромная заслуга в создании символики современной математики принадлежат Л. Эйлеру. Он ввёл (1734) в общее употребление первый знак переменной операции, именно знак функции f (x) (от лат. functio). После работ Эйлера знаки для многих индивидуальных функций, например тригонометрических, приобрели стандартный характер. Эйлеру же принадлежат обозначения постоянных е (основание натуральных логарифмов, 1736), π [вероятно, от греческого περιφερεια (periphereia) — окружность, периферия, 1736], мнимой единицы

(от французского imaginaire — мнимый, 1777, опубликовано в 1794).

В 19 в. роль символики возрастает. В это время появляются знаки абсолютной величины |x| (К. Вейерштрасс, 1841), вектора r̅ (О. Коши, 1853), определителя

(А. Кэли, 1841) и др. Многие теории, возникшие в 19 в., например Тензорное исчисление, не могли быть развиты без подходящей символики.

Наряду с указанным процессом стандартизации З. м. в современной литературе весьма часто можно встретить З. м., используемые отдельными авторами только в пределах данного исследования.

С точки зрения математической логики, среди З. м. можно наметить следующие основные группы: А) знаки объектов, Б) знаки операций, В) знаки отношений. Например, знаки 1, 2, 3, 4 изображают числа, т. е. объекты, изучаемые арифметикой. Знак операции сложения + сам по себе не изображает никакого объекта; он получает предметное содержание, когда указано, какие числа складываются: запись 1 + 3 изображает число 4. Знак > (больше) есть знак отношения между числами. Знак отношения получает вполне определённое содержание, когда указано, между какими объектами отношение рассматривается. К перечисленным трём основным группам З. м. примыкает четвёртая: Г) вспомогательные знаки, устанавливающие порядок сочетания основных знаков. Достаточное представление о таких знаках дают скобки, указывающие порядок производства действий.

Знаки каждой из трёх групп А), Б) и В) бывают двух родов: 1) индивидуальные знаки вполне определённых объектов, операций и отношений, 2) общие знаки «неременных», или «неизвестных», объектов, операций и отношений.

Примеры знаков первого рода могут служить (см. также таблицу):

A₁) Обозначения натуральных чисел 1, 2, 3, 4, 5, 6, 7, 8, 9; трансцендентных чисел е и π; мнимой единицы i.

Б₁) Знаки арифметических действий +, —, ·, ×,:; извлечения корня , дифференцирования

знаки суммы (объединения) ∪ и произведения (пересечения) ∩ множеств; сюда же относятся знаки индивидуальных функций sin, tg, log и т.п.

B₁) Знаки равенства и неравенства =, >, <, ≠, знаки параллельности || и перпендикулярности ⊥, знаки принадлежности ∈ элемента некоторому множеству и включения ⊂ одного множества в другое и т.п.

Знаки второго рода изображают произвольные объекты, операции и отношения определённого класса или объекты, операции и отношения, подчинённые каким-либо заранее оговорённым условиям. Например, при записи тождества (a + b)(a — b) = a² — b² буквы а и b обозначают произвольные числа; при изучения функциональной зависимости у = х² буквы х и у — произвольные числа, связанные заданным отношением; при решении уравнения

x² — 1 = 0

х обозначает любое число, удовлетворяющее данному уравнению (в результате решения этого уравнения мы узнаём, что этому условию соответствуют лишь два возможных значения +1 и —1).

С логической точки зрения, законно такого рода общие знаки называть знаками переменных, как это принято в математической логике, не пугаясь того обстоятельства, что «область изменения» переменного может оказаться состоящей из одного единственного объекта или даже «пустой» (например, в случае уравнений, не имеющих решения). Дальнейшими примерами такого рода знаков могут служить:

A₂) Обозначения точек, прямых, плоскостей и более сложных геометрических фигур буквами в геометрии.

Б₂) Обозначения f, F, φ для функций и обозначения операторного исчисления, когда одной буквой L изображают, например, произвольный оператор вида:

Обозначения для «переменных отношений» менее распространены, они находят применение лишь в математической логике (см. Алгебра логики) и в сравнительно абстрактных, по преимуществу аксиоматических, математических исследованиях.

Лит.: Cajori F., A history of mathematical notations, v. 1—2, Chi., 1928—29.

Источник: Большая советская энциклопедия на Gufo.me

Значения в других словарях

ЗНАКИ МАТЕМАТИЧЕСКИЕ — ЗНАКИ МАТЕМАТИЧЕСКИЕ — условные обозначения, служащие для записи математических понятий, предложений и выкладок. Напр., математические знаки +, -, =, > (больше) — (знак корня) — sin (синус) — (интеграл) и т. Большой энциклопедический словарь
Знаки Математические — Условные обозначения, предназначенные для записи математич. понятий и выкладок. Напр., понятие «квадратный корень из числа… Математическая энциклопедия

Математические символы HTML ± π √ ½ ƒ

Все Символы \| Знаки \| Коды \| HTML
➕	➕	Плюс жёлтого цвета
➖	➖	Минус синего цвета
➗	➗	Разделить зеленого цвета
❌	❌	Умножить красного цвета
−	−	Минус (Символ html)
+	+	Плюс (Символ html)
×	×	Умножить (Символ html)
÷	÷	Разделить (Символ html)
±	±	Плюс-минус
<	<	Меньше
>	>	Больше
≤	≤	Меньше или равно
≥	≥	Больше или равно
π	π	Пи
√	√	Корень квадратный
∡	∡	Корень квадратный
∢	∢	Корень квадратный
∠	∠	Угол
∛	∛
∜	∜
⁄	⁄	Слэш, дробная черта
¬	¬	Отрицание
°	°	Градус
∼	∼	Оператор тильда
≅	≅	Геометрическая эквивалентность
≈	≈	Приблизительное равенство
≠	≠	Не равно
≡	≡	Тождественное равенство
Математические Дроби символы коды HTML
%	%	Простая дробь «ноль на ноль»
¼	¼	Дробь одна четвертая
½	½	Дробь одна вторая
¾	¾	Дробь три четвертых
⅓	⅓	Дробь одна третья
⅔	⅔	Дробь две третих
⅕	⅕	Дробь одна пятая
⅖	⅖	Дробь две пятых
⅗	⅗	Дробь три пятых
⅘	⅘	Дробь четыре пятых
⅙	⅙	Дробь одна шестая
⅚	⅚	Дробь пять шестых
⅛	⅛	Дробь одна восьмая
⅜	⅜	Дробь три восьмых
⅝	⅝	Дробь пять восьмых
⅞	⅞	Дробь семь восьмых
Другие математические символы коды HTML
¹	¹	Верхний индекс «1»
²	²	Верхний индекс «2»
³	³	Верхний индекс «3»
∞	∞	Бесконечность
∝	∝	Пропорционально
⊥	⊥	Ортогонально, перпендикуляр
∴	∴	Следовательно
ƒ	ƒ	Функция
∫	∫	Интеграл
∂	∂	Частный дифференциал
∇	∇	Оператор набла
∀	∀	Для всех
∃	∃	Существует
∏	∏	Знак произведения
∑	∑	Сумма последовательности
∧	∧	Логическое И (конъюнкция)
∨	∨	Логическое ИЛИ (дизъюнкция)
∅	∅	Пустой набор = диаметр
∈	∈	Принадлежит
∉	∉	Не принадлежит
∋	∋	Содержит
∩	∩	Пересечение
∪	∪	Объединение
⊂	⊂	Является подмножеством
⊃	⊃	Является надмножеством
⊄	⊄	Не является подмножеством
⊆	⊆	Является подмножеством либо эквивалентно
⊇	⊇	Является надмножеством либо эквивалентно

Что такое математика? | Живая наука

Математика — это наука, которая занимается логикой формы, количества и расположения. Математика вокруг нас, во всем, что мы делаем. Это строительный блок для всего в нашей повседневной жизни, включая мобильные устройства, архитектуру (древнюю и современную), искусство, деньги, инженерию и даже спорт.

С самого начала истории человечества математические открытия были в авангарде каждого цивилизованного общества и используются даже в самых примитивных культурах.Потребности математики возникли исходя из потребностей общества. Чем сложнее общество, тем сложнее математические потребности. Первобытным племенам нужно было немного больше, чем умение считать, но они также полагались на математику для расчета положения солнца и физики охоты.

История математики

Несколько цивилизаций — в Китае, Индии, Египте, Центральной Америке и Месопотамии — внесли свой вклад в математику, какой мы ее знаем сегодня. Шумеры были первыми, кто разработал систему подсчета.Математики разработали арифметику, которая включает в себя основные операции, умножение, дроби и квадратные корни. Шумерская система прошла через Аккадскую империю к вавилонянам около 300 г. до н.э. Спустя шестьсот лет в Америке майя разработали сложные календарные системы и стали искусными астрономами. Примерно в это же время была разработана концепция нуля.

По мере развития цивилизаций математики начали работать с геометрией, которая вычисляет площади и объемы для угловых измерений и имеет множество практических применений.Геометрия используется во всем, от строительства дома до моды и дизайна интерьера.

Геометрия шла рука об руку с алгеброй, изобретенной в девятом веке персидским математиком Мухаммедом ибн-Мусой аль-Ховаризми. Он также разработал быстрые методы для умножения и погружения чисел, которые известны как алгоритмы — искажение его имени.

Алгебра предложила цивилизациям способ разделить наследство и распределить ресурсы. Изучение алгебры означало, что математики решали линейные уравнения и системы, а также квадратики и изучали положительные и отрицательные решения.Математики в древние времена также начали смотреть на теорию чисел. Теория чисел берет свое начало в построении формы, рассматривая образные числа, характеристику чисел и теоремы.

Математика и греки

Изучение математики в ранних цивилизациях было строительным материалом для математики греков, которые разработали модель абстрактной математики через геометрию. Греция с ее невероятной архитектурой и сложной системой управления была образцом математических достижений до наших дней.Греческие математики были разделены на несколько школ:

Ионийская школа , основанная Фалесом, которому часто приписывают первые дедуктивные доказательства и разработку пяти основных теорем в геометрии плоскости.
Пифагорейская школа , основанная Пифагором, который изучал пропорции, плоскую и твердую геометрию и теорию чисел.
Элеатическая школа , в которую входил Зено Элеа, известный своими четырьмя парадоксами.
Софистская школа , которая зачисляется за предоставление высшего образования в передовых греческих городах.Софисты давали инструкции по публичным дебатам, используя абстрактные рассуждения.
Школа Платона , основанная Платоном, который поощрял исследования в области математики в обстановке, очень похожей на современный университет.
Школа Евдокса , основанная Евдоксом, который разработал теорию пропорциональности и величины и создал много теорем в геометрии плоскости.
Школа Аристотеля , также известная как Лицей, была основана Аристотелем и следовала за Платоническая школа.

В дополнение к греческим математикам, перечисленным выше, ряд греков оставил неизгладимый след в истории математики. Архимед, Аполлоний, Диофант, Паппус и Евклид все пришли из этой эпохи. Чтобы лучше понять последовательность и то, как эти математики влияли друг на друга, посетите этот график.

За это время математики начали работать с тригонометрией. Вычислительная по своей природе тригонометрия требует измерения углов и вычисления тригонометрических функций, которые включают синус, косинус, тангенс и их обратные значения.Тригонометрия опирается на синтетическую геометрию, разработанную такими греческими математиками, как Евклид. Например, теорема Птолемея дает правила для хорды суммы и разности углов, которые соответствуют формулам суммы и разности для синусов и косинусов. В прошлых культурах тригонометрия применялась в астрономии и для вычисления углов в небесной сфере.

После падения Рима развитие математики взяли на себя арабы, а затем европейцы. Фибоначчи был одним из первых европейских математиков и был известен своими теориями по арифметике, алгебре и геометрии.Ренессанс привел к успехам, которые включали десятичные дроби, логарифмы и проективную геометрию. Теория чисел была значительно расширена, и такие теории, как вероятность и аналитическая геометрия, открыли новую эру математики с исчислением на переднем крае.

Развитие исчисления

В 17 веке Исаак Ньютон и Готфрид Лейбниц независимо разработали основы для исчисления. Развитие исчисления прошло три периода: ожидание, развитие и строгость.На стадии ожидания математики пытались использовать методы, которые включали бесконечные процессы, чтобы найти области под кривыми или максимизировать определенные качества. На стадии разработки Ньютон и Лейбниц свели эти методы вместе через производную и интегральную. Хотя их методы не всегда были логически обоснованы, математики в 18-м веке вышли на этап ригоризации и смогли их обосновать и создать заключительную стадию исчисления. Сегодня мы определяем производную и интегральную с точки зрения ограничений.

В отличие от исчисления, являющегося типом непрерывной математики, другие математики выбрали более теоретический подход. Дискретная математика — это раздел математики, который имеет дело с объектами, которые могут принимать только отдельные, отдельные значения. Дискретные объекты могут быть охарактеризованы целыми числами, тогда как непрерывные объекты требуют действительных чисел. Дискретная математика является математическим языком информатики, так как включает в себя изучение алгоритмов. Области дискретной математики включают комбинаторику, теорию графов и теорию вычислений.

Люди часто задаются вопросом, какое значение имеют математики сегодня. В современном мире математика, такая как прикладная математика, не только актуальна, но и важна. Прикладная математика — это отрасли математики, которые участвуют в изучении физического, биологического или социологического мира. Идея прикладной математики заключается в создании группы методов, которые решают проблемы в науке. Современные области прикладной математики включают математическую физику, математическую биологию, теорию управления, аэрокосмическую инженерию и математические финансы.Прикладная математика не только решает проблемы, но также обнаруживает новые проблемы или развивает новые инженерные дисциплины. Прикладные математики требуют опыта во многих областях математики и науки, физической интуиции, здравого смысла и сотрудничества. Общий подход в прикладной математике состоит в том, чтобы построить математическую модель явления, решить модель и разработать рекомендации по улучшению производительности.

Хотя чистая математика не обязательно противоположна прикладной математике, она руководствуется абстрактными проблемами, а не проблемами реального мира.Многое из того, что преследуют чистые математики, может корениться в конкретных физических проблемах, но более глубокое понимание этих явлений приводит к проблемам и техническим аспектам. Эти абстрактные проблемы и технические особенности — это то, что пытается решить чистая математика, и эти попытки привели к крупным открытиям для человечества, включая Универсальную Машину Тьюринга, теоретизированную Аланом Тьюрингом в 1937 году. Универсальная Машина Тьюринга, которая началась как абстрактная идея, позже заложил основу для развития современного компьютера.Чистая математика абстрактна и основана на теории, и поэтому она не ограничена ограничениями физического мира.

Согласно одному чистому математику, чистые математики доказывают теоремы, а прикладные математики строят теории. Чистые и прикладные не являются взаимоисключающими, но они уходят корнями в разные области математики и решения проблем. Хотя сложная математика, используемая в чистой и прикладной математике, не поддается пониманию большинства обычных американцев, решения, разработанные на основе этих процессов, повлияли и улучшили жизнь всех людей.

общих символов в математике | SkillsYouNeed

Математические символы могут вводить в заблуждение и могут служить реальным препятствием для обучения и понимания основ счета.

Эта страница дополняет наши страницы по умению считать и предоставляет краткий глоссарий общих математических символов с краткими и краткими определениями.

Мы что-то упустили? Получите это прикосновение, чтобы сообщить нам.

+ дополнение

Символ сложения + обычно используется для указания того, что два или более чисел следует сложить вместе, например, 2 + 2.

Символ + также можно использовать для обозначения положительного числа, хотя это встречается реже, например, +2. Как объясняется на нашей странице о положительных и отрицательных числах , число без знака считается положительным, поэтому плюс обычно не требуется.

Смотрите нашу страницу на Дополнение для получения дополнительной информации.

— Вычитание или минус

Этот символ имеет два основных применения в математике:

— используется, когда необходимо вычесть одно или несколько чисел, например, 2 — 2.
Символ — также обычно используется, чтобы показать минус или отрицательное число, такое как -2.

Смотрите нашу страницу на Вычитание для получения дополнительной информации.

× или * или. Умножить

Эти символы имеют одинаковое значение; обычно × используется для обозначения умножения при написании от руки или, например, на калькуляторе 2 × 2.

Символ * используется в электронных таблицах и других компьютерных приложениях для обозначения умножения, хотя * имеет и другие более сложные значения в математике.

Реже умножение также может обозначаться точкой. или вообще ни одним символом. Например, если вы видите число, написанное вне скобок без оператора (символ или знак), то оно должно быть умножено на содержимое скобок: 2 (3 + 2) равно 2 x (3 + 2).

Смотрите нашу страницу на Умножение для получения дополнительной информации.

÷ или / Разделить

Эти символы используются для обозначения деления в математике. ÷ используется обычно в рукописных расчетах и на калькуляторах, например, 2 ÷ 2.

/ используется в электронных таблицах и других компьютерных приложениях.

Смотрите нашу страницу на Дивизион для получения дополнительной информации.

= равно

Символ = равен используется для отображения результата расчета, 2 + 2 = 4.

Вы также можете встретить другие связанные символы, хотя они встречаются реже:

≠ означает не равно. Например, 2 + 2 × 5 — 2. В компьютерных приложениях (например, в Excel) символы <> означают, что они не равны.
≡ означает идентичный. Аналогично, но не совсем так же, как и у равных. Если сомневаетесь, придерживайтесь =.
≈ означает приблизительно равно или почти равно. Обе стороны отношения, обозначенные этим символом, будут , а не , достаточно точными для математического манипулирования.

<меньше чем>> больше чем

Этот символ < означает меньше, например, 2 <4 означает, что 2 меньше 4.

Этот символ > означает больше, чем, например, 4> 2.

≤ ≥ Эти символы означают «меньше или равно» и «больше или равно» и обычно используются в алгебре. В компьютерных приложениях используются <= и> =.

≫ ≫ Эти символы встречаются реже и означают намного меньше или намного больше, чем.

± плюс или минус

Этот символ ± означает «плюс или минус». Он используется для указания, например, доверительных интервалов вокруг числа.

Ответ называется «плюс или минус» другого числа или, другими словами, в пределах диапазона вокруг данного ответа.

Например, 5 ± 2 на практике может быть любым числом от 3 до 7.

∑ Сумма

Символ means означает сумму.

∑ является символом греческой столицы сигма. Обычно используемый в алгебраических функциях, вы также можете заметить это в Excel — кнопка AutoSum имеет значок сигма.

° градус

градусов ° используются несколькими различными способами.

В качестве меры вращения — угол между сторонами фигуры или вращение круга. Круг 360 °, а прямой угол 90 °. Смотрите наш раздел на Geometry для более подробной информации.
Мера температуры. градусов Цельсия или Цельсия используются в большинстве стран мира (за исключением США). Вода замерзает при 0 ° С и кипит при 100 ° С. В США Фаренгейт используется по шкале Фаренгейта, вода замерзает при 32 ° F и кипит при 212 ° F.Смотрите нашу страницу: Системы измерения для получения дополнительной информации.

∠ Угол

Символ угла ∠ используется как сокращение в геометрии (изучение форм) для описания угла.

Выражение ∠ABC используется для описания угла в точке B (между точками A и C). Аналогично, ∠BAC будет использоваться для описания угла точки A (между точками B и C). Подробнее об углах и других геометрических терминах см. На наших страницах Geometry .

√ квадратный корень

√ символ квадратного корня.Квадратный корень — это число, которое при умножении на себя дает исходное число.

Например, квадратный корень из 4 равен 2, потому что 2 x 2 = 4. Квадратный корень из 9 равен 3, потому что 3 x 3 = 9.

Смотрите нашу страницу: Специальные числа и концепции для получения дополнительной информации о квадратных корнях.

² Мощность

Этот символ используется для числа 3 3010159 , например, означает 3 в степени 2 или 3 в квадрате (3 x 3).

Число с надстрочным индексом является степенью, поэтому 4 ³ означает 4 в степени 3 или 4 куба, то есть 4 × 4 × 4.

См. Наши страницы на Расчет площади и Расчет объема для примеров использования квадратов и чисел в кубах

. Десятичная точка

символ десятичной точки, часто называемый просто «точкой».

, разделитель тысяч

Запятую можно использовать для разделения больших чисел и облегчения их чтения.

Тысяча может быть записана как 1000, а также 1000 и миллион как 1,000,000 или 1000000.Запятая разбивает большие числа на блоки из трех цифр.

В большинстве англоязычных стран математическая функция не имеет, она просто используется для облегчения чтения чисел.

В некоторых других странах, особенно в Европе, вместо десятичной точки может использоваться запятая.

() Кронштейны

Квадратные скобки () используются для определения порядка вычисления в соответствии с правилом BODMAS.

Части вычисления, включенные в скобки, рассчитываются первыми, например,

5 + 3 × 2 = 11
(5 + 3) × 2 = 16

% Процент

Символ% означает процент или число из 100.

Узнайте все о процентах на нашей странице: Введение в проценты

∞ Бесконечность

Символ ∞ означает бесконечность, концепцию, что числа продолжаются вечно.

Какое бы ни было большое число, у вас всегда может быть большее, потому что вы всегда можете добавить к нему одно.

Бесконечность — это не число, а идея и чисел, которые существуют вечно. Вы не можете добавить один к бесконечности, больше, чем вы можете добавить один к человеку, или любить или ненавидеть.

x-bar Mean

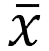
x-bar — это среднее значение всех возможных значений x.

Этот символ чаще всего встречается в статистике.

Смотрите нашу страницу на В среднем для получения дополнительной информации.

! Факториал

! является символом факториала.

n! является произведением всех чисел от n до 1 включительно, то есть n x (n − 1) x (n − 2) x… x 2 x 1.

∝ Пропорциональный

∝ означает ‘пропорционально ’ и используется для отображения чего-то, что отличается от другого.Например, если x = 2y, то x ∝ y.

∴ Поэтому

— это полезная сокращенная форма слова «поэтому», используемая в математике и естествознании.

∵ Потому что

— это полезная сокращенная форма «потому что», которую не следует путать с «поэтому».

математика | Определение и история

Математика , наука о структуре, порядке и отношениях, которая возникла из элементарной практики подсчета, измерения и описания форм объектов. Это имеет дело с логическим рассуждением и количественным вычислением, и его развитие вовлекало увеличивающуюся степень идеализации и абстракции его предмета. С 17-го века математика была незаменимым дополнением к физическим наукам и технологиям, и в последнее время она играет аналогичную роль в количественных аспектах наук о жизни.

Британика Викторина

Математика: факт или вымысел?

Вы можете сделать все римские цифры своими руками.

Во многих культурах — под воздействием потребностей практических занятий, таких как торговля и сельское хозяйство — математика вышла далеко за рамки базового счета.Этот рост был самым большим в обществах, достаточно сложных для того, чтобы поддерживать эту деятельность и обеспечить досуг для размышлений и возможность использовать достижения более ранних математиков.

Все математические системы (например, евклидова геометрия) представляют собой комбинации наборов аксиом и теорем, которые могут быть логически выведены из аксиом. Изучение логической и философской основы математики сводится к вопросу о том, обеспечивают ли аксиомы данной системы ее полноту и непротиворечивость.Для полной обработки этого аспекта, см. Математика , основы.

Эта статья предлагает историю математики с древних времен до наших дней. В результате экспоненциального роста науки большая часть математики развивалась с 15-го века до н.э., и это исторический факт, что с 15-го века до конца 20-го века новые разработки в области математики были в основном сосредоточены в Европе и Северной Америке , По этим причинам основная часть этой статьи посвящена европейским разработкам с 1500 года.

Получите эксклюзивный доступ к контенту из нашего первого издания 1768 года с вашей подпиской. Подпишитесь сегодня

Это, однако, не означает, что события в других местах были не важны. Действительно, чтобы понять историю математики в Европе, необходимо знать ее историю, по крайней мере, в древней Месопотамии и Египте, в древней Греции и в исламской цивилизации с 9 по 15 века. То, как эти цивилизации влияли друг на друга, и важный прямой вклад, который Греция и ислам внесли в последующие события, обсуждаются в первых частях этой статьи.

Вклад Индии в развитие современной математики был сделан благодаря значительному влиянию достижений Индии на исламскую математику в годы ее становления. Отдельная статья, южноазиатская математика, посвящена ранней истории математики на индийском субконтиненте и развитию там современной десятичной системы счисления. В статье «Восточноазиатская математика» освещается в основном самостоятельное развитие математики в Китае, Японии, Корее и Вьетнаме.

Основные разделы математики рассматриваются в нескольких статьях. См. алгебра; анализ; арифметическая; комбинаторика; теория игры; геометрия; теория чисел; численный анализ; оптимизация; теория вероятности; теория множеств; статистика; тригонометрия.