Прямоугольник. Ось симметрии фигуры

Если в четырехугольнике все углы прямые, то его называют прямоугольником.

На рисунке 125 изображен прямоугольник ABCD.

Стороны AB и BC имеют общую вершину B. Их называют соседними сторонами прямоугольника ABCD. Также соседними являются, например, стороны BC и CD.

Соседние стороны прямоугольника называют его длиной и шириной.

Стороны AB и CD не имеют общих вершин. Их называют противоположными сторонами прямоугольника ABCD. Также противолежащими являются стороны BC и AD.

Противолежащие стороны прямоугольника равны.

На рисунке 125 AB = CD, BC = AD. Если длина прямоугольника равна a, а ширина − b, то его периметр вычисляют по уже знакомой тебе формуле:

P = 2a + 2b

Прямоугольник, у которого все стороны равны, называют квадратом (рис. 126).

Проведем прямую l, проходящую через середины двух противолежащих сторон прямоугольника (рис.

127). Если лист бумаги перегнуть по прямой l, то две части прямоугольника, лежащие по разные стороны от прямой l, совпадут.

Аналогичным свойством обладают фигуры, изображенные на рисунке 128. Такие фигуры называют симметричными относительно прямой. Прямую l называют осью симметрии фигуры.

Итак, прямоугольник − это фигура, имеющая ось симметрии. Также ось симметрии имеет равнобедренный треугольник (рис. 129).

Фигура может иметь более одной оси симметрии. Например, прямоугольник, отличный от квадрата, имеет две оси симметрии (рис. 130), а квадрат − четыре оси симметрии (рис. 131). Равносторонний треугольник имеет три оси симметрии (рис. 132).

Изучая окружающий мир, мы часто встречаемся с симметрией. Примеры симметрии в природе показаны на рисунке 133.

Объекты, имеющие ось симметрии, легко воспринимаются и приятные для глаза. Недаром в Древней Греции слово «симметрия» служило синонимом слов «гармония», «красота». \circ$) $S_l$ относительно некоторой прямой $l$, отличной от $Ox$, $Oy$ и $ Oz$, то одна из этих трех осей должна переходить сама в себя, а две остальные — друг в друга.

У правильного тетраэдра три оси симметрии — прямые, соединяющие середины его ребер. Чтобы убедиться в этом, удобно достроить тетраэдр до куба, проведя через каждое ребро тетраэдра плоскость, параллельную противоположному ребру (рис. $2$). Ясно, что любое самосовмещение тетраэдра будет также самосовмещением этого описанного куба. Из девяти осевых симметрий, отображающих куб на себя, лишь три будут переводить в себя тетраэдр.

б) Пусть дан многогранник $M$, у которого более одной оси симметрии.

Лемма $1$ Если $l$ и $m$ — оси симметрии многогранника $M$, то $S_l (m) = m’$ — также ось симметрии $М$.

В самом деле, если точки $P$ и $P’$ многогранника $M$ симметричны относительно $m$, то $S_l (P)$ и  $S_l (P’)$ будут симметричными относительно $m’$. Короче: $S_{m’}  = S_l O S_m O S_l$.

Лемма $2$ Если $l$ и $m$ — оси симметрии многогранника $M$, пересекающиеся в точке $O$ и перпендикулярные друг к другу, то прямая $n$, перпендикулярная им обоим и проходящая через точку $O$, также служит осью симметрии $M$.

Действительно, $S_n = S_m O S_l$. Это легко проверить, приняв данные прямые за оси координат, или построив прямоугольный параллелепипед с центром в точке $O$ и осями симметрии $l$, $m$, $n$ с произвольной вершиной $P$ (рис. $3$).

Леммы $1$ и $2$ позволяют, фиксировав какую-то одну ось симметрии $l$, разбить все остальные на пары: если $m$ удовлетворяет условия леммы $2$, то пару с ней образует $n$, а если нет, то $m’ = S_l(m) \ne m$. Отсюда сразу следует утверждение задачи б).

Возникает естественный вопрос: какое вообще (конечное) множество прямых может быть множеством всех осей симметрии некоторого многогранника?

Различные примеры даются множеством осей симметрии $n$-угольной правильной призмы (здесь количество осей $p=n$ при $n$ нечетном и $p=n+1$ при $n$ четном), тетраэдра (или прямоугольного параллелепипеда с разными ребрами, $p=3$), куба (или октаэдра $p=9$) и додекаэдра (или икосаэдра, $p=15$).

Попробуйте доказать, что других множеств осей симметрии (состоящих более чем из одной прямой) не бывает. Конечно, тут не обойтись без такой очень полезной леммы, которую многие читатели применили и в решении задачи б).

Лемма $3$ Оси симметрии любого многогранника пересекаются в одной точке.

Предположим, что $l$, $m$ — непересекающиеся оси симметрии многогранника $M$. Пусть $n$ — общий перпендикуляр $l$, $m$; рассмотрим прямоугольную систему координат с началом в точке $O = l \cap n$, с осью $Oz$ направленной по лучу $OA$, где $A = n \cap m$; пусть $|OA| = a$. Тогда при симметрии относительно оси $l$ координата $z$ любой точки переходит в $(-z)$, а при симметрии относительно $m$ — в $(2a-z)$. Поэтому при композиции этих двух симметрий $z$ изменяется на $2a$. Повторяя эту композицию достаточное число раз, мы «выгоним» любую точку за пределы многогранника $M$.  Противоречие!

Вот еще более короткое доказательство леммы $3$ (правда, использующее понятие, заимствованное из механики): пусть $O$ — центр масс одинаковых грузиков, помещенных в вершинах многогранника $M$; ясно, что при любом самосовмещении многогранника $M$ грузики лишь меняются местами, поэтому точка $O$ переходит в себя; в частности, все оси симметрии многогранника $M$ проходят через точку $O$.

Н. Васильев, В. Сендеров, А. Сосинский

Поделиться ссылкой:

Похожее

§15. Прямоугольник. Ось симметрии фигуры

ВОПРОСЫ

1. Какой четырехугольник называют прямоугольником?

Если в четырехугольнике все углы прямые, то его называют прямоугольником.

2. Какие стороны прямоугольника называют соседними? Противолежащими?

3. Что называют длиной и шириной прямоугольника?

Соседние стороны прямоугольника, т.е. стороны имеющие общую вершину, называют его длиной и шириной.

4. Каким свойством обладают противолежащие стороны прямоугольника?

Противолежащие стороны прямоугольника равны.

5. Какую фигуру называют квадратом?

Квадратом называют прямоугольник, у которого все стороны равны. 

6. Объясните, какие фигуры называют симметричными относительно прямой.

7. Как называют прямую, относительно которой симметрична фигура?

Прямую, относительно которой симметрична фигура, называют осью симметрии фигуры.

8. Какие вы знаете фигуры, имеющие ось симметрии?

Прямоугольник, квадрат, равнобедренный и равносторонний треугольники.

9. Сколько осей симметрии имеет прямоугольник, отличный от квадрата? Квадрат? Равносторонний треугольник?

---

РЕШАЕМ УСТНО

1. Каждая сторона треугольника равна 12 см. Как называют такой треугольник? Чему равен его периметр?

2. Периметр равнобедренного треугольника равен 32 см, а одна из его сторон — 12 см. Найдите длины двух других сторон треугольника. Сколько решений имеет задача?

3. Найдите сторону равностороннего треугольника, если она меньше его периметра на 10 см.

4. Вычислите значение по формуле y= x*x+ 12, если: 1) x = 1; 2) x = 10.

---

УПРАЖНЕНИЯ

359. Постройте: 1) прямоугольник, соседние стороны которого равны 4 см и 2 см; 2) квадрат со стороной 3 см.

360. Постройте прямоугольник, соседние стороны которого равны 25 мм и 35 мм.

361. Вычислите периметр: 1) прямоугольника, соседние стороны которого равны 42 см и 23 см; 2) квадрата со стороной 8 дм.

362. Найдите периметр прямоугольника, соседние стороны которого равны 13 мм и 17 мм.

363. Какие из букв, изображенных на рисунке 135, имеют ось симметрии?

А, Е, Т.

364. Сколько осей симметрии имеет многоугольник, изображенный на рисунке 136?

365.  1) Длина одной из сторон прямоугольника равна 14 см, что на 5 см больше длины соседней стороны. Найдите периметр прямоугольника.
2) Периметр прямоугольника равен 34 см, а одна из его сторон — 12 см. Найдите длину соседней стороны прямоугольника.

366. Одна сторона прямоугольника равна 8 см, а соседняя — в 4 раза больше. Найдите периметр прямоугольника.

367. Квадрат со стороной 12 см и прямоугольник, одна из сторон которого равна 8 см, имеют равные периметры. Найдите неизвестную сторону прямоугольника.

368. Прямоугольник, соседние стороны которого равны 42 см и 14 см, и квадрат имеют равные периметры. Найдите длину стороны квадрата.

369. Сколько квадратов изображено на рисунке 137?

370. Из куска проволоки сделали модель пятиугольника (рис. 138). Какие из моделей перечисленных фигур, длины сторон которых выражаются натуральным числом сантиметров, можно сделать из этого куска проволоки: 1) квадрат; 2) пятиугольник, все стороны которого равны; 3) равносторонний треугольник?

371. Прямоугольник АВCD разрезали на квадраты так, как показано на рисунке 139. Сторона наименьшего из квадратов равна 4 см. Найдите длины сторон прямоугольника АВСD.

372. Начертите прямоугольник, соседние стороны которого равны 3 см и 6 см. Разделите его на три равных прямоугольника. Вычислите периметр каждого из полученных прямоугольников. Сколько решений имеет задача?

373. Существует ли среди прямоугольников с периметром 12 см такой, который можно разделить на два равных квадрата? В случае положительного ответа выполните рисунок и вычислите периметр каждого из полученных квадратов.

374.  Как надо разрезать квадрат на четыре равные части, чтобы из них можно было сложить два квадрата?

375. Как надо разрезать равнобедренный прямоугольный треугольник на четыре равные части, чтобы из них можно было сложить квадрат?

376. Как надо разрезать прямоугольник со сторонами 8 см и 4 см на четыре части, чтобы из них можно было сложить квадрат?

377. Как надо разрезать квадрат на треугольник и четырехугольник, чтобы из них можно было сложить треугольник?

378. Как надо разрезать квадрат со стороной 6 см на две части по ломаной, состоящей из трех звеньев, чтобы из полученных частей можно было сложить прямоугольник?

---

УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ

379. Проведите прямую МК, луч PS и отрезок АВ так, чтобы луч РS пересекал отрезок АВ и прямую МК, а прямая МК не пересекала отрезок АВ.

380. В магазине имеются лимоны, апельсины и мандарины, всего 740 кг. Если бы продали 55 кг лимонов, 36 кг апельсинов и 34 кг мандаринов, то оставшиеся массы лимонов, апельсинов и мандаринов оказались бы равными. Сколько килограммов фруктов каждого вида имеется в магазине?

381. От дома до дачи можно доехать на автобусе, или на электропоезде, или на маршрутном такси. В таблице указано время, которое надо затратить на каждый участок пути. Какой наименьшее время потребуется на дорогу? Каким видом транспорта надо воспользоваться?

382. Найдите сумму корней уравнений:

---

ЗАДАЧА ОТ МУДРОЙ СОВЫ

383. Как с помощью пятилитрового бидона и трехлитровой банки набрать на берегу реки 4 л воды?

Куб

Куб

Куб Самый популярный многогранник из семейства Платоновых тел. Куб или гексаэдр (от греческого hex — шесть и hedra — грань) составлен из 6 квадратов.

Каждая из 8 вершин куба является вершиной 3 квадратов, поэтому сумма плоских углов при каждой вершине равна 270°. У куба 12 ребер, имеющих равную длину. Примем длину ребра куба за а и представим числовые характеристики его элементов.

Сумма длин всех ребер	12а
Площадь поверхности	6а2
Объем	V = а3
Радиус описанной сферы
Радиус вписанной сферы	r = a/2

Кубу свойственны все виды симметрии.

	Центром симметрии является точка пересечения диагоналей куба. Через центр симметрии проходят 9 осей симметрии. Ось симметрии куба может проходить либо через середины параллельных ребер, не принадлежащих одной грани, либо через точку пересечения диагоналей противоположных граней.
	Плоскостей симметрии у куба также 9 и проходят они либо через противоположные ребра ( таковых плоскостей 6), либо через середины противоположных ребер (таких — 3).

В мире нет места для некрасивой математики.
Готфрид Харди

Правильные многогранники — самые выгодные фигуры.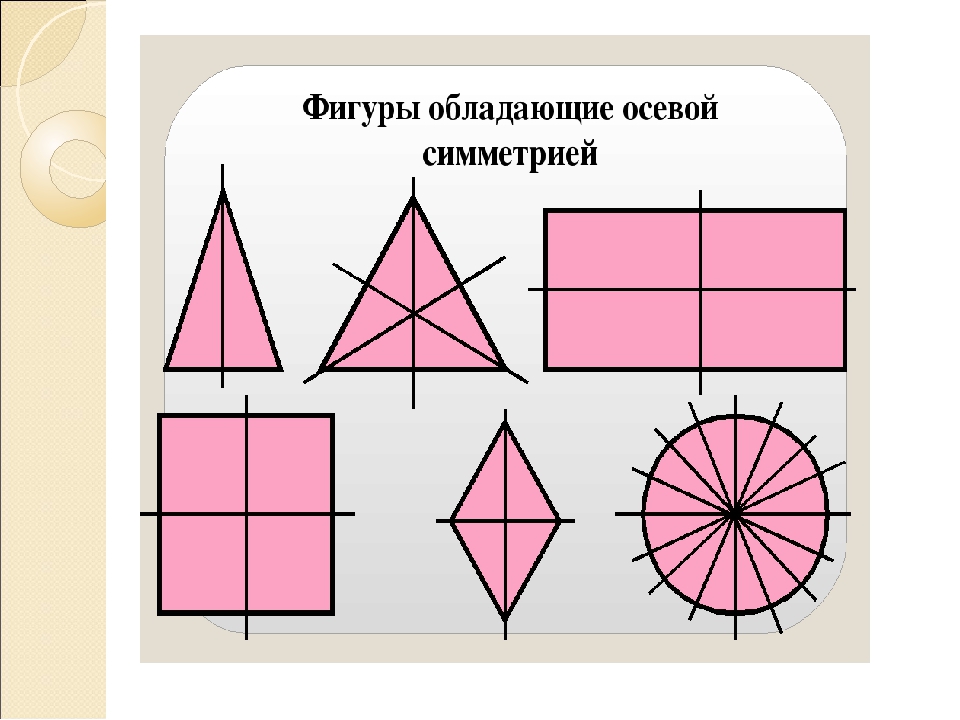 И природа этим широко пользуется. Кристаллы некоторых знакомых нам веществ имеют форму правильных многогранников.

Куб передает форму кристаллов поваренной соли NaCl.

Форму куба имеют кристаллические решётки многих металлов (Li, Na, Cr, Pb, Al, Au, и другие), кристалл алмаза, кристаллическая решётка хлорида цезия CsCl.

В 2009 г. должно исполниться 500 лет со времени выхода в свет книги Луки Пачоли «Божественная пропорция», а следовательно, и изобретения Леонардо да Винчи для ее иллюстрации метода жестких ребер.

Леонардо изображал своим способом не только индивидуальные многогранники, но и, например, плотную упаковку кубов. Этим изображением Леонардо на три века предвосхитил гипотезу о периодическом строении кристаллов, высказанную французскими кристаллографами аббатом Рэнэ-Жюстом Гаюи (1743-1822) и морским офицером Огюстом Бравэ (1811-1863).

Можно сравнить этот рисунок Леонардо с похожей работой Маурица Эшера, относящейся к 1952 г. , «Ячейки кубического пространства».

Не менее интересна другая работа Маурица Эшера. В центре гравюры «Водопад» расположен комплекс конструкций, поднимающийся на фоне ландшафта с террасами. Вертикальная ось создается двумя мощными башнями, каждая из которых увенчана острогранными многогранниками слева — три пересекающиеся куба, а справа также три пересекающихся правильных октаэдра. Маленькие домики примыкают к башням слева и справа в едином комплексе. Слева на первом плане картины изображен маленький садик со странными, необычными подводными растениями. Центральным действием картины является ручей, который падает на колесо и крутит его. Он течет слегка полого вниз и извивается, проходя через башни, при этом он трижды протекает через точку, в которой уже проходил. Абсурдность доходит до нас через круг неправильных соединений куба. В результате невольного восприятия зрительная точка оказывается самой ближней, а самая высокая точка становится самой низкой.

Водопад на картине Маурица Эшера осуществляет то,что мы считаем невозможным — вечное движение.

Урок повторения по теме «Симметрия»

Урок повторения по теме «Симметрия»

Математика, 6 класс

Чебанькова Татьяна Александровна, учитель высшей категории

МОУ СОШ № 57 Кировского района г. Волгограда

Учебник: Математика. 6 класс. И.И.Зубарева, А.Г.Мордкович «Мнемозина», 2006

Цели:

• Обобщить и систематизировать знания обучающихся по теме «Симметрия»;

• Продолжить формирование ряда умений осознать проблему, анализировать, сравнивать, делать выводы и обобщения.

• Воспитание умения работать в малых группах и ответственности за результаты совместной работы.

Ход урока

Организационный момент

Страница 1. Учащимся предлагается три ряда картинок (рис. 1)

Подумайте, по какому признаку они собраны в ряды. Попробуйте распределить по этим группам данные четыре фигуры.

рис.1

Несложно, заметить, что в 1 ряду фигуры обладают центральной симметрией, и значит к ним необходимо «перетащить» фигуру — «мозаика». Второй ряд не обладает особенными свойствами – таким образом «вензель» и «птичка» относятся именно к этим фигурам. Фигуры третьего ряда обладают осевой симметрией, а, значит, к ним учащиеся добавляют «бабочку».

После того как учащиеся смогут определить признаки, по которым составлены ряды фигур, учитель совместно с учащимися формулирует тему урока.

Беседа по теме «Симметрия»

Понятие симметрии проходит через всю многовековую историю человеческого творчества. Оно встречается уже у истоков человеческого знания; его широко используют все без исключения направления современной науки. Принципы симметрии играют важную роль не только в математике, но и … в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке.

Симметрия делится на два типа симметрии. Первый тип – это та симметрия, которую можно непосредственно видеть. Она может быть названа геометрической симметрией. Второй тип – эта та симметрия, которая лежит в законах природы и физических явлениях. Ее можно назвать физической симметрией.

В процессе беседы учащиеся вспоминают примеры симметрии в жизни, и различных областях наук (симметрией мы встречаемся везде – в природе, технике, искусстве, науке. Отметим, например, симметрию, свойственную бабочке и кленовому листу, симметрию форм автомобиля и самолета, симметрию в ритмическом построении стихотворения и музыкальной фразы, симметрию орнаментов и бордюров, симметрию атомной структуры молекул и кристаллов)

Термин «симметрия» по-гречески означает «соразмерность, пропорциональность, одинаковость в расположении частей». А какой же смысл вкладывали люди в это слово на протяжении многих столетий?

Страница 2. Учащимся предлагается выполнить несложные вычисления и расшифровать слово «гармония» (рис. 2)

рис. 2

Проверить себя они смогут, использую функцию интерактивной доски « ластик», стерев желтый цвет, они увидят верный ответ.

Страница 3 и 4. Следующее задание, найди центр симметрии и оси симметрий простейших геометрических фигур (рис. 3). С помощью функций «перо» и «умное перо» учащиеся смогут показать оси и центр симметрий.

рис.3

Страница 5 и 6. Задания на узнавание вида симметрии, определение центров симметрии и осей (рис. 4).

рис. 4

Помогите роботу обрести себя. Данное задание является своеобразным мостиком от простых фигур к более сложным. Учащиеся используют функции интерактивной доски «выбрать» и «перетащить объект».

Страница 7. Выберите из данных фигур только те, которые имеют ось симметрии (рис. 5).

рис. 5

Используется дополнительная функция «непрозрачный экран», который закрывает второй вопрос к этому заданию: есть ли среди фигуры, у которых более двух осей симметрии? Учащиеся используют функции интерактивной доски «выбрать» и «перетащить объект».

Страница 8. На странице представлена 21 фигура, и четыре области (рис. 6). Учащиеся, получают аналогичный набор картинок на парту. За 2 минуты им нужно придумать, каким образом они разделят эти фигуры, по каким признакам. Учащиеся используют функции интерактивной доски «выбрать» и «перетащить объект».

рис. 6

Построение симметричных фигур.

Учащимся всегда легче определить визуально по картинке обладает ли она симметрией, нежели построить самостоятельно симметричные фигуры. Следующий этап урок вспомнить алгоритмы построения симметричных точек и простейших геометрических фигур. Презентация поможет без труда восполнить пробелы учащихся по данному вопросу (рис. 7).

рис. 7

Работа в парах. Учащимся предоставляется две карточки, на которых в декартовой системе координат изображен рисунок, требуется продолжить их таким образом, чтобы они обладали либо центральной симметрией, либо осевой. Учащиеся самостоятельно выбирают вид симметрии. Так учитель увидит, какой вид симметрии не достаточно усвоен. Проверить себя они смогут, сравнив свой рисунок с образцом на доске. Используются дополнительные функции «непрозрачный экран» и «таймер».

Страница 9. Последнее задание «Парад стран».(5мин) Учащимся представлены флаги стран мира, им требуется удалить те флаги, которые не обладают симметрией (рис.8). Проблемой является два флага с нечетким маленьким рисунком.

рис.8

Для рассмотрения учащиеся могут использовать функцию интерактивной доски «лупа». Кроме этого в центре находится ящик с подсказками названий стран, удалив, его они смогут воспользоваться ими.

Подведение итогов.

Домашнее задание. Придумать рисунок, иллюстрирующий осевую или центральную симметрии, и изобразить его на отдельном листе.

Симметрия и её виды | Обучонок

1. Симметрия и ее виды

Понятие симметрии проходит через всю историю человечества. Оно встречается уже у истоков человеческого знания. Возникло оно в связи с изучением живого организма, а именно человека. И употреблялось скульпторами ещё в 5 веке до нашей эры. Слово “симметрия” греческое, оно означает “соразмерность, пропорциональность, одинаковость в расположении частей”.

Его широко используют все без исключения направления современной науки. Немецкий математик Герман Вейль сказал: “Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство”. Его деятельность приходится на первую половину ХХ века. Именно он сформулировал определение симметрии, установил по каким признакам усмотреть наличие или, наоборот, отсутствие симметрии в том или ином случае. Таким образом, математически строгое представление сформировалось сравнительно недавно – в начале ХХ века.

1.1. Осевая симметрия

Две точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему (Рисунок 2.1). Каждая точка прямой а считается симметричной самой себе.

Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой a также принадлежит этой фигуре (Рисунок 2.2).

Прямая а называется осью симметрии фигуры.

Говорят также, что фигура обладает осевой симметрией.

Осевой симметрией обладают такие геометрические фигуры как угол, равнобедренный треугольник, прямоугольник, ромб (Рисунок 2.3).

Фигура может иметь не одну ось симметрии. У прямоугольника их две, у квадрата – четыре, у равностороннего треугольника – три, у круга – любая прямая, проходящая через его центр.

Если присмотреться к буквам алфавита (Рисунок 2.4)., то и среди них можно найти, имеющие горизонтальную или вертикальную, а иногда и обе оси симметрии. Объекты, имеющие оси симметрии достаточно часто встречаются в живой и неживой природе.

Имеются фигуры, у которых нет ни одной оси симметрии. К таким фигурам относятся параллелограмм, отличный от прямоугольника, разносторонний треугольник.

В своей деятельности человек создаёт много объектов (в том числе и орнаменты), имеющих несколько осей симметрии.

1.2 Центральная симметрия

Две точки А и А1 называются симметричными относительно точки О, если О — середина отрезка АА1. Точка О считается симметричной самой себе (Рисунок 2.5).

Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре [1].

Простейшими фигурами, обладающими центральной симметрией, является окружность и параллелограмм (Рисунок 2.6).

Точка О называется центром симметрии фигуры. В подобных случаях фигура обладает центральной симметрией. Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма — точка пересечения его диагоналей.

Прямая также обладает центральной симметрией, однако в отличие от окружности и параллелограмма, которые имеют только один центр симметрии у прямой их бесконечно много — любая точка прямой является её центром симметрии. Примером фигуры, не имеющей центра симметрии, является треугольник.

1.3. Поворотная симметрия

Предположим, что объект совмещается сам с собой при повороте вокруг некоторой оси на угол, равный 360°/n (или кратный этой величине), где n = 2, 3, 4, … В этом случае о поворотной симметрии, а указанную ось называют поворотной осью n-го порядка.

Рассмотрим примеры со всеми известными буквами «И» и «Ф». Что касается буквы «И», то у нее есть так называемая поворотная симметрия. Если повернуть букву «И» на 180° вокруг оси, перпендикулярной к плоскости буквы и проходящей через ее центр, то буква совместится сама с собой.

Иными словами, буква «И» симметрична относительно поворота на 180°. Заметим, что поворотной симметрией обладает также буква «Ф».

На рисунке 2.7. даны примеры простых объектов с поворотными осями разного порядка – от 2-го до 5-го. [3]

Перейти к разделу: 1.4. Зеркальная симметрия

Осевая симметрия как основополагающий закон вселенной

Осевая симметрия как основополагающий закон вселенной

Фридрих  В.А. 1

---

1Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа № 6», г. Александровск, Пермский край

Дементьева  В.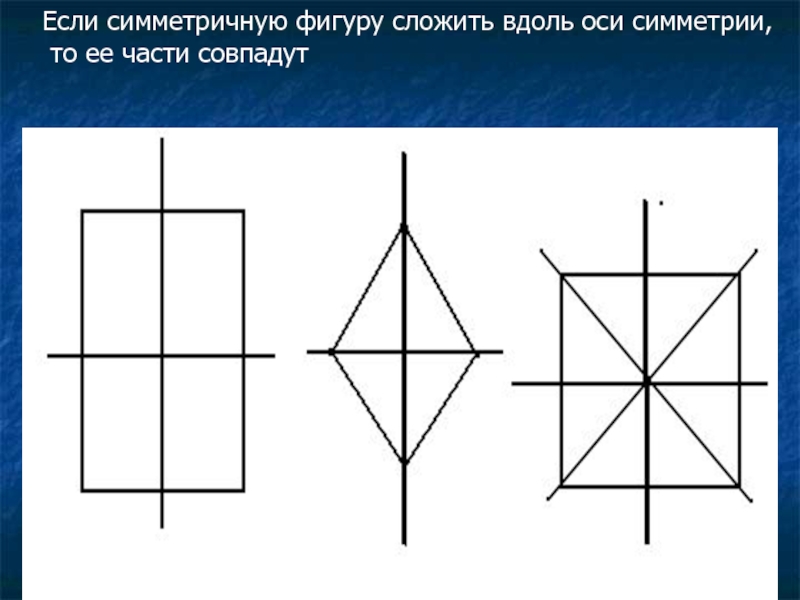 В. 1

---

1Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа № 6», г. Александровск, Пермский край

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

«Стоя перед черной доской и рисуя на ней

мелом разные фигуры,

я вдруг был поражен мыслью:

почему симметрия приятна глазу?

Что такое симметрия?

Это врожденное чувство, отвечал я сам себе»

Л.Н. Толстой

В учебнике математика 6 класс, автор Никольский С. М., на страницах 132 – 133 раздел Дополнительные задачи к главе № 3, имеются задания для исследования фигур на плоскости, симметричных относительно прямой. Меня заинтересовала данная тема, я решила выполнить задания и более подробно изучить данную тему.

Объект исследования – симметрия.

Предмет исследования – симметрия как основополагающий закон вселенной.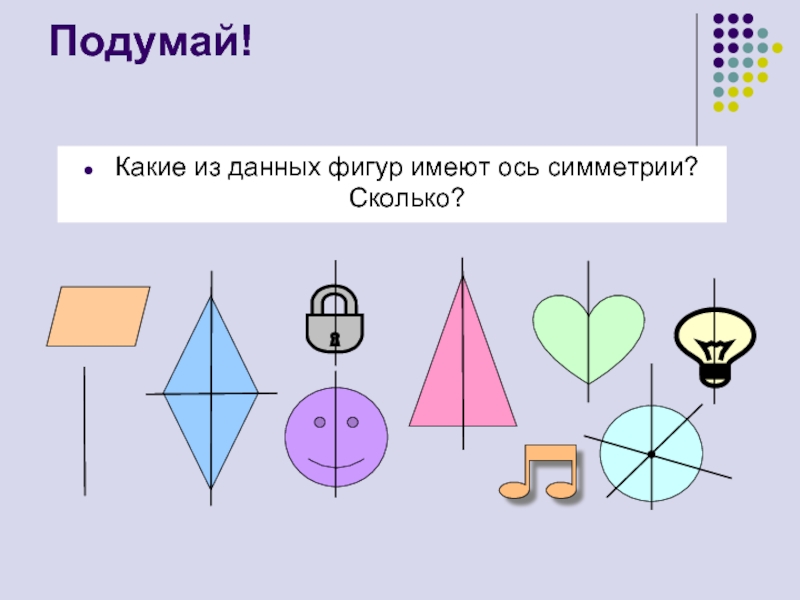

Какую гипотезу я буду проверять:

Я считаю, что осевая симметрия является не только математическим и геометрическим понятием, и применяется только для решения соответствующих задач, но и является основой гармонии, красоты, равновесия и устойчивости. Принцип симметрии используется практически во всех науках, в нашей повседневной жизни и является одним из «краеугольных» законов, на котором базируется мироздание в целом.

Актуальность темы

Понятие симметрия проходит через всю многовековую историю человеческого творчества. Оно встречается уже у истоков его развития. В наше время, наверное, трудно найти человека, который не имел бы какого-либо представления о симметрии. Мир, в котором мы живём, наполнен симметрией домов, улиц, творениями природы и человека. С симметрией мы встречаемся буквально на каждом шагу: в технике, искусстве, науке.

Поэтому, знание и понимание о симметрии в окружающем нас мире, является обязательным и необходимым, которое пригодится в дальнейшем для изучения других научных дисциплин. В этом и заключается актуальность избранной мной темы.

Цель и задачи

Цель работы: выяснить, какую роль играет симметрия в повседневной жизни человека, в природе, архитектуре, в быту, музыке и других науках.

Для достижения поставленной цели, мне необходимо выполнить следующие задачи:

1. Найти необходимую информацию, литературу и фотографии. Установить наибольшее количество данных, необходимых для моей работы, с помощью доступных для меня источников: учебники, энциклопедии или другие носители информации, соответствующих заданной теме.

2. Дать общие понятие о симметрии, видах симметрии и истории происхождения термина.

3. Для подтверждения своей гипотезы, создать поделки и провести эксперимент с данными фигурами, имеющими симметрию и не несимметричными.

4. Продемонстрировать и представить результаты наблюдений в своём исследовании.

Для практической части исследовательской работы мне необходимо сделать следующее, для чего я составила план работы:

1. Создать своими руками поделки с заданными свойствами — симметричные и не симметричные модели, композицию, используя цветную бумагу, картон, ножницы, фломастеры, клей и т.д.;

2. Провести эксперимент с моими поделками, с двумя вариантами симметрии.

3. Исследовать, проанализировать и систематизировать полученные результаты, составив таблицу.

4. Для наглядного и интересного закрепления полученных знаний, с помощью приложения «Paint 3 D» создать рисунки для наглядности, а так же нарисовать картинки, с заданиями – дорисовать симметричную половинку (начиная с простых рисунков и заканчивая сложными) и объединить их, создав электронную книгу.

Методы исследования:

1. Анализ статей и всей информации о симметрии.

2. Компьютерное моделирование (обработка фотографий средствами графического редактора).

3. Обобщение и систематизация полученных данных.

Основная часть.

Осевая симметрия и понятие совершенства

С древних времен человек выработал представления о красоте и пытался постигнуть смысл совершенства. Красивы все творения природы. По-своему прекрасны люди, восхитительны животные и растения. Радует взор зрелище драгоценного камня или кристалла соли, сложно не любоваться снежинкой или бабочкой. Но почему так происходит? Нам кажется правильным и завершенным вид объектов, правая и левая половина которых выглядит одинаково.

Видимо, первыми о сути красоты задумывались люди искусства.

Впервые обосновали это понятие художники, философы и математики Древней Греции. Древние скульпторы, изучавшие строение человеческого тела, еще в V веке до н.э. стали применять понятие «симметрия». Это слово имеет греческое происхождение и означает гармоничность, пропорциональность и похожесть расположения составляющих частей. Древнегреческий мыслитель и философ Платон утверждал, что прекрасным может быть лишь то, что симметрично и соразмерно.

И действительно, «радуют глаз» те явления и формы, которые имеют пропорциональность и завершенность. Их мы называем правильными.

Виды симметрии

В геометрии и математике рассматриваются три вида симметрии: осевая симметрия (относительно прямой), центральная (относительно точки) и зеркальная (относительно плоскости).

Осевая симметрия как математическое понятие

Точки симметричны относительно некой прямой (оси симметрии), если они лежат на прямой, перпендикулярной данной прямой, и на одинаковом расстоянии от оси симметрии.

Фигура считается симметричной относительно прямой, если для каждой точки рассматриваемой фигуры, симметричная для неё точка относительно данной прямой также находится на этой фигуре. Прямая является в этом случае осью симметрии фигуры.

Фигуры, симметричные относительно прямой равны. Если геометрической фигуре свойственна осевая симметрия, определение зеркальных точек можно наглядно представить, просто перегнув ее по оси и сложив равные половинки «лицом к лицу». Искомые точки при этом соприкоснутся.

Примеры оси симметрии: биссектриса неразвернутого угла равнобедренного треугольника, любая прямая, проведенная через центр окружности, и т.д. Если геометрической фигуре свойственна осевая симметрия, определение зеркальных точек можно наглядно представить, просто перегнув ее по оси и сложив равные половинки «лицом к лицу». Искомые точки при этом соприкоснутся.

Фигуры могут иметь несколько осей симметрии:

· осью симметрии угла является прямая, на которой лежит его биссектриса;

· осью симметрии окружности и круга является любая прямая, проходящая через их диаметр;

· равнобедренный треугольник имеет одну ось симметрии, равносторонний треугольник – три оси симметрии;

· прямоугольник имеет 2 оси симметрии, квадрат – 4, ромб – 2 оси симметрии.

Ось симметрии — это воображаемая линия разделяющая объект на симметричные части. На моём рисунке она изображена для наглядности.

Имеются фигуры, у которых нет ни одной оси симметрии. К таким фигурам относится параллелограмм, отличный от прямоугольника и ромба, разносторонний треугольник.

Осевая симметрия в природе

Природа мудра и рациональна, поэтому почти все ее творения имеют гармоничное строение. Это относится и к живым существам, и к неодушевленным объектам.

Внимательное наблюдение показывает, что основу красоты многих форм, созданных природой, составляет симметрия. Ярко выраженной симметрией обладают листья, цветы, плоды. Их зеркальная, радиальная, центральная, осевая симметрия – очевидны. В значительной степени она обусловлена явлением гравитации.

Геометрические формы кристаллов с их плоскими поверхностями представляют собой удивительное явление природы. Однако подлинная физическая симметрия кристалла проявляется не столько в его внешнем виде, сколько во внутреннем строении кристаллического вещества.

Осевая симметрия в животном мире

Симметрия в мире живых существ, проявляется в закономерном расположении одинаковых частей тела относительно центра или оси. Чаще в природе встречается осевая симметрия. Она обуславливает не только общее строение организма, но и возможности его последующего развития. Каждому виду животных присущ характерный окрас. Если в расцветке фигурирует рисунок, то, как правило, он дублируется с обеих сторон.

Осевая симметрия и человек

Если взглянуть на любое живое существо, сразу бросается в глаза симметричность устройства организма. Человек: две руки, две ноги, два глаза, два уха и так далее.

Это означает, что существует некая линия, по которой животные и люди могут быть визуально «поделены» на две идентичные половинки, то есть в основе их геометрического устройства лежит осевая симметрия.

Как видно из приведённых примеров, любой живой организм природа создает не хаотично и бессмысленно, а согласно общим законам мироустройства, ведь во Вселенной ничто не имеет чисто эстетического, декоративного назначения. Это обусловлено закономерной необходимостью.

Конечно, природе редко присуща математическая точность, но похожесть элементов организма все равно поразительна.

Симметрия в архитектуре

С древнейших времен архитекторы хорошо знали математическую пропорцию и симметрию, и использовали их при строительстве архитектурных сооружений. Например, архитектура русских православных храмов и соборов Руси: Кремль, собор Христа Спасителя г. Москва, Казанский и Исаакиевский соборы г. Санкт-Петербург и др.

А также другие всемирно известные достопримечательности, многие из которых во всех странах мира, мы можем видеть и сейчас: Египетские пирамиды, Лувр, Тадж-Махал, Кёльнский собор и т.д. Все они, как мы видим, имеют симметрию.

Симметрия в музыке

Я учусь в музыкальной школе, для меня было интересно найти примеры симметрии в данной области. Не только музыкальные инструменты обладают явной симметрией, но и части музыкальных произведений звучат в определённом порядке, в соответствии с партитурой и замыслом композитора.

Например, реприза — (франц. reprise, от reprendre -возобновлять). Повторение темы или группы тем после этапа её (их) развития или изложения нового тематического материала.

Также в одномерном повторении во времени через равные интервалы состоит музыкальный принцип ритма.

Симметрия в технике

Мы живем в стремительно — меняющемся высокотехнологическом, информационном обществе, и не задумываемся, почему некоторые окружающие нас предметы и явления пробуждают чувство прекрасного, а другие нет. Мы их не замечаем, даже не задумываемся, об их свойствах.

Но кроме этого, данные технические и механические устройства, детали, механизмы, агрегаты не смогут правильно работать и вообще функционировать, если при этом не будет соблюдена симметрия, а вернее, некая ось, в механике это — центр тяжести.

Сбалансированность по центру, в данном случае, является обязательным техническим требованием, соблюдение которого строго регламентируется ГОСТ или ТУ и должно соблюдаться.

Симметрия и космические объекты

Но, пожалуй, самыми загадочными, волновавшими умы многих, ещё с древнейших времён, являются космические объекты. Которые также имеют симметрию – солнце, луна, планеты.

Эту цепочку можно продолжать, но мы сейчас говорим о чем-то едином: о том, что осевая симметрия является основополагающим законом вселенной, является основой красоты, гармонии и пропорциональности, и во взаимосвязи этого с математикой.

Практическая часть

Найдя необходимую информацию, изучив литературу, я убедилась в правоте своей гипотезы и сделала вывод о том, что в глазах человека несимметричность чаще всего ассоциируется с неправильностью или ущербностью. Поэтому в большинстве творений людских рук прослеживается симметричность и гармония, как необходимое и обязательное требование.

Это хорошо видно на моём рисунке, где изображён поросёнок, с непропорциональными частями тела, что сразу бросается в глаза!

И только после того, как подольше приглядишься к нему, посчитаешь его милым?

Несмотря на то, что данная тема известна, хорошо изучена, но все эти данные рассмотрены отдельно в каждой дисциплине. Обобщённых данных о том, что принцип симметрии используется, и именно на нём базируются многие другие науки, и их взаимосвязи с математикой я не встретила.

Поэтому я решила доказать своё утверждение с помощью самого простого и доступного для меня способа. Таким решением, я считаю, будет проведение эксперимента с испытаниями.

Для наглядного доказательства того, что асимметричные модели не устойчивы, не обладают необходимыми требованиями и жизненно необходимыми навыками, и подтверждения своей гипотезы мне необходимо создать поделки, рисунки и композицию:

1 вариант – симметричны относительно оси;

2 вариант — с явным нарушением симметрии.

Поскольку я считаю, что такой дисбаланс будет хорошо виден на следующих примерах, для чего я создала поделки-оригами (самолёт и лягушонок) из цветной бумаги. Для чистоты эксперимента они сделаны из одинаковой цветной бумаги и тестировались в одинаковых условиях. И композицию «Маяк», где маяк сделан из пустой пластиковой бутылки, обклеен цветной бумагой. Для украшения композиции использованы игрушечные фигуры человека, модели парусника и лодки, декоративные камни, а для имитации света я использовала светящийся от батарейки элемент.

Я провела испытания с данными поделками, все показатели зафиксировала и занесла в таблицу (все показатели можно посмотреть в приложении № 1 стр. 18 — 21).

Все поделки делались с соблюдением техники безопасности (приложение № 2 стр. 21)

Все полученные данные я проанализировала, вот что у меня получилось.

Анализ полученных данных

Эксперимент № 1

Испытание – прыжок лягушек в длину, замер этого расстояния.

Лягушонок Зелёный (симметричный) прыгает ровно, на большее расстояние, а Красный (не симметричный) ни разу не прыгнул ровно, всегда с поворотом или переворотом в сторону, на расстояние в 2 — 3 раза меньше.

Таким образом, можно сделать вывод, что такое животное не сможет быстро охотиться или наоборот убегать, эффективно добывать пищу, что уменьшает шансы на выживание, это доказывает, что в природе всё сбалансировано, пропорционально, правильно — симметрично.

Эксперимент № 2

Вид испытания – запуск самолётов в полёт и измерение расстояния длины полёта.

Самолётик № 1 «Розовый» (симметричный) летит из 10 раз, 8 раз ровно и прямо, на максимальную длину, (т.е. на всю длину моей комнаты), а траектория полёта самолётика № 2 «Оранжевый» (не симметричный) из 10 раз — ни разу не летел ровно, всегда с поворотом или переворотом, на меньшее расстояние. То есть, если бы это был настоящий самолёт, то он не смог бы лететь ровно, в правильном направлении. Такой полёт был бы очень неудобен или даже опасен для человека (также как и для птиц), а машины и другие транспортные средства передвижения, не смогли бы ехать, плыть и т.д. в необходимую сторону.

Эксперимент № 3

Вид испытания – проверка устойчивости здания «Маяка», при уменьшении угла наклона сооружения, относительно поверхности.

1. Создав композицию «Маяка», я установила его прямо, т.е. перпендикулярно (под углом 90⁰) относительно стен сооружения к поверхности. Данная конструкция стоит ровно, выдерживает установленный световой элемент и фигурку человека.

2. Для дальнейшего проведения эксперимента мне было необходимо расчертить основание башни на углы, равные 10⁰.

После чего я отрезала от основания угол равный 10⁰.

Под углом в 80⁰ здание стоит криво, шатается, но дополнительную нагрузку выдерживает.

3. Отрезав ещё 10⁰ , получился угол наклона в 70⁰, при котором вся моя конструкция рушится.

Данный опыт доказывает, что исторически сложившиеся традиция строительства под прямым углом и соблюдение при этом симметрии самого здания, является необходимым условием для устойчивого, надёжного возведения и эксплуатации архитектурных зданий и сооружений.

Для наглядного примера осевой симметрии и доказательства утверждения о том, что человек воспринимает любые окружающие его предметы, образы животных и т.д. только симметрично, то есть, когда обе стороны, «половинки» одинаковы, равны, я создала электронную раскраску, которую можно распечатать, составив детскую книжку-раскраску. Данное пособие поможет всем желающим лучше усвоить тему, интересно и с удовольствием провести свободное время (Титульный лист изображён на этом рисунке, остальные рисунки расположены в приложении № 3 стр. 21 -24).

Проведённые мною эксперименты доказывают, что симметрия является не только математическим и геометрическим понятием, а является сферой, средой нашего проживания, неким техническим требованием, так же необходимым условием для выживания в целом, как для людей, так и для животных. Симметрия объединяет всё это воедино, и уходит далеко за пределы обычной науки!

Заключение

Выводы:

Я выяснила, что симметрия является одной из главных составляющих в повседневной жизни человека, в предметах быта, в архитектуре, технике, в природе, музыке, науке и т. д.

Результат:

Я нашла необходимую информацию, доказала свою гипотезу, проверила и подтвердила её опытным путём. Я создала поделки, композицию, рисунки и электронную раскраску для наглядного проведения эксперимента.

Я выяснила, что все законы природы – биологические, химические, генетические, астрономические связаны с симметрией. Практически, всё то, что нас окружает, что создано человеком — подчинено общим для нас всех принципам симметрии, поскольку имеют завидную системность. Таким образом, сбалансированность, тождественность как принцип имеет всеобщий масштаб.

Можно сказать, что симметрия является основополагающим законом, на котором базируются основные законы науки? Наверное, да.

Эту тайну пытались осмыслить великие мыслители человечества. Сегодня в разгадку этой тайны погрузились и мы.

Один из известных математиков Герман Вейль писал, что «симметрия — является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство».

Может мы нашли секрет создания красоты, совершенства или даже создания основных законов вселенной? Может это симметрия?

Приложения

Приложение № 1 Таблица испытаний:

Эксперимент № 1
Попытка №	Вид испытания	Результат и характеристика испытания «Зелёная лягушка» (симметричная)	Результат и характеристика испытания «Красная лягушка» (не симметричная)
1	Прыжок лягушки в длину (измерение в см.)	16,5 ровно	6,0 в левую сторону
2		14,4 с небольшим поворотом вправо	9,0 переворот назад
3		10,5 почти ровно	2,0 переворот
4		9,5 с небольшим поворотом вправо	5,0 переворот в левую сторону
5		10,6 с небольшим поворотом вправо	3,0 в левую сторону
6		17,0 ровно	12,0 назад
7		9,0 переворот	9,0 поворот влево
8		13,5 почти ровно	1,5 назад, с поворотом влево
9		15,5 ровно	9,5 влево с переворотом
10		21,2 почти ровно	4,5 влево с переворотом
Эксперимент № 2
		Самолёт «Розовый» (Симметричный)	Самолёт «Оранжевый» (Не симметричный)
1	Запуск самолётика в длину Максимальная длина комнаты (5,1 метра)	5,1 с 2 переворотами	3,04 с переворотами вправо
2		5,1 ровно	2,78 с переворотами вправо
3		5,1 с наклоном вправо	3, 65 с переворотами вправо
4		5,1 с наклоном вправо	1,51 почти ровно
5		5,1 почти ровно	4,73 с переворотами вправо
6		5,1 с наклоном в левую сторону	3,82 поворот вправо
7		5,1 почти ровно	3,41 с переворотами
8		5,1 почти ровно	3,37 поворот влево
9		5,1 с переворотом	3,51 с переворотами влево
10		5,1 почти ровно	3,19 с переворотами вправо

Эксперимент № 3
Попытка №	Характеристика свойств объекта	Вид и характеристика испытания	Результат
1	Сооружение стоит перпендикулярно поверхности (т.е. под углом в 90 0)	Установка дополнительной нагрузки: светящийся элемент и игрушечная фигура человека	Маяк стоит ровно, надёжно
2	Под углом 800	От основания маяка я наметала и отрезала угол в 100	Маяк выдерживает нагрузку, но стоит ненадёжно, шатается
3	Под углом 700	От основания маяка я ещё раз отрезала 100	Сооружение падает и рушится

Приложение № 2

При изготовлении моих поделок соблюдалась техника безопасности, а именно:

Ножницы или нож должны быть хорошо заточены и отрегулированы.

Хранить необходимо в определенном и безопасном месте или коробке.

При пользовании ножниц (ножа), нельзя отвлекаться, нужно быть максимально внимательными, дисциплинированными.

Передавая ножницы (нож), держать их за сомкнутые лезвия (остриё).

Ножницы (нож) класть справа сомкнутыми лезвиями (остриём) направленными от себя.

При резании узкое лезвие ножниц (остриё ножа) должно быть внизу.

После использования клея вымыть руки.

Приложение № 3

Электронная книга-раскраска

Симметрия-

Это означает то, что одна часть предмета похожа на другую.

Осевая симметрия- это симметрия относительно прямой (линии).

Ось симметрии — это воображаемая линия разделяющая объект на симметричные части. На рисунках она изображена для наглядности.

В этой книге нужно закончить рисунки, соединяя точки.

Затемможнораскрашиватьто, чтополучилось.

Попробуй закончить эти рисунки:

Сердечко

Треугольник Домик

Звёздочка Листочек

Мышка Ёлочка

Собачка Замок

Кроме осевой симметрии есть и симметрия относительно точки.

Этот шар симметричен

И ёщё один вид симметрии — зеркальная симметрия.

Зеркальная симметрия-

это симметрия относительно плоскости. Например, относительно зеркала.

Попробуй прочитать с зеркалом:

Симметрия это—

Используемая литература

1. Автор Атанасян Л. С., Геометрия 7- 9 класс.

2. Герман Вейль «Симметрия» (Издательство «Наука» главная редакция физико-математической литературы, Москва 1968 г.)

3. Автор Никольский С.М., Математика 6 класс.

4. Мои рисунки и фотографии.

5. Справочник машиностроителя, том 1, (Государственное научно – техническое издательство машиностроительной литературы, Москвы 1960 г.)

6. Фотографии и рисунки из сети «Интернет».

Просмотров работы: 1189

СОВЕТ 74 Чтобы нарисовать бутылку, начните с оси симметрии

.

Нарисуем современный чайник, который на самом деле похож на бутылку.

Кузов сбоку симметричный. Сложность здесь состоит в том, чтобы изгибы стороны были симметричными. Для этого. Я рекомендую начать с рисования оси симметрии.

Поначалу это упражнение может показаться немного неуклюжим. Если вы правша, левая кривая может заканчиваться немного пологой. И наоборот, если вы левша.Это просто из-за нашего собственного ограничения движений тела .

Я люблю эти корейские ручки — Monami

Обычно я говорю: переверните бумагу, и ваши кривые будут рисоваться намного проще. Однако здесь, если вы поворачиваете бумагу, ваш мозг может быть отсоединен от оси симметрии ссылки.

Итак, держите бумагу и ось симметрии вертикально, , и потренируйтесь рисовать обе стороны кривых чайной бутылки. Могу поспорить, что поначалу это будет немного раздражать, но ваша рука научится новым движениям!

Уловка состоит в том, чтобы предвидеть каждый угол перед тем, как начертить кривые.Если ваши линии неправильные, перерисуйте поверх них, чтобы скорректировать их.

Не забудьте использовать Ghost Drawing!

Обратите внимание, что для быстрых эскизов обе кривые не обязательно должны быть на 100% симметричными. Но вам нужны плавные линии.

Следуйте своему ощущению, чтобы делать красивые изгибы. Ваш мозг должен думать: гладкий и чистый.

Вы будете удивлены, увидев, как такое мышление повлияет на ваши строки. (особенно для изделий из стекла, металла, фарфора…)

Практикуясь, вы станете естественно становиться все более точными.Этот трюк работает со стаканом, ручкой, трубкой, цветочным горшком, шляпой…

Если вы освоите этот трюк, вы уже можете много чего рисовать! (только вид сбоку)

Если вы хотите попрактиковаться в рисовании линий с помощью некоторых упражнений по рисованию для начинающих, я приглашаю вас зарегистрироваться и пришлю вам Designer Starter Kit, который вы можете увидеть ниже.

Увидимся на следующий совет дня!

алгебра колледжа — симметрия

В общих чертах, двумерный график считается симметричным относительно определенной линии, если часть графика на одной стороне линии является зеркальным отображением той части графика, которая находится на другая сторона линии.Например, график ниже считается симметричным относительно оси y (линия x = 0), потому что четверть круга слева от оси y является зеркальным отображением четверти круга справа от оси y. ось. Фактически, если бы вы могли сложить эту страницу по оси Y, две четверти круга идеально совпали бы.

Нас интересуют четыре типа симметрии:

(1) симметрия относительно оси y
(2) симметрия относительно оси x
(3) симметрия относительно начала координат
(4) симметрия относительно прямой y = x

Почему кого-то волнует симметрия?

Одна из причин заключается в том, что знание того, что график симметричен относительно линии, уменьшает объем работы, которую нужно сделать, чтобы описать кривую.Если вы пытаетесь описать, где на графике есть пик, впадина или разрыв, вам нужно будет исследовать только одну половину графика — другая половина графика (ее зеркальное отображение) будет просто дубликатом. Это может быть особенно полезно, если вы работаете в трехмерном пространстве, как это делается в многомерном исчислении.

Есть несколько уровней понимания симметрии, которые мы собираемся развивать в этом классе:

(1) общее понимание концепции, чтобы вы могли взглянуть на двумерный график и составить мнение относительно его возможной симметрии (относительно оси y, оси x, начала координат или y = x)

(2) пространственная перспектива, чтобы вы могли нарисовать эскиз графика, который был бы симметричен данному графику

(3) способность проверить уравнение графика на симметрию, прежде чем вы когда-либо увидите график.Последний особенно полезен, когда мы переходим к трехмерным графам, и симметрию сложнее определить, глядя на фигуру.

Это чтение предназначено, чтобы помочь вам развить интуитивное понимание симметрии в основу тестов на симметрию, которые мы используем для уравнений.

Графическое представление симметрии

Взгляните на этот график из пяти точек.Черная точка представляет исходную точку, а цветные точки демонстрируют четыре типа симметрии.

Черная и красная точки симметричны относительно оси y.
Черная и синяя точки симметричны относительно оси x.
Черная и зеленая точки симметричны относительно начала координат
Черная и розовая точки симметричны относительно y = x

Симметрия относительно оси Y

Посмотрите еще раз на черную и красную точки.Обратите внимание, что x-координаты являются аддитивно обратными друг другу. То есть, если b — координата x одной точки, то — b — координата x другой точки. Таким же образом мы проверяем уравнение кривой, чтобы убедиться, что кривая симметрична относительно оси y.

Проверка симметрии относительно оси Y: замените x на (-x). Упростите уравнение. Если полученное уравнение эквивалентно исходному уравнению, тогда график симметричен относительно оси y.

Пример: Используйте тест на симметрию относительно оси y, чтобы определить, симметричен ли график y — 5x ² = 4 относительно оси y.

исходное уравнение: y — 5x ² = 4

тест: y — 5 (-x) ² = 4

упростить: y — 5x ² = 4

Заключение: Поскольку результирующее уравнение эквивалентно исходному уравнению, график симметричен относительно оси Y

Симметрия относительно оси x

Проверка на симметрию относительно оси x аналогична предыдущей проверке.Посмотрите снова на черные и синие точки. Обратите внимание, что теперь y-координаты аддитивно инвертируют друг друга. То есть, если c — координата y одной точки, то — c — координата y другой точки. Таким же образом мы проверяем уравнение кривой, чтобы убедиться, что кривая симметрична относительно оси x.

Проверка симметрии относительно оси x: замените y на (-y). Упростите уравнение. Если полученное уравнение эквивалентно исходному уравнению, тогда график симметричен относительно оси x.

Пример: Используйте тест на симметрию относительно оси x, чтобы определить, симметричен ли график y — 5x ² = 4 относительно оси x.

исходное уравнение: y — 5x ² = 4

тест: (-y) — 5x ² = 4

упростить: — y — 5x ² = 4

Заключение: Поскольку результирующее уравнение НЕ эквивалентно исходному уравнению, график НЕ является симметричным относительно оси x

Вот набросок кривой.Тот факт, что кривая симметрична z относительно оси y и НЕ симметрична относительно оси y, довольно очевиден.

Симметрия относительно начала координат

Тест на симметрию относительно начала координат также имеет сходство с предыдущими тестами. Посмотрите на черные и зеленые точки. Обе координаты x и y являются аддитивными обратными. То есть (b, c) и (-b, -c) симметричны относительно начала координат.Вы можете думать о симметрии относительно начала координат как о отражении относительно оси y, а также оси x. Тест на симметрию относительно начала координат объединяет элементы из первых двух тестов.

Проверка симметрии относительно начала координат: замените y на (-y) И x на (-x). Упростите уравнение. Если полученное уравнение эквивалентно исходному уравнению, то график симметричен относительно начала координат.

Пример: Используйте тест на симметрию относительно начала координат, чтобы определить, симметричен ли график xy — 5x ² = 4 относительно начала координат.

исходное уравнение: xy — 5x ² = 4

тест: (-x) (- y) — 5 (-x) ² = 4

упростить: xy — 5x ² = 4

Заключение: Поскольку результирующее уравнение эквивалентно исходному уравнению, график симметричен относительно начала координат.

Вот набросок кривой. Мы должны сначала решить для y (в терминах x), чтобы использовать графический калькулятор.

На этот раз симметрию не так легко увидеть на эскизе.

Симметрия относительно прямой y = x

Для последней симметрии вернемся к черной и розовой точкам. В этом случае координаты x и y поменялись местами на . То есть (b, c) и (c, b) симметричны относительно прямой y = x. Большая часть нашей более поздней работы с этим типом симметрии будет связана с функциями.В этом случае нас будет интересовать создание уравнения, график которого симметричен (относительно y = x) с заданным графиком. Мы делаем это, меняя местами

x и y.

Пример: Создайте уравнение графика, которое будет симметричным

(около y = x) с графиком y = x ³ ,

для x> или = 0.

исходное уравнение: y = x ³

новое уравнение: x = y ³

решить относительно y: y = x ^1/3 , x> or = 0

Вот два графика.Обратите внимание, что они являются зеркальным отображением линии y = x.

Вы увидите гораздо больше этой симметрии, когда мы перейдем к обсуждению функций и их обратных.

© 1999 Джо Стейг

---

Симметрия | ZBrush Docs

Симметрия позволяет моделировать одну сторону модели и обновлять другую сторону с учетом ваших изменений. Есть три типа симметрии:

• • Симметрия по оси
  • Возможная симметрия
  • Радиальная симметрия

Элементы управления «Симметрия» находятся на палитре «Преобразование».

Симметрия поперек оси

Скульптура с X-симметрией

Симметрия по оси относится к ориентации вашей модели. Чтобы включить симметрию относительно оси:

1. 1. Нажмите Transform> Активировать симметрию .
   2. Нажмите X, Y или Z в зависимости от оси, по которой вы хотите отразить свои действия.

Возможная симметрия

Poseable Symmetry использует технологию ZBrush SmartResym для автоматического создания симметрии на основе топологии, а не мирового пространства.

Нормальная симметрия требует, чтобы модель имела одинаковую форму по осям X, Y или Z. Однако когда вы позиционируете модель, она перестает быть одинаковой по любой оси и не может быть симметрично скульптурирована с помощью инструментов нормальной симметрии.

Poseable Symmetry решает эту проблему, используя симметрию на основе вашей топологии. Топология должна быть симметричной относительно одной оси. Однако он не может быть симметричным относительно двух или более осей, таких как сфера или куб. Он не использует UV и на 100% зависит от топологической симметрии меша от одной стороны к другой.

Чтобы использовать Poseable Symmetry , просто выберите ось, по которой должна работать симметрия, в палитре преобразования. Затем нажмите Use Poseable Symmetry .

Следующие шаги подробно описывают процесс использования возможной симметрии:

1. 1. Нажмите «Преобразовать»> «Активировать симметрию».
   2. Установите Tool> Geometry> SDiv на самый высокий уровень разрешения, на котором вы будете лепить.
   3. Нажмите X, Y или Z в зависимости от оси топологии, по которой вы хотите отразить свои действия.
   4. Пресс-трансформация> Использовать возможную симметрию

• • Если топология модели не на 100% симметрична от одной стороны к другой, инструмент выйдет из строя.
  • Если ваша модель симметрична более чем по одной оси, она также выйдет из строя. Например, сфера симметрична по всем трем осям.

Возможная симметрия определяется радиусом зеленой кисти.

• • Если радиус кисти зеленый, у вас активна возможная симметрия
  • Если радиус кисти красный, у вас не активна возможная симметрия

Подсказки

Если вы разделите вашу сетку после установки Poseable Symmetry, вы вернетесь к нормальной симметрии. Просто нажмите Use Poseable Symmetry еще раз, чтобы вернуться к Poseable Symmetry.

Если вы сталкиваетесь с симметрией около 50% и ваша модель имеет n-угольники, возможно, что петля кромок вашей модели не на 100% одинакова от одной стороны к другой.

Если ваша модель пришла из более ранних версий ZBrush и имела n-угольники в базовой сетке, то петля ребер может быть непостоянной по оси. ZBrush имеет функцию при импорте OBJ с n-угольниками для создания симметричных треугольников.

Радиальная симметрия

Радиальная симметрия может быть активирована следующим образом:

1. 1. Нажмите Transform> Активировать симметрию .
   2. Нажмите X, Y или Z в зависимости от оси, по которой вы хотите отразить свои действия.
   3. Пресс-трансформация> R
   4. Установите Transform: Radial Count на количество раз, которое вы хотите симметрично отразить ваши действия вдоль поверхности.

советов по рисованию симметрии | Sciencing

На симметричном чертеже есть идентичные части, отражающие друг друга по линии симметрии. Эту симметрию можно найти во всей природе, включая человеческое тело, форму листьев и крыльев бабочки. Создание искусства, демонстрирующего симметрию, может быть трудным, поскольку две половинки, пересекающие линию симметрии, должны быть идентичны.Художник использует практику и несколько полезных руководств, чтобы рисовать симметричные изображения.

Практика зеркального отображения

Вы можете практиковать симметрию в рисовании, практикуясь с зеркалом. Проведите прямую линию с помощью линейки на вертикальной или горизонтальной оси. С одной стороны от прямой нарисуйте половину фигуры. Например, нарисуйте половину креста или сердечка. Используйте линейку, чтобы определить размеры нарисованной вами половинки. Используйте эти измерения, чтобы создать зеркальное отображение полуформы на другой стороне линии симметрии.Практикуйтесь в использовании различных форм, например, с прямыми линиями и углами, а также с изогнутыми линиями. Чем больше у вас будет практики с основными формами, тем лучше вы будете позже создавать более детализированные симметричные изображения.

Линии сетки

Сетки — еще один способ создания симметричных изображений. Нарисуйте сетку, используя отметки светлым карандашом и линейку. Важно, чтобы все линии сетки были прямыми, а прямоугольники были одинакового размера. Если коробки неправильные, рисунок тоже будет.Определите, какая линия сетки является центром или линией симметрии сетки. Нарисуйте половину изображения, которое вы хотели сделать. Используйте сетки как способ измерения расстояния от линии симметрии и размера объектов. Как только рисунок будет завершен, сотрите все линии сетки.

Произвольный набросок

Произвольный набросок также можно использовать для тренировки симметрии. Используйте изображение объекта в качестве ориентира и от руки нарисуйте основной контур объекта. Используйте легкие карандашные отметки, чтобы создать набросок от руки, потому что большая часть этих отметок будет стерта или изменена позже.Определите, где находится линия симметрии на объекте, и с помощью линейки проведите эту линию. Используйте набросок в качестве ориентира, чтобы добавить более подробные изображения на одну сторону линии симметрии. Создайте зеркальное отображение детального изображения на другой стороне линии симметрии.

Лица

Лица сложно нарисовать, и они редко бывают идеально симметричными. Однако вы можете попрактиковаться в рисовании симметричных лиц с помощью фотографий. Возьмите изображение лица и проведите вертикальную линию через центр носа, чтобы создать линию симметрии.Вырежьте изображение по этой линии. Прикрепите к изображению белый лист бумаги, чтобы нарисовать другую сторону лица. Вначале может быть полезно использовать технику сетки, чтобы запечатлеть все черты лица. По мере улучшения снимите сетку и нарисуйте зеркальное отображение лица.

Изучение художественных концепций — рабочие листы с линиями симметрии

Изучите концепцию симметрии с этими рабочими листами с линиями симметрии. Простые подсказки для рисования «половин» помогут вам, художники!

Что такое симметрия…

Симметрия — это качество изготовления одинаковых частей, обращенных друг к другу или вокруг оси.Симметрию можно увидеть везде — в природе, графическом дизайне, архитектуре, даже в людях. Как только ваши дети поймут, что такое симметрия, они смогут распознать ее, глядя на чужие работы, и использовать ее как инструмент в своих собственных работах.

Создавая симметричные изображения, которые составляют только половину, ваш молодой художник вдохновляется рисовать оставшуюся часть изображения.

Для большей симметрии художественных идей прочтите этот пост. Более элементарный рабочий лист симметрии плюс классический проект симметрии с полным видеоуроком завершат ваше исследование симметрии.

Различные виды симметрии….

Отражательная симметрия — линия может быть проведена посередине фигуры, а фигура на одной стороне линии «отражается» на другую сторону. Отраженная форма будет точно такой же, как оригинал.

Радиальная симметрия — состояние, при котором аналогичные части равномерно расположены вокруг центральной оси.

Существуют и другие, более специфические виды симметрии, такие как вращательная, двусторонняя и диагональная симметрия .На мой взгляд, понимание основных концепций отражающей радиальной симметрии упрощает понимание других концепций. Эти термины могут быть добавлены в словарный запас ваших студентов по мере необходимости.

Вы хотите сегодня взять эти рабочие листы симметрии….

Вы можете использовать их дома или в классе — бесплатно! Используйте форму ниже, чтобы стать подписчиком KTC. Затем проверьте свою электронную почту и подтвердите подписку. После подтверждения вы получите еще одно электронное письмо с паролем только для подписчика.Этот пароль откроет мою бесплатную библиотеку ресурсов, где вы найдете эскиз этих таблиц симметрии под заголовком «Элементы, принципы и связанные концепции». Щелкните миниатюру, и PDF-файл откроется.

Вы также получите доступ к сотням других бесплатных печатных форм, которые помогут вам проявлять творческий подход с вашими детьми. Кроме того, я работаю над тем, чтобы поделиться растущим числом цифровых ресурсов, таких как действия в Google Презентациях, которыми вы можете поделиться со своими детьми!

Подписавшись, вы также начнете получать мои электронные письма KTC.Мои новейшие веселые проекты и бесплатные ресурсы для печати будут доставлены прямо вам на почту!

Вы уже являетесь подписчиком Kitchen Table Classroom….

Если да, то вам не нужно подписываться снова, чтобы получить эти забавные листы симметрии. Просто используйте этот пароль подписчика для входа в систему и загрузки.

Если вы потеряли пароль, потому что вы человек, и это то, что мы делаем, не волнуйтесь! Проверьте нижнюю часть любого информационного бюллетеня от меня. Вы увидите ссылку на мою библиотеку ресурсов и пароль.

Знаете ли вы кого-нибудь еще, кому нужны эти рабочие листы с линиями симметрии? Поделись, пожалуйста!

Каждая публикация в социальных сетях помогает мне предлагать вам больше увлекательных проектов и бесплатных печатных листов искусства, подобных этим!

Техническая поддержка — The Molecular Symmetry Painter

Molecular Symmetry Painter — это приложение на основе Java, которое позволяет интерактивно рисовать элементы симметрии на молекулярных моделях в трех измерениях.Художник использует Jmol для молекулярной визуализации и был построен как открытый инструмент, позволяющий загружать любую молекулу и рисовать любой элемент. Художник может быть использован для обучения и практики основных концепций молекулярной симметрии. Его также можно использовать для подготовки высококачественных изображений и презентаций.

Системные требования для использования Molecular Symmetry Painter

1. Браузер: Internet Explorer версии 7.0 или выше

2. Java JRE 5.0: Требуется для трехмерного просмотра молекул. Чтобы загрузить и установить обновление 5 среды выполнения J2SE 5.0, щелкните здесь.

При входе в Molecular Symmetry Painter может появиться следующее сообщение:

Щелкните Run , чтобы разрешить загрузку молекул с персонального компьютера пользователя. Щелкните Отмена , чтобы отключить эту опцию и работать только со встроенной молекулярной базой данных.

Экран для рисования молекулярной симметрии

Экран программы Molecular Symmetry Painter разделен на несколько областей:

1. Область Commands расположена в левой части экрана и содержит меню для выбора молекулы и элементов для рисования.
2. Область Display находится в центре экрана. Он содержит окно Jmol , в котором отображается молекула. Название молекулы отображается в теге над окном. Щелчок правой кнопкой мыши внутри окна Jmol открывает меню Jmol. Чтобы получить справку по этому меню, перейдите на страницу справки Jmol, щелкнув знак вопроса в левом верхнем углу экрана. Над окном Jmol есть две кнопки отображения:
   Нажмите эту кнопку, чтобы отобразить декартову систему координат.Щелкните еще раз, чтобы скрыть это.
   Нажмите эту кнопку, чтобы переключаться между отображением мяча и клюшки и отображением каркаса.
3. Окно History находится в правой части экрана и позволяет отображать или скрывать элементы, созданные пользователем.

Работа с программой Molecular Symmetry Painter

Обратите внимание: значок вопросительного знака на каждом шаге отображает краткое объяснение шага при наведении курсора мыши.

Шаг 1. Выбор молекулы

Щелкните стрелку, чтобы просмотреть список молекул, доступных в базе данных Painter. Молекулы расположены в алфавитном порядке их химической формулы. Выберите молекулу, которая будет отображаться в окне Jmol .

Комментарий: Чтобы загрузить молекулу с персонального компьютера пользователя, выберите «Обзор» в конце списка. Откроется окно просмотра, из которого можно перейти в конкретный каталог и выбрать файл.Молекулы могут отображаться в различных химических форматах. Обновленный список молекулярных форматов файлов см. На http://jmol.sourceforge.net.

Шаг 2: Выбор элемента

Выберите элемент, который хотите нарисовать:

Выберите Axis для создания оси, Plane для создания плоскости и Point для создания точки.

Откроется таблица координат для выбранного элемента. Для оси таблица включает две линии (см. Изображение ниже), для плоскости — три линии, а для точки — одну линию.

Шаг 3: Ввод координат

Рисование элемента симметрии требует определения точек на этом элементе. Одна точка необходима для определения точки инверсии, а две — для оси вращения. Для зеркальной плоскости необходимы три точки, которые не находятся на одной прямой. Чтобы выбрать координаты, выполните следующие действия:

1. Посмотрите на молекулу и попробуйте решить, через какие точки проходит элемент симметрии. На сложных органических молекулах атомы водорода могут быть скрыты для лучшего обзора молекулярного скелета.Щелкните правой кнопкой мыши в окне Jmol и перейдите по меню:

   Стиль → Атомы → Показать атомы водорода

   
   
2. Выберите этот вариант еще раз, чтобы показать атомы водорода.
3. Щелкните этот значок над окном Jmol, чтобы отобразить молекулу в каркасном формате с порядковыми номерами атомов.
4. Щелкните этот значок над окном Jmol, чтобы отобразить декартову систему координат.
5. Выберите точки, через которые проходит элемент.Обратите внимание, что каждая точка может быть одним из трех вариантов:
   1. Атом в молекуле (например, C1, h3, O3)
   2. Середина между двумя атомами (например, между C2 и H5)
   3. Любая другая точка в пространстве
   
   

Каждая точка в таблице представляет собой точку в пространстве. В левой ячейке каждой строки выберите тип точки (атом, средняя точка между атомами или введите координаты вручную).

Заполните остальные ячейки в строке:

1. Atom — Щелкните левой кнопкой мыши по выбранному атому в окне Jmol.Тип атома и его координаты появятся в таблице. Например:
   
2. Средняя точка между атомами — Щелкните левой кнопкой мыши по двум атомам в окне Jmol. Имена атомов и координаты точки появятся в таблице. Например:
   
3. Ввести координаты вручную — введите значения x, y и z точки в соответствующие ячейки. Декартова система координат (объясненная выше) может помочь в выборе правильных значений.

Шаг 4: Представляем элемент симметрии

Когда таблица будет заполнена, нажмите кнопку создания, чтобы отобразить элемент в молекуле.

Обратите внимание, что после нажатия кнопки создания имя элемента появляется в окне истории. Например:

Шаг 5: Переход между элементами

Molecular Symmetry Painter позволяет создавать множество элементов симметрии и перемещаться между ними через окно истории.Отображение всех элементов, созданных пользователем, является настройкой по умолчанию. При выборе другой молекулы список истории удаляется. Чтобы просмотреть конкретный элемент симметрии, щелкните его имя в окне истории. Используйте клавишу Shift, чтобы выбрать несколько элементов. Чтобы скрыть все элементы симметрии, щелкните слово «История».

Обратите внимание: для каждой молекулы, отображаемой в окне Jmol, можно нарисовать любое количество осей и плоскостей, но только одну точку инверсии.

Шаг 6: Тест

Используя определенные команды Jmol, пользователи могут отображать фактические элементы симметрии и сравнивать их со своими собственными элементами.Если фактические элементы и элементы пользователя совпадают, элементы пользователя верны.

В меню Jmol щелкните Console , чтобы открыть окно командной строки. В нижней части окна введите одну из следующих команд:

Команда	Результат
вычислить POINTGROUP	Имя группы симметрии отображается в верхней части окна консоли.
нарисовать POINTGROUP X где X — одно из следующих: Cn, C2, C3, C4, C5, C6, C8, Sn, S3, S4, S5, S6, S8, S10, S12, Cs, Ci	Отображаются все элементы симметрии определенного типа. Например, draw POINTGROUP C2 вызывает отображение всех возможных осей C 2 ; draw POINTGROUP C3 2 рисует только вторую ось C 3 .
розыгрыш POINTGROUP	Отображаются все элементы симметрии молекулы.
нарисовать УДАЛИТЬ	Все элементы удаляются, включая элементы, созданные пользователем.

Симметрия в искусстве с использованием Autodesk SketchBook

Об авторе

Мари-Ли — исследователь мира изобразительного искусства и начинающий дизайнер / художник. Она любит путешествовать по миру и узнавать обо всех культурах и историях каждого места.Мари-Ли — инук, выросла в провинции Квебек, но сейчас живет в Икалуите, Нунавут.

Художественный дизайн

Руководство

---

Введение

Вы когда-нибудь смотрели на домашнее задание по математике и думали, что оно красивое? Возможно, вы так не думаете, но математики находят красоту не только в математических вычислениях, но и в геометрических объектах, обладающих симметрией.Симметрия — это слово из греческого языка, которое означает «иметь согласие в размерах и пропорциях». Симметрия встречается во многих областях, таких как природа, архитектура, музыка и математика. У объекта может быть много типов симметрии, но сегодня мы сосредоточимся на отражающей или зеркальной симметрии, чтобы помочь нам создать цифровое искусство, вдохновленное цветочными рисунками / бисером.

Словарь

• Прозрачность: , сколько света может пройти через изображение.
• Непрозрачность: В графическом дизайне это означает, насколько прозрачным является изображение.Чем больше непрозрачность изображения, тем меньше оно прозрачности.
• Эллипс: геометрическая форма, которая выглядит как овал или сплющенный круг.
• Motif: декоративный рисунок или узор.
• Ось, множественное число осей: воображаемая линия, фиксируемая с целью измерения координат. В двухмерных плоскостях есть горизонтальная ось X и вертикальная ось Y

• Симметрия: 2D-объект является симметричным, если вы можете провести через него линию, и обе стороны линии выглядят одинаково.В математике это объект, который не изменяется, когда он претерпевает преобразования, такие как отражение, вращение, перемещение и масштабирование.
  • Вращательная / радиальная симметрия: Объект или изображение обладают вращательной симметрией, когда они выглядят одинаково после некоторого вращения вокруг центральной оси.

Эти снежинки радиально симметричны по 6 осям

• Двусторонняя симметрия: На этих изображениях показаны примеры двусторонней симметрии, поскольку обе половины изображения с каждой стороны оси идентичны.

Симметрия в природе

Эта морская звезда имеет радиальную симметрию

У этого тигра двусторонняя симметрия рисунка меха

Симметрия в искусстве

Christi Belcourt, Water Song , (2010–11).

---

Материалы

Загрузить Autodesk SketchBook

---

Компьютерная активность

1. Откройте Autodesk Sketchbook и узнайте расположение ваших инструментов, посмотрев на панель инструментов в верхней части экрана.

2. Выберите кисть, чтобы рисовать точками. В правой части нашей панели инструментов нажмите кнопку Brush Palette . Это откроет окно с различными вариантами кисти.

3. Теперь мы установим размер и непрозрачность нашей кисти. Дважды щелкните кнопку шариковой ручки, чтобы открыть окно свойств кисти. Здесь вы найдете базовую вкладку и расширенную вкладку. На основной вкладке у нас есть два ползунка для регулировки размера и непрозрачности (темноты) наших мазков кисти.Установите ползунок размера на максимум (4,0) и непрозрачность на 100%

4. Теперь мы установим интервал между мазками. Щелкните вкладку «Дополнительно», и вы найдете различные раскрывающиеся меню. Нажмите «Штамп», и появится ползунок «Интервал». Установите значение 10. Это добавит пробел между мазками кисти и создаст точечный вид.

5. Нажмите кнопку редактора цвета на панели инструментов. Это откроет редактор цвета, который изменит цвет наших мазков.Выберите черный.

6. Мы будем использовать некоторые вспомогательные инструменты, которые помогут нам создавать формы круга. Эти пунктирные круги помогут нам рисовать формы и сохранять их пропорциональными. На панели инструментов выберите инструмент эллипс. Сдвиньте его к середине страницы, нажав кнопку в центре, и перетащите его в середину страницы. Чтобы нарисовать круг, нажмите и удерживайте кнопку мыши и перетащите ее по направляющей круга.

7. Теперь мы увеличим нашу направляющую круга, чтобы нарисовать больший круг снаружи.Нажмите левую кнопку и перетащите круг / кнопку, чтобы сделать круг побольше.

Повторите шаги 6 и 7, чтобы сделать еще два круга, так что всего у вас будет три круга. Должно получиться так:

8. Закройте направляющую, нажав кнопку X в нижней части инструмента направляющей эллипса.

9. Теперь мы можем начать рисовать цветочные узоры с помощью инструмента симметрии на нашей панели инструментов. Выберите кнопку симметрии.Это откроет разные варианты. Мы выберем Симметрию Y и Симметрию X. Это покажет пунктирную линию на осях x и y с кнопкой, где они пересекаются. Нажмите эту кнопку, чтобы перетащить наши линии симметрии к центру наших кругов.

10. Теперь мы будем использовать чернильное перо, чтобы нарисовать контур нашего дизайна. Выберите чернильное перо в параметрах кисти и дважды щелкните, чтобы открыть свойства. Измените размер на 3,0.

11. Добавьте несколько длинных лепестков, щелкнув левой кнопкой мыши и перетащив мышь от центра нашего первого круга вверх, пока мы не дойдем до второго.

Нарисуйте ту же фигуру по горизонтали слева направо.

12. Продолжайте добавлять формы в свой дизайн, например, эту форму сердца. Начиная с центрального круга, проведите прямую линию между двумя лепестками.

Добавьте вторую линию, чтобы сделать основу сердца.

Нарисуйте верхнюю часть сердца изогнутыми линиями

Отлично, давайте добавим немного листьев. Чтобы повернуть страницу, удерживайте клавишу пробела, щелкните и перетащите страницу, чтобы переместить ее.Мы нарисуем две слегка изогнутые линии от второго круга к третьему, чтобы получился наш первый лист.

На каждой стороне этого первого листа добавьте форму второго листа.

Вот наш готовый план!

13. Теперь мы заполним фигуры в нашем дизайне с помощью инструмента заливки заливкой. Нажмите кнопку ведра на панели инструментов и выберите нужный цвет с помощью редактора цветов.

Продолжайте и залейте остальную часть вашего дизайна цветом!

Если вы допустили ошибку, нажмите Ctrl-Z на клавиатуре, чтобы отменить действие, или вы можете использовать красную стрелку на панели инструментов.

---

Заключение

Мы хотим видеть то, что вы создаете! Сделайте фото или видео и поделитесь с нами своей работой по электронной почте [email protected] или отметив @pinnguaq в Facebook, Twitter или Instagram. Не забудьте добавить хэштег #LearnWithPinnguaq!

---

Ресурсы

Дизайн, вдохновленный Эруомой Авашиш

Подробнее о традиционном искусстве

Посмотреть наш план урока «Создание традиционного метис-точечного искусства»

Ресурсы социальных сетей

---

Поделитесь своим мнением!

Не могли бы вы уделить время заполнению нашего опроса? Это позволит нам лучше понять типы интересующего вас контента, чтобы мы могли создавать больше подобных ресурсов в будущем.