Конспект урока математики «Равенства. Неравенства» 1 класс
Черняева Валентина Викторовна
Учитель начальных классов
ГУ «Средняя общеобразовательная школа- гимназия №9» г.Павлодара
Класс 1
Краткосрочное планирование по теме:
РЕВЕНСТВА. НЕРАВЕНСТВА.
Цели: Формировать понятие о равенстве и неравенстве групп предметов по количеству, способность к записи результатов сравнения с помощью знаков «больше», «меньше», «равно», распознавать среди математических записей равенства и неравенства, составлять равенства и неравенства
Развивать восприятие, внимание, мышление, навыки работы в паре, группе
Воспитывать интерес к математике, умение адекватно оценивать свою деятельность на уроке и деятельность товарищей
Ожидаемый результат:
А: знать, что такое равенство и неравенство
В: уметь соотносить и составлять равенства и неравенства, применять полученные знания на практике
С: уметь выражать свои мысли, формулировать затруднения, работать в паре, группе
Ресурсы: учебник, видеоурок «Равенства и неравенства» https://www.
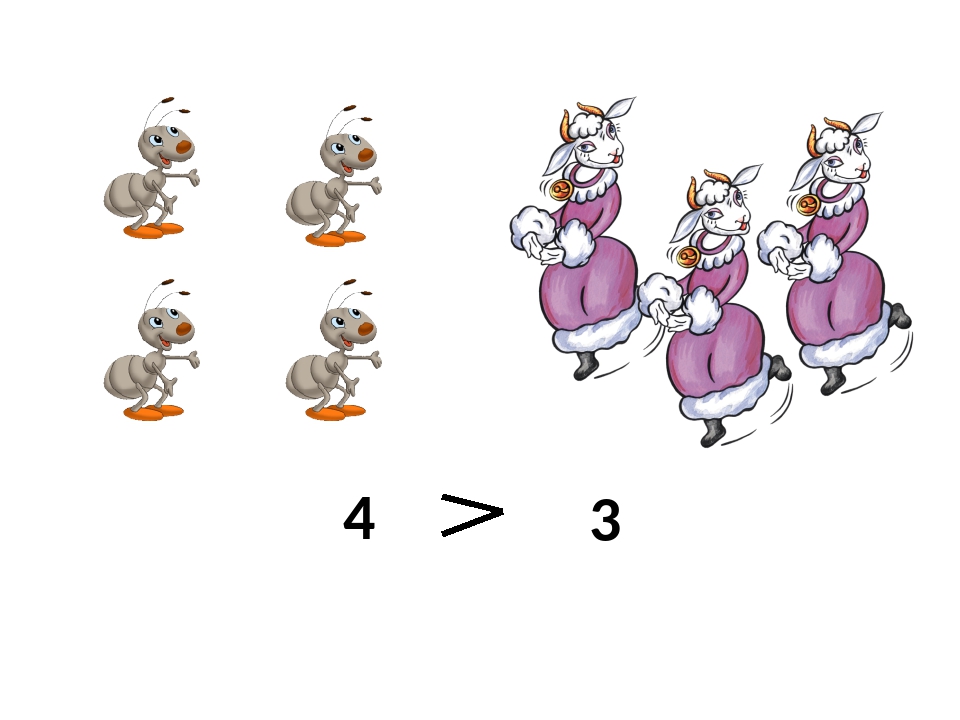

Просмотр содержимого документа
«Конспект урока математики «Равенства. Неравенства» 1 класс »
Черняева Валентина Викторовна
Учитель начальных классов
ГУ «Средняя общеобразовательная школа- гимназия №9» г.Павлодара
Класс 1
Краткосрочное планирование по теме:
Ревенства. НЕравенства.
Цели: Формировать понятие о равенстве и неравенстве групп предметов по количеству, способность к записи результатов сравнения с помощью знаков «больше», «меньше», «равно», распознавать среди математических записей равенства и неравенства, составлять равенства и неравенства
Развивать восприятие, внимание, мышление, навыки работы в паре, группе
Воспитывать интерес к математике, умение адекватно оценивать свою деятельность на уроке и деятельность товарищей
Ожидаемый результат:
А: знать, что такое равенство и неравенство
В: уметь соотносить и составлять равенства и неравенства, применять полученные знания на практике
С: уметь выражать свои мысли, формулировать затруднения, работать в паре, группе
Ресурсы: учебник, видеоурок «Равенства и неравенства» https://www. youtube.com/watch?v=FzgppzPRfIM, презентация для устного счёта
youtube.com/watch?v=FzgppzPRfIM, презентация для устного счёта
Этапы урока Используемые модули | Деятельность учителя | Формы работы | Деятельность учащихся | Оценивание |
Организационный этап НП – создание колаб.среды | Приём «5 пожеланий» | Прикасаются каждым пальчиком к пальчикам соседа, и высказывают ему пожелания | ||
Актуализация знаний ИКТ — презентация | Устный счёт 1.Каждый вариант получает лист А4 с примерами: 4+2= 9-1= 5-2= 8-2= 2+1= 5+2= 6-1= 7-1= 11-1= 7+1= 10+1= 9+1= 4+2= 9+2= 2. | ПР ФР | Решают на скорость, проверяют с помощью анимации в презентации 10 | Взаимооценивание смайликами |
Ориентационный этап Учёт ВО –задания в соотв с возрат. УиЛ – уч-уч при группой работе | 1.Сравнение чисел 1 * 1 2 * 3 4 * 1 2 * 2 — Сравните числа. 1 = 1 2 1 2 = 2 — На какие группы можно разделить эти записи? — Как называются записи первой группы? Второй? — Как называется тема нашего урока? — Что мы должны знать и уметь к концу урока? | ГР | 1 = 1 2 = 2 — равенства 2 1 – неравенства ЗНАТЬ… УМЕТЬ… | Взаимооценивание «Сигналы рукой» |
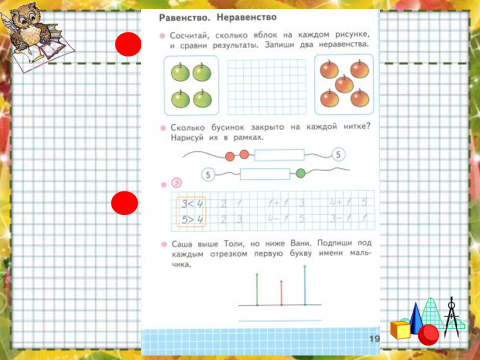
Операционный этап НП -ПР Физкультминутка ИКТ — видео | 1. — НА ГЛАЗ — ИЗМЕРЕНИЕМ — НАЛОЖЕНИЕМ — СОЕДИНИТЬ ПАРАМИ 2.Просмотр видеофильма «Равенства. Неравенства. — Посмотрите фильм и запомните ещё один способ сравнения чисел 3.Закрепление — Сравните числа с помощью числового луча, запишите равенства и неравенства в тетрадь. 2 * 4 4 * 3 3 * 3 1 * 2 — Вставьте числа, так, чтобы равенства и неравенства были верными. … …. 4.Работа по учебнику, с.46 №1 — Составьте равенства и неравенства по картинкам 5.Работа по уч Петерсон Л.Г. С.52 №2-5 ( в учебнике) | ПР ИР | Обсуждение в паре способов сравнения групп предметов, чисел,… Сравнение чисел с помощью числового луча Сравнивают числа, используя числовой луч | «Сигналы рукой» Самооценивание по готовому образцу Взаимооценивание «Сигналы рукой» |
Творческое задание Обучение ТиО –тв. | Известно, что В меньше А. Найдите знак для соотношения А и В. = | ГР | Взаимооценивание в группе | |
Итог урока | — Какую цель ставили на уроке? — Достигли ли мы цели? -Какое задание было трудным? — Над чем нам надо ещё поработать? | |||
Домашнее задание | П.с. 53 № 2,3,4,5* все в учебнике | |||
Рефлексия | Приём «Острова» |
Урок математики в первом классе(учебник А. А. Аргинской) по теме: «Преобразование равенств в неравенства и неравенств в равенства». | Методическая разработка по математике (1 класс) по теме:
Урок математики в 1 классе по системе Занкова.
Автор-составитель: Галицына Валентина Александровна- учитель начальных классов..
Тема: «Преобразование равенств в неравенства и
неравенств в равенства».
Цели и задачи: 1. Расширить представления учащихся о равенствах и неравенствах, способах преобразования равенств в неравенства и неравенств в равенства.
2. Развивать умения находить критерии оценки и сравнения объектов, строить логические цепочки рассуждений и доказательств.
3.Формирование межличностных отношений: сотрудничества в работе,
коррекции деятельности партнёров, оценки их деятельности.
- Организационный момент. (слайд 1)
— Ну-ка проверь, дружок,
Ты готов начать урок?
Всё ль на месте,
Всё ль в порядке,
Ручка, книжка, линейка,
Цифры, карандаш, тетрадка?
Все ли правильно сидят?
Все ль внимательно глядят?
Тут затеи, и задачи,
Игры, шутки, всё для вас!
Пожелаем всем удачи –
За работу, в добрый час
— Сегодня мы проведём цветочный урок — соревнование. Догадайтесь, как это: цветочный урок? (варианты ответов детей)
Догадайтесь, как это: цветочный урок? (варианты ответов детей)
— За каждую, хорошо выполненную работу вы получите один цветок в вазу для букета.( вывешиваются ваза)
2. Работа над каллиграфией. (Задание учебника №95.)
-Нарисуй цветок, потерявший лепесток.
-Напиши строку цифры, обозначающей количество оставшихся лепестков.
2 2 2 2 2 2 2 2 2 …
3. Разминка.
— Начинаем разминку.
а) — «Эстафета». (Дети выбегают по очереди, записывают значение одного выражения и передают эстафету следующему).
1-к: 3+4 2-к: 3+3
5+1 4+1
6-5 4-3
5+2 7-6
6+3 5+4
2+3 1+4
4+2 3+2
7+1 6+1
б) – Эксперты проверяют работу команд и подчеркивают неверные равенства.
А команды в это время получают от меня по 2 задания: приготовьте цифры.
а) 1 команда: Стали числа танцевать:
2 плюс 3, конечно…5!
3 плюс 2 – …тоже 5
Получается опять…
— Почему? ( Применили переместительное свойство сложения)
2 команда: 3 плюс 5 равно …8.
Быстро кружатся они –
Получилось 5 плюс 3…
8, что ни говори!
— Почему? Как называются выражения, о которых я прочитала вам стихи? (Это суммы).
б)1-команда: Что такое 3 и 5? (слагаемые)
2-команда: Как назвать 8?(значение суммы)
(Команды получают цветы за выполненные задания и крепят их в свои вазы на доске)
3.Работа над новым материалом.
а) — Измените неверные равенства так, чтобы записи стали верными. Что можно изменить? Что получится, если изменить знаки, а не числа? ( Выслушиваются и обсуждаются все предложения учеников: можно изменить одно из чисел, а можно знак равно на знак сравнения).
б) – А теперь внимание на экран (слайд 2- 4):
Задание №94.
(Выполняется задание в тетрадях, с комментированием. Команды работают по очереди. Цветок получает команда, не допустившая ошибок в постановке знаков).
Вывод: Чьи способы исправления вы нашли при работе над заданием «Эстафеты»?
4. Физ. минутка. «Непослушная голова», «Ребро, ладонь, кулак».
5.Выделение «лишнего» рисунка на основе анализа рисунков.
а) Задание учебника №96. ( слайд 5).
Запись: 3+5 3+2 4+4 5+3
— Сравни суммы.
б)1-команда: — Начерти отрезок, имеющий длину самого маленького значения суммы.
5см.
2-команда: — Начерти отрезок, имеющий длину равную большим значениям сумм.
8см…………………..
(Учитель просматривает работы в тетрадях и смотрит у какой команды меньше или совсем нет ошибок, той выдаётся цветок).
5.Развитие комбинаторного мышления.
Задание №98 (слайд 6).
6. Составление и работа с математическими рассказами. (слайд 7)
7. «Делу – время, потехе – час». (Компьютерная игра «Супердетки»). Цель: развитие внимания и логического мышления.
(Компьютерная игра «Супердетки»). Цель: развитие внимания и логического мышления.
8. Итог урока. Рефлексия.
-Чему научились? Нарисуйте на полях тетради смайлка, который подскажет мне как вы себя чувствовали на уроке.
— Проверяем букеты, выявляем победителей.
— Что будем делать с букетами? (Подарим их всем гостям и поздравим с наступающим женским праздником).
Тетрадкин Град — Урок математики в 1 классе «Равенство. Неравенство»
Основное меню
- Главная страница
- Оценка деятельности руководителя общеобразовательной организации
- Техники запоминания
- Мнемонические фразы для школьников
- Противодействие жестокому обращению с детьми
- Странные и необычные предметы в школах мира
- Стихи про школьные предметы
Конспекты уроков
- Начальные классы
- Русский язык
- Литература
- Иностранный язык
- История
- Обществознание
- Биология
- Экология
- География
- Математика
- Информатика
- Физика
- Химия
- ОБЖ
- Физкультура
- Инклюзивное обучение
- Классный час
- Внеклассные мероприятия
Начальная школа
- Обучение грамоте
- Задания по обучению грамоте
- Дидактические игры по обучению грамоте
- Русский язык
- Словарная работа
- Тренажер «Написание словарных слов»
- Тексты для списывания
- Творческие задания по русскому языку
- Карточки по русскому языку для начальной школы
- Шарады, кроссворды, ребусы по русскому языку
- Математика
- Задачки по математике в стихах
- Занимательные задачки по математике
- Веселые рифмованные задачки
- Задания по математике для одаренных учеников
- Заниматика по математике
- Окружающий мир
- Как устроен человек
- Если хочешь быть здоров
- Знакомство со Вселенной
- Задания по окружающему миру «Природные сообщества»
- Задания по ОБЖ для 1-2 классов
- 10 000 заданий и упражнений для четвероклассника
- Викторины для младших школьников
- Игры для организации подвижной переменки в начальной школе
Русский язык
- Педагогическая симптоматика трудностей при изучении русского языка
- Игровые технологии на уроках русского языка
- Орфоэпия
- Речь учащихся: о причинах смещения орфоэпических норм
- Мнемонические карточки по орфоэпии
- Задания по орфоэпии
- Тесты «Языковые нормы»
- Сказка-быль в орфоэпических тонах «Сливаться или сочетаться»
- Конкурс для школьников «Рекламный»
- Фразеология
- О происхождении фразеологизмов
- Фонетика и графика
- Задания по теме «Фонетика»
- Контрольно-тренировочные упражнения по теме «Фонетика»
- Неправильные правила, или Как запомнить словарные слова
- Лексика
- Обогащение словарного запаса на уроках русского языка
- Задания по теме «Омонимы»
- Задания по теме «Синонимы»
- Задания по теме «Стилистически нейтральные синонимы»
- Историзмы и архаизмы
- Слова, утратившие первоначальный смысл
- Шпаргалка для школьника
- Рабочая тетрадь «Лингвистическая разминка».
 5 класс
5 класс - Лингвистические задачки
- Приемы обучения орфографии на уроках русского языка
- Нескучные уроки практической грамотности
- Тест «Знаете ли вы, как пишутся эти слова?»
- Изучение лексики, орфографии и пунктуации на материале пословиц и поговорок
- Морфология
- Жизнь языка: части речи
- Глагол и его формы. Обобщение материала
- «Наречие». Обобщение материала
- Предлоги: проблемы изучения и обучения
- Тренинги «Служебные части речи»
- Как различать грамматические омонимы?
- Карточки по русскому языку
- Синтаксис
- Задания по теме «Простое осложнённое предложение»
- Задания по теме «Словосочетание и предложение»
- Фразы, которые ошибочно считают вводными
- Задания по пунктуации.
 9 класс
9 класс - Задания на умение находить и классифицировать синтаксические ошибки
- Задания по теме «Вводные слова и предложения»
- Работа с текстом
- Как построить работу с текстом
- Метапредметный подход в работе с текстом
- Задания на умение работать с текстом
- Предтекстовая работа по осмысленному восприятию художественного текста
- Изложения
- Русский язык. Повторяем и закрепляем
- Культура речи
- Как говорить по-русски правильно
- Классификация речевых ошибок
- Факторы загрязнения речи
- Многословие ведет к ошибкам
- Задания на исправление речевых ошибок
- Тонкости этимологии слов
- Учимся писать сочинение
- Пишем сочинение: правила и раскрытые темы
- Сочиняем собственный текст: советы
- Тесты по русскому языку
- 5 класс
- 6 класс
- Проверочные работы по русскому языку
- 5 класс
- 6 класс
- 7 класс
- Задания по русскому языку
- Банк заданий «Выразительность русской речи»
- Игры и нестандартные задания на уроках русского языка
- Задания для грамотеев по русскому языку
- Тренировочные задания по русскому языку
- Дидактический материал по русскому языку.
 8 — 11 классы
8 — 11 классы - Система упражнений «Поиск и исправление грамматических ошибок»
Литература
- Учителю литературы
- Тематическое планирование по литературе 5 класс
- Изучение обзорных тем в школьном курсе литературы
- Опорные схемы по литературе
- Смысловое чтение при изучении биографии писателя
- Проблемное обучение на уроках литературы
- Изучение творчества писателя в школе
- Изучение творчества Крылова
- Изучение творчества Чехова в школе
- Методические аспекты изучения повести Пушкина «Капитанская дочка»
- Методические рекомендации по изучению повестей о любви А.
 И. Куприна в школе
И. Куприна в школе - Изучение творчества Татьяны Толстой в школе
- Занимательно о классиках литературы
- Эссе о русских писателях
- Изучение литературных произведений
- Прототипы литературных героев
- Внеклассные мероприятия по литературе
- Литературно-лингвистический конкурс для школьников. 5-8 классы
- Читательская грамотность
- Совершенствование читательской грамотности при работе с текстом
- Реализация проекта «Семейное чтение»
- Пословицы и поговорки
- Расшифтуйте пословицы и поговорки
- Продолжение известных пословиц и поговорок
- Сказки
- Зашифрованные послания для взрослых в сказке «Алиса в Стране чудес»
- Тест «Чем на самом деле закончились всем известные сказки?»
- Карточки по литературе
- Литературные диктанты по зарубежной литературе
- Лабораторные работы по литературе.
 7 класс
7 класс - Наш Пушкин
- В садах Лицея. На брегах Невы
- Михайловское в судьбе Пушкина
- Город Пушкина
- Развитие речи на уроках литературы
- Изобразительно-выразительные средства в художественном произведении. Задания
- Фразы-клише по элементам структуры эссе
- Цитируем классиков
- Занимательный материал к урокам литературы
- 5 класс
- 6 класс
Сложное неравенство — математика с отличием, часть 1 — оценка ppt скачать
Презентация на тему: «Сложные неравенства — Часть 1 с отличием по математике — 8 класс» — стенограмма презентации:
1 Сложные неравенства — Часть 1 с отличием по математике — 8 класс
2
Приготовьтесь к уроку Американские горки Mind Eraser в Six Flags в Балтиморе, штат Мэриленд, представляют собой американские горки с перевернутой стальной гусеницей. 3
Составное неравенство, содержащее и Два неравенства, соединенных словом и образующих составное неравенство.Составное неравенство, содержащее «и», верно только в том случае, если верны оба неравенства. Его график является пересечением графиков двух неравенств. Решение должно удовлетворять обоим неравенствам. Сложное неравенство, к которому присоединяется слово И, называется союзом. 4
Изобразите множество решений составного неравенства. x -2 Изобразите 1-е неравенство. x <3 Изобразите 2-е неравенство. x> -2 Найдите пересечение. 5
Изобразите множество решений составного неравенства. p 2 Изобразите 1-е неравенство. p <6 Изобразите 2-е неравенство. p> 2 Найдите пересечение. Где пересекаются графики? Это представляет собой перекресток. Набор решений: 2 6
Изобразите множество решений составного неравенства.-5 7
Изобразите множество решений составного неравенства.6 При работе с неравенствами, включающими показатели степени, эти неравенства ведут себя во многом как традиционные уравнения.Неравенства с четным показателем обычно имеют два решения, а неравенства с нечетным показателем имеют одно решение. Неравенство с нечетным показателем ведет себя точно так же, как неравенство без показателя или традиционное уравнение с нечетным показателем. Единственное предостережение — которое также относится к неравенствам без показателей — это то, что вы должны знать знак переменной, прежде чем вы сможете делить или умножать ее (см. Умножение и деление с неравенствами). x 3 <27 2x 3 + 14> 30 Как указано выше, неравенство с четным показателем обычно имеет два решения. Причина в том, что x может быть как положительным, так и отрицательным. Следовательно, при вычислении четного показателя в неравенстве мы имеем дело с двумя случаями: x положительно, x отрицательно. Случай 1: x положительный Случай 2: x отрицательный Решение можно представить графически. 3x 2 <27 Множественные неравенства с показателями решаются так же, как решаются множественные неравенства без показателей. 1.) Решите каждое неравенство отдельно. x 2 <9 2.) Объедините каждое неравенство и найдите перекрытие (т.е. области, в которых каждое неравенство выполняется — эта область является решением). Область перекрытия, то есть решение набора неравенств — это где x <2 и x> -2 Для многих студентов вышеуказанный набор неравенств лучше всего можно понять графически. Решением множества неравенств является перекрывающаяся графическая область. На этой странице рассказывается о решении неравенств. После изучения этого раздела вы сможете: Неравенства: квадратичные выражения Когда вы решаете неравенства, это точно так же, как если бы вы решали алгебраические уравнения. x 2 + 4x + 1 <–2 Не забывайте обращаться со знаком неравенства как со знаком равенства. Это дает нам x 2 + 4x + 1 = –2 Первое, что вам нужно сделать, это переставить неравенство (уравнение) так, чтобы оно имело вид ax 2 + bx + c = 0. Все, что вам нужно сделать, это перенести –2 в левую часть. Это дает нам x 2 + 4x + 3 = 0. Мы можем разложить это уравнение на две скобки: (x + 3) (x + 1) = 0 Решениями этого квадратного уравнения являются –3 и –1. Затем мы можем подумать о наброске этого уравнения: Вот как будет выглядеть кривая, если мы ее начертим (обратите внимание также на общую U-образную форму). Теперь мы должны рассмотреть исходное неравенство. Помните, что исходное неравенство было следующим: (x + 3) (x + 1) <0 Это часть графика, которая находится ниже линии y = 0 (заштрихована). Это означает, что решение этого неравенства: –3 Подумайте, какие части графика удовлетворяют этому неравенству: (x + 3) (x + 1)> 0 Неравенства по одной переменной ≤ означает «меньше или равно» ≥ означает «больше или равно» Неравенства могут отображаться числовыми линиями. Первое неравенство охватывает целые числа -1, 0, 1. Второе неравенство охватывает только 3. Правила манипулирования неравенствами аналогичны правилам для уравнений, за исключением того, что умножение или деление каждой стороны на отрицательное число изменяет направление знака неравенства. Примеры: а) Решите неравенство 4 (х-2)> х + 10 4x — 8> x + 10 (развернуть скобку) 4x> x + 18 (прибавить 8 к обеим сторонам) 3x> 18 (вычесть x с обеих сторон) x> 6 (разделить обе стороны на 3) б) Решить 1/3 (4 — 4а) ≤ 8 4-4a ≤ 24 (умножить обе стороны на 3) -4a ≤ 20 (вычтем 4 с обеих сторон) -a ≤ 5 (разделить обе части на 4) a ≥ -5 (умножить обе стороны на -1) c) Найдите все возможные целые значения n, которые удовлетворяют 3n + 1 ≤ 27 <5n - 6. Разделение неравенств: 3n + 1 ≤ 27 2n ≤ 26, n ≤ 8,66666, поэтому n = 8, 7, 6, 5,… 27 <5n - 6 33 <5n, n> 6,6, поэтому n = 7, 8, 9,… Целые числа, удовлетворяющие обоим значениям 7 и 8. ПРИМЕЧАНИЕ: Неравенства по двум переменным Для неравенства с двумя переменными: 2x — y> 1. Ниже приведен график для 2x-y = 1. Формулу можно изменить как y = 2x -1 и получить прямую линию. ПРИМЕЧАНИЕ. Помните, что уравнение в форме y = 2x — 1 имеет градиент 2 и точку пересечения y (где оно пересекает ось y) равное –1, На приведенном ниже графике показана линия 2x-y = 1, в то время как область под линией охватывает значения 2x-y> 1, а область выше покрывает 2x-y <1. Могут отображаться одновременно несколько неравенств. Заштрихованная область удовлетворяет условиям y ≤ x, x + y ≤ и y ≥ 1. Если вы изучаете у нас продвинутую алгебру, то наверняка возникнет тема алгебраических неравенств. Обязательно начните с первой части перед просмотром этого видео, которое является второй частью нашего обсуждения. В этом видео мы поговорим еще о нескольких идеях, связанных с неравенством.Прежде всего, предположил, что в задаче задано более одного неравенства. Что нам разрешено делать с двумя отдельными неравенствами? Итак, комбинируя неравенства, если у нас есть два уравнения, прежде всего a = b и b = c, мы, безусловно, можем объединить их, чтобы получить a = c технически, что называется транзитивным свойством равенства. Примерно так же, если мы знаем, что r меньше s, а s меньше t, мы можем сделать вывод, что r меньше s меньше t, и, следовательно, r меньше t.Итак, это тоже транзитивное свойство. Обратите внимание, что для того, чтобы комбинация работала, общий термин s должен быть больше одного члена и меньше другого, и это очень, очень важно. Если один и тот же термин больше, чем оба других условия, или меньше, чем оба других термина, мы не можем сделать какой-либо вывод. Если c меньше f, а d также меньше f, мы знаем, что c и d меньше f, но мы не знаем, как они сравниваются друг с другом. Так, например, если f равно 100, то оба числа c и d меньше 100, но нам ничего не известно, какое из них больше другого. Вторая проблема, добавление неравенства. Напомним, что нам разрешено складывать или вычитать любые два уравнения. Оказывается, уравнения в этом отношении очень просты. С неравенством нам нужно быть более осторожными. Предположим, у нас есть два неравенства: a меньше b и c меньше d. Какие виды сложения и вычитания разрешены? Прежде всего, мы можем добавить неравенства с тем же направлением. Другими словами, неравенства указывают в одном направлении.Итак, если a больше b и c больше d, то мы можем просто сложить их вместе. A + c должно быть больше, чем b + d. И в этом есть смысл, что если мы сложим две большие вещи, получится больше, чем сумма двух маленьких вещей. Например, 5 больше 2 и 11 больше 8, это два истинных неравенства. Мы можем добавить их, когда направления совпадают. Поэтому, когда мы добавляем, конечно, мы получаем еще одно истинное утверждение, 16 больше, чем 10. Мы не обязательно получим что-то разумное, если добавим неравенства, которые имеют разные направления. Так, например, эти два неравенства теперь мы перевернули, чтобы они имели противоположное направление. Сложив их, мы получим 13 с обеих сторон, и на самом деле это вовсе не неравенство, а уравнение. И если мы выберем разные начальные значения, мы сможем получить сумму, которая будет либо больше, либо меньше, либо равна. Значит, общего правила нет. Когда вы начинаете добавлять неравенства, где знак указывает в противоположных направлениях, в основном вы получаете математическую чепуху.Невозможно предсказать, что вы получите. Таким образом, в этом случае для вычитания неравенств мы не можем вычитать неравенства с одинаковым направлением. Итак, вот куча неравенств, это действительные неравенства, все выстроенные в одну линию с неравенствами в одном направлении. Обратите внимание, что если мы вычитаем, мы можем получить знак «меньше», «знак равенства» или «знак больше». Если мы вычтем неравенства в том же направлении, мы сможем получить любой из этих знаков. Опять же, это чисто математическая чепуха. Если вычесть два неравенства в одном направлении, невозможно предсказать, какие отношения получатся. Но в этом случае мы можем вычесть неравенства, имеющие противоположные направления. Итак, если a больше, чем b, а c больше, чем d, у нас нет возможности сравнить размер a-c с размером b-d. Изображение Neirfy Если мы сделаем большой минус большой и маленький минус маленький, что ж, трудно сказать, как это будет сравниваться. Но мы можем перевернуть последнее, сделать его d- c, а затем мы можем вычесть, a- d больше, чем b- c.Другими словами, большой минус маленький всегда будет больше, чем маленький минус большой. Итак, это работает. Подумайте об этом заявлении. Если a больше b, а d меньше c, тогда a- d больше b- c. Давайте рассмотрим числовые примеры, предположим, что a = 20, b = 15, c = 12 и d = 10. Ясно, что 20 больше 15, ясно, что 10 меньше 12, и когда мы вычитаем, получаем 10 больше 3. Обратите внимание, что результирующее неравенство следует направлению исходного неравенства, из которого мы вычитаем.Итак, это задает тон. То первое, из которого мы вычитаем, мы вычитаем из этого что-то в противоположном направлении. И результат, разница будет такая же, как у оригинала. Нет правил умножения и деления неравенств. Опять же, это всегда приводит к математической чепухе, вы не можете этого сделать. Вы можете подумать, что если бы a было больше, чем b, а c было больше, чем d, это всегда привело бы к тому, что x, умноженное на c, больше, чем b, умноженное на d.Почему бы не сделать так, чтобы большое, умноженное на большое, всегда больше, чем маленькое, умноженное на малое? Если бы мы могли гарантировать, что все числа положительные, тогда это сработало бы. Но рассмотрим этот пример: -10 явно меньше +2, а -8 явно меньше +3. Но если мы умножим, мы получим -8 умножить на -10, и отрицательное умножение на отрицательное даст нам положительное 80, которое больше, чем 6, 2 умноженное на 3, что равно 6. Итак, это пример, когда умножение двух кавычек, удаление меньших чисел в кавычки, отрицательное числа дает очень положительный, очень большой продукт. Изображение carmen2011 Если мы знаем, что число отрицательное, нам не нужно вычислять его точное значение. Мы точно знаем, что только по тому факту, что оно отрицательное, оно всегда меньше любого положительного числа.Также имейте в виду, что добавление любого положительного числа всегда увеличивает число. Так, например, x + 10 должно быть больше x. Фактически, любое положительное число может быть дробью x + две пятых должно быть больше x. Но точно так же, вычитание любого положительного или добавление любого отрицательного всегда делает число меньше. Таким образом, x должен быть больше, чем x- 3, вычитание 3 обязательно делает все меньше. Вот практическая задача. Поставьте видео на паузу, а потом мы поговорим об этом.В частности, это очень похожая на тест проблема. Это проблема, похожая на тест, потому что она разработана с некоторыми ловушками, которые могут наказать людей, которые очень наивно думают о числах. Кто думает, что все числа — это числа, которые они могут пересчитать на пальцах, они забывают о других видах чисел. Итак, во-первых, это первое утверждение действительно верно. Если мы прибавим 2, не имеет значения, является ли число положительным, отрицательным или дробным. Неважно, если мы прибавим 2, мы сделаем его больше.Таким образом, это всегда больше, чем x, и поскольку я должен быть включен в ответ, мы можем исключить ответ D, потому что он не включает I. Хорошо, а как насчет 2х? Всегда ли 2x больше x? Если вы думаете о положительных числах, здесь вы можете столкнуться с проблемой. Потому что, конечно, если вы удвоите любое положительное число, оно станет больше. 6 больше 3, 20 больше 10 и тому подобное. Проблема в том, что мы получаем отрицательные числа. Если у меня -10 и вдвое больше, то -20, -10 больше -20.Один из способов подумать об этом: что лучше: вы бы предпочли иметь 10 долларов в долгах или 20 долларов в долгах? Вам будет гораздо лучше в финансовом отношении, если у вас 10 долларов в долг, а не 20 долларов. Итак, можно думать об этом, -10 определенно больше, чем -20. Так что с отрицательными числами это просто не работает. Итак, II не всегда верно, и это означает, что мы можем исключить любой из ответов, которые включают II. Итак, теперь мы подошли к A и C. Наконец, квадрат x. Это особенно сложно, потому что, конечно, с большинством положительных чисел вы возводите его в квадрат, и оно становится больше.А отрицательные числа возводят в квадрат отрицательное, и оно становится положительным. Так что, конечно, это больше еще и потому, что любое позитивное больше негативного. Так что может показаться, что все готово. Прежде всего, обратите внимание на пару чисел, которые мы возведем в квадрат как 1 и 0. Возводим 1 в квадрат, получаем 1, если возводим в квадрат 0, получаем 0. Что ж, это не неравенство, это равенство. 1 в квадрате равно 1, оно не больше 1. А также подумайте о десятичной дроби между 1 и 0. Если возвести половину в квадрат, мы получим одну четвертую, а одна четвертая меньше половины.Когда мы возводим дроби в квадрат, они становятся меньше. Итак, это означает, что этот последний не всегда верен, и поэтому мы можем исключить другие ответы, и просто путем исключения работает единственный вариант ответа A. Таким образом, мы можем комбинировать неравенства, если общий член меньше одного и больше другого. Мы можем объединить все в одном направлении. Итак, a меньше b, b меньше c, мы можем объединить это в a меньше b меньше c, что прямо говорит нам, что a меньше c.Мы можем складывать неравенства одного и того же направления, мы можем вычитать неравенства в противоположных направлениях. Не существует общего правила для неравенства умножения или деления. Любое положительное число больше любого отрицательного числа. И снова, это очень удобный ярлык во многих обстоятельствах. И, наконец, добавление положительного числа увеличивает число, вычитание положительного — уменьшает. 888-338-2283 НАЖМИТЕ, чтобы позвонить МЕНЮ НАЧАТЬ ЗВОНИТЕ МЕСТОПОЛОЖЕНИЯ МЕНЮ НАЧАТЬ НАЙТИ МЕСТО Поезда подвешены под путями. Чтобы кататься на этом подстаке, вы должны быть ростом не менее 52 дюймов и не более 72 дюймов. Напишите неравенство, чтобы представить эту ситуацию. Пусть h представляет рост всадника. Не менее 52 дюймов и не более 72 дюймов. Приведенные выше неравенства можно объединить в 52
Поезда подвешены под путями. Чтобы кататься на этом подстаке, вы должны быть ростом не менее 52 дюймов и не более 72 дюймов. Напишите неравенство, чтобы представить эту ситуацию. Пусть h представляет рост всадника. Не менее 52 дюймов и не более 72 дюймов. Приведенные выше неравенства можно объединить в 52  Где пересекаются графики? Это представляет собой перекресток. Набор решений: -2
Где пересекаются графики? Это представляет собой перекресток. Набор решений: -2 Показатели и неравенства — GMAT Math Study Guide
Определения
Например, 20x <40 - это неравенство, а x = 2 - это уравнение.
Например, 4x = 40 — это уравнение, а 4x> 40 — неравенство.
Например, в выражении 5 8 число 8 является показателем степени. Оперируя неравенствами: экспоненты

Нечетные экспоненты
(x 3 ) 1/3 <27 1/3
x <3 [переворачивать знак неравенства нет необходимости, поскольку отрицательные числа не используются]
В качестве проверки , если x = 4 (вне множества решений), x 3 = 64, что не укладывается в неравенство (т.е. 64 не меньше 27). Однако, если x = 2 (внутри набора решений), x 3 = 8, что соответствует неравенству (т.е. 8 меньше 27).
2x 3 + 14 — 14> 30 — 14
2x 3 > 16
x 3 > 8
(x 3 ) 1/3 > 8 1/3
x> 2
В качестве проверки, если x = 0 (вне набора решений), 2x 3 + 14 = 14, что не соответствует неравенству (т. е.е., 14 не больше или равно 30). Однако, если x = 2 (внутри набора решений), 2x 3 + 14 = 30, что соответствует неравенству (т.е. 30 больше или равно 30).
е.е., 14 не больше или равно 30). Однако, если x = 2 (внутри набора решений), 2x 3 + 14 = 30, что соответствует неравенству (т.е. 30 больше или равно 30). Четные экспоненты
x 2 > 16
x> 4
x <-4
Примечание. Знак неравенства изменился, поскольку мы взяли корень отрицательного числа.
В качестве проверки, если x = -5 (в наборе решений), 2x 2 = 50, что соответствует неравенству. Однако, если x = -2 (вне набора решений), 2x 2 = 8, что не соответствует неравенству.
x 2 <9
Случай 1: x положителен
x <3
Случай 2: x отрицателен
x> -3 Множественные неравенства
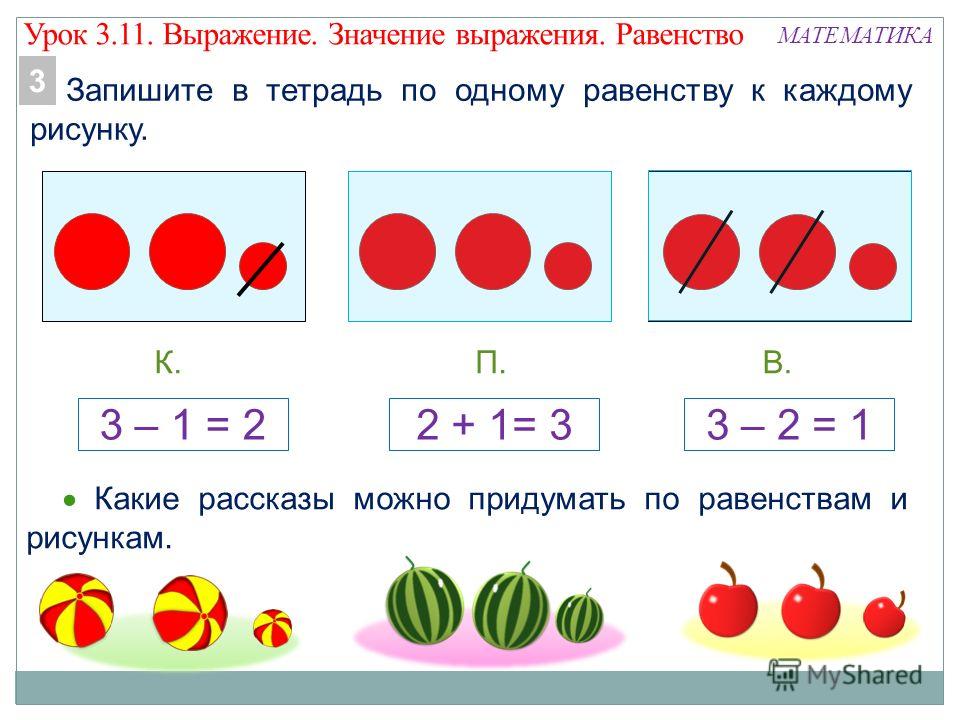
2x 2 + 5 <13
2x 2 <8
x 2 <4
x <2 AND x> -2
x <3 AND x> -3
x <2
x> -2
x <3
x> -3 Inequalities — Maths GCSE Revision
 Попробуем решить следующую задачу:
Попробуем решить следующую задачу:
При работе с двойными неравенствами начните с решения двух неравенств. Целое число — это любое целое число, положительное отрицательное или ноль.
При решении неравенств не забывайте, что умножение или деление на отрицательное число меняет знак неравенства:
−x> 3, становится x <−3 (умножение на −1).
другими словами y = (градиент) x + (y -перехват) Продвинутая алгебра: алгебраические неравенства — II
Множественные алгебраические неравенства
Добавление неравенств
Умножение и деление алгебраических неравенств
И вот почему нет никаких правил для умножения и деления неравенств. Определенно верно, что любое положительное число больше любого отрицательного числа. Это может быть очевидное утверждение, но в определенных обстоятельствах это может оказаться полезным сокращением. Практическая задача
Сводка
Репетиторство по математике для 1-го класса и Помощь по математике для 1-го класса
.

 Повторение способов сравнения предметов.
Повторение способов сравнения предметов. задание
задание 5 класс
5 класс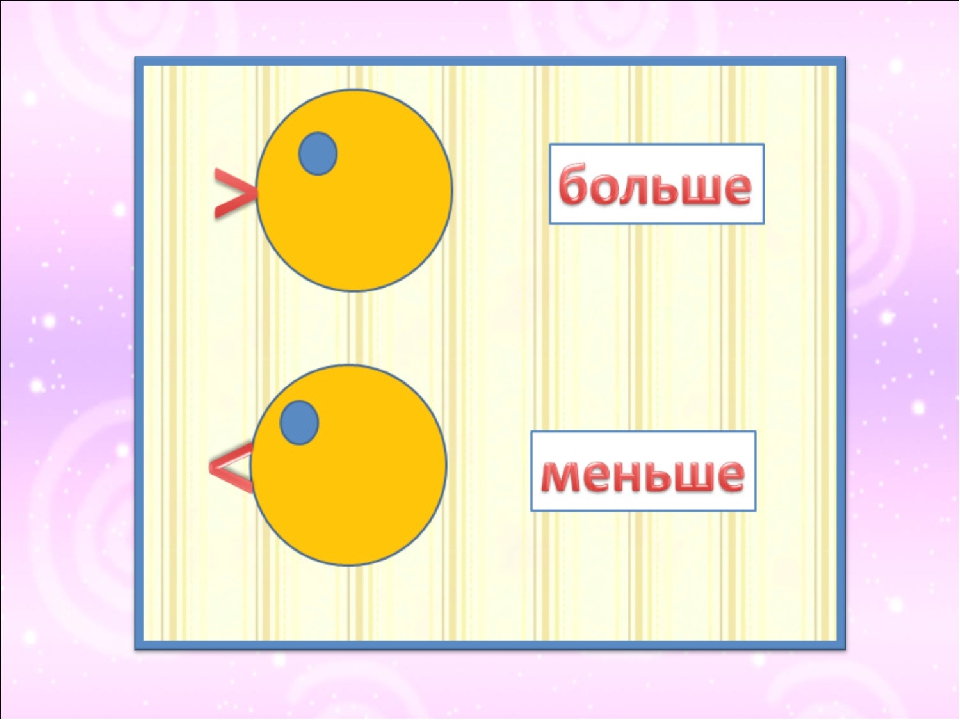 9 класс
9 класс 8 — 11 классы
8 — 11 классы И. Куприна в школе
И. Куприна в школе 7 класс
7 класс