выбираем для типа «прямоугольник» женские прически и стрижки с челкой, макияж и оправы

Каждая девушка хочет выглядеть великолепно, а лицо – это первое, на что обращают внимание окружающие. В зависимости от формы лица подбираются макияж, прическа и аксессуары. Прямоугольная форма лица имеет свои особенности. Каждой обладательнице таких черт нужно знать, как подчеркнуть все достоинства и скрыть недостатки.

Особенности

Прямоугольное лицо считается довольно редким и необычным. Его обладательницы имеют маленький подбородок и четко выраженные скулы. Ширина лица почти вдвое меньше длины, что влияет на ширину лба.

Если у вас именно такой типаж, вы заметили, что волосы не имеют четкой линии роста. Спустя некоторое время после стрижки вам приходится вновь подравнивать кончики, чтобы получить опрятный вид.

Прямоугольная форма лица считается довольно сложной, но к ней можно легко привыкнуть. Создав правильный образ, вы заставите окружающих восхищаться вашей красотой и уникальностью. Девушки с таким личиком отлично получаются на фотографиях.

Большинство известных моделей и признанных красавиц имеют именно прямоугольное вытянутое лицо. Правильная прическа и макияж способны творить чудеса, делая верный акцент на скулах.

Многие голливудские актрисы, которые признаны мировыми эталонами красоты, имеют прямоугольную форму лица. Из этого следует, что обладательницы такого типа внешности способны добиваться многого в своей карьере. Сильный внутренний стержень, а также неоспоримая сила воли помогают справляться со многими проблемами и принципами.

Стрижки

Правильно подобранная стрижка способна творить чудеса, подчеркивать вашу красоту. Ведь не зря девушки столько внимания уделяют своей голове и часто посещают салоны красоты.

Длинные волосы

Если вы счастливая обладательница длинных густых волос, то помните о многослойности при создании образа. Такая простая стрижка как лесенка идеально подходит для прямоугольного лица. Пряди должны начинать ниспадать от области скул.

• Стрижка лесенкой подойдет и девушкам с волнистыми волосами – на них каскад смотрится более эффектно.
• Кудрявые волосы могут придать лицу необходимую полноту, сгладить углы и добавить округлости чертам. Если вам это необходимо, то можете смело использовать плойку или бигуди, если нет возможности посетить профессионала.

• Длинные волосы прямого типа нужно разделить боковым пробором, отведя большую часть в сторону. Полуовальный срез кончиков помогает сделать лицо более мягким, скрыв остроту и грубость. Челка при длинных прямых волосах помогает скрыть лоб, визуально сделать лицо более коротким. Пряди, спадающие на подбородок, способны скрыть широкую челюсть, сделав лицо аккуратным и миниатюрным.

Кудрявые от природы волосы должны быть максимально длинными. Наберитесь терпения и отрастите необходимую длину.

При этом не запрещается подравнивать кончики. Многослойность здесь никто не отменял, поэтому учитывайте данный принцип при выборе стрижки.

Волосы средней длины

Средняя длина прически для лица типа «прямоугольник» считается более подходящим вариантом. На таких волосах намного проще создать объемную укладку, которая идеально сочетается с острыми чертами, делая их более приветливыми. Объемная прическа добавляет лицу свежести, омолаживает и подчеркивает все прелести.

При выборе стрижки отдайте предпочтение закругленным внутрь концам, которые отвлекут внимание от широких и острых скул. Многослойность так же является главным принципом, поэтому каскадные стрижки должны быть в приоритете. Острый подбородок помогут скрыть спадающие пряди, слегка закрывающие острые углы.

Градуированный боб считается наиболее подходящей стрижкой для средней длины волос. Текстурные срезы кончиков смягчат прямоугольник, превратив его визуально в приятный овал. При всем этом объем не добавит лишней тяжести прическе, создав плавные, но четкие линии.

Боб любого типа отлично подходит для средней длины волос. Вы можете каждый день экспериментировать и обновлять свою прическу. Сегодня вам захочется завить кончики, а завтра – сделать ровную укладку. Какой образ бы вы ни выбрали, ваш боб будет помогать вам быть идеальными.

Если вы выбираете такую стрижку, то пусть она будет похожа на каре с удлинением. Это значит, на затылке волосы должны быть не намного короче, чем спереди. В противном случае, вы только сделаете акцент на прямоугольных чертах лица.

Короткие волосы

Если ваш выбор прически сводится к короткой стрижке, она должна быть объемной, с перистыми прядками вокруг лица. Такой вариант поможет сделать акцент на скулах, скрыв широту челюсти.

Создаваемый объем должен идти вбок, а не вверх. Во втором варианте стрижка удлинит лицо, сделав черты еще более грубыми. В области лба и глаз должен быть максимальный акцент, созданный с помощью боковых срезов.

Избегайте сильно коротких стрижек, где невозможно будет создать объем из-за недостаточного количества волос. Асимметричные укладки являются наиболее удачными для прямоугольной формы лица и укороченных волос.

Стрижка боб также подходит для недлинных волос, но в этом случае верх стрижки должен быть круглым, внешние пряди – перистыми, а внутренние – прямыми. Такая многослойность с различными типами прядей выигрышно смотрятся, отлично сглаживая все углы.

Стрижки Пикси подходит для очень коротких волос. Легкая небрежность, и взъерошенность сделает ваше лицо идеальным, способным конкурировать даже с самым правильным овалом.

Многослойная челка должная спадать на бок, но не закрывать глаза.

Короткая стрижка при прямоугольном лице не делает черты мужественными, как это может показаться сначала. Вы получите привлекательный, мягкий, легкий и загадочный образ. При этом вы точно будете выделяться из толпы, и останавливать на себе взгляды окружающих.

Челка

При любой длине волос челка является главным козырем в создании образа. Вы можете сделать стрижку, выделив косую, прямую или многослойную челочку. Короткая челка – это то, что является строгим запретом для прямоугольного типа лица. Она только добавит угловатости, усугубив ситуацию.

Если вы никогда не прикрывали лоб волосами, то сейчас самое время это сделать. С одной стороны, челка является не очень удобным дополнением к стрижке, за которым нужно тщательно следить.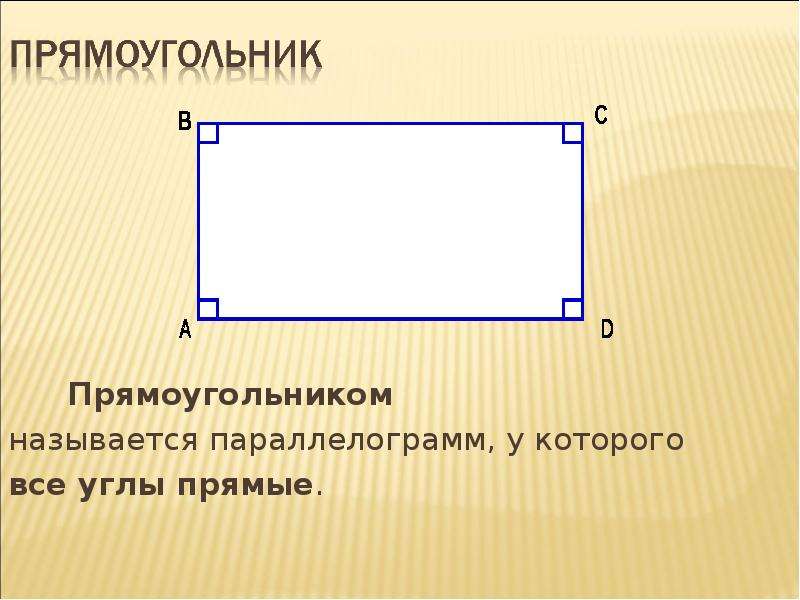 Но с другой стороны, у вас есть прекрасная возможность скрыть все недостатки на лбу. Особенно это актуально в жаркий летний период, когда лоб сильно потеет и начинает блестеть.

Короткие стрижки практически невозможно представить без челки. Если вы решили оставить лоб открытым, то это будет большой ошибкой. При прямоугольной форме лица лоб и так сильно широкий, а укороченные волосы подчеркнут эту широту в большей степени.

При окрашивании попробуйте поэкспериментировать с оттенками, уделив внимание челке. Вам помогут хорошо сочетающиеся между собой оттенки, плавно чередующиеся между собой.

Прически

Подходящие женские прически при прямоугольном типе лица – это те, которые делают лицо максимально приближенным к овалу.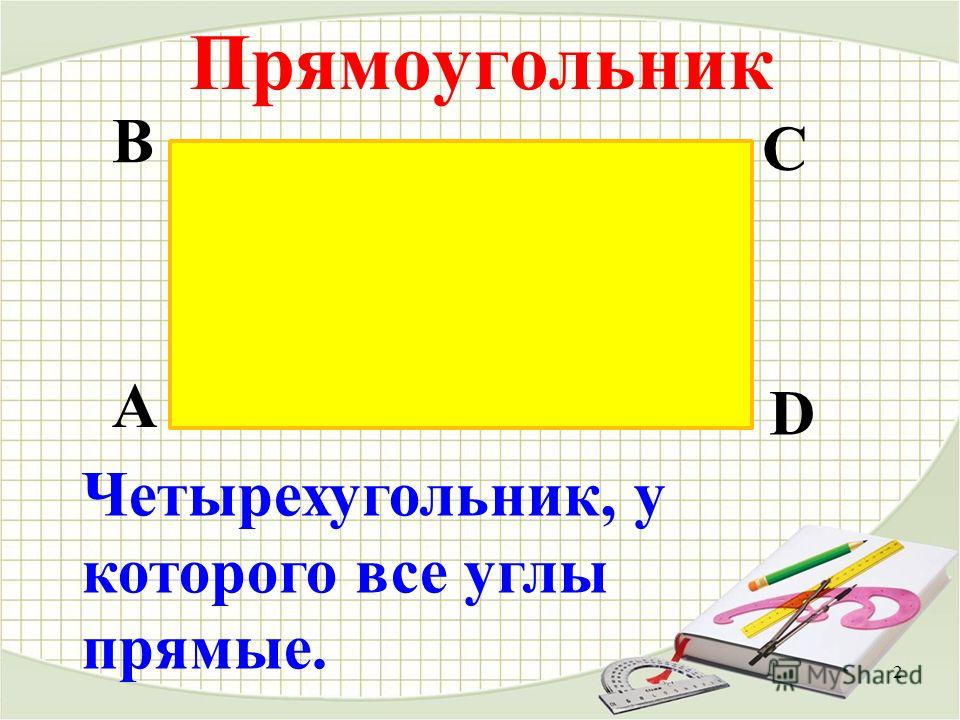 Если у вас возникла необходимость сделать прическу, то она должна быть объемной.

Косой пробор, а также разное количество волос с двух сторон добавят объема, сгладят остроту. Забудьте про приглаженные локоны – вам они совершенно не подходят.

При создании вечернего образа оставьте ниспадающие пряди на скулах. Такая прическа подчеркивает все достоинства, делая лицо нежным и пропорциональным. Всевозможные косы, которые плетутся на бок, также имеют место быть.

Если на мероприятии нет строго табу для причесок, то вы можете просто закрутить локоны, слегка подобрав волосы на макушке. Как уже упоминалось, кудри, и волнистые пряди отлично сочетаются с прямоугольником.

Макияж

При создании образа с помощью макияжа стоит уделить внимание всем деталям, начиная с тональной основы.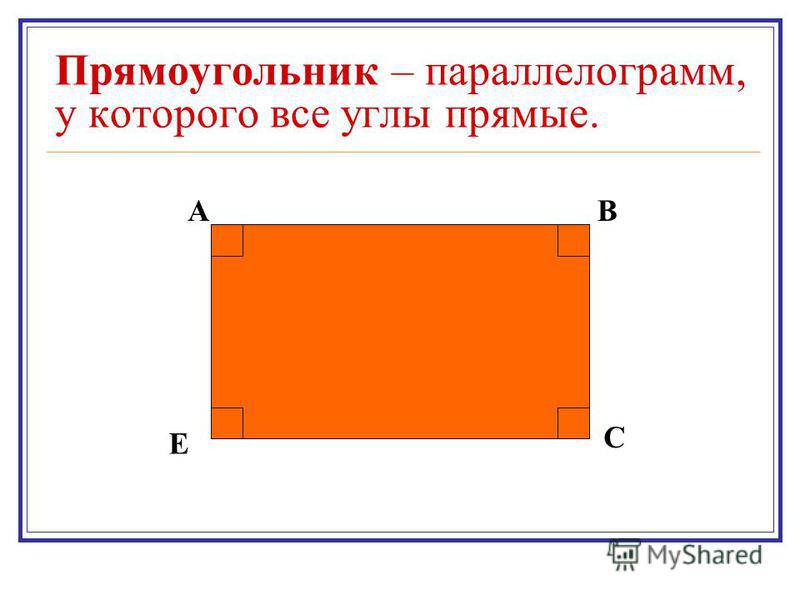 Ее оттенок должен быть немного темнее природного цвета. После тонального крема нанесите пудру или румяна так, чтобы сделать акцент на центре лица, смягчив скулы и острый подбородок. Для этого нужно наносить пудру вдоль линии роста волос и поверх скул.

Глаза являются вашим сильным оружием для создания мягкого и гармоничного образа. Сделав акцент на макияже глаз, вы отвлечете внимание от остроты ваших форм. В этом вам поможет полюбившиеся многим «Смоки айз» с классическим или более яркими оттенками теней.

При макияже глаз не стоит использовать подводки, заменив их хорошей тушью или накладными ресницами.

Если вы решили сделать акцент на губах, то только они должны быть яркими, а остальной макияж – спокойным. Выбирайте насыщенный оттенок в зависимости от того, какой цвет вам подходит. Чаще всего – это классический красный или бордо.

Аксессуары

Очки – незаменимый аксессуар, который обязательно должен присутствовать в арсенале обладательниц прямоугольного лица. В вашем случае отлично подойдут большие круглые очки. Вы можете подобрать модную широкую или узкую оправу, приблизив свое лицо к идеальным овальным формам.

Избегайте узких очков, которые не только не смогут подчеркнуть все достоинства, но и значительно усугубят ситуацию. Лицо будет казаться более вытянутым, а акцент на острых скулах только усилится.

О том, как скорректировать прямоугольное лицо, смотрите в следующем видео.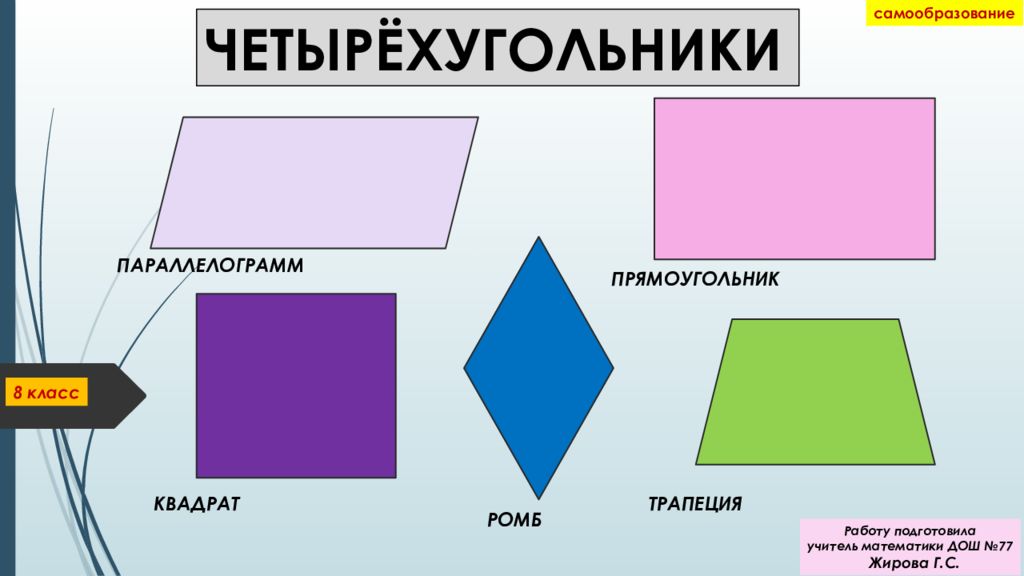

Геометрические логотипы

Андрей Батурин, 22 сентября, 2015

АНДРЕЙ БАТУРИН

При создании логотипов дизайнеры часто используют простые геометрические формы, такие, как круг, квадрат, треугольник и т.д. или их сочетание.

Это связано с тем, что логотипы, содержащие простые геометрические формы, легко воспринимаются глазом и хорошо запоминаются. Чего не скажешь о логотипах с изображением сложных и витиеватых форм.

Многие известные логотипы компаний выполнены с использованием простых геометрических фигур. И все они узнаваемы миллионами потребителей.

Давайте разберемся, что символизируют простые геометрические фигуры и как это можно выгодно использовать при создании логотипа компании.

ЛОГОТИПЫ В ФОРМЕ КРУГА

Самые распространенные геометрические логотипы – логотипы в форме круга.

Круг – это фигура, не имеющая ни начала, ни конца, ни направления, ни ориентировки. Поэтому он ассоциируется с завершенностью и бесконечностью одновременно. Круг также по форме напоминает Солнце и Луну, поэтому вызывает чувство доверия.

Логотипы в форме круга символизируют активность устремлений компании и ее подвижность.

Пример круглого логотипа, который разработали мы

Круглый логотип мы разработали для компании по доставке еды Fitness Food. Выглядит он так:

Кейс: Fitness Food

Многие логотипы автомобилей известных марок имеют форму круга.

Volkswagen

Firefox

LG

BMW

ЛОГОТИПЫ В ФОРМЕ КВАДРАТА

Геометрическая фигура квадрат символизирует комбинацию и упорядочивание четырех разных элементов.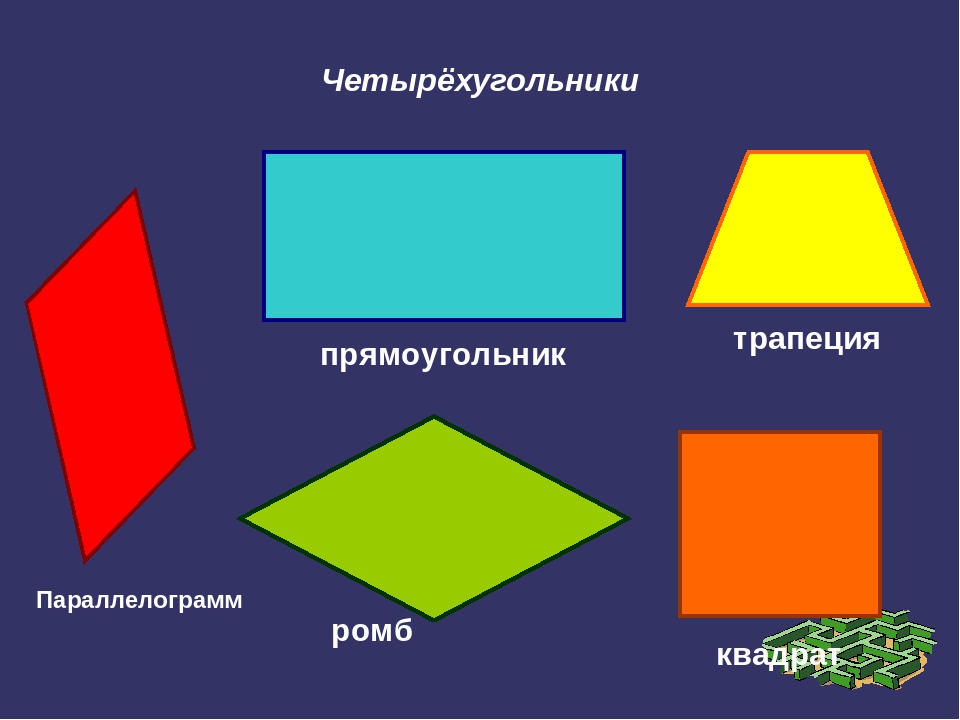 Таких, например, как четыре стихии или четыре времени года.

Форма квадрата вызывает ощущение стабильности, прочности, консервативности и уравновешенности сторон.

Логотипы, в которых доминирует геометрическая фигура квадрат часто используют большие и серьезные организации.

Givenchy

Microsoft

MTC

Columbia Sportswear

ЛОГОТИПЫ В ФОРМЕ ТРЕУГОЛЬНИКА

Треугольник – один из самых мощных и универсальных символов. Распространен в современной айдентике благодаря тому, что вызывает чувство уравновешенности.

Треугольник, расположенный вершиной вверх, символизирует целеустремленность, власть и гармонию; вершиной вниз – развитие, плодовитость, углубленность. Пересекающиеся треугольники образуют гексаграмму и символизируют синтез, союз противоположностей.

Применение треугольников в логотипах символизирует движение вверх, развитие, совершенствование, единство разных направлений.

Пример работы нашей студии

Логотип в форме треугольника мы сделали для компании “Миграционный юрист”. Хоть здесь и есть изогнутые линии, образ этой геометрический фигуры все равно заметен:

Кейс: Миграционный юрист

Google Drive

Reebok

Loomers Auto

Toblerone

ЛОГОТИПЫ В ФОРМЕ ПРЯМОУГОЛЬНИКА

Прямоугольник – это самая правильная, рациональная и надежная фигура. Именно благодаря этим свойствам прямоугольник всегда был и остается самой любимой формой человека, с помощью которой он приспосабливает все для своего быта. Например, комната, дом, стол, кровать имеют прямоугольную форму.

Прямоугольник в логотипах компаний символизирует устойчивость, рациональность и надежность.

Универсальность прямоугольника обуславливает популярность его использования, как составной части сложного логотипа.

Tommy Hilfiger

Youtube

Visa

Hewlett Packard

ЛОГОТИПЫ В ФОРМЕ ЭЛЛИПСА

Часто используется в логотипах геометрическая форма эллипс. Он ассоциируется с развитием, движением, стремлением к совершенству. Две стороны эллипса символизируют снижение и восхождение, инволюцию и эволюцию. Наклонный эллипс олицетворяет напор, динамику, инновационность.

Использование такой формы в логотипах подходит для современных быстроразвивающихся, амбициозных компаний. Наверное, по этой причине логотипы в форме эллипса часто используют автомобильные компании.

Toyota

Samsung

Ford

Cadbury

ЛОГОТИПЫ В ФОРМЕ ГЕКСАГОНА

Гексагон – это правильный шестиугольник, у которого все углы и стороны равны. Он часто встречается в природе: снежинки, пчелиные соты, кристаллы некоторых молекул и атомов, и многое другое имеют форму гексагона.

Логотипы в форме гексагона лаконичны и гармоничны. Они ассоциируются с совершенством, природной наполненностью, гармонией, красотой, изобилием, свободой.

Пример работы нашей студии

В форме гексагона мы сделали лого для компании «МосМастерКамень».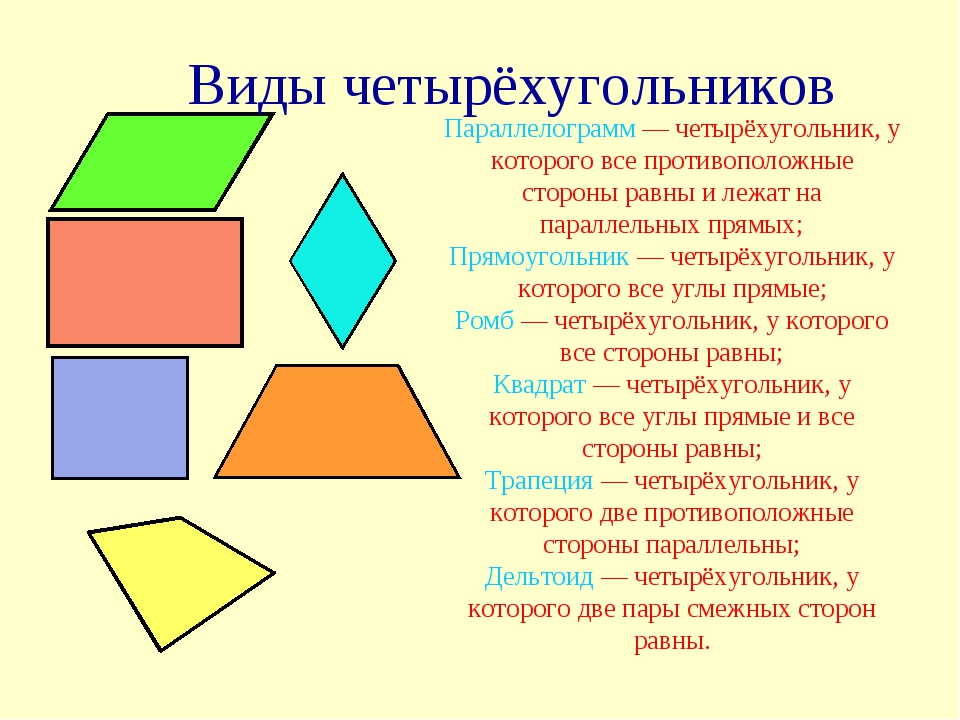

Кейс: МосМастерКамень

EndoCarbon

Malerex

Express Home Services

Hexagon Metrology

ЛОГОТИПЫ В ФОРМЕ КУБА

Символически куб идентичен квадрату. И кроме того, куб – это символ Земли. Он ассоциируется с устойчивым основанием, идеальной стабильностью. Куб считается эмблемой правды.

В древние времена монархи (египетские фараоны, например) изображались сидящими на кубическом камне, который символизировал устойчивость их царства.

Поэтому использование куба в логотипах компании ассоциируется со стабильностью и верностью корпоративным принципам.

Пример нашей студии

Кубический логотип мы разработали для поставщика медицинских изделий “Национальные проект”:

Кейс: Национальные проект

Dropbox

Next

Red Cube Design Studio

The Garver Group

Хотите заказать логотип?

CEO WebEvolution — Андрей Батурин

• 14 лет практики
• 350 выполненных проектов

Хотите заказать логотип?

Обращайтесь к нам — разработаем лого, который отразит ценности вашей компании и привлечет внимание клиентов. Консультация бесплатна.

Оставить телефон Получите бесплатную консультацию эксперта

Другие статьи по тегам

логотипы

на эту тему

Использование негативного пространства в логотипах Логотипы, которые содержат скрытый смысл Значение цвета в фирменном стиле компании «Экспресс» – создаем профессиональный логотип быстро и дешево Фирменный стиль Логотип — важнейшая часть бренда

Суть метода прямоугольников — Мегаобучалка

Составные квадратурные формулы

В случае разбиения отрезка интегрирования на элементарных отрезков приведённые выше формулы применяются на каждом из этих элементарных отрезков между двумя соседними узлами. В результате, получаютсясоставные квадратурные формулы

1. Для левых прямоугольников:

2. Для правых прямоугольников:

3. Для средних прямоугольников:

Формулу с вычислением значения в средней между двумя узлами точке можно применять лишь тогда, когда подынтегральная функция задана аналитически, либо каким-нибудь иным способом, допускающим вычисление значения в произвольной точке. В задачах, где функция задана таблицей значений остаётся лишь вычислять среднее значение между интегралами, посчитанными по формулам левых и правых прямоугольников соответственно, что приводит к составной квадратурной формуле трапеций.

Поскольку составные квадратурные формулы являются ни чем иным, как суммами, входящими в определение интеграла Римана, при они сходятся к точному значению интеграла. Соответственно, с увеличением точность получаемого по приближённым формулам результата возрастает.

Сравнение применения различных формул прямоугольников
Формула левых прямоугольников   Формула средних прямоугольников   Формула правых прямоугольников

Составные формулы для равномерных сеток [править]

Равномерную сетку можно описать следующим набором формул:

где — шаг сетки.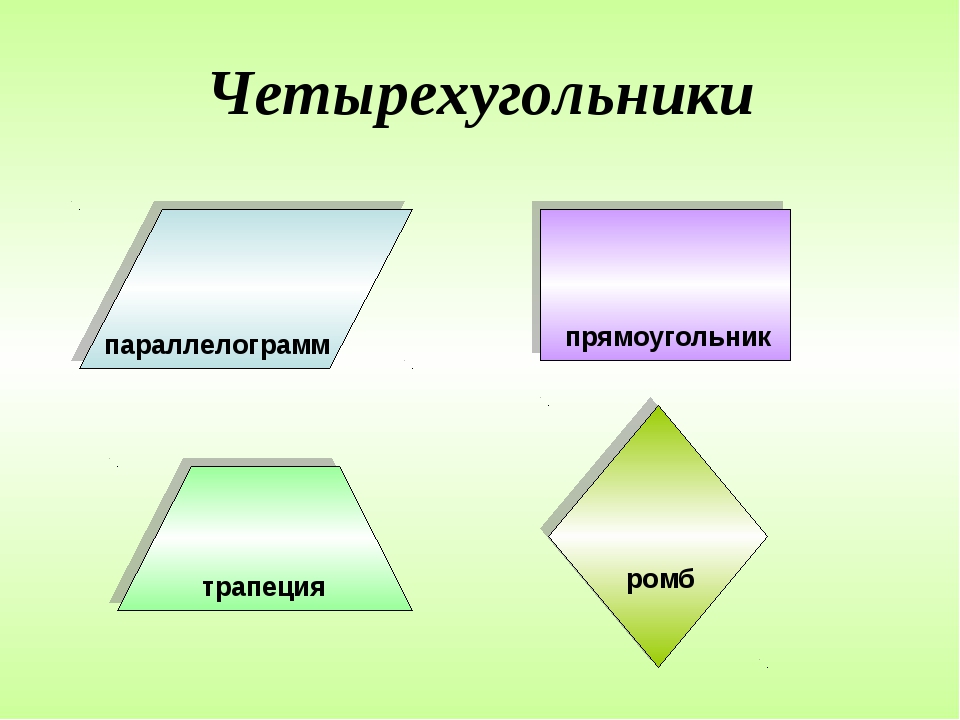

Для равномерных сеток формулы прямоугольников можно записать в виде следующих формул Котеса:

1. Составная формула левых прямоугольников:

2. Составная формула правых прямоугольников:

Погрешность метода

Для формул правых и левых прямоугольников погрешность составляет

Для формулы прямоугольников (средних)

Для составных формул правых и левых прямоугольников на равномерной сетке:

Для составной формулы прямоугольников:

 

Суть метода и решение примеров

Суть метода прямоугольников.

Пусть функция y = f(x) непрерывна на отрезке [a; b]. Нам требуется вычислить определенный интеграл .

Обратимся к понятию определенного интеграла. Разобьем отрезок [a;b] на n частей точками . Внутри каждого отрезка выберем точку . Так как по определению определенный интеграл есть предел интегральных сумм при бесконечном уменьшении длины элементарного отрезка разбиения , то любая из интегральных сумм является приближенным значением интеграла .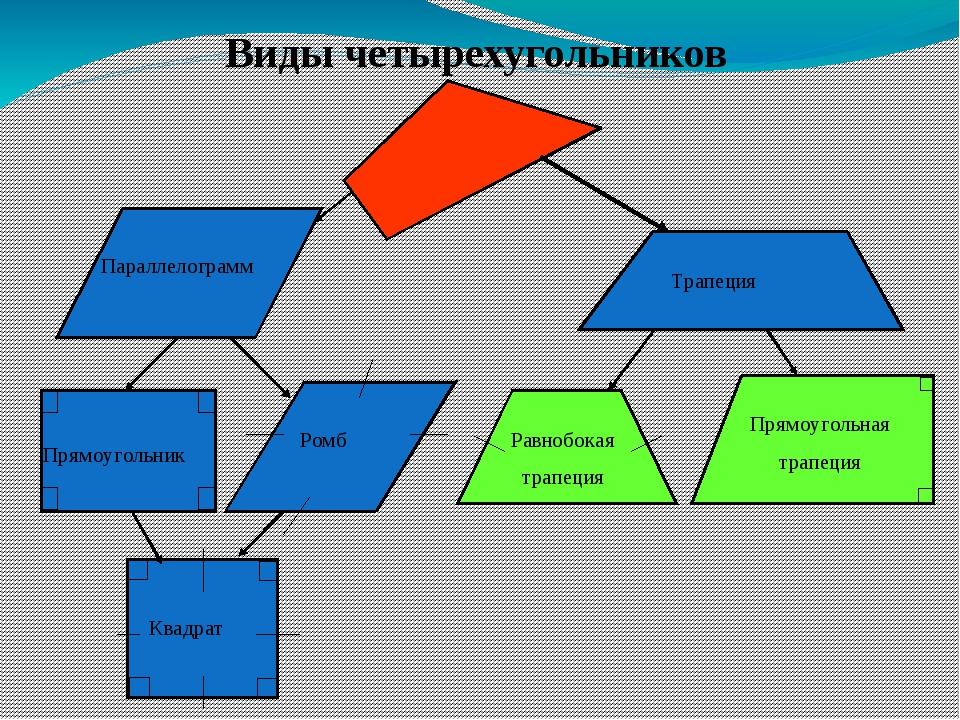

Суть метода прямоугольников заключается в том, что в качестве приближенного значения определенного интеграла берут интегральную сумму (далее мы покажем, какую именно интегральную сумму берут в методе прямоугольников).

Прямоугольник

(переход к области прямоугольника или периметру прямоугольника)

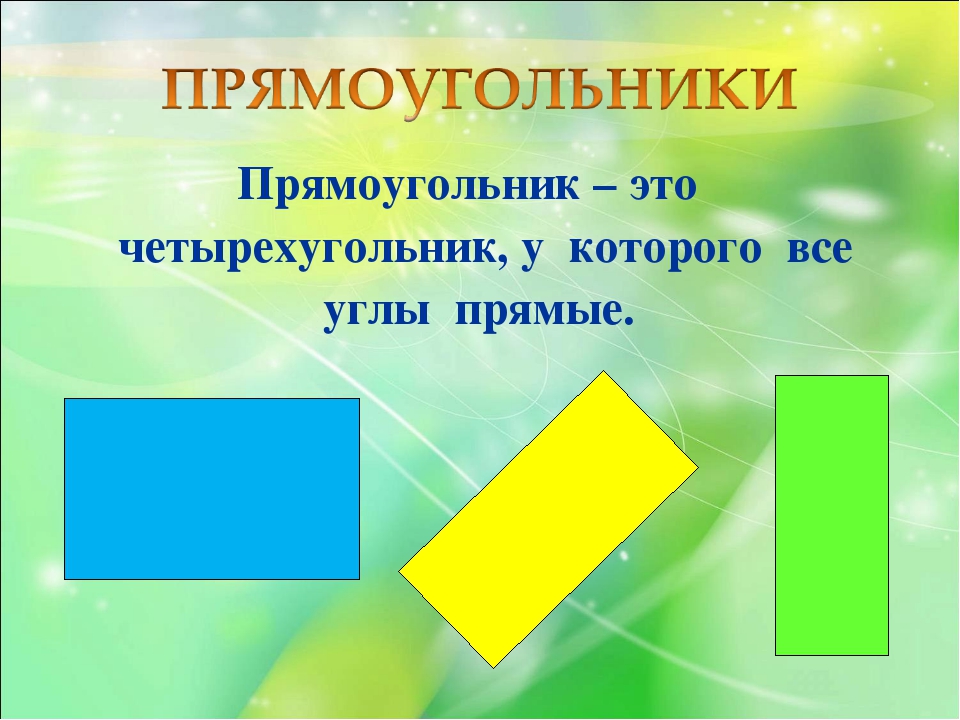
Прямоугольник — это четырехсторонняя плоская форма, каждый угол которой является прямым (90 °).

		означает «прямой угол»
		равны
		равны

Играть с прямоугольником:

Площадь прямоугольника

Площадь = a × b

Пример: прямоугольник шириной 6 м и высотой 3 м, какова его площадь?

Периметр прямоугольника

Периметр — это расстояние по краям.

Периметр 2 раза (a + b) : Периметр = 2 (a + b)

Пример: прямоугольник имеет длину 12 см и высоту 5 см, каков его периметр?

Периметр = 2 × (12 см + 5 см)

= 2 × 17 см

= 34 см

Диагонали прямоугольника

Прямоугольник имеет две диагонали, они равны по длине и пересекаются посередине.

Длина диагонали — это квадратный корень из (a в квадрате + b в квадрате) : Диагональ «d» = √ (a 2 + b 2 )

Пример: прямоугольник имеет ширину 12 см и высоту 5 см. Какова длина диагонали?

d = √ (12 ² + 5 ² )

= √ (144 + 25)

= √169

= 13 см

Золотой прямоугольник

Существует также специальный прямоугольник, называемый Золотым прямоугольником:

Типы четырехугольников

Существует шесть типов четырехугольников, и эти четырехугольники можно классифицировать по соотношению сторон и углов.

Как определить параллелограмм

Параллелограмм — это четырехсторонний многоугольник с двумя парами параллельных и равных сторон. Следующий рисунок представляет собой параллелограмм.

Для параллелограмма справедливо все следующее:

• Противоположные стороны параллельны (AB || DC и AD || BC)

• Противоположные стороны равны (AB = DC и AD = BC)

• Противоположные углы равны (угол A = угол C и угол B = угол D)

Как определить прямоугольник

Прямоугольник — это параллелограмм с четырьмя прямыми углами.Следующий рисунок представляет собой прямоугольник.

В прямоугольнике справедливо все следующее:

• Противоположные стороны параллельны (HG || EF и HE || GF)

• Противоположные стороны равны (HG = EF и HE = GF)

• Все четыре угла равны 90 градусам (угол E = угол F = угол G = угол H = 90 градусов)

Как определить квадрат

Квадрат — это прямоугольник с 4 равными сторонами. Следующая фигура квадратная.

В квадрате справедливо все следующее:

• Противоположные стороны параллельны (JK || IL и JI || KL)

• Все четыре стороны равны (JI = KL = JK = IL)

• Все четыре угла равны 90 градусам (угол I = угол J = угол K = угол L = 90 градусов)

Ромб: Ромб — это параллелограмм с 4 равными сторонами.Следующий рисунок представляет собой ромб.

В ромбе справедливо все следующее:

• Противоположные стороны параллельны (PO || MN и PM || ON)

• Все четыре стороны равны (PO = ON = NM = MP)

• Противоположные углы равны (угол M = угол O и угол N = угол P)

Как определить трапецию

Трапеция: Трапеция — это четырехугольник, у которого всего одна пара параллельных сторон. Есть три типа трапеций. Масштабная трапеция: Разносторонняя трапеция — это трапеция без равных сторон. Далее следует разносторонняя трапеция. Прямоугольная трапеция: Прямоугольная трапеция — это трапеция с двумя прямыми углами. Далее следует прямоугольная трапеция. Равнобедренная трапеция: У равнобедренной трапеции непараллельные стороны равны. Ниже изображена равнобедренная трапеция.

Как определить воздушный змей

Воздушный змей — это четырехугольник с двумя парами смежных сторон, которые равны.Кроме того, нет равных противоположных сторон.

Типы четырехугольников викторины. Быстро проверьте, поняли ли вы этот урок.

1. Введение в физику

   18 ноя, 20 13:20

   Первоклассное введение в физику. Универсальный ресурс для глубокого понимания важных концепций физики

   Подробнее

Новые уроки математики

Ваша электронная почта в безопасности.Мы будем использовать его только для информирования вас о новых уроках математики.

Типы углов

Есть много разных видов углов. Мы определим их в этом уроке. Внимательно изучите изображения, чтобы понять их.

Острый угол:

Угол, размер которого меньше 90 градусов. Далее следует острый угол.

Прямой угол:

Угол, размерность которого составляет 90 градусов.Следующее — прямой угол.

Тупой угол:

Угол, размер которого больше 90 градусов, но меньше 180 градусов. Таким образом, он составляет от 90 до 180 градусов. Далее следует тупой угол.

Прямой угол

Угол, размер которого составляет 180 градусов. Таким образом, прямой угол выглядит как прямая линия.Далее следует прямой угол.

Угол отражения:

Угол, размер которого больше 180 градусов, но меньше 360 градусов. Ниже приводится угол отражения.

Типы углов: как назвать пары углов

Смежные углы:

Угол с общей вершиной и одной общей стороной.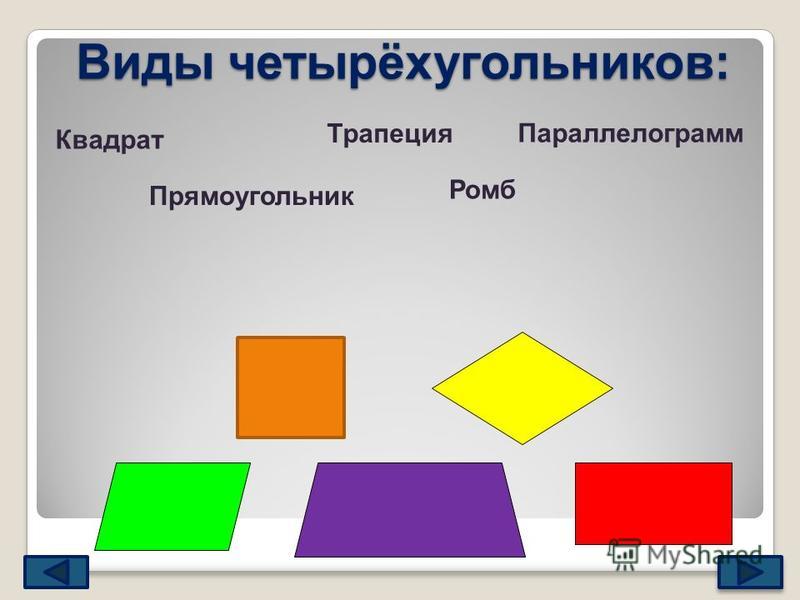 <1 и <2, являются смежными углами.

Дополнительные углы:

Два угла, сумма которых составляет 90 градусов.Угол 1 и угол 2 являются дополнительными углами, потому что вместе они образуют прямой угол.

Обратите внимание, что угол 1 и угол 2 не обязательно должны быть смежными. должны быть дополнительными, пока они в сумме составляют 90 градусов.

Дополнительные углы:

Два угла, сумма которых составляет 180 градусов. Ниже приведены дополнительные углы.

Вертикальные углы:

Углы с общей вершиной, стороны которых образованы одними и теми же линиями.Следующие (угол 1 и угол 2) — это вертикальные углы.

Когда две параллельные линии пересекаются третьей линией (поперечной), образуется 8 углов. Взгляните на следующий рисунок Углы 3,4,5,8 — внутренние углы

Углы 1,2,6,7 — внешние углы

Альтернативные внутренние углы:

Пары внутренних углов на противоположных сторонах трансверсали.

Например, угол 3 и угол 5 являются альтернативными внутренними углами. Угол 4 и угол 8 также являются альтернативными внутренними углами.

Альтернативные внешние углы:

Пары внешних углов на противоположных сторонах трансверсали.

Угол 2 и угол 7 являются альтернативными внешними углами.

Соответствующие углы:

Пары углов, находящихся в аналогичных положениях.

Угол 3 и угол 2 — соответствующие углы.

Угол 5 и угол 7 — соответствующие углы

Ну вот! Внимательно изучите типы углов.Здесь начинается любое серьезное изучение геометрии.

Типы углов викторины. Посмотрите, насколько хорошо вы можете распознавать углы.

1. Введение в физику

   18 ноя, 20 13:20

   Первоклассное введение в физику. Универсальный ресурс для глубокого понимания важных концепций физики

   Подробнее

Новые уроки математики

Ваша электронная почта в безопасности.Мы будем использовать его только для информирования вас о новых уроках математики.

Свойства четырехугольника — прямоугольник, квадрат, параллелограмм, ромб, трапеция

В евклидовой геометрии четырехугольник — это четырехугольная двумерная фигура, сумма внутренних углов которой равна 360 °. Слово четырехугольник образовано от двух латинских слов «quadri» и «latus», что означает четыре и сторона соответственно. Поэтому определение свойств четырехугольников важно при попытке отличить их от других многоугольников.

Итак, каковы свойства четырехугольника? Четырехугольники обладают двумя свойствами:

• Четырехугольник должен быть замкнутой формы с 4 сторонами
• Сумма всех внутренних углов четырехугольника составляет 360 °

В этой статье вы получите представление о 5 типах четырехугольников и познакомитесь со свойствами четырехугольников.

Это то, что вы прочитаете в статье:

Вот видео, объясняющее свойства четырехугольника:

На приведенной ниже диаграмме показан четырехугольник ABCD и сумма его внутренних углов.Сумма всех внутренних углов составляет 360 °.

Таким образом, A + ∠B + ∠C + ∠D = 360 °

Различные типы четырехугольников

Существует 5 типов четырехугольников в зависимости от их формы. Эти 5 четырехугольников:

1. прямоугольник
2. Квадрат
3. Параллелограмм
4. Ромб
5. Трапеция

Давайте подробно обсудим каждый из этих пяти четырехугольников:

Вот вопросы, которые научат вас применять свойства всех пяти четырехугольников, которые вы узнаете в этой статье.

Прямоугольник

Прямоугольник — это четырехугольник с четырьмя прямыми углами. Таким образом, все углы в прямоугольнике равны (360 ° / 4 = 90 °). Причем противоположные стороны прямоугольника параллельны и равны, а диагонали делят друг друга пополам.

Свойства прямоугольников

Прямоугольник имеет три свойства:

• Все углы прямоугольника равны 90 °
• Противоположные стороны прямоугольника равны и параллельны
• Диагонали прямоугольника делят друг друга пополам

Формула прямоугольника — Площадь и периметр прямоугольника

Если длина прямоугольника L, а ширина B, то

1. Площадь прямоугольника = длина × ширина или L × B
2. Периметр прямоугольника = 2 × (L + B)

Эти практические вопросы помогут вам закрепить свойства прямоугольников

Площадь

Квадрат — четырехугольник с четырьмя равными сторонами и углами.Это также правильный четырехугольник, так как его стороны и углы равны. Как и прямоугольник, квадрат имеет четыре угла по 90 ° каждый. Его также можно рассматривать как прямоугольник, две смежные стороны которого равны.

Недвижимость квадрата

Чтобы четырехугольник стал квадратом, он должен обладать определенными свойствами. Вот три свойства квадратов:

• Все углы квадрата равны 90 °
• Все стороны квадрата равны и параллельны друг другу
• Диагонали пересекают друг друга перпендикулярно

Формула квадрата — Площадь и периметр квадрата

Если сторона квадрата — «а», тогда

1. Площадь квадрата = a × a = a²
2. Периметр квадрата = 2 × (a + a) = 4a

Эти практические вопросы помогут вам закрепить свойства квадратов

Если вы наберете Q50-51 за GMAT, вы сможете набрать 700+ баллов за GMAT.Почему бы вам не начать подготовку к GMAT с помощью наших бесплатных подготовительных ресурсов и не начать свой путь к получению Q50-51 на GMAT. Учитесь у Кэрри Лоу, у которой за 3 недели показатель улучшился с Q35 до Q50.

Параллелограмм

Параллелограмм, как следует из названия, представляет собой простой четырехугольник, противоположные стороны которого параллельны. Таким образом, у него две пары параллельных сторон. Более того, у параллелограмма противоположные углы равны, а его диагонали делят друг друга пополам.

Свойства параллелограмма

Четырехугольник, удовлетворяющий указанным ниже свойствам, будет классифицирован как параллелограмм.У параллелограмма четыре свойства:

• Противоположные углы равны
• Противоположные стороны равны и параллельны
• Диагонали пересекают друг друга
• Сумма любых двух смежных углов равна 180 °

Формулы параллелограмма — Площадь и периметр параллелограмма

Если длина параллелограмма равна «l», ширина — «b», а высота — «h», тогда:

1. Периметр параллелограмма = 2 × (l + b)
2. Площадь параллелограмма = l × h

Эти практические вопросы помогут вам закрепить свойства параллелограмма

Ромб

Ромб — это четырехугольник, все четыре стороны которого равны по длине, а противоположные стороны параллельны друг другу.Однако углы не равны 90 °. Ромб с прямыми углами стал бы квадратом. Другое название ромба — «ромб», так как он похож на ромб в игральных картах.

Свойства ромба

Ромб — это четырехугольник, обладающий следующими четырьмя свойствами:

• Противоположные углы равны
• Все стороны равны, противоположные стороны параллельны друг другу
• Диагонали пересекают друг друга перпендикулярно
• Сумма любых двух смежных углов равна 180 °

Формулы ромба — Площадь и периметр ромба

Если сторона ромба — это, то периметр ромба = 4a

Если длина двух диагоналей ромба равна d ₁ и d ₂ , то площадь ромба = ½ × d ₁ × d ₂

Эти практические вопросы помогут вам закрепить свойства ромба

Трапеция

Трапеция (в США ее называют трапецией) — это четырехугольник, у которого есть только одна пара параллельных сторон.Параллельные стороны называются «основаниями», а две другие стороны называются «ножками» или боковыми сторонами.

Свойства трапеции

Трапеция — это четырехугольник, в котором одно свойство:

• Только одна пара противоположных сторон параллельна друг другу

Формулы трапеции — Площадь и периметр трапеции

Если высота трапеции « h» (как показано на диаграмме выше), то:

1. Периметр трапеции = Сумма длин всех сторон = AB + BC + CD + DA
2. Площадь трапеции = ½ × (Сумма длин параллельных сторон) × h = ½ × (AB + CD) × h

Эти практические вопросы помогут вам закрепить свойства трапеции

Свойства четырехугольника

В таблице ниже суммированы все свойства четырехугольников, которые мы изучили до сих пор:

Свойства четырехугольника	Прямоугольник	Площадь	Параллелограмм	Ромб	Трапеция
Все стороны равны	✖	✔	✖	✔	✖
Противоположные стороны равны	✔	✔	✔	✔	✖
Противоположные стороны параллельны	✔	✔	✔	✔	✔
Все углы равны	✔	✔	✖	✖	✖
Противоположные углы равны	✔	✔	✔	✔	✖
Сумма двух смежных углов 180	✔	✔	✔	✔	✖
Разделить пополам	✔	✔	✔	✔	✖
Перпендикулярно пополам	✖	✔	✖	✔	✖

На изображении ниже также показаны свойства четырехугольника:

Важные четырехугольные формулы

В таблице ниже приведены формулы площади и периметра четырехугольников различных типов:

Четырехугольные формулы	Прямоугольник	Квадрат	Параллелограмм	Ромб	Трапеция
Площадь	д × ш	a²	д × в	½ × d1 × d2	½ × (Сумма параллельных сторон) × высота
Периметр	2 × (д + б)	4a	2 × (д + б)	4a	Сумма всех сторон

Дополнительная литература:

Четырехсторонние вопросы

Попрактикуемся в применении свойств четырехугольника на следующих типовых вопросах:

Вопрос 1

Адам хочет построить забор вокруг своего прямоугольного сада длиной 10 метров и шириной 15 метров.Сколько метров забора нужно купить, чтобы ограждать весь сад?

1. 20 метров
2. 25 метров
3. 30 метров
4. 40 метров
5. 50 метров

Решение

Шаг 1: Дано

• У Адама прямоугольный сад.
  • Он имеет длину 10 метров и ширину 15 метров.
  • Он хочет построить вокруг него забор.

Шаг 2: найти

• Длина, необходимая для строительства ограды вокруг всего сада.

Шаг 3: подход и разработка

Забор можно строить только вокруг внешней стороны сада.

• Итак, общая необходимая длина забора = Сумма длин всех сторон сада.
  • Так как сад прямоугольный, сумма длин всех сторон — это не что иное, как периметр сада.
  • Периметр = 2 × (10 + 15) = 50 метров

Следовательно, необходимая длина забора — 50 метров.

Следовательно, вариант E — правильный ответ.

Вопрос: 2

Стив хочет покрасить одну прямоугольную стену своей комнаты. Стоимость покраски стены — 1,5 доллара за квадратный метр. Если длина стены 25 метров, а ширина 18 метров, то какова общая стоимость покраски стены?

1. 300 долл. США
2. $ 350
3. $ 450
4. 600 $
5. $ 675

Решение

Шаг 1: Дано

• Стив хочет покрасить одну стену своей комнаты.
  • Стена 25 метров в длину и 18 метров в ширину.
  • Стоимость покраски стены составляет 1,5 доллара за квадратный метр.

Шаг 2: найти

• Общая стоимость покраски стены.

Шаг 3: подход и разработка

• Стена окрашена по всей площади.
  • Итак, если мы найдем общую площадь стены в квадратных метрах и умножим ее на стоимость покраски 1 квадратного метра стены, мы сможем получить общую стоимость.
  • Площадь стены = длина × ширина = 25 метров × 18 метров = 450 квадратных метров
  • Общая стоимость покраски стены = 450 × 1,5 $ = 675 $

Следовательно, правильный ответ — вариант E.

Мы надеемся, что к настоящему времени вы узнали о различных типах четырехугольников, их свойствах и формулах, а также о том, как применять эти концепции для решения вопросов о четырехугольниках. Применение четырехугольников важно для решения вопросов по геометрии на GMAT.Если вы планируете сдавать GMAT, мы можем помочь вам с высококачественными учебными материалами, к которым вы можете получить доступ бесплатно, зарегистрировавшись здесь.

Вот еще несколько статей по математике:

1. Повысьте точность ответов на вопросы по математике по многоугольникам
2. Вопросы о геометрии — самые распространенные ошибки | GMAT Quant Prep

Если вы планируете сдавать GMAT, мы можем предоставить вам доступ к качественному онлайн-контенту для подготовки. Наша компания по подготовке к GMAT является самой обсуждаемой компанией на gmatclub: более 1950 отзывов.

Почему бы вам не воспользоваться бесплатным испытанием и не судить сами?

Напишите нам по адресу [email protected] в случае возникновения каких-либо вопросов.

прямоугольников, ромбов и квадратов | Ресурсы Wyzant

По мере того, как мы продвигались четырехугольников, мы стали все более и более конкретизировать тип фигур, с которыми мы имеем дело.Сначала мы рассматривали всевозможные полигоны, а потом мы сузили его до четырехугольников, называемых четырехугольниками. Оттуда мы узнал об особом типе четырехугольника, противоположные стороны которого параллельны, называется параллелограмм. В этом разделе мы станем еще более конкретными, изучив свойства различных параллелограммов. Давайте узнаем, что делает прямоугольники, ромбы и квадраты особые фигуры.

Прямоугольники

Определение: Прямоугольник — это четырехугольник с четырьмя прямыми углами.

Обратите внимание, что мы используем «четырехугольник» в нашем определении прямоугольников. Мы могли бы иметь также сказал, что прямоугольник — это параллелограмм с четырьмя прямыми углами, поскольку и четырехугольник с четырьмя прямыми углами также является параллелограммом (потому что их противоположные стороны будут параллельны).

Прямоугольники обладают парой свойств, которые помогают отличить их от других параллелограммов. Изучая эти свойства, мы сможем различать различные типы параллелограммов и классифицируйте их более конкретно. Имейте в виду, что все фигуры в этом разделе имеют общие свойства параллелограммов. То есть все они иметь

(1) противоположные стороны, которые параллельны,

(2) противоположных углов, которые совпадают,

(3) противоположных сторон, которые совпадают,

(4) последовательных углов, которые являются дополнительными, и

(5) диагоналей, пересекающих друг друга.

Теперь давайте посмотрим на свойства, которые делают прямоугольники особым типом параллелограмма.

(1) Все четыре угла прямоугольника — прямые.

(2) Диагонали прямоугольника совпадают.

Ромбы

Определение: Ромб — это четырехугольник с четырьмя конгруэнтными сторонами.

Подобно определению прямоугольника, мы могли бы использовать слово «параллелограмм». вместо «четырехугольника» в нашем определении ромба. Таким образом, у ромбов есть все свойств параллелограммов (указанных выше), а также некоторые другие. Давайте посмотрите на эти свойства.

(1) Последовательные стороны ромба совпадают.

(2) Диагонали ромба делят пополам пары противоположных углов.

(3) Диагонали ромба перпендикулярны.

Квадраты

Определение: Квадрат — это параллелограмм с четырьмя равными сторонами и четырьмя сторонами. конгруэнтные углы.

Обратите внимание, что определение квадрата — это комбинация определений прямоугольник и ромб.Следовательно, квадрат — это и прямоугольник, и ромб, что означает, что свойства параллелограммов, прямоугольников и ромбов все применить к квадратам. Поскольку квадраты обладают комбинацией всех этих различных свойств, это очень специфический тип четырехугольника.

Посмотрите на иерархию четырехугольников ниже. Этот рисунок показывает прогрессию наших знаний о многоугольниках, начиная с четырехугольников и заканчивая квадратами.

Обратите внимание на две стрелки, указывающие на квадрат. Это потому, что квадрат обладает всеми свойствами прямоугольника и ромба.

Теперь, когда мы знаем о свойствах прямоугольников, ромбов и квадратов, давайте поработайте над несколькими упражнениями, которые позволят оценить наше понимание этого материала.

Упражнение 1

Обозначьте каждый параллелограмм как прямоугольник, ромб или квадрат.

Ответ:

Во-первых, давайте взглянем на параллелограмм A. На рисунке показано, что у него четыре конгруэнтных стороны и что его диагонали пересекаются перпендикулярно. Потому что его стороны совпадают, мы знаем, что параллелограмм не является прямоугольником. Тот факт, что параллелограмм А пересечение диагоналей перпендикулярно нам не помогает, потому что и ромбы, и квадраты разделяют эту характеристику.Угол в вершине параллелограмма A не равен но под прямым углом. Следовательно, мы знаем, что это не квадрат. Параллелограмм А — ромб.

В параллелограмме B мы видим, что есть четыре прямых угла и что пары противоположные стороны конгруэнтны. Однако последовательные стороны не совпадают, поэтому мы можем исключить из наших вариантов ромбы и квадраты. Таким образом, параллелограмм B является прямоугольник.

Давайте теперь посмотрим на параллелограмм C. Отметим, что он имеет пару прямых углов и четыре конгруэнтных стороны. Наша склонность заставляет нас думать, что этот параллелограмм квадрат, но давайте на всякий случай убедимся. Мы знаем, что два прямых угла данные нам имеют сумму 180 ° . Поскольку внутренние углы четырехугольника это 360 ° , мы знаем, что оставшиеся два угла должны иметь сумму 180 ° (потому что 360-180 = 180 ).Противоположные углы параллелограммов конгруэнтны, что означает, что недостающие углы должны иметь меру из 90 ° (начиная с 180 ÷ 2 = 90 ). Это говорит нам, что есть на самом деле четыре прямых угла в параллелограмме C, поэтому мы знаем, что это квадрат (и ромб).

Упражнение 2

Найдите значение x для прямоугольника ABCD ниже.

Ответ:

Мы знаем, что ABCD — это прямоугольник, поэтому давайте воспользуемся некоторыми свойствами прямоугольника. чтобы помочь нам выяснить, что такое x . Кажется, что в центре внимания это упражнение по диагоналям фигуры. Сверху мы знаем, что диагонали прямоугольника совпадают, поэтому давайте установим сегменты AC и BD равны между собой:

Итак, получаем x = 12 .

Упражнение 3

Ответ:

Давайте рассмотрим информацию, полученную в результате упражнения, чтобы вывести из него больше информации. Мы знаем, что EKIN — параллелограмм, и что ? 1 ?? 2 . Поскольку EKIN — параллелограмм, мы знаем, что что его противоположные стороны параллельны.Следовательно, сегменты EK и В параллельны.

Затем мы можем использовать теорему об альтернативных внутренних углах , чтобы утверждать, что ? 1 ?? 4 и ? 2 ?? 3 . Напомним, что альтернативные внутренние углы совпадают. тогда и только тогда, когда трансверсаль пересекает пару параллельных прямых. В этом случае, наша пара параллельных линий EK и IN , а наша поперечная это сегмент NK .

По транзитивности можно сказать, что ? 1 ?? 3 и ? 2 ?? 4 . Давайте посмотрите на нашу цепочку сравнений, чтобы убедиться, что предыдущие утверждения правда.

Диагональ делит наш параллелограмм на два треугольника. Фактически, потому что два угла каждого треугольника совпадают, можно сказать, что ? EKN и ? INK — равнобедренные треугольники.Обратное к теореме о равнобедренном треугольнике гласит: что стороны, противоположные конгруэнтным углам равнобедренных треугольников, совпадают, поэтому мы знаем, что сегмент EK соответствует сегменту EN , и что сегменты IK и IN совпадают.

Теперь можно сказать, что сегменты EK и IN совпадают, как и EN и IK , потому что противоположные стороны параллелограмма конгруэнтны.По транзитивности мы знаем, что EN? EK? IN? IK . Давайте смотреть на нашей новой иллюстрации.

Таким образом, параллелограмм EKIN является ромбом, потому что он имеет четыре равных стороны. Наши Геометрическое доказательство этого упражнения из двух столбцов показано ниже.

Упражнение 4

Каким должно быть значение и , чтобы ромб PQRS стал квадратом?

Ответ:

Прежде чем мы сможем вычислить наши и , мы должны определить, какое значение имеет х есть.В конечном итоге мы хотим, чтобы ромб PQRS был квадратом, это означает, что PQRS должно иметь четыре прямых угла.

Начнем с выяснения того, что такое x . Это относительно просто, потому что мы можем просто установить сегмент PQ равным PS :

Теперь, когда мы знаем, что такое x , мы можем подставить его в меру угла, данного нас.Но сначала нам нужно выяснить, какова общая величина ? QSR . Мы знаем что мы хотим, чтобы ? PSR было 90 ° . Также мы знаем, что диагонали квадрата пополам пары противоположных углов. Следовательно, ? PSR следует разделить пополам на сегмент QS , разделив угол вверх на два равных угла 45 ° (потому что 90 ÷ 2 = 45 ).Теперь мы можем установить ? QSR равно 45 ° . Получаем:

Теперь мы заменяем 7 на x :

Таким образом, значение y должно быть 4 , чтобы ромб PQRS также был квадратом.

диагоналей прямоугольника с калькулятором

диагоналей прямоугольника с калькулятором — Math Open Reference

Попробуй это Перетащите любую вершину прямоугольника ниже. Он останется прямоугольником, и будет рассчитана длина диагонали.

Прямоугольник имеет две диагонали. Каждый из них отрезок нарисованный между противоположным вершины (углы) прямоугольника. Диагонали обладают следующими свойствами:

• Две диагонали конгруэнтные (одинаковой длины).На рисунке выше нажмите «показать обе диагонали», затем перетащите оранжевую точку в любую вершину прямоугольника и убедитесь, что это так.
• Каждая диагональ делит пополам другой. Другими словами, точка, где диагонали пересечь (крест), делит каждую диагональ на две равные части
• Каждая диагональ делит прямоугольник на две части. конгруэнтные прямоугольные треугольники. Поскольку треугольники совпадают, они имеют одинаковую площадь, и каждый треугольник имеет половину площади прямоугольника

Длина по диагонали

На рисунке выше нажмите «Сброс».Как видите, диагональ прямоугольника делит его на две части. прямоугольные треугольники, BCD и DAB. Диагональ прямоугольника — это гипотенуза этих треугольников. Мы можем использовать Теорема Пифагора чтобы найти длину диагонали, если мы знаем ширину и высоту прямоугольника.

В виде формулы: где:
w — ширина прямоугольника
h — высота прямоугольника

Калькулятор

Воспользуйтесь калькулятором выше, чтобы вычислить свойства прямоугольника.

Введите длину двух сторон, и оставшаяся часть будет рассчитана. Например, введите длину двух сторон. Будут найдены площадь, периметр и длина диагонали.

Что попробовать

1. На рисунке вверху страницы нажмите «сбросить» и «скрыть детали». Затем перетащите углы, чтобы создать произвольный прямоугольник. Рассчитайте длину диагоналей. Нажмите «Показать подробности», чтобы проверить свой ответ.
2. Прямоугольник имеет высоту 12 и диагональ 31.Найдите ширину прямоугольника и используйте анимацию или калькулятор выше, чтобы проверить свой ответ.

Другие темы полигонов

Общий

Типы многоугольника

Площадь различных типов полигонов

Периметр различных типов полигонов

Углы, связанные с многоугольниками

Именованные полигоны

(C) Открытый справочник по математике, 2011 г.
Все права защищены.

.

No related posts.