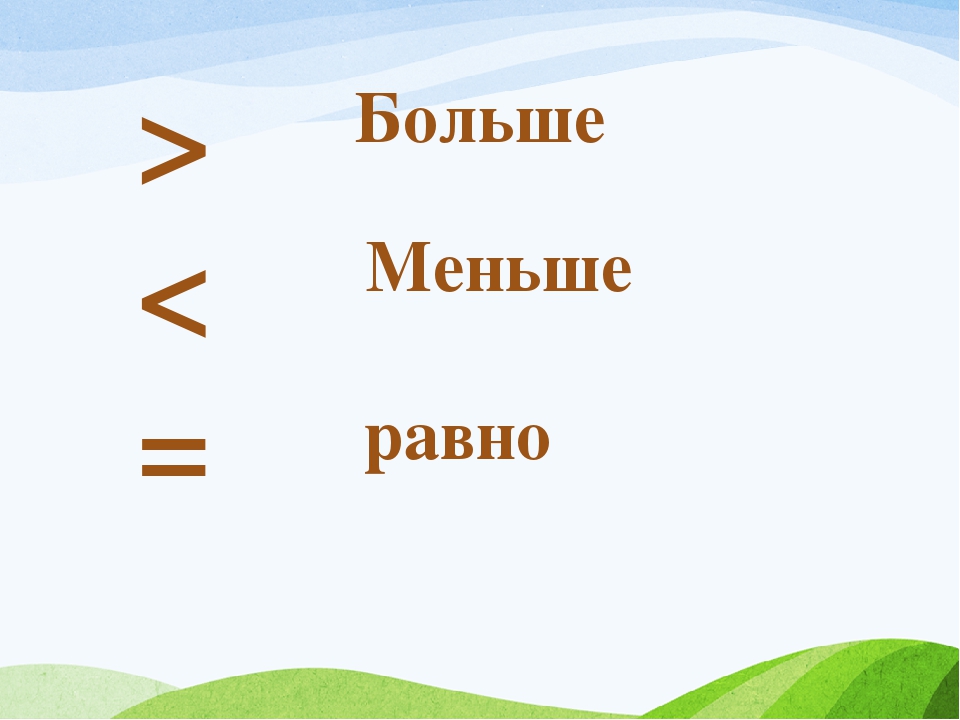
Знаки больше, меньше, равно

Технологическая карта урока по математике в 1 классе «Школа России»

Тема урока: Знаки сравнения «больше», «меньше», «равно».

Цель урока: в ходе практической работы и наблюдений познакомить со знаками >, <, =; научить выполнять записи с этими знаками; закреплять знания состава чисел, развивать умение рассуждать.

Планируемые результаты: учащиеся научатся сравнивать любые два числа и записывать результат сравнения, используя знаки >, <, =; читать записи; выполнять мыслительные операции анализа и синтеза и делать умозаключения; применять полученные ранее знания в измененных условиях; слушать собеседника и вести диалог; слушать учителя и выполнять его требования; оценивать себя, границы своего знания и незнания; работать в паре и оценивать товарища.

Познавательные УУД:

1. Ориентироваться в учебнике.

2. Понимать информацию, представленную в виде текста, рисунка, схем.

3. Сравнивать предметы, объекты: находить общее и различие.

4. Классифицировать предметы, объекты по заданным критериям.

Регулятивные УУД:

1. Организовывать свое рабочее место.

2. Осуществлять контроль в форме сличения своей работы с заданным эталоном..

3. Вносить дополнения, исправления в свою работу.

Коммуникативные УУД:

1. Соблюдать нормы речевого этикета.

2. Вступать в диалог.

3. Сотрудничать с товарищами при выполнении заданий в паре: устанавливать и соблюдать очередность действий, корректно сообщать товарищу об ошибках.

4. Участвовать в коллективном обсуждении учебной проблемы.

Оборудование: для учителя — интерактивная доска или проектор; карточки Учи.Ру, магнитный набор цифр и знаков, геометрических фигур; учебник «Математика, 1 класс»; рабочая тетрадь с печатной основой;

для учащихся – геометрический набор; большие карточки с цифрами; учебник; рабочая тетрадь, пенал.

Ход урока.

Деятельность ученика,

ссылки на карточки платформы Учи. Ру

1

2

3

1

Самоопределение к деятельности.

Приветствие детей, психологический настрой детей на урок.

Учитель:

Прозвенел звонок для нас.

Все зашли спокойно в класс.

Встали все у парт красиво,

Поздоровались учтиво.

Тихо сели, спинки прямо.

Вижу, класс наш хоть куда.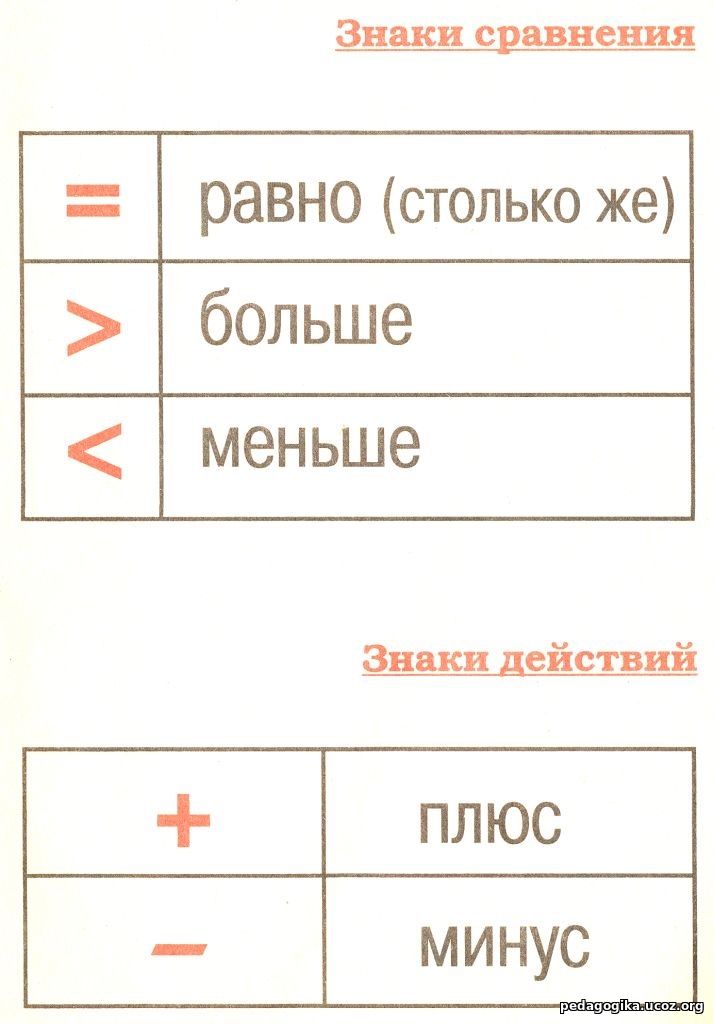

Мы начнём урок, друзья.

Приветствие учителя.

2

Устный счет. 1.

Игра «Назови соседа»

3 2 4

5 1 3

Игра «Весёлый счет» Поможем ёжику сосчитать грибы.

— Сегодня мы отправимся в математическое путешествие, но сначала нам нужно выбрать транспортное средство. Путешествие сказочное, поэтому, прибывать на станции мы будем всегда одновременно.

-как вы думаете на каком же транспорте мы отправимся с вами в путешествие? Для того, чтобы отправится мы должны ответить на вопросы. Посмотрите на доску.

— На каких рисунках столько же фигур? (Корабль, легковая машина.)

— На каких рисунках меньше всего? (Маленький грузовик.)

— На каких больше 6, но меньше 9? (Ракета.)

-Ребята, мы отправимся на том транспорте в котором наименьшее количества фигур. И это?

— Внимание! Путешествие начинается. Чтобы попасть на математическую станцию, необходимо хором вести отсчет. Закрыли глаза. Считаем

от1 до 5.

— Мы прибываем на станцию ( Чтение хором, на доске появляется запись.)

1 задание (Работа с большими карточками, цифры от 1 до 5.)

— Дети, получившие карточки, выходят к доске и строятся по порядку. (Проверка.)

— Делайте шаг вперед, если ответом является число на карточке и называйте его.

1) Какое число следует за числом 3? 4?

2) Какое число стоит между числами 1 и 3? 3 и 5?

3) Какое число предшествует числу 4? 5? 2?

4) Назовите соседей числа 3? 2?

2 задание (Задачи в стихах. Дети показывают карточку с ответом.)

1) Карандаш один у Миши,

Карандаш один у Гриши.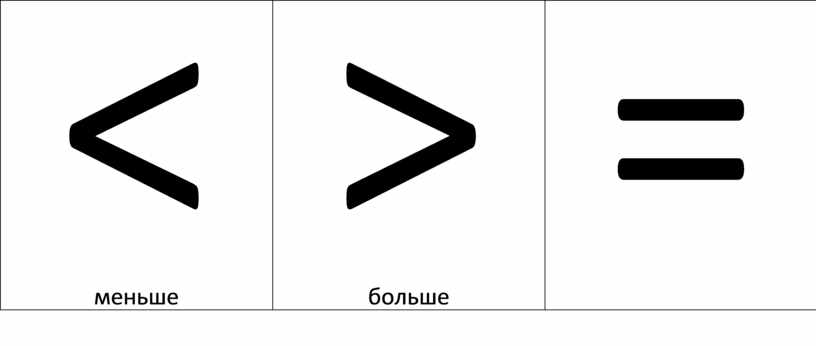

Сколько всего карандашей у малышей?

2) Четыре краски есть у Сани,

Одна у маленького брата.

Все краски посчитайте сами.

Ну, постарайтесь-ка, ребята!

3) Четыре сороки пришли на уроки.

Одна из сорок не знала урок.

Сколько прилежно трудилось сорок?

4) Два щенка – баловника бегают, резвятся.

К шалунишкам три дружка с громким лаем мчатся.

Вместе лучше – веселей.

Сколько будет всех друзей?

— Вы справились с заданиями, и мы отправляемся на следующую станцию.

— Закрываем глаза, путешествие продолжается.

— Хором считаем от 3 до 8.

(Дети встают и выполняют зарядку.)

Мы читали, мы считали,

А теперь тихонько встали.

Раз – присели, два – нагнулись,

На носочках потянулись.

Руки ставим на бочок:

На носочках скок, скок, скок.

А теперь все тихо сели,

Продолжаем наш урок.

— Закрыли глаза. Считаем от 7 до 3.

— Вы должны зажечь окошки в домиках. (Работа ведется около доски и с места, ответ дети показывают карточками.)

— Закрыть глаза – продолжить состав чисел.

2 – это 1 и ?

3 – это 2 и ?

4 – это 2 и ?

4 – это 1 и ?

5 – это 4 и ?

5 – это 2 и ?

Устный счет

https://uchi.ru/teachers/groups/10076038/subjects/1/course_programs/1/cards/485

https://uchi.ru/teachers/groups/10076038/subjects/1/course_programs/1/cards/424

https://uchi. ru/teachers/groups/10076038/subjects/1/course_programs/1/cards/5110

https://uchi.ru/teachers/groups/10076038/subjects/1/course_programs/1/cards/5101

3

1) Фронтальная работа

— Закрыли глаза. Считаем от 10 до 5.

— Перечислите знаки, которые вы знаете. (Дети выходят к доске и берут карточки со знаками +, -, =. )

Дети выкладывают на парте примеры (счетный набор)

2 3=5 — Какие карточки перевернуты? Выйти к доске и заполнить

пропуски.

5 1=4

3 1 4

Физкультминутка на внимание.

Покажите, что вы готовы к работе.

— левую руку вверх

— 3 вращения кистью

— правую руку вверх

— 2 хлопка

— правую руку вперед

— 3 вращения кистью

— левую руку вперед

— 2 хлопка

— Сложили руки на столе.

(Вернуться к изображениям транспортных средств. Индивидуальная работа (дети используют счетный набор) и фронтальная (на доске – магнитные цифры).

— Сравните количество фигур корабля и легковой машины. Как это записать? (10=10)

— А теперь сравните по количеству фигуры грузовиков. Где фигур больше? Как же мы запишем сравнение? (Ответы детей.)

— Мы не можем воспользоваться знаком =. Нужен новый знак. В математике этот знак называется больше >.

9 > 6

(Читает учитель. Читают все дети.)

— На каком рисунке фигур меньше? Значит, какое число меньше 6 или 9? В записи мы будем использовать знак меньше <.

6 < 9

(Читает учитель. Читают все дети.)

— Что вам напоминают эти знаки? (уголки, клювики, ротики)

Открытый ротик направлен к большему числу, уголочек – к меньшему.

Физкультминутка

2) Работа по учебнику

— Откройте учебник на с. 46. Как называются знаки вверху страницы? (Больше, меньше, равно.)

— Прочитайте, что мы будем делать сегодня на уроке.

— Что мы уже узнали? (Как обозначаются слова «больше», «меньше», «равно».)

— Как вы думаете, для чего нужны эти знаки? (Чтобы экономить время при записи.)

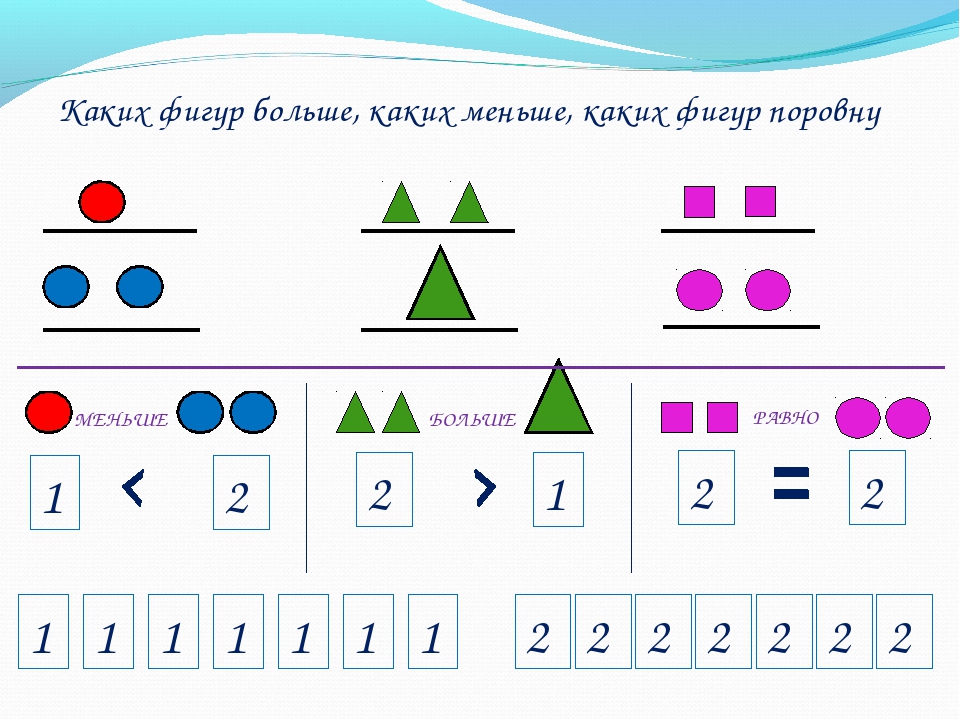
— Посмотрите на левый верхний рисунок. Какие фигуры вы видите? (Два зеленых квадрата и три синих круга)

— Чего больше? Как это записать? Чего меньше? Прочитайте запись.

(По аналогии разбираются картинки справа, иллюстрирующие записи 5>4, 4<5 и 5=5.)

— Посмотрите на рисунок с птицами. Составьте рассказ по записи.

(Было 3 птицы, прилетела еще 1. Птиц стало 4.)

— Птиц стало больше или меньше? Как это записали?

— Составьте рассказ по второй записи. (Было 4 птицы, одна птица улетела. Осталось 3 птицы.)

— Птиц стало больше или меньше? Прочитайте запись. (Три меньше четырех.)

Работа в паре.

— Вместе с соседом по парте составьте записи к картинкам с вишнями.

(Проверка. Записи приведены на доске: 3+1=4, 4>1, 4-3=1, 1<4.)

https://uchi.ru/teachers/groups/10076038/subjects/1/course_programs/1/cards/60903

https://uchi.ru/teachers/groups/10076038/subjects/1/course_programs/1/lessons/129

5

Закрепление изученного материала

1) Работа в тетради с печатной основой.

— Откройте тетрадь на с. 18. Прочитайте первое задание. Самостоятельно запишите, какое время показывают часы.

(Фронтальная проверка.)

— Посмотрите на знаки, приведенные ниже. Как называется знак, который записан первым? Вторым?

(Объяснение, показ, запись знаков в тетради.)

— Посмотрите на рисунок с мячами.

(Записать количество, заполнить пропуски рисунками, с помощью новых знаков составить запись 5>3, 3<5.)

2) Работа по учебнику.

— Рассмотрите рисунок на с. 47. вспомните сказку В. Сутеева «Мешок яблок». За что звери принесли зайцу столько подарков? (За доброту.)

Работа в паре.

— Пользуясь рисунком, расскажите соседу по парте, как можно получить число 5.

(Проверка. Выходит к доске пара для ответа. Спросить несколько пар.)

— Посмотрите на следующий рисунок. Сколько желтых полосок нужно положить, чтобы накрыть розовую? А сколько зеленых? Почему получили разные ответы? (Полоски разной длины.) Каких полосок нужно больше?

https://uchi.ru/teachers/groups/10076038/subjects/1/course_programs/1/lessons/133

6

Рефлексия

— Наше путешествие заканчивается.

— Оцените, как вы поняли новую тему, с помощью «Светофора».

— С какими знаками мы сегодня познакомились?

— Покажите знак «больше».

— Покажите знак «меньше».

«Знаки сравнения «больше», «меньше», «равно»

Муниципальное бюджетное образовательное учреждение
дополнительного образования детей
«Районный центр детского и юношеского творчества»

Красногвардейский район Республики Крым

Конспект занятия по ФЭМП
Тема: «Знаки сравнения «больше», «меньше», «равно»

составитель: Яценко Анастасия Васильевна
педагог дополнительного образования
МБОУ ДОД «РЦДЮТ»

пгт Красногвардейское, 2019

Дата проведения: 10. 10.2019

Группа 2 (6-7 лет).

Цели: создать условия для ознакомления со знаками сравнения «больше», «меньше», «равно»; развития навыков счёта; закрепления знаний состава изученных чисел; учить писать знаки сравнения «больше», «меньше»; прививать аккуратность.
Планируемые результаты: знать названия и последовательность чисел от 1 до 5; использовать при сравнении чисел знаки сравнения «больше», «меньше», «равно».
Универсальные учебные действия:
Познавательные: стремиться к расширению своей познавательной сферы, стараться производить логические мыслительные операции (анализ, сравнение) для решения познавательной задачи.
Регулятивные: уметь оценивать результат своей работы на уроке.
Коммуникативные: уметь участвовать в диалоге на уроке и в жизненных ситуациях; отвечать на вопросы учителя, товарищей по классу.
Личностные: проявляют интерес к новому материалу, касающемуся конкретных фактов, но не теории (учебно-познавательный интерес на уровне реакции на новизну).
Ход занятия:
Устный счёт.
— Обратный счет от 10 до 1
– Назовите соседей числа:
3 2 4
– Назовите число, которое:
следует за числом 1;
предшествует числу 5;
между 3 и 5
II. Закрепление пройденного материала.
Для проведения этой работы использовать наборное полотно «Дом цифр».
Затем, пользуясь различными фигурками счётного материала и наборным полотном, дети составляют разными способами числа 3,4,5.
Устное решение записей на карточках 1 + 1, 2 + 1, 3 + 1, 5 – 1, 2 + 2, 3 – 1
Решение задач (устно)
В класс вошла Маринка,
За нею – Иринка,
Потом пришел Игнат.
Сколько всех ребят?
На плетень взлетел петух,
Повстречал еще там двух.
Сколько стало петухов?
У кого ответ готов?
Найти и назвать все линии, которые мы с вами изучили на рисунке (рисунок находится на доске) – луч, отрезок, ломанная линия, многоугольник, круг, кривая линия.

Ребята, чем отличается луч от отрезка?
А что интересного вы знаете о прямой?
Физкультминутка
Раз — подняться, подтянуться,
Два – нагнуться, разогнуться,
Три – в ладоши три хлопка,
Головою три кивка,
На четыре — руки шире,
Пять руками помахать,
Шесть на место тихо сесть.
III. Изучение нового материала.
Знакомство со знаками сравнения.
– Используя наборное полотно, сравните группы различных предметов.
Например: 2 желтых круга и 3 фиолетовых круга;
— Каких меньше?
— Почему вы так решили?
– Какое число меньше 2 или 3?
Сегодня мы научимся записывать это математически.
Математика удивительная наука, она очень точная и не любит лишних слов.
Мы не будем писать слово меньше или больше, для этого есть специальные математические знаки.
2 < 3, а что мы можем сказать по отношению к трем кругам?
Что три больше двух.
– Чтобы уметь отличать знак больше от знака меньше, я сейчас открою вам маленький секрет. Все готовы меня слушать?
Кто сейчас меня внимательно будет слушать, тот никогда не перепутает их.
Какой рукой мы работаем больше всего? Правой. Теперь посмотрите. (Поворачиваюсь к детям спиной, прикладываю правую руку к доске).
Поднимите правую руку и сделайте как я – это знак больше, а левой рукой мы работаем меньше – это знак меньше.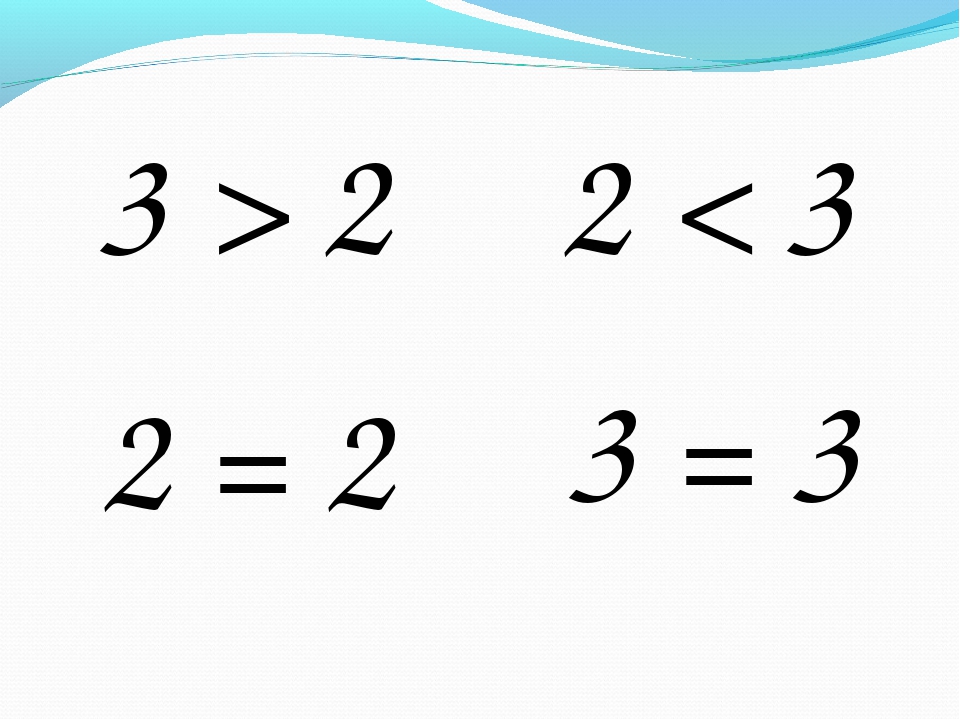
А теперь мы с вами поиграем. У вас есть знаки больше и меньше, чтобы вам было легче внизу есть точка, запомните точка должна быть внизу. Я буду называть сравнения, а вы будете показывать знак больше или меньше. В нашем классе мальчиков больше, чем девочек. Покажите знак.
В нашем классе стульев больше, чем столов.
В нашем классе дверей меньше, чем окон.
IV. Составление и чтение равенств и неравенств.
Учащиеся, под руководством педагога составляют и читают неравенства и равенства (хором).
Например:
«На ветке сидело 3 птички, к ним прилетела ещё одна. Стало 4 птички. К 3 прибавить 1 получится 4.Четыре больше трёх.
На ветке сидело 4 птички, одна улетела, осталось 3 птички. Из 4 вычесть 1 получится 3. Три меньше четырёх». И т. д.
V. Пропись знаков сравнения.
Показываю учащимся, как правильно писать знаки сравнения «больше», «меньше», и ученики прописывают их в тетрадях (задание 2, с. 18).
Далее на наборное полотно выставляется равное количество каких-либо предметов, например: 3 листика и 3 гриба.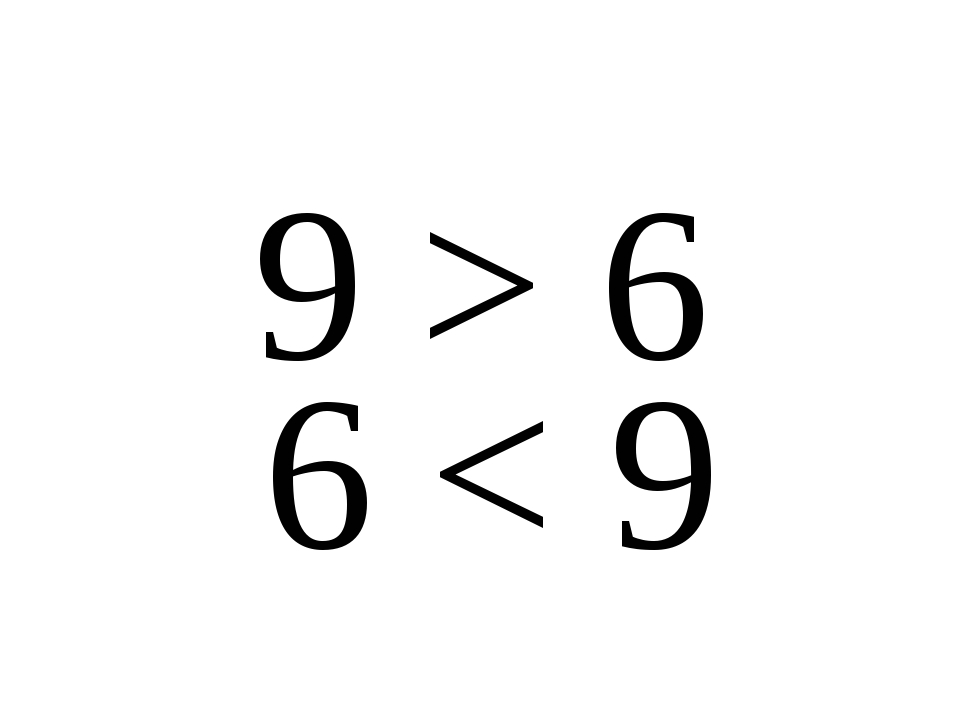
– Сравните количество листьев и грибов.
– Как бы вы записали, что количество листьев и грибов одинаково?
Учащиеся могут сами предложить использовать знак «равно» (=) в данной записи.
Физкульминутка
Еж спешил к себе домой,
Нес запасы он с собой.
Через кочки еж скакал,
Быстро по лесу бежал.
Вдруг он сел и изменился –
В шарик круглый превратился.
А потом опять вскочил
И к детишкам поспешил.

VI. Работа над составом числа 5.
В заключение урока педагог может предложить задание на развитие логического мышления.

VII. Итог урока.
Вопросы: Что нового узнали на уроке? Покажите знак больше, знак меньше.
Если все понятно зажгите зеленый свет, если нужна помощь, зажгите желтый свет, если срочно нужна моя помощь зажгите красный свет.
(У каждого ученика находится зеленый, желтый и красный кружок)

Таблица знаков (символов) в алгебре и их значения

Символ / знак	Название	Значение / описание	Пример
x	переменная x	неизвестная переменная, которую нужно найти	если 2x = 6, значит x = 3
≡	эквивалентность	логическая равнозначность или эквиваленция	A ≡ B, A эквивалентно B
~	приблизительно равно	приближенное равенство (слабое)	15 ~ 14
≈	приблизительно равно	приближенное равенство	01) ≈ 0.01</nobr>» data-order=»<nobr>sin (0.01) ≈ 0.01</nobr>»>sin (0.01) ≈ 0.01
∝	пропорционально	пропорциональность величин	y ∝ x, если: y = kx, а k — константа
∞	бесконечность	отсутствие границ или количественной меры
≪	намного меньше	A намного меньше, чем B	5 ≪ 50000
≫	намного больше	A намного больше, чем B	50000 ≫ 5
( )	круглые скобки	выражение в скобках считается в первую очередь	4 ⋅ (2+3) = 20
[ ]	квадратные скобки	выражение в скобках считается в первую очередь	[(6-3)⋅(2+7)] = 27
{ }	фигурные скобки	различное применение
⌊x⌋	нижние квадратные скобки	округление числа x до нижнего целого (пол)	3⌋ = 5</nobr>» data-order=»<nobr>⌊5.3⌋ = 5</nobr>»>⌊5.3⌋ = 5
⌈x⌉	верхние квадратные скобки	округление числа x до верхнего целого (потолок)	3⌉ = 6</nobr>» data-order=»<nobr>⌈5.3⌉ = 6</nobr>»>⌈5.3⌉ = 6
x!	восклицательный знак	факториал	5! = 1⋅2⋅3⋅4⋅5 = 120
log	логарифм	logab Это степень, в которую нужно возвести a, чтобы получить b	log28=3
| x |	одиночная вертикальная черта	абсолютная величина (модуль)	| -7 | = 7
f (x)	функция с переменной x	величина x определяет значение величины f (x)	f (x) = 5x + 2
(f ∘ g)	композиция функций	е. применение одной функции к результату другой» data-order=»<nobr>(f∘ g) (x) = f (g(x)),</nobr><br>т.е. применение одной функции к результату другой»>(f∘ g) (x) = f (g(x)), т.е. применение одной функции к результату другой	f (x)=5x, g (x)=x-2 ⇒ (f ∘ g (x)) = 5 (x-2)
(a,b)	открытый интервал	(a,b) = {x | a < x < b}	x ∈ (3,7)
[a,b]	закрытый интервал	[a,b] = {x | a ≤ x ≤ b}	x ∈ [3,7]
∆	дельта	изменение/разница	∆t = t2 — t1
∆	дискриминант	Δ = b2 — 4ac	y = x2 + 3x — 5 Δ = 32 — 4⋅1⋅(-5) = 29
∑	сигма	сумма всех значений в выбранном диапазоне	..+x<sub>n</sub></em></span></nobr>» data-order=»<nobr><span class="math"><em>∑ x<sub>i</sub>= x<sub>1</sub>+x<sub>2</sub>+…+x<sub>n</sub></em></span></nobr>»>∑ xi= x1+x2+…+xn
∑∑	сигма	двойная сигма	png" class="stbSkipLazy alignnone size-full" width="230" height=&quot»/>

НОД по ФЭМП Знакомство с знакми «больше, меньше, равно» | План-конспект занятия по математике (подготовительная группа):

Государственное бюджетное дошкольное образовательное учреждение

Детский сад №1 комбинированного вида

Невского района Санкт-Петербурга

Конспект непрерывной образовательной деятельности

по формированию элементарных математических понятий

Знакомство с математическими знаками

 больше, меньше, равно»

для детей подготовительной группы.

Воспитатель: Муромцева Е.А.

Санкт-Петербург, 2020

Цель: знакомство детей со знаками больше, меньше, равно

Задачи:

Образовательные — освоение знаковой системы соотношений между числами

Развивающие — Закрепить порядок чисел в числовом ряду, умение называть число на один меньше или больше. Закрепить умение называть соседей чисел

Воспитательные — воспитание выдержки, развитие внимания.

Материалы и обородувание: раздаточные карточки с цифрами от 1 до 6, демонстрационные знаки больше, меньше , равно, изготовленных из картона в виде крокодилов с открытой пастью, магнитные карточки с фруктами. Демонстрационный материал: две группы кружков по 4 и 5 разного цвета, знаки «больше, меньше, равно», наборное полотно, мяч, указка, две группы кружков по 4 и 5 разного цвета, 1/2 альбомного листа, разделенного пополам, знаки «больше, меньше, равно», карточки для самостоятельной работы, простой карандаш.

Методы: словесный, наглядный

Ход занятия:

Воспитатель: Ребята, мы сегодня с вами познакомимся с математическими знаками «больше, меньше, равно». Посмотрите на доску, как они обозначаются. На что похожи эти знаки? Варианты детей. Я согласна с вами. Больше они похожи на пасть крокодила. Посмотрите, к нам приплыли крокодильчики. Каждый крокодильчик плывет с открытой пастью к тем предметам, которых больше. А если количество предметов одинаковое, то крокодильчики плывут вместе с закрытой пастью. Садитесь за столы, ребята перед вами лежат геометрические фигуры и полотно (1/2 альбомного листа, разделенного пополам). Выложите слева 4 квадрата, а справа 5 кругов.

Воспитатель дублирует работу детей на магнитной доске

А теперь давайте сравним квадраты и круги. Чего больше? (кругов) Как вы узнали, что кругов больше? (посчитали) Значит у нас квадратов меньше, чем кругов. Каким же знаком мы укажем неравенство фигур? Поставьте между своими цифрами нужный знак. Давайте прочитаем нашу запись: 4 меньше 5. А  теперь добавьте два квадрата слева. Каких фигур больше? Каким знаком укажем? Давайте проговорим: 6 больше 5. А теперь прибавьте один круг справа. Сколько квадратов? Сколько кругов? Каких фигур меньше? Правильно. Одинаково. 6=6. Между цифрами ставим знак равенства.

Физминутка

Игра «Сделай движение на одно меньше (больше) »

Дети встают в круг, а воспитатель говорит: прыгните на один раз больше, чем я хлопну в ладоши (хлопаю в ладоши 6 раз), сделайте приседаний на одно меньше, чем я хлопну в ладоши и т. д.

Самостоятельная работа

Молодцы! А сейчас садитесь за столы. Посмотрите, перед вами лежат карточки и математические знаки. Расставьте правильно знаки «больше», «меньше», «равно»

Дети самостоятельно ставят знаки «больше», «меньше», «равно»

Воспитатель проверяет работы детей.

Дидактическая игра «Соседи». Воспитатель бросает мяч и называет число, ребенок называет соседнее большее или меньшее, в соответствии с заданием.

Математические задачки

— Что больше – 3 стула или 4 кровати?

— Чего меньше – 5 яблок или 2 груши?

— Чего больше – 6 конфет или 6 пряников?

Рефлексия: Как обозначаются знаки больше, меньше, равно? На что они похожи? Где эти знаки ставятся?

Открытый урок по математике » Знаки:Больше, меньше или равно» | План-конспект урока по математике (1 класс) на тему:

Тема: Знаки: > (больше),

Продолжительность урока: 35 мин.

Тип учебного занятия: урок изучения нового материала.

Цели:

Личностные:

• сохранять мотивацию к учебе, ориентироваться на понимание причин успеха в учебе,
• проявлять интерес к новому учебному материалу, развивать способность к самооценке.

Регулятивные:

• принимать и сохранять учебную задачу, учитывать выделенные учителем ориентиры действия,
• осуществлять итоговый
• и пошаговый контроль,
• адекватно воспринимать оценку учителя, различать способ и результат действия.

Познавательные:

• сравнивать множества, рассматривать параметры абсолютного (много — мало) и относительного (больше — меньше) сравнения.
• устанавливать взаимно — однозначные соответствия между элементами множеств как основу отношений «больше», «меньше», «равно» между соответствующими рассматриваемым множествам числами.
• использовать знаки для обозначения этих отношений (=, >,
• сравнивать числа на основе сравнения соответствующих им множеств.
• анализировать объекты, выделять главное, осуществлять синтез (целое из частей), проводить сравнение,
• строить рассуждения об объекте, обобщать (выделять класс объектов по какому-либо признаку).

Коммуникативные:

• допускать существование различных точек зрения,
• учитывать разные мнения,
• стремиться к координации,
• формулировать собственное мнение и позицию в высказываниях, задавать вопросы по существу.

Ход урока

1. Организационный момент.
2. Актуализация раннее изученного.

Устный счет.

— Мы сегодня отправимся с вами на прогулку в сказочный лес.

По тропинке в лесок

Покатился колобок.

Встретил серого зайчишку,

Встретил волка, встретил мишку

Да плутовку – лису

Повстречал еще в лесу.

Отвечай поскорей,

Сколько встретил он зверей?

— Назовите соседей числа 4.

— Какое число следует за числом 5?

— Какое число стоит перед числом 10?

— Какое число стоит между числами 6 и 8?

— Молодцы! Продолжаем свой путь.

— Посмотрите, какие чудесные елочки повстречались нам на пути. Давайте нарядим их.

— С каждого ряда один ученик выходит и вставляет нужные числа. (Числа записаны на шишках.)

— Проверка.

— Значит, 3 — это 2 и 1, 1 и 2; 4 – это 2 и 2,3 и 1, 1 и 3, 5 – это 2 и 3, 3 и 2, 4 и 1, 1 и 4.

Физминутка.

В небе плавает луна,

В облака зашла она.

1, 2, 3, 4, 5 – можем мы луну достать,

6, 7, 8, 9, 10 – и пониже перевесить.

III. Объяснение нового материала.

— Мы вышли на полянку. Какие грибы вы видите? (Белые и мухоморы)

— На какие другие две группы их можно разбить? (Съедобные и несъедобные)

— Передо мной две корзины. В одну положите съедобные грибы, в другую несъедобные грибы.

— Какие еще съедобные грибы знаете? Помните об этом, когда собираетесь в лес за грибами.

— Посчитаем, сколько тех и других грибов (3 и 2)

— В какой корзине больше грибов? Почему?

— Как вы сравнивали? (Поставили парами, друг под другом)

— Какой вывод делаем? (Белому грибу не хватило пары, значит белых грибов больше)

— Сколько белых грибов? (3)

— Какой цифрой обозначим? (3)

— Сколько мухоморов? (2)

— Какой цифрой обозначим? (2)

— Сравните количество грибов?

— Какое число при счете называют раньше: 3 или 2?

— Сравнили числа вы верно, но как это записать? (Ответы детей).

— Для того чтобы не писать слова «больше», «меньше», «равно» математики договорились обозначать их специальными знаками. Так слово «больше» мы будем обозначать знаком «>». Посмотрите. На, что он похож? (На клювик птички).  

Вы должны запомнить, что острие знака всегда показывает на меньшее число.

— Прочитаем запись (три больше двух): 3 > 2.

-Что мы можем сказать про число мухоморов? (Их два).

— Сколько белых? (3).

— Сделаем вывод: 2

— Читаем вслух (два меньше трёх).

— О чём должны помнить при записи неравенства? (Что остриё всегда показывает на меньшее число).

— Как сделать, чтобы грибов стало поровну? (Надо прибавить один мухомор) Работа у доски.

— Сколько белых грибов? (3).

— Сколько мухоморов? (3)

— Что можно сказать про их количество?

— 3=3.

— Прочитаем запись (три равно трём).

— Как по-другому можно сделать одинаковое количество грибов, уравнять их? (Один белый гриб убрать).

— Сколько стало белых грибов?(2).

— Сколько мухоморов?(2).

— Что мы можем сказать про их количество? (Одинаковое)

— Как записать?

— 2=2.

— Прочитаем запись (два равно двум).

— Хорошо! Посмотрите, какая у нас получилась запись. Скажите, с какими знаками вы сегодня познакомились?

Физминутка.

Буратино потянулся,

Раз – нагнулся, два – нагнулся

Руки в стороны развел –

Видно ключик не нашел.

Чтобы ключик нам достать,

Надо на носочки встать.

IV. Закрепление.

— Сколько и какие фигуры изображены наверху страницы? Давайте внимательно прочитаем математические записи под фигурами.

— Составьте рассказ о птицах по левому рисунку. Прочитайте записи. Поработаем также по правому рисунку.

— Придумайте рассказ о вишнях и восстановите записи.

 Физминутка для глаз.

— Закройте, ребята, глаза. Посмотрите вверх, вниз, вправо, влево, прислушайтесь. Слышите, как в нашем волшебном лесу поют птички.

— Молодцы! Открываем глазки, садимся.

— Волшебные птицы приглашают нас к тетради.

Тетрадь №1 с. 11.

— Найдите задание под первым кругом. Кто может прочитать, что надо сделать?

Самостоятельное составление примеров. Один ученик работает у доски.

— посмотрите, что случилось с часами внизу страницы? Надо восстановить пропавшие цифры.

— Переходим к последнему заданию. Как называется знак в верхней строке? В нижней? Закончите строки знаков.

V. Итог урока.

-Что нового узнали на уроке?

— О чем должны помнить, когда ставим знаки сравнения?

VI. Рефлексия:

— Кто остался доволен своей работой на уроке?

— Кто считает, что мог работать лучше?

ЗНАКИ СРАВНЕНИЯ «БОЛЬШЕ», «МЕНЬШЕ», «РАВНО» | План-конспект урока по математике (1 класс) на тему:

ЗНАКИ СРАВНЕНИЯ «БОЛЬШЕ», «МЕНЬШЕ», «РАВНО»

Педагогические цели: создать условия для ознакомления со знаками сравнения «больше», «меньше», «равно»; развития навыков счёта; закрепления знаний состава изученных чисел; учить писать знаки сравнения «больше», «меньше»; прививать аккуратность.

Планируемые результаты (предметные): знать названия и последовательность чисел от 1 до 5; использовать при сравнении чисел знаки сравнения «больше», «меньше», «равно».

Универсальные учебные действия (метапредметные):

Познавательные: стремиться к расширению своей познавательной сферы, стараться производить логические мыслительные операции (анализ, сравнение) для решения познавательной задачи.

Регулятивные: уметь оценивать результат своей работы на уроке.

Коммуникативные: уметь участвовать в диалоге на уроке и в жизненных ситуациях; отвечать на вопросы учителя, товарищей по классу; соблюдать простейшие нормы речевого этикета: здороваться, прощаться, благодарить; слушать и понимать речь других; осуществлять работу в паре.

Личностные: совместно договариваются о правилах общения и поведения в школе и следуют им; проявляют интерес к новому материалу, касающемуся конкретных фактов, но не теории (учебно-познавательный интерес на уровне реакции на новизну).

Ход  урока

I. Устный счёт.

– Назовите соседа.

3        2        4

– Назовите число, которое:

следует за числом 1;        на 1 больше числа 3;

предшествует числу 5;        на 1 меньше числа 2.

Целесообразнее, чтобы на данном этапе урока ученики пользовались карточками с цифрами.

II. Закрепление состава изученных чисел.

Для проведения этой работы учитель может использовать задание 1 (с. 46 учебника), а также воспользоваться счётным материалом и наборным полотном.

Выполняя задание учебника и пользуясь рисунками и данными равенствами, ученики рассказывают, как можно получить число 5.

Затем, пользуясь различными фигурками счётного материала и наборным полотном, дети составляют разными способами числа 4, 3.

III. Изучение нового материала.

1. Знакомство со знаками сравнения.

– Используя наборное полотно, сравните группы различных предметов.

Например: 5 зайчиков и 4 лисички;

2 розы и 3 ромашки и т. д.

– Можно ли то, что вы сказали, записать?

– В математике существуют специальные знаки. Для того чтобы показать, что одно число больше другого, используют знак «больше» (>), а для того чтобы показать, что одно число меньше другого, используют знак «меньше» ().

2. Пропись знаков сравнения.

Учитель показывает учащимся, как правильно писать знаки сравнения «больше», «меньше», и ученики прописывают их в тетрадях (задание 2, с. 18).

Далее на наборное полотно выставляется равное количество каких-либо предметов, например: 3 груши и 3 яблока.

– Сравните количество груш и яблок.

– Как бы вы записали, что количество груш и яблок одинаково?

Учащиеся могут сами предложить использовать знак «равно» (=) в данной записи.

IV. Составление и чтение равенств и неравенств.

Учащиеся, используя рисунки заданий 1, 2 учебника (с. 46), под руководством учителя составляют и читают неравенства и равенства (хором).

Например:

«На ветке сидело 3 птички, к ним прилетела ещё одна. Стало 4 птички. К 3 прибавить 1 получится 4.Четыре больше трёх.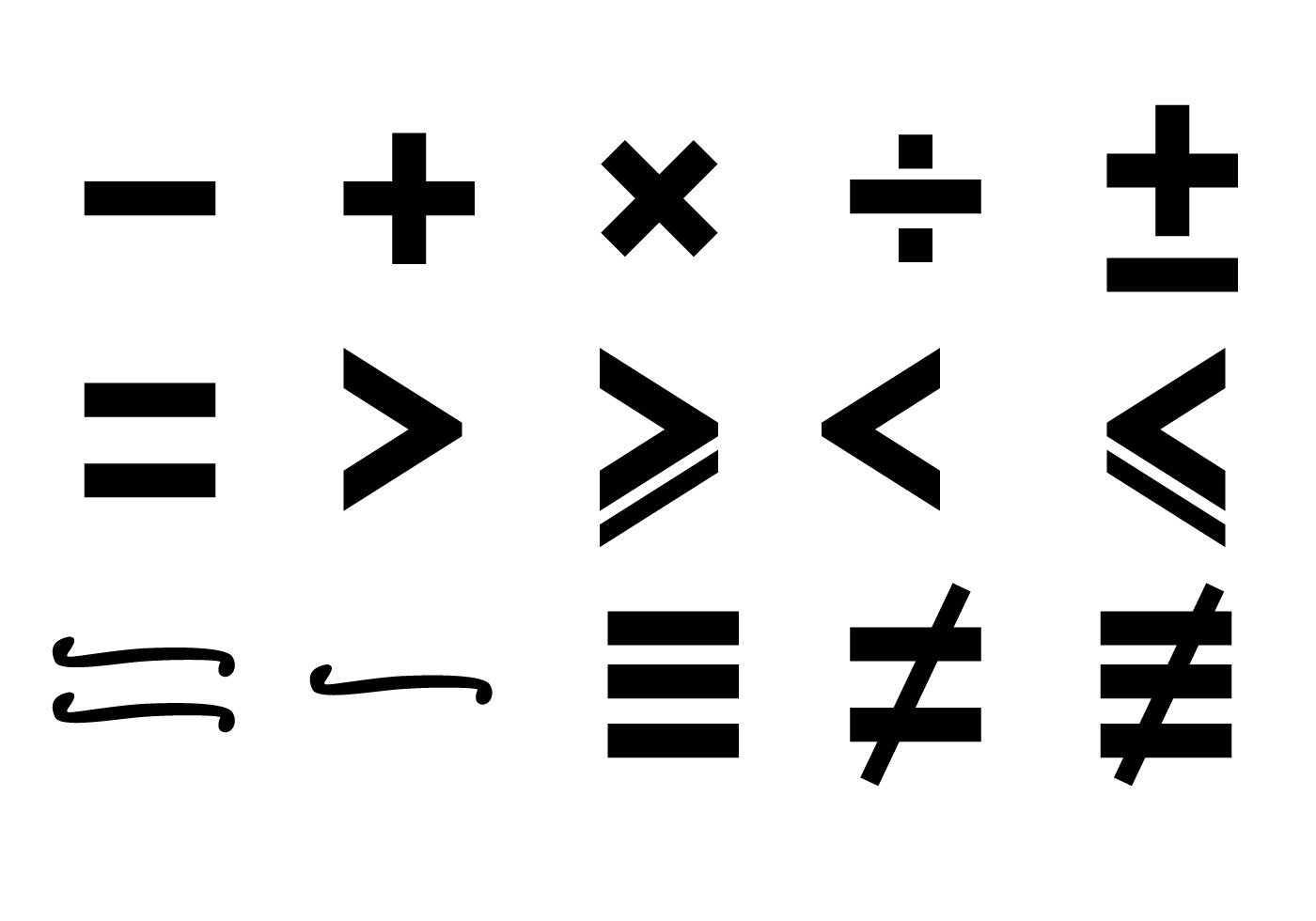

На ветке сидело 4 птички, одна улетела, осталось 3 птички. Из 4 вычесть 1 получится 3. Три меньше четырёх». И т. д.

V. Работа над составом числа 5.

В заключение урока учитель может предложить задание на развитие логического мышления. Например, задание, данное на полях учебника (с. 47).

VI. Итог урока.

Вопросы: Что нового узнали на уроке? Какое задание особенно понравилось?

п \]

Как видите, способ отображения уравнений зависит от разделителя, в данном случае \ [\] и \ (\) .

Открыть пример на обороте

LaTeX допускает два режима записи математических выражений: режим inline и режим отображения . Первый используется для написания формул, являющихся частью текста. Второй используется для записи выражений, которые не являются частью текста или абзаца и поэтому помещаются в отдельные строки.2 \] обнаружен в 1905 году Альбертом Эйнштейном. В натуральных единицах ($ c $ = 1) формула выражает тождество \ begin {уравнение} E = m \ end {уравнение}

Чтобы напечатать уравнения в режиме отображения , используйте один из следующих разделителей: \ [\] , \ begin {displaymath} \ end {displaymath} или \ begin {Equation} \ end {equal}

Важное примечание: Equation * Среда предоставляется внешним пакетом, обратитесь к статье amsmath .

Открыть пример на обороте

Ниже представлена ​​таблица с некоторыми общими математическими символами. Для более полного списка см. Список греческих букв и математических символов:

Различные классы математических символов характеризуются разным форматированием (например, переменные выделяются курсивом, а операторы — нет) и разным интервалом.

Открыть пример на обороте

Математический режим в LaTeX очень гибкий и мощный, с его помощью можно сделать гораздо больше:

Что значит быть успешным в математике? | Помощь детям в изучении математики

с коэффициентом n ³ , они могут понять многие ситуации, в которых объекты любой формы пропорционально увеличиваются или уменьшаются.(Они могут понять, например, почему чашка на 16 унций, имеющая ту же форму, что и чашка на 8 унций, намного меньше, чем в два раза по высоте.)

Знания, полученные с пониманием, обеспечивают основу для запоминания или реконструкции математических фактов и методов, для решения новых и незнакомых проблем и для генерирования новых знаний. Например, студенты, которые хорошо разбираются в операциях с целыми числами, могут распространить эти концепции и процедуры на операции с десятичными знаками.

Понимание также помогает учащимся избежать серьезных ошибок при решении проблем, особенно проблем значительного масштаба.Любой учащийся с хорошим пониманием чисел, который умножает 9,83 и 7,65 и получает за ответ 7 519,95, должен немедленно увидеть, что что-то не так. Ответ не может быть больше 10 умножить на 8 или 80, так как одно число меньше 10, а другое меньше 8. Это рассуждение должно наводить на мысль учащемуся, что десятичная запятая была неправильно установлена.

(2) Вычисления: выполнение математических процедур, таких как сложение, вычитание, умножение и деление чисел гибко, точно, эффективно и надлежащим образом.

Вычислительная техника включает свободное владение процедурами сложения, вычитания, умножения и деления мысленно или с помощью бумаги и карандаша, а также знание того, когда и как использовать эти процедуры надлежащим образом. Хотя слово вычисление подразумевает арифметическую процедуру, в этом документе оно также относится к свободному владению процедурами из других разделов математики, таких как измерение (измерение длины), алгебра (решение уравнений), геометрия (построение подобных фигур) и статистика (графические данные). Свободное владение означает умение выполнять процедуру эффективно, точно и гибко.

Ученикам необходимо быстро и точно вычислить основные числовые комбинации (6 + 7, 17–9, 8 × 4 и т. Д.). Они также должны стать точными и эффективными с помощью алгоритмов — пошаговых процедур для сложения, вычитания, умножения и деления многозначных целых чисел, дробей и десятичных знаков, а также для выполнения других вычислений. Например, у всех учащихся должен быть понятный им алгоритм умножения 64 и 37, который является достаточно эффективным и достаточно общим, чтобы использовать его с другими двузначными числами, и который может быть расширен для использования с более крупными числами.

Использование калькуляторов не должно угрожать развитию вычислительных навыков учащихся. Напротив, калькуляторы могут улучшить как понимание

GRE Предметный тест по математике (для тестируемых)

Обзор

• Тест состоит из примерно 66 вопросов с несколькими вариантами ответов, взятых из курсов, обычно предлагаемых на уровне бакалавриата.
• Примерно 50 процентов вопросов связаны с исчислением и его приложениями — предметом, который считается общим для почти всех математических специальностей.
• Около 25 процентов вопросов в тесте относятся к элементарной алгебре, линейной алгебре, абстрактной алгебре и теории чисел. Остальные вопросы касаются других областей математики, которые в настоящее время изучаются студентами многих учебных заведений.

Характеристики содержимого

Следующие ниже описания содержания могут помочь участникам подготовиться к экзамену. Указанные проценты являются приблизительными; Фактические проценты будут несколько отличаться от одного выпуска теста к другому.

РАСЧЕТ — 50%

Материал, изучаемый в обычной последовательности курсов элементарного исчисления — дифференциальное и интегральное исчисление одной или нескольких переменных, — включая приложения на основе исчисления и связи с координатной геометрией, тригонометрией, дифференциальными уравнениями и другими разделами математики.

АЛГЕБРА — 25%

• Элементарная алгебра: основные алгебраические методы и манипуляции, приобретенные в средней школе и используемые в математике
• Линейная алгебра: матричная алгебра, системы линейных уравнений, векторные пространства, линейные преобразования, характеристические многочлены, собственные значения и собственные векторы
• Абстрактная алгебра и теория чисел: элементарные разделы теории групп, теории колец и модулей, теории поля и теории чисел

ДОПОЛНИТЕЛЬНЫЕ ТЕМЫ — 25%

• Вводный реальный анализ: последовательности и ряды чисел и функций, непрерывность, дифференцируемость и интегрируемость, а также элементарная топология R и R ⁿ
• Дискретная математика: логика, теория множеств, комбинаторика, теория графов и алгоритмы
• Другие темы: общая топология, геометрия, комплексные переменные, вероятность и статистика, численный анализ

Приведенное выше описание тем, охваченных тестом, не следует считать исчерпывающим; необходимо понимать многие другие связанные концепции. Предполагаемые участники тестирования должны знать, что вопросы, требующие не более чем хорошего предвычисления, могут быть довольно сложными; такие вопросы могут входить в число самых сложных вопросов теста. В целом вопросы предназначены не только для проверки запоминания информации, но и для оценки понимания фундаментальных концепций и способности применять эти концепции в различных ситуациях.

Скачать учебник

<Вернуться к: Содержание теста

Обзор тем | MIT математики

Учебная программа бакалавриата по математике Массачусетского технологического института богата и разнообразна, и нет двух студентов пройти через него тем же путем.Для этого есть как минимум три причины: математика Массачусетского технологического института. мейджоры преследуют самые разные карьерные цели; у них широкий выбор фонов и препараты; и сама математика, как представлено исследовательскими интересами Преподавательский состав Массачусетского технологического института настолько широк, что немногие студенты могут освоить действительно репрезентативную часть его.

Это усложняет выбор предметов, но отсутствие общепринятого список тем для освещения означает, что студенты могут исследовать, не опасаясь пропустить важные составные части.Варианты степени, отличные от общего В разделе «Математика» указываются предметы, которые могут считаться центральными в своих областях.

Некоторые предметы не имеют формальных предпосылок — они требуют только интереса к математика. Это 18,01, 18,510 и 18,781.

Еще несколько тем откроются, как только у вас будет балл за 18.01 — 18.062J = 6.042J, а серия лекций IAP 18.095 — но для большинства требуется как минимум 18.01 и 18.02. (Все варианты 18.01 и 18.02 служат для выполнения предварительных требований.)

18.03 требуется по специальности «Математика». 18.03 имеет 18.01 как предварительное условие и имеет 18.02 в качестве обязательного условия: вы можете использовать 18.02 и 18.03 одновременно. (Обратите внимание, что в В особых случаях вместо 18.03 могут использоваться предметы верхнего уровня 18.152 или 18.303.)

Есть несколько субъектов, которые перечисляют только 18.02 в качестве обязательного условия:
18.05, 18.06, 18.100, 18.200, 18.600, 18.700 и 18.703.

После того, как вы закончите 18.03, откроются многие дополнительные предметы бакалавриата, такие как как 18.04, 18.300, 18.330. На странице основных планов по математике представлены инструкции по соответствующим классам для различных областей и приложений математики, примерно отсортированные в том порядке, в котором они могут быть взяты.

Вместо 18.03 достаточно продвинутые студенты могут заменить 18.152 или 18.303. В таком случае эти предметы не будут считаться RESTs и не будут использоваться в качестве одного из восемь обязательных предметов сверх 18.03.

Замена 18,650 на 15,075, 18,05 на 6,041 или 18,615 на 6,262 или от 18.600 до 15.079 будет предоставлено по запросу для математических специальностей, но не для несовершеннолетних. Обратите внимание, однако, что разрешена только одна такая замена. Отправить запрос по электронной почте Дебби Бауэр ([email protected]). Другие занятия в Массачусетском технологическом институте, не относящиеся к курсу 18, вряд ли будут рассматриваться на замену.

По всем остальным вопросам отправляйте электронное письмо профессору Джу-Ли Киму (juleekim @ mit.эду).

Математика состоит из шести факультативов по естественным наукам и технологиям: 18.03, 18.032 (ранее 18.034), 18.05, 18.06, 18.600 и 18.700.

Начиная с осени 2019 г., следующие предметы были перенумерованы:
18,175 изменено на 18,675
18,176 изменено на 18,676
18,177 изменено на 18,677

Многие математические предметы были перенумерованы с 2015-1016 учебного года. Для диаграммы старых номеров и новых смотрите здесь.

Номера предметов в курсе 18 дают представление о математической области предмета. В первая цифра обозначает поле. Каждый элемент ниже связан с краткой аннотацией предметы бакалавриата в данной области, включая сравнение аналогичных предметов. Эти комментарии неофициальные. Проконсультируйтесь с каталог для достоверной информации о содержании, предпосылках, наличии предмет, семестр и так далее.

18.0x Предметы начального уровня и специальности

18,1x Анализ

18,2x Дискретная прикладная математика

18,3x Непрерывная прикладная математика

18,4x Теоретическая информатика

18,5x Логика и теория множеств

18,6x Вероятность и статистика

18,7x Алгебра и теория чисел

18,8x Лабораторные объекты

18.9x Топология и геометрия и специальности

Выпускная программа по математике Прием

Подать заявку на программу PhD Подать заявку на программу магистра

О нашей выпускной программе

Посмотрите видео-тур о жизни аспирантов по математике и прочтите нашу брошюру.Ознакомьтесь с нашими выпускниками PhD и их вакансиями и посмотрите нашу брошюру о программе актуарных наук, если это вас интересует.

См. Информацию о программе ниже для

Щелкните ссылки справа, чтобы подать заявление о приеме и финансировании (освобождение от платы за обучение, стипендии для преподавателей и исследователей, стипендии).

Познакомьтесь с некоторыми нынешними аспирантами …

Антон Бернштейн Я выбрал Иллинойс для аспирантуры, потому что математический факультет в Иллинойсе очень большой и разнообразный, что позволяет найти экспертов, работающих практически в любой области.Узнать больше	Ванесса Ривера-Киньонес Я решила поступить в Университет Иллинойса, потому что хотела поступить в аспирантуру, которая заботилась об успехах студентов и обеспечивала дружескую атмосферу для студентов. Я был членом Ассоциации женщин-математиков. Узнать больше
Ашиш Кумар Пандей Урбана-Шампейн — один из лучших студенческих городков, в которых я был.Мне нравятся университетские библиотеки, а также публичные библиотеки. Еще мне очень нравится Центр развлечений и отдыха в Иллинойсе, в котором есть множество удобств, и это отличное место, чтобы немного повеселиться после целого дня математики. Узнать больше	Cara Monical В штате Иллинойс есть большая программа, которая предоставила мне различные возможности для изучения. Студенты поддерживают друг друга и счастливы быть здесь. Я регулярно участвую в нашем студенческом отделении Ассоциации женщин-математиков, которое проводит мероприятия в поддержку аспирантов, а также проводит информационные мероприятия в сообществе.Узнать больше
Юнь Ши Мне нравится этот маленький и удобный городок. Многие мои друзья живут недалеко от кампуса, и мы часто собираемся вместе, чтобы поговорить о математике или заняться другими делами. В Центре отдыха на кампусе я могу заниматься всеми видами спорта, которые мне нравятся. Центр исполнительских искусств Краннерта — отличное место для наслаждения представлениями. Узнать больше

Кандидат математических наук

Кандидаты должны обладать сильным опытом в области математики на бакалавриате.Для получения докторской степени обычно требуется от четырех до шести лет обучения. В 2015–2016 годах среднее время получения степени составляло 5,5 лет, а у 88% наших аспирантов — 6 лет или меньше. Основные этапы:

• Комплексные требования
• Предварительная экспертиза (диссертация)
• Докторская диссертация

Студенты, желающие получить докторскую степень, должны подавать заявки непосредственно на программу PhD. Студенты обычно могут получить степень магистра по пути к докторской степени.

Подробные требования к ученой степени см. В Руководстве для аспирантов по математике.

Кандидат наук по актуарной науке и аналитике рисков

The Concentration привлекает студентов, проявляющих большой интерес к аналитике финансовых рисков и актуарным приложениям математики, и предоставляет им передовые аналитические инструменты для профессиональной и академической карьеры. Студенты Концентрации завершают курсовую работу или профессиональные экзамены по вероятности, моделированию и анализу рисков, математической статистике, теории финансов и актуарным моделям для непредвиденных обстоятельств жизни или финансовой экономики.Студентам-концентраторам требуется , а не , необходимые для изучения абстрактной алгебры.

PhD приложений для студентов, в настоящее время обучающихся по программе MS в Департаменте математики Иллинойса

Эта форма только для использования студентами магистратуры факультета математики, желающими поступить в аспирантуру по математике. Ваша заявка будет рассмотрена наравне со всеми другими полученными заявками, но при использовании этой формы вам не придется платить дополнительный сбор за подачу заявки.

Магистр математики

Программа «Магистр математики» предоставляет студентам широкий выбор курсов и может предложить хорошую подготовку либо к работе в промышленности, либо к получению докторской степени по математике в другом университете. Редко, хотя и возможно, студенты поступают на докторскую программу в Иллинойсском университете после получения степени магистра математики. Для получения степени требуется 32 кредитных часа, и ее обычно можно получить за 18 месяцев. Магистерская диссертация не является обязательной.Заявки принимаются на осенний семестр каждый год. Финансовая помощь, как правило, недоступна, хотя студентов, участвующих в этой программе, иногда нанимают в качестве помощников преподавателей после зачисления.

Подробные требования к ученой степени см. В Руководстве для аспирантов по математике.

Учащиеся, поступающие на программу, должны пройти не менее шести курсов математики на уровне младших и старших классов (помимо математики). Настоятельно рекомендуется, чтобы поступающий студент прошел курсы, охватывающие следующие программы:

• Математика 417 — Введение в абстрактную алгебру
• Math 447 — Действительные переменные
• Курс компьютерного программирования

Магистр прикладной математики

Программа «Магистр прикладной математики» предназначена для студентов, желающих продолжить карьеру в области прикладной математики.Он также подходит для подготовки к поступлению в аспирантуру по прикладной математике. Студенты редко поступают на программу докторантуры в Университете Иллинойса после получения этой степени. Студенты могут выбрать один из трех направлений: Оптимизация и алгоритмы, Приложения к науке или Вычислительные науки и инженерия. Эта программа на получение степени требует 32 кредитных часа и обычно может быть завершена за 18 месяцев. Магистерская диссертация не является обязательной. Заявки принимаются на осенний семестр. Финансовая помощь, как правило, недоступна, хотя студентов, участвующих в этой программе, иногда нанимают в качестве помощников преподавателей после зачисления.

Подробные требования к ученой степени см. В Руководстве для аспирантов по математике.

Учащиеся, поступающие на программу, должны пройти не менее шести курсов математики на уровне младших и старших классов (помимо математики). Для варианта «Оптимизация и алгоритмы » и «» настоятельно рекомендуется, чтобы поступающий студент прошел хотя бы один курс по каждой из дисциплин линейной алгебры, реального анализа, вероятности или статистики и прошел курс теоретической информатики, отличный от курса программирования. .Для вариантов Applications to the Sciences и Computational Science & Engineering настоятельно рекомендуется, чтобы поступающий студент прошел хотя бы один курс по каждой из линейной алгебры, реального анализа, вероятности или статистики, а также дифференциальных уравнений и прошел подготовку. в компьютерном программировании.

Магистр актуарных наук

Эта программа готовит студентов к карьере в области актуарных наук; он обеспечивает основу для большей части материала по основным профессиональным актуарным экзаменам.Требуется, чтобы поступающий студент прошел последовательность исчисления и хотя бы один курс вероятности или статистики. Также полезно пройти обучение компьютерному программированию и изучение экономики или финансов. Подробные требования к степени см. В Руководстве для аспирантов по математике.

Для поступления на эту программу не требуется степень бакалавра в области актуарных наук, но студенты, которые еще не сдали первый актуарный экзамен (теория вероятностей), должны быть готовы сдать его в течение первого семестра.Студент, который поступает со значительным актуарным опытом, также сможет продолжить более продвинутую курсовую работу в области актуарных наук, математики, статистики и финансов.

Студент, успешно завершивший программу, обычно усвоил материал, охваченный большинством или всеми основными актуарными экзаменами (экзамены P, FM, MLC, MFE и C), и будет иметь возможность изучать финансы, экономику, или другие области потенциального применения в актуарной работе. Программа требует 32 кредитных часа и обычно может быть завершена за 18 месяцев.Финансовая помощь обычно недоступна; однако небольшому количеству студентов, которые являются носителями английского языка или которые выполнили требования к уровню владения английским языком для международных ассистентов преподавателя, могут быть предложены ассистенты преподавателя, которые предусматривают полный отказ от платы за обучение (независимо от классификации студента по месту жительства), частичный отказ от платы, и стипендия, достаточная для проживания в Шампейн-Урбана. Студенты могут начать программу либо в осеннем, либо в весеннем семестре.

Для получения информации о курсах актуарных наук, преподавательском составе, а также о социальных и сетевых мероприятиях, организуемых студентами, см. Страницу программы «Актуарные науки».

Магистр математики

Магистр преподавания математики предназначен для тех, кто хочет преподавать в средней школе или местном колледже. Это не приводит к сертификации для преподавания в государственных школах. Программа требует 32 кредитных часа и обычно может быть завершена за 18 месяцев.

Ассистент преподавателя и полный отказ от платы за обучение (плюс частичный отказ от платы) будут предложены в течение трех семестров всем допущенным абитуриентам, которые являются носителями английского языка или удовлетворяют требованиям к уровню владения английским языком для международных ассистентов преподавателей.

Подробные требования к ученой степени см. В Руководстве для аспирантов по математике.

Учащиеся, поступающие на программу, должны пройти не менее шести курсов математики на уровне младших и старших классов (помимо математики). Настоятельно рекомендуется, чтобы поступающий студент прошел курсы, охватывающие следующие программы:

• Math 402 — Неевклидова геометрия
• Математика 417 — Введение в абстрактную алгебру
• Math 444 — Элементарный вещественный анализ
• Курс прикладной статистики / вероятности
• Курс программирования или информатики

Математика Graduate Office
267 Altgeld Hall
Эл. Почта: math-grad @ illinois.edu
Телефон: 217-333-5749

Математика | Таусонский университет

Учебная программа по математике является целенаправленной и гибкой, с вариантами, которые помогут подготовить вас за карьеру в правительстве, бизнесе, промышленности и образовании или дальнейшее обучение в аспирантуре или профессиональном училище.

Математика предлагает четыре уровня концентрации:

Программа ускоренного обучения от бакалавра до магистра

Кафедра математики предлагает программу ускоренного обучения от бакалавриата до магистратуры.Ускоренные программы позволяют вам начать учебу в аспирантуре в качестве бакалавра, предлагая вам возможность сэкономить время и деньги, продвигая свою академическую карьеру. Комбинированный Б.С. по математике / М.С. Программа «Прикладная и промышленная математика» позволяет студентам заменить девять кредитов по программе «Прикладная и промышленная математика» на курсы бакалавриата по специальности «Математика».

Почему университет Таусона?

Академические преимущества

• Ресурсы большой школы с вниманием малой школы
• Высоко индивидуализированные консультации и всесторонняя поддержка студентов
• три активных студенческих математических клуба, предлагающие приглашенных докладчиков и мероприятия, связанные с решению проблем и подготовке к карьере
• Лаборатория прикладной математики, в которой избранные продвинутые студенты работают над исследованиями для местной промышленности или бизнеса

.

No related posts.