Найди формы геометрических фигур в картинках

Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок. Подобные занятия позволяют без лишних слов объяснить детям важный факт математической науки: все, что мы видим вокруг, имеет определенную геометрическую форму, начиная от маленького семечка в земле и заканчивая земным шаром. Конечно, это задание затрагивает данный вопрос не настолько глобально, как хотелось бы, но все-таки для дошкольника этого материала будет достаточно, чтобы увидеть геометрические формы во всех окружающих нас предметах (или по крайней мере в большинстве из них). 

1. Формы геометрических фигур — Найди их в картинках:

Чтобы начать искать формы геометрических фигур с помощью заданий в картинках, скачайте во вложениях файл задания, распечатайте его на цветном принтере и положите на стол. После этого предложите ребенку внимательно посмотреть на картинки и ответить, видит ли он знакомые формы среди них? Постарайтесь добиться того, чтобы малыш нашел как можно больше геометрических форм в этих изображениях.

Например, пирамидка напоминает форму треугольника, клубок с нитками — круг и так далее.

Можете сделать процесс поиска более содержательным, предложив ребенку найти геометрические формы в предметах вашей комнаты. Если это занятие его заметно увлечет, то можете продолжить научную экскурсию по дому, заглядывая в каждую комнату и каждый уголок с целью найти нужные геометрические формы.

Скачать задание — Формы геометрических фигур — вы можете во вложениях внизу страницы.

2. Найди фигуры на картинке — Задание-раскраска для распечатки

Здесь вы можете скачать еще одно задание — Найди фигуры на картинке, где малыш также должен проявить внимательность и знание основных геометрических фигур — кругов, треугольников и прямоугольников (в том числе, квадратов). Это упражнение не такое уж легкое, как кажется на первый взгляд. Ведь ребенку предстоит рассмотреть фигуры в множественных узорах и формах, из которых состоят нарисованные на картинке животные.

Более того, найденные фигуры необходимо еще и пересчитать, вписав полученные числа в специальные поля внизу бланка с заданием. После того, как ребенок выполнит все задания, картинку можно раскрасить произвольными цветами.  

Скачать задание «Найди фигуры на картинке» вы можете во вложениях внизу страницы.

3. Сложи картинку из геометрических фигур

Чтобы сложить картинку из геометрических фигур в нашем следующем задании, нужно вспомнить довольно популярную игру в собирание картинки из пазлов. Здесь принцип тот же. Задание развивает наглядное-образное и логическое мышление детей. Подготовьте распечатанные бланки с заданиями, простой карандаш, клей и ножницы.

Как проводить занятие. В каждом бланке дается несколько картинок-форм, но только одна из них может полностью вместить в себя заданные геометрические фигуры, нарисованнные вверху бланка. То есть, вам нужно заполнить этими фигурами одну из сложных форм.

Подбирать правильный ответ нужно визуально, без использования карандаша. Но если это для ребенка сложно, то в качестве исключения можно использовать простой карандаш, чтобы наметить контуры фигур.  

После того, как правильный ответ будет найден, можно его проверить наглядным образом. Для этого нужно вырезать геометрические фигуры в верхней части бланка и наклеить их на ту форму, которую ребенок выбрал.

Скачать задание — Сложи картинку из геометрических фигур — вы можете во вложениях

Бланк №1 — Квадраты

Бланк №2 — Треугольники

Бланк №3 — Прямоугольники

4. Найди и заполни геометрическими фигурами каждую форму.

Еще одно практическое занятие, помогающее закрепить умение ребенка видеть геометрические формы в различных объектах. На этот раз задание состоит в том, чтобы в каждой сложной фигуре обнаружить несколько геометрических фигур и нарисовать их, полностью заполнив ими большую фигуру.

Как выполнять задание. Дайте ребенку бланк №1 для заполнения данными фигурами (квадрат и треугольник) всех сложных фигур на бланке. В качестве подсказки используйте бланк №2 — именно так должно получится у ребенка, если он все сделает правильно.

Внимание! Размеры фигур, которые рисует ребенок, должны точно соответствовать нарисованным на бланке!

Вооружайте ребенка простым карандашом и ластиком, распечатывайте бланк с заданием и смело приступайте к упражнению.

Скачать задание 3 вы можете во вложениях внизу страницы

Бланк №1

Бланк №2

Также вам будут полезны и другие материалы по изучению геометрических фигур: 

Рисунки из геометрических фигур — Задания в картинках и раскраски

Веселые и красочные задания для детей «Рисунки из геометрических фигур» являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических форм:

Геометрические фигуры и их названия — Задания в картинках

Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках.

 

Геометрические фигуры — Раскраска для дошкольников

Задания ознакомят ребенка с основными фигурами геометрии — кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.

 

Плоские геометрические фигуры — Обведи и дорисуй

Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги.

Наложение фигур друг на друга — Задание для детей

Наложение фигур друг на друга — это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение. Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры. 

Свойства геометрических фигур для дошкольников

Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер.

 

Счет геометрических фигур — Картинки с заданиями

Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.

 

Чертежи геометрических тел — Задание для детей

В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел. По сути, это занятие представляет собой мини-урок по начертательной геометрии

Геометрические фигуры из бумаги — Вырезаем и занимаемся

Здесь мы подготовили для вас объемные геометрические фигуры из бумаги, которые нужно вырезать и склеить. Куб, пирамиды, ромб, конус, цилиндр, шестигранник,  распечатать их на картоне (или цветной бумаге, а затем наклеить на картон), а затем дать ребенку для запоминания. 

Прописи-цифры от 1 до 10 для распечатки — Скачай и обводи

Здесь вы можете скачать прописи цифры, распечатать их на принтере и использовать в домашнем обучении для подготовки детей к школе

 

И еще можете поиграть в математические игры онлайн от лисенка Бибуши:

Игра «Что лишнее? — Геометрические формы»

В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок.

При этом необходимо руководствоваться признаками геометрических форм.

 

Фигуры из геометрических фигур. Картинки для детей, дошкольников, 1-2 класс. Шаблоны для аппликаций

Фигуры и цвета малыши начинают изучать с самого детства с помощью различных методик, в частности, через аппликации. Эти аппликации складываются из геометрических фигур, которые ребенок приклеивает к картонной или бумажной основе.

С какого возраста можно начинать учить с ребенком геометрические фигуры

По мнению ученых, обучать малыша следует с самого рождения, при этом его проводят в несколько этапов:

1. После рождения малыш почти ничего не запоминает, однако приучается смотреть на мир во всех его аспектах. В это время рекомендуется разговаривать с младенцем, проговаривая каждую фигуру, читать небольшие детские стихи, петь песни.
2. Когда ребенку исполнится 6 месяцев, он постарается узнать о мире побольше. Для этого он будет трогать и покусывать предметы. Важно подобрать правильные игрушки. Подойдет набор мягких квадратов, на которых нарисованы цветы, бабочки, птички.
3. Следующий этап начинается тогда, когда малыш учится говорить. Необходимо проговаривать все названия фигур, начиная с самых простых (круг, треугольник, квадрат). Затем придет черед трапеции, прямоугольника и других. На этом этапе поможет игрушечная пирамидка, пластмассовые кубики, из которых строят башню, и рисование.

Изучение геометрических фигур с ребенком можно начинать с самого раннего возраста

Таким образом, обучение можно с рождения ребенка, используя разные методики.

Изучение геометрических фигур: названия, форма, цвет, размер

С возрастом ребенок должен узнавать все больше фигур и цветов.

К 2 годам необходимо знать:

• треугольник;
• квадрат;
• круг.

В этом же возрасте нужно знать основные цвета:

• синий;
• красный;
• желтый;
• зеленый;
• белый.

К 2 годам ребенок должен знать основные геометрические фигуры и цвета

Некоторые дети в 2 года знают несколько больше цветов:

• оранжевый;
• фиолетовый;
• черный;
• розовый.

К 6 годам ребенок узнает о более сложных, комбинированных цветах и оттенках, знакомится с составными (состоящими из основных) фигурами.

Дети обучаются через игры, они бывают разной сложности, поэтому давать их ребенку рекомендуется в следующей последовательности:

• Нарисованные на картоне круги, треугольники, квадраты разных размеров и цветов. Называйте изображения своими именами, проговаривая их вслух.
• Нарисовать на картоне только контуры фигур, причем все контуры должны быть разных цветов, чтобы малыш обводил их соответствующими цветами, раскрашивал и проговаривал названия вслух. В возрасте от 2 лет следует начинать сравнивать размеры.

Сортер с геометрическими фигурами помогает детям в их изучении

• Вырезать фигуры и разложить на видных местах в доме, чтобы малыш искал рисунки. Каждый раз, когда ребенок находит изображение, он должен назвать следующие характеристики: фигуру, цвет и размер.
• Игровые наборы, предназначенные для изучения выше перечисленного. Например, пирамидка, грибы разных цветов и размеров на подставке, мозаика и другие. Такие игры развлекут ребенка, привлечет его внимание.
• Поиск геометрических фигур в окружающем мире. Например, стол – это прямоугольник, шкатулка – квадрат, а мячик – круг. Рекомендуется рассматривать и более сложные формы: стакан – цилиндр, а праздничный колпак – пирамида.

Разработано множество методик, предназначенных для изучения фигур и цветов. Они рассчитаны для детей разного возраста, а также учитывают их любимые занятия.

Изучение сложных геометрических фигур с помощью простых: польза занятий для детей

Фигуры из геометрических фигур, или составные фигуры, проще изучать через простые формы. Необходимо вырезать несколько квадратов, кругов и треугольников и складывать их.

Примеры составления сложных фигур:

• Трапеция: квадрат + 2 треугольника.
• Прямоугольник: 2 и более квадратов.
• Ромб: 2 равных треугольника.
• Параллелограмм: 2 квадрата + 2 равных треугольника.

Ребенок должен быть полностью вовлечен в процесс обучения, в противном случае обучение будет бесполезным. Обучение в формате игры – лучший способ привлечь внимание ученика и сделать процесс интересным. Делая открытия самостоятельно, малыш пожелает продолжить обучение.

Уроки начертательной геометрии для детей

Начертательная геометрия направлена на развитие пространственного мышления. Ребенок учится представлять сложные объемные фигуры, раскладывая их на простые и плоские. Задания предусматривают не только выбор правильных ответов, но и объяснение своего выбора и почему другие ответы неверны.

Дорисовать фигуру по образцу

Закрепить урок поможет рисование.

Что нужно сделать:

1. Показать ребенку фигуры, рассказать о них, привести примеры вещей соответствующей формы, которые находятся в комнате.
2. Распечатать бланки, на которых пунктирной линией изображены недорисованные фигуры (пример бланка приведен выше).
3. Задание: продолжить пунктир, сказать, которое изображение является кругом, квадратом, прямоугольником.
4. Обговорить получившиеся результаты.

Вместо пунктирных линий могут быть и обычные, но прерывающиеся. Это упрощенный вариант упражнения. Чтобы усложнить задание, необходимо распечатать бланк, на котором часть фигуры закрашена, но не повторяет контуры. Это запутает малыша.

Кроме дорисовывания, появляется необходимость закрасить оставшуюся часть фигуры.

Обведение фигуры по точкам

Упражнение по соединению точек развивает воображение, позволяя представить, какие точки нужно соединить, чтобы получилась заданная фигура. Этот навык развивает способность к выполнению заданий по образцу, что пригодится в школе. Ребенок должен рисовать карандашом, чтобы он мог исправить ошибки.

Как делать упражнение:

1. Распечатать бланки заданий.
2. На каждом бланке слева представлен образец рисунка, а справа множество точек, из которых нужно составить такой же рисунок.
3. Ребенок должен заметить, что точки разные: есть точки с крестиками, черные точки и белые. Одинаковые точки соединять нельзя.
4. Справа точек больше, чем нужно – некоторые останутся вне рисунка.

Поиск геометрических фигур на изображении

Фигуры из геометрических фигур привлекают внимание детей. Им становится интересно, как же разделить сложный рисунок на простой, а простой собрать в сложный. В этом задание предлагается найти круги, квадраты, треугольники. В усложненном варианте добавляются прямоугольники, трапеции, овалы и ромбы.

Легкий рисунок «бабочка» для девочек:

• Круги разных размеров – туловище.
• 2 пары одинаковых треугольников – нижние и верхние крылья.
• По 2 штуки маленьких, средних и больших кругов – украшение крыльев.

В рисунке «дом» можно найти:

• Квадрат – основная часть дома.
• Прямоугольник – дверь.
• Два круга или овала – окна.
• Маленький круг – дверная ручка.
• Треугольник – крыша.

Усложненный рисунок «кораблик»:

• Трапеция – корпус корабля.
• 3 круга – окна кают.
• 2 прямоугольника разных размеров – возвышение на палубе.
• Треугольники – паруса.

Рисунок «робот»:

• Квадрат – тело робота.
• 2 равных прямоугольника – ноги.
• 2 одинаковых равносторонних треугольника – ступни.
• 2 равных ромба – кнопки на теле робота.
• Длинный прямоугольник – плечи.
• 2 круга, 2 прямоугольника и 2 круга – руки.
• Небольшой квадрат – лицо.
• 2 маленьких круга – глаза.
• Треугольник – нос.
• Тонкий прямоугольник – рот.
• Трапеция (в длине должна быть больше квадрата лица) – шляпа.

Примеры рисунков расположены по степени сложности (от легкого к сложного).

Раскрашивание геометрических фигур

Задание развивает пространственное мышление, так как ребенок должен закрасить фигуры так, чтобы одна перекрывала другую.

Как проводить упражнение:

1. Нарисовать на листе бумаги пары круг-квадрат, треугольник-круг, квадрат-треугольник и другие так, чтобы их концы пересекались, перекрывая друг друга.
2. Предоставить ребенку лист и цветные карандаши.
3. Попросить малыша раскрасить фигуры так, чтобы одна из пары находилась сверху друг друга, проговаривая вслух цвета.

Чтобы облегчить задачу, необходимо заранее показать ребенку объемные фигуры, дать ему возможность подвигать их и поиграть.

Пазл из геометрических фигур: как сложить нужные формы

Фигуры из геометрических фигур не сразу понятны малышам. Для упрощения обучения рекомендуется собирать своеобразные «пазлы».

Фигуры из геометрических фигур ребенку поможет научиться собирать игра в пазлы

Как проводить первый вариант упражнения:

1. Распечатать бланки, на которых сверху нарисованы простые фигуры, а внизу несколько сложных форм.
2. Ребенок должен найти, какой из вариантов на нижней части листа совмещает в себе все перечисленные формы на верхней части листа.
3. Также необходимо объяснить получившиеся ответы.

Вначале следует давать простые рисунки, в которых фигуры соединяются без наклона. Также форма может содержать только квадраты или только треугольники.

Упражнение развивает фантазию и ориентацию в плоскости фигур.

Группировка простых фигур в сложные

Это задание обратно предыдущему.

Как выполнять упражнение:

1. Распечатать на картоне несколько кругов, квадратов, треугольников и трапеций, вырезать их.
2. Задача ребенка – составить как можно больше разных форм, состоящих из перечисленных выше фигур.
3. Чтобы выучить цифры, необходимо считать каждый вид фигур.

Чтобы усложнить задачу, ребенок должен составить определенный рисунок (птицу, корабль).

Второй вариант выполнения упражнения:

1. Показать ребенку закрашенное изображение и предоставить фигуры, необходимые для составления этого рисунка.
2. Задача заключается в составлении идентичного изображения.

Этот вариант предназначен для детей от 6 лет.

Примеры и пошаговые инструкции для создания аппликаций из геометрических фигур

В зависимости от возраста ребенка аппликации выполняют по-разному:

• До 2,5 лет дети не умеют вырезать, поэтому это делает взрослый. На усмотрение взрослого, приклеивать бумажные детали к картону может ребенок или сам взрослый. Во втором случае, следует советоваться с малышом, куда именно приклеить деталь.
• От 2,5 до 5 лет дети умеют вырезать ножницами, но делают это неровно, поэтому при необходимости следует исправлять неровности.
• От 5 лет дети учатся ровно резать, поэтому участие взрослого в процесс создания аппликации минимально.

С 2 до 5 лет дети еще неровно вырезают фигуры и способн делать самые простые аппликации

В маленьком возрасте малыш старается упростить форму, которую видит. Например, облака, похожие на кудри, упрощаются до овала.

Для детей 3-5 лет

Привлечь маленьких детей могут необычные картинки и процесс их создания. Аппликация «Ежик» нестандартна, но проста в создании. В качестве иголок используются ладошки из коричневой или черной бумаги.

Их можно сделать двумя способами:

• Приложить ладошку ребенка к бумаге с обратной стороне листа и обвести простым карандашом. Вырезать ладошку по контуру.
• Раскрасить ладошку малыша краской и приложить к бумаге. Контуры обводить не следует. Вырезать деталь.

Понадобится 4 ладошки.

Также понадобятся следующие детали:

• «Лодочка», состоящая из овала и кривого треугольника. Эта деталь послужит телом и носом ежика.

• Небольшой круг – кончик носа.
• Красный полукруг – рот.
• Белый полукруг – часть глаза.
• Маленький черный круг – зрачок.
• Круг с подрезанными верхней и нижней частью зеленого цвета – яблоко.
• Темно-зеленые ромбы – 2 листа яблока.
• Деталь, похожая на капсулу белого цвета – ножка гриба.
• Коричневый полукруг – шляпка гриба.
• Четыре трапеции разных размеров – ноги.

Детали следует приклеивать в той последовательности, в которой они перечислены выше. При этом 2 ладошки расположены пальцами вверх, одна – по диагонали, последняя – вбок.

Конец тела располагается около последней ладошки.

Аппликация «Объемная божья коровка»:

• Половина черного овала – голова.

• Два красных или розовых круга – тело. Круги нужно согнуть пополам: одну половину приклеить к картону, вторую оставить. Половину второго круга приклеить рядом с первой так, чтобы из приклеенной части образовался круг.
• Черные круги – точки. Они располагаются как на приклеенных, так и на отступающих частях тела.
• Покупные глаза разного размера.
• Усики и круги на их концах дорисовать черным фломастером.

Картина привлекает своим объемом. Ребенок может поиграть с выступающими частями божьей коровки.

Как сделать аппликацию «цветочная поляна»:

1. Раскрасить картонный лист зеленой краской.
2. Небольшой квадрат сложить 4 раза так, чтобы получился квадрат меньшего размера. Обрезать 3 угла (кроме угла сгиба). Разогнуть лист.
3. В центр получившихся из квадрата лепестков приклеить круг контрастного цвета.
4. Сделать несколько цветков.
5. Приклеить цветы на раскрашенный лист картона.

Картина получится многоцветной, поэтому ребенку станет интересно рассмотреть цветы поближе.

Для учеников 1 класса

Первоклассники способны создавать более сложные аппликации, используя новые материалы.

Аппликация «Сирень»:

• Раскрасить картонный лист акварельной краской. При желании, можно сделать плавный переход от одного цвета к другому (от красного к фиолетовому, от фиолетового к синему или от синего к бледно-голубому).
• Дать фону подсохнуть.
• Вырезать прямоугольник и круг для вазы.
• Приклеить к основе сначала прямоугольник, а круг – сверху него.
• Вырезать из гофрированной бумаги зеленого цвета 4 тонкие короткие полоски. Эти полоски будут стеблями.
• Равномерно приклеить стебли к концу вазы.
• Вырезать из цветной салфетки 6 деталей овальной или яйцеобразной формы. Эти детали помогут обозначить границы соцветий сирени.

• Приклеить детали рядом со стеблями. Так как соцветий больше, чем стеблей, необходимо соотнести 4 соцветия со стеблями, а остальные приклеить по краям вазы.
• Разрезать салфетки на маленькие квадраты.
• Некоторые квадрату скомкать, остальные сначала порвать, а потом скомкать.
• Смазать соцветие клеем, распределить на нем комочки из салфеток.
• Повторить пункты 9-11 для остальных соцветий.
• Вырезать 6 листов из гофрированной бумаги: 4 приклеить на стебли, остальные – по краям.
• В некоторых местах объемных соцветий нанести пятна розовой акварельной краски.

Выполнить аппликацию «Гусеница» под силу каждому ребенку в 7 лет. Процесс создания занимает немного времени, поэтому подойдет, чтобы занять ребенка на небольшой период времени.

Как делать:

• Вырезать несколько разноцветных кругов одинакового размера.
• Приклеить на картон круги друг за другом. При желании, расположить круги с подъемами, будто гусеница ползет.

• На первом кругу нарисовать улыбку, приклеить глаза и дорисовать ресницы.
• Приклеить рожки – два треугольника.

Для детей 2-4 класса

Фигуры, изученные детьми до 11 лет, позволяют создавать сложные и интересные рисунки. Составление комбинаций из геометрических фигур и вырезание мелких деталей развивает мелкую моторику. В частности, этому способствует аппликация «Мыши».

Детали, необходимые для первой мыши:

• Серый полукруг – тело.
• 2 черных круга разных размеров – нос и глаз.
• 2 одинаковых серых круга – уши.
• 2 отрезка черной проволоки – усы.
• Отрезок белой толстой нити – хвост.

Сначала следует приклеивать к основе одно ухо, затем тело, которое немного перекрывает ухо, затем остальные детали.

Детали, необходимые для второй мыши:

• Серый овал с заостренными концами – тело.
• 2 серых круга – уши.
• 2 маленьких черных круга – глаза.
• Черный круг большего размера – нос.
• 2 отрезка черной проволоки – усы.
• Отрезок толстой белой нити – хвост.

Кусок сыра – равносторонний желтый треугольник. Его необходимо сложить пополам и склеить. На двойном треугольнике нарисовать круги и вырезать с помощью маникюрных ножниц. Нижнюю часть треугольника обрезать так, чтобы треугольник оказался равносторонним.

Как расположить элементы на листе:

1. Приклеить сыр так, чтобы угол был направлен в верхнюю правую диагональ.
2. Первую мышь приклеить над сыром ближе к основанию. Хвост опустить вниз и вправо так, чтобы он находился на сыре.
3. Вторую мышь расположить под сыром ближе к его концу так, чтобы нос почти упирался в край сыра.

В качестве фона может выступать не только однотонный картон, но и картон с необычным орнаментом (клетка рубашки или круги). Дети в возрасте 8-10 лет способны комбинировать разные элементы, создавая сложные сюжеты.

Чтобы создать аппликацию «Космос», необходимо сделать следующие модели ракет:

1. Вырезать корпус ракеты, который показан на фото ниже.
2. Вырезать 3 круга контрастного цвета одинакового размера.
3. Вырезать 3 круга меньшего размера.
4. В каждый круг из пункта 2 приклеить по одному кругу из пункта 3. Получатся окна.
5. Приклеить окна на корпус ракеты.

Вторая модель ракеты:

1. Вырезать корпус ракеты по фото.
2. Вырезать два круга разного размера.
3. Вклеить в маленький круг в большой.
4. Вырезать овал, разрезать его на 4 части (2 части – крылья ракеты).
5. Приклеить окно и крылья к корпусу ракеты.

Необходимо сделать несколько ракет и приклеить к листу так, чтобы они летели в разных направлениях.  Оставшуюся площадь заполнить небольшими кругами и звездами. В мультфильмах из хвоста ракет вырывается огонь или дым, который можно изобразить овалами или спиральной деталью.

Геометрическая аппликация «Транспорт»

Фигуры из геометрических фигур складываются в полноценные картины при их правильном распределении.

Ниже рассмотрены аппликации разных видов транспорта. Аппликация «Поезд» состоит из вагонов двух типов: первого вагона и остальных. Вначале перечислены фигуры, необходимые для первого вагона.

Аппликация	Фигуры, которые используются в процессе создания аппликации	Часть транспорта, которую изображает фигура	Особенности расположения
«Поезд»	Прямоугольник	Корпус	Полукруг находится слева от прямоугольника
	Полукруг
	Большой и маленький прямоугольники	Кабина водителя	Один из прямоугольников — окно
	Треугольник	Труба	Часть фигуры перекрывается прямоугольником корпуса
	Треугольник меньшего размера	Фонарь	Частично перекрыт полукругом корпуса
	Прямоугольник	Основа для колес	Клеится под корпусом
	3 круга	Колеса	Располагаются под корпусом, крепятся на прямоугольник
	Круг большего размера	Колесо	Клеится под кабиной водителя, частично ее перекрывая
	Тонкие прямоугольники	Цепи, соединяющие вагоны	—
	Прямоугольники	Вагоны	—
	По 4 круга 1 вагон
«Автобус»	Большой прямоугольник	Корпус	—
	2 круга	Колеса	Перекрывают часть корпуса, располагаются ближе к краям прямоугольника
	2 прямоугольника	Двери	Располагаются около колес
	4 более тонких прямоугольника	Окна дверей	На каждую дверь 2 окна
	2 квадрата	Окна на корпусе	Квадратные окна располагаются по краям от дверей, а прямоугольное окно – между ними
	Прямоугольник
«Корабль»	Треугольник с обрезанными краями	Основная часть корабля	—
	3 круга	Окна	—
	Тонкий длинный прямоугольник	Палка, на которую крепятся паруса	Клеится левее середины основного треугольника
	Треугольник	Паруса	Клеятся с двух сторон от палки
	Полукруг
	Квадрат	Флаг	Располагается в верхней части палки
	Прямоугольные треугольники
«Грузовик»	2 прямоугольника разных размеров	Кабина водителя и передняя часть	Меньший прямоугольник крепится сбоку от большого
	Квадрат	Окно	—
	Прямоугольник	Кузов	—
	2 круга	Колеса	Один круг располагается под кабиной водителя, а второй – под кузовом. Часть кругов перекрывает ту часть грузовика, к которому крепится.
	Треугольник	Груз	—

Аппликации из геометрических фигур «Животные»

Животных могут изобразить даже самые маленькие.

Аппликация «Мартышка» состоит из следующих фигур:

• Овал – тело.
• 4 тонких овала – руки и ноги.
• Изогнутый тонкий овал – хвост.
• Круг – лицо.
• 4 круга (2 маленьких и 2 средних) – уши.
• Круг – нос.
• 2 белых и 2 черных круга – глаза.

Аппликация «Медведь» состоит из тех же фигур, но в качестве ушей используются 2 полукруга, а хвост не виден.

Аппликация «Цыпленок»:

1. Вырезать 2 овала и приклеить на расстоянии друг от друга. Эти овалы станут крыльями.
2. Вырезать желтый овал – тело будущего цыпленка. Приклеить тело между крыльями так, чтобы оно перекрывало часть крыльев.
3. Сверху приклеить круг – лицо цыпленка.
4. Вырезать маленький оранжевый круг. Внутрь приклеить еще более маленький черный круг.
5. Склеенные круги приклеить на лицо сбоку, будто цыпленок смотрит вправо или влево.
6. Вырезать 3 красных треугольника.
7. Один треугольник приклеить сбоку от лица рядом с глазом – этот треугольник будет клювом.
8. Остальные треугольники приклеить под телом – это лапы птицы.
9. Один прямоугольный желтый треугольник приклеить с той стороны, где не расположен клюв. Этот треугольник – хвост.

Чтобы составить полноценную картину, необходимо добавить траву, состоящую из овалов разных размеров и длины, рядом с лапами цыпленка. Таким образом, птица будто бегает по полю.

Аппликация слон складывается из следующих деталей:

• Круг – тело.
• Прямоугольники – ноги.
• Полукруги – ступни.
• Тонкий треугольник – хвост.
• Полукруг большего размера – ухо.
• Небольшой круг – голова.
• Прямоугольник – хобот.
• Белый и черный круги – глаз.

Рекомендуется дать ребенку выбрать самостоятельно, какое животное он хочет изобразить и как хочет это сделать.

Рисунки из геометрических фигур: задания для детей

Изучив геометрические фигуры, ребенку необходимо понять, как их комбинировать в сложные рисунки.

Фигуры из геометрических фигур – первый этап изучения. Второй этап – складывание фигур в рисунки окружающих предметов.

Варианты упражнений на знание геометрических фигур:

• Распечатать бланк, на котором изображены различные предметы. Задача ребенка – назвать фигуры, которые он видит в представленных предметах.
• Разделить лист на 2 части. В левой части нарисовать по пары из двух одинаковых фигур. Упражнение заключается в том, что ребенок должен нарисовать в правой части фигуры, которые можно получить из пар фигур слева (2 прямоугольных треугольника – прямоугольник).

• Распечатать бланки, на которых изображены различные предметы (поезд, корабль, елка с шариками). Задание: посчитать количество каждой из фигур на рисунках.
• Распечатать бланки, на которых нарисованы картинки и задано определенное количество какой-либо фигуры. Необходимо найти рисунок, на котором присутствует указанное количество заданной фигуры.

Перечисленные выше задания помогают ребенку запомнить фигуры и научиться правильно считать. С геометрическими фигурами ребенок начинает знакомиться с самого рождения, узнавая все больше информации об окружающем мире. Обучение рекомендуется проводить в форме игры, составляя с ребенком разные комбинации из фигур.

Автор: mariamur1

Оформление статьи: Натали Подольская

Видео про геометрические фигуры

Как сделать фигуры из геометрических фигур — поделки для детей в этом видео:

Презентация к уроку по математике (средняя группа) на тему: Презентация «Геометрические фигуры»

Слайд 1

Геометрические фигуры ( для средней группы) Воспитатель: Андрусенко О.Н Муниципальное дошкольное образовательное учреждение детский сад № 8

Слайд 2

Задачи: 1.Учить детей выделять особые признаки фигур (наличие или отсутствие углов и др.) 2.Познакомить детей с прямоугольником, сравнивая его с кругом, квадратом, треугольником. 3.Формировать представление о том, что фигуры могут быть разных размеров: большой, маленький. 4.Учить соотносить форму предметов с известными геометрическими фигурами: тарелка-круг, платок-квадрат, мяч-шар, дверь-прямоугольник и др. 5.Развивать умения различать пространственные направления: вверху-внизу, справа-слева. Цель: развивать представления детей о геометрических фигурах: круге, квадрате, треугольнике.

Слайд 3

Он давно знакомый мой, Каждый угол в нём прямой, Все четыре стороны Одинаковой длины. Вам его представить рад Как зовут его? Квадрат

Слайд 5

Словно стол стоит квадрат. Он гостям обычно рад. Он квадратное печенье Положил для угощенья. Он — квадратная корзина И квадратная картина. Все четыре стороны У квадратика равны. Квадрат

Слайд 7

На фигуру посмотри И в альбоме начерти Три угла. Три стороны Меж собой соедини. Получился не угольник, А красивый… Треугольник

Слайд 9

Треугольник Треугольный треугольник Угловатый своевольник. Он похож на крышу дома И на шапочку у гнома. И на острый кончик стрелки, И на ушки рыжей белки. Угловатый очень с виду Он похож на пирамиду!

Слайд 11

Круг Прикатилось колесо, Ведь похожее оно, Как наглядная натура Лишь на круглую фигуру. Догадался, милый друг? Ну, конечно, это …

Слайд 13

Круг Круглый круг похож на мячик, Он по небу солнцем скачет. Круглый словно диск луны, Как бабулины блины, Как тарелка, как венок, Как веселый колобок, Как колеса, как колечки, Как пирог из теплой печки!

Слайд 15

Растянули мы квадрат И представили на взгляд, На кого он стал похожим Или с чем-то очень схожим? Не кирпич, не треугольник — Стал квадрат… Прямоугольник

Слайд 17

Прямоугольник Как окно прямоугольник, Аккуратный, словно школьник. Он похож на дверь , на книжки, И на ранец у мальчишки. На автобус, на тетрадку, На большую шоколадку. На корыто поросенка И на фантик у ребенка.

Слайд 19

Если взял бы я окружность, С двух сторон немного сжал, Отвечайте дети дружно — Получился бы … Овал

Слайд 21

Овал С высоты кружок упал. Он теперь не круг – овал! Он овальный, как жучок, Он похож на кабачок, На глаза и на картошку, А еще похож на ложку, На орех и на яйцо, На овальное лицо!

Слайд 23

Взял треугольник и квадрат, Из них построил домик. И этому я очень рад: Теперь живет там гномик. Поиграем

Слайд 25

Мы встречаем их везде: На земле и на воде В небесах и под землей, Нам они нужны с тобой! Будем их мы называть, В окружении искать. Треугольник, круг, квадрат, Тем фигурам каждый рад! Различить их с вами сможем, Мы без них никак не можем!

Слайд 26

Физкультминутка «Все умеем мы считать» Раз, два, три, четыре, пять — Все умеем мы считать. Раз! Подняться потянуться. ( Под счет воспитателя дети выполняют потягивани я.) Два! Согнуться, разогнуться . (Наклоны. Повороты туловища.) Три! В ладоши три хлопка, Головою три кивка. ( Движения головой.) На четыре — руки шире. ( Хлопки в ладоши.) Пять — руками помахать . ( Движения руками.) Шесть — на стульчик тихо сесть. ( Прыжки. Ходьба на месте.)

Слайд 27

СОБЕРИ КРУГИ

Слайд 28

СОБЕРИ КВАДРАТЫ

Слайд 29

СОБЕРИ ТРЕУГОЛЬНИКИ

Слайд 30

ИЗ КАКИХ ФИГУР СОСТОИТ КАРТИНКА

Слайд 31

ИЗ КАКИХ ФИГУР СОСТОИТ КАРТИНКА

Геометрические фигуры схемы

Как сделать объемные геометрические фигуры из бумаги, развертки для склеивания: куба, конуса, схемы и шаблоны для вырезания цилиндра, пирамиды, треугольника

Любому ребенку нравится делать яркие и объемные поделки.

Головоломки · Фель Нелля Аркадьевна. Персональный сайт

Игры — головоломки развивают пространственное воображение, комбинаторные способности, сообразительность, смекалку, находчивость. Простые в понимании, но достаточно трудные в решении, головоломки находятся на тонкой грани, соединяющей увлекательную игру и интеллектуальное развитие.

Головоломка Сфинкс

Головоломка «Сфинкс» состоит из разнообразных геометрических фигур: из 4 треугольников и 3 четырехугольников с разным соотношением сторон. Из элементов можно собрать силуэты птиц, человека, животных, развивая наблюдательность и геометрическое воображение.

Инструкция содержит схемы для построения более двух десятков фигур: конструктивная схема для сборки фигуры методом наложения, схемы в уменьшенном варианте и схемы для сборки головоломки по теням.

Многообразие и различная степень сложности фигур позволяет учитывать возрастные особенности детей, их склонности, возможности, уровень подготовки.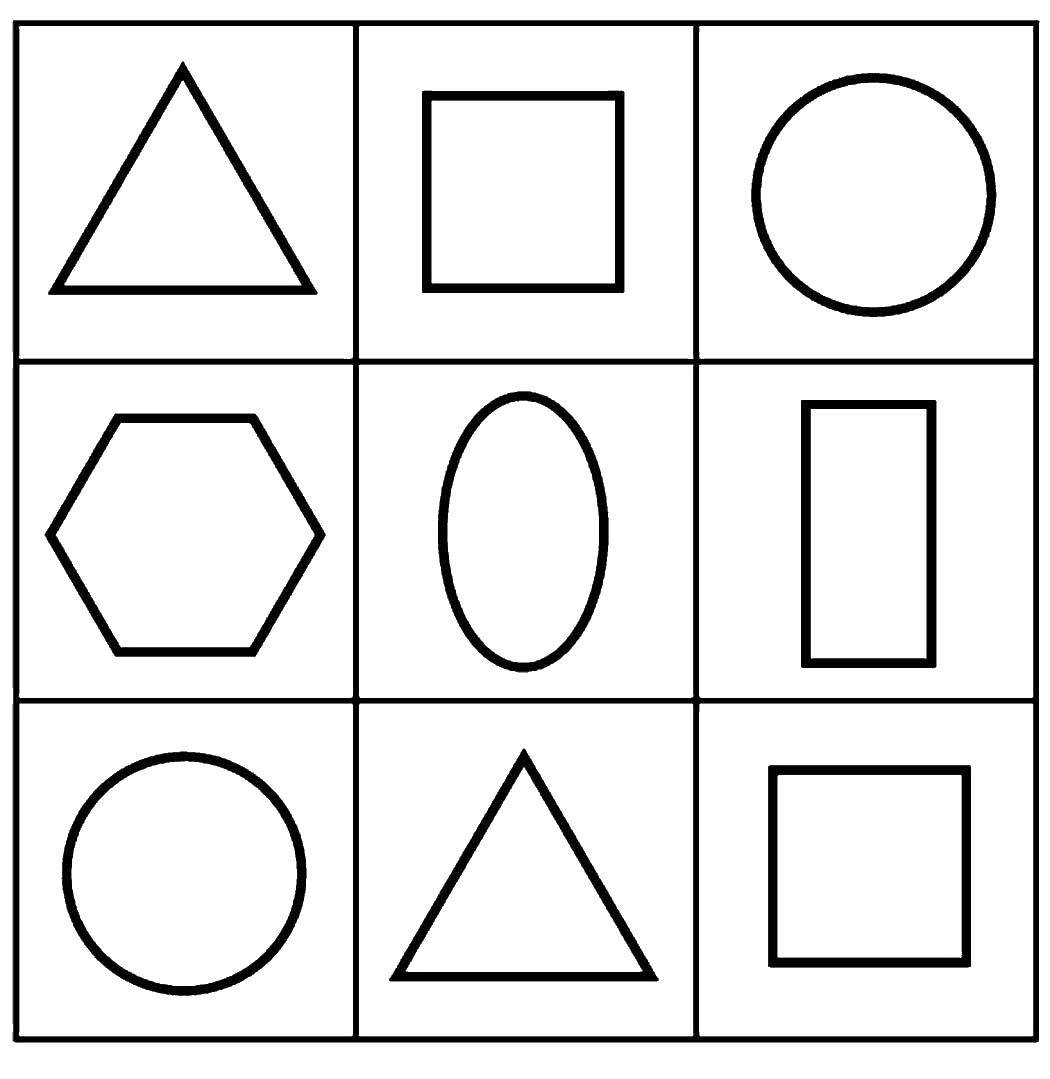

Головоломка Танграм

В набор головоломки “Танграм” входит квадрат, состоящий из пяти треугольников (два больших, один средний и два маленьких), квадрата, равного по размерам двум маленьким треугольникам, и параллелограмма, по площади равного квадрату. Танграм – это древняя китайская головоломка и суть её заключается не только в собирании первоначальной фигуры, которую мы видим на планшете. Из разрезанных элементов можно сложить цифры, буквы, предметы домашнего обихода, фигуры животных, игрушек и многого другого.

Все игры — головоломки представляют собой различные геометрические фигуры, разделенные на части. В результате игры получается плоскостное силуэтное изображение — условное, схематичное, но, образ которого легко угадывается по его строению, основным характерным признакам предмета, пропорциональному соотношению частей и форме.

Каждая игра имеет свой комплект элементов, из которых можно сложить только определенные плоскостные силуэты. Игры позволяют создавать абстрактные изображения разнообразной конфигурации, узоры, геометрические фигуры.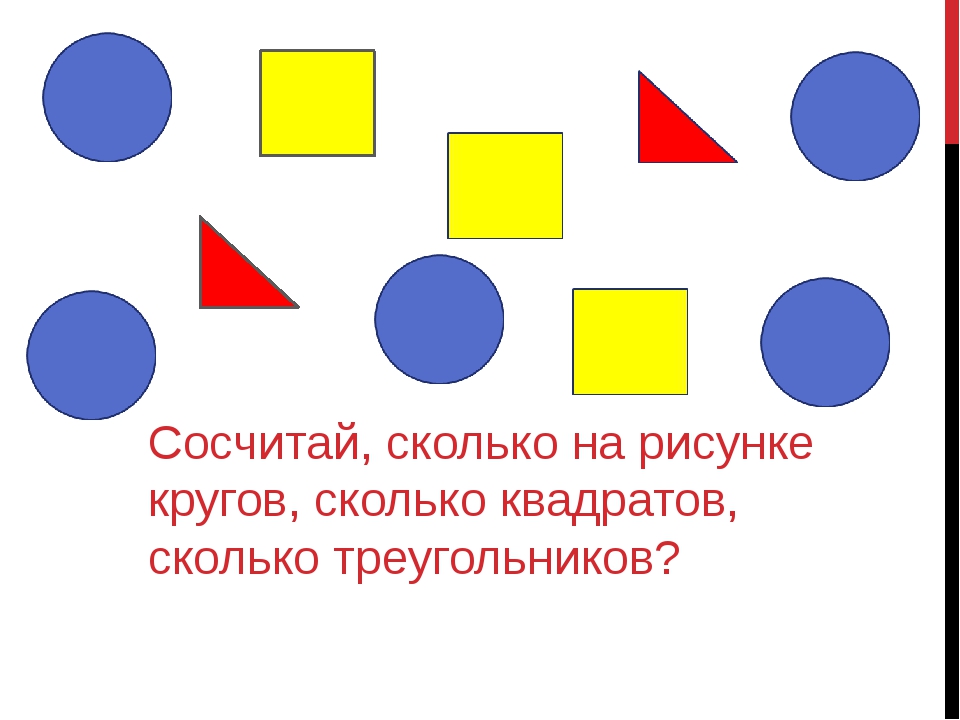

Основное правило: нужно обязательно использовать все элементы Танграма и никогда не накладывать их друг на друга. Для каждой игры разработаны различные схемы изображений, апробированные в работе с детьми. Многие из них являются результатами детского творчества. В качестве образцов используются изображения реальных предметов, силуэтное изображение которых можно воссоздать из набора геометрических фигур той или иной формы.

Развивающая головоломка Танграм для дошкольников способствует развитию:

• внимания;
• понимания цвета, величины и формы,
• абстрактного и пространственного мышления;
• воображения;
• логического мышления;
• комбинаторных способностей.

Логическая игра Листик

Логическая игра Листик — это головоломка-пазл, состоящая из геометрических фигур, которые в свою очередь образуют фигуру, напоминающую схематичное изображение человеческого сердца или листа дерева сирени, разделенная на 9 элементов. С помощью этого набора можно начинать знакомство малыша с геометрическими фигурами. Головоломка состоит и простейших геометрических форм, расположенных на специальной подложке.

Прежде всего, игра развивает логическое мышление, фантазию, внимательность и заставляет думать и размышлять.

Перед началом игры вместе с малышом повторите названия геометрических форм и вспомните как они выглядят.

Сперва попросите ребенка собрать из фигур лист, опираясь на картинку в инструкции. А потом уже предложите малышу самому составить из них какую-нибудь фигуру или реальный предмет. Также малыш может попробовать придумать свой вариант фигуры или просто обводить их, используя как трафареты.

В набор входит инструкция для родителей и педагогов, где подробно описаны все варианты игры.

Особенно хорошо из элементов этой головоломки получаются силуэты различных видов транспорта. Полученные изображения напоминают детские рисунки (собачки, птички, человечки). Конструируя простые образные фигуры, дети учатся восприятию формы, способности выделять, фигуру из фона, выделению основных признаков объекта.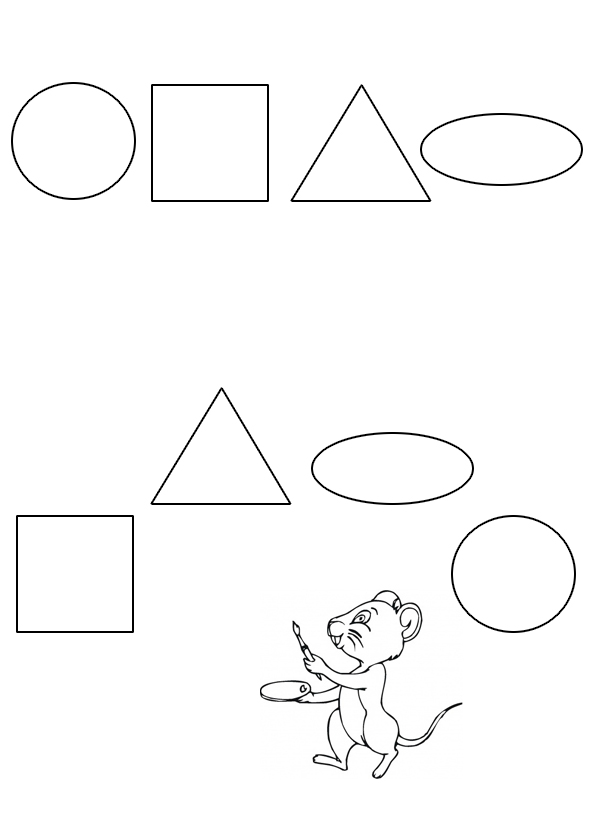 Головоломка развивает глазомер, аналитико-синтетические функции, воображение (репродуктивное и творческое), зрительно-моторную координацию, умение работать по правилам.

Головоломка Пифагора

Набор из 7-ми геометрических фигур, полученных при делении квадрата. Мировые и авторские головоломки являются эффективным средством развития умственных и творческих способностей.

Суть игр заключается в построении из плоских геометрических фигур различных силуэтов – животных, людей, растений, предметов окружающего мира. Каждая игра имеет свой комплект элементов, и методические рекомендации по ее использованию.

К каждой игре прилагается набор изображений – заданий для сборки разного уровня сложности. Игры развивают восприятие формы, способность выделять фигуру из фона, способность к выделению основных признаков объекта, глазомер, воображение (репродуктивное и творческое), зрительно-моторную координацию, мышление, зрительный анализ/синтез, умение работать по правилам.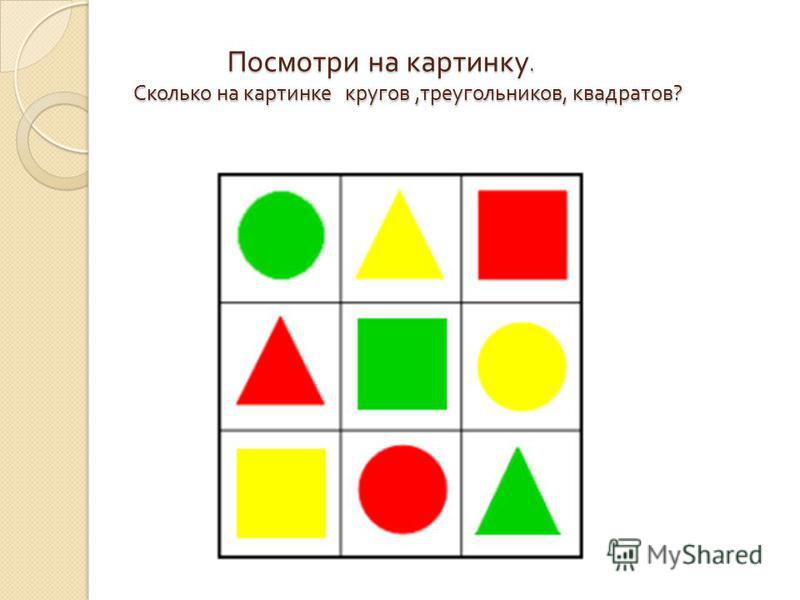 Материал игр (фанера) позволяет обводить карандашом как отдельные геометрические фигуры, так и получаемые из них силуэты. Это можно использовать для тренировки изобразительных умений ребенка.

Головоломка Колумбово яйцо

Для развития творческих плюс умственных способностей деток идеально подходят головоломки. Одной из таких является геометрических конструктор-игра “Колумбово яйцо”. Суть игры — конструирование на плоскости различных силуэтов, напоминающих фигурки животных, людей, всевозможных предметов быта, транспорт, а также буквы, цифры, цветы и прочее.

Такая игра развивает пространственное воображение, сообразительность, смекалку, комбинаторные способности, усидчивость и мелкую моторику.

Колумбово яйцо представляет собой овал, который необходимо разрезать на 10 частей. В результате получатся

Плоские геометрические фигуры: свойства и основные формулы

В статье дается определение, основные свойства и формулы для следующих геометрических фигур:

Четырёхугольник

Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три точки не лежат на одной прямой.

Основные свойства:

• Сумма углов четырёхугольника равна 360°
• Не существует четырёхугольников, у которых все углы острые или все углы тупые.
• Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов.
• Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон.

В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны. Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.

Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°.Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.

Квадрат

Квадрат —  правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.

Основные формулы:

Периметр: P=4a, где P-периметр, a-сторона
Площадь: S=a²или S=d²/2
Сторона и диагональ связаны соотношениями: a=d/√2, d=a√2
Радиус описанной окружности: R=d или R=a/√(2)
Радиус вписанной окружности: r=a/2

где a-сторона, d-диагональ, P-периметр, S-площадь
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(2) – корень квадратный из 2.

Свойства:

• Все стороны равны, все углы равны и составляют 90°;
• Диагонали квадрата равны и перпендикулярны;
• У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей;
• Квадрат является одновременно частным случаем ромба и прямоугольника.

Прямоугольник

Прямоугольник — четырехугольник, у которого все углы прямые.

Основные формулы:

Периметр: P=(a+b)*2
Площадь по сторонам: S = a*b
Площадь по диагонали и углу между ними: S =  d²* sin γ. / 2
Стороны и диагональ связаны соотношением: d=√(a²+b²)/2 (теорема Пифагора)
Радиус описанной окружности: R= √(a²+b²)/2 (теорема Пифагора)

где a, b — длины сторон прямоугольника, d-диагональ, P-периметр, S-площадь
γ – угол между диагоналями
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(a²+b²) – корень квадратный из (a²+b²).

Свойства:

• Диагонали прямоугольника равны и делятся точкой пересечения пополам.
• Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали.

Параллелограмм

Параллелограмм — четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.

Определения:

Высота параллелограмма — это перпендикуляр, проведённый из вершины параллелограмма к противоположной стороне.

Основные формулы:

Стороны и диагональ связаны соотношением: (d₁)²+(d₂)²=(a²+b²)*2
Периметр: P=(a+b)*2
Площадь по стороне и высоте:  S = a*h
Площадь по двум сторонам и углу между ними: S=a*b*sin α
Площадь по двум диагоналям и углу между ними:  S=(d₁*d₂)/2*sin γ

где a, b — длины сторон, d₁, d₂ –диагонали, P-периметр, S-площадь,
h-высота, проведенная к противоположной стороне
α — угол между сторонами параллелограмма,
γ — угол между диагоналями параллелограмма (острый).

Свойства:

• У параллелограмма противоположные стороны равны и противоположные углы равны.
• Сумма любых двух соседних углов параллелограмма равна 180°.
• Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
• Каждая диагональ делит параллелограмм на два равных треугольника.
• Две диагонали параллелограмма делят его на четыре равновеликих треугольника (равны площади всех 4-х треугольников)
• Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
• Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.

Ромб

Ромб — это параллелограмм, у которого все стороны равны.

Основные формулы:

Периметр: P=4*a
Площадь по стороне и высоте: S=a*h
Площадь по диагоналям: S = (d₁*d₂)/2
Площадь по стороне и радиусу вписанной окружности: S=2*a*r
Площадь по стороне и углу: S = a² · sin α
Радиус окружности, вписанной в ромб: r=h/2 или  r =(d₁*d₂)/4a

где a — длина стороны, d₁, d₂ –диагонали, P-периметр, S-площадь,
h -высота, проведенная к противоположной стороне
α — угол между сторонами ромба

Свойства:

• Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.
• В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей. Радиус окружности: r=h/2 или r = d₁*d₂/4a.

Трапеция

Трапеция — четырёхугольник, у которого только две противолежащие стороны параллельны.

Определения:

• Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.
• Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.  
• Средняя линия (первая средняя линия) трапеции — отрезок, который соединяет середины боковых сторон данной трапеции.Средняя линия трапеции параллельна её основаниям и равна их полусумме.
• Средняя линия (вторая средняя линия) — отрезок, соединяющий середины оснований, проходит через точку пересечения диагоналей.
• Равнобокая трапеция – трапеция,у которой боковые стороны равны (c=d). У равнобокой трапеции:диагонали равны, углы при основании равны, сумма противолежащих углов равна 180°.Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая.
• Прямоугольная трапеция — трапеция, у которой одна из её боковых сторон перпендикулярна основаниям.

Основные формулы:

Периметр: P=a+b+c+d
Площадь определить: S=h*(a+b)/2
Стороны и диагональ равнобокой трапеции: d² = ab+c²
Радиус вписанной окружности: r = h/2

где a,b — основания, c,d — боковые стороны (с – боковые стороны в случае, если трапеция равнобокая), d₁, d₂ –диагонали,
P-периметр, S-площадь, h -высота, проведенная к противоположной стороне

Свойства:

В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон (a+b=c+d). Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.

Треугольник

Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).

Определения:

• Углами (внутренними углами) треугольника называются три угла, каждый из которых образован лучами, выходящими из вершин треугольника и проходящими через две другие вершины.
• Высота треугольника — перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны
• Медиана треугольника — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
• Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне
• Равные треугольники – треугольники, у которых соответствующие стороны равны и соответствующие углы равны
• Равнобедренный треугольник— треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
• Равносторонний или правильный треугольник – треугольник, у которого все стороны равны.
• Прямоугольный треугольник — треугольник, у которого есть прямой угол. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.

Основные формулы:

Периметр: P=a+b+c
Площадь по стороне и высоте: S=(a*h)/2
Площадь по сторонам и углу между ними:  S=(a*b)/2* sin γ
Площадь по трем сторонам и радиусу описанной окружности: S=(a*b*c)/4R
Площадь по трем сторонам и радиусу вписанной окружности: S=(a+b+c)/2*r
Площадь прямоугольного треугольника: S=(a*b)/2
Стороны прямоугольного треугольника: c²=a²+b² (Теорема Пифагора)

где a,b, c — стороны (a,b –катеты , с – гипотенуза в случае прямоугольного треугольника)
d₁, d₂ –диагонали, h -высота, проведенная к противоположной стороне,
P-периметр, S-площадь, γ  — угол между сторонами a и b
r — радиус вписанной окружности, R — радиус описанной окружности

Свойства:

• В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.
• Сумма углов треугольника равна 180°:
• Длина каждой стороны треугольника больше разности и меньше суммы длин двух других сторон: |a-b| <c<a+b
• Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.
• Медиана делит треугольник на два равновеликих (с равными площадями) треугольника. Три медианы треугольника делят его на шесть равновеликих треугольников
• Биссектрисы внутренних углов треугольника пересекаются в одной точке, находящейся внутри треугольника, равноудалённой от трёх его сторон, которая является центром окружности, вписанной в данный треугольник
• В равнобедренном треугольнике углы при основании равны. В равнобедренном треугольнике медиана, проведённая к основанию, является и биссектрисой и высотой.
• Все углы равностороннего треугольника равны 60°. Каждая медиана равностороннего треугольника совпадает с биссектрисой и высотой.
• В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: c²=a²+b² (Теорема Пифагора).В прямоугольном треугольнике гипотенуза всегда больше любого из катетов.

Окружность

Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра окружности), которая лежит в той же плоскости, что и кривая.

Определения:

• Радиус — отрезок, который соединяет центр окружности с любой её точкой.
• Хорда — отрезок, который соединяет какие-либо две точки окружности (AB).
• Диаметр — хорда, проходящая через центр окружности(d).  Диаметр – наибольшая хорда окружности. Наименьшей хорды окружности не существует. 
• Касательная — прямая, которая лежит в одной плоскости с окружностью и имеет с ней только одну общую точку (E)
• Секущая — прямая, которая пересекает окружность в двух различных точках.

Основные формулы:

Длина окружности: L = 2πR
Площадь круга: S = π*r² или S = π*d²/4

где π = 3,14 (3,1415926535) – величина постоянная,
где r-радиус, d –диаметр, L – длина окружности, S-площадь.

 

Раскраски с более 80 фигурами ✨ Цветные квадраты, круги, треугольники

Геометрические и вычурные формы для раскрашивания.

Color with Fuzzy!

Раскраски с легкими формами сделают урок математики более увлекательным! Изучение форм — это такое же искусство, как и словарный запас или математика. Маленьким детям нравится раскрашивать некоторые из этих детских страниц.

В художественном классе нам часто нужны формы для узоров, таких как цветы, бриллианты и сердечки. Обожаю сердечки! Вы?

Родителям и учителям нравятся печатные формы с контуром фигур для малышей и дошкольников.Мне нравится печатать некоторые из этих фигур на карточках у себя на столе, когда я рисую. Я могу обвести форму в любое время, когда захочу.

Кроме того, я сделал их так, чтобы вы могли добавлять примечания, детали или сообщения.

~ Нечеткое

Раскраска

Список фигур

Перейти к фотографиям на этой странице:

Детям дошкольного и младшего школьного возраста понравятся эти PDF-раскраски без рекламы для печати . Они забавные настроить и раскрасить для домашней школы онлайн.

Добавьте свое имя или напишите сообщение о дне рождения в своем любимые шрифтов , РАЗМЕРЫ и цветов . Вам понравится использовать интерактивные раскраски для печати! См. Нашу домашнюю страницу для получения дополнительной информации о цифровых загрузках.

• Используйте настройку буклета вашего принтера для поздравительных открыток .
• Используйте установку кратных для печатных форм размером с куклу от двух до четырех.Детсадовцы любят это!

Также приготовьте свои любимые мелки, цветные карандаши и акварели для моих расслабляющих раскрасок для взрослых!

~ Нечеткое

Я могу получить небольшую комиссию, если вы будете покупать по моим ссылкам. Смотрите мое раскрытие здесь.

Атрибуция: Многие изображения CWF лицензированы на GraphicsFactory.com.

Многообразные раскраски

1. Круглые формы для вырезания и раскраски

Круги имеют одну сторону.Что ж, эта «сторона» одинаково проходит вокруг центральной точки. Выберите простой кружок для дошкольного образования и детского сада или кружок по математике для детей старшего возраста.

Сферы — это трехмерные круги. Думайте о шарах и воздушных шарах, когда рассказываете о сферах. Совместите это с географией с глобусом. У меня также есть конусы, которые нужно раскрасить.

1А. Раскраски Круг

Я могу получить небольшую комиссию, если вы будете покупать по моим ссылкам. Смотрите мое раскрытие здесь.

1Б.Конусы, цилиндры и сферы для раскрашивания

Дошкольники развлекаются с формами для раскрашивания и вырезания. Одна картинка показывает, что конус на самом деле представляет собой полукруг. Раскрасьте фигуры и вырежьте их, чтобы надеть конус шляпы для вечеринки.

2. Раскраски треугольной формы.

Многоугольники с тремя сторонами называются треугольниками. Треугольник может иметь разные формы: прямоугольные, равнобедренные, равносторонние и другие.

Каждый треугольник назван в соответствии с его углами или сторонами.Например, равносторонний треугольник имеет равные стороны.

Равный означает равный, а поперечный означает боковой.

Пирамида — это трехмерный треугольник с квадратным или треугольным основанием.

2А. Треугольники

2Б. Пирамиды

3. Квадратные и прямоугольные формы

Квадраты и прямоугольники — это многоугольники, четыре стороны которых соединяются под прямым углом.

Создайте трехмерный квадрат или прямоугольник, и вы нарисовали куб. Кубики отлично подходят для обучения тому.

3А. Квадратные раскраски

У меня здесь больше квилтов и квадратных форм.

3С. Кубики и блоки

4. Больше полигонов

Поли означает много, поэтому многоугольник означает множество сторон. Хотите раскрасить пятиугольник, шестиугольник или восьмиугольник?

Пентагоны имеют пять сторон, шестиугольники — шесть сторон, а восьмиугольники — восемь сторон.

Префикс указывает количество сторон.

5. Забавные фигуры в цвете

Цветы, сердечки, звезды и ромбики превращаются в забавные вырезанные проекты.Используйте их на карточках в качестве узоров или трафаретов, если вы используете ножницы, чтобы удалить внутренности.

Мне нравится, когда мои дети раскрашивают раскраски с фигурами, прежде чем вырезать их, чтобы улучшить цвет по краям.

У меня есть много других раскрасок в виде цветов, сердец, геометрических фигур и звезд.

Fuzzy любит раскрашивать фигуры!

Урок математики доставляет больше удовольствия, когда вы изучаете формы.

Если вы покажете детям, сколько раз мы видим круги (светофоры, цветы, луны), квадраты или прямоугольники (здания, коробки, грузовики), они смогут нарисовать свои собственные картинки.

Их измерение — математическая сторона, рисование или раскраска — художественная сторона.

В художественном классе нам часто нужны формы для узоров. Узоры позволяют дошкольникам и детсадовцам вырезать желтые круги в центре цветов или аккуратные квадраты, расположенные вдоль рамки картины.

Держите под рукой несколько раскрасок фигур, чтобы дети могли рисовать разные формы для рисунков. Обожаю фигурные распечатки для детского сада и первого класса. Чем они старше, тем лучше дети обращаются с мелками и ножницами.

Взрослые любят показывать детям оптические иллюзии в некоторых формах. Земной шар катится? Куб с отступом? Иногда взрослые сами находят, что окрашивание — прекрасная терапия для снятия стресса. Наслаждайтесь!

Спасибо за раскрашивание с помощью Fuzzy!

Раскраски Фигуры

Треугольник круг квадратной формы Иконки

• Авторы
• Пакеты
• Дополнительные инструменты

  Прочие товары

  Freepik Бесплатные векторы, фото и PSD Онлайн-редактор Freepik Редактируйте свои шаблоны Freepik Slidesgo Бесплатные шаблоны для презентаций Рассказы Бесплатные редактируемые иллюстрации

  Инструменты

  Образец значка Создавайте шаблоны значков для своих обоев или социальных сетей

  Google Workspace

  Иконки для слайдов и документов +2.5 миллионов бесплатных настраиваемых значков для ваших слайдов, документов и таблиц
• английский
  • Español
  • английский
  • Deutsch
  • Português
  • 한국어

Базовая геометрия: Площадь (многоугольник, треугольник, круг, квадрат) Учебное пособие

Площадь (многоугольник, треугольник, круг, квадрат)

Площадь — это пространство внутри двухмерной фигуры.Если вы подумаете о полу в своей спальне, то это будет максимальная площадь пола, на которую вы можете бросить свои вещи, прежде чем вы не увидите ни одного оставшегося пола.

Площадь всегда выражается в квадратных единицах ( единиц ² ). Это потому, что он двумерный (длина и высота).

Вы можете определить площадь фигур, посчитав квадраты внутри фигур. На этих трех рисунках каждая клетка представляет.

• Рисунок A занимает 25 маленьких коробок, поэтому его площадь составляет
• Рисунок B занимает 36 маленьких коробок, поэтому его площадь составляет
• Рисунок C занимает 21 полную коробку и 7 половинных коробок, поэтому его площадь составляет

Площадь прямоугольника = основание x высота

Вот.

Если мы разделим его на секцию шириной 1 см, это будет выглядеть так:

Каждая строка содержит 10 квадратов и 6 рядов, что в сумме дает 10 × 6 квадратных см. Это то же самое, что умножение основания на высоту:.

Площадь треугольника = ½ (основание × высота)

Вот треугольник с основанием 5 см и высотой 6 см.

Если мы поместим еще один треугольник с такой же высотой и основанием поверх этого, мы получим.

Теперь мы уже знаем, как вычислить площадь прямоугольника (основание × высота). Итак, площадь прямоугольника

. Однако нам нужен только треугольник, который составляет половину прямоугольника. По сути, мы взяли ½ площади всего прямоугольника или ½ (основание × высота).

Площадь параллелограмма = основание × высота

Теперь давайте посмотрим на параллелограмм с основанием 6 см и высотой 3 см.

Если переместить маленький треугольник слева до упора вправо, эта форма станет прямоугольником с основанием 6 и высотой 3 см.

Поскольку вы уже знаете, как найти площадь прямоугольника (основание × высота), у вас есть все инструменты, необходимые для определения площади этого параллелограмма.

Площадь трапеции = ½ (основание ₁ + основание ₂ ) x высота

Представьте, что вы отрезаете треугольный нижний левый угол и вставляете его в верхний правый угол следующим образом:

Теперь у нас есть еще один прямоугольник, но с новой основой.База этой новой цифры — это среднее значение исходной базы. Площадь этой новой фигуры равна .Просто будьте осторожны, потому что основание, которое мы используем, является средним из двух исходных оснований!

Площадь круга = πr ²

Наконец, мы рассмотрим красивый круг. Вот такой, радиусом 6 см.

Вот тот же круг, но с линиями, проведенными через каждые сантиметры.

Сначала мы объединили части квадрата, чтобы получился полный квадрат, затем мы очень тщательно и старательно пересчитали каждый из этих квадратов и обнаружили, что там примерно 113 квадратов.Это почти равно.

Площадь круга, треугольника, квадрата, прямоугольника, параллелограмма, трапеции, эллипса и сектора

Площадь — это размер поверхности!
Узнайте больше о площади или воспользуйтесь калькулятором площади.

Пример: Какова площадь этого прямоугольника?

Формула:

Площадь = ш × в
ш = ширина
в = высота

Мы знаем, что w = 5 и h = 3 , поэтому:

Площадь = 5 × 3 = 15

Пример: Какова площадь этого круга?

Радиус = r = 3

Площадь		= π × r 2
		= π × 3 2
		= π × (3 × 3)
		= 3.14159 … × 9
		= 28,27 (до 2 знаков после запятой)

Пример: Какова площадь этого треугольника?

Высота = h = 12

База = b = 20

Площадь = ½ × b × h = ½ × 20 × 12 = 120

Более сложный пример:

Пример: Сэм косит траву по цене 0,10 доллара за квадратный метр

Сколько зарабатывает Сэм, обрабатывая эту область:

Разобьем область на две части:

Часть A — квадрат:

Площадь A = ² = 20 м × 20 м = 400 м ²

Часть B представляет собой треугольник.При взгляде сбоку он имеет основание 20 м и высоту 14 м.

Площадь B = ½b × h = ½ × 20 м × 14 м = 140 м ²

Итого общая площадь:

Площадь = Площадь A + Площадь B = 400 м ² + 140 м ² = 540 м ²

Сэм зарабатывает 0,10 доллара за квадратный метр

Сэм зарабатывает = 0,10 доллара × 540 млн ² = 54 доллара

Развлечение с фигурами Тоня Мартин.Как называется эта форма? Квадратный круг треугольник прямоугольник.

Презентация на тему: «Развлечение с фигурами, Тоня Мартин. Как называется эта фигура? Квадрат, круг, треугольник, прямоугольник». — стенограмма презентации:

1 Развлечения с фигурами Тоня Мартин

2 Как называется эта форма? Квадратный Круг Треугольник Прямоугольник

3 Ой! Попробуй еще раз.Эта форма не была кругом. Круг круглый, как шар, без сторон и углов. Вот 2 круга: эта форма не была кругом. Круг круглый, как шар, без сторон и углов. Вот 2 круга:

4 Попробуй еще раз! Форма — это не квадрат. У квадрата 4 стороны одинаковой длины. Вот изображение квадрата.

5 Ой! Мы знаем, что у прямоугольников верх и низ имеют одинаковую длину, а левая и правая стороны одинаковы, поэтому попробуйте еще раз.Мы знаем, что у прямоугольников верх и низ имеют одинаковую длину, а левая и правая стороны одинаковы, поэтому попробуйте еще раз.

6 Прекрасная работа! Ты прав! Эта форма — треугольник. У него 3 стороны и 3 угла. Вы правы! Эта форма — треугольник. У него 3 стороны и 3 угла.

8 Как называется эта форма? Прямоугольникпрямоугольник кругкруг треугольниктреугольник квадратквадрат

9 Ой-ой.Это не прямоугольник. Давайте вместе вспомним, как выглядит прямоугольник. Давайте вместе вспомним, как выглядит прямоугольник. Верх и низ имеют одинаковую длину, а левый и правый — одинаковой длины. Верх и низ имеют одинаковую длину, а левый и правый — одинаковой длины.

10 Попробуй еще раз! Эта форма не была квадратом. Помните, что у квадрата 4 равные стороны. Помните, что у квадрата 4 равные стороны.

Лучшая цена, круг, квадрат, треугольник, прямоугольник — Выгодные сделки на круг, квадрат, треугольник, прямоугольник от продавцов, глобальный круг, квадрат, треугольник, прямоугольник

Отличные новости !!! Вы находитесь в правильном месте для круга, квадрата, треугольника, прямоугольника. К настоящему времени вы уже знаете, что что бы вы ни искали, вы обязательно найдете это на AliExpress. У нас буквально тысячи отличных продуктов во всех товарных категориях.Ищете ли вы товары высокого класса или дешевые и недорогие оптовые закупки, мы гарантируем, что он есть на AliExpress.

Вы найдете официальные магазины торговых марок наряду с небольшими независимыми продавцами со скидками, каждый из которых предлагает быструю доставку и надежные, а также удобные и безопасные способы оплаты, независимо от того, сколько вы решите потратить.

AliExpress никогда не уступит по выбору, качеству и цене.Каждый день вы будете находить новые онлайн-предложения, скидки в магазинах и возможность сэкономить еще больше, собирая купоны. Но вам, возможно, придется действовать быстро, поскольку этот прямоугольник с верхним кругом, квадратом, треугольником должен стать одним из самых востребованных бестселлеров в кратчайшие сроки. Подумайте, как вам будут завидовать друзья, когда вы скажете им, что получили свой прямоугольник в виде круга, квадрата, треугольника на AliExpress. Благодаря самым низким ценам в Интернете, дешевым тарифам на доставку и возможности получения на месте вы можете еще больше сэкономить.

Если вы все еще не уверены в том, что круг, квадрат, треугольник, прямоугольник, и думаете о выборе аналогичного товара, AliExpress — отличное место для сравнения цен и продавцов. Мы поможем вам решить, стоит ли доплачивать за высококлассную версию или вы получаете столь же выгодную сделку, приобретая более дешевую вещь. И, если вы просто хотите побаловать себя и потратиться на самую дорогую версию, AliExpress всегда позаботится о том, чтобы вы могли получить лучшую цену за свои деньги, даже сообщая вам, когда вам будет лучше дождаться начала рекламной акции. , а также ожидаемую экономию.AliExpress гордится тем, что у вас всегда есть осознанный выбор при покупке в одном из сотен магазинов и продавцов на нашей платформе. Реальные покупатели оценивают качество обслуживания, цену и качество каждого магазина и продавца. Кроме того, вы можете узнать рейтинги магазина или отдельных продавцов, а также сравнить цены, доставку и скидки на один и тот же продукт, прочитав комментарии и отзывы, оставленные пользователями. Каждая покупка имеет звездный рейтинг и часто имеет комментарии, оставленные предыдущими клиентами, описывающими их опыт транзакций, поэтому вы можете покупать с уверенностью каждый раз.Короче говоря, вам не нужно верить нам на слово — просто слушайте миллионы наших довольных клиентов.

А если вы новичок на AliExpress, мы откроем вам секрет. Непосредственно перед тем, как вы нажмете «купить сейчас» в процессе транзакции, найдите время, чтобы проверить купоны — и вы сэкономите еще больше. Вы можете найти купоны магазина, купоны AliExpress или собирать купоны каждый день, играя в игры в приложении AliExpress.Вместе с бесплатной доставкой, которую предлагают большинство продавцов на нашем сайте, мы думаем, вы согласитесь, что вы получите прямоугольник, квадрат, треугольник по самой выгодной цене.

У нас всегда есть новейшие технологии, новейшие тенденции и самые обсуждаемые лейблы. На AliExpress отличное качество, цена и сервис всегда в стандартной комплектации. Начните самый лучший шоппинг прямо здесь.

.

No related posts.